Частота это в физике определение: Частота — это… Что такое Частота?

Частота в физике, теория и онлайн калькуляторы

Определение частоты

Определение

Частотой называют физическую величину, характеризующую периодический процесс.

Она равна числу повторений или реализации событий за единицу времени. Обозначают частоту $\nu ,$ могут встречаться другие варианты обозначений частоты, например $f$ или $F$.

Частота (наряду со временем) — это наиболее точно измеряемая величина.

Частота колебаний

Частота служит одним из основных параметров, характеризующих колебания.

Определение

Частота — это физическая величина обратная периоду колебаний (T). Частота — это число полных колебаний, которые совершаются за единицу времени.

\[\nu =\frac{1}{T}\left(1\right).\]

В Международной системе единиц (СИ) частота измеряется в герцах или обратных секундах:

\[\left[\nu \right]=с^{-1}=Гц.\]

Герц — единица измерения частоты периодического процесса, при которой за время в одну секунду протекает один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, о близкими по величине частотами (${\nu }_1\ и\ {\nu }_2$) равна:

\[{\nu =\nu }_1-\ {\nu }_2\left(2\right).\]

Другой характеристикой колебаний является циклическая частота, которая равна:

\[{\omega }_0=2\pi \nu \left(3\right).\]

Циклическая частота измеряется в радианах, деленных на секунду:

\[\left[{\omega }_0\right]=\frac{рад}{с}.\]

Частота колебаний тела, массой$\ m,$ подвешенного на пружине с жесткостью $k$ равна:

\[\nu =\frac{1}{2\pi \sqrt{{m}/{k}}}\left(4\right).\]

Выражение (4) выполняется для упругих, малых колебаний. Масса пружины должна быть мала в сравнении с массой тела.

Частота колебаний математического маятника, длина нити которого $l$:

\[\nu =\frac{1}{2\pi \sqrt{{l}/{g}}}\left(5\right),\]

где $g$ — ускорение свободного падения.

Частота колебаний физического маятника:

\[\nu =\frac{1}{2\pi \sqrt{{J}/{mgd}}}\left(6\right),\]

где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.

Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее результаты дают эти формулы.

Частота дискретных событий, частота вращения

Определение

Частотой дискретных колебаний ($n$) — называют физическую величину, которая равна количеству действий (событий) в единицу времени.

Если время, которое занимает одно событие обозначить как $\tau $, то частота дискретных событий равна:

\[n=\frac{1}{\tau }\left(7\right).\]

Единицей измерения частоты дискретных событий является обратная секунда:

\[\left[n\right]=\frac{1}{с}.\]

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Частотой вращения ($n$) — называют величину, ра

Единица измерения частоты, теория и онлайн калькуляторы

Прежде чем перейти к единицам измерения частоты, скажем о том, что следует выделить: частоту периодических процессов (колебаний, излучений и т.д.), частоту дискретных событий (импульсов и т.д. ) и частоту вращения.

Герц — единица измерения частоты периодического процесса в системе СИ

Определение

Частота периодических процессов ($\nu$) — это физическая величина, которая равна количеству циклов, которые происходят в единицу времени. Это определение говорит о том, что:

\[\nu =\frac{1}{T}\left(1\right),\]

где $T$ — период процесса.

Из выражения (1) очевидно, что единицей измерения частоты служит обратная секунда:

\[\left[\nu \right]=с^{-1}.\]

В Международной системе единиц (СИ) эта единица измерения имеет специальное название, ее называют герцем (Гц) с 1960 г (начала существования системы). Герц — единица измерения частоты периодического процесса, при которой за время в одну секунду протекает один цикл процесса.

Единица измерения частоты периодического процесса называется в честь немецкого ученого Г. Герца, который много и успешно занимался электродинамикой.

Герц, как единица измерения частоты может использоваться со стандартными приставками системы СИ для обозначения десятичных кратных и дольных единиц. Например, гГц (гектогерц): $1г\ Гц=100\ Гц$; мкГц (микрогерц): $1мкГц={10}^{-6}Гц.$ Биения здорового человеческого сердца в спокойном состоянии происходят с частотой 1Гц.

Иногда частоту периодических колебаний обозначают буквой $f$.

Часто в расчётах используют циклическую частоту (угловую частоту, радиальную частоту, круговая частота) ($\omega $), которая равна:

\[\omega =2\pi {\mathbf \nu }\left(2\right).\]

Угловая частота измеряется в радианах, деленных на секунду:

\[\left[\omega \right]=\frac{рад}{с}.\]

В системах СИ и СГС единицы измерения круговой частоты одинаковы.

Секунда в минус первой степени — единица измерения частоты дискретных событий

Частота дискретных колебаний ($n$) — это физическая величина, которая равна количеству действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $\tau $, то частота дискретных событий равна:

\[n=\frac{1}{\tau }\left(3\right).\]

Из определения (3) следует, что обратная секунда (секунда в минус первой степени) — единица измерения частоты дискретных событий:

\[\left[n\right]=\frac{1}{с}.\]

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Секунда в минус первой степени — единица измерения частоты вращения

Частота вращения ($n$) — это величина, равная количеству полных оборотов в единицу времени. Если $\tau $ — время, затрачиваемое на один полный оборот, то:

\[n=\frac{1}{\tau }\left(4\right).\]

Секунда в минус первой степени —

Формула частоты в физике

Определение

Частота — это физический параметр, которые используют для характеристики периодических процессов. Частота равна количеству повторений или свершения событий в единицу времени.

Чаще всего в физике частоту обозначают буквой $\nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.

Частота (наряду со временем) является самой точно измеряемой величиной.

Формула частоты колебаний

При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$

\[\nu =\frac{1}{T}\left(1\right).\]

Частота, в этом случае — это число полных колебаний ($N$), совершающихся за единицу времени:

\[\nu =\frac{N}{\Delta t}\left(2\right),\]

где $\Delta t$ — время за которое происходят $N$ колебаний.

Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:

\[\left[\nu \right]=с^{-1}=Гц.\]

Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${\nu }_1\ и\ {\nu }_2$) равна:

\[{\nu =\nu }_1-\ {\nu }_2\left(3\right).\]

Еще одно величиной характеризующей колебательный процесс является циклическая частота (${\omega }_0$), связанная с частотой как:

\[{\omega }_0=2\pi \nu \left(4\right).\]

Циклическая частота измеряется в радианах, деленных на секунду:

\[\left[{\omega }_0\right]=\frac{рад}{с}.\]

Частота колебаний тела, имеющего массу$\ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:

\[\nu =\frac{1}{2\pi \sqrt{{m}/{k}}}\left(5\right).\]

Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.

Для математического маятника частоту колебаний вычисляют как: длина нити:

\[\nu =\frac{1}{2\pi \sqrt{{l}/{g}}}\left(6\right),\]

где $g$ — ускорение свободного падения; $\ l$ — длина нити (длина подвеса) маятника.

Физический маятник совершает колебания с частотой:

\[\nu =\frac{1}{2\pi \sqrt{{J}/{mgd}}}\left(7\right),\]

где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.

Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.

Формулы для вычисления частоты дискретных событий, частота вращения

дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $\tau $, то частота дискретных событий равна:

\[n=\frac{1}{\tau }\left(8\right).\]

Единицей измерени

Частота колебаний — это… Что такое Частота колебаний?



Частота колебаний

        число полных колебаний (См. Колебания)в единицу времени. Для гармонических колебаний Ч. к. f = 1/T, где Т — период колебаний. Единица Ч. к. — одно колебание в секунду, или Герц. Часто пользуются величиной ω = 2πf, которая называется циклической или круговой частотой.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Частота кадров
• Частота электрического тока

Смотреть что такое «Частота колебаний» в других словарях:

• частота колебаний — число колебаний в 1 с. Обозначается f или ν. Если Т  период колебаний, то f = 1/T; измеряется в герцах (Гц). Угловая частота колебаний ω = 2πf = 2π/T рад/с. * * * ЧАСТОТА КОЛЕБАНИЙ ЧАСТОТА КОЛЕБАНИЙ, число колебаний в 1 с. Обозначается f или n.… …   Энциклопедический словарь

• частота колебаний — (f[v]) Величина, обратная периоду колебаний. [ГОСТ 7601 78] частота колебаний Число колебаний в единицу времени [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] частота колебаний частота Количество периодов… …   Справочник технического переводчика

• ЧАСТОТА КОЛЕБАНИЙ — число колебаний в 1 с. Обозначается f или ?. Если T период от колебаний, то f = 1/T; измеряется в герцах (Гц). Угловая частота колебаний ??= 2?f = 2?/T рад/с …   Большой Энциклопедический словарь

• ЧАСТОТА КОЛЕБАНИЙ — величина, обратная периоду колебаний T(f=1/Т), т. е. равная числу периодов колебаний (числу колебаний), совершаемых в единицу времени. Обычно Ч. к. измеряется в герцах: 1 Гц соответствует одному колебанию в секунду. Часто используется также… …   Физическая энциклопедия

• Частота колебаний — 14. Частота колебаний v Средняя частота спектра лазерного излучения в пределах интервала частот линии спонтанного излучения Источник: ГОСТ 24453 80: Измерения пара …   Словарь-справочник терминов нормативно-технической документации

• частота колебаний — svyravimų dažnis statusas T sritis automatika atitikmenys: angl. oscillation frequency vok. Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d oscillation, f …   Automatikos terminų žodynas

• частота колебаний — virpesių dažnis statusas T sritis automatika atitikmenys: angl. oscillation frequency vok. Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d oscillations, f …   Automatikos terminų žodynas

• частота колебаний — svyravimų dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Svyruojamojo judesio dažnis. atitikmenys: angl. oscillation frequency vok. Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d’oscillations, f ryšiai:… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• частота колебаний — virpesių dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Tam tikros sistemos virpėjimo dažnis. atitikmenys: angl. oscillation frequency vok. Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d’oscillations, f… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• частота колебаний — virpesių dažnis statusas T sritis chemija apibrėžtis Virpesių skaičius per 1 sekundę. atitikmenys: angl. oscillation frequency rus. частота колебаний …   Chemijos terminų aiškinamasis žodynas

• частота колебаний — svyravimų dažnis statusas T sritis fizika atitikmenys: angl. oscillation frequency vok. Schwingfrequenz, f; Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d’oscillations, f …   Fizikos terminų žodynas

Книги

• Школа музыки. 40 уроков для юных музыкантов, певцов и композиторов, Боуэн Майриг, Боуэн Рэйчел. О книгеЗамечательное продолжение одной из наших любимых книг об искусстве `Школы искусств`. Теперь пришло время обратить внимание на музыку!Мы снова стоим на пороге невероятной школы, где вас… Подробнее  Купить за 1063 грн (только Украина)
• Решение волновых задач сейсмостойкости методом граничных элементов, С.П. Гордеева. Программа вычисляет напряженно-деформированное состояние (НДС) сооружений неограниченной формы (плотины совместно с основанием, подземные сооружения, откосы каньонов) при волновом… Подробнее  Купить за 970 грн (только Украина)
• Решение волновых задач сейсмостойкости методом граничных элементов, С.П. Гордеева. Программа вычисляет напряженно-деформированное состояние (НДС) сооружений неограниченной формы (плотины совместно с основанием, подземные сооружения, откосы каньонов) при волновом… Подробнее  Купить за 863 руб

Частота электрического тока: определение, формула, характеристики

Переменный ток имеет ряд важных характеристик, влияющих на его физические свойства. Одним из таких параметров является частота переменного тока. Если говорить с точки зрения физики, то частота – это некая величина, обратная периоду колебания тока. Если проще – то это количество полных циклов изменения ЭДС, произошедших за одну секунду.

Известно, что переменный ток заставляет электроны двигаться в проводнике сначала в одну сторону, потом — в обратную. Полный путь «туда-обратно» они совершают за некий промежуток времени, называемый периодом переменного тока. частота же является количеством таких колебаний за 1 секунду. В качестве единицы измерения частоты во всем мире принят 1 Гц (в честь немецкого ученого Г.Герца), который соответствует 1 периоду колебания за 1 секунду.

В республиках бывшего СССР стандартной считается частота тока в 50 Гц.

Это значит, что синусоида тока движется в течение 1 секунды 50 раз в одном направлении, и 50 — в обратном, 100 раз проходя чрез нулевое значение. Получается, что обычная лама накаливания, включенная в сеть с такой частотой, будет затухать и вспыхивать примерно 100 раз за секунду, однако мы этого не замечаем в силу особенностей своего зрения.

Для измерения частоты переменного тока применяют приборы, называемые частотомерами. Частотомеры используют несколько основных способов измерения, а именно:

• Метод дискретного счета;

• Метод перезаряда конденсатора;

• Резонансный метод измерения частот.

• Метод сравнения частот;

Метод дискретного счета основывается на подсчете импульсов необходимой частоты за конкретный промежуток времени. Его наиболее часто используют цифровые частотомеры, и именно благодаря этому простому методу можно получить довольно точные данные.

Более подробно о частоте переменного тока Вы можете узнать из видео:

Метод перезаряда конденсатора тоже не несет в себе сложных вычислений. В этом случае среднее значение силы тока перезаряда пропорционально соотносится с частотой, и измеряется при помощи магнитоэлектрического амперметра. Шкала прибора, в таком случае, градуируется в Герцах.

Погрешность подобных частотомеров находится в пределах 2%, и поэтому такие измерения вполне пригодны для бытового использования.

Резонансный способ измерения базируется на электрическом резонансе, возникающем в контуре с подстраиваемыми элементами. Частота, которую необходимо измерить, определяется по специальной шкале самого механизма подстройки.

Такой метод дает очень низкую погрешность, однако применяется только для частот больше 50 кГц.

Метод сравнения частот применяется в осциллографах, и основан на смешении эталонной частоты с измеряемой. При этом возникают биения определенной частоты. Когда же частота этих биений достигает нуля, то измеряемая частота становится равной эталонной. Далее, по полученной на экране фигуре с применением формул можно рассчитать искомую частоту электрического тока.

Ещё одно интересное видео о частоте переменного тока:

Частота — Большая советская энциклопедия

Частота́

Какого-либо события А, отношение m/n числа m появлений этого события в данной последовательности испытаний к общему числу n испытаний. Если испытания независимы и существует определённая вероятность р наступления события А в отдельном испытании, то, сколь бы мало ни было число ε > 0 при достаточно большом m, практически несомненно, что частота m/n удовлетворяет неравенству.

.

См. Больших чисел закон, Вероятность.

Термин «Ч.» к.-л. признака употребляется также в математической статистике для обозначения числа элементов совокупности, обладающих этим признаком.

Источник: Большая советская энциклопедия на Gufo.me

---

Значения в других словарях

1. частота — частота I ж. Отвлеч. сущ. по прил. частый I II ж. Величина, выражающая количество одинаковых движений, колебаний и т.п. в единицу времени. Толковый словарь Ефремовой
2. частота — орф. частота, -ы, мн. -оты, -от Орфографический словарь Лопатина
3. частота — -ы, мн. -тоты, ж. 1. Свойство и состояние по знач. прил. частый. Люди сидят близко друг к другу и могут слышать частоту дыхания соседа. Бахметьев, Преступление Мартына. 2. спец. Число повторений одинаковых движений, колебаний в какую-л. единицу времени. Частота вращения. Частота колебаний маятника. Малый академический словарь
4. частота — ЧАСТОТ’А, частоты, мн. (спец.) частоты, частот, ·жен. (·книж. ). 1. только ед. ·отвлеч. сущ. к частый. Частота случаев. Частота ритма. Повышение частоты пульса. Частота тока. Толковый словарь Ушакова
5. частота — (ν или f) Число повторений некоторого явления в единицу времени. В случае волнового процесса частота представляет собой число волн, проходящих через фиксированную точку за одну секунду. Основная единица частоты — герц (Гц). Большой астрономический словарь
6. ЧАСТОТА — ЧАСТОТА — англ. frequency; нем. Haufigkeit. 1. Проявления случайного события; отношение т/п, где число т обозначает отношение этого события в данной последовательности испытаний к общему числу испытаний — п. 2. Социологический словарь
7. частота — ЧАСТОТА — частота движений. Одна из характеристик скоростных способностей, измеряется числом движений в единицу времени. — частота дыхания. Один из показателей внешнего дыхания. Измеряется числом дыхательных актов в единицу времени. Словарь спортивных терминов
8. частота — См. частый Толковый словарь Даля
9. частота — сущ., кол-во синонимов: 3 видеочастота 1 радиочастота 1 частость 9 Словарь синонимов русского языка
10. частота — ЧАСТОТА, ы, мн. оты, от, ж. 1. см. частый. 1. Величина, выражающая число повторений чего-н. в единицу времени (спец.). Ч. электромагнитных волн. Ч. колебаний маятника. | прил. частотный, ая, ое. Толковый словарь Ожегова
11. ЧАСТОТА — ЧАСТОТА, показатель, выражающий собой число повторений или возникновения событий (процессов). В статистике частота — это цифра, показывающая, сколько раз за какой-то период происходило некоторое событие… Научно-технический словарь
12. частота — • большая ~ • высокая ~ Словарь русской идиоматики
13. частота — Частота, частоты, частоты, частот, частоте, частотам, частоту, частоты, частотой, частотою, частотами, частоте, частотах Грамматический словарь Зализняка
14. частота — Част/от/а́. Морфемно-орфографический словарь
15. частота — ЧАСТОТА -ы; частоты; ж. 1. к Частый (1 зн.). Следить за частотой повторения ходов. Необходимая ч. посадки картофеля. Обратить внимание на частоту пульса. 2. Число повторений одинаковых движений, колебаний в какую-л. единицу времени. Ч. вращения колеса. Толковый словарь Кузнецова

Теория радиоволн: ликбез / Хабр

Думаю все крутили ручку радиоприемника, переключая между «УКВ», «ДВ», «СВ» и слышали шипение из динамиков.
Но кроме расшифровки сокращений, не все понимают, что скрывается за этими буквами.
Давайте ближе познакомимся с теорией радиоволн.

Радиоволна

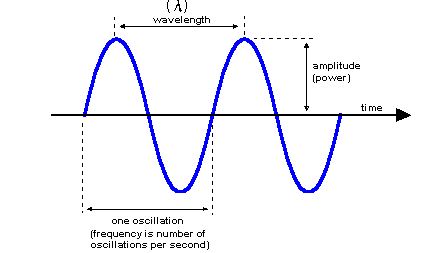
Длина волны(λ) — это расстояние между соседними гребнями волны.
Амплитуда(а) — максимальное отклонения от среднего значения при колебательном движении.
Период(T) — время одного полного колебательного движения
Частота(v) — количество полных периодов в секунду

Существует формула, позволяющая определять длину волны по частоте:

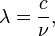
Где: длина волны(м) равна отношению скорости света(км/ч) к частоте (кГц)

«УКВ», «ДВ», «СВ»

Сверхдлинные волны — v = 3—30 кГц (λ = 10—100 км).
Имеют свойство проникать вглубь толщи воды до 20 м и в связи с этим применяются для связи с подводными лодками, причем, лодке не обязательно всплывать на эту глубину, достаточно выкинуть радио буй до этого уровня.
Эти волны могут распространяться вплоть до огибания земли, расстояние между земной поверхностью и ионосферой, представляет для них «волновод», по которому они беспрепятственно распространяются.

Длинные волны(ДВ) v = 150—450 кГц (λ = 2000—670 м).

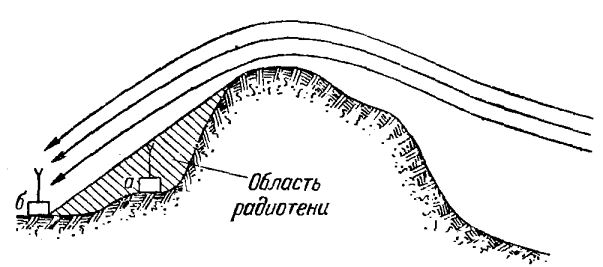
Этот тип радиоволны обладает свойством огибать препятствия, используется для связи на большие расстояния. Также обладает слабой проникающей способностью, так что если у вас нет выносной антенны, вам вряд ли удастся поймать какую-либо радиостанцию.

Средние волны (СВ) v = 500—1600 кГц (λ = 600—190 м).

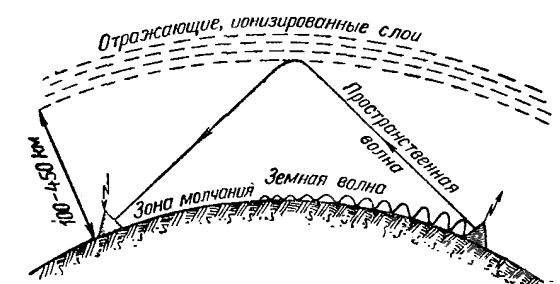
Эти радиоволны хорошо отражаются от ионосферы, находящейся на расстоянии 100-450 км над поверхностью земли.Особенность этих волн в том, что в дневное время они поглощаются ионосферой и эффекта отражения не происходит. Этот эффект используется практически, для связи, обычно на несколько сотен километров в ночное время.

Короткие волны (КВ) v= 3—30 МГц (λ = 100—10 м).

Подобно средним волнам, хорошо отражаются от ионосферы, но в отличии от них, не зависимо от времени суток. Могут распространяться на большие расстояния(несколько тысяч км) за счет пере отражений от ионосферы и поверхности земли, такое распространение называют скачковым. Передатчиков большой мощности для этого не требуется.

Ультракороткие Волны(УКВ) v = 30 МГц — 300 МГц (λ = 10—1 м).

Эти волны могут огибать препятствия размером в несколько метров, а также имеют хорошую проникающую способность. За счет таких свойств, этот диапазон широко используется для радио трансляций. Недостатком является их сравнительно быстрое затухание при встрече с препятствиями.
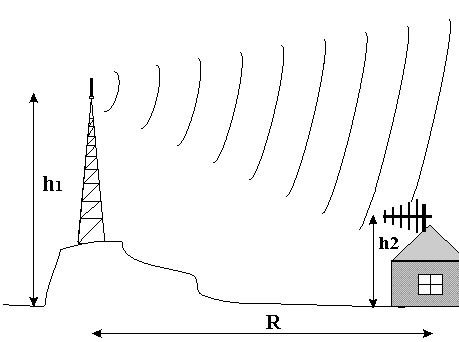
Существует формула, которая позволяет рассчитать дальность связи в УКВ диапазоне:

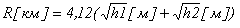
Так к примеру при радиотрансляции с останкинской телебашни высотой 500 м на приемную антенну высотой 10 м, дальность связи при условии прямой видимости составит около 100 км.

Высокие частоты (ВЧ-сантиметровый диапазон) v = 300 МГц — 3 ГГц (λ = 1—0,1 м).
Не огибают препятствия и имеют хорошую проникающую способность. Используются в сетях сотовой связи и wi-fi сетях.
Еще одной интересной особенностью волн этого диапазона, является то, что молекулы воды, способны максимально поглощать их энергию и преобразовывать ее в тепловую. Этот эффект используется в микроволновых печах.
Как видите, wi-fi оборудование и микроволновые печи работают в одном диапазоне и могут воздействовать на воду, поэтому, спать в обнимку с wi-fi роутером, длительное время не стоит.

Крайне высокие частоты (КВЧ-миллиметровый диапазон) v = 3 ГГц — 30 ГГц (λ = 0,1—0,01 м).
Отражаются практически всеми препятствиями, свободно проникают через ионосферу. За счет своих свойств используются в космической связи.

AM — FM

Зачастую, приемные устройства имеют положения переключателей am-fm, что же это такое:

AM — амплитудная модуляция

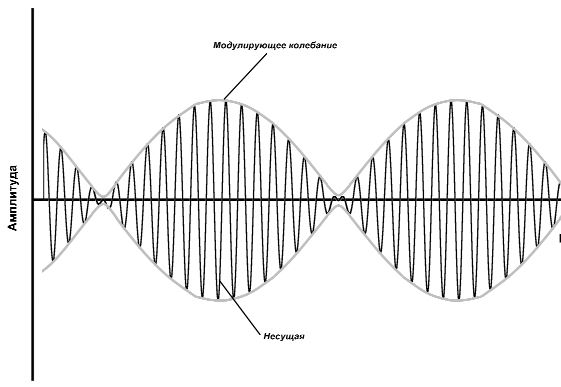
Это изменение амплитуды несущей частоты под действием кодирующего колебания, к примеру голоса из микрофона.
АМ — первый вид модуляции придуманный человеком. Из недостатков, как и любой аналоговый вид модуляции, имеет низкую помехоустойчивость.

FM — частотная модуляция

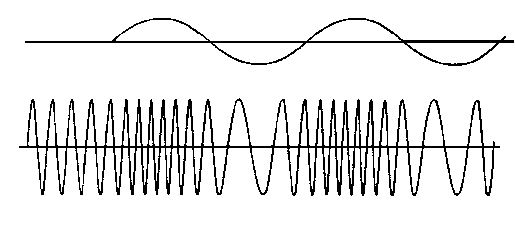
Это изменение несущей частоты под воздействие кодирующего колебания.
Хотя, это тоже аналоговый вид модуляции, но он имеет более высокую помехоустойчивость чем АМ и поэтому широко применяется в звуковом сопровождении ТВ трансляций и УКВ вещании.

На самом деле у описанных видом модуляции есть подвиды, но их описание не входит в материал данной статьи.

Еще термины

Интерференция — в результате отражений волн от различных препятствий, волны складываются. В случае сложения в одинаковых фазах, амплитуда начальной волны может увеличиться, при сложении в противоположных фазах, амплитуда может уменьшиться вплоть до нуля.
Это явление более всего проявляется при приеме УКВ ЧМ и ТВ сигнала.

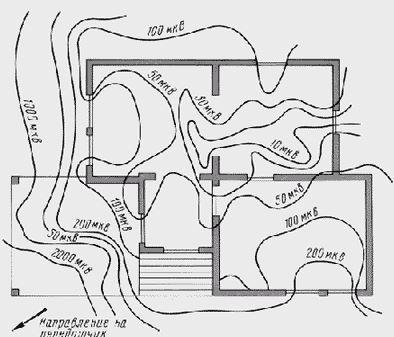
Поэтому, к примеру внутри помещения качество приема на комнатную антенну ТВ сильно «плавает».

Дифракция — явление, возникающее при встрече радиоволны с препятствиями, в результате чего, волна может менять амплитуду, фазу и направление.
Данное явление объясняет связь на КВ и СВ через ионосферу, когда волна отражается от различных неоднородностей и заряженных частиц и тем самым, меняет направление распространения.
Этим же явлением объясняется способность радиоволн распространяться без прямой видимости, огибая земную поверхность. Для этого длина волны должна быть соразмерна препятствию.

PS:

Надеюсь, информация описанная мной будет полезна и принесет некоторое понимание по данной теме.Частота

| Определение, символы и формулы

Частота , в физике, количество волн, которые проходят фиксированную точку за единицу времени; также, количество циклов или колебаний, которым подвергается тело в периодическом движении за одну единицу времени. Считается, что тело, находящееся в периодическом движении, претерпело один цикл или одну вибрацию после прохождения серии событий или положений и возвращения в свое исходное состояние. См. Также угловая скорость; простые гармонические колебания.

Подробнее по этой теме

излучение: Диапазон частот

Электромагнитные волны охватывают огромный диапазон частот (количество колебаний в секунду), только небольшая часть из которых приходится на…

Если период или временной интервал, необходимый для завершения одного цикла или вибрации, составляет ¹ / ₂ секунд, частота равна 2 в секунду; если период составляет ¹ / ₁₀₀ часов, частота составляет 100 в час. В общем, частота является обратной величиной периода или временного интервала; т.е. частота = 1 / период = 1 / (временной интервал). Частота обращения Луны вокруг Земли составляет немногим более 12 циклов в год. Частота струны ля скрипки составляет 440 колебаний или циклов в секунду.

Чаще всего для обозначения частоты используются символы f и греческие буквы nu (ν) и омега (ω). Nu чаще используется при указании электромагнитных волн, таких как свет, рентгеновские лучи и гамма-лучи. Омега обычно используется для описания угловой частоты, то есть того, насколько объект вращается или вращается в радианах в единицу времени. Обычно частота выражается в герцах, названных в честь немецкого физика XIX века Генриха Рудольфа Герца, один герц равен одному циклу в секунду, сокращенно Гц; один килогерц (кГц) равен 1000 Гц, а один мегагерц (МГц) равен 1000000 Гц.В спектроскопии иногда используется другая единица частоты — волновое число.

.

определение частоты по The Free Dictionary

Но какая конкретная частота может быть абсолютно необходимой для этой цели, по-видимому, не поддается никакому точному расчету и должна зависеть от множества обстоятельств, с которыми она может быть связана. Его поиск в различных книгах убедил его, что он обнаружил всевозможные ошибки, чаще всего повторяющиеся в комбинации, и с большой легкостью расположил их в правильном порядке из-за частоты, с которой он просматривал увлекательную книгу с алфавитными картинками.Он вынул из кармана книгу и начал энергично читать ее, судя по точности и частоте, с которой он переворачивал листья, поэтому в течение следующих двух лет его посещения города стали более частыми, а его пребывания там неуклонно увеличивались. Частота таких сообщений привела к установлению среди рабов изречения о том, что неподвижный язык делает умную голову. Аттерсон настолько привык к неизменному характеру этих сообщений, что понемногу терял в частоте его посещений.Бывают моменты, когда я рад побыть одному — горевать и роптать, когда никто не разделит мою печаль: и эти моменты начинают приходить ко мне все чаще и чаще. Всегда в своих воспоминаниях я нахожу что-то необъяснимое, но в то же время очень привлекательное — настолько, что в течение нескольких часов, проведенных вместе, я остаюсь нечувствительным к своему окружению, забывая о реальности. Этот курс вскоре привел его к развилке Маленького Миссури, примерно в ста ярдах широкая и напоминающая великую реку с одноименным названием силой своего течения, мутной воды, частым появлением зарослей и затонувших деревьев.Он бывал в Винчестере и Оксфорде, и его беседы с большой частотой впечатляли этот факт. Когда он узнал подробности воспитания Филиппа, его манера поведения стала еще более покровительственной. Это происходило очень часто, потому что однажды в полном крике собаки были склонны забываться в азарте погони, в то время как Белый Клык никогда не забывал себя. действовала по политическим мотивам, а также из удовольствия от частоты ее посещений в Делафорде; ибо ее желание свести вместе Марианну и полковника Брэндона было не менее искренним, хотя и более либеральным, чем то, что выразил Джон.Один, на который, если мы можем судить по частоте его повторения, больше всего полагаются, это то, что Палата представителей недостаточно многочисленна для приема всех различных классов граждан, чтобы объединить интересы и чувства каждой части сообщества, и вызвать должное сочувствие между представительным органом и его составляющими. .Определение

в кембриджском словаре английского языка

ЧАСТОТА | Определение в кембриджском словаре английского языка

частота имя существительное (ПРОИСХОДИТ)

Тезаурус: синонимы и родственные слова .

Угловая частота — Простая английская Википедия, бесплатная энциклопедия

По физике угловая частота. ω. (также называется угловой скоростью , радиальной частотой и радианной частотой) — это мера скорости вращения. Высокая угловая частота означает, что что-то вращается очень быстро. Угловая частота — это величина вектора угловой скорости , которая также известна как вектор угловой частоты . ω → {\ displaystyle {\ vec {\ omega}}} .

Угловая частота — это мера того, насколько быстро объект вращается.

Это полезно во многих областях математики и естествознания, так как позволяет понять многие свойства физических объектов в нашем мире. В единицах СИ угловая частота измеряется в радианах в секунду с размерами t ^-1 , поскольку радианы безразмерны.

Угловая частота часто выражается в радианах в секунду ( т — 1 {\ displaystyle t ^ {- 1}} ), так как с ним легче работать.Таким образом, угловая частота определяется выражением

  
    
      
        ω
        знак равно
        
          
            
              2
              π
            
            Т
          
        
        знак равно
        2
        π
        ж
      
    
    {\ displaystyle \ omega = {\ frac {2 \ pi} {T}} = 2 \ pi f}
  
 
 

где Т {\ displaystyle T} — время (период) одного оборота (оборота) и ж {\ displaystyle f} это частота.

Если колесо поворачивается на угол θ {\ displaystyle \ theta} вовремя т {\ displaystyle t} тогда угловая частота в любой момент определяется выражением

  
    
      
        ω
        знак равно
        
          
            
              d
              θ
            
            
              d
              т
            
          
        
      
    
    {\ displaystyle \ omega = {\ frac {d \ theta} {dt}}}
  
   
 

Если скорость вращения постоянна, это становится,

  
    
      
        ω
        знак равно
        
          
            θ
            т
          
        
      
    
    {\ displaystyle \ omega = {\ frac {\ theta} {t}}}
  
 
 

и так похоже на скорость.

Для объектов, движущихся по кругу, угловая частота также может быть задана как (в радианах),

  
    
      
        ω
        знак равно
        
          
            v
            р
          
        
      
    
    {\ displaystyle \ omega = {\ frac {v} {r}}}
  
 
 

где v {\ displaystyle v} это скорость и р {\ displaystyle r} это расстояние от середины круга.

Угловая частота важна для определения того, может ли объект оставаться над землей против силы тяжести или же волчок может стоять. Это также важно для создания частоты подачи электроэнергии в сеть и уменьшения нагрева из-за трения в двигателях.

спутников [изменить | изменить источник]

Объекты притягиваются к земле под действием силы тяжести. Чтобы противостоять этому, спутник должен лететь достаточно быстро, чтобы не коснуться земли. Чтобы силы равнялись друг другу,

  
    
      
        
          
            
              грамм
              M
              м
            
            
              р
              
                2
              
            
          
        
        знак равно
        м
        
          ω
          
            2
          
        
        р
      
    
    {\ displaystyle {\ frac {GMm} {r ^ {2}}} = m \ omega ^ {2} r}
  
 
 

где M {\ displaystyle M} масса большего тела и грамм {\ displaystyle G} — гравитационная постоянная.Чтобы получился круг, угловая частота должна быть равна,

  
    
      
        
          ω
          
            c
            я
            р
            c
            л
            е
          
        
        знак равно
        
          
            
              
                грамм
                M
              
              
                р
                
                  3
                
              
            
          
        
      
    
    {\ displaystyle \ omega _ {круг} = {\ sqrt {\ frac {GM} {r ^ {3}}}}}
  
 
 

, что ведет к одному из законов Иоганна Кеплера.

Сетевое питание [изменить | изменить источник]

Генераторы на электростанциях вращаются с определенной частотой. Скорость, с которой они вращаются, дает нам частоту, с которой работают наши источники электроэнергии. Их можно замедлить с помощью больших тормозов или больших тяжелых колес, которые не позволяют генераторам вращаться слишком быстро.

Примеры измерения угловой частоты включают [изменить | изменить источник]

.

No related posts.