В чем измеряются единицы емкости конденсаторов
Конденсатор представляет собой электрическое устройство, которое обладает возможностью накапливать заряд, состоит из обкладок и слоя диэлектрика между ними. Одной из важнейших характеристик прибора является ёмкость.
Конденсатор
Единица измерения емкости
В Международной системе СИ за единицу измерения ёмкости конденсатора принимают фарад:
[C] = Ф, где С – обозначение ёмкости устройства.
Международное обозначение – F. Названа в честь английского физика М.Фарадея и используется в Международной системе СИ с 1960г.
Формула для расчёта электроёмкости записывается следующим образом:
С = Dq / U (1), где:
- Dq – заряд (измеряется в кулонах, или Кл),
- U – разность потенциалов между обкладками (измеряется в вольтах или В).
Следовательно, 1Ф = 1Кл / 1В.
То есть конденсатор ёмкостью в 1 фарад накапливает на обкладках заряд, равный 1 кулон, создавая напряжение между ними, равное 1 вольт.
В фарадах измеряются электроёмкости проводников и конденсаторов.
Согласно правилам написания, принятых в СИ, если название происходит от фамилии учёного, то полное её название «фарад» пишется с маленькой (строчной) буквы, а её сокращённое название «Ф» – с прописной.
Единица измерения электроёмкости в других системах
Помимо СИ, есть ещё устаревшая система СГС, которой пользовались ранее. Первые три символа в названии обозначают:
- С – сантиметр,
- Г – грамм,
- С – секунда.
Существует две разновидности системы: СГСЭ и СГСМ. Символ Э в СГСЭ обозначает электростатическую систему, а символ М – магнитную. В системе СГСЭ емкость конденсатора измеряется в сантиметрах, или см. Для пересчёта используют соотношение:
- 1см » 1,1126 · 10-12Ф,
- 1Ф » 8,99 · 1011 статФ.
Сантиметр по-другому может называться статфарад, или статФ.
В системе СГСМ единицей измерения является абфарад, или абФ. Абфарад связан с фарадом следующим образом:
1абф = 1·109 Ф = 1ГФ.
Для перевода из СГСЭ и СГСМ в СИ в сети Интернет имеются специальные сервисы, которые позволяют автоматизировать эти действия.
Онлайн переводчик из СГС в СИ
Фарады через основные единицы системы СИ
Для выражения фарады через основные единицы СИ воспользуемся следующими формулами.
Единица измерения заряда вычисляется как:
Dq = I · Dt (2), где:
- I – сила тока (измеряется в амперах или А),
- Dt – время прохождения заряда (измеряется в секундах или с).
В свою очередь, напряжение определяется как работа, которую нужно выполнить для перемещения заряда в электростатическом поле:
U = А / Dq (3), где А – работа по перемещению заряда, определяется в джоулях, или Дж.
Из механики известно, что:
А = F · s = m · a · s (4), где:
- m – масса, измеряется в килограммах, или кг,
- s – перемещение, рассчитывается в метрах, или м,
- a – ускорение, определяется в м/с2.
Из формул 1-4 имеем:
Таким образом, 1 фарад через единицы СИ определяется как:
Кратные единицы ёмкости
При покупке радиодеталей невозможно купить конденсатор с электроёмкостью даже в несколько единиц фарад. Они выпускаются с гораздо меньшими параметрами. Это объясняется тем, что ёмкость в 1 фарад является очень большой величиной. Например, такую электроёмкость может иметь изолированный проводник в форме шара с радиусом в 13 раз больше радиуса Солнца.
Именно по этой причине для характеристики емкостных устройств применяют дольные единицы, которые рассчитываются как доля от определённого числа фарад. Для обозначения используют приставки, которые применяются для сокращения длины записываемого числа.
Таблица перевода дольных единиц
| Приставка | Обозначение | Множитель | |
|---|---|---|---|
| деци | дФ | dF | 10^-1 |
| санти | сФ | sF | 10^-2 |
| милли | мФ | mF | 10^-3 |
| микро | мкФ | F или uF | 10^-6 |
| нано | нФ | nF | 10^-9 |
| пико | пФ | pF, mmF, uuF | 10^-12 |
| фемто | фФ | fF | 10^-15 |
| атто | аФ | aF | 10^-18 |
| зепто | зФ | zF | 10^-21 |
| йокто | иФ | yF | 10^-24 |
Таким образом, если параметр указывается равным 5 uF, то для перевода в фарады необходимо умножить цифру 5 на соответствующий множитель. Получаем 5 uF = 5 · 10-6 F.
В радиотехнике наиболее популярны модели, ёмкость которых измеряется в микрофарадах, нанофарадах (микромикрофарадах) или пикофарадах.
Также промышленность выпускает устройства ионисторы, которые представляют собой конденсаторы, имеющие двойной электрический слой. У некоторых ионисторов ёмкость может измеряться в килофарадах.
Ионистор с характеристикой в 1F
Маркировка конденсаторов в зависимости от ёмкости
Кодировка маленьких по размерам устройств
Существует специальная цифровая кодировка. Её используют для маркировки маленьких по размерам приборов. Кодировка электроёмкости выполняется согласно стандарту EIA.
Внимание! Ёмкость небольших конденсаторов, например, керамических или танталовых, обычно измеряется в пикофарадах, а больших, например, алюминиевых электролитических, в микрофарадах.
Существует специальная таблица таких обозначений, с помощью которой можно быстро подобрать такую же или аналогичную радиодеталь по соответствующему коду. Её можно свободно найти в Интернете.
В старых маркировках использовалась следующая кодировка. Если нанесено целое двузначное число, значит, значение ёмкость измеряется в пикофарадах, а если нанесена десятичная дробь, значит, параметр определяется в микрофарадах.
Например, радиодеталь с параметром 1000 nF =1 uF будет иметь маркировку 105, с параметрами 820 nF = 0, 82 uF – маркировку 824, а 0,27 uF = 270nF будет обозначено кодом 274.
В настоящее время, если на устройстве нанесено значение, не содержащее буквы, то оно обозначает ёмкость в пикофарадах. Если перед цифрами или после них стоит символ «н» («n»), то это означает, что значение даётся в нанофарадах, если «мк» («m», «u») – микрофарадах. В том случае, когда символ располагается перед числом, цифры в нём обозначают сотые доли. Например, n61 расшифровывается как 0,61нФ. Если символ располагается посередине значения, то на место символа нужно поставить запятую. Сам символ покажет единицы измерения. Например, 5u2 обозначает 5,2 мкФ.
Также в настоящее время используется цифровая кодировка, содержащая три числа. Первые две цифры являются числовыми характеристиками ёмкости. Параметр при этом измеряется в пикофарадах. Если значение меньше 1, то первая цифра – 0. Третья цифра определяет множитель, на который нужно умножить число, получаемое из первых двух цифр.
В случае, когда последнее число находится в диапазоне от 0 до 6, к значению дописывают количество нулей, равное третьей цифре. Например, если указано число 270, то устройство имеет параметр 27 пФ, если 271 – то на 270 пФ.
Трёхзначная кодировка
Если число равно 8, то в этом случае множитель равен 0,01. То есть если указано число 278, то ёмкость будет равна 27 · 10-2 = 0,27. Когда третье число равно 9, то множитель будет 0,1. Например, маркировка 109 указывает на электроёмкость в 1 пФ.
Если в кодировке присутствует символ «R», то параметр указывается в пикофарадах, а символ показывает место расположения запятой. Например, 4R1 расшифровывается как 4,1пФ.
Кодировка больших по размерам устройств
На больших по габаритным размерам конденсаторах маркировка наносится сверху на корпус, причём в данном случае будет присутствовать полная информация о параметрах устройства.
В обозначениях может встречаться значение MF. В приставках Международной системы единиц СИ если перед единицей измерения располагается большая буква М, то это обозначает, что должен использоваться множитель 106. В случае с конденсатором это всё равно будет обозначать микрофарады.
Также может встречаться обозначение МFD или mfd. В данном случае сочетание символов «fd» обозначает farad. Таким образом, если на корпусе написано 5 mfd, то значит, что конденсатор используется на 5 микрофарад.
Маркировка больших по размерам конденсаторов
Таким образом, при ремонте электросхемы, содержащей конденсатор, нужно правильно читать маркировку устройства и соответственно информации подбирать нужный прибор.
Видео
Оцените статью:jelectro.ru
Электрическая ёмкость — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 июля 2019; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 июля 2019; проверки требуют 2 правки.Электри́ческая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками
В Международной системе единиц (СИ) ёмкость измеряется в фарадах, в системе СГС — в сантиметрах.
Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид
- C=Qφ,{\displaystyle C={\frac {Q}{\varphi }},}
где Q{\displaystyle Q} — заряд, φ{\displaystyle \varphi } — потенциал проводника.
Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ):
- C=4πε0εrR,{\displaystyle C=4\pi \varepsilon _{0}\varepsilon _{r}R,}
где ε0 — электрическая постоянная, равная 8,854⋅10−12Ф/м, εr — относительная диэлектрическая проницаемость.
Вывод формулы Известно, что φ1−φ2=∫12Edl⇒φ=∫R∞Edl=14πεrε0∫R∞qr2dr=14πεε0qR.{\displaystyle \varphi _{1}-\varphi _{2}=\int _{1}^{2}E\,dl\Rightarrow \varphi =\int _{R}^{\mathcal {\infty }}E\,dl={\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}\int _{R}^{\mathcal {\infty }}{\frac {q}{r^{2}}}\,dr={\frac {1}{4\pi \varepsilon \varepsilon _{0}}}{\frac {q}{R}}.} Так как C=qφ{\displaystyle C={\frac {q}{\varphi }}}, то подставив сюда найденный φ{\displaystyle \varphi }, получим, что C=4πε0εrR.{\displaystyle C=4\pi \varepsilon _{0}\varepsilon _{r}R.} |
Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком или вакуумом, — к конденсатору. В этом случае ёмкость (взаимная ёмкость) этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:
- C=ε0εrSd,{\displaystyle C=\varepsilon _{0}\varepsilon _{r}{\frac {S}{d}},}
где S — площадь одной обкладки (подразумевается, что обкладки одинаковы), d — расстояние между обкладками, εr — относительная диэлектрическая проницаемость среды между обкладками.
Электрическая ёмкость некоторых систем[править | править код]
Вычисление электрической ёмкости системы требует решение Уравнения Лапласа ∇2φ = 0 с постоянным потенциалом φ на поверхности проводников. Это тривиально в случаях с высокой симметрией. Нет никакого решения в терминах элементарных функций в более сложных случаях.
В квазидвумерных случаях аналитические функции отображают одну ситуацию на другую, электрическая ёмкость не изменяется при таких отображениях. См. также Отображение Шварца — Кристоффеля.
Величина обратная ёмкости называется эластанс (эластичность). Единицей эластичности является дараф (daraf), но он не определён в системе физических единиц измерений СИ[10].
- ↑ Шакирзянов Ф. Н. Ёмкость электрическая // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 28—29. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ 1 2 Jackson, J. D. Classical Electrodynamics. — Wiley, 1975. — P. 80.
- ↑ Binns. Analysis and computation of electric and magnetic field problems / Binns, Lawrenson. — Pergamon Press, 1973. — ISBN 978-0-08-016638-4.
- ↑ 1 2 Maxwell, J. C. A Treatise on Electricity and Magnetism. — Dover, 1873. — P. 266 ff. — ISBN 0-486-60637-6.
- ↑ Rawlins, A. D. Note on the Capacitance of Two Closely Separated Spheres (англ.) // IMA Journal of Applied Mathematics (англ.)русск. : journal. — 1985. — Vol. 34, no. 1. — P. 119—120. — DOI:10.1093/imamat/34.1.119.
- ↑ Jackson, J. D. Classical Electrodynamics. — Wiley, 1975. — P. 128, problem 3.3.
- ↑ Maxwell, J. C. On the electrical capacity of a long narrow cylinder and of a disk of sensible thickness (англ.) // Proc. London Math. Soc. : journal. — 1878. — Vol. IX. — P. 94—101. — DOI:10.1112/plms/s1-9.1.94.
- ↑ Vainshtein, L. A.
- ↑ Jackson, J. D. Charge density on thin straight wire, revisited (неопр.) // Am. J. Phys. — 2000. — Т. 68, № 9. — С. 789—799. — DOI:10.1119/1.1302908. — Bibcode: 2000AmJPh..68..789J.
- ↑ Тензорный анализ сетей, 1978, с. 509.
ru.wikipedia.org
В чем измеряется емкость конденсатора?
Давайте начнем с предложенной Вами задачи. Основой для ее решения является формула, определяющая емкость:
Переведем данные из задачи в единицы системы СИ: нКл=Кл; кВ=В. Теперь можно вычислить емкость конденсатора:
Теперь разберемся, в чем измеряется емкость конденсатора. Емкость конденсатора, как и емкость любого другого проводящего тела, измеряется в фарадах. Обозначается фарада буквой (Ф). Название данная единица получила в честь М. Фарадея. 1Ф равен емкости конденсатора, если заряд его пластин равен 1 Кл, а напряжение между обкладками 1 В. Если фарад выражать через основные единицы системы СИ, то получим: Ф=Aкг м.
Поэтому часто на практике используют пикофарады (пФ): 1 пФ=Ф; нанофарады: 1 нФ=Ф; микрофарфды 1 мкФ=Ф.
Тогда ответ в нашей задаче удобнее записать как пФ.
Подробнее о конденсаторах можно прочитать в ответах на вопросы: «Как работает конденсатор?», «Каково обозначение конденсаторов на схеме?», «Для чего нужен конденсатор?», «Как измерить емкость конденсатора?».
как найти, отчего зависит напряжение на этом элементе
Конденсатор — это электротехнический элемент, позволяющий накапливать заряд. Самая простая его форма представляет две пластины, разделенные слоем диэлектрика. Если на пластины подать напряжение, то оно сохранится какое-то время после его снятия. Важно знать, в чем измеряется емкость конденсатора, для правильного построения схем с этими элементами.
Применение в технике
Конденсаторы применяются в различной электро- и радиоаппаратуре. Эти элементы способны накапливать заряд и поддерживать напряжение (например, сетевое) на должном уровне во время незначительных перебоев с питанием. Конденсаторы большой емкости сами используются как питающие элементы для малогабаритной мобильной аппаратуры. Они еще называются ионисторы. Их недостатком является необходимость частого подзаряда.
Большое значение имеют эти элементы и в фильтрующих устройствах, приборах, задача которых не пропустить помехи в полезный сигнал, или уловить нужный сигнал в постоянном напряжении повышенного уровня.
Без конденсаторов не обходится ни один генератор переменного сигнала. Их назначение — задать частоту генерации, период и другие временные параметры. Здесь используются очень точные элементы, с допуском по номиналу не более 1%.
Конденсаторы бывают как постоянной, так и переменной емкости. Элементы переменной емкости используются в аппаратуре, требующей настройки на разные частоты. Например, это широко используется в настройке радиочастот в FM -приемниках.
Формулы для расчета конденсаторов
Для решения задач техники и прикладных теоретических расчетов нужно знать законы, по которым электрические величины взаимодействуют друг с другом. Эти законы выражаются формулами. Например, напряжение на конденсаторе зависит от его емкости и заряда, накопленного им.
Определение емкости
Это значение зависит от нескольких параметров. Чтобы его рассчитать, нужно знать, в чем измеряется емкость конденсатора. Эта величина эквивалентна тому, сколько кулон заряда накапливается элементом при напряжении в 1 вольт, приложенном к нему. Измеряется она в фарадах. Емкость этих элементов зависит также и от их формы.
Плоские конденсаторы — самая простая разновидность накопителей заряда. Как найти емкость конденсатора, имеющего плоскую форму, можно узнать, если определить все параметры, влияющие на это. На его емкость влияет расстояние между его обкладками (токопроводящие пластины) d, площадь самих обкладок S, диэлектрическая проницаемость вещества между обкладками ε и электрическая постоянная ε0, которая равна 8,85 ⋅ 10 -12 фарад на метр. Формула конденсатора такова:
Плоские конденсаторы — самая простая разновидность накопителей заряда. Как найти емкость конденсатора, имеющего плоскую форму, можно узнать, если определить все параметры, влияющие на это. На его емкость влияет расстояние между его обкладками (токопроводящие пластины) d, площадь самих обкладок S, диэлектрическая проницаемость вещества между обкладками ε и электрическая постоянная ε0, которая равна 8,85 ⋅ 10 -12 фарад на метр. Формула конденсатора такова:С = ε ⋅ ε0 ⋅ S/d
- Цилиндрический конденсатор также состоит из двух заряженных обкладок, обе они имеют форму цилиндров, расположенных один внутри другого. Внутренний цилиндр цельный, внешний — полый. Расстояние между обкладками равно разности радиусов этих цилиндров. Формулу емкости конденсатора можно представить такой же, как в предыдущем случае, с той разницей, что площадь обкладок рассчитывается исходя из их высоты и радиуса:
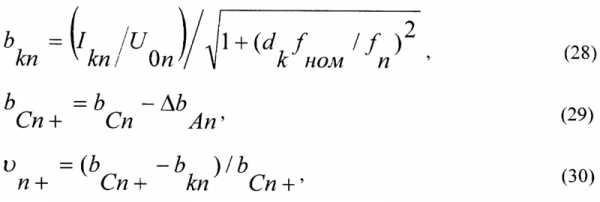
С = 2 ⋅ π ⋅ ε ⋅ ε0 ⋅ h ⋅ R вн /(R нар — R вн) = ε ⋅ ε0 ⋅ S / d
где h — высота обкладки,
Rвн — внутренний радиус, R нар — наружный радиус,
π = 3,14.
- Зарядом может обладать не только тело с двумя обкладками, но и проводящий шарообразный объект. Если подать на него напряжение, а потом измерить потенциал между ним и землей, то потенциал будет ненулевым. Формула для расчета шарообразного накопителя заряда:
С = 4 ⋅ π ⋅ ε ⋅ ε0 ⋅ R
где R — радиус шара.
Если в формулу подставить радиус Земли и диэлектрическую проницаемость воздуха, можно получить значение емкости Земли в фарадах. После расчетов:
С (Земли) = 700 микрофарад
Такую емкость могут иметь современные электролитические конденсаторы.
Если разместить один шар внутри другого и подать между ними напряжение, то полученная конструкция тоже будет накапливать заряд между поверхностями шаров. Определение емкости такой конструкции можно провести по формуле:
С = ε ⋅ ε0 ⋅4⋅π ⋅ R1 ⋅ R2 / (R2 — R1)
где R2 и R1 — радиусы соответствующих шарообразных поверхностей.
Емкость конденсатора зависит также и от типа используемого диэлектрика. Наиболее распространены керамические, электролитические, бумажные, воздушные и слюдяные наполнители.
Вычисление энергии
Накопители заряда обладают и другими параметрами. Один из них — это энергия. При зарядке конденсатора на его обкладках накапливается потенциальная энергия.
Она создаёт силу, притягивающую разноименно заряженные пластины, а также ток, который питает электроприборы, если использовать ионистор как источник питания. Энергию можно выразить как зависимость от напряжения обкладок и емкости:
W = C ⋅ U 2 /2
Ток утечки через диэлектрик
I ут = U/R d
где I ут — ток утечки,
U — напряжение на обкладках,
R d — сопротивление изоляции диэлектрика.
Соединение элементов
При создании схем применяется различное соединение элементов. Элементы схемы могут быть соединены:
- Параллельно;
- Последовательно;
- Параллельно — последовательно (смешанно).
Как найти ёмкость параллельно соединенных элементов? Нужно понять, что является общим при таком типе соединения. Так как напряжение прикладывается одновременно ко всем обкладкам, то оно является общим. Заряд же будет для каждого своим. По формуле:
q = C ⋅ U, здесь q — суммарный заряд, то есть
q = ΣC i ⋅ U = U ⋅ ΣC i
С общее будет равняться сумме всех С.
При последовательном соединении элементов общим для всех них будет заряд. В то же время напряжение будет для каждого из них разным, и общее будет складываться из всех по отдельности.
U = q / C, здесь U — сумма напряжений на всех элементах
U общее = q ⋅ Σ (1/ C i)
1/С общее = 1/С 1 +1/С 2 +… +1/C i
При таком соединении значение общей емкости будет меньше самого маленького значения этой величины в группе.
В случае использования смешанного соединения необходимо вычислить отдельно общую емкость для параллельного и отдельно для последовательного соединения. После этого по формуле последовательного соединения найти общее для двух получившихся величин значение.
220v.guru
Электрическая емкость
Дата публикации: .
Категория: Электротехника.
Сообщение электрического разряда проводнику называется электризацией. Чем больший заряд принял проводник, тем больше его электризация, или, иначе говоря, тем выше его электрический потенциал.
Между количеством электричества и потенциалом данного уединенного проводника существует линейная зависимость: отношение заряда проводника к его потенциалу есть величина постоянная:
Для какого-либо другого проводника отношение заряда к потенциалу есть также величина постоянная, но отличная от этого отношения для первого проводника.
Одной из причин, влияющих на эту разницу, являются размеры самого проводника. Один и тот же заряд, сообщенный различным проводникам, может создать различные потенциалы. Чтобы повысить потенциал какого-либо проводника на одну единицу потенциала, необходим определенный заряд.
Электрическая емкость и ее единица измерения
Свойство проводящих тел накапливать и удерживать электрический заряд, измеряемое отношением заряда уединенного проводника к его потенциалу, называется электрической емкостью, или просто емкостью, и обозначается буквой С.
Приведенная формула электрической емкости позволяет установить единицу электрической емкости.
Практически заряд измеряется в кулонах, потенциал в вольтах, а емкость в фарадах:
Емкостью в 1 фараду обладает проводник, которому сообщают заряд в 1 кулон и при этом потенциал проводника увеличивается на 1 вольт.
Единица измерения электрической емкости – фарада (обозначается ф или F) очень велика. Поэтому чаще пользуются более мелкими единицами – микрофарадой (мкф или μF), составляющей миллионную часть фарады:
1 мкф = 10-6ф ,
и пикофарадой (пф), составляющей миллионную часть микрофарады:
1 пф = 10-6мкф = 10-12ф .
Найдем выражение практической единицы – фарады в абсолютных единицах:
Электрический конденсатор
Устройство, предназначенное для накопления электрических зарядов, называется электрическим конденсатором.
Рисунок 1. Модель простейшего конденсатора
Конденсатор состоит из двух металлических пластин (обкладок), разделенных между собой слоем диэлектрика. Чтобы зарядить конденсатор, нужно его обкладки соединить с полюсами электрической машины. Разноименные заряды, скопившиеся на обкладках конденсатора, связаны между собой электрическим полем. Близко расположенные пластины конденсатора, влияя одна на другую, позволяют получить на обкладках большой электрический заряд при относительно невысокой разности потенциалов между обкладками. Электрическая емкость конденсатора есть отношение заряда конденсатора к разности потенциалов между его обкладками:
Как показывают измерения, емкость конденсатора увеличится, если увеличить поверхность обкладок или приблизить их одну к другой. На емкость конденсатора оказывает влияние также материал диэлектрика. Чем больше электрическая проницаемость диэлектрика, тем больше емкость конденсатора по сравнению с емкостью того же конденсатора, диэлектриком в котором служит пустота (воздух). Выбирая диэлектрик для конденсатора, нужно стремиться к тому, чтобы диэлектрик обладал большой электрической прочностью (хорошими изолирующими качествами). Плохой диэлектрик приводит к пробою его и разряду конденсатора. Несовершенный диэлектрик повлечет за собой утечку тока через него и постепенный разряд конденсатора.
Длинные линии передачи высокого напряжения можно рассматривать как своеобразные обкладки конденсатора. Емкость провода нужно рассматривать не только относительно другого провода, но также относительно земли, стен помещений и окружающих предметов. Значительной емкостью обладают подводные и подземные кабели ввиду близкого расположения токоведущих жил между собой.
Конденсатор постоянной емкости
Конденсаторы, емкость которых изменять нельзя, называются конденсаторами постоянной емкости.
Рисунок 2. Схема устройства конденсатора
постоянной емкости
Наиболее распространенные в настоящее время конденсаторы постоянной емкости состоят из очень тонких металлических (станиолевых) листов с парафинированной бумажной или слюдяной прослойкой между ними.
Для увеличения емкости (увеличения площади пластин конденсатора) чаще всего берут по нескольку станиолевых листов и соединяют их в две группы, входящие одна в другую и разделенные диэлектриком, как схематически показано на рисунке 2. Иногда также берут две длинные станиолевые пластины, прокладывают между ними и снаружи парафинированную бумагу и затем свертывают все в компактный пакет или трубку. Конденсаторы большой емкости во многих случаях помещают в металлическую коробку и заливают парафином.
Рисунок 3. Внешний вид современных конденсаторов постоянной емкости
Определим емкость плоского конденсатора. Возьмем произвольную замкнутую поверхность вокруг одной из пластин конденсатора. Тогда по теореме Гаусса поток вектора напряженности, проходящий через любую замкнутую поверхность, внутри которой находится электрический заряд, равен:
| (1) |
Предполагая, что поле конденсатора однородно (пренебрегая искажением поля у краев пластин), получаем напряженность электрического поля в конденсаторе:
| (2) |
где d – расстояние между пластинами или толщина диэлектрика. Подставив значение E из формулы (2) в формулу (1), получим:
откуда
Так как
то выражение емкости плоского конденсатора примет вид:
где S – площадь пластин в м²; d – толщина диэлектрика в м; ε – относительная электрическая проницаемость диэлектрика (диэлектрическая проницаемость).
Таким образом, для увеличения емкости плоского конденсатора нужно увеличить площадь его пластин (обкладок) S, уменьшить расстояние между ними d и в качестве диэлектрика поставить материал с большой относительной электрической проницаемостью (ε).
Видео об устройстве конденсатора постоянной емкости:
Конденсатор переменной емкости
Конденсаторы, емкость которых можно менять, называются конденсаторами переменной емкости.
Наиболее простой конденсатор переменной емкости имеет несколько (реже один) медных или алюминиевых полудисков, соединенных между собой электрически и укрепленных неподвижно. Другой ряд таких же полудисков собран на общей оси. При повороте этой оси каждый из укрепленных на ней полудисков входит меду двумя неподвижными полудисками. Поворачивая ось и меняя таким образом взаимное расположение подвижных и неподвижных полудисков, мы можем менять емкость конденсатора. На рисунке 3 показана схема устройства и на рисунке 4 – общий вид воздушного конденсатора переменной емкости.
Рисунок 3. Схема устройства конденсатора переменной емкости
Рисунок 4. Общий вид конденсатора переменной емкости
Видео об устройстве серийного конденсатора переменной емкости:
Видео о том, как можно сделать самодельный конденсатор переменной емкости своими руками:
Электролитические конденсаторы
В радиотехнике применяются также электролитические конденсаторы. Эти конденсаторы изготовляются двух типов: жидкостные и сухие. В обоих типах конденсаторов употребляется оксидированный алюминий. Путем специальной электрохимической обработки на поверхности алюминия получают тонкий (порядка нескольких десятков микрон) слой оксида алюминия Al2O3, представляющий так называемую оксидную изоляцию алюминия. Оксидная изоляция обладает электроизолирующими свойствами, а также является механически прочной, нагревостойкой, но гигроскопичной.
В жидкостных электролитических конденсаторах алюминиевую оксидированную пластину помещают внутрь металлического корпуса, который служит второй пластиной. В корпус заливают электролит, состоящий из раствора борной кислоты с некоторыми примесями.
Сухие электролитические конденсаторы изготовляют путем сворачивания трех лент. Одна лента представляет собой алюминиевую оксидированную фольгу (тонко раскатанный лист металла). Другой пластиной является лента из алюминиевой фольги. Между двумя металлическими лентами помещается бумажная или марлевая лента, пропитанная вязким электролитом. Плотно свернутые ленты помещаются в алюминиевый корпус и заливаются битумом. Тонкий оксидный изолирующий слой с высокой электрической проницаемостью (ε = 9) позволяет получить дешевые конденсаторы с большой удельной емкостью.
Видео об устройстве электролитического конденсатора:
Параллельное соединение конденсаторов
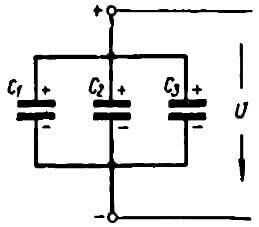
Рисунок 5. Параллельное
соединение конденсаторов
Когда емкость конденсатора мала, то соединяют несколько конденсаторов параллельно (рисунок 5).
При параллельном соединении конденсаторов напряжение на обкладках каждого конденсатора одно и то же. Поэтому можно написать:
U1 = U2 = U3 = U .
Количество электричества (заряд) каждого конденсатора:
q1 = C1 × U; q2 = C2 × U; q3 = C3 × U .
Общий заряд батареи конденсаторов:
q = q1 + q2 + q3 ;
q = C1 × U + C2 × U + C3 × U = U (C1 + C2 + C3) .
Обозначая емкость батареи конденсаторов через C, получаем:
q = C × U ,
тогда
C × U = U × (C1 + C2 + C3)
или окончательно формула емкости при параллельном соединении конденсаторов примет вид:
C = C1 + C2 + C3 .
Следовательно, при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов. При параллельном соединении каждый конденсатор окажется включенным на полное напряжение сети.
Последовательное соединение конденсаторов
Рисунок 6. Последовательное
соединение конденсаторов
Рассмотрим последовательное соединение конденсаторов (рисунок 6).
Если левая обкладка первого конденсатора заряжена положительно (+), то вследствие электростатической индукции правая обкладка этого конденсатора получит отрицательный заряд (–), перешедший с левой обкладки второго конденсатора, которая сама зарядится положительно, и так далее. Значит, при последовательном соединении каждый конденсатор независимо от величины его емкости получит один и тот же заряд, то есть
q1 = q2 = q3 = q .
Напряжение, приложенное ко всей батареи конденсаторов, равно сумме напряжений на обкладках каждого конденсатора:
U = U1 + U2 + U3 .
Так как
для всей батареи
теперь можно написать
или, сокращая на q, получим окончательно, что емкость конденсаторов при последовательном соединении равна:
Таким образом, при последовательном соединении конденсаторов обратная величина общей емкости равна сумме обратных величин емкостей отдельных конденсаторов. Каждый из конденсаторов включен на меньшее напряжение, чем напряжение сети.
Конденсаторы широко применяются в радиотехнике, рентгенотехнике, высокочастотной промышленной электротехнике, для увеличения коэффициента мощности электроустановок и так далее.
Источник: Кузнецов М.И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.
www.electromechanics.ru
Что такое конденсатор и как они используются
Приветствую, друзья!
Мы уже рассматривали, как устроены «кирпичики», из которых собран компьютер.
Вы уже знаете, как устроены и как работают полупроводниковые диоды, полевые и биполярные транзисторы.
Вы уже знакомы с таким понятием, как SMD компоненты.
Давайте познакомимся с еще одной интереснейшей штуковиной — конденсатором.
Из всего многообразия конденсаторов мы рассмотрим лишь те, которые используются в компьютерах и периферийных устройствах.
Что такое конденсатор?
Конденсатор — это деталь с двумя выводами (двухполюсник), позволяющая накапливать энергию.
Конденсатор характеризуется такой величиной, как ёмкость.
Чем больше ёмкость конденсатора, тем больше энергии он может накопить и тем (грубо говоря) больше его габариты.
Конденсатор может не только накапливать энергию, но и отдавать ее.
Именно в таком режиме он чаще всего и работает.
Конденсатор, в отличие от транзистора, является пассивным компонентом, т.е. есть он не может генерировать или усиливать сигнал.
Как устроен конденсатор?
В простейшем случае конденсатор состоит из двух металлических пластин (обкладок) и диэлектрика (изолятора) между ними. Чем больше размер пластин и чем меньше зазор между ними, тем больше емкость конденсатора.Вообще говоря, конденсатор накапливает на обкладках заряд (множество элементарных частиц, каждая из которых обладает элементарным зарядом). Чем больший заряд накоплен, тем большая запасена энергия. Ёмкость конденсатора зависит также и от вида диэлектрика.
Две пластины, разделенные тонким воздушным слоем (воздух — тоже диэлектрик), обладают очень небольшой емкостью, и в таком виде конденсаторы не используются.
С помощью специальных материалов и технологических ухищрений научились достаточно большую ёмкость втискивать в очень небольшой объём.
Самый характерный пример — электролитические конденсаторы.
В них две металлические обкладки в виде длинных полос (чаще всего из алюминиевой фольги) разделены слоем бумаги, пропитанной электролитом.
Электролит вызывает образование тонкой пленки оксида (окисла), которая является хорошим диэлектриком.
Поэтому электролитические конденсаторы называют ещё оксидными. Полосы сворачивают и помещают в цилиндрический алюминиевый корпус.
Раньше выводы конденсаторов делали из меди – как из материала с высокой электропроводностью. Теперь же их нередко делают из более дешевых сплавов на основе железа. В этом можно убедиться, если поднести к ним магнит. Фирмачи научились экономить!
В керамических конденсаторах диэлектриком служит пластинка из керамики, а обкладками – напыленные на керамику пленки металлических сплавов.
В каких единицах измеряется емкость конденсатора?
Основная единица для измерения ёмкости – Фарад (Ф, старое название – Фарада).
Но это очень большая величина, поэтому на практике используются её производные — пикофарад (пФ, пикофарада), нанофарад (нФ, нанофарада), микрофарад (мкФ, микрофарада).
Один микрофарад = 1 000 нанофарад = 1 000 000 пикофарад.
В компьютерных блоках питания и в материнских платах используются электролитические конденсаторы ёмкостью несколько сотен или тысяч микрофарад.
Там же применяется малогабаритные керамические конденсаторы ёмкостью несколько сотен или тысяч пикофарад.
Керамические конденсаторы используются чаще всего в виде SMD компонентов.
Как обозначаются конденсаторы в электрических схемах?
Конденсаторы в электрических схемах обозначается в виде двух вертикальных черточек, разделенных небольшим пространством. Графическое изображение напоминает те самые две пластины, разделенные воздушным диэлектриком.
У электролитических конденсаторов возле одной из черточек (обкладок) помещается знак «+».
Это потому, что электролитические конденсаторы обычно имеют полярность, которую надо соблюдать при монтаже.
Отметим, что в некоторых случаях применяются электролитические неполярные конденсаторы.
Рядом наносится значение ёмкости конденсатора.
А если конденсатор электролитический — то и величина его рабочего напряжения.
Записи вида 1000 p (1000 pF) и 3,9 n (3,9 nF) означают соответственно 1000 пикофарад и 3,9 нанофарад (или 3900 пикофарад).
Запись вида 1000uFx16V означает емкость 1000 микрофарад и рабочее напряжение 16 Вольт.
Напротив отрицательного электрода на корпусе конденсатора наносится соответствующая маркировка (знак «-»).
Где и как используются конденсаторы?
Перед тем как начать рассказывать об области применения конденсаторов, вспомним, что конденсатор это — две пластины, разделенные диэлектриком. Поэтому ток через конденсатор (в первом приближении) идти не может. Однако в цепи с конденсатором могут происходить процессы заряд и разряда. И во время этих процессов в цепи будут протекать токи заряда или разряда.
Таким образом, если переменное напряжение будет приложено к цепи с конденсатором, в ней будет протекать переменный ток. Поэтому конденсатор можно охарактеризовать такой величиной как емкостное сопротивление (обозначается в технической литературе как Хс).
Емкостное сопротивление зависит от ёмкости конденсатора и частоты приложенного напряжения. Чем ёмкость и частота больше, тем меньше емкостное сопротивление. На этих эффектах основано применение конденсаторов в схемах фильтрации источников питания.
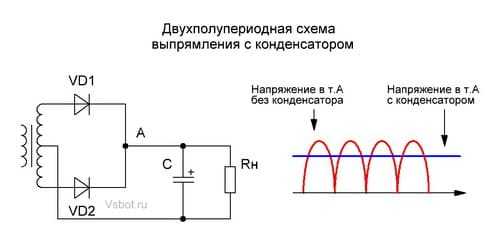
В компьютерных блоках питания для получения постоянных напряжений +3,3, +5, и +12 В используется двухполупериодная схема выпрямление с двумя диодами и фильтрующим конденсатором. Без конденсатора на нагрузке будет пульсирующее напряжение одной полярности.
Источник постоянного напряжения можно представить в виде эквивалентной схемы из генератора и двух сопротивлений, где R1 — это внутреннее сопротивление выпрямителя, а R2 — емкостное сопротивление конденсатора.
Генератор – это сумма постоянного и переменного напряжений (пульсирующее напряжение содержит в себе постоянную и переменную составляющую).
Таким образом, сигнал с генератора подается на частотно-зависимый делитель напряжения. Выходной сигнал снимается с нижнего плеча (конденсатора). Для постоянного напряжения сопротивление конденсатора очень велико, гораздо больше сопротивления выпрямителя. Поэтому уменьшения постоянного напряжения не происходит.
Для переменного напряжения сопротивления конденсатора очень мало, гораздо меньше сопротивления выпрямителя, поэтому происходит сильное ослабление переменной составляющей.
В реальной схеме ситуация несколько сложнее, так как к нижнему плечу делителя подключена нагрузка, обладающая сопротивлением. Поэтому полностью избавиться от пульсаций нельзя, можно только свести их к какому-то небольшому значению.
Вообще, такая комбинация активного сопротивления и конденсатора называется фильтром нижних частот, который пропускает постоянную составляющую и какой-то диапазон низких частот.
Чем выше частота входного переменного напряжения, тем сильнее оно ослабляется.
Так как необходимо сильное подавление пульсаций переменного напряжения, то используется электролитические конденсаторы большой емкости.
Назначение керамических SMD конденсаторов на материнской плате — подавлять высокочастотные помехи, возникающие при переключении транзисторов в микросхемах. Таким образом, электролитические конденсаторы фильтруют относительно низкочастотные помехи и пульсации, а керамические — более высокочастотные.
Приведем еще один пример разделения переменной и постоянной составляющей. Пусть в схеме на рисунке сигнал в точке А будет иметь постоянную составляющую 5 В и переменную амплитудой 2 В.
После конденсатора, в точке В будет уже только переменная составляющая той же амплитудой 2 В (если емкостное сопротивление конденсатора мало для такой частоты). Интересно, не правда ли?
По существу, это тоже частотно-зависимый делитель напряжения, где в виде нижнего плеча выступает сопротивление нагрузки. Такую комбинацию называют фильтром верхних частот, который не пропускает постоянную составляющие и низкие частоты, так как в емкостное сопротивление будет для них большим.
Заканчивая, отметим маленькую деталь: так как максимальное напряжение на конденсаторе будет равно сумме постоянной и переменной составляющей, его рабочее напряжение должно быть не менее этой величины.
Купить конденсаторы можно здесь:
Продолжение следует.
vsbot.ru
§52. Конденсаторы, их назначение и устройство
Заряд и разряд конденсатора. Конденсатор представляет собой устройство, способное накапливать электрические заряды. Простейшим конденсатором являются две металлические пластины (электроды), разделенные каким-либо диэлектриком. Конденсатор 2 можно зарядить, если соединить его электроды с источником 1 электрической энергии постоянного тока (рис. 181, а).
При заряде конденсатора свободные электроны, имеющиеся на одном из его электродов, устремляются к положительному полюсу источника, вследствие чего этот электрод становится положительно заряженным. Электроны с отрицательного полюса источника устремляются ко второму электроду и создают на нем избыток электронов, поэтому он становится отрицательно заряженным. В результате протекания зарядного тока i3 на обоих электродах конденсатора образуются равные, но противоположные по знаку заряды и между ними возникает электрическое поле, создающее между электродами конденсатора определенную разность потенциалов. Когда эта разность потенциалов станет равной напряжению источника тока, движение электронов в цепи конденсатора, т. е. прохождение по ней тока i3 прекращается. Этот момент соответствует окончанию процесса заряда конденсатора.
При отключении от источника (рис. 181,б) конденсатор способен длительное время сохранять накопленные электрические заряды. Заряженный конденсатор является источником электрической энергии, имеющим некоторую э. д. с. ес. Если соединить электроды заряженного конденсатора каким-либо проводником (рис. 181, в), то конденсатор начнет разряжаться. При этом по цепи пойдет ток iр разряда конденсатора. Начнет уменьшаться и разность потенциалов между электродами, т. е. конденсатор будет отдавать накопленную электрическую энергию во внешнюю цепь. В тот момент, когда количество свободных электронов на каждом электроде конденсатора станет одинаковым, электрическое поле между электродами исчезнет и ток станет равным нулю. Это означает, что произошел полный разряд конденсатора, т. е. он отдал накопленную им электрическую энергию.
Емкость конденсатора. Свойство конденсатора накапливать и удерживать электрические заряды характеризуется его емкостью. Чем больше емкость конденсатора, тем больше накопленный им заряд, так же как с увеличением вместимости сосуда или газового баллона увеличивается объем жидкости или газа в нем.
Емкость С конденсатора определяется как отношение заряда q, накопленного в конденсаторе, к разности потенциалов между его электродами (приложенному напряжению)U:
C = q / U (69)
Емкость конденсатора измеряется в фарадах (Ф). Емкостью в 1 Ф обладает конденсатор, у которого при сообщении заряда
Рис. 181. Заряд и разряд конденсатора
в 1 Кл разность потенциалов возрастает на 1 В. В практике преимущественно пользуются более мелкими единицами: микрофарадой (1 мкФ=10-6 Ф), пикофарадой (1 пФ = 10-12 мкФ).
Емкость конденсатора зависит от формы и размеров его электродов, их взаимного расположения и свойств диэлектрика, разделяющего электроды. Различают плоские конденсаторы, электродами которых служат плоские параллельные пластины (рис. 182, а), и цилиндрические (рис. 182,б).
Свойствами конденсатора обладают не только специально изготовленные на заводе устройства, но и любые два проводника, разделенные диэлектриком. Емкость их оказывает существенное влияние на работу электротехнических установок при переменном токе. Например, конденсаторами с определенной емкостью являются два электрических провода, провод и земля (рис. 183, а), жилы электрического кабеля, жилы и металлическая оболочка кабеля (рис. 183,6).
Устройство конденсаторов и их применение в технике. В зависимости от применяемого диэлектрика конденсаторы бывают бумажными, слюдяными, воздушными (рис. 184). Используя в качестве диэлектрика вместо воздуха слюду, бумагу, керамику и другие материалы с высокой диэлектрической проницаемостью, удается при тех же размерах конденсатора увеличить в несколько раз его емкость. Для того чтобы увеличить площади электродов конденсатора, его делают обычно многослойным.
Рис. 182. Плоский (а) и цилиндрический (б) конденсаторы
В электротехнических установках переменного тока обычно применяют силовые конденсаторы. В них электродами служат длинные полосы из алюминиевой, свинцовой или медной фольги, разделенные несколькими слоями специальной (конденсаторной) бумаги, пропитанной нефтяными маслами или синтетическими пропитывающими жидкостями. Ленты фольги 2 и бумаги 1 сматывают в рулоны (рис. 185), сушат, пропитывают парафином и помещают в виде одной или нескольких секций в металлический или картонный корпус. Необходимое рабочее напряжение конденсатора обеспечивается последовательным, параллельным или последовательно-параллельным соединениями отдельных секций.
Всякий конденсатор характеризуется не только значением емкости, но и значением напряжения, которое выдерживает его диэлектрик. При слишком больших напряжениях электроны диэлектрика отрываются от атомов, диэлектрик начинает проводить ток и металлические электроды конденсатора замыкаются накоротко (конденсатор пробивается). Напряжение, при котором это происходит, называют пробивным. Напряжение, при котором конденсатор может надежно работать неограниченно долгое время, называют рабочим. Оно в несколько раз меньше пробивного.
Конденсаторы широко применяют в системах энергоснабжения промышленных предприятий и электрифицированных железных дорог для улучшения использования электрической энергии при переменном токе. На э. п. с. и тепловозах конденсаторы используют для сглаживания пульсирующего тока, получаемого от выпрямителей и импульсных прерывателей, борьбы с искрением контактов электрических аппаратов и с радиопомехами, в системах управления полупроводниковыми преобразователями, а также для созда-
Рис. 183. Емкости, образованные проводами воздушной линии (а) и жилами кабеля (б)
Рис. 184. Общие виды применяемых конденсаторов: 1 — слюдяные; 2 — бумажные; 3 — электролитический; 4 — керамический
Рис. 185. Устройство бумажного (а) и электролитического (б) конденсаторов
Рис. 186. Устройство конденсатора переменной емкости
ния симметричного трехфазного напряжения, требуемого для питания электродвигателей вспомогательных машин. В радиотехнике конденсаторы служат для создания высокочастотных электромагнитных колебаний, разделения электрических цепей постоянного и переменного тока и др.
В цепях постоянного тока часто устанавливают электролитические конденсаторы. Их изготовляют из двух скатанных в рулон тонких алюминиевых лент 3 и 5 (рис. 185,б), между которыми проложена бумага 4, пропитанная специальным электролитом (раствор борной кислоты с аммиаком в глицерине). Алюминиевую ленту 3 покрывают тонкой пленкой окиси алюминия; эта пленка образует диэлектрик, обладающий высокой диэлектрической проницаемостью. Электродами конденсатора служат лента 3, покрытая окисной пленкой, и электролит; вторая лента 5 предназначена лишь для создания электрического контакта с электролитом. Конденсатор помещают в цилиндрический алюминиевый корпус.
При включении электролитического конденсатора в цепь постоянного тока необходимо строго соблюдать полярность его полюсов; электрод, покрытый окисной пленкой, должен быть соединен с положительным полюсом источника тока. При неправильном включении диэлектрик пробивается. По этой причине электролитические конденсаторы нельзя включать в цепи переменного тока. Их нельзя также использовать в устройствах, работающих при высоких напряжениях, так как окисная пленка имеет сравнительно небольшую электрическую прочность.
В радиотехнических устройствах применяют также конденсаторы переменной емкости (рис. 186). Такой конденсатор состоит из двух групп пластин: неподвижных 2 и подвижных 3, разделенных воздушными промежутками. Подвижные пластины могут перемещаться относительно неподвижных; при повороте оси 1 конденсатора изменяется площадь взаимного перекрытия пластин, а следовательно, и емкость конденсатора.
Способы соединения конденсаторов. Конденсаторы можно соединять последовательно и параллельно. При последовательном
Рис. 187. Последовательное (а) и параллельное (б) соединения конденсаторов
Рис. 188. Схема подключения цепи R-C к источнику постоянного тока (а) и кпивые тока и напряжения при переходном процессе (б) кривые
Рис. 189. Схема разряда емкости С на резистор R (а) и кривые тока и напряжения при переходном процессе (б)
Рис. 190. Кривая пилообразного напряжения
соединении нескольких (например, трех), конденсаторов (рис. 187, а) эквивалентная емкость
1 /Cэк = 1 /C1 + 1 /C2 + 1 /C3
эквивалентное емкостное сопротивление
XCэк= XC1 + XC2 + XC3
результирующее емкостное сопротивление
Cэк = C1 + C2 + C3
При параллельном соединении конденсаторов (рис. 187,б) их результирующая емкость
1 /XCэк = 1 /XC1 + 1 /XC2 + 1 /XC3
Включение и отключение цепей постоянного тока с конденсатором. При подключении цепи R-C к источнику постоянного тока и при разряде конденсатора на резистор также возникает переходный процесс с апериодическим изменением тока i и напряжения uc При подключении к источнику постоянного тока цепи R-C выключателем В1 (рис. 188,а) происходит заряд конденсатора. В начальный момент зарядный ток Iнач=U /R. Но по мере накопления зарядов на электродах конденсатора напряжение его и с будет возрастать, а ток уменьшаться (рис. 188,б). Если сопротивление R мало, то в начальный момент подключения конденсатора возникает большой екачок тока, значительно превышающий номинальный ток данной цепи. При разряде конденсатора на резистор R (размыкается выключатель В1 на рис. 189, а) напряжение на конденсаторе uс и ток i постепенно уменьшаются до нуля (рис. 189,б).
Скорость изменения тока i и напряжения ис при переходном процессе отделяется постоянной времени
T = RC
Чем больше R и С, тем медленнее происходит заряд конденсатора.
Процессы заряда и разряда конденсатора широко используют в электронике и автоматике. С помощью их получают периодаческие несинусоидальные колебания, называемые релаксационными, и, в частности, пилообразное напряжение, необходимое для работы систем управления тиристорами, осциллографов и других устройств. Для получения пилообразного напряжения (рис. 190) периодически подключают конденсатор к источнику питания, а затем к разрядному резистору. Периоды Т1 и T2, соответствующие заряду и разряду конденсатора, определяются постоянными времени цепей заряда Т3 и разряда Тр, т. е. сопротивлениями резисторов, включенных в эти цепи.
electrono.ru
