Фарадей электромагнитная индукция – Закон электромагнитной индукции Фарадея — Википедия — specable.ru

Закон электромагнитной индукции Фарадея — Википедия

Зако́н электромагни́тной инду́кции Фараде́я является основным законом электродинамики, касающимся принципов работы трансформаторов, дросселей, многих видов электродвигателей и генераторов.^[1] Закон гласит:

или другими словами:
Генерируемая ЭДС пропорциональна скорости изменения магнитного потока.
При этом индукционный ток направлен таким образом, что его действие противоположно действию причины, вызвавшей этот ток (правило Ленца).^[2]
Электромагнитная индукция была обнаружена независимо друг от друга Майклом Фарадеем и Джозефом Генри в 1831 году, однако Фарадей первым опубликовал результаты своих экспериментов^[3]^[4].
В первой экспериментальной демонстрации электромагнитной индукции (август 1831) Фарадей обмотал двумя проводами противоположные стороны железного тора (конструкция похожа на современный трансформатор). Основываясь на своей оценке недавно обнаруженного свойства электромагнита, он ожидал, что при включении тока в одном проводе особого рода волна пройдёт сквозь тор и вызовет некоторое электрическое влияние на его противоположной стороне. Он подключил один провод к гальванометру и смотрел на него, когда другой провод подключал к батарее. В самом деле, он увидел кратковременный всплеск тока (который он назвал «волной электричества»), когда подключал провод к батарее, и другой такой же всплеск, когда отключал его.
[5] В течение двух месяцев Фарадей нашёл несколько других проявлений электромагнитной индукции. Например, он увидел всплески тока, когда быстро вставлял магнит в катушку и вытаскивал его обратно, он генерировал постоянный ток во вращающемся вблизи магнита медном диске со скользящим электрическим проводом («диск Фарадея»)^[6].
Фарадей объяснил электромагнитную индукцию с использованием концепции так называемых силовых линий. Однако, большинство учёных того времени отклонили его теоретические идеи, в основном потому, что они не были сформулированы математически.
[7] Исключение составил Максвелл, который использовал идеи Фарадея в качестве основы для своей количественной электромагнитной теории.^[7]^[8]^[9] В работах Максвелла аспект изменения во времени электромагнитной индукции выражен в виде дифференциальных уравнений. Оливер Хевисайд назвал это законом Фарадея, хотя он несколько отличается по форме от первоначального варианта закона Фарадея и не учитывает индуцирование ЭДС при движении. Версия Хевисайда является формой признанной сегодня группы уравнений, известных как уравнения Максвелла.
Эмилий Христианович Ленц сформулировал в 1834 году закон (правило Ленца), который описывает «поток через цепь» и даёт направление индуцированной ЭДС и тока в результате электромагнитной индукции.
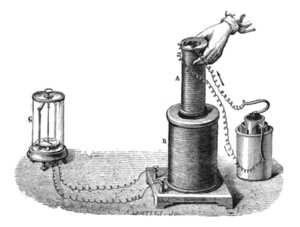Эксперимент Фарадея, показывающий индукцию между витками провода: жидкостная батарея (справа) даёт ток, который протекает через небольшую катушку (A), создавая магнитное поле. Когда катушки неподвижны, ток не индуцируется. Но когда маленькая катушка вставляется или извлекается из большой катушки (B), магнитный поток через катушку изменяется, вызывая ток, который регистрируется гальванометром (G).^[10]
Закон Фарадея как два различных явления[править | править код]
Некоторые физики отмечают, что закон Фарадея в одном уравнении описывает два разных явления: двигательную ЭДС, генерируемую действием магнитной силы на движущийся провод, и трансформаторную ЭДС, генерируемую действием электрической силы вследствие изменения магнитного поля. Джеймс Клерк Максвелл обратил внимание на этот факт в своей работе О физических силовых линиях в 1861 году. Во второй половине части II этого труда Максвелл даёт отдельное физическое объяснение для каждого из этих двух явлений. Ссылка на эти два аспекта электромагнитной индукции имеется в некоторых современных учебниках.
[11] Как пишет Ричард Фейнман:^[12]
Таким образом, «правило потока» о том, что ЭДС в цепи равна скорости изменения магнитного потока через контур, применяется независимо от причины изменения потока: то ли потому что поле изменяется, то ли потому что цепь движется (или и то, и другое)…. В нашем объяснении правила мы использовали два совершенно различных закона для двух случаев – v×B{\displaystyle {\stackrel {\mathbf {v\times B} }{}}} для «движущейся цепи» и ∇ x E = −∂ tB{\displaystyle {\stackrel {\mathbf {\nabla \ x\ E\ =\ -\partial _{\ t}B} }{}}} для «меняющегося поля».

Мы не знаем никакого аналогичного положения в физике, когда такие простые и точные общие принципы требовали бы для своего реального понимания анализа с точки зрения двух различных явлений.
— Ричард Фейнман, Фейнмановские лекции по физике
Отражение этой очевидной дихотомии было одним из основных путей, которые привели Эйнштейна к разработке специальной теории относительности:

Известно, что электродинамика Максвелла — как её обычно понимают в настоящее время — при применении к движущимся телам приводит к асимметрии, которая, как кажется, не присуща этому явлению. Возьмем, к примеру, электродинамическое взаимодействие магнита и проводника. Наблюдаемое явление зависит только от относительного движения проводника и магнита, тогда как обычное мнение рисует резкое различие между этими двумя случаями, в которых либо одно, либо другое тело находится в движении. Ибо, если магнит находится в движении, а проводник покоится, в окрестности магнита возникает электрическое поле с определенной плотностью энергии, создавая ток там, где расположен проводник. Но если магнит покоится, а проводник движется, то в окрестности магнита никакое электрическое поле не возникает. В проводнике, однако, мы находим электродвижущую силу, для которой не существует соответствующей энергии самой по себе, но которая вызывает — предполагая равенство относительного движения в двух обсуждаемых случаях — электрические токи по тому же направлению и той же интенсивности, как в первом случае.
Примеры подобного рода вместе с неудачной попыткой обнаружить какое-либо движение Земли относительно «светоносной среды» предполагают, что явления электродинамики, а также механики не обладают свойствами, соответствующими идее абсолютного покоя.
— Альберт Эйнштейн, К электродинамике движущихся тел^[13]
Поток через поверхность и ЭДС в контуре[править | править код]
Определение поверхностного интеграла предполагает, что поверхность Σ поделена на мелкие элементы. Каждый элемент связан с вектором dA, величина которого равна площади элемента, а направление — по нормали к элементу во внешнюю сторону. Векторное поле F(r, t) определено во всём пространстве, а поверхность Σ ограничена кривой ∂Σ, движущейся со скоростью v. По этой поверхности производится интегрирование поля.

Закон электромагнитной индукции Фарадея использует понятие магнитного потока Φ_B через замкнутую поверхность Σ, который определён через поверхностный интеграл:
:Φ=∬SBn⋅dS,{\displaystyle \Phi =\iint \limits _{S}\mathbf {B_{n}} \cdot d\mathbf {S} ,}
где dS — площадь элемента поверхности Σ(t), B — магнитное поле, а B·dS — скалярное произведение B и dS. Предполагается, что поверхность имеет «устье», очерченное замкнутой кривой, обозначенной ∂Σ(t). Закон индукции Фарадея утверждает, что когда поток изменяется, то при перемещении единичного положительного пробного заряда по замкнутой кривой ∂Σ возникает ЭДС E{\displaystyle {\mathcal {E}}}, величина которой определяется по формуле:
|E|=|dΦdt| ,{\displaystyle |{\mathcal {E}}|=\left|{{d\Phi } \over dt}\right|\ ,}
где |E|{\displaystyle |{\mathcal {E}}|} — величина электродвижущей силы (ЭДС) в вольтах, а Φ
B — магнитный поток в веберах. Направление электродвижущей силы определяется законом Ленца.
Для плотно намотанной катушки индуктивности, содержащей N витков, каждый с одинаковым магнитным потоком Φ_B, закон индукции Фарадея утверждает, что:
|E|=N|dΦBdt|,{\displaystyle |{\mathcal {E}}|=N\left|{{d\Phi _{B}} \over dt}\right|,}
где N — число витков провода, Φ_B — магнитный поток в веберах на один виток.
При выборе пути ∂Σ(t) для нахождения ЭДС заметим, что путь должен удовлетворять двум основным требованиям: (i) путь должен быть замкнутым, и (ii) путь должен охватывать относительное движение частей контура (источник происхождения t-зависимости в ∂Σ(t)). К требованиям не относится то, что путь должен совпадать с линией тока, но, конечно, ЭДС, которая находится по закону потока, будет считаться по выбранному пути. Если путь не совпадает с линией тока, то подсчитанная ЭДС, возможно, будет не та ЭДС, которая вызывает ток.

Пример 1: пространственно меняющееся магнитное поле[править | править код]
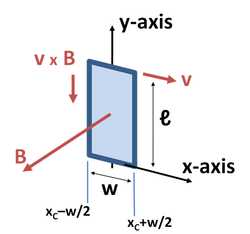Рис. 3. Замкнутый прямоугольный провод движется вдоль оси x со скоростью v в магнитном поле, которое изменяется вдоль x.
Рассмотрим случай на рисунке 3, на котором прямоугольная замкнутая проволочная петля, расположенная в плоскости xy, перемещается в направлении оси x со скоростью v. Центр петли x_C удовлетворяет условию v = dx_C / dt. Петля имеет длину ℓ в направлении оси y и ширину w в направлении оси x. Зависящее от времени пространственно меняющееся магнитное поле B(x) показано в направлении z. Магнитное поле на левой стороне равно B(x_C − w / 2), а на правой стороне B(x_C + w / 2). Электродвижущую силу можно найти либо с помощью закона Лоренца, либо, что эквивалентно, используя вышеизложенный закон индукции Фарадея.

Закон Лоренца[править | править код]
Заряд q в проводнике на левой стороне петли испытывает силу Лоренца q v × B k = −q v B(x_C − w / 2) j (j, k — единичные векторы в направлениях y и z; см. векторное произведение векторов), что вызывает ЭДС (работу на единицу заряда) v ℓ B(x_C − w / 2) по всей длине левой стороны петли. На правой стороне петля аналогичное рассуждение показывает, что ЭДС равна v ℓ B(x_C + w / 2). Две противоположные друг другу ЭДС толкают положительный заряд по направлению к нижней части петли. В случае, когда поле B возрастает вдоль х, сила на правой стороне будет больше, а ток будет течь по часовой стрелке. Используя правило правой руки, мы получаем, что поле B, создаваемое током, противоположно приложенному полю.^[14] ЭДС, вызывающая ток, должна увеличиваться по направлению против часовой стрелки (в отличие от тока). Складывая ЭДС в направлении против часовой стрелки вдоль петли мы находим:

E=vℓ[B(xC+w/2)−B(xC−w/2)] .{\displaystyle {\mathcal {E}}=v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ .}
Закон Фарадея[править | править код]
В любой точке петли магнитный поток через неё равен:
ΦB=±∫0ℓdy∫xC−w/2xC+w/2B(x)dx{\displaystyle \Phi _{B}=\pm \int _{0}^{\ell }dy\int _{x_{C}-w/2}^{x_{C}+w/2}B(x)dx}
=±ℓ∫xC−w/2xC+w/2B(x)dx .{\displaystyle \qquad =\pm \ell \int _{x_{C}-w/2}^{x_{C}+w/2}B(x)dx\ .}
Выбор знака определяется по принципу, имеет ли нормаль к поверхности в данной точке то же направление, что и B, или противоположное. Если нормаль к поверхности имеет то же направление, что и поле B наведённого тока, этот знак отрицательный. Производная по времени от потока (найденная с помощью методов дифференцирования сложной функции или по правилу Лейбница дифференцирования интеграла) равна:
dΦBdt=(−)ddxC[∫0ℓdy ∫xC−w/2xC+w/2dxB(x)]dxCdt {\displaystyle {\frac {d\Phi _{B}}{dt}}=(-){\frac {d}{dx_{C}}}\left[\int _{0}^{\ell }dy\ \int _{x_{C}-w/2}^{x_{C}+w/2}dxB(x)\right]{\frac {dx_{C}}{dt}}\ }
=(−)vℓ[B(xC+w/2)−B(xC−w/2)] ,{\displaystyle \qquad =(-)v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ ,}
(где v = dx_C / dt является скоростью движения петли в направлении оси х), что приводит к:
E=−dΦBdt=vℓ[B(xC+w/2)−B(xC−w/2)] ,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}}=v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ ,}
как и в предыдущем случае.
Эквивалентность этих двух подходов является общеизвестной, и в зависимости от решаемой задачи более практичным может оказаться либо тот, либо другой метод.
Пример 2: проводник, движущийся в постоянном магнитном поле[править | править код]
Рис. 4. Два проводника замкнутые на проводящие обода образуют «рамку» вращающуюся с угловой скоростью ω в радиальном, направленном наружу магнитном поле B фиксированной величины. Ток подается щётками, касающимися верхнего и нижнего дисков с проводящими ободами.
На рис. 4 показан шпиндель, образованный двумя дисками с проводящими ободами, и проводники, расположенные вертикально между этими ободами. ток скользящими контактами подается на проводящие обода. Эта конструкция вращается в магнитном поле, которое направлено радиально наружу и имеет одно и то же значение в любом направлении. то есть мгновенная скорость проводников, ток в них и магнитная индукция, образуют правую тройку, что заставляет проводники вращаться.
Сила Лоренца[править | править код]
В этом случае на проводники действует Сила Ампера, а на единичный заряд в проводнике Сила Лоренца — поток вектора магнитной индукции B , ток в проводниках, соединяющих проводящие обода, направлен нормально к вектору магнитной индукции, тогда сила, действующая на заряд в проводнике, будет равна
F=qBv,{\displaystyle F=qBv\,,}
где v = скорости движущегося заряда^[15]
Следовательно, сила действующая на проводники
F=IBℓ,{\displaystyle {\mathcal {F}}=IB\ell ,}
где l — длина проводников
Здесь мы использовали B как некую данность, на самом деле она зависит от геометрических размеров ободов конструкции, и это значение можно вычислить, используя Закон Био — Савара — Лапласа . Данный эффект используется и в другом устройстве, называемом Рельсотрон
Закон Фарадея[править | править код]
Интуитивно привлекательный, но ошибочный подход к использованию правила потока выражает поток через цепь по формуле Φ_B = B w ℓ, где w — ширина движущейся петли.
Ошибочность такого подхода в том, что это не рамка в обычном понимании этого слова. Прямоугольник на рисунке образован отдельными проводниками, замкнутыми на обод. Как видно на рисунке, ток по обоим проводникам течет в одном направлении, то есть здесь отсутствует понятие «замкнутый контур»
Наиболее простое и понятное объяснение этому эффекту дает понятие сила Ампера. То есть вертикальный проводник может быть вообще один, чтобы не вводить в заблуждение. Или же проводник конечной толщины может быть расположен на оси, соединяющей обода. Диаметр проводника должен быть конечным и отличаться от нуля, чтобы момент силы Ампера был ненулевой.
Рис. 6. Иллюстрация теоремы Кельвина-Стокса с помощью поверхности Σ, её границы ∂Σ и ориентации n , установленной правилом правой руки.
Переменное магнитное поле создаёт электрическое поле, описываемое уравнением Фарадея — Максвелла:
∇×E=−∂B∂t,{\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}},}
где:
∇×{\displaystyle \nabla \times } обозначает ротор
E — электрическое поле
B — плотность магнитного потока.
Это уравнение присутствует в современной системе уравнений Максвелла, часто его называют законом Фарадея. Однако, поскольку оно содержит только частные производные по времени, его применение ограничено ситуациями, когда заряд покоится в переменном по времени магнитном поле. Оно не учитывает^{[уточнить]} электромагнитную индукцию в случаях, когда заряженная частица движется в магнитном поле.
В другом виде закон Фарадея может быть записан через интегральную форму теоремы Кельвина-Стокса:^[16]
∮∂Σ⁡E⋅dℓ=−∫Σ∂∂tB⋅dA.{\displaystyle \oint _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=-\int _{\Sigma }{\partial \over {\partial t}}\mathbf {B} \cdot d\mathbf {A} .}
Для выполнения интегрирования требуется независимая от времени поверхность Σ (рассматриваемая в данном контексте как часть интерпретации частных производных). Как показано на рис. 6:
Σ — поверхность, ограниченная замкнутым контуром ∂Σ, причём, как Σ, так и ∂Σ являются фиксированными, не зависящими от времени,
E — электрическое поле,
dℓ — бесконечно малый элемент контура ∂Σ,
B — магнитное поле,
dA — бесконечно малый элемент вектора поверхности Σ.
Элементы dℓ и dA имеют неопределённые знаки. Чтобы установить правильные знаки, используется правило правой руки, как описано в статье о теореме Кельвина-Стокса. Для плоской поверхности Σ положительное направление элемента пути dℓ кривой ∂Σ определяется правилом правой руки, по которому на это направление указывают четыре пальца правой руки, когда большой палец указывает в направлении нормали n к поверхности Σ.
Интеграл по ∂Σ называется интеграл по пути или криволинейным интегралом. Поверхностный интеграл в правой части уравнения Фарадея-Максвелла является явным выражением для магнитного потока Φ_B через Σ. Обратите внимание, что ненулевой интеграл по пути для E отличается от поведения электрического поля, создаваемого зарядами. Генерируемое зарядом E-поле может быть выражено как градиент скалярного поля, которое является решением уравнения Пуассона и имеет нулевой интеграл по пути.
Интегральное уравнение справедливо для любого пути ∂Σ в пространстве и любой поверхности Σ, для которой этот путь является границей.
Рис. 7. Площадь заметания элемента вектора dℓ кривой ∂Σ за время dt при движении со скоростью v.
Используя^[17]
ddt∫AB dA=∫A(∂B∂t+v div B+rot(B×v))dA{\displaystyle {\frac {\text{d}}{{\text{d}}t}}\int \limits _{A}{\mathbf {B} }{\text{ d}}\mathbf {A} =\int \limits _{A}{\left({\frac {\partial \mathbf {B} }{\partial t}}+\mathbf {v} \ {\text{div}}\ \mathbf {B} +{\text{rot}}\;(\mathbf {B} \times \mathbf {v} )\right)\;{\text{d}}}\mathbf {A} }
и принимая во внимание divB=0{\displaystyle {\text{div}}\mathbf {B} =0} (Ряд Гаусса),
ru.wikipedia.org
Электромагнитная индукция – FIZI4KA
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
источник – переменное магнитное поле;
обнаруживается по действию на заряд;
не является потенциальным;
линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь \( S \) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции \( B \), площади поверхности \( S \), пронизываемой данным потоком, и косинуса угла \( \alpha \) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – \( \Phi \), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла \( \alpha \) магнитный поток может быть положительным (\( \alpha \) < 90°) или отрицательным (\( \alpha \) > 90°). Если \( \alpha \) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из \( N \) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением \( R \):
При движении проводника длиной \( l \) со скоростью \( v \) в постоянном однородном магнитном поле с индукцией \( \vec{B} \) ЭДС электромагнитной индукции равна:
где \( \alpha \) – угол между векторами \( \vec{B} \) и \( \vec{v} \).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
определить направление линий магнитной индукции внешнего магнитного поля;
выяснить, как изменяется магнитный поток;
определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции \( \varepsilon_{is} \), возникающая в катушке с индуктивностью \( L \), по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток \( \Phi \) через контур из этого проводника пропорционален модулю индукции \( \vec{B} \) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности \( L \) между силой тока \( I \) в контуре и магнитным потоком \( \Phi \), создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
закона электромагнитной индукции;
ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3 (60%) 2 votes
fizi4ka.ru
Электромагнитная индукция — Википедия
Электромагни́тная инду́кция — явление возникновения электрического тока, электрического поля или электрической поляризации при изменении во времени магнитного поля или при движении материальной среды в магнитном поле^[1]. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года^[2]. Он обнаружил, что электродвижущая сила (ЭДС), возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Согласно закону электромагнитной индукции Фарадея (в СИ):
E=−dΦBdt,{\displaystyle {\mathcal {E}}=-{{d\Phi _{B}} \over dt},}
где
E{\displaystyle {\mathcal {E}}} — электродвижущая сила, действующая вдоль произвольно выбранного контура,
ΦB{\displaystyle \Phi _{B}} =∬SB→⋅dS→{\displaystyle =\iint \limits _{S}{\vec {B}}\cdot d{\vec {S}}} — магнитный поток через поверхность, ограниченную этим контуром.
Знак «минус» в формуле отражает правило Ленца, названное так по имени российского физика Э. Х. Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
E=−NdΦBdt=−dΨdt,{\displaystyle {\mathcal {E}}=-N{{d\Phi _{B}} \over dt}=-{{d\Psi } \over dt},}
где
E{\displaystyle {\mathcal {E}}} — электродвижущая сила,
N{\displaystyle N} — число витков,
ΦB{\displaystyle \Phi _{B}} — магнитный поток через один виток,
Ψ{\displaystyle \Psi } — потокосцепление катушки.
Векторная форма[править | править код]
В дифференциальной форме закон Фарадея можно записать в следующем виде:
rotE→=−∂B→∂t{\displaystyle \operatorname {rot} \,{\vec {E}}=-{\partial {\vec {B}} \over \partial t}} (в системе СИ)
или
rotE→=−1c∂B→∂t{\displaystyle \operatorname {rot} \,{\vec {E}}=-{1 \over c}{\partial {\vec {B}} \over \partial t}} (в системе СГС).
В интегральной форме (эквивалентной):
∮∂S⁡E→⋅dl→=−∂∂t∫SB→⋅ds→{\displaystyle \oint _{\partial S}{\vec {E}}\cdot {\vec {dl}}=-{\partial \over \partial t}\int _{S}{\vec {B}}\cdot {\vec {ds}}}(СИ)
или
∮∂S⁡E→⋅dl→=−1c∂∂t∫SB→⋅ds→{\displaystyle \oint _{\partial S}{\vec {E}}\cdot {\vec {dl}}=-{1 \over c}{\partial \over \partial t}\int _{S}{\vec {B}}\cdot {\vec {ds}}} (СГС).
Здесь E→{\displaystyle {\vec {E}}} — напряжённость электрического поля, B→{\displaystyle {\vec {B}}} — магнитная индукция, S {\displaystyle S\ } — произвольная поверхность, ∂S{\displaystyle \partial S} — её граница. Контур интегрирования ∂S{\displaystyle \partial S} подразумевается фиксированным (неподвижным).
Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).
В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)^[3].
Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство E=−dΦ/dt{\displaystyle {\mathcal {E}}=-{{d\Phi }/dt}} продолжает соблюдаться, но ЭДС в левой части теперь не сводится к ∮⁡E→⋅dl→{\displaystyle \oint {\vec {E}}\cdot {\vec {dl}}} (которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула остаётся справедливой, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).
Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год^[4] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п. к формуле E=−dΦ/dt{\displaystyle {\mathcal {E}}=-{{d\Phi }/dt}} в случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)^[5]. В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.
Однако возможность (пусть с некоторыми оговорками, уточняющими область применимости) совпадающей формулировки «правила потока» с законом электромагнитной индукции нельзя назвать чисто случайной. Дело в том, что, по крайней мере для определённых ситуаций, это совпадение оказывается очевидным проявлением принципа относительности. А именно, например, для случая относительного движения катушки с присоединённым к ней вольтметром, измеряющим ЭДС, и источника магнитного поля (постоянного магнита или другой катушки с током), в системе отсчёта, связанной с первой катушкой, ЭДС оказывается равной именно циркуляции электрического поля, тогда как в системе отсчёта, связанной с источником магнитного поля (магнитом), происхождение ЭДС связано с действием силы Лоренца на движущиеся с первой катушкой носители заряда. Однако та и другая ЭДС обязаны совпадать, поскольку вольтметр показывает одну и ту же величину, независимо от того, для какой системы отсчёта мы её рассчитали.
Потенциальная форма[править | править код]
При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:
E→=−∂A→∂t{\displaystyle {\vec {E}}=-{\partial {\vec {A}} \over \partial t}} (в случае отсутствия безвихревого поля, то есть тогда, когда электрическое поле порождается полностью только изменением магнитного, то есть электромагнитной индукцией).
В общем случае, при учёте и безвихревого (например, электростатического) поля имеем:
E→=−∇φ−∂A→∂t{\displaystyle {\vec {E}}=-\nabla \varphi -{\partial {\vec {A}} \over \partial t}}
Подробнее
Поскольку вектор магнитной индукции по определению выражается через векторный потенциал так:
B→=rot A→≡∇×A→,{\displaystyle {\vec {B}}=rot\ {\vec {A}}\equiv \nabla \times {\vec {A}},}
то можно подставить это выражение в
rot E→≡∇×E→=−∂B→∂t,{\displaystyle rot\ {\vec {E}}\equiv \nabla \times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}
получая
∇×E→=−∂(∇×A→)∂t,{\displaystyle \nabla \times {\vec {E}}=-{\frac {\partial (\nabla \times {\vec {A}})}{\partial t}},}
и, поменяв местами дифференцирование по времени и пространственным координатам (ротор):
∇×E→=−∇×∂A→∂t.{\displaystyle \nabla \times {\vec {E}}=-\nabla \times {\frac {\partial {\vec {A}}}{\partial t}}.}
Отсюда, поскольку ∇×E→{\displaystyle \nabla \times {\vec {E}}} полностью определяется правой частью последнего уравнения, видно, что вихревая часть электрического поля (та часть, которая имеет ротор, в отличие от безвихревого поля ∇φ{\displaystyle \nabla \varphi }) полностью определяется выражением
−∂A→∂t.{\displaystyle -{\frac {\partial {\vec {A}}}{\partial t}}.}
То есть в случае отсутствия безвихревой части можно записать
E→=−∂A→∂t,{\displaystyle {\vec {E}}=-{\frac {\partial {\vec {A}}}{\partial t}},}
а в общем случае
E→=−∇φ−dA→dt.{\displaystyle {\vec {E}}=-\nabla \varphi -{\frac {d{\vec {A}}}{dt}}.}
В 1820 году Ганс Христиан Эрстед показал, что протекающий по цепи электрический ток вызывает отклонение магнитной стрелки. Если электрический ток порождает магнетизм, то с магнетизмом должно быть связано появление электрического тока. Эта мысль захватила английского ученого М. Фарадея. «Превратить магнетизм в электричество», — записал он в 1822 году в своём дневнике. Многие годы настойчиво ставил он различные опыты, но безуспешно, и только 29 августа 1831 года наступил триумф: он открыл явление электромагнитной индукции. Установка, на которой Фарадей сделал своё открытие, состояла из кольца из мягкого железа примерно 2 см шириной и 15 см диаметром. На каждой половине кольца было намотано много витков медной проволоки. Цепь одной обмотки замыкала проволока, в её витках находилась магнитная стрелка, удаленная настолько, чтобы не сказывалось действие магнетизма, созданного в кольце. Через вторую обмотку пропускался ток от батареи гальванических элементов. При включении тока магнитная стрелка совершала несколько колебаний и успокаивалась; когда ток прерывали, стрелка снова колебалась. Выяснилось, что стрелка отклонялась в одну сторону при включении тока и в другую, когда ток прерывался. М. Фарадей установил, что «превращать магнетизм в электричество» можно и с помощью обыкновенного магнита.
В это же время американский физик Джозеф Генри также успешно проводил опыты по индукции токов, но пока он собирался опубликовать результаты своих опытов, в печати появилось сообщение М. Фарадея об открытии им электромагнитной индукции.
М. Фарадей стремился использовать открытое им явление, чтобы получить новый источник электричества.
↑ Миллер М. А., Пермитин Г. В. Электромагнитная индукция // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 537—538. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
↑ Faraday, Michael. The philosopher’s tree: a selection of Michael Faraday’s writings / Michael Faraday, P. Day. — CRC Press, 1999-02-01. — P. 71. — ISBN 978-0-7503-0570-9.
↑ Это уравнение Максвелла может быть переписано в эквивалентном виде
∮∂S⁡E→⋅dl→=−∫S∂B→∂t⋅ds→{\displaystyle \oint _{\partial S}{\vec {E}}\cdot {\vec {dl}}=-\int _{S}{\frac {\partial {\vec {B}}}{\partial t}}\cdot {\vec {ds}}}
(здесь просто производная по t внесена под знак интеграла). В таком виде уравнение также может быть включено в систему уравнений Максвелла, причем оговорка о неподвижности контура интегрирования теряет актуальность, так как производная теперь очевидно не действует на границу области (на пределы интегрирования), а само интегрирование в любом случае полагается «мгновенным». В принципе, в таком виде это уравнение также могут называть законом Фарадея (чтобы отличить его от других уравнений Максвелла), пусть в таком виде оно и не совпадает прямо с его обычной формулировкой (но эквивалентно ей в своей области применимости).
↑ М. Лившиц. Закон электромагнитной индукции или «правило потока»? // Квант. — 1998. — № 3. — С. 37—38.
↑ Такой отказ объясняется тем, что, в отличие от закона для циркуляции электрического поля, выполняющегося всегда, «правило» корректно работает лишь для случаев, когда контур, в котором вычисляется ЭДС, совпадает физически с проводником (то есть совпадает их движение; в противном же случае правило может не работать (самый известный пример — униполярная машина Фарадея; контур, который в этом случае трудно определить, но кажется довольно очевидным, что он не меняется; во всяком случае, довольно затруднительно указать разумное определение для контура, который бы в этом случае менялся), то есть проявляется парадокс, что для «закона природы» недопустимо.
ru.wikipedia.org
правило Ленца, уравнения Максвелла в интегральной форме, электромагнитная индукция
В статье расскажем что такое электромагнитная индукция, подробно опишем закон Фарадея и правило Ленца, а так же немного затронем тему уравнений Максвелла.
Электромагнитная индукция
Суть электромагнитной индукции заключается в том, что изменение магнитного поля, покрывающего электрическую цепь, вызывает возникновение электродвижущей силы в этой цепи, которая в случае замкнутой цепи вызывает протекание электрического тока. Если цепь, в которой мы должны генерировать электродвижущую силу, состоит из катушки и прикрепленного к ней амперметра, то источник изменяющегося магнитного поля, который включает в себя катушку, может быть адекватно перемещен постоянным магнитом или движущимся электромагнитом, в котором мы меняем ток питания. В каждом из этих случаев магнитное поле, которое пронизывает катушку, изменяется со временем.
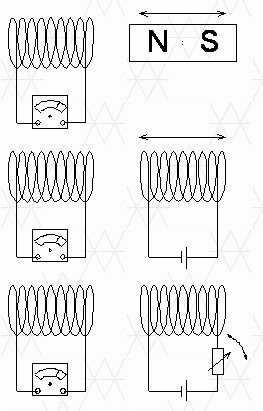
В общем, изменение магнитного потока в цепи амперметра вызывает электрический ток в этой цепи.
Источником индуктивных явлений снова является сила Лоренца F, которая возникает, когда заряд q движется со скоростью v в магнитном поле B
F = q * v * B
Когда направляющая перемещается в поле B, подвижные носители нагрузки будут смещаться под действием силы Лоренца до тех пор, пока в проводнике не появится электрическое поле E, а сила, действующая на носители, F = q * E, уравнивает силу Лоренца. Когда линейный проводник длины l движется с постоянной скоростью v в однородном магнитном поле B, направленном перпендикулярно оси проводника и вектору скорости v , как на чертеже:
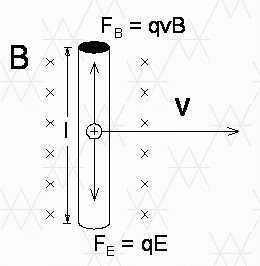
тогда мы сохраним условие баланса между силой Лоренца и силой отталкивания между зарядами в виде уравнения:
q*v*B = q*E ,
следовательно
v*B = E = V / l ,
где V — разность потенциалов на концах проводника длиной l. Следовательно, значение этой разности потенциалов:
Если вектор v не перпендикулярен полю B , но образует с ним угол N , то разность потенциалов на концах направляющей будет:
V = v * B * l * sin θ
Это означает, что перемещение проводника вдоль направления поля B не будет генерировать в нем электродвижущую силу. Нетрудно доказать, что в случае направляющей любой формы разность потенциалов между точками а и b направляющей равна:
Когда прямоугольная рамка со сторонами a и b вращается в однородном магнитном поле B с постоянной угловой скоростью T
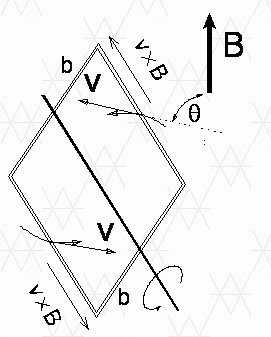
это электродвижущая сила V, генерируемая с обеих сторон рамы:
Магнитные силы, действующие в двух других сторонах петли, перпендикулярны этим сторонам и не влияют на электродвижущую силу. Посредством соответствующего способа получения генерируемого напряжения можно реализовать простейшие модели генераторов переменного тока (а) и постоянного тока (b), как показано на рисунке:
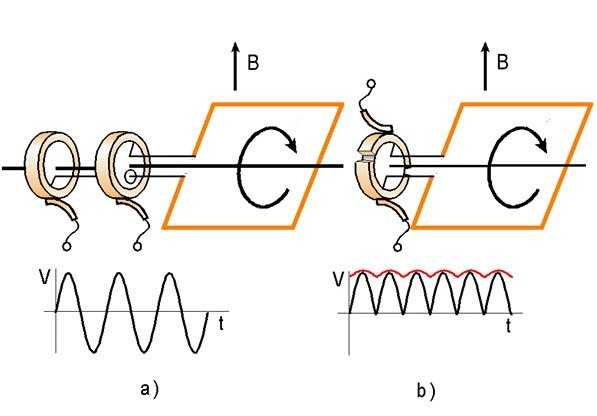
В природе и технике существует огромное количество явлений, вызванных электромагнитной индукцией, то есть генерацией электродвижущей силы в пространстве, где существует изменяющееся магнитное поле. Все эти явления описываются одним замечательным, компактным уравнением, являющимся содержанием закона Фарадея.
Формулы и объяснение закона Фарадея
Большое открытие Майкла Фарадея (1791 — 1867) состояло в том, что он нашел правило, управляющие электромагнитной индукцией. В результате многолетних экспериментов Фарадей заявил, что электродвижущая сила E появляется в проводнике при изменении магнитного поля, окружающего этот проводник, величина генерируемой электродвижущей силы пропорциональна скорости магнитного поля, и что направление индуцированной электродвижущей силы зависит от направления, в котором изменяется магнитное поле. Все эти факты содержатся только в одном уравнении:
где dΦ _B — элементарный поток магнитного поля
В общем случае, даже когда проводников нет, электродвижущая сила равна циркуляции электрического поля E вдоль замкнутого контура:
Таким образом , закон Фарадея может быть записан в обобщенной форме:
Обратите внимание, сколько факторов может изменить значение потока:
1. Изменение значения вектора B ;
2. Изменение значения площади поверхности d A ;
3. Путем изменения угла между B и d А ;
4. Одновременное изменение B и d А ;
5. Одновременное изменение В и угла ;
6. Одновременное изменение d A и угла.
Нельзя не заметить появившийся здесь знак минус! Этот знак минус в законе Фарадея был назван правилом Ленца, который можно понимать как правило неповиновения в электродинамике.
Правило Ленца
Правило Ленца (знак минуса в законе Фарадея) определяет, что индукционный электрический ток в проводнике, возникающий при изменении магнитного потока, направлен таким образом, что его магнитное поле противодействует изменению магнитного потока.
Закон индукции Фарадея вместе с правилом Ленца представляет собой анимацию, в которой движение постоянного магнита вызывает создание электродвижущей силы в катушке, покрытой полем магнита.
Индукционный ток может создаваться не только в обмотках, но и в сплошных металлических блоках, помещенных в изменяющиеся магнитные поля.
Пример: так называемый вихревой ток, схематически показанный на рисунке:
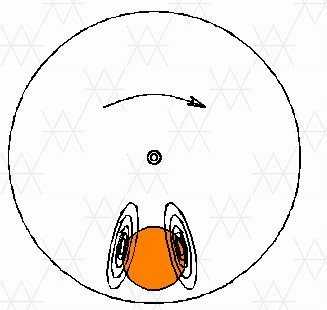
Когда постоянное магнитное поле приложено к вращающейся алюминиевой мишени, то в мишени создаются два семейства противоположно направленных токов. Магнитное поле вихревых токов направлено так, что часть диска, которая выходит из поля, будет втянута обратно в поле, а часть диска, которая входит в область поля, будет вытеснена из этого поля.
Вихревые токи часто нежелательны, например, в сердечниках трансформатора, где они вызывают потери тепла. Для ограничения вихревых токов сердечники трансформатора выполнены в виде стопок из листового металла.
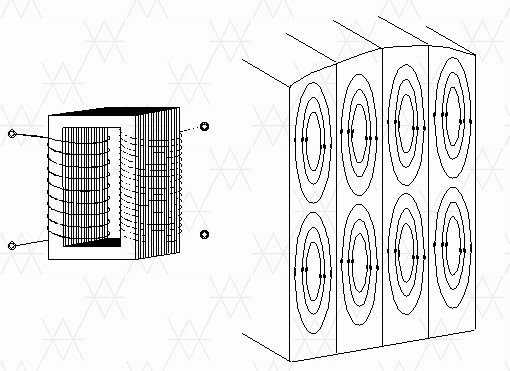
Уравнения Максвелла в интегральной форме
Закон Фарадея содержит: обобщенный закон Ампера, закон Гаусса для электрического поля и закон Гаусса для магнитного поля в системе из четырех уравнений Максвелла. Эти уравнения были представлены применительно к макроскопическим контурам и замкнутым поверхностям. По этой причине мы говорим, что это уравнения Максвелла в интегральной форме. Давайте посмотрим на эти уравнения еще раз.
Закон Фарадея
Обобщенный закон Ампера
Закон Гаусса для электрического поля
Закон Гаусса для магнитного поля
Интегральные уравнения Максвелла описывают электрические и магнитные явления в макроскопическом масштабе. Ведь для их формулировки нужны контуры, замкнутые поверхности, токи и потоки полей. Однако чрезвычайно важно знать, что происходит с электрическими и магнитными полями в отдельных точках, то есть в микроскопическом масштабе. Тогда можно будет описать такие явления как электромагнитные волны.
Для микроскопического описания электрических и магнитных явлений используются уравнения Максвелла в дифференциальной форме. Чтобы получить их, мы применим две математические теоремы к уравнениям в интегральной форме: теорема Гаусса-Остроградского и теорема Стокса.
Следует отметить, что преобразование уравнений Максвелла между целочисленной и дифференциальной формами получается в результате только математических операций. Это означает физическую эквивалентность этих двух форм уравнений Максвелла.
Теорема Гаусса-Остроградского и теорема Стокса, несмотря на их кажущуюся сложность, концептуально совершенно просты и легко интуитивно принимаются. Обе эти тему будут представлены в следующей статье.
meanders.ru
Конспект «Электромагнитная индукция. Опыты Фарадея»
Электромагнитная индукция. Опыты Фарадея
Раздел ОГЭ по физике: 3.13. Электромагнитная индукция. Опыты Фарадея.
Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток. В 1831 г. М. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает индукционный ток. (Индукция в данном случае – появление, возникновение.)
1) Опыт с двумя проволочными спиралями (катушками). Одна из таких спиралей присоединялась к гальванометру, который регистрировал слабые токи. Вторая спираль сообщалась с гальванической батареей. В момент замыкания и размыкания цепи второй катушки индикаторная стрелка гальванометра обязательно отклонялась.
2) Опыт по взаимодействию магнита и катушки с током: при внесении магнита в катушку в цепи возникает электрический ток, при вынесении также возникает ток, но другого направления. Сила тока зависит от скорости внесения (вынесения) магнита.
Явление возникновения электрического поля при изменении магнитного поля называется электромагнитной индукцией.
Индукционный ток в катушке возникает при:
перемещении постоянного магнита относительно катушки;
перемещении электромагнита относительно катушки;
перемещении сердечника относительно электромагнита, вставленного в катушку;
регулировании тока в цепи электромагнита;
замыкании и размыкании цепи.
Если в изменяющееся магнитное поле поместить замкнутый проводящий контур, то появление тока в контуре свидетельствует о действии в контуре сторонних электрических сил (или о возникновении в контуре ЭДС индукции).
Явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного поля, пронизывающего контур, является следствием электромагнитной индукции.
Основные области применения электромагнитной индукции: генерирование тока (индукционные генераторы на всех электростанциях, динамо-машины), трансформаторы.

Конспект урока по физике 8 класса «Электромагнитная индукция. Опыты Фарадея».
Следующая тема: Электромагнитные колебания и волны.

uchitel.pro
ФАРАДЕЙ. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ. Максвелл
ФАРАДЕЙ. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
Одержимый идеями о неразрывной связи и взаимодействии сил природы, Фарадей пытался доказать, что точно так же, как с помощью электричества Ампер мог создавать магниты, так же и с помощью магнитов можно создавать электричество.
Логика его была проста: механическая работа легко переходит в тепло; наоборот, тепло можно преобразовать в механическую работу (скажем, в паровой машине). Вообще, среди сил природы чаще всего случается следующее соотношение: если А рождает Б, то и Б рождает А.
Если с помощью электричества Ампер получал магниты, то, по-видимому, возможно «получить электричество из обычного магнетизма». Такую же задачу поставили перед собой Араго и Ампер в Париже, Колладон — в Женеве.
Фарадей ставит множество опытов, ведет педантичные записи. Каждому небольшому исследованию он посвящает параграф в лабораторных записях (изданы в Лондоне полностью в 1931 году под названием «Дневник Фарадея»). О работоспособности Фарадея говорит хотя бы тот факт, что последний параграф «Дневника» помечен номером 16041. Блестящее мастерство Фарадея-экспериментатора, одержимость, четкая философская позиция не могли не быте вознаграждены, но ожидать результата пришлось долгих одиннадцать лет.
Кроме интуитивной убежденности во всеобщей связи явлений, его, собственно, в поисках «электричества из магнетизма» ничто не поддерживало. К тому же он, как его учитель Дэви, больше полагался на свои опыты, чем на мысленные построения. Дэви учил его:
— Хороший эксперимент имеет больше ценности, чем глубокомыслие такого гения, как Ньютон.
И тем не менее именно Фарадею суждены были великие открытия. Великий реалист, он стихийно рвал путы эмпирики, некогда навязанные ему Дэви, и в эти минуты его осеняло великое прозрение — он приобретал способность к глубочайшим обобщениям.
Первый проблеск удачи появился лишь 29 августа 1831 года. В этот день Фарадей испытывал в лаборатории несложное устройство: железное кольцо диаметром около шести дюймов, обмотанное двумя кусками изолированной проволоки. Когда Фарадей подключил к зажимам одной обмотки батарею, его ассистент, артиллерийский сержант Андерсен, увидел, как дернулась стрелка гальванометра, подсоединенного к другой обмотке.
Дернулась и успокоилась, хотя постоянный ток продолжал течь по первой обмотке. Фарадей тщательно просмотрел все детали этой простой установки — все было в порядке.
Но стрелка гальванометра упорно стояла на нуле. С досады Фарадей решил выключить ток, и тут случилось чудо — во время размыкания цепи стрелка гальванометра опять качнулась и опять застыла на нуле!
Фарадей был в недоумении: во-первых, почему стрелка ведет себя так странно? Во-вторых, имеют ли отношение замеченные им всплески к явлению, которое он искал?
Вот тут-то и открылись Фарадею во всей ясности великие идеи Ампера — связь между электрическим током и магнетизмом. Ведь первая обмотка, в которую он подавал ток, сразу становилась магнитом. Если рассматривать ее как магнит, то эксперимент 29 августа показал, что магнетизм как будто бы рождает электричество. Только две вещи оставались в этом случае странными: почему всплеск электричества при включении электромагнита стал быстро сходить на нет? И более того, почему всплеск появляется при выключении магнита?
На следующий день, 30 августа, — новая серия экспериментов. Эффект ясно выражен, но тем не менее абсолютно непонятен.
Фарадей чувствует, что открытие где-то рядом.
23 сентября он пишет своему другу Р.Филиппсу:
«Я теперь опять занимаюсь электромагнетизмом и думаю, что напал на удачную вещь, но не могу еще утверждать это. Очень может быть, что после всех моих трудов я в конце концов вытащу водоросли вместо рыбы».
К следующему утру, 24 сентября, Фарадей подготовил много различных устройств, в которых основными элементами были уже не обмотки с электрическим током, а постоянные магниты. И эффект тоже существовал! Стрелка отклонялась и сразу же устремлялась на место. Это легкое движение происходило при самых неожиданных манипуляциях с магнитом, иной раз, казалось, случайно.
Следующий эксперимент — 1 октября. Фарадей решает вернуться к самому началу — к двум обмоткам: одной с током, другой — подсоединенной к гальванометру. Различие с первым экспериментом — отсутствие стального кольца — сердечника. Всплеск почти незаметен. Результат тривиален. Ясно, что магнит без сердечника гораздо слабее магнита с сердечником. Поэтому и эффект выражен слабее.
Фарадей разочарован. Две недели он не подходит к приборам, размышляя о причинах неудачи.
Эксперимент триумфальный — 17 октября.
Фарадей заранее знает, как это будет. Опыт удается блестяще.
«Я взял цилиндрический магнитный брусок (3/4 дюйма в диаметре и 8 1/4 дюйма длиной) и ввел один его конец внутрь спирали из медной проволоки (220 футов длиной), соединенной с гальванометром. Потом я быстрым движением втолкнул магнит внутрь спирали на всю его длину, и стрелка гальванометра испытала толчок. Затем я так же быстро вытащил магнит из спирали, и стрелка опять качнулась, но в противоположную сторону. Эти качания стрелки повторялись всякий раз, как магнит вталкивался или выталкивался».
Секрет — в движении магнита! Импульс электричества определяется не положением магнита, а движением!
Это значит, что «электрическая волна возникает только при движении магнита, а не в силу свойств, присущих ему в покое».
Эта идея необыкновенно плодотворна. Если движение магнита относительно проводника создает электричество, то, видимо, и движение проводника относительно магнита должно рождать электричество! Причем эта «электрическая волна» не исчезнет до тех пор, пока будет продолжаться взаимное перемещение проводника и магнита. Значит, есть возможность создать генератор электрического тока, действующий сколь угодно долго, лишь бы продолжалось взаимное движение проволоки и магнита!
28 октября Фарадей установил между полюсами подковообразного магнита вращающийся медный диск, с которого при помощи скользящих контактов (один на оси, другой — на периферии диска) можно было снимать электрическое напряжение. Это был первый электрический генератор, созданный руками человека.
После «электромагнитной эпопеи» Фарадей был вынужден прекратить на несколько лет свою научную работу — настолько была истощена его нервная система…
Опыты, аналогичные фарадеевским, как уже говорилось, проводились во Франции и в Швейцарии. Профессор Женевской академии Колладон был искушенным экспериментатором (он, например, произвел на Женевском озере точные измерения скорости звука в воде). Может быть, опасаясь сотрясения приборов, он, как и Фарадей, по возможности удалил гальванометр от остальной установки. Многие утверждали, что Колладон наблюдал те же мимолетные движения стрелки, что и Фарадей, но, ожидая более стабильного, продолжительного эффекта, не придал этим «случайным» всплескам должного значения…
Действительно, мнение большинства ученых того времени сводилось к тому, что обратный эффект «создания электричества из магнетизма» должен, по-видимому, иметь столь же стационарный характер, как и «прямой» эффект — «образование магнетизма» за счет электрического тока. Неожиданная «мимолетность» этого эффекта сбила с толку многих, в том числе Колладона, и эти многие поплатились за свою предубежденность.
Фарадея тоже поначалу смущала мимолетность эффекта, но он больше доверял фактам, чем теориям, и в конце концов пришел к закону электромагнитной индукции. Этот закон казался тогда физикам ущербным, уродливым, странным, лишенным внутренней логики.
Почему ток возбуждается только во время движения магнита или изменения тока в обмотке?
Этого не понимал никто. Даже сам Фарадей. Понял это через семнадцать лет двадцатишестилетний армейский хирург захолустного гарнизона в Потсдаме Герман Гельмгольц. В классической статье «О сохранении силы» он, формулируя свой закон сохранения энергии, впервые доказал, что электромагнитная индукция должна существовать именно в этом «уродливом» виде.
Независимо к этому пришел и старший друг Максвелла, Вильям Томсон. Он тоже получил электромагнитную индукцию Фарадея из закона Ампера при учете закона сохранения энергии.
Так «мимолетная» электромагнитная индукция приобрела права гражданства и была признана физиками.
Но она никак не укладывалась в понятия и аналогии статьи Максвелла «О фарадеевских силовых линиях». И это было серьезным недостатком статьи. Практически ее значение сводилось к иллюстрации того, что теории близко— и дальнодействия представляют различное математическое описание одних и тех же экспериментальных данных, что силовые линии Фарадея не противоречат здравому смыслу. И это все. Все, хотя это было уже очень много.
Поделитесь на страничке
Следующая глава >
biography.wikireading.ru
Закон Фарадея для электромагнитной индукции в трансформаторах
Электричество обладает способностью генерировать магнитное поле. В 1831 году М. Фарадей ввел понятие электромагнитная индукция. Он смог получить в закрытой системе проводников электричество, появляющееся при изменении показателей магнитного потока. Формула закона Фарадея дала толчок для развития электродинамики.
История развития
После доказательства закона электромагнитной индукции английским ученым М. Фарадеем над открытием работали российские ученые Э. Ленц и Б. Якоби. Благодаря их трудам, сегодня разработанный принцип положен в основу функционирования многих приборов и механизмов.
Основными агрегатами, в которых применяется закон электромагнитной индукции Фарадея, являются двигатель, трансформатор и множество иных приборов.
Индукцией электромагнитно именуется индуцирование в замкнутой проводящей системе электрического тока. Такое явление становится возможным при физическом передвижении через проводниковую систему магнитного поля. Механическое действие влечет за собой появление электричества. Его принято называть индукционным. До открытия закона Фарадея человечество не знало об иных способах создания электричества, кроме гальваники.
Если сквозь проводник пропустить магнитное поле, в нем будет возникать ЭДС индукции. Ее еще именуют электродвижущей силой. При помощи этого открытия удается представить в количественном выражении показатель.
Опытное доказательство
Проводя свои исследования, английский ученый установил, что индукционный ток получается одним из двух способов. В первом опыте он появляется при движении рамки в магнитном поле, создаваемом неподвижной катушкой. Второй способ предполагает неподвижное положение рамки. В этом эксперименте изменяется только поле катушки при ее движении или изменении силы тока в ней.
Опыты Фарадея привели исследователя к выводу, что при генерировании индукционного тока провоцируется увеличением или уменьшением магнитного потока в системе. Также опыты Фарадея позволили утверждать, что значение электричества, полученного опытным путем, не зависит от методологии, которой был изменен поток магнитной индукции. На показатель влияет только скорость такого изменения.
Количественное выражение
Установить количественное значение явления электромагнитной индукции позволяет закон Фарадея. Он гласит, что ЭДС, определяющаяся в системе, меняет значение пропорционально скорости перемещения потока в проводнике. Формула будет иметь такой вид:
Отрицательный знак свидетельствует о том, что ЭДС препятствует появлению изменений внутри контура. Для решения некоторых задач отрицательный знак в формуле не ставят. В этом случае результат записывают в виде модуля.
Система может включать в себя несколько витков. Количество их обозначается латинской буквой N. Все элементы контура пронизываются единым магнитным потоком. ЭДС индукции будет рассчитываться так:
Понятным примером воссоздания электричества в проводнике считается катушка, сквозь которую перемещается постоянный магнит.
Работа Э. Ленца
Направленность индукционного тока предоставляет возможность определить правило Ленца. Краткая формулировка звучит достаточно просто. Появляющийся при изменении показателей поля проводникового контура ток, препятствует благодаря своему магнитному полю такому изменению.
Если в катушку постепенно вводить магнит, в ней повышается уровень магнитного потока. Согласно правилу Ленца, магнитное поле будет иметь направление противоположное увеличению поля магнита. Чтобы понять эту направленность, необходимо смотреть на магнит с северной стороны. Отсюда будет вкручиваться буравчик навстречу северному полюсу. Ток будет перемещаться в сторону движения часовой стрелки.
Если магнит выводится из системы, магнитный поток в ней уменьшится. Чтобы установить направление тока, выкручивается буравчик. Вращения будет направлено в обратную сторону перемещения по циферблату часовой стрелки.
Формулировки Ленца приобретают большое значение для системы с контуром замкнутого типа и отсутствующим сопротивлением. Его принято именовать идеальным контуром. По правилу Ленца, в нем невозможно увеличить или уменьшить магнитный поток.
Понятие самоиндукции
Генерация индукции в идеальной системе, которое имеет место при падении или возрастании электричества в проводнике, именуется самоиндукцией.
Закон Фарадея для самоиндукции выражается равенством, когда при изменении электричества не произошло иных изменений:
где е – ЭДС, L – индуктивность закрытой катушки, ΔI/Δt – скорость, с которой происходят изменения силы тока.
Индуктивность
Отношение, которое показывает пропорциональность между такими категориями, как сила тока в проводящей системе и магнитным потоком именуется индуктивностью. На показатель имеет влияние физические габариты катушки и магнитные характеристики среды. Отношение описывается формулой:
Движущееся в контуре электричество провоцирует появление магнитного поля. Оно пронизывает собственный проводник и влечет появление своего потока сквозь контур. Причем собственный поток пропорционален электричеству, которая его порождает:
Фс = L*I
Значение индуктивности также формируется из закона Фарадея.
Недвижимая система
Сила Лоренца объясняет возникновение ЭДС при движении системы в поле со значением постоянным. Индукционная ЭДС имеет способность возникать и при неподвижной проводящей системе, находящейся в переменном магнитном поле. Сила Лоренца в таком примере не способна объяснить появление ЭДС индукции.
Максвелл для проводящих систем неподвижного типа предложил применять особое уравнение. Оно объясняет возникновение в таких системах ЭДС. Главным принципом закона Фарадея-Максвелла является факт, что переменное поле образует в пространстве вокруг себя электрическое поле. Оно выступает фактором, провоцирующим появление тока индукции в недвижимой системе. Перемещение вектора (Е) по стационарным контурам (L) является ЭДС:
При наличии тока переменного значения законы Фарадея водятся в уравнения Максвелла. Причем они могут быть представлены как в дифференциальной форме, так и в виде интегралов.
Труды в области электролиза
При использовании законов Фарадея описываются закономерности, которые существуют при электролизе. Этот процесс заключается в превращении веществ с разнообразными характеристиками. Это происходит при движении электричества сквозь электролит.
Эти закономерности были доказаны М. Фарадеем в 1834 году. Первое утверждение гласит, что масса вещества, которое образуется на электроде, меняется соответственно заряду, перемещенному сквозь электролит.
Второе утверждение гласит, что эквиваленты компонентов с разными характеристиками пропорциональны химическим эквивалентам этих компонентов.
Оба представленных утверждения совмещаются в объединенный закон Фарадея. Из него следует, что число Фарадея будет равняться электричеству, способному выделить на электролите 1 моль вещества. Ее рассчитывают на единицу валентности. Именно по объединенной формуле в далеком 1874 году был вычислен заряд электрона.
Законы электролиза, установленные Фарадеем, тестировались при различном значении тока, температуры, давления, а также при одновременном выделении двух и более веществ. Электролиз также проводился в разных расплавах и растворителях. Концентрация электролита также отличалась в разных опытах. При этом иногда наблюдались небольшие отклонения от закона Фарадея. Они объясняются электронной проводимостью электролитов, которая определяется наравне с ионной проводимостью.
Открытия, сделанные английским физиком М. Фарадеем, позволили описать множество явлений. Его законы являются основой современной электродинамики. По этому принципу функционирует различное современное оборудование.
protransformatory.ru
No related posts.