Формула напряженности электрического поля – Напряжённость электрического поля — Википедия

Основные законы и формулы

58

ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК

Закон Кулона:

,

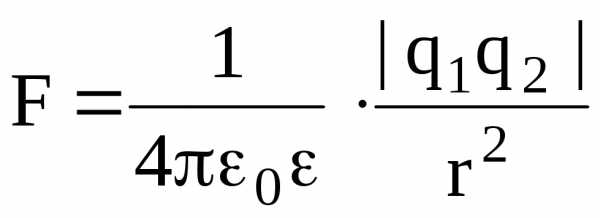где F – сила взаимодействия двух точечных зарядов q₁ и q₂; r – расстояние между зарядами;  — диэлектрическая проницаемость среды; ₀ — электрическая постоянная

.

Закон сохранения заряда:

,

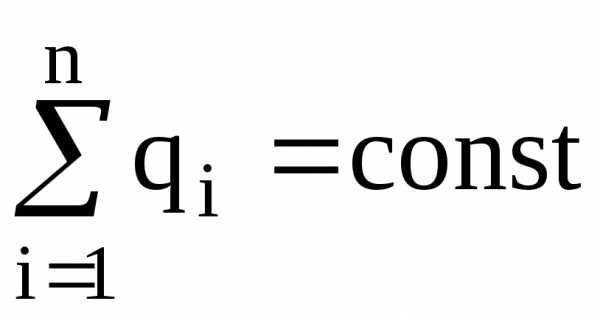где 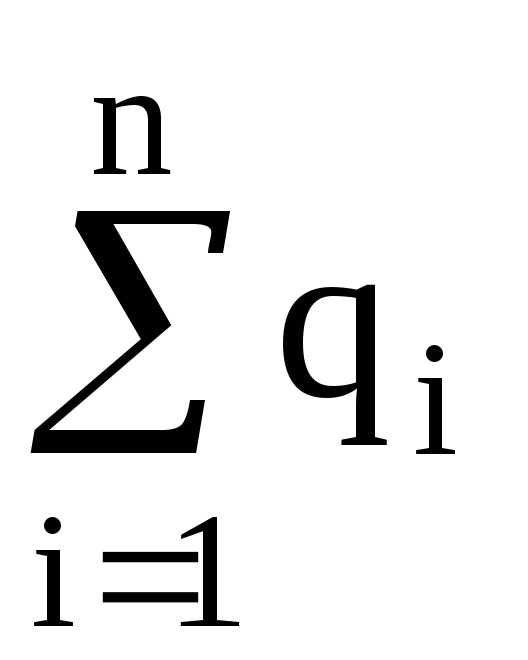– алгебраическая сумма зарядов, входящих в изолированную систему;n – число зарядов.

Напряженность и потенциал электростатического поля:

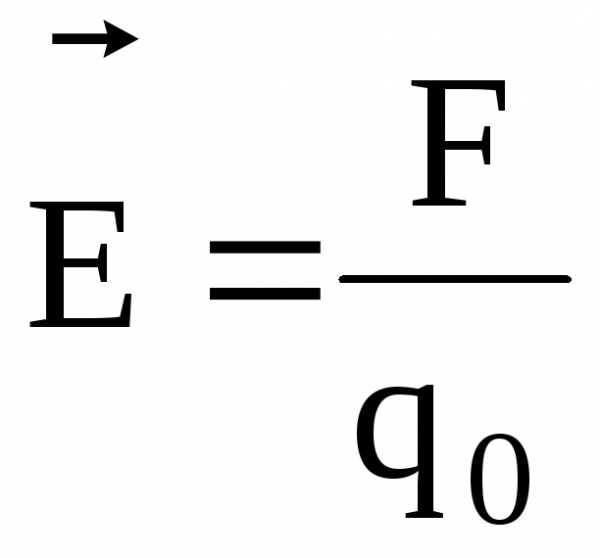
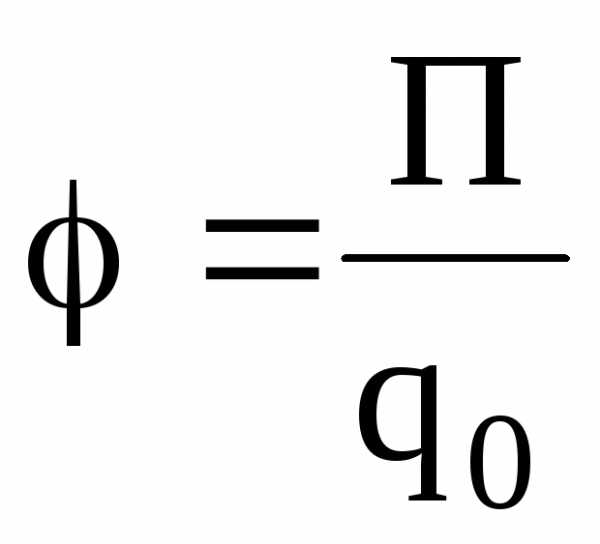; , или,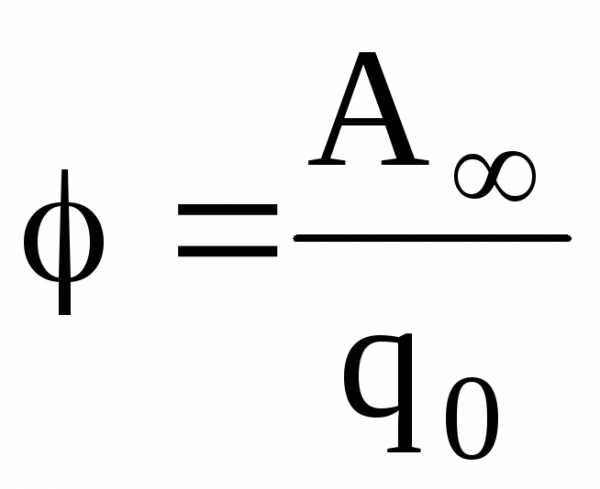

где – сила, действующая на точечный положительный зарядq₀, помещенный в данную точку поля; П – потенциальная энергия заряда; А_∞ — работа, затраченная на перемещение заряда q₀ из данной точки поля в бесконечность.

Поток вектора напряженности электрического поля:

а) через произвольную поверхность S, помещенную в неоднородное поле:

, или ,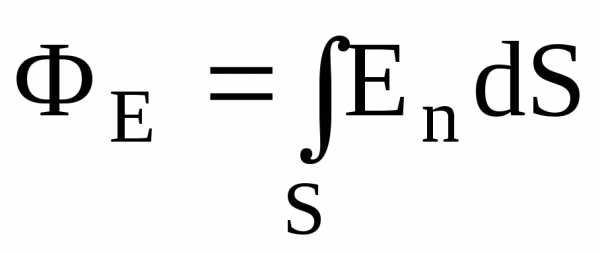

где  – угол между вектором напряженности

и нормальюк элементу поверхности;dS – площадь элемента поверхности; E_n – проекция вектора напряженности на нормаль;

б) через плоскую поверхность, помещенную в однородное электрическое поле:

.

Поток вектора напряженности через замкнутую поверхность –

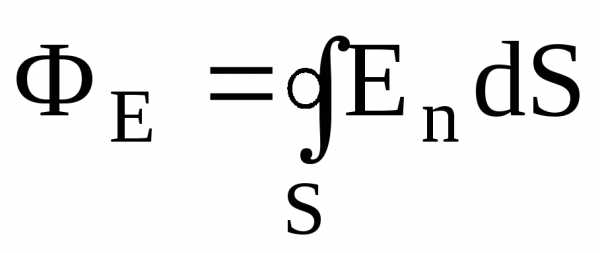
(интегрирование ведется по всей поверхности).

Теорема Остроградского-Гаусса. Поток вектора напряженностичерез любую замкнутую поверхность, охватывающую зарядыq1,q2, …,qn, –

,

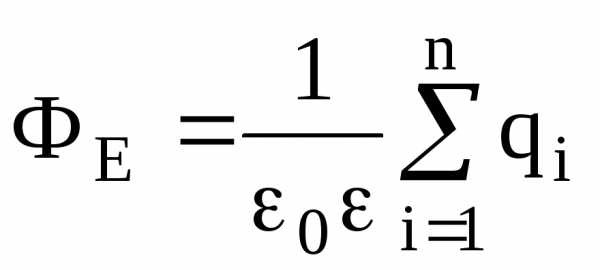где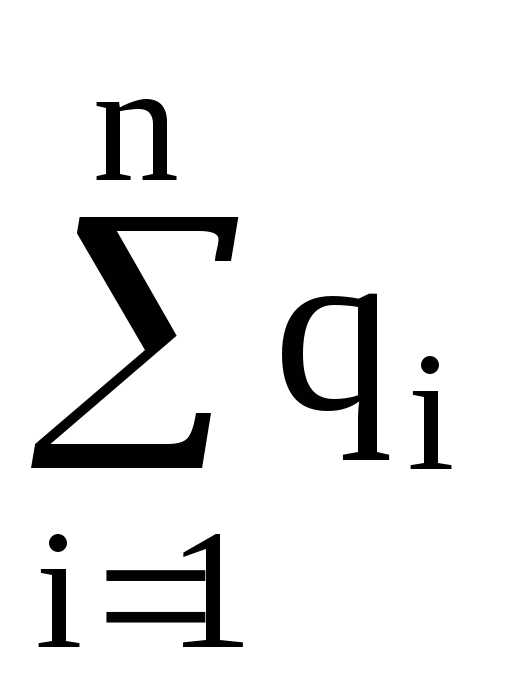

– алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; n – число зарядов.

Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –

.

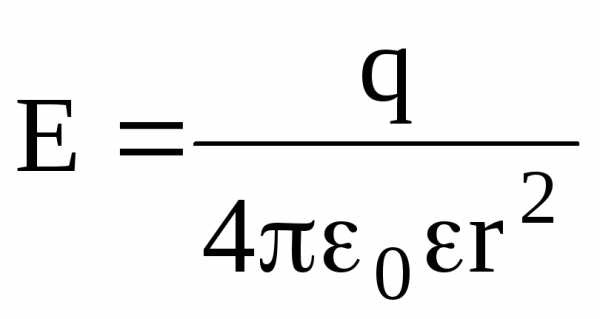Напряженность электрического поля, создаваемого сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы такова:

внутри сферы (r R) Е=0;

на поверхности сферы (r=R) ;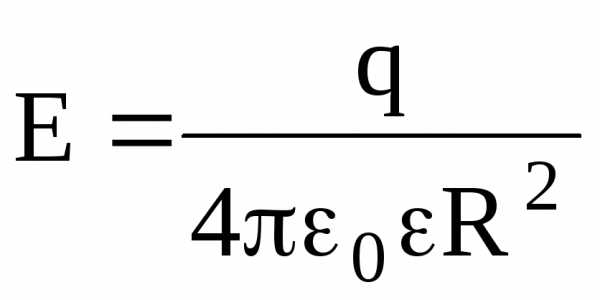

вне сферы (r  R) .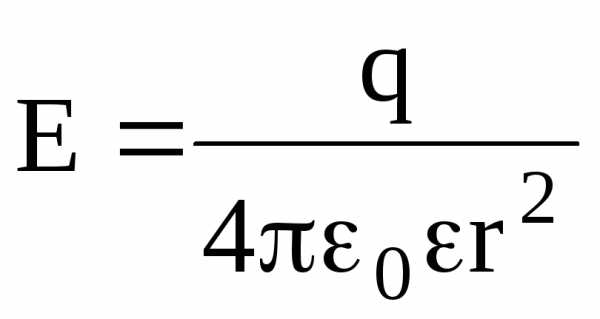

Принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность

результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей, выражается формулой

.

В случае двух электрических полей с напряженностями 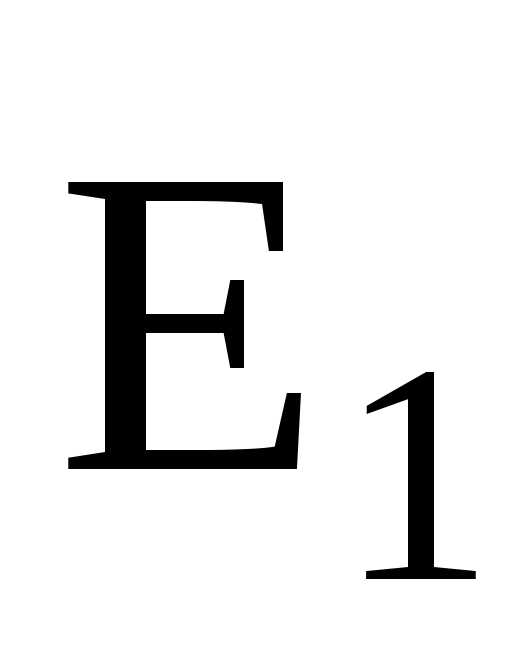иабсолютное значение вектора напряженности составляет

,

где  — угол между векторами 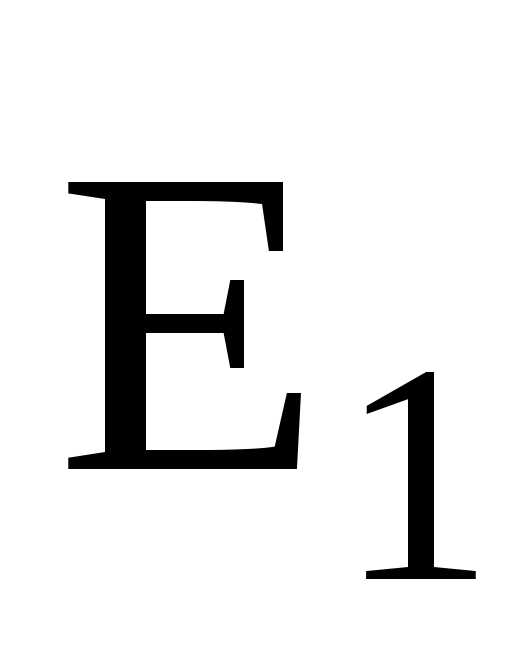и.

Напряженность поля, создаваемого бесконечно длинной и равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси, –

,

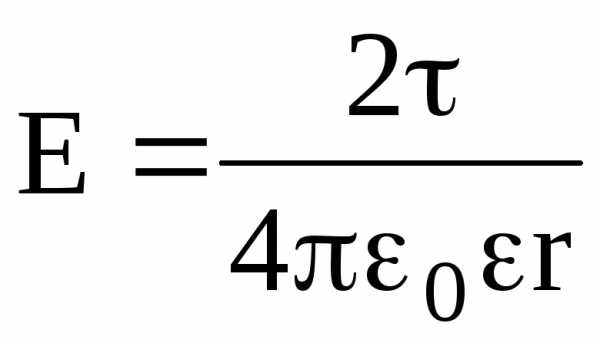где  — линейная плотность заряда.

Линейная плотность заряда есть величина, равная его отношению к длине нити (цилиндра):

.

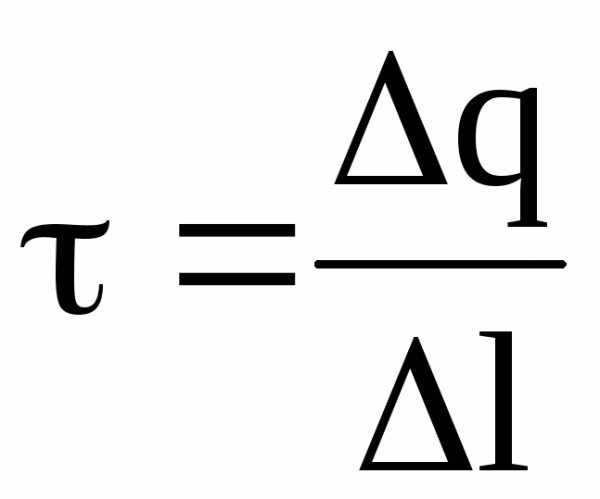Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, –

,

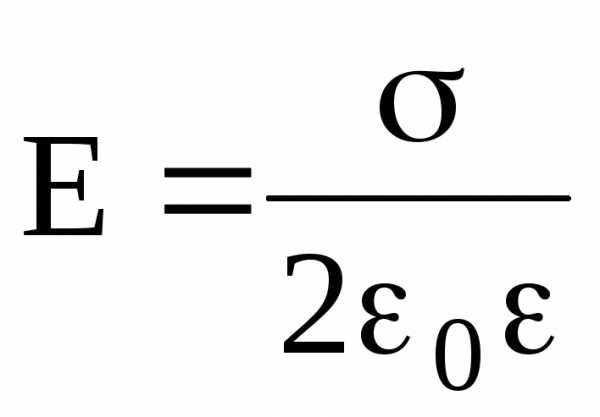где  — поверхностная плотность заряда.

Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к ее площади:

.

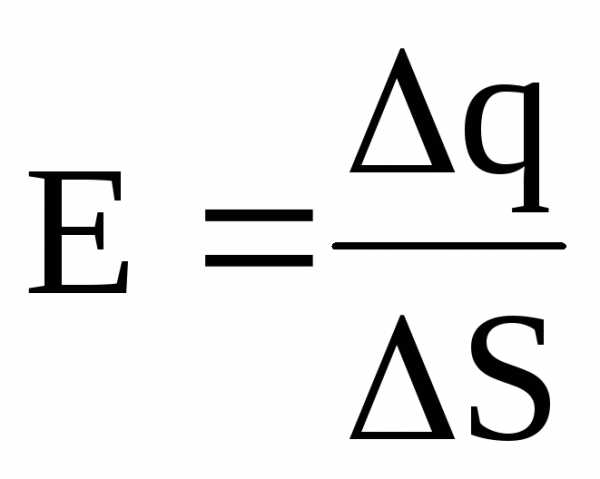Напряженность поля, создаваемого двумя бесконечными и параллельными плоскостями, заряженными равномерно и разноименно, с одинаковой по абсолютному значению поверхностной плотностью заряда (поле плоского конденсатора) –

.

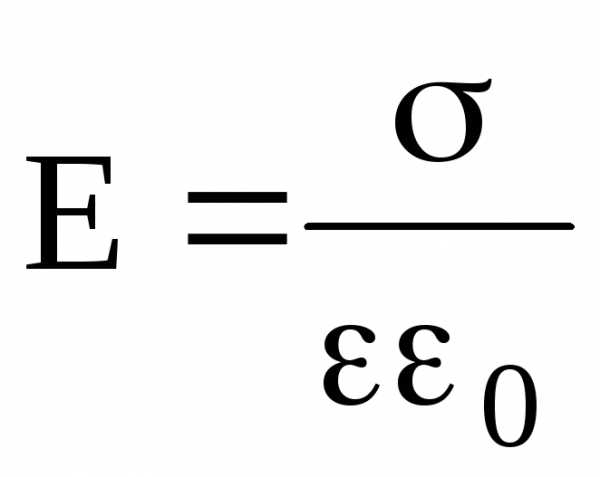Приведенная формула справедлива при вычислении напряженности поля между пластинами плоского конденсатора (в его средней части) только в том случае, если расстояние между пластинами намного меньше линейных размеров пластин конденсатора.

Электрическое смещение связано с напряженностьюэлектрического поля соотношением

,

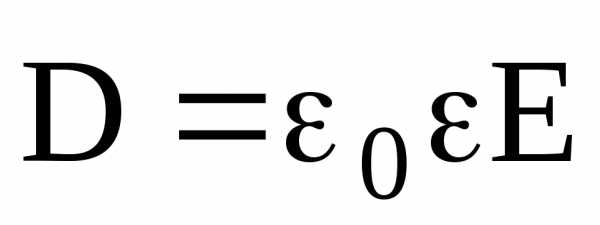которое справедливо только для изотропных диэлектриков.

Потенциал электрического поля есть величина, равная отношению потенциальной энергии и точечного положительного заряда, помещенного в данную точку поля:

.

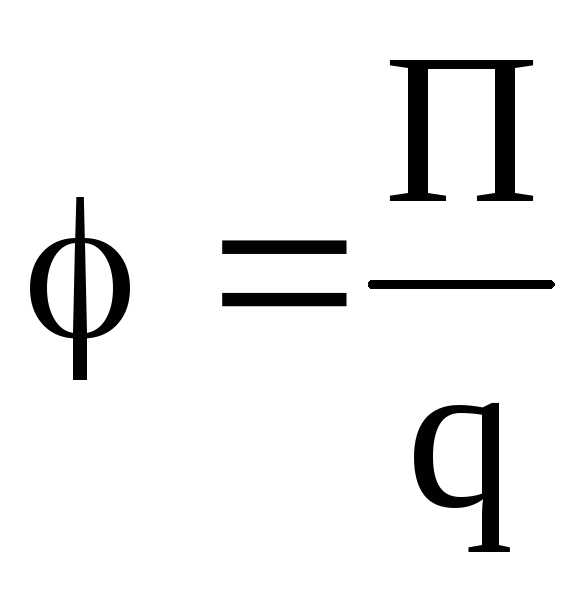Иначе говоря, потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к величине этого заряда:

.

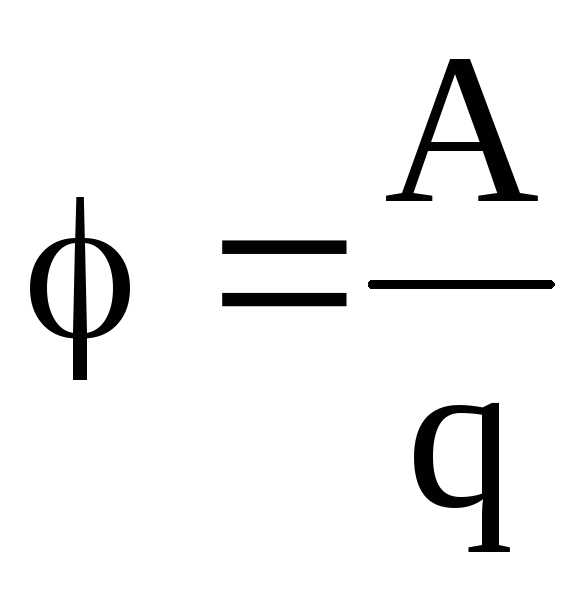Потенциал электрического поля в бесконечности условно принят равным нулю.

Потенциал электрического поля, создаваемый точечным зарядом q на

расстоянии r от заряда, –

.

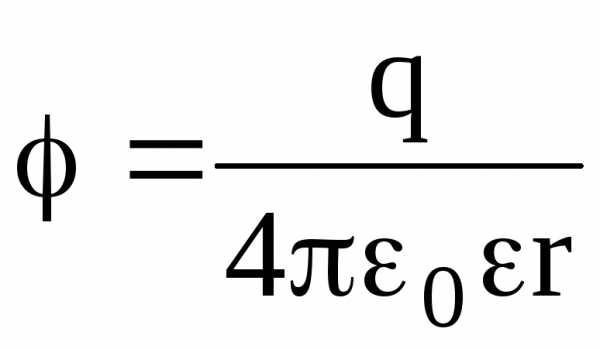Потенциал электрического поля, создаваемый металлической сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы таков:

внутри сферы (r  R)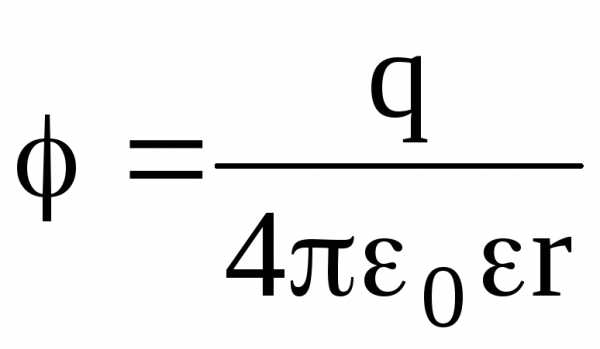

;

на поверхности сферы (r = R) ;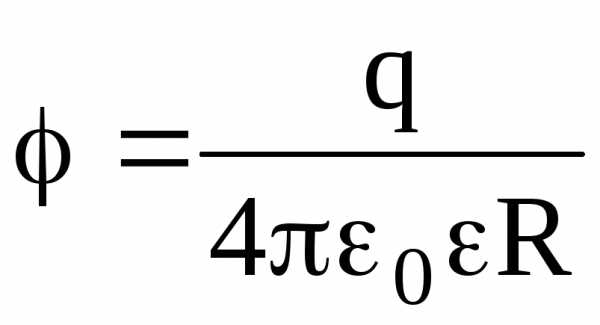

вне сферы (r  R) .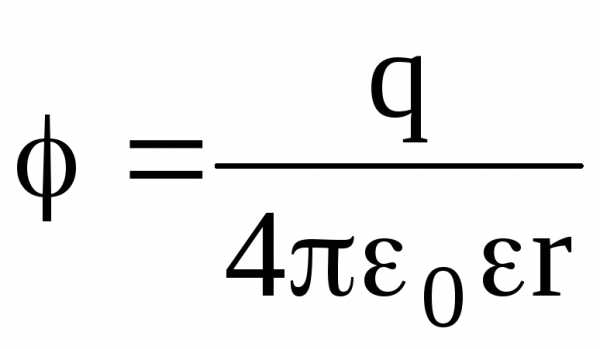

Во всех формулах, приведенных для потенциала заряженной сферы,  есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.

Потенциал электрического поля, образуемого системой n точечных зарядов в данной точке в соответствии с принципом суперпозиции электрических полей, равен алгебраической сумме потенциалов , создаваемых отдельными точечными зарядами:

.

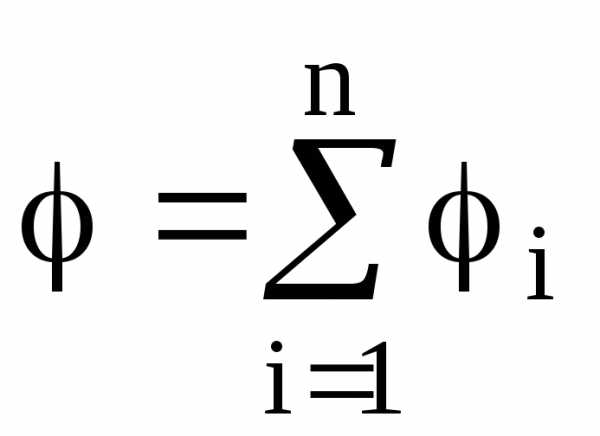Энергия W взаимодействия системы точечных зарядов определяется работой, которую эта система может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой

,

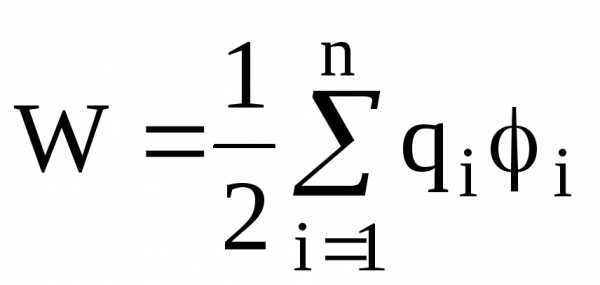где — потенциал поля, создаваемый всеми (n-1) зарядами (за исключением i-го) в точке, где находится заряд .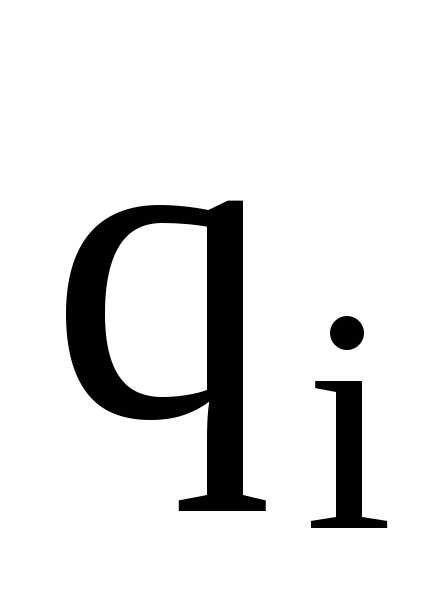

Потенциал связан с напряженностью электрического поля соотношением

.

В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой

,

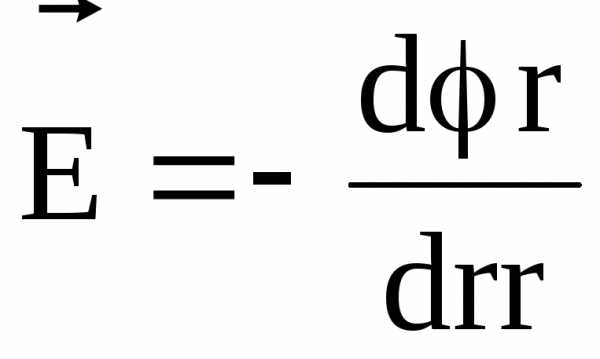или в скалярной форме

.

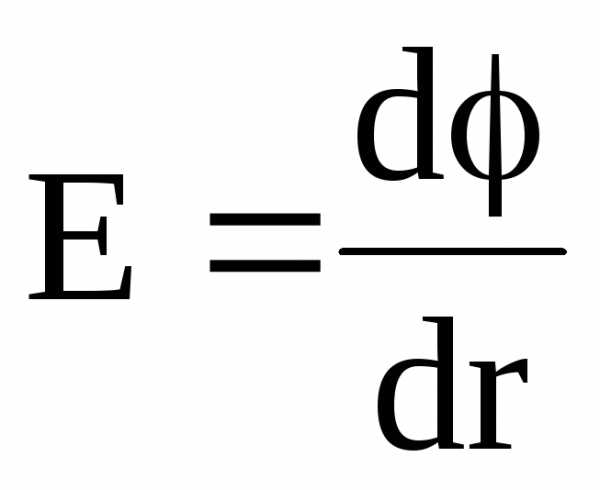
В случае однородного поля, т.е. поля, напряженность которого в каждой его точке одинакова как по абсолютному значению, так и по направлению, –

,

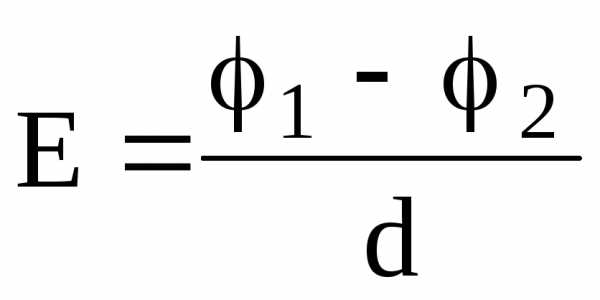где ₁ и ₂ – потенциалы точек двух эквипотенциальных поверхностей; d — расстояние между этими поверхностями вдоль электрической силовой линии.

Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал ₁, в другую, имеющую потенциал ₂, равна

, или ,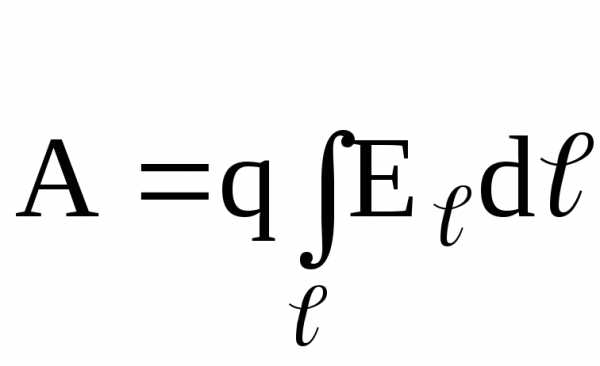

где E – проекция вектора

на направление перемещения;— перемещение.

В случае однородного поля последняя формула принимает вид

,

где 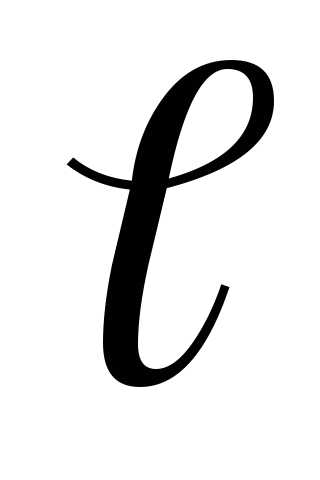– перемещение; — угол между направлениями вектора и перемеще-ния.

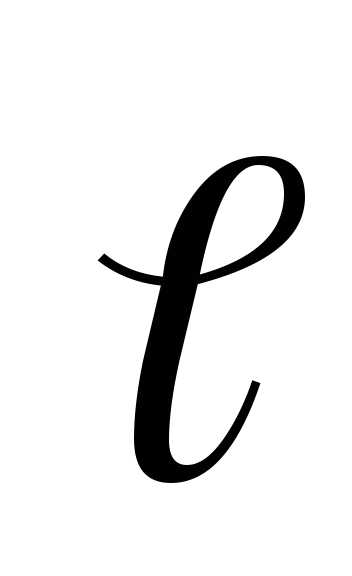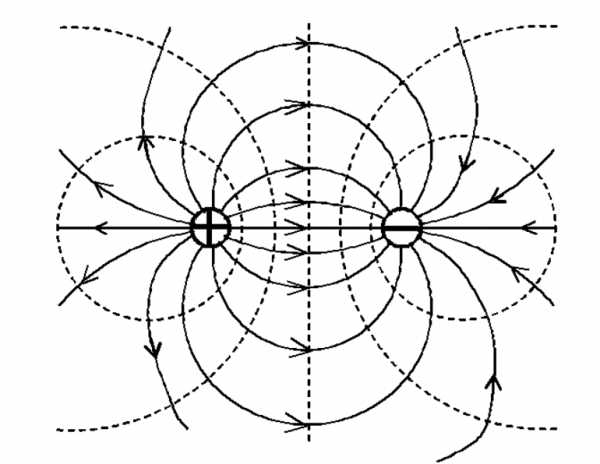
Диполь есть система двух точечных (равных по абсолютному значению и противоположных по знаку) зарядов, находящихся на некотором расстоянии друг от друга.

Электрический момент 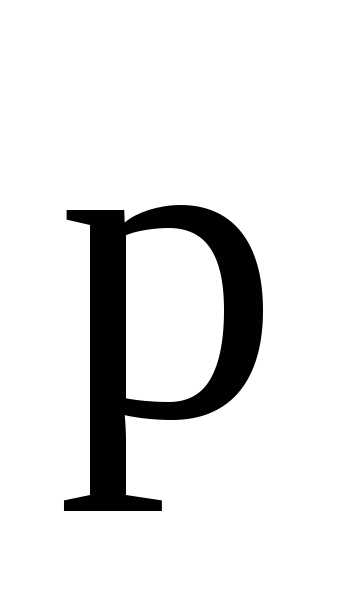диполя есть вектор, направленный от отрицательного заряда к положительному, равный произведению заряда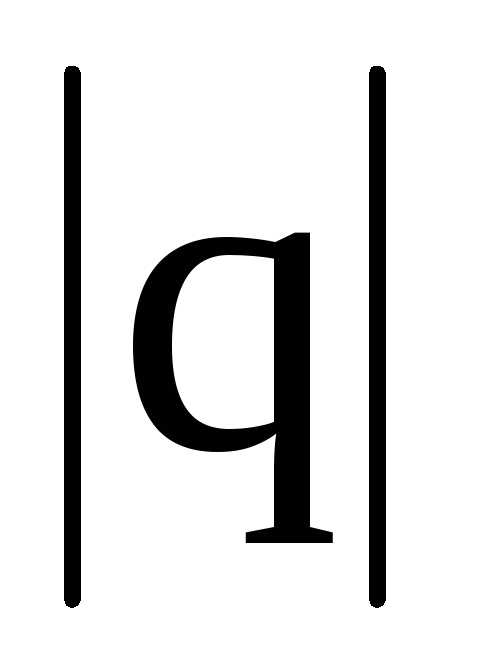на вектор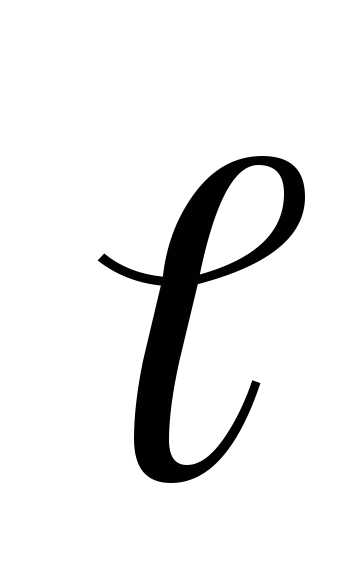, проведенный от отрицательного заряда к положительному, и называемый плечом диполя, т.е.

.

Диполь называется точечным, если его плечо 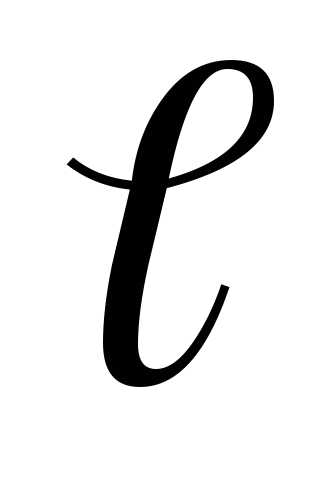намного меньше расстоянияr от центра диполя до точки, в которой нас интересует действие диполя (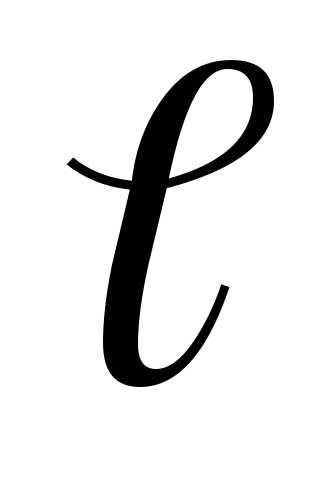 r), см. рис. 1.

Рис. 1

Напряженность поля точечного диполя:

,

где р – электрический момент диполя; r – абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует;  — угол между радиус-вектором и плечомдиполя.

Напряженность поля точечного диполя в точке, лежащей на оси диполя

(=0), находится по формуле

;

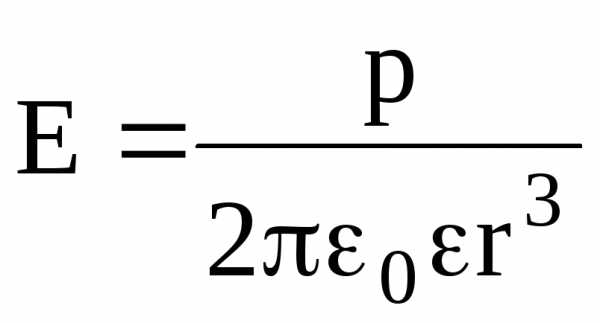в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины , – по формуле

.

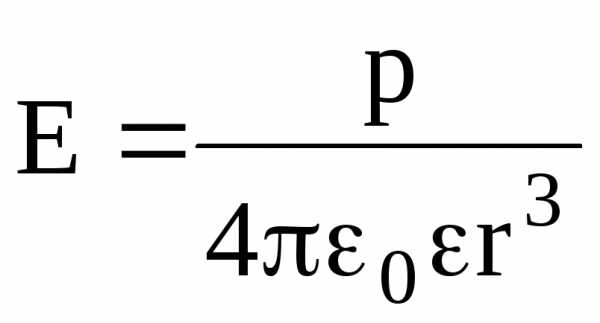Потенциал поля точечного диполя в точке, лежащей на оси диполя (=0), составляет

,

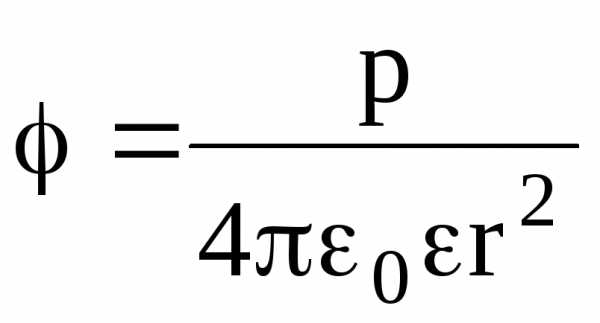а в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины , –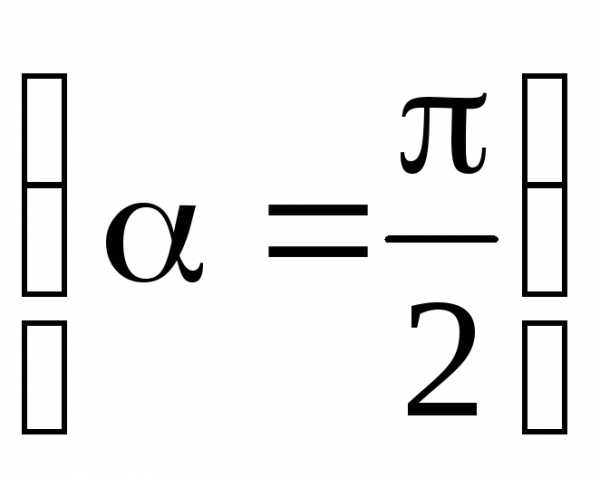

=0.

Напряженность и потенциал неточечного диполя определяются так же как и для системы зарядов.

Механический момент, действующий на диполь с электрическим моментом р, помещенный в однородное электрическое поле с напряженностью Е, –

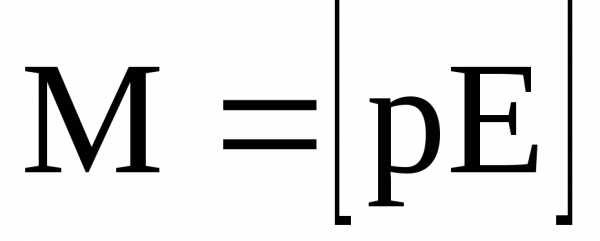, или ,

где  — угол между направлениями векторов 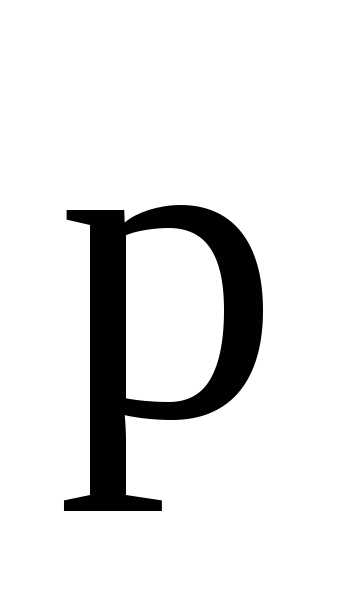и.

Электроемкость уединенного проводника или конденсатора –

,

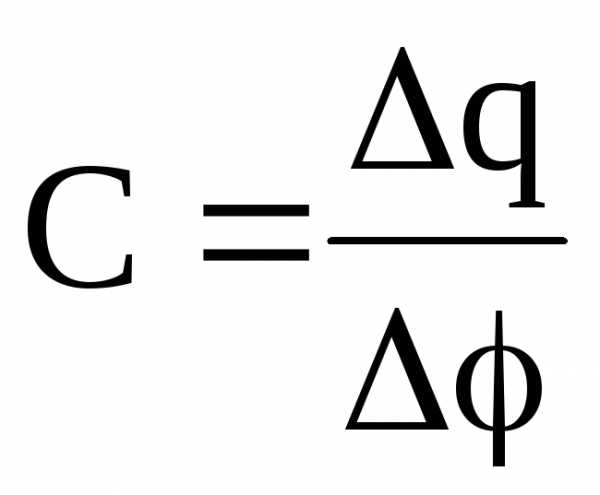где q – заряд, сообщенный проводнику; — изменение потенциала, вызванное этим зарядом.

Электроемкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью , –

.

Если сфера полая и заполнена диэлектриком, то ее электроемкость при этом не изменяется.

Электроемкость плоского конденсатора:

,

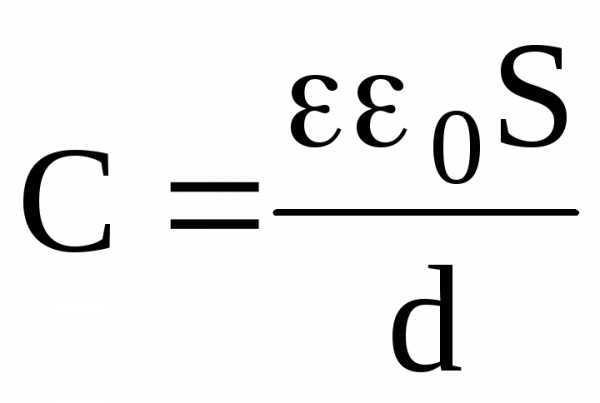где S – площадь каждой пластины конденсатора; d – расстояние между пластинами;  — диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Электроемкость плоского конденсатора, заполненного n слоями диэлектрика толщиной d_i и диэлектрической проницаемостью _i каждый (слоистый конденсатор), составляет

.

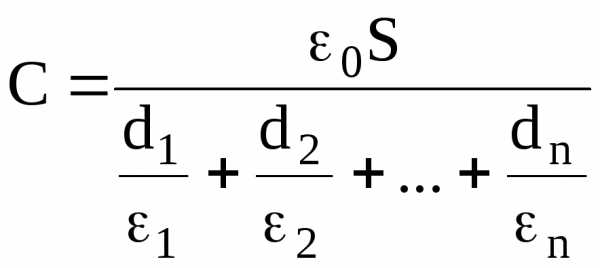Электроемкость сферического конденсатора (две концентрические сферы радиусом R₁ и R₂ , пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ) находится так:

.

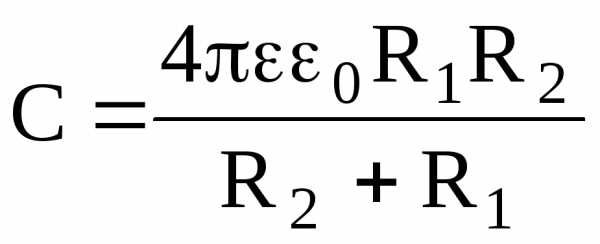Электроемкость последовательно соединенных конденсаторов составляет:

в общем случае –

,

где n – число конденсаторов;

в случае двух конденсаторов –

;

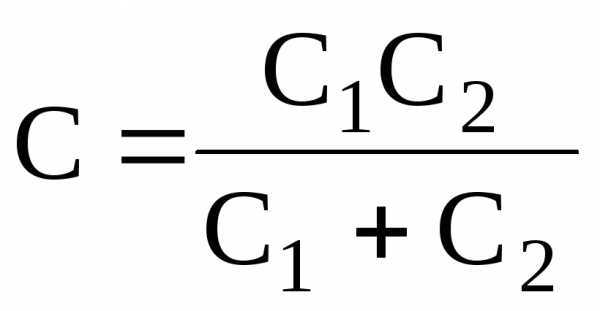в случае n одинаковых конденсаторов с электроемкостью С₁ каждый –

.

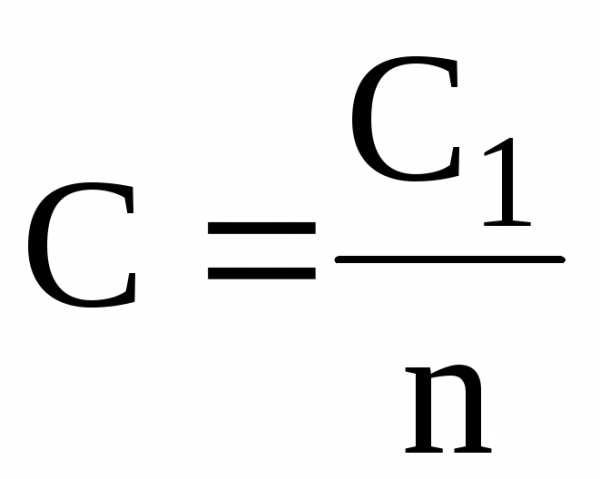Электроемкость параллельно соединенных конденсаторов определяется следующим образом:

в общем случае –

С=С₁+С₂+…+С_n;

в случае двух конденсаторов –

С= С₁+С₂;

в случае n одинаковых конденсаторов с электроемкостью С₁ каждый –

С=nС₁.

Энергия заряженного проводника выражается через заряд q, потенциал  и электроемкость С проводника следующим образом:

.

Энергия заряженного конденсатора –

,

где q – заряд конденсатора; С – электроемкость конденсатора; U – разность потенциалов на его пластинах.

studfile.net

Напряженность электрического поля ⚡ формула, единица измерения, значение, сила напряженности точечного заряда электрического поля, модуль, от чего зависит напряженность

Общее понятие

Электрическое поле представляет собой определенный вид материи, возникающий вокруг частиц или тел, у которых присутствует электрический заряд. В свободной форме поле существует при реформировании магнитного фона, например, при действии электромагнитных волн. Область воздействия не наблюдается непосредственно, но проявляется в результате влияния силы на тела с зарядами.

Электромагнитный фон рассматривается в форме математической модели, которая описывает размер напряженности в заданной точке участка. Поле не является вариантом вещества и относится к вопросам из метафизической области.

Классическая наука в вопросах рассмотрения объектов, которые по размеру больше атома, руководствуется теорией взаимодействия на электрическом участке. Поле считается отдельной составляющей общего электромагнитного фона. В теории квантовой электродинамики оно рассматривается в качестве элемента слабого взаимодействия.

Присутствие поля заключается в измерении числа свободных носителей при действии электростатического фона на плоскость проводящей среды. Этот эффект применяется при работе полевых радиоприемников. Поле воздействует силой на стационарные (относительно зрителя) заряженные частицы или тела. Если предмет является неподвижным в исследуемой сфере, то он не ускоряется при действии силы. Подвижные заряженные элементы ускоряются под влиянием энергетического и магнитного поля.

Напряженностью поля называется векторная размерность, которая определяется отношением действующей силы на положительно заряженную частицу, к величине отдельного потенциала. Вектор напряженности электрического поля совпадает в разных точках внутри исследуемого шара с направлением приложения силы. Величина измеряется в вольтах на метр (в/м) в соответствии с Международной СЕ.

Зависимость между двумя зарядами

Напряженность поля по аналогии с механическим действием характеризуется не только численной величиной, но и зависит от пространственного направления, т. е. представляет собой векторную константу. Если заряд одной частицы принять за единицу, то получится сила, которая действует на единицу потенциала.

Направленность точечного заряда с положительным значением идет по линии радиуса. Напряженность в разноудаленных точках от проводника всегда отличается и уменьшается при удалении в обратно пропорциональной зависимости к расстоянию в квадрате. Для расчета суммирующего показателя интенсивности значение напряженностей складываются, так как силы направляются одна к другой под углом. Такое вычисление происходит по закону параллелограмма. Этим же способом рассчитывается модуль напряженности в разных точках сферы при одном или нескольких зарядах.

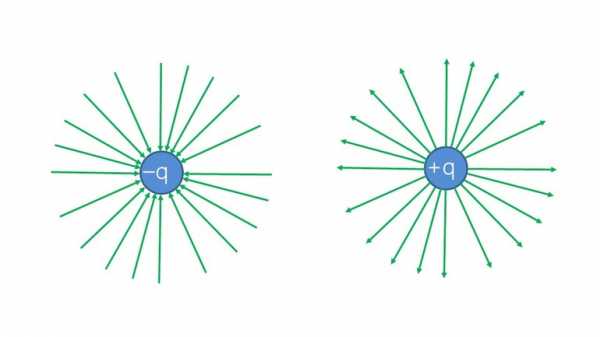
Положительный заряд электричества отталкивается по прямой линии, продолжающей направление радиуса, если он находится в поле с плюсовым потенциалом. Вырисовывается совокупность радиальных линий, которые направляются в разные стороны от шара при перемещении заряда по различным точкам области и после отметок двигательных траекторий. Полученные воображаемые прямые являются силовыми электрическими линиями, по которым передвигается положительно заряженная частица с отсутствием инерции.

В электрически заряженном поле обнаруживается множество силовых линий. С их помощью графически показывается величина напряженности и направление действия электрического потенциала в конкретной точке поля. Иногда используется прием проведения через каждый см² площади, перпендикулярной к силовым линиям на заданном участке пространства, такого количества линий, чтобы их суммарное значение соответствовало напряженности. Величина интенсивности в этой части поля меняет показатель в зависимости от густоты потока силовых векторов.

Однородное поле

Электростатическое поле называется равномерным или однородным, если имеет одинаковые показатели напряжения в различных пространственных областях по направлению и величине. Примером служит поле между большими заряженными пластинами, которые располагаются параллельно одна к другой.

Для изображения применяются прямые линии:

• параллельные друг другу;
• имеющие векторный показатель;
• располагающиеся равномерно и на одинаковом расстоянии.

Одноименные потенциалы отталкиваются при взаимодействии, поэтому электрический заряд может существовать только снаружи проводниковой плоскости. Объем электричества, который действует на единицу площади тела, называется поверхностной плотностью.

Величина показателя зависит:

• от общего количественного значения электричества на внешней площади тела;
• от формы поверхности используемого проводника.

Электрический заряд раздается равномерно при использовании круглых проводников большой длины или сферических фигур правильной формы. В этом случае поверхностная плотность потенциала будет одинаковой на всех участках площади тела. Если тело отличается неправильной геометрией, то заряд делится с нарушением равномерности. Больший показатель плотности определяется на вступающих частях и уменьшается внутри углублений и впадин.

Самый большой показатель поверхностной насыщенности проявляется на острых кромках и ребрах. Части потенциала на таких экстремальных участках отталкиваются и стремятся сбросить заряды с поверхности в проблемных областях. На острие скапливается значительная порция заряда, поэтому образовывается электрическое поле большой силы.

Возникает эффект конденсатора. Под его действием окружающий воздух или иной диэлектрик ионизируется и становится проводником. В этом случае наблюдается «стекание» потенциала с острия.

При изготовлении проводников тщательно убирают все острые выступы и концы, чтобы избежать избыточной электризации в случае применения высокого напряжения.

Электрическая напряженность в быту

Вначале создается электрический потенциал для получения поля. Любой диэлектрик натирается о шерсть, волосы, используется, например, пластиковая ручка или эбонитовая палочка. На поверхности предмета создается потенциал, а вокруг возникает электрическое поле. Ручка с зарядом притягивает мелкие кусочки бумаги. Если подобрать правильное сочетание материала и размера предмета, то в темноте наблюдаются небольшие искры, которые появляются вследствие разрядов электричества.

Электростатический фон часто появляется рядом с экраном телевизора при включении или выключении оборудования. Это поле ощущается в виде поднятых волосков на теле. Избыточный потенциал, полученный проводником извне, сосредотачивается на поверхности предмета, как становится ясно из проведенных опытов. Перемещение заряженных частиц к внешней оболочке свидетельствует о появлении электростатического поля внутри проводника, что дает импульс к переброске.

Существует ошибочное мнение, что электрический фон в заряженном теле исчезает после окончания дислокации электронов, а поле действует определенный промежуток времени. Если бы точка зрения была правильной, то избыточный потенциал мог находиться в условиях равновесия и способствовал бы беспорядочному и хаотичному движению молекул. Такое явление никогда не наблюдается в проводниках и заряженных телах.

Расчет показателей

Напряженность поля, которое возникает под действием системы зарядов в искомой точке исследуемой области, равняется векторному результату аналогичных показателей всех полей, создаваемых отдельными потенциалами.

Формула напряженности электрического поля выглядит как Е= F / q, где параметры обозначаются буквами:

1. Е — напряженность поля.
2. F — сила, которая влияет на заряд, находящийся в определенной точке.
3. Q — потенциал отдельной частицы, измеряется в кулонах.

Направление вектора Е должно совпадать с курсом действия силы, влияющей на положительный заряд, и находится в противоположном русле к давлению, которое оказывается на отрицательную частицу.

Это свойство означает, что действие поля происходит по принципу суперпозиции, который гласит:

• результат влияния на отдельную микрочастицу нескольких наружных сил равняется векторной сумме обособленных влияний;
• каждое сложное передвижение раскладывается на несколько простых.

Иногда принцип принимает другие формулировки, которые по смыслу представляют собой эквивалентную теорию. В соответствии с ней, для нахождения энергии взаимного смещения в системе множества частиц берется сумма активности парных сочетаний между всеми реальными парами зарядов. Уравнения, которые участвуют в описании поведения системы, являются линейными формулами по количеству микрочастиц.

Взаимодействие потенциалов

Элементарные микрочастицы, которые носят название электрических зарядов, создают в собственном окружении электромагнитный фон. Поле переносит силовые связи между отдельными частицами. Электростатическое поле контактирует с носителями заряда и представляет собой носитель информации в современных системах телевещания, радио.

Частицы взаимодействуют между собой и переносятся полем в пространственном континууме с определенной конечной скоростью. Электрический потенциал (заряд) является численной характеристикой в определенной области поля и принимает положительное или отрицательное значение. При этом величина силового действия между элементами, которое осуществляется зарядами, является прямо пропорциональной размеру потенциала. Определение направления силовых линий индукции, идущих со стороны электрического поля, зависит от знака действующего заряда.

Электрический потенциал определенной направленности присутствует в частице в течение всего времени ее существования. В результате происходит отождествление микроэлемента с его зарядом. Для характеристики используется система диполь, применяемая для описания поля или учета распространения колебаний электромагнитных линий вдали от нулевого источника с зарядом, разделенным в пространстве.

Потенциал любого проводника является кратным модулю элементарного заряда частицы. В природе создается одинаковое количество положительных и отрицательных электронов, при этом электрический потенциал молекул и атомов принимается равным нулю. Заряды ионов и катионов в каждом участке кристаллической решетки компенсируются между собой.

Возникновение изолированных систем с определенной полярностью связывается не с появлением новых потенциальных частиц, а с их разделением в некоторых условиях, например, при трении. Электростатическое поле возникает в случае неподвижности зарядов и является идеализированным понятием.

Точечные резервы

Потенциалом называется заряженный предмет или отдельная частица, размеры которой признаются ничтожными по сравнению с дистанциями до других зарядов в искомой системе. Точечный заряд идеализируется так же, как понятие материальной точки в механической теории. Заряд, который помещается в исследуемое тело для получения характеристик и выявления свойств, носит название пробного.

Такой потенциал является довольно малым, чтобы влиять на положение основных зарядов и искажать условия измеряемого поля. Этот элемент служит индикатором электромагнитного фона. Заряд в замкнутом электрическом поле никогда не изменится, если через поверхность не будут поступать заряженные элементарные частицы (закон Фарадея).

Если заряженная система 1 отдает потенциал системе 2, то размер получаемого заряда всегда равен величине отдаваемого количества. Заряд тела является симметричным относительно перемены порядка отсчета и не зависит от ускорения и начальной скорости.

nauka.club

Напряжённость электрического поля — Википедия

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда ^[1]:

.

Из этого определения видно, почему напряжённость электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном^[2] множителе).

В каждой точке пространства в данный момент времени существует своё значение вектора (вообще говоря — разное^[3] в разных точках пространства), таким образом, —- это векторное поле. Формально это выражается в записи

представляющей напряжённость электрического поля как функцию пространственных координат (и времени, так как может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле^[4], и законы, которым оно подчиняется, есть предмет электродинамики.

Напряжённость электрического поля в Международной системе единиц (СИ) измеряется в вольтах на метр [В/м] или в ньютонах на кулон [Н/Кл].

Напряжённость электрического поля в классической электродинамике[править]

Из сказанного выше ясно, что напряженность электрического поля — одна из основных фундаментальных величин классической электродинамики. В этой области физики можно назвать сопоставимыми с ней по значению только вектор магнитной индукции (вместе с вектором напряженности электрического поля образующий тензор электромагнитного поля) и электрический заряд. С некоторой точки зрения столь же важными представляются потенциалы электромагнитного поля (образующие вместе единый электромагнитный потенциал).

Приведем краткий обзор основных контекстов классической электродинамики в отношении напряженности электрического поля.

Сила, с которой действует электромагнитное поле на заряженные частицы[править]

Полная сила, с которой электромагнитное поле (включающее вообще говоря электрическую и магнитную составляющие) действует на заряженную частицу, выражается формулой силы Лоренца:

где q — электрический заряд частицы,  — её скорость,  — вектор магнитной индукции (основная характеристика магнитного поля), косым крестом обозначено векторное произведение. Формула приведена в единицах СИ.

Как видим, эта формула полностью согласуется с определением напряженности электрического поля, данном в начале статьи, но является более общей, так как включает в себя также действие на заряженную частицу (если та движется) со стороны магнитного поля.

В этой формуле частица предполагается точечной. Однако эта формула позволяет рассчитать и силы, действующие со стороны электромагнитного поля на тела любой формы с любым распределением зарядов и токов — надо только воспользоваться обычным для физики приемом разбиения сложного тела на маленькие (математически — бесконечно маленькие) части, каждая из которых может считаться точечной и таким образом входящей в область применимости формулы.

Остальные формулы, применяемые для расчета электромагнитных сил (такие, как, например, формула силы Ампера) можно считать следствиями^[5] фундаментальной формулы силы Лоренца, частными случаями её применения итп.

Однако для того, чтобы эта формула была применена (даже в самых простых случаях, таких, как расчет силы взаимодействия двух точечных зарядов), необходимо знать (уметь рассчитывать) и чему посвящены следующие параграфы.

Уравнения Максвелла[править]

Достаточным вместе с формулой силы Лоренца теоретическим фундаментом классической электродинамики являются уравнения электромагнитного поля, называемые уравнениями Максвелла. Их стандартная традиционная форма представляет собой четыре уравнения, в три из которых входит вектор напряженности электрического поля:

Здесь  — плотность заряда, —- плотность тока,  — электрическая постоянная,  — магнитная постоянная,  — скорость света (уравнения здесь записаны в единицах СИ).

Здесь приведена наиболее фундаментальная и простая форма уравнений Максвелла — так называемые «уравнения для вакуума» (хотя, вопреки названию, они вполне применимы и для описания поведения электромагнитного поля в среде). Подробно о других формах записи уравнений Максвелла — см. основную статью.

Этих четырёх уравнений вместе с пятым — уравнением силы Лоренца — в принципе достаточно, чтобы полностью описать классическую (то есть не квантовую) электродинамику, то есть они представляют её полные законы. Для решения конкретных реальных задач с их помощью необходимы ещё уравнения движения «материальных частиц» (в классической механике это законы Ньютона), а также зачастую дополнительная информация о конкретных свойствах физических тел и сред, участвующих в рассмотрении (их упругости, электропроводности, поляризуемости итд итп), а также о других силах, участвующих в задаче (например, о гравитации), однако вся эта информация уже не входит в рамки электродинамики как таковой, хотя и оказывается зачастую необходимой для построения замкнутой системы уравнений, позволяющих решить ту или иную конкретную задачу в целом.

«Материальные уравнения»[править]

Такими дополнительными формулами или уравнениями (обычно не точными, а приближенными, зачастую всего лишь эмпирическими), которые не входят непосредственно в область электродинамики, но поневоле используются в ней ради решения конкретных практических задач, называемыми «материальными уравнениями», являются, в частности:

Связь с потенциалами[править]

Связь напряженности электрического поля с потенциалами в общем случае такова:

где  — скалярный и векторный потенциалы. Приведем здесь для полноты картины и соответствующее выражение для вектора магнитной индукции:

В частном случае стационарных (не меняющихся со временем) полей, первое уравнение упрощается до:

Это выражение для связи электростатического поля с электростатическим потенциалом.

Электростатика[править]

Важным с практической и с теоретической точек зрения частным случаем в электродинамике является тот случай, когда заряженные тела неподвижны (например, если исследуется состояние равновесия) или скорость их движения достаточно мала чтобы можно было приближенно воспользоваться теми способами расчета, которые справедливы для неподвижных тел. Этим частным случаем занимается раздел электродинамики, называемый электростатикой.

Как мы уже заметили выше, напряженность электрического поля в этом случае выражается через скалярный потенциал как

или

то есть электростатическое поле оказывается потенциальным полем. ( в этом случае — случае электростатики — принято называть электростатическим потенциалом).

• Также и обратно

Уравнения поля (уравнения Максвелла) при этом также сильно упрощаются (уравнения с магнитным полем можно исключить, а в уравнение с дивергенцией можно подставить ) и сводятся к уравнению Пуассона:

а в областях, свободных от заряженных частиц — к уравнению Лапласа:

Учитывая линейность этих уравнений, а следовательно применимость к ним принципа суперпозиции, достаточно найти поле одного точечного единичного заряда, чтобы потом найти потенциал или напряженность поля, создаваемого любым распределением зарядов (суммируя решения для точечного заряда).

Теорема Гаусса[править]

Очень полезной в электростатике оказывается теорема Гаусса, содержание которой сводится к интегральной форме единственного нетривиального для электростатики уравнения Максвелла:

где интегрирование производится по любой замкнутой поверхности S (вычисляя поток через эту поверхность), Q — полный (суммарный) заряд внутри этой поверхности.

Эта теорема дает крайне простой и удобный способ расчета напряженности электрического поля в случае, когда источники имеют достаточно высокую симметрию, а именно сферическую, цилиндрическую или зеркальную+трансляционную. В частности, таким способом легко находится поле точечного заряда, сферы, цилиндра, плоскости.

Напряжённость электрического поля точечного заряда[править]

В единицах СИ[править]

Для точечного заряда в электростатике верен закон Кулона

или

.

.

Исторически закон Кулона был открыт первым, хотя с теоретической точки зрения уравнения Максвелла более фундаментальны. С этой точки зрения он является их следствием. Получить этот результат проще всего исходя из теоремы Гаусса, учитывая сферическую симметрию задачи: выбрать поверхность S в виде сферы с центром в точечном заряде, учесть, что направление будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что E можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса r: , имеем:

откуда сразу получаем ответ для E.

Ответ для получается, тогда, интегрированием E:

Для системы СГС[править]

Формулы и их вывод аналогичны, отличие от СИ лишь в константах.

Напряженность электрического поля произвольного распределения зарядов[править]

По принципу суперпозиции для напряженности поля совокупности дискретных источников имеем:

где каждое

Подставив, получаем:

Для непрерывного распределения аналогично:

где V — область пространства, где расположены заряды (ненулевая плотность заряда), или всё пространство,  — радиус-вектор точки, для которой считаем ,  — радиус-вектор источника, пробегающий все точки области V при интегрировании, dV — элемент объёма. Можно подставить x, y,z вместо , вместо , вместо dV.

Системы единиц[править]

В системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в ньютонах на кулон или в вольтах на метр (русское В/м, международное V/m).

1. ↑ Напряжённость электрического поля // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 246. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
2. ↑ Для любой частицы её электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или если к ней что-то заряженное присоединится.
3. ↑ Хотя иногда его значения могут оказываться и одинаковыми в разных точках пространства; если одинаков всюду в пространстве (или какой-то области пространства), говорят об однородном электрическом поле —- это всего лишь частный случай электрического поля, хотя и наиболее простой; притом что в реальности электрическое поле может быть однородным лишь приближенно, то есть различия в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.
4. ↑ Электромагнитное поле может быть выражено и по-другому, например через электромагнитный потенциал или в несколько иной математической записи (прячущей вектор напряженности электрического поля вместе с вектором магнитной индукции внутрь тензора электромагнитного поля), однако все эти способы записи тесно связаны между собой, таким образом, утверждение о том, что поле  — одна из основных составляющих электромагнитного поля не утрачивает смысла.
5. ↑ Хотя исторически многие из них были открыты раньше.

wp.wiki-wiki.ru

Напряженность поля точечного заряда | Объединение учителей Санкт-Петербурга

Напряженность поля точечного заряда.
Обозначим: q — заряд, создающий поле, q0 — заряд, помещенный в поле (внешний заряд). Закон Кулона: . Напряженность поля: . Тогда напряженность поля точечного заряда:
Теорема  Гаусса. Потоком вектора напряженности наз. величина Ф, равная произведению модуля вектора напряженности на площадь контура S, ограничивающую некоторую площадь, и на косинус угла между вектором напряженности и нормалью (перпендикуляром) к площадке.
Если считать, что напряженность пропорциональна числу силовых линий, приходящихся на единицу площади поверхности (т.е. густоте), то поток напряженности пропорционален полному числу силовых линий, пересекающих данный контур.
Поток линий напряженности электростатического поля через произвольную замкнутую поверхность прямо пропорционален величине заряда, находящегося в области пространства,  ограниченного данной поверхностью.
Применения теоремы Гаусса.
1. Напряженность поля заряженной проводящей сферы радиуса R. Сфера заряжена по поверхности.  А) Внутри сферы заряда нет . Е=0
Б) Снаружи сферы.
На поверхности сферы:
2. Напряженность поля шара заряженного по объему.
Введем понятие объемной плотности заряда:  Объемная плотность заряда показывает, какой заряд содержится в единице объема заряженного по всему объему тела.  Объем шара произвольного радиуса . Обозначим q — заряд шара, q0 — заряд, находящийся внутри объема произвольного радиуса.
Тогда заряд сферы радиуса r , будет:                                 Следовательно: .   – напряженность поля внутри шара, равномерно заряженного по объему. Снаружи — см. 1.
3. Напряженность поля бесконечной заряженной плоскости.
Введем понятие поверхностной плотности заряда: . Тогда . Коэффициент 2 появляется, т.к. плоскость окружена двумя поверхностями площадью S. Поле бесконечной заряженной плоскости не зависит от расстояния от плоскости! Можно пользоваться, когда расстояние много меньше размеров плоскости. 4. Напряженность поля плоского воздушного конденсатора. Из рисунка видим, что снаружи конденсатора поля пластин взаимно скомпенсированы, и общее поле равно нулю. Внутри конденсатора поля складываются. Используя вывод п.3 получаем: . Формула справедлива при условии, что расстояние между пластинами много меньше размеров самих пластин и вдали от краев пластин.

www.eduspb.com

Формула напряженности электрического поля

Все электрически заряженные тела взаимодействуют между собой. Природа этого взаимодействия заключается в наличии вокруг этих тел специальной физической величины. Согласно теории близкодействия, взаимодействие между всеми телами происходит через особую материальную среду, окружающую тела и передающую все изменения, происходящие в пространстве. Эта физическая величина получила название электрического поля. Понятие электрического поля Электрическое поле могут создавать, как подвижные, так и неподвижные заряды. Его наличие проявляется, прежде всего, в способности оказания силового воздействия на заряженные частицы, статические и движущиеся. Кроме того, оно способно производить индукцию электрических зарядов на поверхностях нейтральных тел, способных проводить электрический ток. То поле, которое создано с помощью неподвижных зарядов, получило название электростатического или электрического стационарного поля. Это особый случай одного из видов электромагнитных полей, позволяющий осуществлять силовые взаимодействия среди тел, имеющих электро заряды и движущихся в произвольном порядке, относительно определенной точки отсчета. Основной количественной характеристикой, с которой происходит силовое воздействие на заряженные тела, служит векторная величина. Формула напряженности электрического поля приведена на рисунке. Значение формулы определяется следующим образом. Сила F, действующая на точечный пробный заряд со стороны поля, относится к величине этого заряда, помещенного в исследуемую точку. Это отношение и является величиной напряженности эл.поля. Использование пробного заряда Пробный заряд не принимает участия в создании электрополя и не искажает картину исследования, потому что значение заряда очень мало. Он не влияет на пространственное перераспределение зарядов, с помощью которых происходит создание данного электрического поля. Для наглядного понимания сути вопроса напряженность электрического поля, формула, которой была рассмотрена, может быть отображена графически. На чертежах производится ее изображение в виде непрерывных линий, которые носят название силовых линий или линий напряженности. Все касательные, расположенные в любой точке чертежа, имеют полное совпадение с вектором напряженности эл.поля в конкретной точке. Данные линии не могут пересекаться, поскольку в каждой точке поля, вектор расположен только в одном направлении. Таким образом, с помощью изображения линий напряженности, можно получить реальную картину электрического поля, наглядно показывающую значение напряженности в его различных частях и ее изменение в пространстве.

electric-220.ru

Вектор напряженности электрического поля

По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля.

Характеристика электрического поля

Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле:

E→=F→q, где F→ — сила, действующая со стороны поля на неподвижный (пробный) заряд q. Его значение должно быть настолько мало, чтобы отсутствовала возможность искажать поле, напряженность которого с его помощью и измеряют. По уравнению видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный пробный заряд.

У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным.

Силовые линии

Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий.

Определение 1

Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.

Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться.

Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:

E→=∑i=1nE→i.

Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле:

E→=∫dE→.

Интегрирование E→=∫dE

zaochnik.com

Электростатическое поле. Напряженность электростатического поля

       Почему заряды взаимодействуют? Над этим вопросом ученые работали долгое время, имела место борьба двух теорий: теория дальнодействия – Ньютон, Ампер и теория близкодействия – Фарадей, Максвелл и т.д. Для электростатического поля справедливы обе эти теории.

       Для понимания происхождения и передачи сил, действующих между зарядами, необходимо допустить наличие между зарядами какого-либо физического агента, обуславливающего это взаимодействие. Этим агентом является электрическое поле.

       Вокруг заряда всегда есть электрическое поле, основное свойство которого заключается в том, что на всякий другой заряд, помещенный в это поле, действует сила.

       Электрические и магнитные поля – частный случай более общего – электромагнитного поля (ЭМП). Они могут порождать друг друга, превращаться друг в друга. Если заряды не движутся, то магнитное поле не возникает.

       ЭМП – не абстракция, а объективная реальность – форма существования материи, обладающая определенными физическими свойствами, которые мы можем измерить.

       Не существует статических электрических полей, не связанных с зарядами, как не существует «голых», не окруженных полем зарядов.

       Силовой характеристикой поля создаваемого зарядом q является отношение силы действующей на заряд к величине этого заряда называемое напряженностью электростатического поля, т.е.

,

(1.3.1)

Или в векторной форме

,

(1.3.2)

здесь r – расстояние от заряда до точки, где мы изучаем это поле. Тогда и при , .

       Вектор напряженности электростатического поля равен силе, действующей в данной точке на помещенный в нее пробный единичный положительный заряд.

       Направление вектора напряженности определяет направление силы, действующей на положительный заряд, помещенный в рассматриваемую точку поля.

       Из формулы (1.3.1) следует что единица измерения напряженности электростатического поля – ньютон на кулон (Н/Кл).

       1 Н/Кл – напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н.

       В СИ размерность напряженности .

---

ens.tpu.ru