Замечательные отношения в прямоугольном треугольнике
Категория: ПланиметрияСправочные материалы
Елена Репина 2013-05-22 2013-08-04На всякий случай, уточним, что гипотенузой называется та сторона треугольника, что лежит против угла в 90 градусов, две оставшиеся стороны называются катетами прямоугольного треугольника.
Подробнее про прямоугольный треугольник здесь.
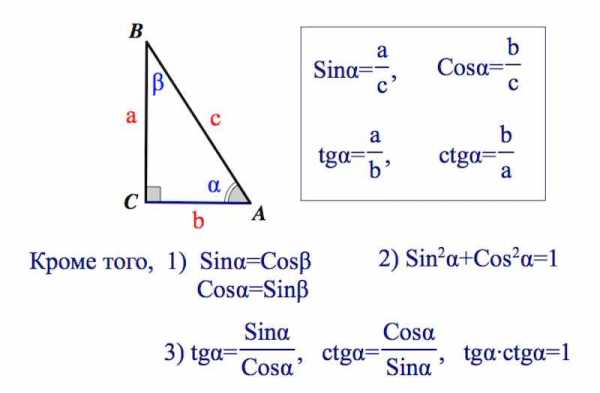
Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
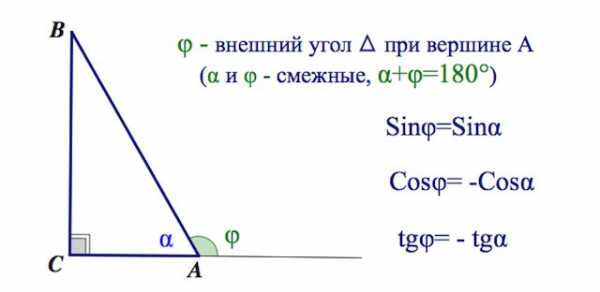
Бывает (и на ЕГЭ, ГИА), что приходится иметь дело с косинусами, синусами и тангенсами внешних углов треугольника. Формулы приведения позволяют увидеть, что есть еще и вот такая связь между смежными углами (помимо того, что их сумма равна 180):
Смотрите подборку задач на применение указанных соотношений в статье «Прямоугольный треугольник. Вычисление длин и углов» часть I, часть II.
Автор: egeMax | комментариев 8 | Метки: шпаргалки-таблицыegemaximum.ru
Тригонометрические функции произвольных углов. Теоремы синусов и косинусов
Тригонометрические функции (синус, косинус, тангенс, котангенс) однозначно определяют острый угол. Это значит, что если нам известно значение хотя бы одной из этих функций, то мы можем найти и сам острый угол, и значение оставшихся трех тригонометрических функций (см. рис. 1).
Рис. 1. Взаимосвязь тригонометрических функций
Взаимосвязь тригонометрических функций:
Например, глядя на определения тангенса и котангенса, легко заметить, что:
Потому что , и наоборот.
Можно переписать в эквивалентном виде:
Если мы знаем, что , то сразу скажем: . Нам даже не надо искать само значение угла.
Кроме того, несложно заметить, что:
И аналогично:
Мы уже почти научились по значению одной тригонометрической функции угла находить остальные. Нужно только связать между собой синус и косинус.
Вспомним, что для прямоугольного треугольника верна теорема Пифагора:
Чтобы перейти к формулам для синуса и косинуса, разделим обе части этого равенства на . Получим:
Откуда, по определению:
Можно получить и другие формулы, связывающие тригонометрические функции одного угла. Например, если мы хотим связать тангенс и косинус, то, взяв формулу
, поделим обе части на , получим:
Откуда:
Аналогично можно получить формулу:
Полученные нами формулы называются основными тригонометрическими тождествами. С их помощью можно, зная значение одной из тригонометрических функций острого угла, найти значения трех остальных. С примером решения такой задачи можно ознакомиться ниже.
Вычисление значений тригонометрических функций
Предположим, что нам известно значение синуса острого угла:
Найдем значения остальных тригонометрических функций этого угла.
Зная синус, несложно найти косинус, используя формулу:
Подставляем, получаем:
Поскольку косинус острого угла, по определению, – это отношение длин двух сторон, то он может принимать только положительные значения. Значит,
Теперь найти тангенс и котангенс не составит проблем:
Можно было действовать и по-другому, например найти котангенс через синус, используя формулу:
Потренируйтесь самостоятельно находить значения остальных тригонометрических функций острого угла по известному тангенсу или котангенсу.
Возникает вопрос: зачем нужно рассматривать целых четыре функции, если можно использовать одну, а все остальные при необходимости выражать через эту одну?
Конечно, можно. Вопрос только в удобстве. Если какая-то конструкция часто используется, то ее удобно обозначить отдельно, а также вывести ее свойства, чтобы использовать их при решении конкретных задач.
К примеру, длину можно было бы измерять только в метрах. Но расстояние между городами или размеры телефона в них измерять не очень удобно. Не говоря уже про размеры бактерий или расстояния между планетами. Поэтому люди используют разные единицы измерения для одной и той же величины (миллиметры, километры, дюймы, мили, световые года и т. д.) в зависимости от удобства при решении той или иной задачи (см. рис. 2).
Рис. 2. Использование различных единиц измерения
Такая же ситуация с тригонометрическими функциями – оказалось, что эти соотношения используются настолько часто, что удобнее ввести и изучать их отдельно, чем выражать через одно.
Более того, можно ввести и другие тригонометрические функции, но они не прижились именно из-за того, что редко встречаются при решении практических задач. Подробнее о них ниже.
vetkaДругие тригонометрические функции
Наблюдательный человек заметит, что при определении тригонометрических функций мы перебрали не все комбинации (см. рис. 3): можно гипотенузу разделить на каждый из катетов.
Рис. 3. Взаимосвязь тригонометрических функций
Взаимосвязь тригонометрических функций:
Действительно, можно ввести еще две функции – секанс и косеканс:
Несложно заметить, что мы получили функции, обратные синусу и косинусу.
В наше время эти функции практически не используют. Слишком просто их заменить синусом и косинусом. Кстати, по этой причине в некоторой литературе не выписываются свойства для котангенса – считается, что его проще выражать через тангенс.
На самом деле, никакой принципиальности в том, чтобы использовать именно эти, а не другие функции, нет. Просто при решении различных задач чаще встречались именно выражения, содержащие синусы, косинусы, тангенсы и котангенсы, поэтому им дали отдельные названия и их подробно изучают.
Какие значения могут принимать тригонометрические функции? Рассмотрим . Поскольку мы определяли синус для острых углов прямоугольных треугольников, то угол может принимать значение от до . Формально, не включая эти значения. Но угол может сколь угодно близко к ним приближаться.
Зафиксируем гипотенузу и уменьшим угол почти до нуля (см. рис. 4).
Рис. 4. Уменьшенный почти до угол при зафиксированной гипотенузе
Почти до нуля уменьшится и катет . А вместе с ним и :
Поэтому можем определить:
Если начать увеличивать (см. рис. 5), то будет увеличиваться и катет , а вместе с ним будет увеличиваться и значение синуса.
Рис. 5. Увеличенный почти до угол
Чем ближе к будет угол, тем ближе катет будет к гипотенузе . Значит:
Поэтому можем определить:
Значение синуса не может превышать – это его максимальное значение. Больше синус быть не может.
interneturok.ru
Тригонометрия для чайников. Урок1. Тригонометрия с нуля
Смотрите бесплатные видео-уроки по теме «Тригонометрия» на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
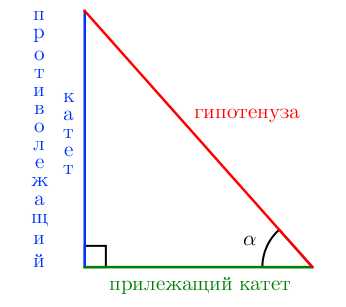
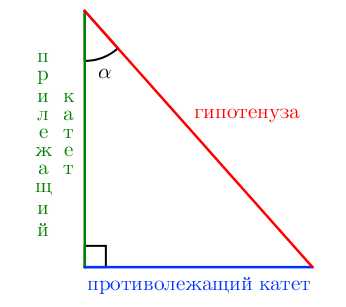
Синус угла – отношение противолежащего катета к гипотенузе.
sinα=Противолежащий катетгипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cosα=Прилежащий катетгипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tgα=Противолежащий катетПрилежащий катет
Котангенс угла
ctgα=Прилежащий катетПротиволежащий катет
Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:
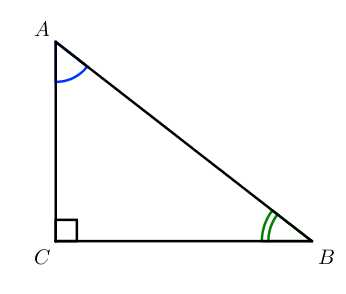
sin∠A=CBAB
cos∠A=ACAB
tg∠A=sin∠Acos∠A=CBAC
ctg∠A=cos∠Asin∠A=ACCB
sin∠B=ACAB
cos∠B=BCAB
tg∠B=sin∠Bcos∠B=ACCB
ctg∠B=cos∠Bsin∠B=CBAC
Тригонометрия на окружности — это довольно интересная абстракция в математике. Если понять основной концепт так называемого «тригонометрического круга», то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках (−1;0) и (1;0), ось y в точках (0;−1) и (0;1)
На данной окружности будет три шкалы отсчета – ось x, ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами (1;0), – то есть от положительного направления оси x, против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A. Рассмотрим ∠SOA, обозначим его за α. Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠SOA=α=∪SA.
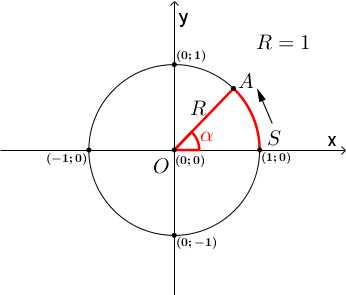
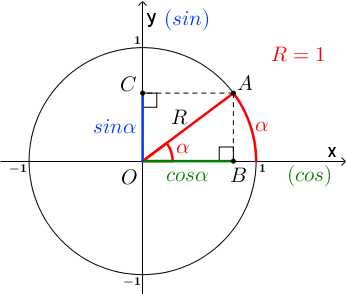
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B) и на ось игрек (точка C).
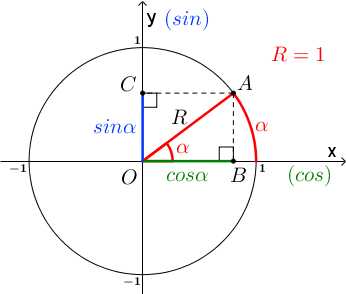
Отрезок OB является проекцией отрезка OA на ось x, отрезок OC является проекцией отрезка OA на ось y.
Рассмотрим прямоугольный треугольник AOB:
cosα=OBOA=OB1=OB
sinα=ABOA=AB1=AB
Поскольку OCAB – прямоугольник, AB=CO.
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α — тупой, то есть больше 90°:
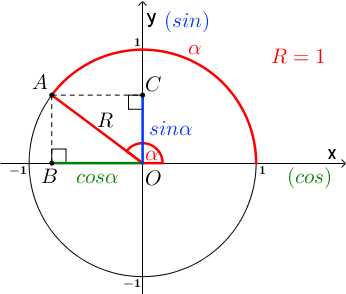
Опускаем из точки A перпендикуляры к осям x и y. Точка B в этом случае будет иметь отрицательную координату по оси x.Косинус тупого угла отрицательный.
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0° до 180°. Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x. (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0°,30°,45°,60°,90°,120°,135°,150°,180°. Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y.
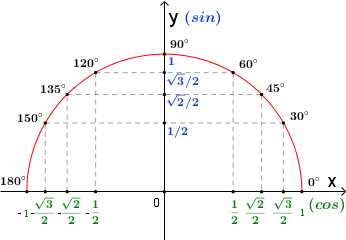
Координата по оси x – косинус угла, координата по оси y – синус угла.
Пример:
cos150°=−32
sin150°=12
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.
sin2α+cos2α=1
Данное тождество – теорема Пифагора в прямоугольном треугольнике OAB:
AB2+OB2=OA2
sin2α+cos2α=R2
sin2α+cos2α=1
| 0° | 30° | 45° | 60° | 90° | |
| sinα | 0 | 12 | 22 | 32 | 1 |
| cosα | 1 | 32 | 22 | 12 | 0 |
| tgα | 0 | 33 | 1 | 3 | нет |
| ctgα | нет | 3 | 1 | 33 | 0 |
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
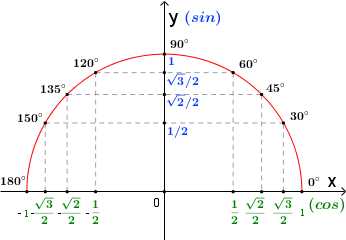
можно заметить, что:
sin180°=sin(180°−0°)=sin0°
sin150°=sin(180°−30°)=sin30°
sin135°=sin(180°−45°)=sin45°
sin120°=sin(180°−60°)=sin60°
cos180°=cos(180°−0°)=−cos0°
cos150°=cos(180°−30°)=−cos30°
cos135°=cos(180°−45°)=−cos45°
cos120°=cos(180°−60°)=−cos60°
Рассмотрим тупой угол β:
Для произвольного тупого угла β=180°−α всегда будут справедливы следующие равенства:
sin(180°−α)=sinα
cos(180°−α)=−cosα
tg(180°−α)=−tgα
ctg(180°−α)=−ctgα
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

asin∠A=bsin∠B=csin∠C
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
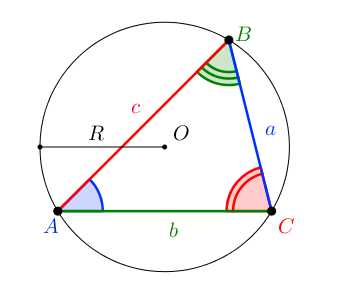
asin∠A=bsin∠B=csin∠C=2R
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a2=b2+c2−2bc⋅cos∠A
b2=a2+c2−2ac⋅cos∠B
c2=a2+b2−2ab⋅cos∠C
Модуль геометрия: задания, связанные с тригонометрией.
Скачать домашнее задание к уроку 1.
epmat.ru
Синус косинус
Синус косинус, определение. Друзья! В прошлой статье, где были рассмотрены задачи на решение прямоугольного треугольника, я пообещал изложить приём запоминания определений синуса и косинуса. Используя его, вы всегда быстро вспомните – какой катет относится к гипотенузе (прилежащий или противолежащий). Решил в «долгий ящик не откладывать», необходимый материал ниже, прошу ознакомиться 😉
Дело в том, что я не раз наблюдал, как учащиеся 10-11 классов с трудом вспоминают данные определения. Они прекрасно помнят, что катет относится к гипотенузе, а вот какой из них — забывают и путают. Цена ошибки, как вы знаете на экзамене – это потерянный бал.
Информация, которую я представлю непосредственно к математике не имеет никакого отношения. Она связана с образным мышлением, и с приёмами словесно-логической связи. Именно так, я сам, раз и на всегда запомнил данные определения. Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.
Напомню определения синуса и косинуса в прямоугольном треугольнике:

Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе:
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Итак, какие ассоциации у вас вызывает слово косинус?
Наверное, у каждого свои 😉 Запоминайте связку:
Таким образом, у вас сразу в памяти возникнет выражение –
«… отношение ПРИЛЕЖАЩЕГО катета к гипотенузе».
Проблема с определением косинуса решена.
Если нужно вспомнить определение синуса в прямоугольном треугольнике, то вспомнив определение косинуса, вы без труда установите, что синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. Ведь катетов всего два, если прилежащий катет «занят» косинусом, то синусу остаётся только противолежащий.
Как быть с тангенсом и котангенсом? Путаница та же. Учащиеся знают, что это отношение катетов, но проблема вспомнить какой к которому относится – то ли противолежащий к прилежащему, то ли наоборот.
Определения:
Тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему:
Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему:
Как запомнить? Есть два способа. Один так же использует словесно-логическую связь, другой – математический.
СПОСОБ МАТЕМАТИЧЕСКИЙ
Есть такое определение – тангенсом острого угла называется отношение синуса угла к его косинусу:
*Запомнив формулу, вы всегда сможете определить, что тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему.
Аналогично. Котангенсом острого угла называется отношение косинуса угла к его синусу:
Итак! Запомнив указанные формулы вы всегда сможете определить, что:
— тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему
— котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему.
СПОСОБ СЛОВЕСНО-ЛОГИЧЕСКИЙ
О тангенсе. Запомните связку:
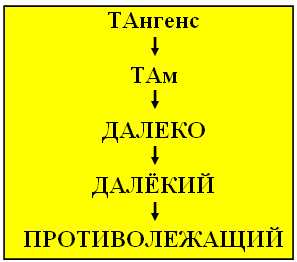
То есть если потребуется вспомнить определение тангенса, при помощи данной логической связи, вы без труда вспомните, что это
«… отношение противолежащего катета к прилежащему»
Если речь зайдёт о котангенсе, то вспомнив определение тангенса вы без труда озвучите определение котангенса –
«… отношение прилежащего катета к противолежащему»
Есть интересный приём по запоминанию тангенса и котангенса на сайте «Математический тандем», посмотрите.
СПОСОБ УНИВЕРСАЛЬНЫЙ
Можно просто зазубрить. Но как показывает практика, благодаря словесно-логическим связкам человек запоминает информацию надолго, и не только математическую.
Надеюсь, материал был вам полезен.
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Синус, косинус угла треугольника
Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.
Если у нас есть треугольник \(ABC\), рисунок выше, для которого \(С\)- прямой угол, то сторонами \(BC\) и \(AC\) будут катеты, а сторона \(AB\) — гипотенуза. Следовательно, по определению, синус угла \(ABC\) равен отношению катета \(АС\) к гипотенузе: синус угла \(ABC=\frac{AC}{AB}\) и синус угла \(BAC=\frac{BC}{AB}\).
косинус угла \(ABC=\frac{BC}{AB}\) и косинус угла \(BAC=\frac{AC}{AB}\).
Чаще всего известно лишь часть данных, например катет и угол, нужно выразить неизвестную величину. Подумайте, как это сделать.
Пример 1. Вычислим синус по двум катетам.
Берем тот же треугольник \(ACB\) с прямым углом \(С\) в котором мы знаем катеты: \(BC = 3\), \(AC = 4\). Для вычисления синуса угла с необходимо разделить катет на гипотенузу: \(sin ∠BAC = \frac{BC} { AB}\).
Гипотенузу вычислим из теоремы Пифагора: \(AC^2+BC^2=AB^2\) \(9+16=25\) \(AB=5\) откуда синус равен:
\(sin ∠ BAC = \frac{3}{5}\)
Пример 2. Вычислим синус угла \(ABC\) по углу\( BAC \) 30° градусов в прямоугольном треугольнике \(ACB\).
Самое главное помнить, что сумма всех углов в треугольнике равна 180 °.Найдем угол \(ABC\):
\(180\)° \(-30\)° \(-90\)°\(=60\)°.
\(sin\) \(60\)° возьмем из табличного значения: \(\frac{ \sqrt{3}} { 2}\)
Табличные значения \(sin\) и \(cos\):
Чтобы лучше понимать значения табличные значения синуса и косинуса представим их на координатной окружности: где ось ординат \((y)\) линия синуса, ось абсцисс \((x)\) – линия косинуса. Если вы забыли значения синуса и косинуса \(90\) и \(180\) можно нарисовать рисунок и посмотреть значения, не забывая, что на первом месте стоит \(x\), на втором \(y\) \((x,y)\);
Теорема синусов:
Теорема косинусов:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Тригонометрия
Катеты BC и AC прямоугольного треугольника ABC (рис. 1) называют противолежащим катетом угла α и прилежащим катетом угла α соответственно.
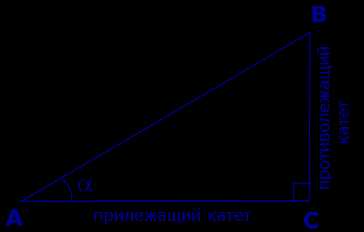
Рис.1
Катеты AC и BC прямоугольного треугольника ABC (рис. 2) называют противолежащим катетом угла β и прилежащим катетом угла β соответственно.
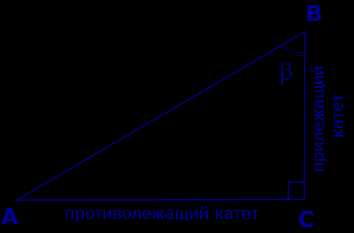
Рис.2
Синусом угла называют дробь:
Косинусом угла называют дробь:
Тангенсом угла называют дробь:
Котангенсом угла называют дробь:
Синус, косинус, тангенс и котангенс, и их комбинации называют тригонометрическими функциями. В данном разделе справочника тригонометрические функции вводятся для острых углов. В следующем разделе даётся определение тригонометрических функций для произвольных углов.
Для синуса, косинуса, тангенса и котангенса угла α используют обозначения
sin α , cos α , tg α , ctg α
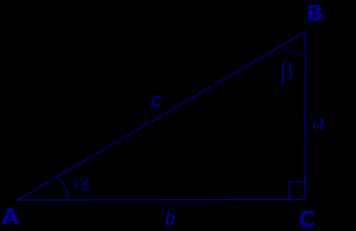
Рис.3
В соответствии с рисунком 3 справедливы формулы:
Следовательно,
Кроме того, справедливы формулы:
sin α = cos β, cos α = sin β, tg α = ctg β, ctg α = tg β,
которые можно переписать в виде:
sin α = cos (90° – α), cos α = sin (90° – α),
tg α = ctg (90° – α), ctg α = tg (90° – α).
Пример. Найти тригонометрические функции углов 30°, 45°, 60°.
Решение. Рассмотрим равносторонний треугольник ABC, сторона которого равна 2 (рис. 4), и проведем высоту BD.
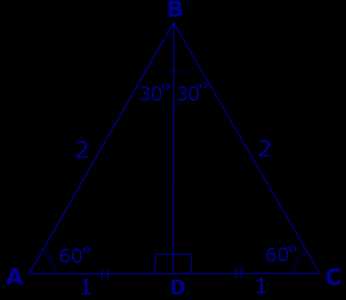
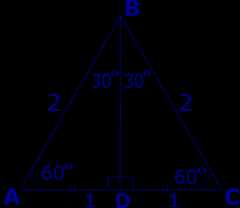
Рис.4
Тогда
Поэтому
Кроме того
Теперь рассмотрим прямоугольный равнобедренный треугольник ABC, катеты которого равны 1 (рис. 5).
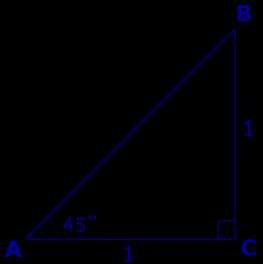
Тогда
Поэтому
Определение тригонометрических функций произвольного угла приводится в разделе справочника «Тригонометрические функции произвольного угла».
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
www.resolventa.ru
Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
Как найти,
гипотенузу или катеты в прямоугольном треугольнике.
a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c — стороны произвольного треугольника
α, β, γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c1 , c2 — отрезки полученные от деления гипотенузы, высотой
α, β — углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.
H — высота треугольника
a — сторона, основание
b, c — стороны
β, γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).
M — медиана
R — радиус описанной окружности
O — центр описанной окружности
с — гипотенуза
a, b — катеты
α — острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a, b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
a — сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Калькулятор — вычислить, найти медиану, биссектрису, высоту
Формулы для вычисления высоты, биссектрисы и медианы.
В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.
L — высота = биссектриса = медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
L— биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC , разделенный биссектрисой пополам
p — полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
www-formula.ru

