Энергия эл поля формула – Энергия электрического поля | Формулы и расчеты онлайн

Энергия электрического поля – Формулы по физике.рф

Энергия электрического поля — Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор

В формуле мы использовали :

— Энергия электрического поля

— Диэлектрическая проницаемость среды

— Диэлектрическая постоянная

— Объем занимаемый электрическим полем

— Напряжение

— Площадь обкладок

— Расстояние между обкладками конденсатора

xn--e1adcbkcgpcji1bjh6h.xn--p1ai

Энергия электромагнитного поля — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016; проверки требуют 3 правки.

Эне́ргия электромагни́тного по́ля — энергия, заключенная в электромагнитном поле^{[источник не указан 2591 день]}. Сюда же относятся частные случаи чистого электрического и чистого магнитного поля.

Работа электрического поля по перемещению заряда[править | править код]

Понятие работы A{\displaystyle A} электрического поля E{\displaystyle E} по перемещению заряда Q{\displaystyle Q} вводится в полном соответствии с определением механической работы:

A=∫F(x)dx=∫Q⋅E(x)dx=Q⋅U,{\displaystyle A=\int F(x)\,dx=\int Q\cdot E(x)\,dx=Q\cdot U,}

где U=∫Edx{\displaystyle U=\int E\,dx} — разность потенциалов (также употребляется термин напряжение).

Во многих задачах рассматривается непрерывный перенос заряда в течение некоторого времени между точками с заданной разностью потенциалов U(t){\displaystyle U(t)}, в таком случае формулу для работы следует переписать следующим образом:

A=∫U(t)dQ=∫U(t)I(t)dt,{\displaystyle A=\int U(t)\,dQ=\int U(t)I(t)\,dt,}

где I(t)=dQdt{\displaystyle I(t)={dQ \over dt}} — сила тока.

Мощность P{\displaystyle P} электрического тока для участка цепи определяется обычным образом, как производная от работы A{\displaystyle A} по времени, то есть выражением:

P(t)=dAdt=U(t)⋅I(t),{\displaystyle P(t)={\frac {dA}{dt}}=U(t)\cdot I(t),}

Это наиболее общее выражение для мощности в электрической цепи.

С учётом закона Ома

U=I⋅R{\displaystyle U=I\cdot R}

электрическую мощность, выделяемую на сопротивлении R{\displaystyle R}, можно выразить как через ток

P=I(t)2⋅R,{\displaystyle P=I(t)^{2}\cdot R,}

так и через напряжение:

P=U(t)2R.{\displaystyle P={{U(t)^{2}} \over R}.}

Соответственно, работа (выделившаяся теплота) является интегралом мощности по времени:

A=∫P(t)dt=∫I(t)2⋅Rdt=∫U(t)2Rdt.{\displaystyle A=\int P(t)\,dt=\int I(t)^{2}\cdot R\,dt=\int {{U(t)^{2}} \over R}\,dt.}

Энергия электрического и магнитного полей[править | править код]

Для электрического и магнитного полей их энергия пропорциональна квадрату напряжённости поля. Строго говоря, термин «энергия электромагнитного поля» является не вполне корректным. Вместо него в физике обычно используют понятие плотности энергии электромагнитного поля (в определённой точке пространства). Общая энергия поля равняется интегралу плотности энергии по всему пространству.

Плотность энергии электромагнитного поля является суммой плотностей энергий электрического и магнитного полей.

В системе СИ:

u=E⋅D2+B⋅h3.{\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} }{2}}+{\frac {\mathbf {B} \cdot \mathbf {H} }{2}}.}

В вакууме (а также в веществе при рассмотрении микрополей):

u=ε0E22+B22μ0=ε0E2+c2B22=E2/c2+B22μ0,{\displaystyle u={\varepsilon _{0}E^{2} \over 2}+{B^{2} \over {2\mu _{0}}}=\varepsilon _{0}{\frac {E^{2}+c^{2}B^{2}}{2}}={\frac {E^{2}/c^{2}+B^{2}}{2\mu _{0}}},}

где E — напряжённость электрического поля, B — магнитная индукция, D — электрическая индукция, H — напряжённость магнитного поля, с — скорость света, ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная и μ0{\displaystyle \mu _{0}} — магнитная постоянная. Иногда для констант ε0{\displaystyle \varepsilon _{0}} и μ0{\displaystyle \mu _{0}} — используют термины диэлектрическая проницаемость и магнитная проницаемость вакуума, — которые являются крайне неудачными, и сейчас почти не употребляются.

В системе СГС:^[1]

u=E⋅D+B⋅H8π.{\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} +\mathbf {B} \cdot \mathbf {H} }{8\pi }}.}

Энергия электромагнитного поля в колебательном контуре[править | править код]

Энергия электромагнитного поля в колебательном контуре:

W=CU22+LI22,{\displaystyle W={\frac {CU^{2}}{2}}+{\frac {LI^{2}}{2}},}

где:

U — электрическое напряжение в цепи,

C — электроемкость конденсатора,

I — сила тока,

L — индуктивность катушки или витка с током.

Потоки энергии электромагнитного поля[править | править код]

Для электромагнитной волны плотность потока энергии определяется вектором Пойнтинга S (в русской научной традиции — вектор Умова — Пойнтинга).

В системе СИ вектор Пойнтинга равен S=E×H{\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} } (векторному произведению напряжённостей электрического и магнитного полей) и направлен перпендикулярно векторам E и H. Это естественным образом согласуется со свойством поперечности электромагнитных волн.

Вместе с тем, формула для плотности потока энергии может быть обобщена для случая стационарных электрических и магнитных полей и имеет тот же вид: S=E×H{\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} }.

Факт существования потоков энергии в постоянных электрических и магнитных полях может выглядеть странно, но не приводит к каким-либо парадоксам; более того, такие потоки обнаруживаются в эксперименте.

ru.wikipedia.org

§11. Электрическая емкость. Энергия электрического поля Основные формулы

Электрическая ёмкость уединенного проводника или конденсатора определяется соотношением

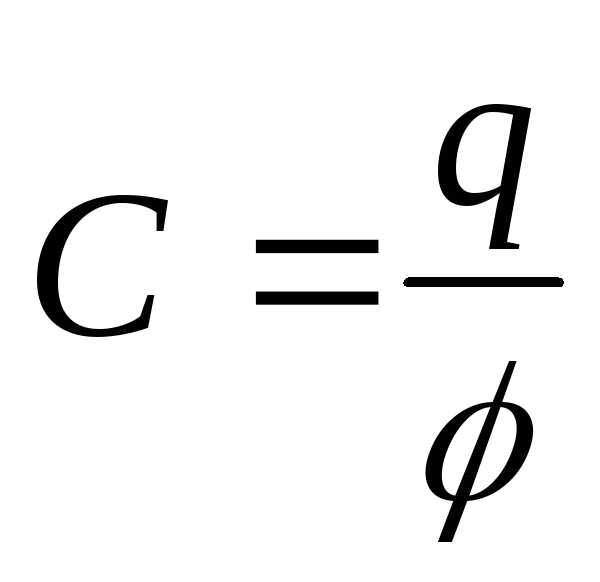, или ,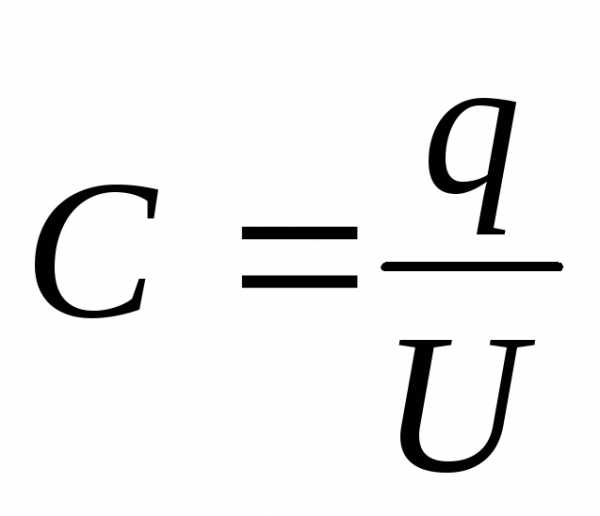

где φ – потенциал уединённого проводника; U – разность потенциалов между пластинами конденсатора; q – заряд проводника или конденсатора.

Электроемкость уединенной проводящей сферы радиуса R равна

.

Электроемкость плоского конденсатора равна

,

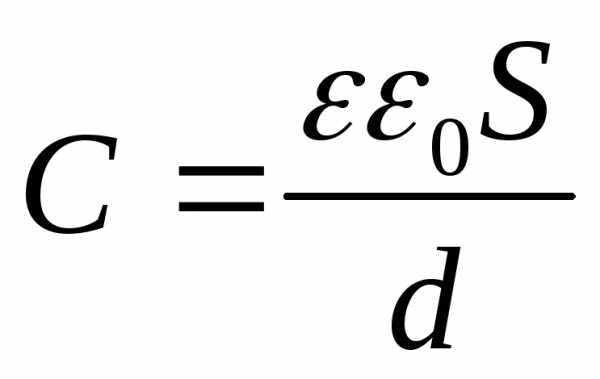где S – площадь каждой пластины конденсатора; d – расстояние между пластинами.

Электроемкость сферического конденсатора определяется формулой

,

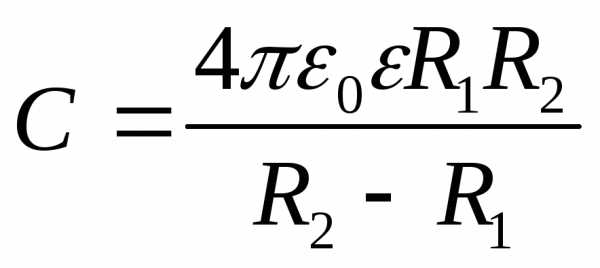где R₁ и R₂ – радиусы концентрических сфер, являющихся обкладками конденсатора; – диэлектрическая проницаемость вещества, находящегося между обкладками.

Электроемкость цилиндрического конденсатора определяется формулой

,

где R₁ и R₂ – радиусы двух коаксиальных цилиндров длины l, являющихся обкладками конденсатора, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ε.

Электроемкость батареи конденсаторов определяется по формулам:

а) при последовательном соединении

;

б) при параллельном соединении

,

где N – число конденсаторов в батарее.

Энергия электрического поля W уединенного заряженного проводника равна

,

где q – заряд проводника; φ– потенциал проводника; С – его электрическая емкость.

Энергия электрического поля заряженного конденсатора равна

,

где q – заряд конденсатора; U – разность потенциалов его обкладок; С – электрическая емкость конденсатора.

Объемная плотность энергии электростатического поля равна

,

где E и D – напряженность и смещение электростатического поля, находящегося в среде с диэлектрической проницаемостью ε.

Задачи

11.1. Найти электроемкость С уединенного металлического шара радиусом R = 1 см, находящегося в вакууме.

11.2. Определить электроемкость С металлической сферы радиу­сом R = 2 см, погруженной в воду.

11.3. Определить электроемкость С Земли, принимая ее за шар радиусом R = 6400 км.

11.4. Два металлических шара радиусами R₁ = 2 см и R₂ = 6 см соединены проводником, емкостью которого можно пренебречь. Шарам сообщен заряд q = l нКл. Найти поверхностную плотность зарядов на шарах.

11.5. Шар радиусом R₁ = 6 см заряжен до потенциала

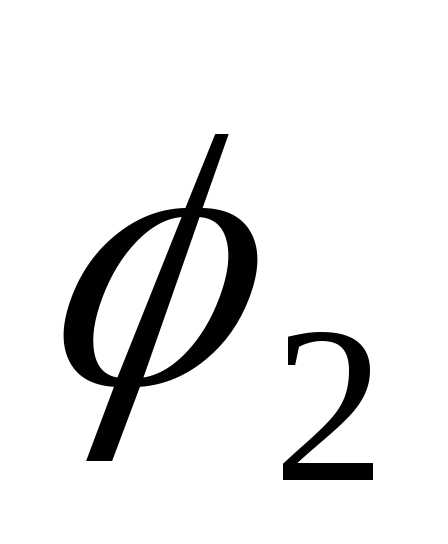= 300 В, а шар радиусом R₂ = 4 см – до потенциала = 500 В. Определить потенциал шаров после того, как их соединили металлическим проводником. Емкостью соединительного проводника пренебречь.

11.6. Определить электроемкость С плоского слюдяного конден­сатора, площадь S пластин которого равна 100 см², а расстояние между ними равно 0,1 мм.

11.7. Найти емкость системы одинаковых конденсаторов между точками А и В, которая показана: а) на рис. 11.1; б) на рис. 11.2.

1

1.8. Четыре одинаковые металлические пластины расположены в воздухе на расстоянии d = 1 мм друг от друга. Площадь каждой пластины S = 220 см². Найти емкость системы между точками А и В, если пластины соединены так, как показано: а) на рис. 11.3; б) на рис. 11.4.

11.9. Найти емкость бесконечной цепи, которая образована повторением одного и того же звена из двух одинаковых конденсаторов, каждый емкости С (рис. 11.5).

11.10. Между пластинами плоского конденсатора, заряженного до разности потенциалов U = 600 В, находятся два слоя диэлектриков: стекла толщиной d₁ = 7 мм и эбонита толщиной d₂ = 3 мм. Площадь S каждой пластины конденсатора равна 200 см². Найти: 1) электроемкость С конденсатора; 2) смещение D, напряженность Е

поля и падение потенциала Δφ в каждом слое.

11.11. На пластинах плоского конденсатора равномерно распределен заряд с поверхностной плотностью = 0,2 мкКл/м². Расстояние d между пластинами равно 1 мм. На сколько изменится разность потенциалов на его обкладках при увеличении расстояния d между пластинами до 3 мм?

11.12. В плоский конденсатор вдвинули плитку парафина толщиной d = 1 см, которая вплотную прилегает к его пластинам. На сколько нужно увеличить расстояние между пластинами, чтобы получить прежнюю емкость?

11.13. Электроемкость С плоского конденсатора равна 1,5 мкФ. Расстояние d между пластинами равно 5 мм. Какова будет электроемкость С конденсатора, если на нижнюю пластину положить лист эбонита толщиной d₁ = 3 мм?

11.14. Между пластинами плоского конденсатора находится плотно прилегающая стеклянная пластинка. Конденсатор заряжен до разности потенциалов

U₁ = 100 В. Какова будет разность потенциалов U₂, если вытащить стеклянную пластинку из конденсатора?

11.15. Две концентрические металлические сферы радиусами R₁ = 2 см и R₂ = 2,1 см образуют сферический конденсатор. Определить его электроемкость С, если пространство между сферами за­полнено парафином.

11.16. К воздушному конденсатору, заряженному до разности потенциалов U = 600 В и отключённому от источника напряжения, присоединили параллельно второй, незаряженный конденсатор таких же размеров и формы, но с диэлектриком (фарфор). Определить диэлектрическую проницаемость фарфора, если после присоединения второго конденсатора разность потенциалов уменьшилось до

U₁= 100 В.

11.17. Два конденсатора электроёмкостями С₁= 3 мкФ и С₂ = 6 мкФ соединены между собой и присоединены к батарее с ЭДС Е = 120 В. Определить заряды q₁и q₂конденсаторов и разности потенциалов U₁и U₂ между их обкладками, если конденсаторы соединены: 1) параллельно; 2) последовательно.

11.18. Конденсатор электроёмкостью С₁ = 0,2 мкФ был заряжен до разности потенциалов U₁ = 320 В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U₂ = 450 В, напряжение U на нём изменилось до 400 В. Вычислить ёмкость

С₂ второго конденсатора.

11.19. Конденсатор электроёмкостью С₁ = 0,6 мкФ был заряжен до разности потенциалов U₁ = 300 В и соединён параллельно со вторым конденсатором электроёмкостью С₂ = 0,4 мкФ, заряженным до разности потенциалов U₂ = 150 В. Найти заряд Δq, перетекший с пластин первого конденсатора на второй.

11.20. Три одинаковых плоских конденсатора соединены последовательно. Электроемкость С такой батареи конденсаторов равна 89 пФ. Площадь S каждой пластины равна 100 см². Диэлектрик – стекло. Какова толщина d стекла?

11.21. Конденсатор емкости С₁ = 1мкФ, заряженный до напряжения U=110B, подключили параллельно к концам системы из двух последовательно соединенных конденсаторов, емкости которых С₂ = 2 мкФ и С₃ = 3мкФ. Какой заряд протечет при этом по соединительным проводам?

11.22. Конденсатору, электроемкость С которого равна 10 пФ, сообщен заряд q = 1 пКл. Определить энергию W конденсатора.

11.23. Расстояние d между пластинами плоского конденсатора равно 2 см, разность потенциалов U = 6 кВ. Заряд q каждой пластики равен 10 нКл. Вычислить энергию W поля конденсатора и силу F взаимного притяжения пластин.

11.24. Какое количество теплоты Q выделится при разряде плоского конденсатора, если разность потенциалов U между пластинами равна 15 кВ, расстояние d = 1 мм, диэлектрик – слюда и площадь S каждой пластины равна 300 см²?

11.25. Сила F притяжения между пластинами плоского воздушного конденсатора равна 50 мН. Площадь S каждой пластины равна 200 см². Найти объемную плотность энергии ω электрического поля конденсатора.

11.26. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом R = 10 см каждая. Расстояние d₁ между пластинами равно 1 см. Конденсатор зарядили до разности потенциалов U = 1,2 кВ и отключили от источника тока. Какую работу А нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d₂ = 3,5 см?

11.27. Плоский воздушный конденсатор электроемкостью С = 1,11 нФ заряжен до разности потенциалов U = 300 В. После отключения от источника тока расстояние между пластинами конденсатора было увеличено в пять раз. Определить: 1) разность потенциалов U₁ на обкладках конденсатора после их раздвижения; 2) работу А внешних сил по раздвижению пластин.

11.28. Внутри плоского конденсатора находится параллельная обкладкам пластина, толщина которой составляет 0,6 расстояния между обкладками. Емкость конденсатора в отсутствие пластины С = 20нФ. Конденсатор сначала подключили к источнику постоянного напряжения U = 200 В, затем отключили и после этого медленно извлекли пластину из зазора. Найти работу, совершенную против электрических сил при извлечении пластины, если она: а) металлическая; б) стеклянная.

11.29. Конденсатор электроемкостью С₁ = 666 пФ зарядили до разности потенциалов U = 1,5 кВ и отключили от источника тока. Затем к конденсатору присоединили параллельно второй, незаряженный конденсатор электроемкостью С₂ = 444 пФ. Определить энергию, израсходованную на образование искры, проскочившей при соединении конденсаторов.

11.30. Конденсаторы электроемкостями С₁ = 1 мкФ, С₂ = 2 мкФ и С₃ = 3мкФ включены в сеть с напряжением U = 1,1 кВ. Определить энергию каждого конденсатора в случаях: 1) последовательного соединения; 2) параллельного соединения.

11.31. Электроемкость С плоского конденсатора равна 111 пФ. Диэлектрик – фарфор. Конденсатор зарядили до разности потенциалов U = 600 В и отключили от источника напряжения. Какую работу А нужно совершить, чтобы вынуть диэлектрик из конденсатора? Трение пренебрежимо мало.

11.32. Найти энергию W уединенной сферы радиусом R = 4 см, заряженной до потенциала φ = 500 В.

11.33. Вычислить энергию W электростатического поля металлического шара, которому сообщен заряд q = 100 нКл, если диаметр d шара равен 20 см.

11.34. Сферическую оболочку радиуса R₁, равномерно заряженную зарядом q, расширили до радиуса R₂. Найти работу, совершенную при этом электрическими силами.

11.35. Сферическая оболочка заряжена равномерно с повер­ хностной плотностью σ. Найти модуль электрической силы на единицу повер­хности оболочки.

studfile.net

Энергия электрического поля | Все формулы

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! 
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

Энергия электрического поля — Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор

В формуле мы использовали :

— Энергия электрического поля

— Диэлектрическая проницаемость среды

— Диэлектрическая постоянная

— Объем занимаемый электрическим полем

— Напряжение

— Площадь обкладок

— Расстояние между обкладками конденсатора

xn--b1agsdjmeuf9e.xn--p1ai

Энергия электрического поля | Все Формулы

   

Энергия электрического поля — Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор

   

Энергия электрического поля

В формуле мы использовали :

   

— Энергия электрического поля

   

— Диэлектрическая проницаемость среды

   

— Диэлектрическая постоянная

   

— Объем занимаемый электрическим полем

   

— Напряжение

   

— Площадь обкладок

   

— Расстояние между обкладками конденсатора

xn—-ctbjzeloexg6f.xn--p1ai

Энергия электрического поля

Опыт показывает, что заряженный конденсатор содержит запас энергии.

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую (рис. 1.7.1). При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов
  при переносе каждой порции Δq внешние силы должны совершить работу

Энергия W_е конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:

Рисунок 1.7.1. Процесс зарядки конденсатора

Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.

Электрическую энергию W_е следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для W_е аналогичны формулам для потенциальной энергии E_р деформированной пружины (см. ч. I, § 2.4)

где k – жесткость пружины, x – деформация, F = kx – внешняя сила.

По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Это легко проиллюстрировать на примере заряженного плоского конденсатора.

Напряженность однородного поля в плоском конденсаторе равна

E = U/d, а его емкость 

Поэтому

где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина

является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.

Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности w_е по всему объему, в котором создано электрическое поле.

questions-physics.ru

эксперименты и формулы :: SYL.ru

Когда рассматривается энергия электрического поля, следует изучать ее накопление и расходование. Накопителями энергии являются электроконденсаторы. При небольших габаритах такое устройство способно сосредотачивать в себе большое количество энергии.

При изучении конденсаторов становится легче понимать электростатические законы и возможности современных приборов. Таковыми являются, например, известные цифровые мультимеры, с помощью которых проводят измерения в пикофарадах. Сначала параметры следует оценивать, используя электростатические методы, а после этого — с применением мультимера.

Электрическая емкость удлиненного проводника

Изучение этого устройства дает лучшее понимание в вопросе, что такое энергия электрического поля. Проводники способны накапливать и сохранять заряды. Это свойство называется электрической емкостью.

Для понимания зависимости потенциала удлиненного проводника от заряда необходимо измерить потенциалы заряженного тела. Удобно это сделать относительно земли.

Электрометр с полым проводящим шаром и заземленным корпусом используют в виде электростатического вольтметра и измеряют потенциал тела относительно земли.

Шариком-пробником касаются электрического источника, перенося таким образом внутрь него заряд. При этом вольтметр покажет наличие определенного потенциала.

Повторяя опыт можно прийти к выводу, что отношение заряда к потенциалу постоянно.

Поменяв полый шар на другой и проделав те же опыты, если вольтметр покажет большие значения по сравнению с предыдущими, можно сделпть вывод о меньшей емкости второго шарика.

В международной системе СИ единица измерения электрической емкости — фарад.

Опыт со сферическим проводником

Если в среде с диэлектрической проницаемостью взять сферический проводник, где потенциал в бесконечности равен нулю, то потенциал в сфере с зарядом будет равен Q/4ПƐ˳ƐR, а электрическая емкость C=4ПƐ˳ƐR,

Получается, что электрическая емкость удлиненного шара пропорциональна его радиусу.

Из опытов следует, что тела считаются удлиненными в случае, если окружающие тела не вызывают существенного перераспределения заряда в них.

Конденсатор

Из двух одинаковых параллельных пластин делают конденсатор и подсоединяют к нему электрометр, который будет работать в виде вольтметра. К его стержню подводят проводящую сферу. Пластину заряжают, перенося заряд с эбонитовой палочки. Тогда вольтметр покажет наличие напряжения, возникшего между пластинами.

Перенеся равные заряды внутрь полой сферы, увеличим показания прибора. Поэтому емкость у пластин будет следующей: C=q/U, способной работать в роли конденсатора, накапливающего заряд электричества (где q – это заряд одной из пластин).

Емкость плоского конденсатора

Емкость плоского конденсатор C=ε̥ε/d, где d – расстояние между пластинами.

Формула может быть подтверждена экспериментом. Собирается плоский конденсатор, заряжается и соединяются пластины с вольтметром. Не изменяя заряд, меняют другие показатели, наблюдая в это время за прибором. Показания будут обратно пропорциональны емкости: U=q/C–1/C.

Делая расстояние между пластинами больше, будем наблюдать увеличение напряжения. Смещая пластины параллельно и увеличивая площадь, получим сокращение напряжения, а емкость при этом увеличится. Если в промежуток между пластинами поместить диэлектрик, то показания вольтметра сократятся.

Так как в ходе эксперимента значение заряда не меняли, получается, что емкость конденсатора прямо пропорциональна перекрытию пластин и обратно пропорциональна d.

Параллельное и последовательное соединение конденсаторов

При параллельном соединении емкости приборов и их напряжения имеют одинаковые значения, а заряды — разное. Общий заряд равен их сумме по отдельности.

При последовательном соединении подключают вольтметр, имеющий полую сферу. Для одной обкладки первого конденсатора дается положительный заряд, тогда другая обкладка приобретет отрицательный, а при соединении с проводником второго прибора — положительный. Тогда оба конденсатора получат идентичные заряды, а напряжения у них будут иметь разные значения.

В результате емкость здесь будет определена по формуле: 1/C=1/C1+1/C2

Энергия плоского и произвольного конденсатора

На пластину подают заряд, имеющий значение, при котором разность потенциалов между пластинами стала равной U. Тогда напряженность будет равна E=U/d, где d – расстояние между объектами.

Одна из пластин находится в электрическом поле другой, где напряженность E/2. Тогда сила притяжения к другой пластине будет f=qE/2. Потенциальная энергия электрического поля заряда равна работе этого поля при сближении пластин.

Подставив ряд значений, получим, что энергия поля W=qU/2=q²/2C=CU²/2.

Такая формула подходит для любого конденсатора. Полная работа поля равна A=1/2qU.

То же самое получится, если применить удлиненный проводник вместо конденсатора.

Определение энергии экспериментальным путем

Замер энергии прибора производится по тепловому действию. В пробирку помещают спираль из металла, закрывают пробкой с трубкой, в которой имеется капелька воды. Получится газовый термометр. К спирали подключают конденсатор, а параллельно — электрометр с шаром, полым внутри.

Конденсатор заряжают при помощи шариков, а затем разряжают посредством спирали. Можно будет заметить перемещение капли в трубке.

После охлаждения воздуха и перемещения капли в начальное положение напряжение увеличивают. Капля переместится на несколько значений выше. Конденсатор меняют на большую емкость в два раза. Зарядив его до начального уровня, можно наблюдать перемещение, увеличенное вдвое.

Плотность энергии электрического поля

Задают энергию такую, чтобы конденсатор не имел значений, а принимались во внимание только величины, характеризующие поле. При этом должна быть вычислена энергия электрического поля на единицу объема.

В результате подстановок плотность энергии получается: ω=W/V=ε̥εΕ²/2, то есть она пропорциональна квадрату напряженности.

Энергия взаимодействия зарядов или энергия в электрическом поле

Итак, для зарядки конденсатора необходима работа, чтобы преодолеть силы электростатического притяжения между разными зарядами при их разделении. За счет этого возникнет запас потенциальной энергии.

Для зарядки любого тела также необходима работа, в данном случае для преодоления электростатического отталкивания между одноименными зарядами.

Взяв уединенный проводник, подаем заряд q. Потенциал поля на бесконечности будет равен нулю, а потенциал проводника — φ(q). Для перенесения малого заряда ∆q требуется работа:

∆A=φ(q)∆q.

Работа по зарядке уединенного проводника определяется по формуле:

A=W=1/2 φ(Q)Q=1/2C(φ(Q))²

На вопрос, где запасается энергия, отвечают двумя вариантами. По одному из них, это энергия взаимодействия зарядов на проводнике, а по другому, энергия — электрического поля получается, так как распределена в окружающем пространстве.

Какому ответу из этих двух отдать предпочтение — личное решение каждого ученика. Но, следует учесть, что при изучении переменных полей возможным становится только второй вариант, где энергия связывается с электрическим полем.

www.syl.ru