Катушка индуктивности. Устройство и принцип работы.
Приветствую всех на нашем сайте!
Мы продолжаем изучать электронику с самых основ, и темой сегодняшней статьи будет катушка индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы.
Устройство и принцип работы катушки индуктивности.
Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку 🙂 То есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:

Важнейшей характеристикой
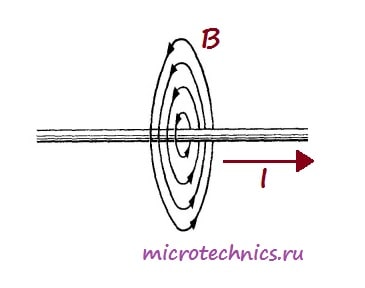
А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:

В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри – это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину индуктивности катушки можно рассчитать по следующей формуле:
L = \frac{\mu_0\thinspace \mu S N^2}{l}
Давайте разберемся, что за величину входят в это выражение:
- \mu_0 – магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению: \mu_0 = 4 \pi \cdot 10^{-7}\medspace\frac{Гн}{м}
- \mu – магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз
- S – площадь поперечного сечения катушки
- N – количество витков
- l – длина катушки
Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.
С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный!
Катушка индуктивности в цепи постоянного тока.
Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет 🙂 Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:
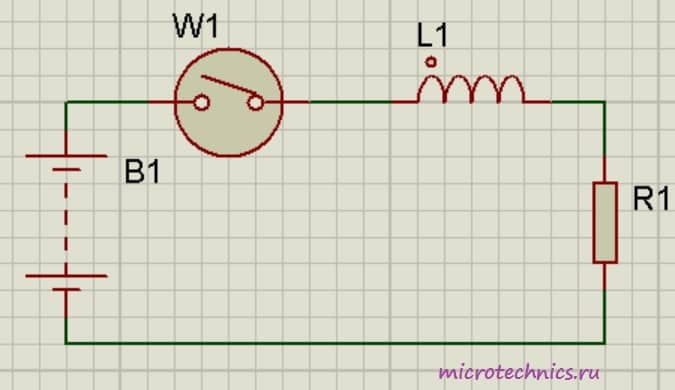
Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель?
Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:
\varepsilon_s = -\frac{d\Phi}{dt}
Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
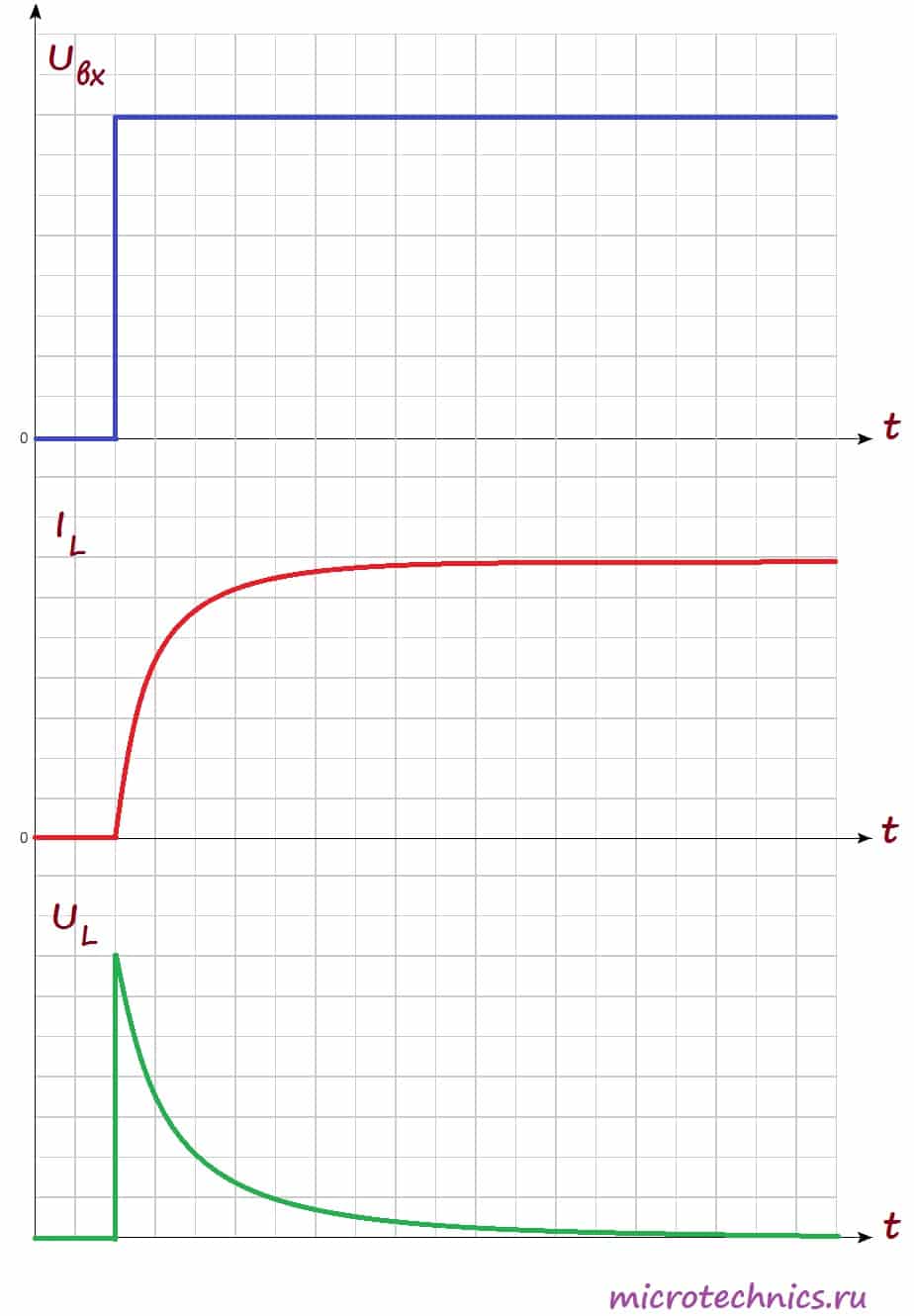
На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать.
Напряжение на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
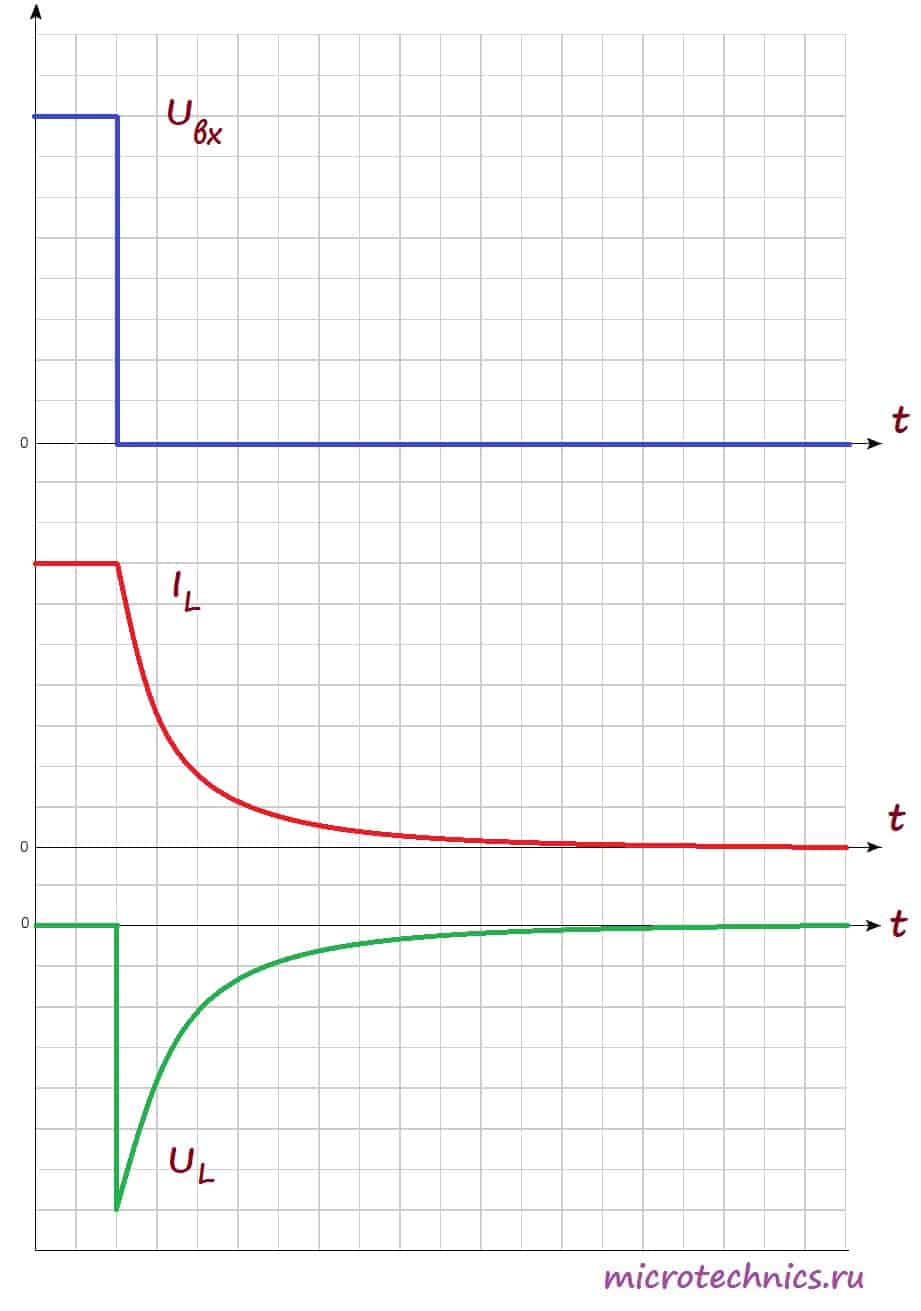
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:
\varepsilon_s = -L\medspace\frac{dI}{dt}
На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.
Катушка индуктивности в цепи переменного тока.
Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:
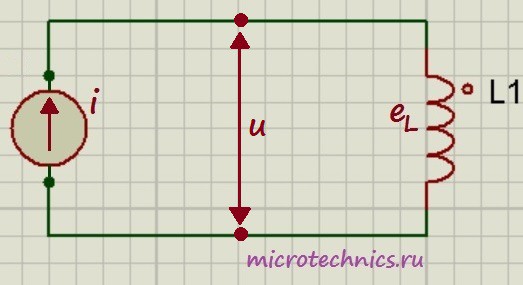
Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:
Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:
\varepsilon_L = -L\medspace\frac{dI}{dt}
Собственно, график нам и демонстрирует эту зависимость! Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.
Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу 🙂
Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: \varepsilon < 0, i > 0, участок 3-4: \varepsilon > 0, i < 0). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника).
А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока).
И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:
X_L = w\medspace L
Где w – круговая частота: w = 2 \pi f. [/latex]f[/latex] – это частота переменного тока. Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный (f = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.
Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение u? Здесь все на самом деле просто! По 2-му закону Кирхгофа:
u + \varepsilon_L = 0
А следовательно:
u = – \varepsilon_L
Построим на одном графике зависимости тока и напряжения в цепи от времени:
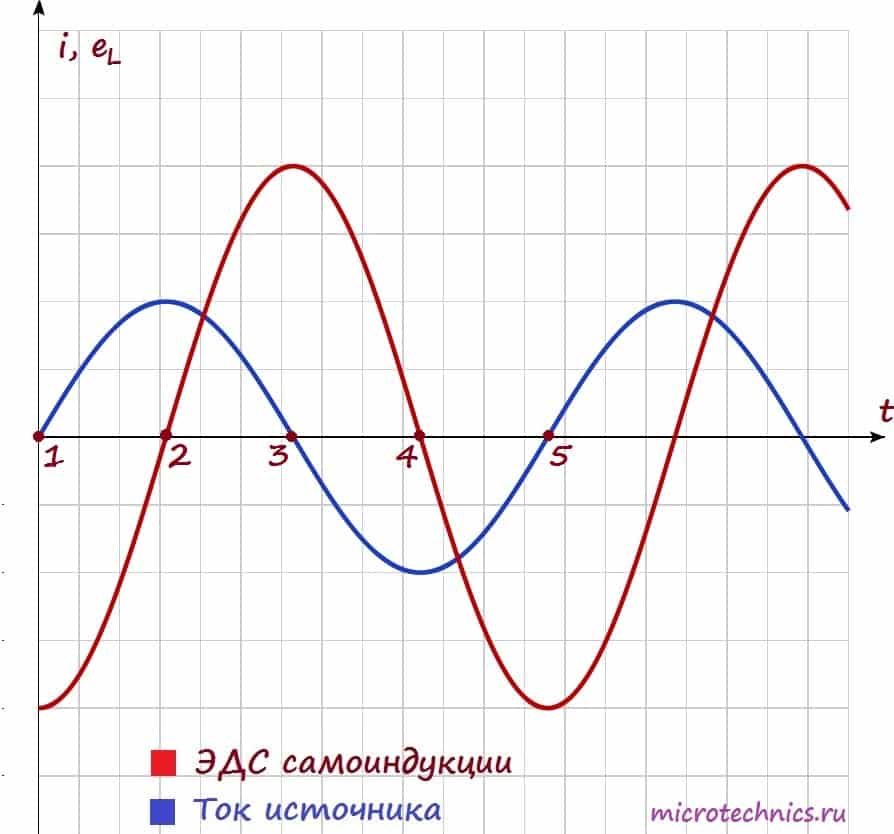
Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:
При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода.
Вот и с включением катушки в цепь переменного тока мы разобрались!
На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому разговор о катушках индуктивности мы продолжим в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!
Катушка индуктивности в цепи постоянного тока. — Студопедия.Нет
Устройство и принцип работы катушки индуктивности.
Мы продолжаем изучать электронику с самого начала, то есть с самых основ и темой сегодняшней статьи будет принцип работы и основные характеристики катушек индуктивности
. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса — резисторы и конденсаторы.
Устройство и принцип работы катушки индуктивности.
Как уже понятно из названия элемента — катушка индуктивности, в первую очередь, представляет из себя именно катушку :), то есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием — витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:

Важнейшей характеристикой
А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:
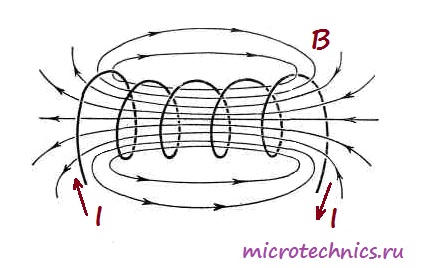
В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри — это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину индуктивности катушки можно рассчитать по следующей формуле:
Давайте разберемся, что за величину входят в это выражение:
§ — магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению:
§ — магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами — магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз.
§ — площадь поперечного сечения катушки
§ — количество витков
§ — длина катушки
Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины — уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.
С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы — в одной будем пропускать через катушку постоянный ток, а в другой -переменный
Катушка индуктивности в цепи постоянного тока.
Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:
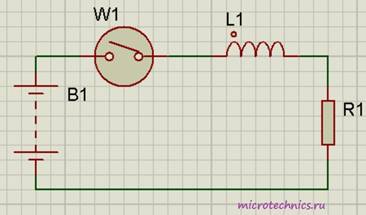
Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь.
Что же произойдет в тот момент когда мы замкнем выключатель?
Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:
Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
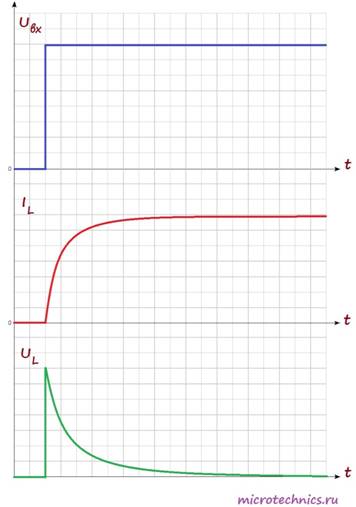
На первом графике мы видим входное напряжение цепи — изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать. Напряжения на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
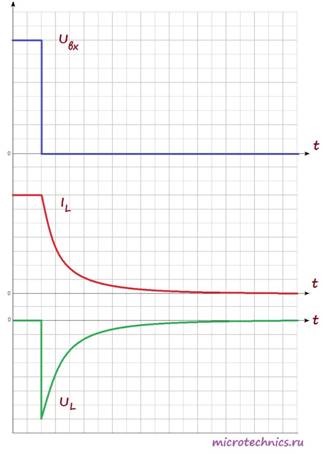
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:
На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим кцепям переменного тока.
Катушка индуктивности в цепи постоянного тока
Катушка индуктивности – это элемент характеризующимся своим свойством накапливать энергию магнитной поля.
Первый закон коммутации гласит: ток, протекающий в катушке индуктивности, в момент коммутации не может измениться скачком.
Это понятно из формулы:

Предположим, что ток iL изменился скачком, то есть:

А значит, что и напряжение в данном случае будет бесконечно велико:

Чего в природе быть не может, так как, следуя закону сохранения энергии, для этого бы потребовался источник энергии бесконечной мощности.

На схеме представлена RL – цепь, запитанная от источника постоянного тока. При замыкании ключа в положение 1, ток протекает по цепи “плюс” источника – резистор R – катушка индуктивности — “минус” источника. Тем самым, происходит накопление энергии магнитного поля в катушке индуктивности.
Напряжение и ток, протекающие в данной цепи, изменяются по экспоненциальному закону. Причем, их изменения взаимообратные, т.е. с увеличением тока, падение напряжения на катушке уменьшается.

Если мы переведем ключ в положение 2, то ток, не изменив своего направления, начнет уменьшаться по экспоненте до нуля. С физической точки зрения, в данном случае катушка отдает накопленную энергию магнитного поля в цепь, где она расходуется на тепловые потери в резисторе.
Одной из характеристик данной цепи является постоянная времени τ. Она зависит от величины индуктивности и активного сопротивления. Примерно за 5 τ ток в цепи достигает своего минимума или максимума.

Реализуем эту схему в программной среде Multisim 13.0 , взяв значения R = 10 Ом, L = 0,1 Гн.

Скачать файл Multisim 13.0
Рассчитаем время, за которое ток в цепи достигает установившегося значения:

Собранная схема запитана от батареи 12 В. Для снятия значений тока, использовался инструмент “current probe”. Внутреннее активное сопротивление катушки индуктивности, принято равным нулю.
Добротность и энергия катушки индуктивности. Варианты соединения.
Продолжаем обсуждение катушек индуктивности! В первой статье (ссылка) мы обсудили все основные аспекты, а именно устройство катушек, принцип работы и их поведение при использовании в цепях постоянного и переменного тока. Но некоторые моменты остались незатронутыми, собственно, их мы и обсудим в этой статье 🙂 И начнем с очень важной характеристики, а именно добротности катушки индуктивности.
Активное сопротивление и добротность катушки индуктивности.
Итак, начнем мы с того, что обсудим некоторые характеристики катушек индуктивности, с которыми мы не успели познакомиться в предыдущей статье. И для начала рассмотрим активное сопротивление катушки.
Рассматривая примеры включения катушек в различные цепи мы считали их активное сопротивление равным 0 (такие катушки называют идеальными). Но на практике любая катушка обладает ненулевым активным сопротивлением. Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:
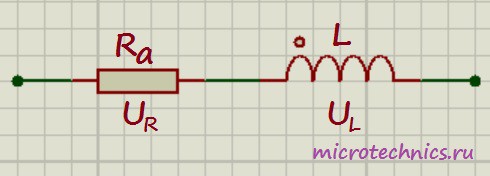
Идеальная катушка, как вы помните, не оказывает никакого сопротивления постоянному току, и напряжение на ней равно 0. В случае с реальной катушкой ситуация несколько меняется. При протекании по цепи постоянного тока напряжение на катушке будет равно:
U_L = IR_а
Ну а поскольку частота тока равна 0 (постоянный ток), то реактивное сопротивление будет равно:
X_L = 2\pi f L = 0
А что же будет происходить при включении реальной катушки индуктивности в цепь переменного тока? Давай разбираться. Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:
u = iR + u_L
Напряжение на идеальной катушке, как вы помните, выражается через ЭДС самоиндукции:
u_L = -\varepsilon_L = L\frac{di}{dt}
И мы получаем для напряжения на реальной катушке индуктивности:
u = iR + L\frac{di}{dt}
Отношение реактивного (индуктивного) сопротивления к активному называется добротностью и обозначается буквой Q:
Q = \frac{X_L}{R}
Раз активное сопротивление R идеальной катушки равно 0, то значит ее добротность Q будет бесконечно большой. Соответственно, чем выше добротность катушки индуктивности, тем она ближе к идеальной. Итак, активное сопротивление катушки мы рассмотрели, давайте перейдем к следующему вопросу.
Энергия катушки индуктивности.
Электрический ток, протекающий через катушку способствует накоплению энергии в магнитном поле катушки. При пропадании/отключении тока эта энергия будет возвращена в электрическую цепь. С этим мы и столкнулись при рассмотрении катушек индуктивности в цепях постоянного тока. Больше тут добавить особо нечего, просто приведу формулу, по которой можно определить величину накопленной энергии катушки индуктивности:
W = \frac{LI^2}{2}
Давайте переходить к вариантам соединения катушек между собой… Все расчеты мы будем производить для идеальных катушек индуктивности, то есть их активные сопротивления равны 0. К слову, в большинстве теоретических задач и примеров, рассматриваются именно идеальные катушки. Но не стоит забывать о том, что в реальных цепях активное сопротивление не равно 0 и его необходимо учитывать при проведении любых расчетов.
Последовательное соединение катушек индуктивности.
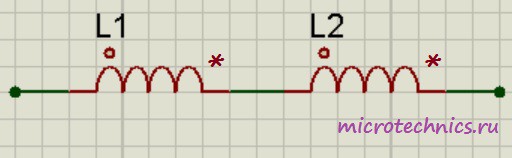
При последовательном соединении катушек индуктивности их можно заменить одной катушкой с величиной индуктивности, равной:
L_0 = L_1 + L_2
Вроде бы все просто, проще некуда, но тут есть один важный момент. Данная формула справедлива только в том случае, если катушки расположены на на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой:
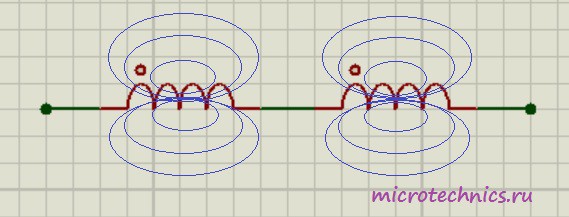
Если же катушки расположены близко друг к другу и часть магнитного поля одной катушки пронизывает вторую, то тут ситуация совсем другая. Возможно два варианта:
- магнитные потоки катушек имеют одинаковое направление
- магнитные потоки направлены навстречу друг другу
Первый случай называется согласным включением катушек – начало второй катушки подключается к концу первой. А второй вариант называют встречным включением – конец второй катушки подключается к началу первой. На схемах начало катушки обозначают символом “*“. Таким образом, на схеме, которая представлена на рисунке мы имеем согласное включение катушек индуктивности. Для этого случая общая индуктивность определяется так:
L = L_1 + L_2 + 2M
Где M – взаимная индуктивность катушек. При встречном включении последовательно соединенных катушек индуктивности:
L = L_1 + L_2\medspace-\medspace 2M
Можно заметить, что если потоки имеют одинаковое направление (согласное включение), то общая индуктивность увеличивается на двойную величину взаимной индуктивности. А если потоки направлены навстречу друг другу – уменьшается на ту же самую величину.
Параллельное соединение катушек индуктивности.
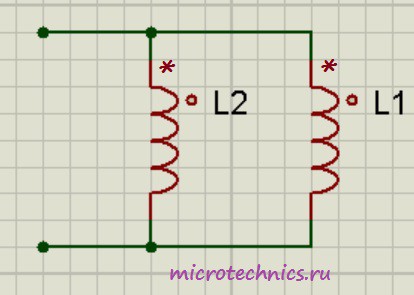
При параллельном соединении катушек индуктивности также возможны три варианта:
- Магнитное поле одной катушки не пересекает витков второй катушки, тогда: \frac{1}{L_0} = \frac{1}{L_1} +\frac{1}{L_2} или L_0 = \frac{L_1L_2}{L_1 + L_2}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены согласно (как изображено на рисунке – то есть начала обеих катушек подключены к одному узлу). В этом случае: L_0 = \frac{L_1L_2\medspace-\medspace M^2}{L_1 + L_2\medspace-\medspace 2M}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены встречно. В этом случае: L_0 = \frac{L_1L_2\medspace-\medspace M^2}{L_1 + L_2 + 2M}
Также как и в случае с последовательным соединением, при согласном включении общая индуктивность будет больше, чем при встречном включении, поскольку знаменатель дроби будет меньше.
Собственно, на этом мы и заканчиваем рассмотрение катушек индуктивности. Ранее мы изучили конденсаторы и резисторы, а в будущих статьях нам предстоит работать с цепями, включающие все эти элементы в разных комбинациях 🙂 Так что подписывайтесь на обновления и не пропускайте новые статьи на нашем сайте!
Катушка индуктивности в цепи постоянного тока — Студопедия.Нет
Первый закон коммутации гласит: ток, протекающий в катушке индуктивности, в момент коммутации не может измениться скачком. Это понятно из формулы:
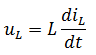

На схеме представлена RL – цепь, запитанная от источника постоянного тока. При замыкании ключа в положение 1, ток протекает по цепи “плюс” источника – резистор R – катушка индуктивности — “минус” источника. Тем самым, происходит накопление энергии магнитного поля в катушке индуктивности.
Напряжение и ток, протекающие в данной цепи, изменяются по экспоненциальному закону. Причем, их изменения взаимообратные, т.е. с увеличением тока, падение напряжения на катушке уменьшается.
Если мы переведем ключ в положение 2, то ток, не изменив своего направления, начнет уменьшаться по экспоненте до нуля. С физической точки зрения, в данном случае катушка отдает накопленную энергию магнитного поля в цепь, где она расходуется на тепловые потери в резисторе.
Одной из характеристик данной цепи является постоянная времени τ. Она зависит от величины индуктивности и активного сопротивления. Примерно за 5 τ ток в цепи достигает своего минимума или максимума.

61. Зарядка конденсатора от источника постоянного напряжения.
Простейшим примеромпереходного процессаможет служить зарядка конденсатора ёмкостью С (рис.) от источника постоянного тока (аккумулятора) с эдс Е и внутренним сопротивлением r через резистор R , ограничивающий ток в цепи. Начиная с момента времени t = 0 , когда замыкается ключ, ток в цепи уменьшается по экспоненциальному закону, приближаясь к нулю, а напряжение увеличивается, асимптотически стремясь к значению, равному эдс источника. Скорость изменения напряжения и тока зависит от ёмкости конденсатора и сопротивления в цепи: чем больше ёмкость и сопротивление, тем длительнее процесс зарядки. Через интервал времени t = (R + r)×C, называемый постоянной времени зарядки конденсатора, напряжение на его обкладках достигает значения uc = 0,63 Е,а сила тока i=0,37 Io, где Io — начальная сила тока, равная отношению эдс к сопротивлению цепи. Через интервал времени 5t uc>0,99 Е, а сила тока i<0,01 I0,и с погрешностью менее 1% Переходные процессы можно считать закончившимся. За время переходного процесса энергия электрического поля конденсатора увеличивается от нуля до Wc=1/2CE2.»

1.  ;
; 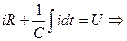
 ;
; 
2. 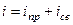
3. 
4. 
 ;
; 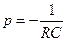 ;
; 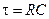
5. 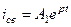 ;
; 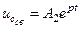
6.  ;
; 
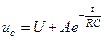 ;
;
 ;
; 
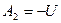
Начальные условия – значения токов через катушки индуктивности и напряжений на конденсаторах, известные из докомутационного режима.
Значения u и i на всех элементах схемы при 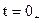 – зависимые начальные условия. Они определяются из независимых с помощью исходного диф. уравнения.
– зависимые начальные условия. Они определяются из независимых с помощью исходного диф. уравнения.
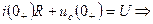
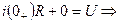
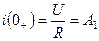
7. 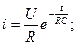
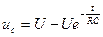

62. Разрядка конденсатора на сопротивление.
Разряд предварительно заряженного конденсатора через активное сопротивление (через резистор) является простейшим переходным процессом.
Пусть конденсатор ёмкостью С заряжен до напряжения U. В момент t=0 замыкается ключ К и конденсатор начинает разряжаться через активное сопротивление R. Так как здесь внешнего воздействия нет, то в цепи будет только свободный процесс.
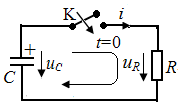 Выбрав направление обхода, запишем для этой цепи второе уравнение Кирхгофа:
Выбрав направление обхода, запишем для этой цепи второе уравнение Кирхгофа:
uR−uC=0,или
iR−uC=0. (1)
А так как для конденсатора ток i здесьявляется разрядным, то 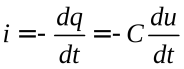 , и тогда
, и тогда 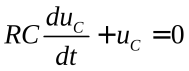 , (2)
, (2)
или 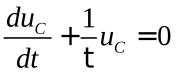 ,
,
где 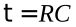 − постоянная времениRC-цепочки.
− постоянная времениRC-цепочки.
Общее решение этого однородного уравнения имеет вид:
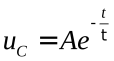 ,где А – коэффициент, определяемый начальным условием, т.е.
,где А – коэффициент, определяемый начальным условием, т.е. 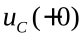 − напряжением на конденсаторев первый момент после замыкания ключа К. Так как, по условию, до замыкания напряжение
− напряжением на конденсаторев первый момент после замыкания ключа К. Так как, по условию, до замыкания напряжение 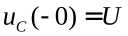 , а напряжение на конденсаторе скачком измениться не может (это привело бы к тому
, а напряжение на конденсаторе скачком измениться не может (это привело бы к тому 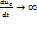 , что, тогда как в уравнении (2) иС – конечно), то
, что, тогда как в уравнении (2) иС – конечно), то
 (это второе правило коммутации).
(это второе правило коммутации).
Это даёт: А=U, и, следовательно,
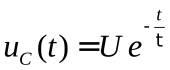 . (3)
. (3)
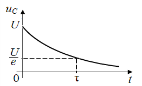
Отсюда видно, что τ – это время, за которое напряжение на конденсаторе убывает в е раз:
 2,7.
2,7.
Реально время переходного процесса оценивается примерно в 3τ, когда напряжение уменьшается в е3 = 20 раз, или когда до установившегося значения осталось лишь 1/20 = 5 % от исходного напряжения U.
63 Нелинейные электрические цепипостоянного тока
 В электрические цепи могут входить пассивные элементы, электрическое сопротивление которых существенно зависит от тока или напряжения, в результате чего ток не находится в прямо пропорциональной зависимости по отношению к напряжению. Такие элементы и электрические цепи, в которые они входят, называют нелинейными элементами. Все электрические цепи являются нелинейными. Они могут считаться линейными в ограниченных диапазонах значений
В электрические цепи могут входить пассивные элементы, электрическое сопротивление которых существенно зависит от тока или напряжения, в результате чего ток не находится в прямо пропорциональной зависимости по отношению к напряжению. Такие элементы и электрические цепи, в которые они входят, называют нелинейными элементами. Все электрические цепи являются нелинейными. Они могут считаться линейными в ограниченных диапазонах значений 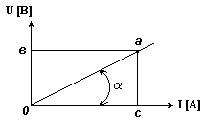 токов и напряжений. Электрическое сопротивление линейного элемента пропорционально тангенсу угла наклона его вольтамперной характеристики к оси тока.
токов и напряжений. Электрическое сопротивление линейного элемента пропорционально тангенсу угла наклона его вольтамперной характеристики к оси тока.
В нелинейной электрической цепи сопротивления ее элементов зависят от величины или направления тока или напряжения. Нелинейные элементы имеют криволинейные вольтамперные характеристики, симметричные или несимметричные относительно осей координат. Сопротивления нелинейных элементов с симметричной характеристикой не зависят от направления тока. Сопротивления нелинейных элементов с несимметричной характеристикой зависят от направления тока. Например, электролампы, термисторы имеют симметричные вольтамперные характеристики , а полупроводниковые диоды — несимметричные характеристики. Элементы нелинейной цепи делят на резистивные,
индуктивные и емкостные. 
64..Статические и динамические сопротивления не линейных элементов
Статическим или интегральным сопротивлением нелинейного элемента называется отношение напряжения на элементе к величине тока. Это сопротивление пропорционально тангенсу угла наклона α между осью тока и прямой, проведенной из начала координат в точку а характеристики. 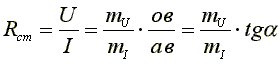
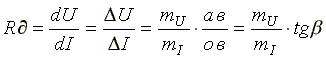 Здесь mU – масштаб напряжений, mI – масштаб токов.
Здесь mU – масштаб напряжений, mI – масштаб токов.
 Дифференциальное или динамическое сопротивление нелинейного элемента — это величина, равная отношению бесконечно малого приращения напряжения на нелинейном сопротивлении к соответствующему приращению тока. Это сопротивление пропорционально тангенсу угла наклона β между осью тока и касательной к точке a характеристики. При переходе от одной точки вольтамперной характеристики к соседней статическое и динамическое сопротивления нелинейного элемента меняются.
Дифференциальное или динамическое сопротивление нелинейного элемента — это величина, равная отношению бесконечно малого приращения напряжения на нелинейном сопротивлении к соответствующему приращению тока. Это сопротивление пропорционально тангенсу угла наклона β между осью тока и касательной к точке a характеристики. При переходе от одной точки вольтамперной характеристики к соседней статическое и динамическое сопротивления нелинейного элемента меняются.
Катушка индуктивности
Катушка индуктивности, как показано на рис. 4.11, представляет собой простомоток провода. Условное обозначение катушки индуктивности показано на рис. 4.12. В отличие от конденсатора, который препятствует изменению приложенного к нему напряжения, катушка индуктивности препятствует изменению протекающего через нее тока. Иными словами,

Рис. 4.12. Условное обозначение катушки индуктивности. Рис. 4.13
если ток, подаваемый в схему, которая содержит катушку, резко увеличить, то ток в схеме будет нарастать плавно до достижения своего максимального значения.
Способность катушки индуктивности препятствовать изменению силы тока, протекающего через нее, носит название индуктивности этой катушки. Индуктивность обозначается буквой L, единицей ее измерения является генри (Гн).
Постоянная времени RС-цепи
На рис. 4.13 последовательная цепочка из конденсатора и резистора соединяется через ключ с источником питания. Когда ключ находится в положении 1, конденсатор постепенно заряжается через сопротивление, пока напряжение на нем не достигнет уровня Е т. е. ЭДС или напряжения источника питания.
Процесс заряда конденсатора показан на рис. 4.14(а) экспоненциальной кривой. Время, за которое напряжение на конденсаторе достигает значения 0,63 от максимума, т. е. в данном случае 0,63Е, называется постоянной времени контура или цепи.
Вернемся к рис. 4.13. Если ключ установить в положение 2, конденсатор будет сохранять запасенную энергию. При переведении ключа в положение3 конденсатор начинает разряжаться на землю через резистор R, и напряжение на нем постепенно падает до нуля. Процесс разряда конденсаторапоказан на рис. 4.14(б). В этом случае постоянной времени цепи называется время, за которое напряжение на конденсаторе уменьшается 0,63 от своего максимального значения.

Рис. 4.14. Кривые заряда (а) и разряда (б) конденсатора, где t — постоянная времени.
Как для случая заряда, так и для случая разряда конденсатора через резистор R постоянная времени цепи выражается формулой
где t — постоянная времени в секундах, С — емкость в фарадах, R — сопротивление, выраженное в омах.
Например, для случая С = 10мкФ и R= 10 кОм постоянная времени цепи равна
На рис. 4.15 изображены графики процессов заряда для цепей с малой и с большой постоянной времени.

Рис. 4.15. Процессы заряда для цепей с малой и с большой постоянной времени.
Постоянная времени RL-цепи
Рассмотрим схему, изображенную на рис. 4.16. Катушка индуктивности L соединена последовательно с резистором R, имеющим сопротивление 1 кОм. В момент замыкания ключа S ток в цепи равен нулю, хотя под действиемЭДС источника он, казалось бы, должен резко увеличиться. Однако катушка индуктивности, как известно, препятствует всякому изменению силы тока, протекающего через нее, поэтому ток в цепи будет возрастать по экспоненциальному закону, как показано на рис. 4.17. Ток будет возрастать до тех пор, пока не достигнет своего максимального значения. После этого увеличение тока прекратится, а падение напряжения на резисторе R станет равным приложенному напряжению Е. Установившееся значение тока равно
E/R = 20 В/1 кОм = 20 мА.
Скорость изменения тока в цепи зависит от конкретных значений R и L. Время, необходимое для того, чтобы сила тока достигла значения, равного 0,63 от его максимальной величины, носит название постоянной времени цепи. Постоянная времени вычисляется по формуле L/R где L выражается в генри, а R — в омах. В этом случае постоянная времени получается в секундах. Используя значения L и R, указанные на рисунке, получаем
Следует заметить, что, чем больше R, тем меньше L/R и тем быстрее изменяется ток в цепи.

Рис. 4.16.

Рис. 4.17. Экспоненциальное увеличение тока, протекающего через катушку индуктивности.
Сопротивление по постоянному току
Катушка индуктивности, включенная в цепь, не препятствует протеканию постоянного тока, если, конечно, но принимать во внимание очень малое сопротивление провода, из которого она сделана. Следовательно, катушка индуктивности имеет нулевое или очень малое сопротивление и может рассматриваться в цепи постоянного тока как цепь короткого замыкания. Конденсатор же в связи с наличием в нем изолирующего диэлектрика имеет бесконечное или очень большое сопротивление и может рассматриваться в цепи постоянного тока как разрыв.
Векторное представление
Сигнал синусоидальной формы может быть представлен в виде вектора ОА, вращающегося против часовой стрелки с угловой скоростью ω= 2πf, где f – частота сигнала (рис. 4.18). По мере того как поворачивается вектор, ордината его конца характеризует показанный на рисунке синусоидальный сигнал. Один полный оборот вектора (360°, или 2π) соответствует одному полному периоду. Половина оборота (180°, или π) соответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода).
Теперь рассмотрим два синусоидальных сигнала, представленных на рис. 4.19(а) векторами ОА и ОВ соответственно. Если оба сигнала имеют одинаковые частоты, то векторы ОА и ОВ будут вращаться с одинаковой угловой скоростью ω= 2πf. Это означает, что угол между этими векторами

Рис. 4.18. Векторное представление синусоидального сигнала.

Рис. 4.19. Разность фаз. Вектор ОА опережает вектор ОВ
(или вектор ОВ отстает от вектора ОА) на угол θ.
изменяться не будет. Говорят, что вектор ОА опережает вектор ОВ на угол θ, а вектор ОВ отстает от вектора ОА на угол в. На рис. 4.19(б) эти сигналы развернуты во времени.
Если оба этих синусоидальных сигнала сложить, то в результате получим другой синусоидальный сигнал, имеющий ту же частоту f, но другую амплитуду. Результирующий сигнал может быть представлен вектором ОТ, который, как показано на рис. 4.19(в), является векторной суммой векторов ОА и ОВ. Вектор ОТ опережает вектор ОВ на угол α и отстает от вектора ОА на угол γ. Дальше вы увидите, что векторное представление является весьма удобным приемом при анализе и расчете цепей переменного тока.
В этом видео рассказывается о катушке индуктивности:
Добавить комментарий
2. Переходные процессы в цепях постоянного тока с катушкой индуктивности | 15. RC и L/R цепи | Часть1
2. Переходные процессы в цепях постоянного тока с катушкой индуктивности
Переходные процессы в цепях постоянного тока с катушкой индуктивности
Характеристики катушек индуктивности противоположны характеристикам конденсаторов. Если конденсаторы накапливают энергию в электрическом поле (создаваемом напряжением между двумя пластинами), то катушки индуктивности накапливают энергию в магнитном поле (создаваемом проходящим через провод током). Из этого можно сделать вывод, что энергия, запасенная в конденсаторе, пытается поддерживать на его выводах постоянное напряжение, а энергия, запасенная в катушке индуктивности, пытается поддерживать постоянный ток в ее обмотке. Таким образом, катушка индуктивности выступает против изменения тока и действует противоположно конденсатору, который выступает против изменения напряжения. Полностью разряженная катушка, ток через которую равен нулю, в момент подключения к источнику питания будет действовать как разомкнутая цепь (пытаясь поддерживать нулевой ток). Напряжение на ее выводах при этом будет максимальным. С течением времени, ток через катушку индуктивности будет возрастать до максимально допустимого значения, а напряжение — соответственно уменьшаться. Как только напряжение на выводах катушки снизится до минимума (ноль — для идеальной катушки), ток через нее достигнет максимального значения, и она будет действовать как короткозамкнутая перемычка.
В момент замыкания контактов выключателя напряжение на катушке индуктивности сразу возрастает до величины напряжения источника питания (действует в качестве обрыва цепи), а затем постепенно снижается до нуля (действует в качестве короткозамкнутой перемычки). Чтобы определить напряжение на катушке индуктивности, нужно рассчитать напряжение на резисторе (с учетом тока через катушку) и вычесть его из напряжения источника питания. Ток в момент замыкания контактов выключателя равен нулю. С течением времени он увеличивается, пока не достигнет величины напряжения источника питания поделенной на последовательное сопротивление 1 Ом. Такое поведение противоположно поведению RC цепи, в которой ток начинается с максимального значения, а напряжение — с нуля. Давайте посмотрим как все это работает, используя реальные значения:
-------------------------------------------------- | Время | Напряжение | Напряжение | Ток | |(секунды) | батареи | катушки | | |------------------------------------------------| | 0 | 15 В | 15 В | 0 | |------------------------------------------------| | 0.5 | 15 В | 9.098 В | 5.902 A | |------------------------------------------------| | 1 | 15 В | 5.518 В | 9.482 A | |------------------------------------------------| | 2 | 15 В | 2.030 В | 12.97 A | |------------------------------------------------| | 3 | 15 В | 0.747 В | 14.25 A | |------------------------------------------------| | 4 | 15 В | 0.275 В | 14.73 A | |------------------------------------------------| | 5 | 15 В | 0.101 В | 14.90 A | |------------------------------------------------| | 6 | 15 В | 37.181 мВ | 14.96 A | |------------------------------------------------| | 10 | 15 В | 0.681 мВ | 14.99 A | --------------------------------------------------
Так же как и для RC цепи, подход напряжения катушки к нулевому значению и подход тока через нее к 15 амперам носит асимптотический характер (обе эти величины с течением времени подходят к окончательным значениям все ближе и ближе, но никогда не достигают их). В практических целях мы можем сказать, что напряжение на катушке в конечном итоге достигнет нулевого значения, а ток в конечном счете будет равен 15 амперам.
Опять же, при помощи программы SPICE мы можем графически отобразить рассмотренное выше асимптотическое уменьшение напряжения и увеличение тока на катушке индуктивности (ток на графике показан с точки зрения напряжения на резисторе, который используется в качестве шунта для измерения данного тока):
inductor charging v1 1 0 dc 15 r1 1 2 1 l1 2 0 1 ic=0 .tran .5 10 uic .plot tran v(2,0) v(1,2) .end
legend: *: v(2) Inductor voltage +: v(1,2) Inductor current time v(2) (*+)------------ 0.000E+00 5.000E+00 1.000E+01 1.500E+01 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 0.000E+00 1.500E+01 + . . * 5.000E-01 9.119E+00 . . + * . . 1.000E+00 5.526E+00 . .* +. . 1.500E+00 3.343E+00 . * . . + . 2.000E+00 2.026E+00 . * . . + . 2.500E+00 1.226E+00 . * . . + . 3.000E+00 7.429E-01 . * . . + . 3.500E+00 4.495E-01 .* . . +. 4.000E+00 2.724E-01 .* . . +. 4.500E+00 1.648E-01 * . . + 5.000E+00 9.987E-02 * . . + 5.500E+00 6.042E-02 * . . + 6.000E+00 3.662E-02 * . . + 6.500E+00 2.215E-02 * . . + 7.000E+00 1.343E-02 * . . + 7.500E+00 8.123E-03 * . . + 8.000E+00 4.922E-03 * . . + 8.500E+00 2.978E-03 * . . + 9.000E+00 1.805E-03 * . . + 9.500E+00 1.092E-03 * . . + 1.000E+01 6.591E-04 * . . + - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Обратите внимание, как напряжение очень быстро уменьшается в начальный момент времени (с левой стороны графика), и практически не меняется в последующем. Аналогичная ситуация и с током: он очень быстро увеличивается в начальный момент времени (с правой стороны графика), и практически не растет в последующем.
Катушка постоянного тока— это … Что такое катушка постоянного тока?
Катушка — сюда перенаправляется обмотка. Для использования в других целях, см Обмотка (значения). Для использования в других целях, см Катушка (значения). Катушка — это серия петель. Спиральная катушка — это структура, в которой сама катушка, в свою очередь, также имеет петлю. Содержание 1…… Википедия
Пускатель прямого включения — Пускатель прямого включения, часто обозначаемый аббревиатурой прямого пуска, является широко используемым методом пуска электродвигателей.Этот термин используется в электротехнике и связан с электродвигателями. Существует много типов пускателей двигателей, самые простые из…… Wikipedia
Коробка передач с прямым переключением передач — Типы трансмиссий Механическая Последовательная ручная Несинхронная Преселекторная Автоматическая Ручная Полуавтоматическая Электрогидравлическая Двойная… Википедия
Токовые клещи — Для регистрации токовых клещей в нейронах см. Электрофизиология # Токовые клещи. В электротехнике и электронике токоизмерительные клещи или токовые пробники — это электрическое устройство, имеющее две губки, которые открываются, чтобы можно было зажать электрический…… Wikipedia
Устройство защитного отключения — Двухполюсное устройство защитного отключения Устройство защитного отключения — это общий термин, охватывающий как RCCB, так и RCBO.Прерыватель цепи остаточного тока (RCCB) — это устройство электропроводки, которое отключает цепь всякий раз, когда обнаруживает, что…… Wikipedia
Электромагнитная катушка — Электромагнитная катушка (или просто катушка) образуется, когда проводник (обычно сплошной медный провод) наматывается на сердечник или форму для создания индуктора или электромагнита. Один виток провода обычно называют витком, а катушка состоит из… Wikipedia
Переменный ток — (зеленая кривая).Горизонтальная ось измеряет время; по вертикали, току или напряжению. В переменном токе (AC, также AC) движение электрического заряда периодически меняет направление. В постоянном токе (DC, также dc) поток электрического заряда… Wikipedia
дроссельная катушка — существительное катушка с низким сопротивлением и высокой индуктивностью, используемая в электрических цепях для пропускания постоянного тока и ослабления переменного тока • Синхронизация: ↑ дроссель, ↑ дроссельная катушка • Гиперонимы: ↑ катушка • Часть Голонимы: ↑ цепь, ↑ электрическая схема, ↑… Полезный английский словарь
катушка зажигания — существительное индукционная катушка, которая преобразует ток от батареи в ток высокого напряжения, необходимый для свечей зажигания • Гиперонимы: индукционная катушка ↑ • Часть Голонимы: ↑ зажигание, ↑ система зажигания * * * (в автомобильном зажигании система) трансформатор…… Полезный английский словарь
дроссельная катушка — существительное катушка с низким сопротивлением и высокой индуктивностью, используемая в электрических цепях для пропускания постоянного и ослабления переменного тока • Синхронизация: ↑ дроссель, ↑ дроссельная катушка • Гиперонимы: ↑ катушка • Часть Голонимы: ↑ цепь, ↑ электрическая схема, ↑… Полезный английский словарь
индукционная катушка — Электр.трансформатор для производства переменного тока высокого напряжения из постоянного тока низкого напряжения, состоящий по существу из двух концентрических катушек с общим сердечником из мягкого железа, первичной катушки с относительно небольшим количеством витков из толстой проволоки и…… Универсалиума
Управление катушкой прямого зажигания
Управление катушкой прямого зажигания| Нажимайте кнопки меню непосредственно ниже, чтобы быстро найти информацию о MegaSquirt®: Безопасность Информация Поддержка Forum
|
Управление катушкой прямого зажигания с помощью процессора MegaSquirt-II ™
Дочерняя плата обновления процессора MegaSquirt-II ™ в сочетании с основной платой V3 может напрямую управлять одной катушкой (ей по-прежнему нужен распределитель, если у вас нет одноцилиндрового двигателя). Для управления двумя катушками, например, для 4-цилиндрового отработанного искры, см. Www.microsquirt.info/dualspark.htm.
В схеме драйвера сильноточной катушки используется специальный драйвер катушки VB921, который ограничивает ток катушки примерно до 7 А (обратите внимание, что более поздние версии MegaSquirt могут иметь BIP373 вместо VB921) .
Подключение катушки к силовому приводу
Чтобы использовать сильноточный драйвер (со специальной микросхемой драйвера катушки VB921), вы должны установить схему сильноточного драйвера зажигания на этапе # 65 сборки вашей основной платы V3.
Убедитесь, что вы не установили R57 . Если вы установили его, удалите его (или обрежьте один провод, чтобы отключить его). R57 расположен примерно в 1 дюйме (25 мм) от DB37 и в 1 дюйме (25 мм) от радиатора. R57 мешает сигналу от процессора к VB921, поэтому его необходимо удалить, иначе ваше время ожидания и время будут неправильными.
Если вы подключили сильноточный драйвер, вы установили перемычки:
- IGBTIN (рядом со стороной радиатора DB37 в нижней части платы) до JS10 (под 40-контактным разъемом ЦП в нижней части платы)
- IGBTOUT – IGN — рядом с теплоотводом DB37 в нижней части печатной платы (это выводит сигнал управления зажиганием на вывод DB37 № 36)
Подключить сильноточную цепь к катушке очень просто.Вам необходимо подать импульсный источник питания 12 В на одну сторону катушки, на положительный (+) вывод. Используйте реле топливного насоса для этого источника, так как катушка не будет запитана во время остановки и т. Д. Вставьте предохранитель на 10 А в этот провод. Другой вывод (отрицательный (-)) подключен к выводу 36 MegaSquirt ® DB37 (он подключается к выводу S5 платы реле, если вы используете плату реле).
Вам необходимо установить параметры в MegaTune. Устанавливать:
- Схема зарядки катушки до «стандартной зарядки катушки»,
- Искровой выход на «высокий (инвертированный)» до 2.Код 886 / ‘По убыванию’ для кода 3.1+.
Наконец, вам нужно настроить параметры задержки, соответствующие вашей катушке. Как правило, вы хотите установить это значение как можно ниже, но при этом не создавать пропусков зажигания. Типичные настройки задержки составляют от 2,5 до 3,5 миллисекунд. Обычно люди должны начинать с примерно 3,0–3,1 миллисекунды, а затем настраивать ее. Опустите его, если пропусков зажигания нет, поднимите, пока они не исчезнут.
При настройке параметров выдержки убедитесь, что у вас достаточно мощности радиатора (и вы использовали смазку для радиатора между VB921 и радиатором), и держите выдержку до точки, в которой она только начинает ограничивать ток.Вот почему в схеме есть резистор 0,01 Ом (R43), поэтому вы можете подключить к нему осциллограф и напрямую измерить нарастание тока.
Контроллеры MegaSquirt ® и MicroSquirt ® — экспериментальные устройства, предназначенные для образовательных целей. Контроллеры
MegaSquirt ® и MicroSquirt ® не предназначены для продажи или использования на транспортных средствах с контролируемым загрязнением. Ознакомьтесь с действующими в вашем регионе законами, чтобы определить, является ли использование контроллера MegaSquirt ® или MicroSquirt ® законным для вашего приложения.
© 2005, 2008 Брюс Боулинг и Эл Гриппо. Все права защищены. MegaSquirt ® и MicroSquirt ® являются зарегистрированными товарными знаками. Этот документ предназначен исключительно для поддержки досок MegaSquirt ® от Bowling и Grippo.
,
Опишите эффект поворота катушки с током в магнитном поле
Опишите эффект поворота катушки с током в магнитном поле
- Токопроводящая катушка в магнитном поле испытывает эффект поворота .
- На рисунке прямоугольная катушка ABCD передает ток в магнитном поле между двумя магнитами магнадура.
(a) По сторонам BC и DA проходят токи с направлением, параллельным магнитному полю.С этих двух сторон не применяется сила.
(b) Сторона AB рядом с южным полюсом испытывает силу. Направление силы можно определить с помощью правила левой руки Флемингса или правила удара правой рукой.
(c) Боковое CD испытывает силу, действующую в противоположном направлении. - Две силы, действующие в противоположных направлениях на двух сторонах катушки, образуют пару и вызывают вращающий эффект на катушке.
- Силы возникают, когда магнитное поле , обусловленное током в катушке, объединяется с внешним магнитным полем , чтобы создать два результирующих поля катапульты вокруг катушки, как показано на рисунке.
- Двумя важными приложениями эффекта поворота катушки с током в магнитном поле являются двигатель постоянного тока и гальванометр с подвижной катушкой.
Люди также спрашивают
Свяжите этот эффект поворота с действием электродвигателя
Двигатель постоянного тока
- Двигатель постоянного тока (двигатель постоянного тока) использует эффект поворота на токе: несущая катушку в магнитном поле.
- Принцип работы двигателя постоянного тока поясняется на рисунке.
Первая половина оборота
- Угольная щетка X контактирует с половиной коллектора.
- Угольная щетка Y соприкасается с другой половиной коллектора.
- Ток течет в катушке по ABCD.
- Магнитная сила на АВ направлена вниз.
- Магнитная сила в CD направлена вверх.
- Катушки вращаются по часовой стрелке.
Вторая половина вращения
- Угольная щетка X находится в контакте с половиной коллектора.
- Угольная щетка Y соприкасается с другой половиной коллектора.
- Ток течет в катушке по DCBA.
- Магнитная сила на CD направлена вниз.
- Магнитная сила в AB направлена вверх.
- Катушки продолжают вращаться по часовой стрелке.
Эффект превращения в действие электродвигателя Эксперимент
Цель: Изучить факторы, влияющие на скорость вращения электродвигателя.
Материалы: Изолированный медный провод (SWG 26), деревянный каркас, тонкий железный стержень в качестве оси, деревянный брус в качестве основания, пара магнадурных магнитов со стальным U-образным хомутом, два шплинта, целлофан лента
Аппарат: Низкое напряжение постоянного тока источник питания
Метод:
- Устройство установлено, как показано на рисунке. Используется катушка с 40 витками вокруг деревянного каркаса.
- Напряжение постоянного тока. напряжение питания установлено на 1 В.Включается электропитание и соблюдается скорость вращения двигателя.
- Шаг 2 повторяется при напряжении 2 В.
- Напряжение постоянного тока. источник питания снова установлен на 1 В.
- Еще одна пара магнитов Magnadur добавлена к U-образному стальному ярму, как показано на рисунке. Включается электропитание и соблюдается скорость вращения двигателя.
- Одна пара магнитов магнадура удалена. Катушка заменяется другой катушкой на 80 витков провода.Включается электропитание и соблюдается скорость вращения двигателя.
Наблюдения:
| Сделанные шаги | Источник питания постоянного тока | Магниты Magnadur | Число витков в катушке | |||||
| 1 V | 1 пара | 40 оборотов | Средняя скорость | |||||
| Шаг 3 | 2 V | 1 пара | 40 оборотов | Более высокая скорость | ||||
| Шаг 5 | Шаг 5 | Шаг 5 | 2 пары | 40 витков | Более высокая скорость | |||
| Шаг 6 | 1 V | 1 пара | 80 витков | Более высокая скорость |
Обсуждение пропорционально Вывод: Амперметр или вольтметр с подвижной катушкой Из-за эффекта самоиндукции катушки (индукторы) создают электродвижущую силу (индуктивную электродвижущую силу), ориентированную таким образом, чтобы противодействовать изменению тока.Следовательно, когда на катушку подается напряжение, ток не начинает течь сразу, а когда напряжение снимается, ток не прекращается немедленно. Неравномерное изменение тока или напряжения, которое происходит, например, в точке включения или выключения переключателя, называется переходной характеристикой (переходным явлением) катушки. Например, в схеме, показанной ниже, где катушка и неоновая лампа (напряжение начала разряда не менее нескольких десятков вольт) подключены параллельно, простое замыкание переключателя батареи (напряжение всего несколько вольт) не приведет к включите неоновую лампу.Но если выключатель разомкнут, когда через катушку течет ток, загорится неоновая лампа. Электродвижущая сила (V), создаваемая катушкой из-за эффекта самоиндукции, пропорциональна коэффициенту изменения тока (ΔI / Δt). Когда переключатель установлен в положение ON, ток постепенно увеличивается, и поэтому электродвижущая сила не превышает напряжения источника питания. Но когда переключатель установлен в положение OFF, протекающий ток мгновенно отключается, что означает, что коэффициент изменения тока большой, вызывая создание большой электродвижущей силы, которой достаточно для зажигания неоновой лампы. В приведенной выше схеме можно зажечь неоновую лампу, поскольку катушка накапливает энергию. Эта энергия пропорциональна индуктивности катушки и квадрату тока.Когда переключатель установлен в положение OFF, накопленная энергия мгновенно высвобождается, создавая высокую электродвижущую силу. Катушка (индуктор) пропускает постоянный ток плавно, но имеет сопротивление переменному току.Сопротивление увеличивается к более высоким частотам. Этот эффект называется индуктивным реактивным сопротивлением (XL) катушки. Между частотой переменного тока (f) и индуктивностью (L) существует следующая зависимость. Переменный ток от коммерческой розетки переменного тока имеет синусоидальную форму.Когда катушка подключена к источнику переменного тока, эффект самоиндукции создает электродвижущую силу, которая ориентирована так, чтобы противодействовать изменению тока. Таким образом, изменение тока задерживается на 90 градусов (1/4 цикла) по отношению к изменению напряжения. Магнитный поток (Φ), создаваемый в катушке, пропорционален индуктивности (L) и протекающему току (I).Поскольку индуктивность пропорциональна магнитной проницаемости, использование магнитного материала с высокой магнитной проницаемостью и приложение большого тока приведет к созданию более сильного магнитного потока. Однако есть пределы способности магнитного материала собирать магнитный поток, и когда ток увеличивается до определенной точки, сердечник достигает магнитного насыщения. Плотность магнитного потока (B) в этой точке называется максимальной плотностью магнитного потока (Bm). Когда сердечник намагничивается, магнитная проницаемость сердечника изменяется.Как показано на графике ниже, магнитная проницаемость (μ) выражается градиентом кривой намагничивания сердечника (θ). Начальный градиент около начала кривой — это начальная магнитная проницаемость (μ0). Эта начальная магнитная проницаемость — это то, что обычно называют магнитной проницаемостью, и это также значение, которое указано в каталогах для ферритовых материалов. Увеличение тока в катушке и, тем самым, увеличение намагниченности в конечном итоге приведет к достижению максимальной магнитной проницаемости.Это называется максимальной магнитной проницаемостью (мкм), после которой значение снова падает. Когда в катушку подается переменный ток, создается электродвижущая сила, которая противодействует изменению магнитного потока, и в сердечнике протекает концентрический ток.Это называется вихревым током, и он лишает систему мощности RI2 (R: сопротивление, I: ток), которая уходит в виде джоулева тепла. Это называется потерей на вихревые токи. У металлических сердечников с низким электрическим сопротивлением потери на вихревые токи более выражены. Ламинированные сердечники, используемые для силовых трансформаторов, представляют собой попытку уменьшить потери на вихревые токи. Однако потери будут увеличиваться по направлению к более высоким частотам, вызывая больше тепла. Поскольку феррит имеет высокое удельное сопротивление, потери на вихревые токи низкие, что делает этот материал пригодным для многих применений, таких как высокочастотные катушки и высокочастотные трансформаторы. 9007 подаваемое напряжение.Сравнивая наблюдения на шагах 2 и 3, скорость вращения увеличивается при увеличении подаваемого напряжения. Следовательно, скорость вращения увеличивается при увеличении тока в катушке.
Скорость вращения электродвигателя увеличивается при увеличении тока в катушке, напряженности магнитного поля или количества витков катушки. Эффект поворота в Амперметр или вольтметр с подвижной катушкой
.Индукторы ― Часть 2 Основы индукторов ② | Electronics ABC | TDK Techno Magazine
Работа индуктора при постоянном токе
Переходная характеристика катушки

Энергия, запасаемая катушкой

Поведение катушки переменного тока
Индуктивное реактивное сопротивление (XL)


Форма кривой напряжения и тока в цепи переменного тока с катушкой

Намагничивание сердечника и магнитная проницаемость
Кривая намагничивания и магнитное насыщение
Процесс намагничивания сердечника и изменение магнитной проницаемости

Вихретоковые потери в сердечнике
 ,
,

