Расчёт LC — фильтров. Онлайн калькулятор ПФ, ФВЧ, ФНЧ.
LC — фильтры я оставил на десерт, подобно бутылке благородного вина, покрытой слоем вековой пыли. Это антиквариат, который на Сотбисе не купишь!
Как ни крути, а не получил бы Александр Степаныч наш Попов звание почётного инженера-электрика, не направь он искровой разряд
напрямик в колебательный контур для обретения благословения свыше и резонанса с передающей антенной.
И заскучала бы братва копателей свободной энергии эфира, не изобрети Никола Тесла свой резонансный трансформатор и
электрический автомобиль с неведомой коробочкой. А то и вовсе, заширялась бы в подъездах, лишённая идей вселенского масштаба.
И начнём мы с расчёта самого простого LC-фильтра — колебательного контура.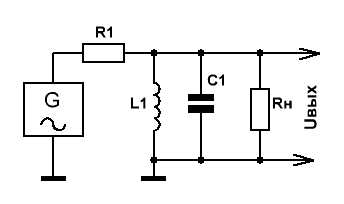
Включённый по приведённой на рис.1 схеме, он представляет собой узкополосный полосовой фильтр, настроенный на частоту
fо= 1/2π√LС.
На резонансной частоте сопротивление контура равно:
Оно в свою очередь рассчитывается по формуле р = √L/C.
Рис.1
На низких (звуковых) частотах конденсаторы практически не вносят потерь, поэтому добротность контура равна добротности катушки
индуктивности, величина которой напрямую зависит от активного сопротивления катушки. Чем ниже частота, тем больше витков и тоньше
провод, тем проще его измерить тестером. Если эта попытка удалась, то Q=2πfL/R, где R – активное сопротивление катушки индуктивности.
На радиочастотах значение активного сопротивления катушки может составлять доли ома, поэтому для расчёта добротности надо — либо
найти сопротивление в Омах по формуле R= 4ρ*L/(πd²), где ρ — удельное сопротивление меди, равное 0,017 Ом•мм²/м, L — длина в
метрах, d — диаметр провода в мм, либо вооружиться генератором сигналов, каким-либо измерителем уровня выходного сигнала с высоким
внутренним сопротивлением, и определить добротность экспериментально.
Нарисуем табличку с расчётом фильтра для низкочастотных приложений.
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ НЧ.
Если параметр активного сопротивления катушки R опущен, его значение принимается равным 200 омам.
Необходимо отметить, что все полученные в таблице данные верны и для последовательного колебательного контура.
При этом, если мы хотим использовать свойства контура полностью, т. е. получить острую резонансную кривую, соответствующую
конструктивной добротности, то параллельный контур надо нагружать слабо, выбирая R1 и Rн намного больше Rо (на практике
десятки кОм), для последовательного же контура, сопротивление генератора R1 наоборот должно быть на порядок меньше
характеристического сопротивления ρ.
Теперь, нарисуем таблицу для расчёта высокочастотных резонансных контуров.
Тут на добротность влияет не только активное сопротивление катушек, но и другие факторы, такие как — потери в ферритах, наличие экрана,
эффект близости витков и т. д.
Поэтому вводить этот параметр в качестве входного я не
стану — будем считать, что добротность катушки вы измерили, или подсмотрели в документации на готовые катушки. Естественным образом
значение добротности катушки должно измеряться на резонансной частоте контура, ввиду прямой зависимости этой величины от рабочей
частоты (Q=2πfL/R).
К тому же я добавлю сюда
параметр добротности конденсатора, особенно актуальный в случае применения варикапов.
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ ВЧ.
Теперь плавно переходим к LC фильтрам верхних и нижних частот (ФВЧ и ФНЧ).
Рис.2
Крутизна спада АЧХ этих фильтров в полосе подавления — 12 дБ/октаву, коэффициент передачи в полосе пропускания К=1 при R1
Однако наилучшие параметры, с точки зрения равномерности АЧХ и передачи максимальной мощности в нагрузку, обеспечиваются
при R1=Rн=ρ. В этом случае фильтр является согласованным, правда коэффициент передачи в полосе пропускания становится равным К=0.5.
Ну да ладно, ближе к делу.
ТАБЛИЦА LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
А если надо рассчитать L и C при известных значениях Fср и ρ ? Не вопрос,
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
Данные ФВЧ и ФНЧ называются Г-образными.
Для получения более крутых скатов АЧХ используют два или более Г-образных звеньев, соединяя их последовательно,
чтобы образовать Т-образное звено (на Рис.3 сверху), или П-образное звено (на Рис.3 снизу).
При этом получаются ФНЧ третьего порядка. Обычно, ввиду меньшего количества катушек, предпочитают П-образные звенья.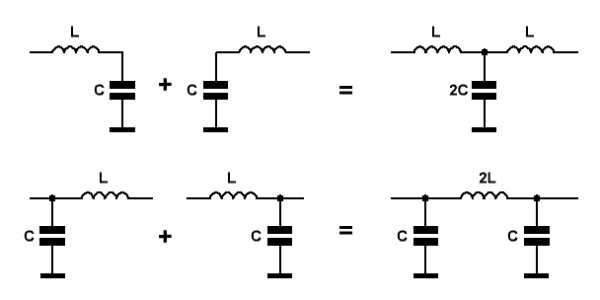
Рис.3
ФВЧ конструируют подобным же образом, лишь катушки заменяются конденсаторами, а конденсаторы — катушками.
Широкополосные полосовые LC — фильтры получают каскадным соединением ФНЧ и ФВЧ.
Что касается многозвенных LC-фильтров высоких порядков, то более грамотным решением (по сравнению с последовательным соединением фильтров низших порядков) будет построение подобных устройств с использованием полиномов товарищей Чебышева или Баттерворта.
Именно такие фильтры 3-го, 5-го и 7-го порядков мы и рассмотрим на следующей странице.


vpayaem.ru
Калькулятор расчёта полосно-заграждающих режекторных фильтров на LC цепях
Что такое режекторный фильтр (он же полосно-заграждающий, он же — фильтр-пробка) и с чем его едят, мы определились на предыдущей странице, рассматривая пассивные и активные режекторные RC-фильтры.
Так же, как и в случаях с НЧ, ВЧ и полосовыми собратьями, LC режекторные фильтры обладают рядом достоинств, таких как: высокая стабильность, низкий уровень собственных шумов, а также возможность работы с широким спектром сигналов, включая СВЧ диапазоны.
Простейший представитель режекторного LC-фильтра 2-го порядка представлен на Рис.1.
Рис.1  Рис.2
Рис.2
Логика работы такого фильтра предельно проста.
На резонансной частоте fо= 1/2π√LС сопротивление параллельного
колебательного контура, образованного катушкой индуктивности L и конденсатором C, принимает максимальное значение, соответственно
максимальное значение принимает и коэффициент подавления сигнала на этой частоте.
Глубина режекции (подавления частоты fo) этого фильтра при работе на согласованную нагрузку, равную характеристическому сопротивлению
колебательного контура ρ = √L/C , достигает 45 дБ.
На Рис.2 представлена схема Г-образного режекторного фильтра 4-го порядка.
Глубина режекции в данной схеме уже может составлять величину 90 дБ.
Приведём таблицу для расчёта элементов этих фильтров.
Не забываем, что характеристическое сопротивление фильтра ρ
должно равняться Rг =Rн.
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ РЕЖЕКТОРНЫХ LC- ФИЛЬТРОВ 2-го и 4-го ПОРЯДКОВ
Для получения больших значений подавления центральной частоты (глубины режекции) используют два или более Г-образных звеньев,
соединяя их последовательно, чтобы образовать Т-образное звено, или П-образное звено.
На Рис.3 приведены схемы типовых полосно-заграждающих LC-фильтров 6-го порядка Т-образной (слева) и П-образной (справа) структур с
глубиной режекции — около 130 дБ.
Рис.3
Ничего не изменилось — последовательная ветвь обладает минимальным полным сопротивлением и оказывает шунтирующее воздействие на
центральной частоте диапазона.
Ее полное сопротивление начинает увеличиваться по обе стороны от частоты резонанса.
Параллельная же ветвь на центральной частоте имеет максимальное сопротивление, и оно уменьшается по обе стороны резонанса.
Центральная частота режекции равна fо= 1/2π√LС,
характеристическое сопротивление ρ = √L/C ,
а значения частотозадающих элементов рассчитываются исходя из следующих равенств:
L1 = L3 = L/2, L2 = L, C1 = C3 = C×2, C2 = C
для Т-образного фильтра,
L 1 = L3 = L×2, L2 = L, C1 = C3 = C/2, C2 = C
для П-образного фильтра.
Приведём таблицу для расчёта элементов и этих фильтров.
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ РЕЖЕКТОРНЫХ Т- и П-образных LC- ФИЛЬТРОВ
Ширина полосы задержания представленных режекторных LC-фильтров составляет величину, примерно равную 50% от значения центральной частоты fo.

vpayaem.ru
Онлайн расчёт многозвенных LC — фильтров. Калькулятор ПФ, ФВЧ, ФНЧ 3-го, 5-го и 7-го порядков.
Одиночный LC-фильтр, как ни бейся, не может обеспечить достаточного подавления сигналов вне заданного диапазона частот, поэтому для
формирования более крутой переходной области обычно используют многозвенные LC — фильтры.
Причём фильтры чётных порядков при равенстве сопротивлений источника и нагрузки вообще теряют актуальность, ведь добавлением всего
одного конденсатора они превращаются в фильтр более высокого порядка.
В низкочастотной схемотехнике LC-фильтры фильтры решительно теряют позиции в пользу активных фильтров высоких порядков, за исключением, пожалуй, сглаживающих фильтров источников питания, LC-фильтров акустических систем, да изредка НЧ фильтров приёмников прямого преобразования.
Зато на непаханых полях радиочастотных диапазонов свободного пространства хоть отбавляй. То-то раздолье тут земледельцу!
По левую руку — входные фильтры приёмников и трансиверов, по правую — фильтры выходных каскадов передатчиков, посередине …
А что, собственно говоря, посередине?
Да всё, что угодно, поля-то — непаханые.
Описания свободных и вынужденных колебаний в электрических цепях, и иже с ними дисперсионные и характеристические уравнения систем различных аппроксимаций оставим бедолагам студентам, а сами играючи воспользуемся таблицами элементов LC фильтров-прототипов, приведённых в справочнике по расчёту фильтров Г. Ханзела.
Как правило, с точки зрения минимизации количества катушек индуктивности, в многозвенных фильтрах используют П-образную схему для ФНЧ и Т-образную для ФВЧ.
На Рис.1 приведены схемы подобных фильтров нижних и верхних частот 3-го, 5-го и 7-го порядков.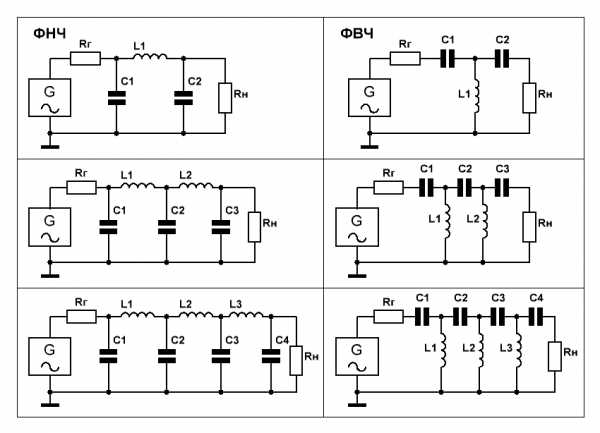
Рис.1
Расчёт поведём доверившись многочленам Пафнутия Львовича нашего Чебышёва.
Почему на сей раз Чебышева, а не вездесущего Баттерворта?
Ответ не сложен — в погоне за максимальным наклоном переходного участка, в жертву некоторой неравномерности АЧХ фильтра в полосе пропускания.
При одном и том же числе элементов схемы у фильтров Чебышева крутизна характеристики ослабления в полосе задерживания
значительно больше, чем у фильтров Баттерворта и может составлять величину 8,5дб на октаву (против менее 6 дБ/окт) на каждый порядок
фильтра.
Значение же неравномерности в полосе пропускания можно ограничивать, выбирая коэффициенты из таблицы фильтра — прототипа. Я посчитал, что
неравномерность 0,28дБ окажется вполне приемлемой.
Ну и хватит, переходим к таблице.
ТАБЛИЦА РАСЧЁТА МНОГОЗВЕННЫХ ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
И как обычно не забываем — многозвенные полосовые LC-фильтры получаются каскадным соединением ФНЧ и ФВЧ, тем более что они отлично друг с другом согласуются.
Ну а если полученный спад амплитудной характеристики не кажется слишком крутым, то нам прямая дорога к эллиптическим фильтрам, которые мы и посчитаем на следующей странице.


vpayaem.ru
Расчёт пассивных RC фильтров. Онлайн калькулятор.
А не фильтрануть ли нам широким махом входной сигнал на предмет подавления помехи относительно единичного уровня
на требуемой частоте, в заданное число раз отличающейся от границы полосы пропускания?
А как насчёт расчёта активных полиномиальных фильтров второго порядка на
звеньях Рауха, Сален-Ки и биквадратного звена?
А кривую изменения реактивного сопротивления ёмкости в зависимости от частоты — не изобразить ли?
«Хватит умничать, пальцем покажи!», — предвижу я законное роптание посетителя, впавшего в соблазн от заголовка страницы.
И действительно. Здесь мне не тут! Базар надо фильтровать, а не безобразия нарушать!
Итак, приступим.
Для начала мы рассмотрим активные и пассивные ФНЧ, ФВЧ, ПФ без использования катушек индуктивности.
Определимся с терминологией.
— Фильтр нижних частот (ФНЧ) представляет собой устройство, которое пропускает сигналы низких частот и задерживает сигналы
высоких частот.
— Фильтр верхних частот (ФВЧ) соответственно пропускает сигналы высоких частот и задерживает сигналы низких.
— Полосовой фильтр (ПФ) пропускает сигналы в некоторой полосе частот и подавляет сигналы и на низких частотах, и на высоких.
— Полоса пропускания определяется как диапазон частот, в котором АЧХ фильтра не выходит за пределы заданной неравномерности
(обычно — 3дБ).
— Частотой среза фильтра называют частоту, ослабление сигнала на которой достигает -3дБ по логарифмической шкале,
или 1/√2 ≈ 0.71 по линейной.
— Неравномерность АЧХ в полосе пропускания — размер флуктуации АЧХ от пика до пика в полосе пропускания.
— Крутизна частотной характеристики фильтра – скорость спада АЧХ в полосе подавления (дБ/октаву или дБ/декаду).
А начнём мы с простейших RC фильтров первого порядка. Слева фильтр нижних частот (ФНЧ), справа фильтр верхних частот (ФВЧ).
Рис.1
Крутизна спада АЧХ таких фильтров в полосе подавления — 6 дБ/октаву.
Частота среза рассчитывается по формуле:  
Теперь надо определиться — из каких соображений выбирать номиналы R и С.
Ёмкость посчитается нашей табличкой, а к выбору сопротивления резистора, для достижения заявленной крутизны, надо подойти со всей
ответственностью.
Номинал этого резистора должен быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного
сопротивления последующего.
РИСУЕМ ТАБЛИЧКУ ДЛЯ ФИЛЬТРОВ ПЕРВОГО ПОРЯДКА
ТЕПЕРЬ ТО ЖЕ САМОЕ С ДРУГИМИ ВВОДНЫМИ
Для получения простейшего полосового фильтра первого порядка, нужно последовательно соединить ФНЧ и ФВЧ с Рис.1, не забывая, что значение сопротивления R второго фильтра должно быть на порядок (в 10 раз) выше сопротивления первого.
Важно понимать, что хорошей крутизны спада АЧХ от таких простейших фильтров добиться не удастся. Тут нам прямая дорога к активным фильтрам, или к фильтрам на LC цепях.
Именно активные фильтры мы и рассмотрим на следующей странице.


vpayaem.ru
Онлайн расчёт полосовых LC — фильтров 3-го, 5-го и 7-го порядков.
Полосовой, он же полосно-пропускающий фильтр — это фильтр, пропускающий частоты в некоторой полосе частот,
находящейся между нижней и верхней частотами среза, и может быть легко представлен в виде последовательности,
состоящей из фильтра нижних частот и фильтра верхних частот.
Однако более рациональными с точки зрения оптимизации характеристик, являются фильтры, рассчитанные через ФНЧ-прототип.
Преобразование фильтра низких частот в полосовой фильтр осуществляется заменой емкостей ФНЧ прототипа параллельными контурами,
а индуктивностей — последовательными.
Примеры таких полосовых фильтров 3-го, 5-го и 7-го порядков приведены на Рис.1. 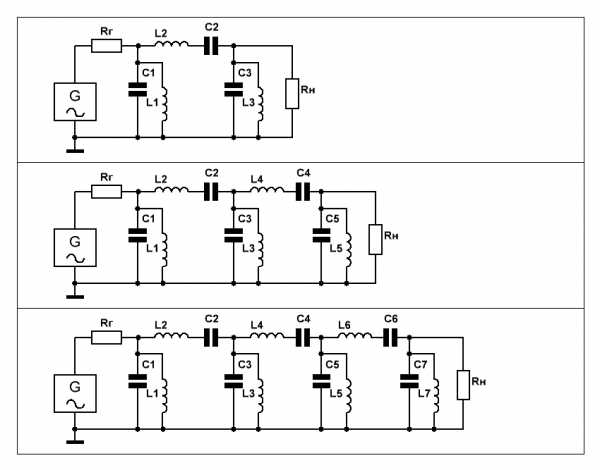
Рис.1
Расчёт поведём, используя прототипы фильтров нижних частот имени уважаемого Пафнутия Чебышева и таблицы не менее уважаемого господина Гранта Ханзела, приведённые в справочнике по расчёту фильтров.
ТАБЛИЦА РАСЧЁТА ПОЛОСОВЫХ LC ФИЛЬТРОВ.
На Рис.2 приведены амплитудно-частотные характеристики полосовых фильтров 3-го, 5-го и 7-го порядков с полосой пропускания 3-5 МГц.
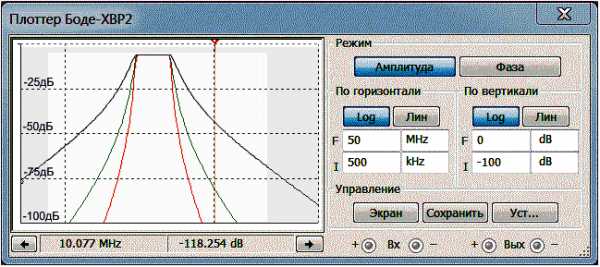
Рис.2
Характеристики затухания фильтров вне полосы пропускания симметричны и составляют величины: 38 дБ на октаву для фильтров 3-го порядка, 75 дБ — для фильтров 5-го порядка и 112 дБ — для фильтров 7-го порядка. Неравномерность в полосе пропускания — менее 0,5 дБ.
Приведённая таблица может стать хорошим подспорьем при расчёте входных диапазонных фильтров радиоприёмников и трансиверов,
однако следует учитывать маленький, но ЖИРНЫЙ «НЮАНС»:
Фильтры Чебышева значительно лучше других справляются с подавлением внеполосных сигналов, но становятся
крайне неудобными (с точки зрения критически малых значений номиналов некоторых элементов) при выборе узкой полосы
прозрачности.
Поэтому наиболее выигрышно они будут смотреться в устройствах относительно широкополосных — с не менее, чем полуоктавной полосой
пропускания.

vpayaem.ru
Электротехника: On-line расчет сглаживающего LC-фильтра.
Для сглаживания пульсаций напряжения и тока в нагрузке может быть применён LC-фильтр нижних частот. Простейший LC-фильтр нижних частот приведён на рисунке 1:Рисунок 1 — Сглаживающий LC-фильтр
E — источник напряжения какой либо формы. RE — резистор имитирующий внутреннее сопротивление источника питания (или внутреннее сопротивление + дополнительное сопротивление фильтра). C — конденсатор LC-фильтра, L — катушка индуктивности фильтра, RH — нагрузка. Такой фильтр может называться Г-фильтром. Помимо Г-фильтров существуют и другие например: Т-фильтр, П-фильтр, двойной Т-фильтр и т.д. (расположение катушек и конденсаторов в П-фильтре напоминает букву «П», в Т-фильтре букву «Т» и т.д.). Достоинством LC-фильтра приведённого на рисунке 1, по сравнению с ёмкостным фильтром, является то что ток источника питания ограничивается катушкой, поэтому в момент подключения питания не будет резкого «скачка» тока. Размеры LC-фильтра могут быть меньше чем ёмкостного или индуктивного при одинаковых амплитудах ненужных высших гармоник в нагрузке. Расчёт Г-образного LC-фильтра (рисунок 1) более сложен чем расчёт ёмкостного или индуктивного и при неправильном подборе ёмкости конденсатора или индуктивности катушки вместо сглаживания, в нагрузке, могут возникнуть колебания. Для расчёта формы напряжения на нагрузке (оно же Uc-напряжение на конденсаторе)(форма тока в нагрузке повторяет форму напряжения на ней т.к. считается что нагрузка активная) и тока катушки IL можно воспользоваться программой приведённой ниже. Для нормальной работы необходимо чтобы браузер поддерживал HTML5. Нажатие на кнопку «Открыть график в виде картинки» приводит к открытию окна с картинкой на которой будут рассчитанные графики (если перед этим была нажата кнопка «Рассчитать и показать график») остальные инструкции те же что и к программе из предыдущей статьи. Если график неправильно рассчитывается то можно попробовать увеличить число точек и уменьшить шаг интегрирования.
HTML5 не поддерживается браузером.
electe.blogspot.com
Фильтры RC. Частота среза. Расчёт онлайн.
Фильтр нижних частот (ФНЧ) — электрическая цепь, эффективно пропускающая частотный спектр сигнала ниже определённой частоты, называемой частотой среза, и подавляющая сигнал выше этой частоты.
Фильтр высших частот (ФВЧ) — электрическая цепь, эффективно пропускающая частотный спектр сигнала выше частоты среза, и подавляющая сигнал ниже этой частоты.
Рассмотрим в качестве фильтра простейшую цепь RC, принцип работы которой основан на зависимости реактивного сопротивления конденсатора от частоты сигнала.
Если к источнику переменного синусоидального напряжения U частотой f подключить последовательно резистор сопротивлением R и конденсатор ёмкостью C, падение напряжения на каждом из элементов можно вычислить исходя из коэффициента деления с импедансом Z.
Импеданс — комплексное (полное) сопротивление цепи для гармонического сигнала.
Z² = R² + X² ; Z = √(R² + X²) , где Х — реактивное сопротивление.
Тогда на выводах резистора напряжение UR будет составлять:
XC – реактивное сопротивление конденсатора, равное 1/2πfC
При равенстве R = XC на частоте f, выражение упростится сокращением R и примет вид:
Следовательно, на частоте f равенство активного и реактивного сопротивлений цепочки RC обеспечит
одинаковую амплитуду переменного синусоидального напряжения на каждом из элементов в √2 раз меньше входного напряжения,
что составляет приблизительно 0.7 от его значения.
В этом случае частота f определится исходя из сопротивления R и ёмкости С выражением:
τ — постоянная времени цепи RC равна произведению RC
Повышение частоты уменьшит реактивное сопротивление конденсатора и падение напряжение на нём, тогда напряжение на выводах резистора возрастёт. Соответственно, понижение частоты увеличит напряжение на конденсаторе и уменьшит на резисторе.
Зависимость амплитуды переменного напряжения от его частоты называют амплитудно-частотной характеристикой (АЧХ).
Если рассмотреть АЧХ напряжения на выводах конденсатора или резистора в RC цепи, можно наблюдать на частоте f = 1/(2π τ) спад уровня до значения 0.7, что соответствует -3db по логарифмической шкале.
Следовательно, цепь RC может быть использована как фильтр нижних частот (ФНЧ) — красная линия на рисунке, или фильтр высших частот (ФВЧ) — синяя линия.
Ниже представлены схемы включения RC-цепочек в качестве фильтров соответственно ФНЧ и ФВЧ.
Частоту f = 1/(2π τ) называют граничной частотой fгр или частотой среза fср фильтра.
Частоту среза фильтра можно посчитать с помощью онлайн калькулятора
Достаточно вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Пост. времени τ RC и частота среза RC-фильтра |
Похожие страницы с расчётами:
Расчёт импеданса.
Расчёт резонансной частоты колебательного контура.
Расчёт компенсации реактивной мощности.
Замечания и предложения принимаются и приветствуются!
tel-spb.ru

