Напряжение переменного тока формула: Переменный электрический ток, действующее напряжение, сила тока. Мощность тока. Курсы по физике

Переменный электрический ток, действующее напряжение, сила тока. Мощность тока. Курсы по физике

Тестирование онлайн

Переменный ток. Основные понятия
Переменный ток

Генератор переменного тока

Устройство, предназначенное для превращения механической энергии в энергию переменного тока, называется генератором переменного тока. В основу работы генератора положено явление электромагнитной индукции.

Рамка вращается в магнитном поле. Поскольку магнитный поток, пронизывающий рамку, изменяется с течением времени, то в ней возникает индуцированная ЭДС:

Ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное.

Основными частями генератора переменного тока являются: индуктор, якорь, коллектор, статор, ротор.

а) устройство ротора; б) работа генератора переменного тока

Переменный ток

Переменный ток изменяется с течением времени по гармоническому закону.

Действующим (эффективным) значением

переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделил бы такое же количество теплоты, что и данный переменный ток.

Мощность переменного тока

Мощность в цепи переменного тока изменяется с течением времени. Поэтому введено понятие мгновенной мощности (мощность в некоторый момент времени) и средней мощности (мощность за длительный промежуток времени).

Рассмотрим цепь переменного тока, состоящую из последовательно соединенных резистора, катушки индуктивности и конденсатора, подключенных к источнику переменного напряжения.

Явление резкого увеличения амплитуды переменного тока в такой цепи получило название резонанса напряжений. Частота, при которой наблюдается резонанс, называется резонансной частотой.

Резонансная частота равна частоте свободных колебаний контура.

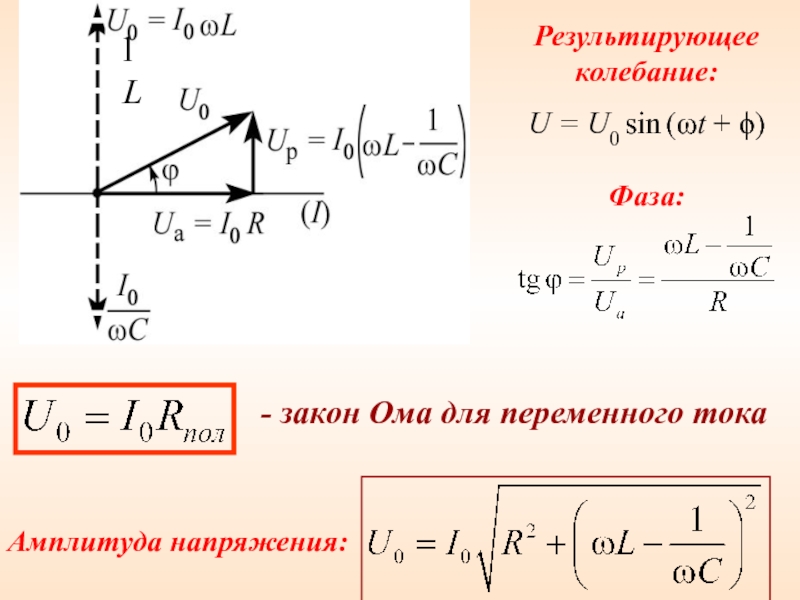
Закон Ома для переменного тока

Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него.

Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы).

В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.

Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю

Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю.

Тогда, падение напряжения на активном сопротивлении определяется по формуле:

(1)

где, U-напряжение на элементе цепи,

I – ток через элемент цепи

R – активное сопротивление элемента

Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:

(2)

где, Um-амплитудное значение напряжения на элементе цепи,

Im – амплитудное значение тока через элемент цепи

R – активное сопротивление элемента

В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис.

2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).

Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов.

Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов.

Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения.

Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:

	(3)
	(4)

где — U_L-падение напряжение на чисто индуктивном сопротивлении ;

U_С—падение напряжения на чисто емкостном сопротивлении;

I— значение тока в через реактивное сопротивление;

L— индуктивность реактивного элемента;

C— емкость реактивного элемента;

ω— циклическая частота.

Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов.

Приведенные выше формулы являются частными случаями закона Ома для переменного тока.

Следовательно, полный закон Ома для переменного тока будет иметь вид:

(5)

Где Z – полное сопротивление цепи переменного тока.

Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены.

Закон Ома для различных типовых цепей переменного тока

Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.)

Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.

Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:

(6)

где —эффективное значение силы тока в А;

U—эффективное значение напряжения в В;

R—активное сопротивление в Ом;

ωL—индуктивное сопротивление в ом.

Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения.

В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.

Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкосного сопротивления.

А закон Ома для такой цепи принимает вид:

(7)

В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6),

Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления.

Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:

(8)

где I-сила тока в А;

U-напряжение в В;

R-активное сопротивление в Ом;

ωL-индуктивное сопротивление в Ом;

1/ωС-емкостное сопротивление в Ом.

Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения.

Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5).

Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов.

а) — параллельное соединение R и L; б) — параллельное соединение R и C.

Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.

Рисунок 8. Эквивалентная схема колебательного контура.

Таким образом закон Ома для переменного тока можно сформулировать следующим образом.

Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Урок 8. переменный электрический ток — Физика — 11 класс

Физика, 11 класс

Урок 8. Переменный электрический ток

Перечень вопросов, рассматриваемых на уроке:

1) Свойства переменного тока;

2) Понятия активного сопротивления, индуктивного и ёмкостного сопротивления;

3) Особенности переменного электрического тока на участке цепи с резистором;

4) Определение понятий: переменный электрический ток, активное сопротивление, индуктивное сопротивление, ёмкостное сопротивление.

Глоссарий по теме

Переменный электрический ток — это ток, периодически изменяющийся со временем.

Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю называют активным сопротивлением.

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Величину Х_C,обратную произведению ωC циклической частоты на электрическую ёмкость конденсатора, называют ёмкостным сопротивлением.

Величину Х_L, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.

Рымкевич А.П. Сборник задач по физике. 10-11 класс.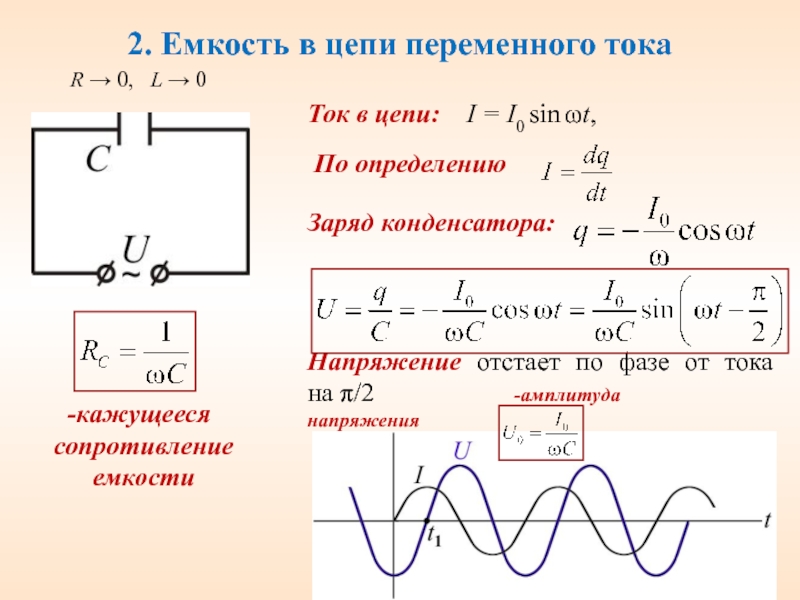 — М.: Дрофа, 2014. – С. 128 – 132.

Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.

Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004

Основное содержание урока

Сейчас невозможно представить себе нашу цивилизацию без электричества. Телевизоры, холодильники, компьютеры – вся бытовая техника работает на нем. Основным источником энергии является переменный ток.

Электрический ток, питающий розетки в наших домах, является переменным А что это такое? Каковы его характеристики? Чем же переменный ток отличается от постоянного? Об этом мы поговорим на данном уроке.

В известном опыте Фарадея при движении полосового магнита относительно катушки появлялся ток, что фиксировалось стрелкой гальванометра, соединенного с катушкой. Если магнит привести колебательное движение относительно катушки, то стрелка гальванометра будет отклоняться то в одну сторону, то в другую – в зависимости от направления движения магнита. Это означает, что возникающий в катушке ток меняет свое направление. Такой ток называют переменным.

Электрический ток, периодически меняющийся со временем по модулю и направлению, называется переменным током.

Переменный электрический ток представляет собой электромагнитные вынужденные колебания. Переменный ток в отличие от постоянного имеет период, амплитуду и частоту.

Сила тока и напряжение меняются со временем по гармоническому закону, такой ток называется синусоидальным. В основном используется синусоидальный ток. Колебания тока можно наблюдать с помощью осциллографа.

Если напряжение на концах цепи будет меняться по гармоническому закону, то и напряженность внутри проводника будет так же меняться гармонически. Эти гармонические изменения напряженности поля, в свою очередь вызывают гармонические колебания упорядоченного движения свободных частиц и, следовательно, гармонические колебания силы тока. При изменении напряжения на концах цепи, в ней с очень большой скоростью распространяется электрическое поле. Сила переменного тока практически во всех сечениях проводника одинакова потому, что время распространения электромагнитного поля превышает период колебаний.

Рассмотрим процессы, происходящие в проводнике, включенном в цепь переменного тока. Сопротивление проводника, в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным. При изменении напряжения на концах цепи по гармоническому закону, точно так же меняется напряженность электрического поля и в цепи появляется переменный ток.

При наличии такого сопротивления колебания силы тока и напряжения совпадают по фазе в любой момент времени.

𝒾 — мгновенное значение силы тока;

ℐ_m— амплитудное значение силы тока.

– колебания напряжения на концах цепи.

Колебания ЭДС индукции определяются формулами:

При совпадении фазы колебаний силы тока и напряжения мгновенная мощность равна произведению мгновенных значений силы тока и напряжения.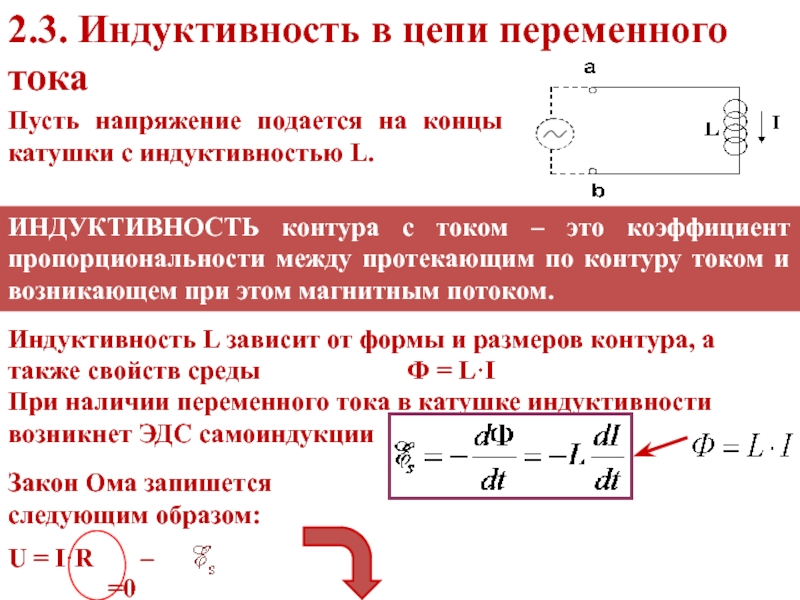 Среднее значение мощности равно половине произведения квадрата амплитуды силы тока и активного сопротивления.

Часто к параметрам и характеристикам переменного тока относят действующие значения. Напряжение, ток или ЭДС, которая действует в цепи в каждый момент времени — мгновенное значение (помечают строчными буквами — і, u, e). Однако оценивать переменный ток, совершенную им работу, создаваемое тепло сложно рассчитывать по мгновенному значению, так как оно постоянно меняется. Поэтому применяют действующее, которое характеризует силу постоянного тока, выделяющего за время прохождения по проводнику столько же тепла, сколько это делает переменный.

U_m — амплитудное значение напряжения.

Действующие значения силы тока и напряжения:

Электрическая аппаратура в цепях переменного тока показывает именно действующие значения измеряемых величин.

Конденсатор включенный в электрическую цепь оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.

Величину Х_C, обратную произведению циклической частоты на электрическую ёмкость конденсатора, называют ёмкостным сопротивлением.

Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току.

Если включить в электрическую цепь катушку индуктивности, то она будет влиять на прохождение тока в цепи, т.е. оказывать сопротивление току. Это можно объяснить явлением самоиндукции.

X_L=ωL

Если частота равна нулю, то индуктивное сопротивление тоже равно нулю.

При увеличении напряжения в цепи переменного тока сила тока будет увеличиваться так же, как и при постоянном токе. В цепи переменного тока содержащем активное сопротивление, конденсатор и катушка индуктивности будет оказываться сопротивление току. Сопротивление оказывает и катушка индуктивности, и конденсатор, и резистор. При расчёте общего сопротивления всё это надо учитывать. Основываясь на этом закон Ома для переменного тока формулируется следующим образом: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

Если цепь содержит активное сопротивление, катушку и конденсатор соединенные последовательно, то полное сопротивление равно

Закон Ома для электрической цепи переменного тока записывается имеет вид:

Преимущество применения переменного тока заключается в том, что он передаётся потребителю с меньшими потерями.

В электрической цепи постоянного тока зная напряжение на зажимах потребителя и протекающий ток можем легко определить потребляемую мощность, умножив величину тока на напряжение. В цепи переменного тока мощность равна произведению напряжения на силу тока и на коэффициент мощности.

Мощность цепи переменного тока

P=IU cosφ

Величина cosφ – называется коэффициентом мощности

Коэффициент мощности показывает какая часть энергии преобразуется в другие виды. Коэффициент мощности находят с помощью фазометров. Уменьшение коэффициента мощности приводит к увеличению тепловых потерь. Для повышения коэффициента мощности электродвигателей параллельно им подключают конденсаторы. Конденсатор и катушка индуктивности в цепи переменного тока создают противоположные сдвиги фаз. При одновременном включении конденсатора и катушки индуктивности происходит взаимная компенсация сдвига фаз и повышение коэффициента мощности. Повышение коэффициента мощности является важной народнохозяйственной задачей.

Разбор типовых тренировочных заданий

1. Рамка вращается в однородном магнитном поле. ЭДС индукции, возникающая в рамке, изменяется по закону e=80 sin 25πt. Определите время одного оборота рамки.

Дано: e=80 sin 25πt.

Найти: T.

Решение:

Колебания ЭДС индукции в цепи переменного тока происходят по гармоническому закону

Согласно данным нашей задачи:

Время одного оборота, т.е. период связан с циклической частотой формулой:

Подставляем числовые данные:

Ответ: T = 0,08 c.

2. Чему равна амплитуда силы тока в цепи переменного тока частотой 50 Гц, содержащей последовательно соединенные активное сопротивление 1 кОм и конденсатор емкости С = 1 мкФ, если действующее значение напряжения сети, к которой подключен участок цепи, равно 220 В?

Дано:

ν=50 Гц,

R=1 кОм=1000 Ом,

C=1 мкФ=10^-6 Ф,

U=220 В.

Найти: I_m

Решение:

Напишем закон Ома для переменного тока:

I=U/Z

Для амплитудных значений силы тока и напряжения, мы можем записать I_m=U_m/Z?

Полное сопротивление цепи равно:

Подставляя числовые данные находим полное сопротивление Z≈3300 Ом. Так как действующее значение напряжения равно:

то после вычислений получаем I_m ≈0,09 Ом.

Ответ: I_m ≈0,09 Ом.

2. Установите соответствие между физической величиной и прибором для измерения.

Физические величины	Физические приборы
Сила тока	Омметр
Напряжение	Вольтметр
Сопротивление	Амперметр
Мощность	Ваттметр

Правильный ответ:

Физические величины	Физические приборы
Сила тока	Амперметр
Напряжение	Вольтметр
Сопротивление	Омметр
Мощность	Ваттметр

Переменный Ток

Рассмотрим процессы, происходящие в проводнике, включенном в цепь переменного тока.

Если индуктивность проводника настолько мала, что при включении его в цепь переменного тока индукционными полями можно пренебречь по сравнению с внешним электрическим полем, то движение электрических зарядов в проводнике определяется действием только внешнего электрического поля, напряженность которого пропорциональна напряжению на концах проводника.

При изменении напряжения по гармоническому закону U = U_m cos wt напряженность электрического поля в проводнике изменяется по такому же закону.

Под действием переменного электрического поля в проводнике возникает переменный электрический ток, частота и фаза колебаний которого совпадает с частотой и фазой колебаний напряжения:

где i — мгновенное значение силы тока, I_m— амплитудное значение силы тока.

Колебания силы тока в цепи являются вынужденными электрическими колебаниями, возникающими под действием приложенного переменного напряжения.

Амплитуда силы тока равна:

При совпадении фаз колебаний силы тока и напряжения мгновенная мощность переменного тока равна:

Среднее значение квадрата косинуса за период равно 0,5. В результате средняя мощность за период

Для того чтобы формула для расчета мощности переменного тока совпадала по форме с аналогичной формулой для постоянного тока (Р = PR), вводится понятие действующих значений силы тока и напряжения. Из равенства мощностей получим

Действующим значением силы тока называют величину, в корень из 2 раз меньшую ее амплитудного значения:

Действующее значение силы тока равно силе такого постоянного тока, при котором средняя мощность, выделяющаяся в проводнике в цепи переменного тока, равна мощности, выделяющейся в том же проводнике в цепи постоянного тока.

Действующее значение переменного напряжения в корень из 2 раз меньше его амплитудного значения:

Средняя мощность переменного тока при совпадении фаз колебаний силы тока и напряжения равна произведению действующих значений силы тока и напряжения:

Сопротивление элемента электрической цепи, в которой происходит превращение электрической энергии во внутреннюю энергию, называют активным сопротивлением. Активное сопротивление участка цепи можно определить как частное от деления средней мощности на квадрат действующего значения силы тока:

Мощность переменного тока. Мощность тока через катушку, резистор, конденсатор

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.

Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .

Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу

Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:

(1)

Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.

Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.

1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).

2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.

Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).

Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.

Мощность тока через резистор

Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:

Поэтому для мгновенной мощности получаем:

(2)

График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:

На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между и . Где же именно?

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно.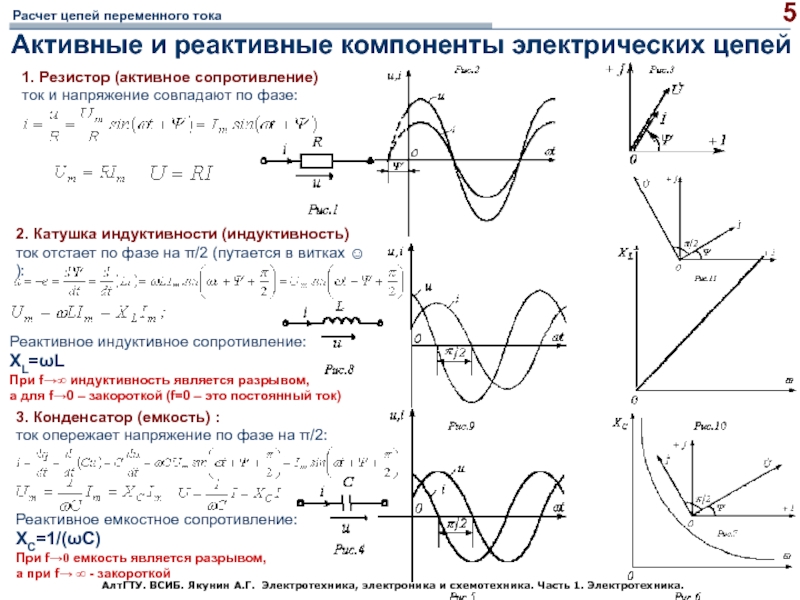 Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно .

Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно

Итак, для среднего значения мощности тока на резисторе имеем:

(3)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):

(4)

Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.

Мощность тока через конденсатор

Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :

Для мгновенной мощности получаем:

График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

Мощность тока через катушку

Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :

Для мгновенной мощности получаем:

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.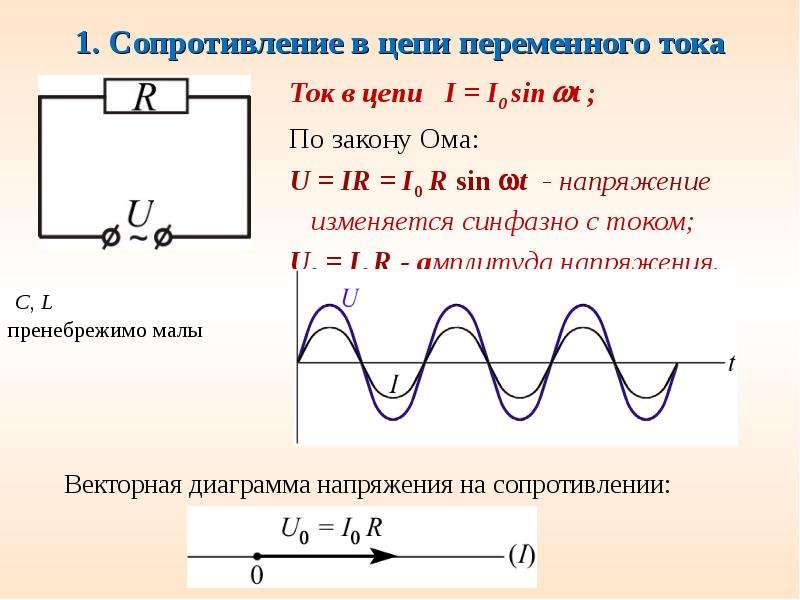

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

Мощность тока на произвольном участке

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .

Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:

Тогда для мгновенной мощности имеем:

(5)

Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:

В результате получим:

(6)

Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:

(7)

Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю.

Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.

С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели.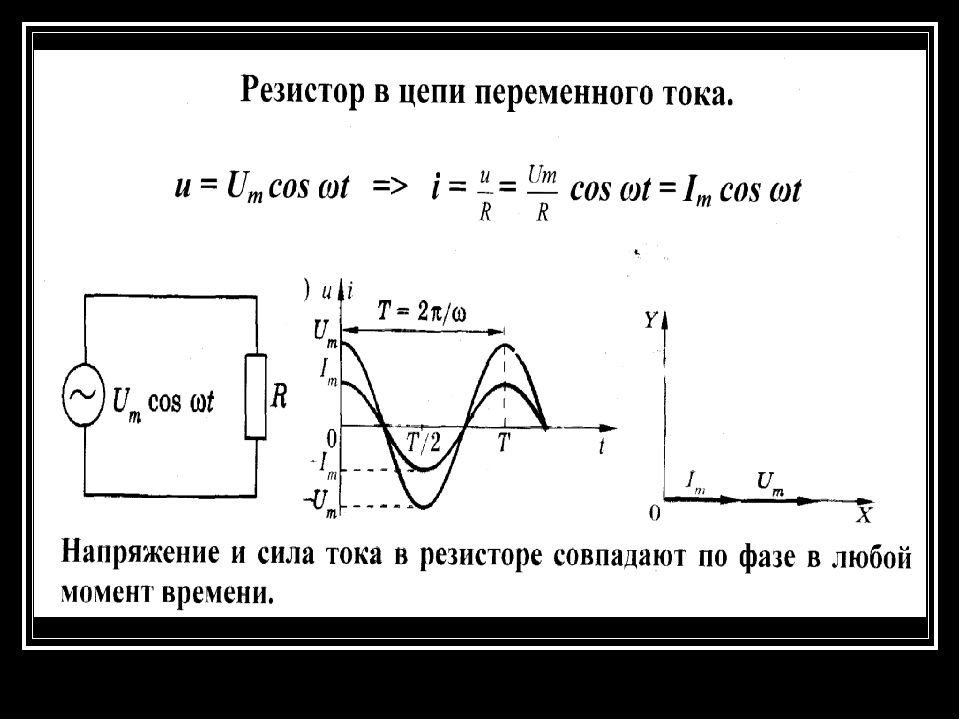 Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.

Напряжение цепи переменного тока | Электрикам

Переменное напряжение — это напряжение, которое изменяется с течением времени. Далее будем рассматривать только гармоническое переменное напряжение (изменяется по синусоиде).

u = U_msin(2πt + Ψ ) = U_msin(ωt + Ψ )

Где u = u(t) — мгновенное значение переменного напряжения [В].

U_m —максимальное значение напряжения (амплитудное значение) [В].

f — частота равная числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с^-1)

ω — угловая частота (омега) (единица угловой частоты — рад/с или с^-1)

ω = 2πf = 2π/T

Аргумент синуса, т.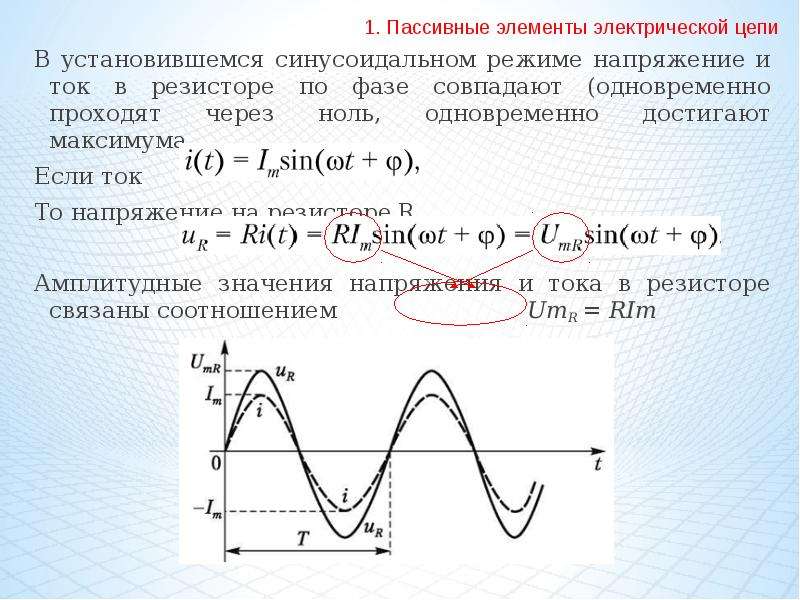 е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.

U — Действующее значение напряжения [В]:

Рассмотрим параметры напряжения в бытовой электросети.

Все мы знаем, что у нас дома в розетке поступает переменный ток, с напряжением 220 вольт и частотой 50 герц (в идеальных условиях) на самом деле допускается не большая погрешность как в меньшую, так и в большую сторону так, что не удивляйтесь если ваш вольтметр покажет не 220, а например 210 или даже 230 В.).

Большинство приборов измеряет не амплитудное, а действующее значение переменного напряжения, тока, мощности так, что если мы говорим что у нас напряжение сети 220, 380 В и т. д. то имеется виду именно действующие значения.

Действующее значение напряжения U = 220 В.
Амплитудное значение напряжения цепи переменного тока U_m= U*√2 = 220 *√2 = 311 В.
Угловая частота ω = 2πf = 3,14*2*50 = 314 рад/с.
Начальная фаза Ψ = 0 град.
Мгновенное значение u = 311sin(314t) В.

Переменный электрический ток. Активное, индуктивное, ёмкостное сопротивления.

Переменный электрический ток

Электромагнитные колебания, как и механические, бывают двух типов: свободные и вынужденные.

Свободные электромагнитные колебания, всегда колебания затухающие. Поэтому на практике они почти не используются. В то время, как вынужденные колебания используются везде и повсеместно. Ежедневно мы с вами можем наблюдать эти колебания.

Все наши квартиры освещены с помощью переменного тока. Переменный ток есть не что иное, как вынужденные электромагнитные колебания. Сила тока и напряжение будут меняться с течением времени согласно гармоническому закону. Колебания, например, напряжения можно обнаружить, если подать напряжение из розетки, на осциллограф.

На экране осциллографа появится синусоида. Можно вычислить частоту переменного тока. Она будет равняться частоте электромагнитных колебаний. Стандартная частота для промышленного переменного тока принята равной 50 Гц. То есть за 1 секунду направление тока в розетке меняется 50 раз.

Изменение напряжения на концах цепи будет вызывать за собой изменение силы тока в цепи колебательного контура. Следует всё же понимать, что изменение электрического поля во всей цепи не происходит мгновенно. Но так как это время, значительно меньше, чем период колебания напряжения на концах цепи, то обычно считают, что электрическое поле в цепи сразу же меняется, как меняется напряжение на концах цепи.

Переменное напряжение создается генераторами на электростанциях. Простейшим генератором можно рассматривать проволочную рамку, которая вращается в однородном магнитном поле.

Магнитный поток, пронизывающий контур, будет постоянно меняться и будет пропорционален косинусу угла между вектором магнитной индукции и нормалью к рамке.

Если рамка вращается равномерно, то угол будет пропорционален времени.

Следовательно, магнитный поток будет изменяться по гармоническому закону:

Ф = BScos(ωt)

Скорость изменения магнитного потока, взятая с обратным знаком, согласно закону ЭМИ, будет равняться ЭДС индукции.

E_i = -Ф’ = E_msin(ωt).

Если к рамке подключить колебательный контур, то угловая скорость вращения рамки определит частот колебаний напряжения на различных участках цепи и силы тока. В дальнейшем мы будем рассматривать только вынужденные электромагнитные колебания.

Они описываются следующими формулами:

u = U_msin(ωt),

u = U_mcos(ωt)

Здесь U_m – амплитуда колебаний напряжения. Напряжение и сила тока меняются с одинаковой частой ω. Но колебания напряжения не всегда будут совпадать с колебаниями силы тока, поэтому лучше использовать более общую формулу:

I = I_msin(ωt +φ), где I_m — амплитуда колебаний силы тока, а φ – сдвиг фаз между колебаниями силы тока и напряжения.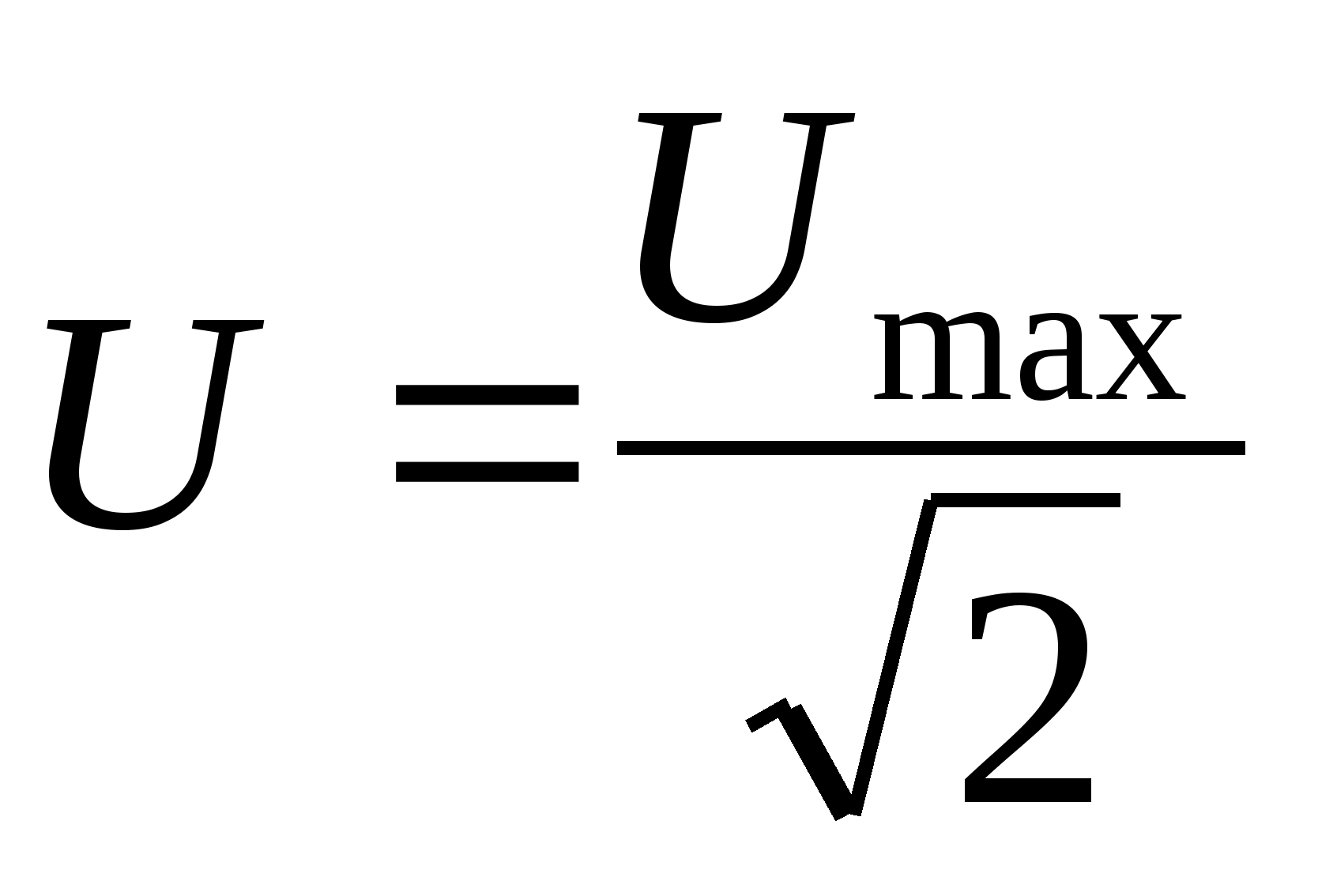

Активное сопротивление

Рассмотрим следующую цепь.

Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.

Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:

U = U_mcos(ωt).

Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения.

I = u/R = U_mcos(ωt)/R = I_mcos(ωt).

Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует.

Действующее значение силы тока

Амплитуда силы тока определяется по следующей формуле:

I_m = U_m/R.

Среднее значение квадрата силы тока за период вычисляется по следующей формуле:

i²= (I_m)²/2.

Здесь I_m есть амплитуда колебания силы тока. Если мы теперь вычислим квадратный корень из среднего значения квадрата силы тока, то получим величину, которая называется действующим значением силы переменного тока.

Для обозначения действующего значения силы тока используется буква I. То есть в виде формулы это будет выглядеть следующим образом:

I = √(i²) = I_m/√2.

Действующее значение силы переменного тока будет равно силе такого постоянного тока, при котором за одинаковый промежуток времени в рассматриваемом проводнике будет выделяться столько же теплоты, сколько и при переменном токе. Для определения действующего значения напряжения используется следующая формула.

U = √(u²) = U_m/√2.

Теперь подставим действующие значения силы тока и напряжения, в выражение I_m = U_m/R.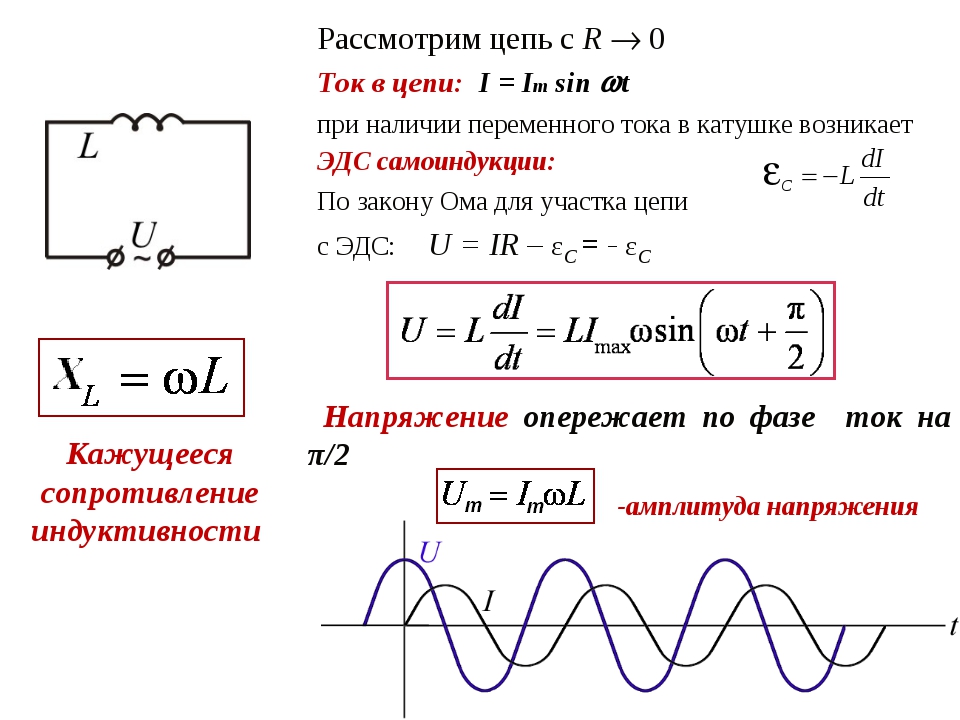 Получим:

I = U/R.

Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний — такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.

Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.

Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.

Для вычисления средней мощности используется следующая формула:

P = I²R = UI.

Отметим, что измерительные приборы (амперметры и вольтметры переменного тока) регистрируют именно действующие значения.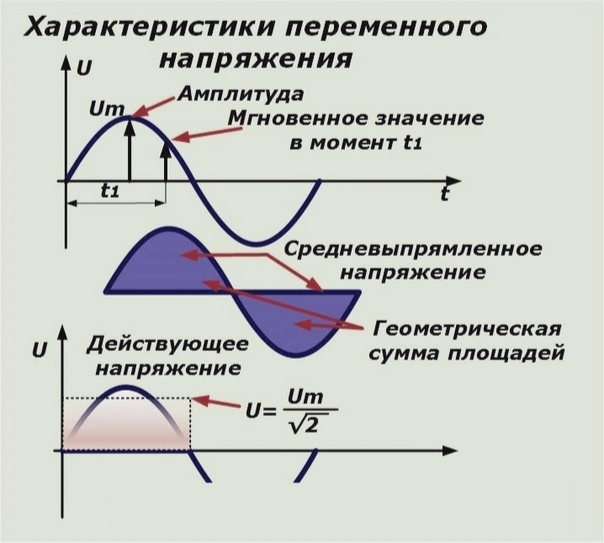 Кроме того, номинальные значения напряжений и токов бытовых приборов также указываются как действующие значения. Так стандартное напряжение в цепи − 220 вольт есть действующее значение, а амплитудное значение этого напряжения равно

При изучении постоянного тока мы узнали, что он не может проходить в цепи, в которой есть конденсатор. Так как конденсатор — это две пластины, разделенные слоем диэлектрика. Для цепи постоянного тока конденсатор будет, как разрыв в цепи. Если конденсатор пропускает постоянный ток, значит, он неисправен.

В отличии от постоянного переменный ток может идти и через цепь, в которой присутствует конденсатор.

Рассмотрим, как будет меняться сила тока в цепи, содержащей конденсатор, с течением времени. При этом будем пренебрегать сопротивлением соединяющих проводов и обкладок конденсатора.

рисунок

Напряжение на конденсаторе будет равняться напряжению на концах цепи. Значит, мы можем приравнять эти две величины.

u = φ₁-φ₂ = q/C, u = U_mcos(ωt).

Имеем:

q/C = U_mcos(ωt).

Выражаем заряд:

q = CU_mcos(ωt).

Видим, что заряд будет изменяться по гармоническому закону. Сила тока — это скорость изменения заряда. Значит, если возьмем производную от заряда, получим выражение для силы тока.

I = q’ = U_mCωcos(ωt+π/2).

Разность фаз между колебаниями силы тока и заряда, а также напряжения, получилась равной π/2. Получается, что колебания силы тока опережают по фазе колебания напряжения на π/2. Это представлено на рисунке.

Из уравнения колебаний силы тока получаем выражение для амплитуды силы тока:

I_m = U_mCω.

Введем следующее обозначение:

Xc = 1/(Cω).

Запишем следующее выражение закона Ома, используя Xc и действующие значения силы тока и напряжения:

I = U/Xc.

Xc — величина, называемая емкостным сопротивлением.

Индуктивность в цепи переменного тока будет влиять на силу переменного тока.

Рассмотрим цепь, в которой есть только катушка индуктивности. При этом значение сопротивления катушки и соединительных проводов пренебрежимо мало.

рисунок

Выясним, как будут связаны напряжение на катушке с ЭДС самоиндукции в ней. При сопротивлении катушки равном нулю, напряженность электрического поля внутри проводника тоже будет равна нулю. Равенство нулю напряженности возможно.

Напряженности электрического поля создаваемого зарядами Eк будет соответствовать такая же по модулю и противоположно направленная напряженность вихревого электрического поля, которое появится вследствие изменения магнитного поля.

Следовательно, ЭДС самоиндукции e_i будет равна по модулю и противоположна по знаку удельной работе кулоновского поля.

Следовательно: e_i= -u.

Сила тока будет изменяться по гармоническому закону: I = I_m sin(ωt).

ЭДС самоиндукции будет равна: Ei = -Li’ = -Lω I_m cos(ωt).

Следовательно, напряжение будет равно: U = Lω I_m cos(ωt) = Lω I_m sin(ωt+ π/2).

Отсюда значение действующего напряжения будет равняться U_m = Lω I_m. Видим, что между колебаниями тока и напряжения получилась разность фаз равная π/2. Следовательно, колебания силы тока отстают от колебания напряжения на π/2. Это наглядно представлено на следующем рисунке.

рисунок

I_m = U_m/(ωL). Введем обозначение XL = ωL. Эта величина называется индуктивное сопротивление.

15.S: Цепи переменного тока (Резюме) — Physics LibreTexts

Ключевые термины

Уравнение

переменный ток	ток, синусоидально колеблющийся во времени с фиксированной частотой
переменное напряжение	напряжение, синусоидально колеблющееся во времени с фиксированной частотой
переменный ток (ac)	Поток электрического заряда, который периодически меняет направление
средняя мощность	среднее время мгновенной мощности за один цикл
ширина полосы	диапазон угловых частот, в которых средняя мощность больше половины максимального значения средней мощности
емкостное реактивное сопротивление	Противодействие конденсатора изменению тока
постоянный ток (dc)	Поток электрического заряда только в одном направлении
импеданс	переменного тока аналог сопротивления в цепи постоянного тока, который измеряет совокупное влияние сопротивления, емкостного реактивного сопротивления и индуктивного реактивного сопротивления
индуктивное сопротивление	Противодействие катушки индуктивности изменению тока
фазовый угол	величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи
Коэффициент мощности	величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе
добротность	безразмерная величина, описывающая резкость пика полосы пропускания; высокая добротность — острый или узкий резонансный пик
резонансная частота	частота, при которой амплитуда тока максимальна, и цепь будет колебаться, если не будет управляться источником напряжения
действующее значение тока	среднеквадратичное значение текущего
действующее напряжение	среднеквадратичное значение напряжения
понижающий трансформатор	трансформатор, понижающий напряжение и увеличивающий ток
повышающий трансформатор	трансформатор, повышающий напряжение и понижающий ток
трансформатор	устройство, преобразующее напряжение из одного значения в другое с помощью индукции
уравнение трансформатора	, показывающее, что отношение вторичного напряжения к первичному в трансформаторе равно отношению количества витков в их обмотках

Ключевые уравнения

Напряжение переменного тока	\ (\ Displaystyle v = V_0sinωt \)
Переменный ток	\ (\ Displaystyle я = I_0sinωt \)
емкостное реактивное сопротивление	\ (\ Displaystyle \ гидроразрыва {V_0} {I_0} = \ гидроразрыва {1} {ωC} = X_C \)
действующее напряжение	\ (\ Displaystyle V_ {rms} = \ frac {V_0} {\ sqrt {2}} \)
действующее значение тока	\ (\ Displaystyle I_ {rms} = \ frac {I_0} {\ sqrt {2}} \)
индуктивное сопротивление	\ (\ Displaystyle \ гидроразрыва {V_0} {I_0} = ωL = X_L \)
Фазовый угол цепи последовательного RLC	\ (\ Displaystyle ϕ = загар ^ {- 1} \ гидроразрыва {X_L − X_C} {R} \)
Вариант закона Ома по переменному току	\ (\ Displaystyle I_0 = \ гидроразрыва {V_0} {Z} \)
Импеданс цепи серии RLC	\ (\ Displaystyle Z = \ sqrt {R ^ 2 + (X_L − X_C) ^ 2} \)
Средняя мощность, связанная с элементом схемы	\ (\ Displaystyle P_ {ave} = \ frac {1} {2} I_0V_0cosϕ \)
Средняя мощность, рассеиваемая резистором	\ (\ Displaystyle P_ {ave} = \ frac {1} {2} I_0V_0 = I_ {rms} V_ {rms} = I ^ 2_ {rms} R \)
Резонансная угловая частота контура	\ (\ Displaystyle ω_0 = \ sqrt {\ frac {1} {LC}} \)
Добротность схемы	\ (\ Displaystyle Q = \ гидроразрыва {ω_0} {Δω} \)
Добротность цепи по параметрам цепи	\ (\ Displaystyle Q = \ гидроразрыва {ω_0L} {R} \)
Уравнение трансформатора с напряжением	\ (\ Displaystyle \ гидроразрыва {V_S} {V_P} = \ гидроразрыва {N_S} {N_P} \)
Уравнение трансформатора с током	\ (\ Displaystyle I_S = \ гидроразрыва {N_P} {N_S} I_P \)

Сводка

15.

2 источника переменного тока

Постоянный ток (dc) относится к системам, в которых напряжение источника постоянно.
Переменный ток (ac) относится к системам, в которых напряжение источника периодически изменяется, особенно синусоидально.
Источник напряжения системы переменного тока выдает напряжение, которое рассчитывается по времени, пиковому напряжению и угловой частоте.
В простой схеме ток определяется делением напряжения на сопротивление.Переменный ток рассчитывается с использованием пикового тока (определяемого делением пикового напряжения на сопротивление), угловой частоты и времени.

15.3 Простые цепи переменного тока

Для резисторов сквозной ток и напряжение совпадают по фазе.
Для конденсаторов мы обнаруживаем, что когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четверть цикла. Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току, называемую емкостным реактивным сопротивлением, которое измеряется в омах.
Для катушек индуктивности в цепях переменного тока мы обнаруживаем, что когда на индуктор подается синусоидальное напряжение, оно опережает ток на одну четверть цикла.
Противодействие катушки индуктивности изменению тока выражается как тип реактивного сопротивления переменного тока. Это индуктивное реактивное сопротивление, измеряемое в омах, зависит от частоты источника переменного тока.

Цепи серии 15,4 RLC с переменным током

Последовательная цепь RLC представляет собой последовательную комбинацию резистора, конденсатора и индуктора через источник переменного тока.
Один и тот же ток течет через каждый элемент последовательной цепи RLC во все моменты времени.
Сопротивлением в цепи постоянного тока является импеданс, который измеряет совокупное влияние резисторов, конденсаторов и катушек индуктивности. Максимальный ток определяется версией закона Ома для переменного тока.
Импеданс измеряется в омах и определяется как сопротивление, емкостное и индуктивное сопротивление.

15.5 Питание в цепи переменного тока

Средняя мощность переменного тока определяется путем умножения среднеквадратичных значений тока и напряжения.
Закон Ома для среднеквадратичного значения переменного тока находится делением действующего напряжения на полное сопротивление.
В цепи переменного тока существует фазовый угол между напряжением источника и током, который можно найти, разделив сопротивление на полное сопротивление.
Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла.
Коэффициент мощности составляет от –1 до 1.

15,6 Резонанс в цепи переменного тока

На резонансной частоте индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению.
График зависимости средней мощности от угловой частоты для цепи RLC имеет пик, расположенный на резонансной частоте; резкость или ширина пика называется полосой пропускания.
Полоса пропускания связана с безразмерной величиной, называемой коэффициентом качества.Высокое значение добротности — это острый или узкий пик.

15,7 Трансформаторы

Электростанции передают высокое напряжение при малых токах для достижения более низких омических потерь на многокилометровых линиях передачи.
Трансформаторы используют индукцию для преобразования напряжения из одного значения в другое.
Для трансформатора напряжения на первичной и вторичной катушках или обмотках связаны уравнением трансформатора.
Токи в первичной и вторичной обмотках связаны количеством первичных и вторичных петель или витков в обмотках трансформатора.
Повышающий трансформатор увеличивает напряжение и снижает ток, тогда как понижающий трансформатор снижает напряжение и увеличивает ток.

Авторы и авторство

Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Цепь

переменного тока — напряжение, ток и мощность

В цепи переменного тока — переменный ток генерируется от источника синусоидального напряжения

Напряжение

Токи в цепях с чисто резистивными, емкостными или индуктивными нагрузками.

Мгновенное напряжение в синусоидальной цепи переменного тока может быть выражено в форме во временной области как

u (t) = U _max cos (ω t + θ) (1)

где

u (t) = напряжение в цепи в момент времени t (В)

U _max = максимальное напряжение при амплитуде синусоидальной волны (В)

t = время (с)

ω = 2 π f

= угловая частота синусоидальной волны (рад / с)

f = частота (Гц, 1 / с)

θ = фазовый сдвиг синусоидальной волны (рад)

Мгновенное напряжение альтернативно может быть выражено в частотной области (или векторном) как

U = U (jω) = U _max e ^jθ (1a)

где

U (jω) = U = комплексное напряжение (В)

Вектор — это комплексное число, выраженное в полярной форме, состоящее из величины, равной пиковой амплитуде синусоидального сигнала, и фазы.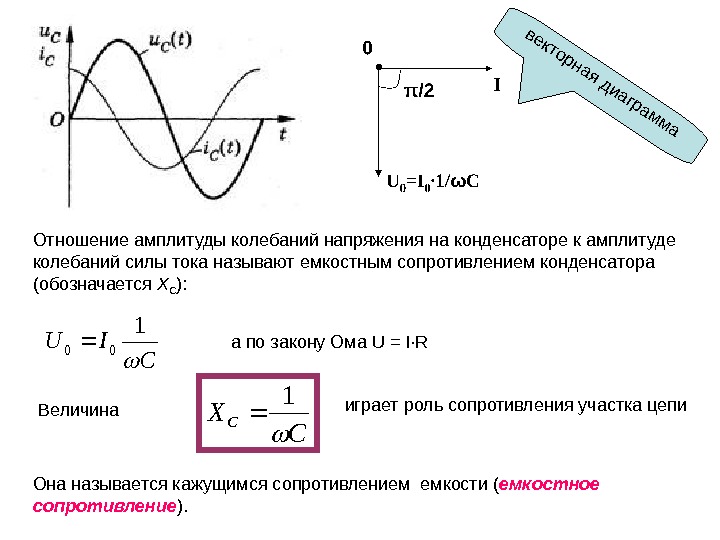 угол, равный фазовому сдвигу синусоидального сигнала относительно косинусоидального сигнала.

Обратите внимание, что конкретная угловая частота — ω — явно не используется в выражении вектора.

Ток

Мгновенный ток можно выразить в форме во временной области как

i (t) = I _m cos (ω t + θ) (2)

где

i (t) = ток в момент времени t (A)

I _max = максимальный ток при амплитуде синусоидальной волны (A)

Токи в цепях с чистые резистивные, емкостные или индуктивные нагрузки показаны на рисунке выше.Ток в «реальной» цепи с резистивной, индуктивной и емкостной нагрузками указан на рисунке ниже.

Мгновенный ток в цепи переменного тока альтернативно можно выразить в частотной (или векторной) форме как

I = I (jω) = I _max e ^jθ (2a)

, где

I = I (jω) = комплексный ток (A)

Частота

Обратите внимание, что частота большинства систем переменного тока является фиксированной — например, 60 Гц в Северной Америке и 50 Гц в большей части остального мира.

Угловая частота для Северной Америки составляет

ω = 2 π 60

= 377 рад / с

Угловая частота для большей части остального мира составляет

ω = 2 π 50

= 314 рад / с

Резистивная нагрузка

Напряжение на резистивной нагрузке в системе переменного тока может быть выражено как

U = RI (4)

где

R = сопротивление (Ом)

Для резистивной нагрузки в цепи переменного тока напряжение составляет в фазе с током.

Индуктивная нагрузка

Напряжение на индуктивной нагрузке в системе переменного тока может быть выражено как

U = j ω LI (5)

где

L = индуктивность (генри)

Для индуктивной нагрузки ток в цепи переменного тока составляет π / 2 (90 ^o) фаза после напряжения (или напряжение перед током).

Емкостная нагрузка

Напряжение на индуктивной нагрузке в системе переменного тока может быть выражено как

U = 1 / (j ω C) I (6)

где

C = емкость (фарад)

Для емкостной нагрузки ток в цепи переменного тока опережает напряжение на π / 2 (90 ^o) фаза .

В реальной электрической цепи есть смесь резистивных, емкостных и индуктивных нагрузок со сдвигом фазы напряжение / ток в диапазоне — π / 2 <= φ <= π / 2 , как показано на рисунок ниже.

Ток в «реальной» цепи со смесью резистивных, индуктивных и емкостных нагрузок. φ — фазовый угол между током и напряжением.

Импеданс

Закон Ома для сложного переменного тока может быть выражен как

U _z = I _z Z (7)

где

U _z = падение напряжения при нагрузке (вольт, В)

I _z = ток через нагрузку (ампер, А)

Z = импеданс нагрузки (Ом, Ом)

Полное сопротивление в цепи переменного тока можно рассматривать как комплексное сопротивление. Импеданс действует как частотно-зависимый резистор, где сопротивление является функцией частоты синусоидального возбуждения.

Импедансы в серии

Результирующий импеданс для последовательных сопротивлений может быть выражен как

Z = Z ₁ + Z ₂ (7b)

Сопротивление параллельно

Результирующее сопротивление для параллельных сопротивлений может быть выражено как

1 / Z = 1 / Z ₁ + 1 / Z ₂ (7c)

Полная проводимость

Полная проводимость — это инвертированный импеданс

Y = 1 / Z (8)

, где

Y = проводимость (1 / Ом)

RMS или эффективное напряжение

RMS значение — это эффективное значение синусоидального напряжения или тока.

RMS — среднеквадратичное значение — или эффективное напряжение может быть выражено как

U _rms = U _eff

= U _max / (2) ^1/2

= 0,707 U _макс. (9)

где

U _{действ. = максимальное напряжение (амплитуда) источника синусоидального напряжения (В)}

RMS — среднеквадратическое значение — или эффективный ток может быть выражен как

I _rms = I _eff

= I _max / (2) ^1/2

= 0.707 I _макс. (10)

где

I _{среднеквадратичное значение} = I _eff

= действующее значение тока (A)

_{макс. = максимальный ток (амплитуда) источника синусоидального напряжения (A)}
Вольтметры и амперметры переменного тока показывают среднеквадратичное значение напряжения или тока — или 0,707 максимальных пиковых значений. Максимальные пиковые значения равны 1.В 41 раз больше значений вольтметра.
Пример
для системы 230 В U _{среднеквадратичное значение} = 230 В и U _{макс. U _макс. = 169 В}
Трехфазное напряжение переменного тока — линия к линии и линия к нейтрали
В трехфазной системе переменного тока напряжение может подаваться между линиями и нейтралью (фазный потенциал), или между линиями (линейный потенциал).Результирующие напряжения для двух общих систем — европейской системы 400/230 В и североамериканской системы 208/120 В указаны для одного периода на рисунках ниже.
400/230 В переменного тока
печать 400/230 В трехфазная диаграмма
L1, L2 и L3 — это три фазы, соединяющие потенциалы нейтрали — потенциалы фаз
L1 — L2, L1 — L3 и L2 — L3 — это трехфазные линейные потенциалы — линейные потенциалы
L2, L2 и L3 — результирующий потенциал трех фаз в сбалансированной цепи — результирующий потенциал = 0
Величина линейных потенциалов равна 3 ^1/2 (1. 73) величина фазового потенциала.
U _{действующее значение, линия} = 1,73 U _{действующее значение, фаза} (11)
208 В / 120 В переменного тока
печать 208/120 В Трехфазная диаграмма
Мощность
Активная — или действительная или истинная — мощность, которая выполняет фактическую работу в цепи — может быть рассчитана как
P = U _{действующее значение} I _{среднеквадратичное значение} cos φ (12)
, где
P = активная активная мощность (Вт)
φ = фазовый угол между током и напряжением (рад, градусы)
Cos φ также называется коэффициентом мощности.
Реактивная мощность в цепи может быть рассчитана как
Q = U _{действующее значение} I _{среднеквадратичное значение} sin φ (13)
Q = реактивная мощность (ВАР)
Мощность в цепи переменного тока — Университет Физика Том 2
Цели обучения
К концу раздела вы сможете:
Опишите, как среднюю мощность от цепи переменного тока можно записать в терминах пикового тока и напряжения, а также среднеквадратичных значений тока и напряжения
Определите соотношение между фазовым углом тока и напряжения и средней мощностью, известное как коэффициент мощности
Элемент схемы рассеивает или вырабатывает мощность в зависимости от того, где I — ток через элемент, а В — напряжение на нем. Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность также зависит от времени. График p ( t ) для различных элементов схемы показан на (Рисунок). Для резистора i ( t ) и v ( t ) синфазны и поэтому всегда имеют один и тот же знак (см. (Рисунок)). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разницы фаз (см. (Рисунок) и (Рисунок)).Следовательно, p ( t ) в некоторые моменты положительный, а в другие — отрицательный, что указывает на то, что емкостные и индуктивные элементы вырабатывают мощность в одни моменты и поглощают ее в другие.
Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. То, что нас почти всегда интересует, — это усредненная по времени мощность, которую мы называем средней мощностью. Он определяется средним по времени мгновенной мощностью за один цикл:
где — период колебаний.С заменами и этот интеграл становится
Используя тригонометрическое соотношение, получаем
Вычисление этих двух интегралов дает
и
Следовательно, средняя мощность, связанная с элементом схемы, равна
В технических приложениях известен как коэффициент мощности, который представляет собой величину, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе.Для резистора, поэтому средняя рассеиваемая мощность составляет
Ом.
Сравнение p ( t ) и показано на (Рисунок) (d). Чтобы выглядеть как его аналог постоянного тока, мы используем среднеквадратичные значения тока и напряжения. По определению это
где
С получаем
Затем мы можем написать для средней мощности, рассеиваемой резистором,
Это уравнение дополнительно подчеркивает, почему при обсуждении выбирается среднеквадратичное значение, а не пиковые значения.Оба уравнения для средней мощности верны для (Рисунок), но среднеквадратичные значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не требуется.
Переменные напряжения и токи обычно описываются их действующими значениями. Например, напряжение 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника равна. Поскольку большинство измерителей переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, помещенный в бытовую розетку, будет показывать 110 В.
Для конденсатора и катушки индуктивности соответственно. Поскольку мы находим из (Рисунок), что средняя мощность, рассеиваемая любым из этих элементов, равна Конденсаторам, а катушки индуктивности поглощают энергию из цепи в течение одного полупериода, а затем разряжают ее обратно в цепь в течение другого полупериода. Это поведение проиллюстрировано на графиках (Рисунок), (b) и (c), которые показывают, что p ( t) колеблется синусоидально около нуля.
Фазовый угол генератора переменного тока может иметь любое значение.Если генератор выдает мощность; если он поглощает энергию. В терминах среднеквадратичных значений средняя мощность генератора переменного тока записывается как
Для генератора в цепи RLC ,
и
Отсюда средняя мощность генератора
Это также можно записать как
, который означает, что мощность, производимая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится делением среднеквадратичного напряжения на импеданс.
Проверьте свое понимание Вольтметр переменного тока, подключенный к клеммам генератора переменного тока 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.
Проверьте свое понимание Покажите, что среднеквадратичные значения напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока, где среднеквадратичный ток выражается соответственно. Определите эти значения для компонентов цепи RLC (рисунок).
Сводка
Средняя мощность переменного тока определяется путем умножения среднеквадратичных значений тока и напряжения.
Закон Ома для среднеквадратичного значения переменного тока находится делением действующего напряжения на полное сопротивление.
В цепи переменного тока существует фазовый угол между напряжением источника и током, который можно найти, разделив сопротивление на полное сопротивление.
Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла.
Коэффициент мощности находится в диапазоне от –1 до 1.
Концептуальные вопросы
При каком значении фазового угла между выходным напряжением источника переменного тока и током средняя выходная мощность источника является максимальной?
Обсудите разницу между средней мощностью и мгновенной мощностью.
Мгновенная мощность — это мощность в данный момент. Средняя мощность — это мощность, усредненная за цикл или количество циклов.
Средний переменный ток, подаваемый в цепь, равен нулю.Несмотря на это, мощность в цепи рассеивается. Объяснять.
Может ли мгновенная выходная мощность источника переменного тока быть отрицательной? Может ли средняя выходная мощность быть отрицательной?
Мгновенная мощность может быть отрицательной, но выходная мощность не может быть отрицательной.
Номинальная мощность резистора, используемого в цепях переменного тока, относится к максимальной средней мощности, рассеиваемой в резисторе. Как это соотносится с максимальной мгновенной мощностью, рассеиваемой на резисторе?
Глоссарий
средняя мощность
среднее время мгновенной мощности за один цикл
коэффициент мощности
величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе
Расчет мощности переменного тока — Видео и стенограмма урока
Power Equations
Но этот урок называется «Мощность переменного тока», так как же нам рассчитать мощность, используемую цепью переменного тока? Как обсуждалось в другом видеоуроке, мощность — это энергия, используемая в секунду, измеряемая в ваттах (или джоулях в секунду).А в схеме его можно вычислить, умножив ток на напряжение. Мы можем сделать то же самое для цепи переменного тока; мы просто используем среднеквадратичное значение тока и среднеквадратичное напряжение. Итак, ниже представлено наше основное уравнение для мощности в цепи переменного тока: действующее значение напряжения, измеренное в вольтах, умноженное на действующее значение тока, измеренное в амперах.
Основное уравнение мощности
Но что, если вы не знаете действующее значение напряжения или тока? Что, если вместо этого вы знаете пиковое напряжение V-ноль и пиковое значение тока I-ноль? Что ж, тогда нам нужно будет использовать предыдущие уравнения для среднеквадратичного напряжения и действующего тока.Но чтобы не использовать более одного уравнения, мы можем подставить эти уравнения в уравнение мощности, например:
Уравнение мощности
Это упрощает представление о том, что мощность, используемая в цепи переменного тока, равна пиковому току, умноженному на пиковое напряжение, деленному на два.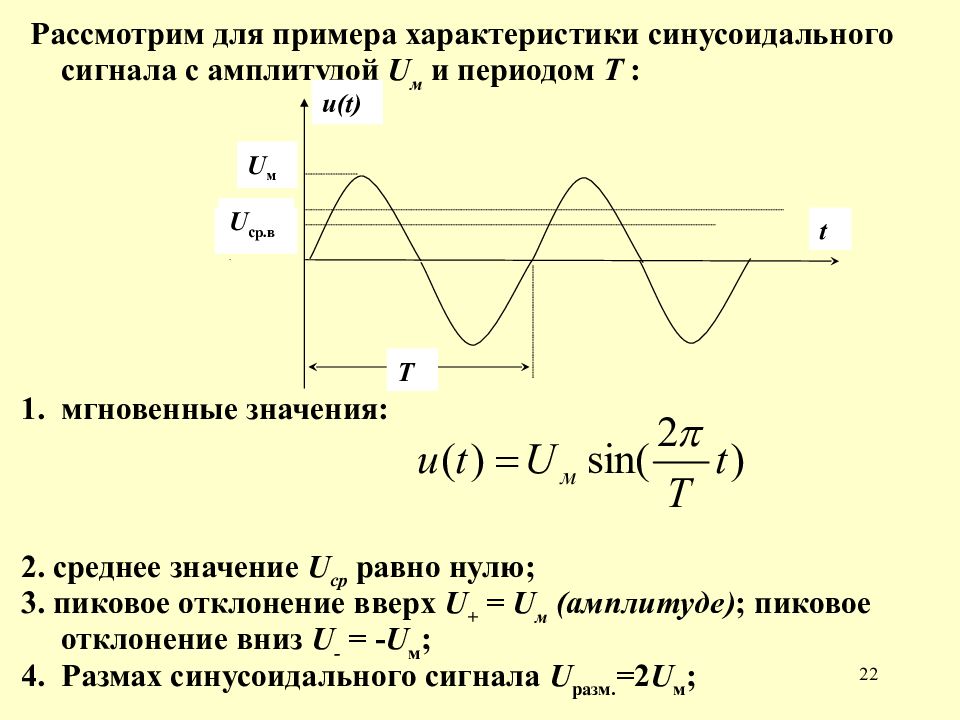
Пример расчета
Хорошо, давайте попробуем пример! Вы проводите испытания энергосберегающей лампочки.Вы обнаружите, что максимальное напряжение, которое он когда-либо использует, составляет 240 вольт, а максимальный ток, который проходит через него, составляет 0,12 ампер. Для обычной лампочки вы просматриваете некоторые значения и обнаруживаете, что среднеквадратичное напряжение составляет 120 вольт, а среднеквадратичный ток — 0,5 ампер. Какая разница в мощности, используемой двумя лампочками?
Итак, нам нужно выяснить, сколько энергии потребляет каждая лампочка, а затем сравнить их. Для первого нам даны максимальные значения, а для второго — среднеквадратичные значения.Итак, нам нужно использовать разные уравнения для каждого, а затем сравнить два значения мощности.
Что касается энергосберегающей лампочки, мы знаем, что V-ноль составляет 240 вольт, а I-ноль — 0,12 ампер. Итак, мы можем вычислить мощность, используя это уравнение: (240 * 0,12) / 2 = 14,4 Вт.
Для обычной лампочки мы знаем, что среднеквадратичное напряжение составляет 120 вольт, а среднеквадратичное значение — 0,5 ампер. Итак, все, что нам нужно сделать здесь, это использовать это уравнение и умножить два вместе: 120 * 0,5 = 60 Вт.
Наконец, чтобы найти разницу между ними, вычтите меньшее число из большего: 60 — 14.4 = 45,6 Вт. Таким образом, разница в потребляемой мощности между двумя лампочками составляет 45,6 Вт. И все — готово!
Краткое содержание урока
Почти все электрические устройства, которые мы используем в повседневной жизни, питаются от переменного тока. Переменный ток (или AC) — это когда ток очень быстро переключает направление, а не течет только в одном направлении по цепи — в одну сторону, а затем в противоположную, снова и снова. Это создает ток, который изменяется синусоидально, что означает, что он изменяется в форме синусоидальной кривой, например, этой:
Синусоидальная кривая цепи переменного тока
Поскольку ток переключается, изменяется и напряжение, и потребляемая мощность. Все они следуют синусоиде. Из-за этого мы склонны выражать ток и напряжение в виде специальных средних значений, называемых среднеквадратичных (или среднеквадратичных ). Цепь переменного тока будет иметь среднеквадратичный ток и среднеквадратичное напряжение, и эти значения определяются следующими уравнениями, где V-ноль — пиковое или максимальное напряжение, а I-ноль — пиковый или максимальный ток. Это вершина и основание синусоиды.
Уравнения
Как обсуждалось в другом уроке, мощность — это энергия, используемая в секунду, измеряемая в ваттах (или джоулях в секунду).В цепи переменного тока есть два основных уравнения, которые вы можете использовать для расчета мощности: верхнее уравнение, в котором вы умножаете среднеквадратичное напряжение на среднеквадратичное значение тока; или нижний, где вы умножаете пиковое напряжение на пиковый ток, а затем делите на два. Основываясь на том, что вам задают в вопросе, вы можете выяснить, какое из двух уравнений использовать.
Результаты обучения
По завершении этого урока вы должны уметь:
Определить переменный ток (AC), среднеквадратичное значение и мощность
Определите синусоидальную кривую переменного тока, напряжения и мощности
Объясните, как использовать два основных уравнения для расчета мощности в цепи переменного тока.
Пиковое напряжение переменного тока, размах напряжения, среднеквадратичное значение напряжения
(DC) — постоянный ток
Элементы и батареи вырабатывают электрический ток, который всегда протекает по цепи одним и тем же прямым, это называется постоянным током (DC).
(AC) — переменный ток
В Великобритании электросеть поставляется с напряжением около 230 вольт и подается как (переменный) или переменный ток. Это означает, что ток течет в одном направлении, а затем в другом по цепи. Ток постоянно меняет направление (чередуется), поэтому его называют (переменным) переменным током. В Великобритании частота электросети составляет 50 Гц , что означает 50 циклов в секунду.
Сигналы переменного тока
Мы можем использовать осциллограф для представления сигнала переменного тока.
Мы можем использовать осциллограмму осциллографа в качестве вольтметра, если мы знаем, какое усиление по оси Y установлено на осциллографе. Используя диаграмму выше и зная, что усиление по оси Y было установлено на 10 В / дел, мы можем это решить;
размах напряжения = 6 квадратов от самой высокой точки до самой низкой, и каждый квадрат стоит 10В. Таким образом, размах напряжения = 60 В.
пиковое значение напряжение (В _o) = половина пикового напряжения = 60/2 = 30 В
Когда мы знаем пиковое напряжение (V _o) и сопротивление (R) в цепи, мы можем вычислить пиковый ток (I _o) , используя уравнение V = IR.
Среднеквадратичные значения
Как п.о. и ток непрерывно изменяются в сигнале переменного тока, нам нужно представить среднее значение для p.d. и ток.
Среднеквадратичные значения p.d. (V _rms) и ток (I _rms) представляют собой действующее значение п.о. и ток в цепи переменного тока.
В _{среднеквадратичное значение} = среднеквадратичная разность потенциалов в вольтах, В
В _o = пиковое напряжение в вольтах, В
I = среднеквадратичный ток в амперах, А
I _o = пиковый ток в амперах, A
Зависимость переменного тока от постоянного
Большинство рассмотренных до сих пор примеров, особенно те, которые используют батареи, имеют источники постоянного напряжения.Как только ток установлен, он также становится постоянным. Постоянный ток (DC) — это поток электрического заряда только в одном направлении. Это установившееся состояние цепи постоянного напряжения. Однако в большинстве известных приложений используется источник напряжения, изменяющийся во времени. Переменный ток (AC) — это поток электрического заряда, который периодически меняет направление. Если источник периодически меняется, особенно синусоидально, цепь называется цепью переменного тока.Примеры включают коммерческую и бытовую энергетику, которая удовлетворяет многие наши потребности. На рисунке 1 показаны графики зависимости напряжения и тока от времени для типичных источников постоянного и переменного тока. Напряжение и частота переменного тока, обычно используемые в домах и на предприятиях, различаются по всему миру.
Рис. 1. (a) Постоянное напряжение и ток постоянны во времени после установления тока. (б) График зависимости напряжения и тока от времени для сети переменного тока 60 Гц. Напряжение и ток синусоидальны и совпадают по фазе для простой цепи сопротивления.Частоты и пиковое напряжение источников переменного тока сильно различаются.
Рис. 2. Разность потенциалов V между клеммами источника переменного напряжения колеблется, как показано на рисунке. Математическое выражение для V дается как [латекс] V = {V} _ {0} \ sin \ text {2} \ pi {ft} \\ [/ latex].
На рисунке 2 показана схема простой схемы с источником переменного напряжения. Напряжение между клеммами колеблется, как показано на рисунке: напряжение переменного тока определяется значением
.
[латекс] V = {V} _ {0} \ sin \ text {2} \ pi {ft} \\ [/ latex],
, где В — напряжение в момент времени t , В ₀ — пиковое напряжение, а f — частота в герцах.Для этой простой цепи сопротивления I = V / R , поэтому переменный ток равен
[латекс] I = {I} _ {0} \ sin 2 \ pi {ft} \\ [/ latex],
, где I — ток в момент времени t , а I ₀ = V ₀ / R — пиковый ток. { 2} \ text {2} \ pi {ft} \\ [/ latex], как показано на рисунке 3.
Установление соединений: домашний эксперимент — лампы переменного / постоянного тока
Помашите рукой между лицом и люминесцентной лампой. Вы наблюдаете то же самое с фарами на своей машине? Объясните, что вы наблюдаете. Предупреждение: Не смотрите прямо на очень яркий свет .
Рис. 3. Мощность переменного тока как функция времени. Поскольку напряжение и ток здесь синфазны, их произведение неотрицательно и колеблется между нулем и I ₀ V ₀.Средняя мощность (1/2) I ₀ V ₀.
Чаще всего нас беспокоит средняя мощность, а не ее колебания — например, у лампочки мощностью 60 Вт в настольной лампе средняя потребляемая мощность 60 Вт. Как показано на Рисунке 3, средняя мощность P _ave составляет
[латекс] {P} _ {\ text {ave}} = \ frac {1} {2} {I} _ {0} {V} _ {0} \\ [/ latex].
Это очевидно из графика, поскольку области выше и ниже линии (1/2) I ₀ V ₀ равны, но это также можно доказать с помощью тригонометрических тождеств.Точно так же мы определяем средний или действующий ток I _{среднеквадратичное значение} и среднее значение или действующее значение напряжения В _{среднеквадратичное значение}, соответственно, равное
[латекс] {I} _ {\ text {rms}} = \ frac {{I} _ {0}} {\ sqrt {2}} \\ [/ latex]
и
[латекс] {V} _ {\ text {rms}} = \ frac {{V} _ {0}} {\ sqrt {2}} \\ [/ latex].
, где среднеквадратичное значение означает среднеквадратичное значение, особый вид среднего. Как правило, для получения среднеквадратичного значения конкретная величина возводится в квадрат, определяется ее среднее значение (или среднее значение) и извлекается квадратный корень.Это полезно для переменного тока, так как среднее значение равно нулю. Сейчас,
P _{среднеквадратичное значение} = I _{среднеквадратичное значение} V _{среднеквадратичное значение},
, что дает
[латекс] {P} _ {\ text {ave}} = \ frac {{I} _ {0}} {\ sqrt {2}} \ cdot \ frac {{V} _ {0}} {\ sqrt {2}} = \ frac {1} {2} {I} _ {0} {V} _ {0} \\ [/ latex],
, как указано выше. Обычно указываются I _{среднеквадратичное значение}, V _{среднеквадратичное значение} и P _{среднеквадратичное значение}, а не пиковые значения.Например, напряжение в большинстве домашних хозяйств составляет 120 В переменного тока, что означает, что В, , _{, среднеквадратичное значение,}, составляет 120 В. Обычный автоматический выключатель на 10 А прервет постоянное напряжение I _{среднеквадратичное значение} более 10 А. микроволновая печь потребляет P _пр. = 1,0 кВт и т. д. Вы можете рассматривать эти среднеквадратичные и средние значения как эквивалентные значения постоянного тока для простой резистивной цепи. Подводя итог, при работе с переменным током закон Ома и уравнения для мощности полностью аналогичны таковым для постоянного тока, но для переменного тока используются среднеквадратические и средние значения.{2} R \\ [/ латекс].
Пример 1. Пиковое напряжение и мощность для переменного тока
(a) Каково значение пикового напряжения для сети переменного тока 120 В? (b) Какова пиковая потребляемая мощность лампочки переменного тока мощностью 60,0 Вт?
Стратегия
Нам говорят, что V _rms составляет 120 В, а P _ave составляет 60,0 Вт. Мы можем использовать [латекс] {V} _ {\ text {rms}} = \ frac {{V} _ {0}} {\ sqrt {2}} \\ [/ latex], чтобы найти пиковое напряжение, и мы можем манипулировать определением мощности, чтобы найти пиковую мощность из заданной средней мощности.
Решение для (a)
Решение уравнения [латекс] {V} _ {\ text {rms}} = \ frac {{V} _ {0}} {\ sqrt {2}} \\ [/ latex] для пикового напряжения В ₀ и замена известного значения на V _rms дает
[латекс] {V} _ {0} = \ sqrt {2} {V} _ {\ text {rms}} = 1,414 (120 \ text {V}) = 170 \ text {V} \\ [/ latex ]
Обсуждение для (а)
Это означает, что напряжение переменного тока изменяется от 170 В до –170 В и обратно 60 раз в секунду.Эквивалентное постоянное напряжение составляет 120 В.
Решение для (b)
Пиковая мощность равна пиковому току, умноженному на пиковое напряжение. Таким образом,
[латекс] {P} _ {0} = {I} _ {0} {V} _ {0} = \ text {2} \ left (\ frac {1} {2} {I} _ {0} {V} _ {0} \ right) = \ text {2} {P} _ {\ text {ave}} \\ [/ latex].
Мы знаем, что средняя мощность составляет 60,0 Вт, поэтому
P ₀ = 2 (60,0 Вт) = 120 Вт.
Обсуждение
Таким образом, мощность меняется от нуля до 120 Вт сто двадцать раз в секунду (дважды за каждый цикл), а средняя мощность составляет 60 Вт.
цепей переменного тока | Безграничная физика
Индуктивность
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока, например изменением тока в проводнике.
Цели обучения
Опишите свойства индуктора
Основные выводы
Ключевые моменты
В случае электроники индуктивность — это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике, называемое самоиндукцией, так и в любых соседних проводниках, называемое взаимной индуктивностью.
Согласно закону Ленца, изменяющийся электрический ток в цепи с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока.
Взаимная индуктивность обозначена как. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в форме уравнения как [латекс] \ text {emf} _2 = — \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]. M то же самое для обратного процесса.
Самоиндукция — это действие закона индукции Фарадея устройства на самого себя. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока, задаваемой [latex] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ латекс].
Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.
Ключевые термины
взаимная индуктивность : отношение напряжения в цепи к изменению тока в соседней цепи.
самоиндукция : Отношение напряжения к изменению тока в той же цепи.
индуктор : Пассивное устройство, которое вводит индуктивность в электрическую цепь.
Индуктивность
ОБЗОР
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. В частности, в случае электроники индуктивность — это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике (самоиндукция), так и в любых соседних проводниках (взаимная индуктивность).Этот эффект основан на двух фундаментальных физических наблюдениях: во-первых, постоянный ток создает постоянное магнитное поле, а во-вторых, изменяющееся во времени магнитное поле индуцирует напряжение в соседнем проводнике (закон индукции Фарадея). Согласно закону Ленца, изменяющийся электрический ток через цепь с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока (если бы это было не так, можно легко увидеть, что энергия не может быть сохранена, при этом изменяющийся ток усиливает изменение тока. петля положительной обратной связи).
ВЗАИМНАЯ ИНДУКТИВНОСТЬ
Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. Посмотрите, где простые катушки наводят друг на друга ЭДС.
Взаимная индуктивность катушек : Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает в катушке 2 ЭДС.(Обратите внимание, что «E2 индуцированная» представляет наведенную ЭДС в катушке 2.)
Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в форме уравнения как
[латекс] \ text {emf} _2 = — \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]
, где M определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Единицы измерения для M : (V⋅s) / A = Ωs, который назван генри (H) в честь Джозефа Генри (обнаружил самоиндукцию). То есть 1 H = 1 Ом.
Природа здесь симметрична. Если мы изменим ток I ₂ в катушке 2, мы индуцируем ЭДС ₁ в катушке 1, что равно
[латекс] \ text {emf} _1 = — \ text {M} \ frac {\ Delta \ text {I} _2} {\ Delta \ text {t}} [/ latex]
, где M то же самое, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M.
Большая взаимная индуктивность M может быть или нежелательна. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки против ветра, чтобы нейтрализовать создаваемое магнитное поле.(Видеть ).
Противоточная намотка : Нагревательные катушки электрической сушилки для белья могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.
САМОИНДУКЦИЯ
Самоиндуктивность, действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение магнитного потока полностью связано с изменением тока ΔI через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
[латекс] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ latex]
, где L — собственная индуктивность устройства.Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.
.
Обозначение индуктора
Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться.Чтобы избежать этого эффекта, необходимо добиться небольшого L, например, за счет встречной намотки катушек, как в.
СОЛЕНОИДЫ
Можно рассчитать L для катушки индуктивности, учитывая ее геометрию (размер и форму) и зная создаваемое ею магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Индуктивность L обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму.{2} \ text {A}} {\ mathscr {\ text {l}}} [/ latex] (соленоид).
Поучительно вывести это уравнение, но это оставлено читателю в качестве упражнения. (Подсказка: начните с того, что отметьте, что индуцированная ЭДС определяется законом индукции Фарадея как ЭДС = −N (Δ / Δt), а по определению самоиндукции задается как ЭДС = −L (ΔI // Δt) и приравняем эти два выражения). Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением.
Цепи RL
Цепь RL состоит из катушки индуктивности и резистора, включенных последовательно или параллельно друг другу, с током, управляемым источником напряжения.{\ frac {- \ text {t}} {\ tau}}) [/ latex]. {\ frac {- \ text {t }} {\ tau}} [/ латекс].В первом временном интервале τ ток падает в раз [латекс] \ frac {1} {\ text {e}} [/ latex] до [latex] 0,368 \ cdot \ text {I} _0 [/ latex].
Ключевые термины
характеристическая постоянная времени : Обозначается $ \ tau $, в цепях RL она задается $ \ tau = \ frac {L} {R} $, где R — сопротивление, а L — индуктивность. Когда переключатель замкнут, это время, за которое ток затухает с коэффициентом 1 / e.
катушка индуктивности : Устройство или компонент цепи, который демонстрирует значительную самоиндукцию; устройство, которое хранит энергию в магнитном поле.
RL Схемы
Цепь резистор-индуктор (цепь RL) состоит из резистора и катушки индуктивности (последовательно или параллельно), приводимых в действие источником напряжения.
Обзор
Напомним, что индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. Взаимная индуктивность — это действие закона индукции Фарадея одного устройства на другое, в то время как самоиндукция — это действие закона индукции Фарадея устройства на самого себя.Катушка индуктивности — это устройство или компонент схемы, который демонстрирует самоиндукцию.
Энергия индуктора
Из закона Ленца мы знаем, что индукторы противодействуют изменениям тока. Мы можем думать об этой ситуации с точки зрения энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, а также время, чтобы истощить ее; следовательно, есть противодействие быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства.{2} [/ латекс].
Катушки индуктивности в цепях
Мы знаем, что ток через катушку индуктивности L нельзя включить или выключить мгновенно. Изменение тока изменяет магнитный поток, вызывая противодействие изменению ЭДС (закон Ленца). Как долго длится противостояние? Текущий будет течь, а можно выключить , но сколько времени это займет? На следующем рисунке показана схема переключения, которую можно использовать для измерения тока через катушку индуктивности как функции времени.
Ток в цепи RL : (a) Схема RL с переключателем для включения и выключения тока. В положении 1 батарея, резистор и катушка индуктивности включены последовательно, и устанавливается ток. В положении 2 аккумулятор извлекается, и ток в конечном итоге прекращается из-за потери энергии в резисторе. (b) График роста тока в зависимости от времени, когда переключатель перемещен в положение 1. (c) График уменьшения тока, когда переключатель перемещен в положение 2.
Когда переключатель сначала перемещается в положение 1 (при t = 0 ), ток равен нулю и в конечном итоге возрастает до I ₀ = В / R , где R — полное сопротивление цепи, а V — напряжение батареи.{\ frac {- \ text {t}} {\ tau}}) [/ latex]
— это ток в цепи RL при включении. (Обратите внимание на сходство с экспоненциальным поведением напряжения на зарядном конденсаторе.) Начальный ток равен нулю и приближается к I ₀ = В / R с характеристической постоянной времени для цепи RL , задаваемой формулой :
[латекс] \ tau = \ frac {\ text {L}} {\ text {R}} [/ latex],
где [latex] \ tau [/ latex] имеет единицы измерения в секундах, поскольку [latex] 1 \ text {H} = 1 \ Omega \ cdot \ text {s} [/ latex].В первый период времени [латекс] \ tau [/ latex] ток возрастает от нуля до 0,632I ₀, поскольку I = I ₀ (1-e ^-1) = I ₀ ( 1−0,368) = 0,632I ₀. В следующий раз ток составит 0,632 от остатка. Хорошо известным свойством экспоненциальной функции является то, что конечное значение никогда не достигается точно, но 0,632 остатка от этого значения достигается за каждое характерное время [латекс] \ тау [/ латекс]. Всего за несколько кратных [latex] \ tau [/ latex] времени, конечное значение почти достигнуто (см. Часть (b) на рисунке выше).
Характерное время [латекс] \ тау [/ латекс] зависит только от двух факторов: индуктивности L и сопротивления R . Чем больше индуктивность L , тем она больше, что имеет смысл, поскольку большая индуктивность очень эффективна в противодействии изменению. Чем меньше сопротивление R, тем больше [латекс] \ тау [/ латекс]. Опять же, это имеет смысл, поскольку небольшое сопротивление означает большой конечный ток и большее изменение, чтобы добраться до него. В обоих случаях (большой L и маленький R) больше энергии хранится в катушке индуктивности, и требуется больше времени для ее ввода и вывода.
Когда переключатель в (a) перемещается в положение 2 и отключает батарею из цепи, ток падает из-за рассеивания энергии резистором. Однако это также не происходит мгновенно, поскольку катушка индуктивности противодействует уменьшению тока, вызывая ЭДС в том же направлении, что и батарея, управляющая током. Кроме того, в катушке индуктивности накапливается определенное количество энергии, (1/2) LI ₀ ², и она рассеивается с конечной скоростью. Когда ток приближается к нулю, скорость убывания замедляется, поскольку скорость рассеяния энергии составляет I ² R.{\ frac {- \ text {t}} {\ tau}} [/ латекс]
В (c), в первый период времени [latex] \ tau = \ text {L} / \ text {R} [/ latex] после того, как переключатель замкнут, ток падает до 0,368 от его начального значения, поскольку I = I ₀ e ⁻¹ = 0,368I ₀. В каждый последующий раз [латекс] \ тау [/ латекс] ток падает до 0,368 от предыдущего значения, а через несколько кратных [латекс] \ тау [/ латекс] ток становится очень близким к нулю.
Цепь серии
RLC: на больших и малых частотах; Фазорная диаграмма
Отклик цепи RLC зависит от частоты возбуждения — на достаточно больших частотах преобладает индуктивный (емкостной) член.
Цели обучения
Различать поведение цепей серии RLC на больших и малых частотах
Основные выводы
Ключевые моменты
RLC-схемы можно описать (обобщенным) законом Ома. Что касается фазы, когда прикладывается синусоидальное напряжение, ток отстает от напряжения на 90 ° по фазе в цепи с индуктором, в то время как ток опережает напряжение на 90 ° в цепи с конденсатором.
На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока только с индуктор.Следовательно, среднеквадратичный ток будет Vrms / XL, а ток отстает от напряжения почти на 90 °.
На достаточно малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex], схема почти эквивалентна цепи переменного тока только с конденсатор. Следовательно, среднеквадратичное значение тока будет равно _В / X _C,, а ток опережает напряжение почти на 90 ^∘.
Ключевые термины
Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
резонанс : Увеличение амплитуды колебаний системы под действием периодической силы, частота которой близка к собственной частоте системы.
среднеквадратичное значение : Среднеквадратичное значение: статистическая мера величины переменной величины.
В предыдущих версиях Atoms мы узнали, как последовательная цепь RLC, показанная на рисунке, реагирует на источник переменного напряжения. Объединив закон Ома (I _{среднеквадратичное значение} = V _{действующее значение} / Z; I _{среднеквадратичное значение} и V _{среднеквадратичное значение} представляют собой среднеквадратичное значение тока и напряжения) и выражения для импеданса Z из:
Цепь последовательного RLC : Последовательная цепь RLC: резистор, катушка индуктивности и конденсатор (слева).2}} [/ латекс].
Из уравнения мы изучили условия резонанса для контура. Мы также изучили фазовые соотношения между напряжениями на резисторе, конденсаторе и катушке индуктивности: при приложении синусоидального напряжения ток отстает от напряжения на фазу 90º в цепи с катушкой индуктивности, в то время как ток опережает напряжение на 90 ^∘. в цепи с конденсатором. Теперь мы исследуем отклик системы в пределах больших и малых частот.
на больших частотах
На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex], X _L намного больше, чем X _C .Если частота достаточно высока, так что X _L также намного больше, чем R, то в импедансе Z доминирует индуктивный член. Когда [latex] \ text {Z} \ приблизительно \ text {X} _ \ text {L} [/ latex], схема почти эквивалентна цепи переменного тока с одним индуктором. Следовательно, среднеквадратичный ток будет составлять _В / X _L, а ток отстает от напряжения почти на 90, ^∘. Этот отклик имеет смысл, потому что на высоких частотах закон Ленца предполагает, что полное сопротивление катушки индуктивности будет большим.
на малых частотах
В импедансе Z на малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] преобладает емкостный член, предполагая, что частота достаточно высока, так что X _C намного больше R. Когда [latex] \ text {Z} \ приблизительно \ text {X} _ \ text {C} [/ latex], схема почти эквивалентна AC схема только с конденсатором. Следовательно, среднеквадратичное значение тока будет равно _В / X _C,, а ток опережает напряжение почти на 90 ^∘.
Резисторы в цепях переменного тока
В цепи с резистором и источником питания переменного тока по-прежнему действует закон Ома ( В, = IR ).
Цели обучения
Применить закон Ома для определения силы тока и напряжения в цепи переменного тока
Основные выводы
Ключевые моменты
При напряжении переменного тока, определяемом по формуле: [latex] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex], ток в цепи определяется как : [latex] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex] Это выражение происходит от Ohm закон: [латекс] \ text {V} = \ text {IR} [/ latex].2} {2 \ text {R}} [/ латекс].
Ключевые термины
Закон Ома : Согласно наблюдениям Ома, постоянный ток, протекающий в электрической цепи, состоящей только из сопротивлений, прямо пропорционален приложенному напряжению.
Постоянный ток (DC) — это поток электрического заряда только в одном направлении. Это установившееся состояние цепи постоянного напряжения. Однако в большинстве известных приложений используется источник переменного напряжения. Переменный ток (AC) — это поток электрического заряда, который периодически меняет направление.Если источник периодически меняется, особенно синусоидально, цепь называется цепью переменного тока. Примеры включают коммерческую и бытовую энергетику, которая удовлетворяет многие наши потребности. показывает графики зависимости напряжения и тока от времени для типичных источников постоянного и переменного тока. Напряжение и частота переменного тока, обычно используемые в домах и на предприятиях, различаются по всему миру.
Синусоидальное напряжение и ток : (a) Напряжение и ток постоянного тока постоянны во времени после установления тока.(б) График зависимости напряжения и тока от времени для сети переменного тока 60 Гц. Напряжение и ток синусоидальны и совпадают по фазе для простой цепи сопротивления. Частоты и пиковое напряжение источников переменного тока сильно различаются.
Мы изучили закон Ома:
[латекс] \ text {I} = \ frac {\ text {V}} {\ text {R}} [/ latex]
, где I — ток, В, — напряжение, а R — сопротивление цепи. Закон Ома применяется как к цепям переменного тока, так и к цепям постоянного тока.Следовательно, с напряжением переменного тока, определяемым по формуле:
[латекс] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex]
, где В ₀ — пиковое напряжение, а [latex] \ nu [/ latex] — частота в герцах, ток в цепи задается как:
[латекс] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex]
В этом примере, в котором у нас есть резистор и источник напряжения в цепи, напряжение и ток считаются синфазными, как показано на (b). 2} {\ text {R}} \ cdot \ sin (2 \ pi \ nu \ text {t}) [/ latex]
Чтобы найти среднюю мощность, потребляемую этой схемой, нам нужно взять среднее значение функции по времени.2} {2 \ text {R}} [/ latex]
Конденсаторы
в цепях переменного тока: емкостное сопротивление и фазовые диаграммы
Напряжение на конденсаторе отстает от тока. Из-за разности фаз для описания этих схем полезно вводить векторы.
Цели обучения
Объясните преимущества использования векторного представления
Основные выводы
Ключевые моменты
Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.
Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно.
Действующее значение тока в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}}} {\ text {X} _ \ text {C}} [/ latex], где [latex] \ text {X} _ \ text {c} [/ latex] — емкостное реактивное сопротивление.
Ключевые термины
среднеквадратичное значение : Среднеквадратичное значение: статистическая мера величины переменной величины.
В предыдущем Атоме «Резисторы в цепях переменного тока» мы представили источник питания переменного тока и изучили, как резисторы ведут себя в цепях переменного тока. Там мы использовали закон Ома (V = IR), чтобы получить соотношение между напряжением и током в цепях переменного тока. В этом и последующих разделах «Атомы» мы обобщим закон Ома, чтобы мы могли использовать его, даже если в цепи присутствуют конденсаторы и катушки индуктивности. Чтобы добраться туда, мы сначала представим очень общий графический способ представления синусоидальной волны с помощью фазора.

Конденсаторы в цепях переменного тока с фазорами
Фазор
Ключевая идея представления вектора состоит в том, что сложный, изменяющийся во времени сигнал может быть представлен как произведение комплексного числа (которое не зависит от времени) и сложного сигнала (которое зависит от времени). Фазоры разделяют зависимости от A (амплитуда), [latex] \ nu [/ latex] (частота) и θ (фаза) на три независимых фактора. Это может быть особенно полезно, потому что частотный коэффициент (который включает временную зависимость синусоиды) часто является общим для всех компонентов линейной комбинации синусоид.{\ text {i} \ theta} [/ латекс]. Поскольку векторы представлены величиной (или модулем) и углом, они графически представлены вращающейся стрелкой (или вектором) в плоскости x-y.
Рис. 3 : Вектор можно рассматривать как вектор, вращающийся вокруг начала координат в комплексной плоскости. Функция косинуса — это проекция вектора на действительную ось. Его амплитуда — это модуль вектора, а его аргумент — полная фаза \ omega t + \ theta. Фазовая постоянная \ theta представляет собой угол, который вектор образует с действительной осью при t = 0.
Конденсаторы в цепях переменного тока
Ранее в предыдущем Atom мы изучали, как напряжение и ток меняются со временем. Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно. Мы говорим, что ток и напряжение совпадают по фазе.
Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.Ток имеет максимум (пик) за четверть цикла до пика напряжения. Инженеры говорят, что «ток опережает напряжение на 90 ^∘». Это показано на.
Рис. 2 : Пик тока (имеет максимум) за четверть волны до напряжения, когда конденсатор подключен к переменному напряжению.
Для цепи с конденсатором мгновенное значение V / I непостоянно. Однако значение V _max / I _max полезно и называется емкостным реактивным сопротивлением (X _C) компонента.Поскольку это по-прежнему напряжение, деленное на ток (например, сопротивление), единицей измерения является ом. Значение X _C (C означает конденсатор) зависит от его емкости (C) и частоты (f) переменного тока. [латекс] \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ latex].
Конденсатор влияет на ток, имея возможность полностью его остановить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором.Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I _{, действующее значение} в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}}} {\ text {X} _ \ text {C}} [/ latex], где V _rms — это действующее значение напряжения. Обратите внимание, что X _C заменяет R в версии закона Ома для постоянного тока.
Фазовое представление
Поскольку напряжение на конденсаторе отстает от тока, вектор, представляющий ток и напряжение, будет иметь вид.На схеме стрелки вращаются против часовой стрелки с частотой [латекс] \ ню [/ латекс]. (Следовательно, ток ведет к напряжению.) В следующих атомах мы увидим, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.
Рис. 4 : Фазорная диаграмма для цепи переменного тока с конденсатором
Индукторы в цепях переменного тока: индуктивно-реактивные и фазовые диаграммы
В цепи переменного тока с катушкой индуктивности напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца.
Цели обучения
Объясните, почему напряжение на катушке индуктивности «опережает» ток в цепи переменного тока с катушкой индуктивности.
Основные выводы
Ключевые моменты
При использовании катушки индуктивности в цепи переменного тока напряжение опережает ток на одну четверть цикла или на фазовый угол 90 °.
Среднеквадратичное значение тока I _{действующее значение} через катушку индуктивности L определяется версией закона Ома: [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ { \ text {rms}}} {\ text {X} _ \ text {L}} [/ latex].X _L называется индуктивным реактивным сопротивлением, которое задается как [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex].
Фазоры — это векторы, вращающиеся против часовой стрелки. Вектор для катушки индуктивности показывает, что напряжение опережает ток по фазе 90º.
Ключевые термины
Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
среднеквадратичное значение : Среднеквадратичное значение: статистическая мера величины переменной величины.
phasor : представление комплексного числа в виде комплексной экспоненты.
Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рисунке. Разумно предположить, что сопротивление пренебрежимо мало, потому что на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на схему. График показывает напряжение и ток как функции времени.(б) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля, затем повышается до своего пика после управляющего им напряжения (как показано в предыдущем разделе, когда было включено напряжение постоянного тока).
Источник переменного напряжения, подключенный последовательно с индуктором : (a) Источник переменного напряжения, подключенный последовательно с индуктором, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.
Когда напряжение становится отрицательным в точке a, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным.Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c, где оно начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Следовательно, когда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.
Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока вызывает ЭДС.Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I _RMS через катушку индуктивности L определяется версией закона Ома: [latex] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text { rms}}} {\ text {X} _ \ text {L}} [/ latex] где V _rms — среднеквадратичное напряжение на катушке индуктивности, а [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex] с [latex] \ nu [/ latex] частота источника переменного напряжения в герцах. X _L называется индуктивным реактивным сопротивлением. Поскольку катушка индуктивности препятствует прохождению тока, X _L имеет единицы измерения в омах (1 H = 1 Ωs, так что частота, умноженная на индуктивность, имеет единицы (циклов / s) (Ωs) = Ω), что соответствует его роли эффективное сопротивление.
Представление векторов
Напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца. Следовательно, вектор, представляющий ток и напряжение, будет иметь вид. Опять же, вектора — это векторы, вращающиеся против часовой стрелки с частотой [latex] \ nu [/ latex] (вы можете видеть, что напряжение опережает ток) . В последующих выпусках Atoms будет обсуждаться, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.
Векторная диаграмма : Векторная диаграмма для цепи переменного тока с индуктором.

Фазоры для индукторов в цепях переменного тока
Резонанс в цепях RLC
Резонанс — это тенденция системы к колебаниям с большей амплитудой на некоторых частотах — в последовательной цепи RLC он возникает на [latex] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}} }[/латекс].
Цели обучения
Сравнить резонансные характеристики цепей с более высоким и низким сопротивлением
Основные выводы
Ключевые моменты
Условие резонанса последовательной цепи RLC может быть получено приравниванием X _L и X _C, так что два противоположных вектора компенсируют друг друга.
В резонансе влияние катушки индуктивности и конденсатора компенсируется, так что Z = R, а I _{среднеквадратичное значение} является максимальным.
Цепи с более высоким сопротивлением не резонируют так сильно по сравнению с цепями с более низким сопротивлением, и при этом они не будут такими избирательными, например, в радиоприемнике.
Ключевые термины
реактивное сопротивление : Противодействие изменению протекания тока в цепи переменного тока из-за индуктивности и емкости; мнимая часть импеданса.
среднеквадратичное значение : Среднеквадратичное значение: статистическая мера величины переменной величины.
импеданс : мера сопротивления течению переменного тока в цепи; совокупность его сопротивления, индуктивного и емкостного сопротивления. Обозначается символом Z.
Резонанс — это тенденция системы колебаться с большей амплитудой на одних частотах, чем на других. Частоты, при которых амплитуда отклика является относительным максимумом, известны как резонансные частоты системы.2}} [/ latex],
, где I _rms и V _rms — среднеквадратичные значения тока и напряжения соответственно. Реактивные сопротивления изменяются в зависимости от частоты [латекс] \ nu [/ latex], при этом X _L большое на высоких частотах и X _C большое на низких частотах, представленных как:
[латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L}, \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ латекс].
На некоторой промежуточной частоте [latex] \ nu_0 [/ latex] реактивные сопротивления будут равны и отменены, давая Z = R — это минимальное значение для импеданса, а максимальное значение для I _{rms. Результат}.Мы можем получить выражение для [latex] \ nu_0 [/ latex], взяв X _L = X _C. Подстановка определений X _L и X _C дает:
[латекс] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} [/ латекс].
[latex] \ nu_0 [/ latex] — это резонансная частота последовательной цепи RLC. Это также собственная частота, на которой цепь будет колебаться, если не будет управляться источником напряжения. В [latex] \ nu_0 [/ latex] эффекты катушки индуктивности и конденсатора нейтрализуются, так что Z = R, а I _rms является максимальным.Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы.
Приемник в радиостанции — это RLC-схема, которая лучше всего колеблется в своем [latex] \ nu_0 [/ latex]. Переменный конденсатор часто используется для регулировки резонансной частоты, чтобы получить желаемую частоту и отклонить другие. представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик в I _rms в [латексе] \ nu_0 = \ text {f} _0 [/ latex].Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них. Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепи с более высоким сопротивлением не резонируют так сильно, и, например, в радиоприемнике они не будут такими избирательными.
Зависимость тока от частоты : График зависимости тока от частоты для двух цепей серии RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f0, но для более высокого сопротивления он ниже и шире.Источник управляющего переменного напряжения имеет фиксированную амплитуду V0.
Мощность
Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается сопротивлением в цепи и задается как [латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms }} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ latex]. Здесь [latex] \ phi [/ latex] называется фазовым углом.
Цели обучения
Рассчитать мощность, подаваемую в цепь переменного тока серии RLC с учетом тока и напряжения.
Основные выводы
Ключевые моменты
Фазовый угол ϕ — это разность фаз между напряжением источника V и током I.См. Векторную диаграмму в.
На резонансной частоте или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны.
Среднюю мощность, рассеиваемую в цепи RLC, можно рассчитать, взяв среднее значение мощности по времени, P (t) = I (t) V (t), за период.
Ключевые термины
среднеквадратичное значение : Среднеквадратичное значение: статистическая мера величины переменной величины.
Если ток изменяется в зависимости от частоты в цепи RLC, то мощность, подаваемая на него, также зависит от частоты.Однако средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных схемах. Как было замечено в предыдущих атомах, напряжение и ток в цепи RLC не совпадают по фазе. Между напряжением источника V и током I существует фазовый угол ϕ, равный
[латекс] \ cos {\ phi} = \ frac {\ text {R}} {\ text {Z}} [/ latex], как показано на рисунке
Векторная диаграмма для последовательной цепи RLC : Векторная диаграмма для последовательной цепи RLC. \ phi — фазовый угол, равный разности фаз между напряжением и током.
Например, на резонансной частоте [латекс] (\ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}}) [/ latex] или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем в резонансе, потому что напряжение и ток не совпадают по фазе, а I _rms ниже.
Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь.Можно показать, что средняя мощность составляет
[латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms}} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ латекс]
(уравнение, полученное путем взятия среднего значения мощности по времени, P (t) = I (t) V (t), за период. I (t) и V (t) — это ток и напряжение в момент времени t). Таким образом, cosϕ называется коэффициентом мощности, который может находиться в диапазоне от 0 до 1. Коэффициенты мощности, близкие к 1, желательны, например, при проектировании эффективного двигателя. На резонансной частоте cosϕ = 1.
Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается только сопротивлением.Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают энергию из цепи. Скорее, они передают энергию вперед и назад друг другу, а резистор рассеивает именно то количество, которое источник напряжения дает цепи. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора (например, радиоволн).
Схема аналогична колесу автомобиля, движущемуся по гофрированной дороге, как показано на рисунке. Неровности на дороге с равномерным интервалом аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз.
No related posts.