Урок 51. названия компонентов и результата действия умножения — Математика — 2 класс
Математика, 2 класс
Урок № 51. Названия компонентов и результата действия умножения
Перечень вопросов, рассматриваемых в теме:
— Связь умножения со сложением, умение заменять сумму одинаковых слагаемых произведением и произведение – суммой одинаковых слагаемых
Глоссарий по теме:
Умножение – математическое действие, посредством которого из двух чисел получается новое число, которое содержит слагаемым первое число столько раз, сколько единиц во втором.
Произведение – это результат умножения.
Основная и дополнительная литература по теме урока:
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А. Бантова, Г.В. Бельтюкова и др. –
8-е изд. – М.: Просвещение, 2017. – с.54.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций.

7-е изд., дораб. – М.: Просвещение, 2016. – с.46.
Открытые электронные ресурсы по теме урока:
1.https://knowworld.ru/fakty/interesnyie-faktyi-o-matematike/
2. https://dic.academic.ru/
3. https://kopilkaurokov.ru/matematika/uroki/
Теоретический материал для самостоятельного изучения
Составьте выражения к рисункам:
2 3
Учимся рассуждать. Числа разные: 2 и 3.
К данному рисунку можем составить выражение на сложение: 2 + 3 = 5
2
Числа одинаковые: 2, 2, 2. К данному рисунку можем составить выражение на умножение:
2 · 3 = 6
Компоненты каждого математического действия имеют название.
Компоненты сложения указывают на производимое действие – сложение: первое слагаемое, второе слагаемое, сумма.
Компоненты вычитания указывают на производимое действие — вычитание: уменьшаемое, вычитаемое, разность.
Компоненты умножения указывают на производимое действие — умножение.
Названия носят города и реки,
Вам от рождения фамилия дана.
И каждому числу при умножении
Особенные дали имена.
Так же, как и при сложении и вычитании, числа при умножении тоже имеют свое название.
Первое число при умножении называется первый множитель. Второе число при умножении называется второй множитель. Результат умножения называют произведение.
Зная, как называются числа при умножении, можно использовать эти термины при чтении выражений.
Равенство 5 · 2 = 10 можно прочитать несколькими способами:
— Первый множитель – пять, второй множитель – два, произведение – десять.
— Произведение пяти и двух равно десяти.
— Пять умножить на два, равняется десять.
Рассмотрим задание: слагаемое 12 повторяется 4 раза. Запишите такую сумму в виде произведения.
Назовите первый множитель этого произведения. Что он обозначает?
Что он обозначает?
Первый множитель этого произведения обозначает слагаемое.
Слагаемое 12 повторяется 4 раза.
Назовите второй множитель этого произведения. Что он обозначает? Второй множитель этого произведения обозначает количество слагаемых.
Слагаемое 12 повторяется 4 раза.
Получилась запись: 12+12+12+12=12·4
Помните, что заменить сложение умножением можно там, где находятся суммы одинаковых слагаемых.
Тренировочные задания.
1. Запишите пример на умножение там, где это возможно:
8 + 8 + 8 + 8 + 8 + 8 =
4 + 4 + 3 + 4 + 4 + 4 =
Правильные ответы:
8 + 8 + 8 + 8 + 8 + 8 = 8 · 6
2. Соедините сумму и произведение:
2 + 2 + 2 5 · 2
1 + 1 + 1 + 1 6 · 4
3 + 3 + 3 + 3 + 3 1 · 4
5 + 5 3 · 5
6 + 6 + 6 + 6 2 · 3
Правильный вариант:
2 + 2 + 2 = 2 · 3
1 + 1 + 1 + 1 = 1 · 4
3 + 3 + 3 + 3 + 3 = 3 · 5
5 + 5 = 5 · 2
6 + 6 + 6 + 6 = 6 · 4
Урок «Компоненты вычитания: уменьшаемое, вычитаемое, разность»
Конспект урока по математике для 1 класса по теме «Компоненты вычитания: уменьшаемое, вычитаемое, разность» УМК « Школа России», 1 класс учебник «Математика», ч. 2, Авт. М.И. Моро и др.,
2, Авт. М.И. Моро и др.,
Тип урока: Комбинированный
Форма урока: Получение новых знаний
Цели:
образовательные:
-познакомить учащихся с названиями компонентов при вычитании;
-научить читать выражения, используя данные термины.
— закрепить умение применять правила в процессе выполнения упражнений;
— формировать навыки самостоятельной работы;
развивающие:
— развивать математическую речь, вычислительные навыки;
— развивать умение применять полученные знания к решению прикладных задач;
воспитывающие:
— воспитание познавательного интереса к предмету;
Оборудование:
— мультимедийный проектор;
— компьютер;
— индивидуальные карточки;
— математический диктант;
— карточки для устной работы;
— схемы./3fa0d5fa597f86c.s.siteapi.org/img/d48671e05016c6f1f1632ec98bf0efee3bbf1ecf.png)
Вид урока: Урок –игра «В гостях у Фиксиков»
План урока:
Организационный этап (2 мин.)
Актуализация знаний (6 мин)
Открытие нового. Введение компонентов вычитания.( 10 мин)
Физкультминутка (3 мин)
Повторение изученного материала. (17 мин.)
Рефлексия (2 мин)
Ход урока:
1. Организационный этап.
Долгожданный дан звонок –
Начинается урок!
Куда сегодня с вами попадем-
Увидите вы скоро.
В известный мультике мы пойдем
К помощникам веселым.
Вы лучше всех
Вас на уроке ждет успех.
— А как вы думаете, от кого зависит успех нашего урока? (Успех урока зависит от успеха каждого из нас. )
)
— Сегодня у нас урок-игра и вы будете работать в группах. Давайте с вами вспомним правила работы в группе. В ходе работы внимательно слушайте друг друга, уважайте мнения одноклассников, командиры групп следите за работой, помогайте ребятам, если будет трудно (правила работы в группах – вывесить на доску).
2.Актуализация знаний
Ребята, к нам пришло письмо с просьбой помочь героям мультфильма, но оно разорвано на части. Чтобы его собрать и соединить надо решить примеры и разместить ответы(числа) в порядке возрастания.
(Дети получают 3 фрагмента числа, на обратной стороне даны примеры на сложение:
3 + 2 + 4 = 9
5+2=7
4+2=5)
Молодцы, вы справились, прочитаем что же к нам пришло:
«ДОРОГИЕ ДРУЗЬЯ!
МОЙ БРАТ, НОЛИК ПОПАЛ В БЕДУ.
ОН ЗАСТРЯЛ В МИХАНИЗМАХ ЧАСАХ И ЧТОБЫ ЕГО СПАСТИ НАДО ЗНАТЬ НА СКОЛЬКО ЧАСОВ НАЗАД НАДО ПЕРЕВЕСТИ СТРЕЛКИ.
ПОМОГИТЕ, ВАША СИМКА»
Итак, поможем, симке?
Но перед этим надо узнать какая тема нашего урока. Отгадайте ребус на слайде.
Верно, вычитание.
Запишите тему урока Компоненты вычитания: уменьшаемое, вычитаемое, разность
3. Открытие нового. Введение компонентов вычитания.
Итак, чтобы помочь нолику надо сделать открытие. У вас на портах лежат карточки с равенствами
Подумайте, на какие две группы их можно разделить?
1+4=5 5+3=8
2+7=8 9-4=6
7-1=4 10-7=3
(Неверные и верные равенства)
А теперь давайте превратим неверные равенства в верные. ( Ученик выходит к доске и решает данную задачу)
( Ученик выходит к доске и решает данную задачу)
А теперь на какие группы можно разделить полученные равенства (сложение, вычитание)
А как называются числа при сложении(ученики отвечают: слагаемые, сумма). Прочитайте данные равенства.
А можем ли мы прочитать равенства с минусом математическим способом? Итак, давайте поставим цель на сегодняшний урок, какое же открытие просят сделать нас фиксики? (научится читать равенства с минусом математическим способом)
Значит, сегодня на уроке мы узнаем, как же называются числа при вычитании, и научимся читать данные равенства.
Приступим к нашему исследованию.
7-4=3
Вначале вспомним, что может означит слово «вычесть»? (убрать, отнять, …)
Что обозначает первое число в равенстве? (сколько было вначале)
А что обозначает второе число в равенстве? (сколько взяли)
А что обозначает третье число в равенстве? (сколько осталось в результате выполнения действия)
Итак, какое число из трех всех больше? (первое)
Что же с ним происходит при вычитании? (Оно становится меньше, уменьшается).
И как мы можем называть это число? (УМЕНЬШАЕМОЕ).
А что происходит со вторым числом? (Его вычитают)
Значит, как его называют? (ВЫЧИТАЕМОЕ)
А третье число изображает разницу между первым числом и вторым. (РАЗНОСТЬ)
Если результат вычитания называется “разность”, то равенство со знаком минус можно назвать так же.
Давайте все вместе повторим названия чисел при вычитании (дети хором проговаривают названия компонентов действия вычитания).
Итак, какое мы совершили открытие? (узнали, как называются числа при вычитании)
Давайте сверим своё открытие с учебником. Откройте 62 № 1.
Назовите вычитаемое.
Назовите разность.
Как теперь можно прочитать выражение со знаком минус? (Разность чисел 7 и 3 равна 4).
Молодцы теперь мы готовы помочь фискам. Давайте отдохнем и продолжим наш путь.
Давайте отдохнем и продолжим наш путь.
4. Физкультминутка
Посмотрите на слайд и повторяйте за героями.
5. Повторение изученного материала.
Итак, мы готовы помочь нашим героям, но вот не задача. Опять сложности. Перед входом в комнату Дим димыча. Нас хочет проверить Папус. Не верит, что мы сможем помочь. Примем его испытание?
Итак, на слайде показано, что нам необходимо сделать.
Вам показана таблица из уменьшаемых и вычитаемых. Надо составить выражение и найти разность. Прочтите равенства математическим способом
уменьшаемое | вычитаемое | разность |
10 8 5 7 9 | 8 6 3 7 3 |
(Ребята выполняют в парах, потом читают равенства по одному разные ребята)
Хорошо, мы получили доступ в комнату Дим Димыча. Но где же у нас здесь часы? Какие виды часов вы знаете? (Ручные часы, электронные, напольные, будильник, часы с кукушкой настенные и другие)
Но где же у нас здесь часы? Какие виды часов вы знаете? (Ручные часы, электронные, напольные, будильник, часы с кукушкой настенные и другие)
На слайде можно найти часы? ( Ребята не находят)
Да, не очень чисто у Дим Димыча. Давайте поможем ему прибраться и найдем часы. Чтобы разложить вещи по местам, надо решать примеры и распределять объект в нужное место.
( Даны 4 конверта с цифрами 5,6,9, 1. Надо решить примеры на обратной стороне предметов и положить их в нужный конверт – Работа в группах)
12-7=
15-6=
7-6=
21-15=
25-16=
10-9=
27-22=
Хорошо, справились. Посмотрите снова на слайд и укажите где часы. ( Ребята находят часы)
Отлично, теперь осталось совсем немного и мы спасем фиксика.
И последнее задание: Покажите, умеете ли вы решать задачи.
— Прежде, давайте вспомним, из каких частей состоит задача (из условия и вопроса)
— Открываем тетради в клеточку.
Чтение задачи учителем.
Часы отбивают каждый час столько ударов сколько они показывают, С одного часа они отбили 6 раз. Сколько часов прошло?
Даю 2 минутки посовещаться и подумать.
Ответ: 1+2+3=6
6-1-2-3=0
6.Рефлексия
— Вот и выполнили мы все задания. И спасли нолика. Фиксики нам очень благодарены!
Ребята, понравился ли вам сегодняшний урок? Довольны ли вы своей работой?
На партах у вас лежат кружочки. Если вы довольны работой, то поднимите красный, если не очень, то зеленый и если не довольны, то синий.
Молодцы.
Какое открытие мы сделали на уроке?/data/files/o1513791867.pptx (Компоненты вычитания: уменьшаемое, вычитаемое, разность)
Знакомство с названиями компонентов действий сложения и вычитания. КРАТКОСРОЧНЫЙ ПЛАН
Постановка цели
Предположение
-Как вы думаете, компоненты вычитания также называются, как и компоненты сложения?
-Хотите узнать, как называются компоненты вычитания?
-Назовите тему урока: Знакомство с названиями компонентов действия вычитания
-Определите цель урока
1. Узнать, как называются компоненты вычитания
2. Научиться читать и записывать выражения, используя названия компонентов вычитания
-Рассмотрите картинку (7 яблок висят на яблоне. 3 яблока упали)
-Составьте выражение по картинке 7-3
-Это выражение называется РАЗНОСТЬ
-Сколько было яблок? Количество яблок на дереве уменьшилось или увеличилось, когда 3 яблока упали?
Число,
которое уменьшаем, называется УМЕНЬШАЕМЫМ, а которое вычитаем –
ВЫЧИТАЕМОЕ.
7 — 3 = 4 – значение разности
уменьшаем вычитаемое
разность
-Сколько яблок осталось на дереве?
— 4 это значение разности чисел 7 и 3
-Прочитайте выражение
Уменьшаемое — 7, вычитаемое – 3, значение разности — 4
Разность чисел 7 и 3 равна 4
Заучивание
Слева — уменьшаемое,
Справа — вычитаемое,
А в ответе всем на радость
Нас встречает наша разность.
Уменьшаемое вычитаемое значение разности
Физминутка
-Прыгните столько раз, сколько будет если от 10 -5,
-Наклонитесь вперёд столько раз, сколько будет, если от 6-2
-Сядьте слолько раз, сколько будет, если к 5+1
-Хлопните в ладоши столько раз, сколько будет, если к 5+2
(ФО) ЦО 1.5.2.4
Навык: знание, применение
Критерий оценивания: используют названия компонентов действия вычитания при чтении и записи выражений
(К)— Как называются компоненты вычитания?
(П) Посмотрите на доску.
9-6 9-3 9-4
—Обсудите в парах, чем похожи выражения и чем отличаются.
(Заслушиваются ответы)
(П) Прочитайте выражения (на доске), используя название компонентов вычитания: 6-3=3, 5-2=3, 8-4=4, 4-1=3
(ФО) Заслушиваются ответы. Дети оценивают с помощью сигнальных карточек
(К/И) Составление выражений. Выполнение «цепочкой»
-Один диктует выражение на вычитание, выкладывает его с помощью демонстрационных карточек на дополнительной доске, остальные выкладывают с помощью карточек на рабочем месте.
(ФО) Взаимооценивание
Дескриптор:
- называет разность
- называет уменьшаемое
- называет вычитаемое
- называет значение разности
У братишки контролка19 мая.Контрольная работа.Тестирование.1. В альбоме 8 листов. Маша нарисовала на
19 мая.
Контрольная работа.
Тестирование.
1. В альбоме 8 листов. Маша нарисовала на 3-х листах. Сколько чистых листов осталось в альбоме?
А)4
Б) 5
В)3
2. Уменьшаемое 18, вычитаемое 9. Найдите разность.
Б) 2
В) 4
3. Найди частное чисел 6 и 3 .
А) 6-3=3
Б) 6:3 =2
В) 6×3=18
4. Сравни числа 134 □143
А) больше
Б) меньше
В) равно
5. Укажи число, в котором
1 дес. и 5 ед.
А) 15
Б) 17
В) 25
6. Что называют многоугольником?
А) фигура с множеством углов и сторон
Б) фигура , у которой 3 угла
В) фигура , у которой 2 угла
7. Назовите компоненты сложения.
А) уменьшаемое, вычитаемое , разность
Б) слагаемое , уменьшаемое, сумма
В) слагаемое , слагаемое, сумма
8. Назовите компоненты вычитания
А) уменьшаемое , вычитаемое , разность
Б) слагаемое , уменьшаемое , сумма
В ) слагаемое , слагаемое , сумма
9. Сколько сантиметров в 1 метре ?
А) 1
Б) 10
В) 100
10.
 Сколько сантиметров в 1 дециметре ?
Сколько сантиметров в 1 дециметре ?Б) 10
В) 100
11. Отрезок — это…
А) линия, которая имеет начало, но не имеет конца
Б) линия , которая имеет и конец и начало
В) линия , которая не имеет ни начала , ни конца
12. При умножении любого числа на нуль получается …
А) 1
Б) 0
В) 5
13. Назовите компоненты умножения.
А) уменьшаемое , вычитаемое, разность
Б) 1 множитель, 2 множитель , произведение
В) слагаемое , слагаемое , сумма
14. Назовите компоненты деления.
А) делимое , делитель , частное
Б) слагаемое , уменьшаемое, сумма
В) слагаемое , слагаемое, сумма
15. Найди частное чисел 28 и 7
А) 4
Б) 6
В) 8 Всего ответов: 2
Ответы
1. 5
2. 9
3. 18
4. 134 меньше 143
5. 15
6. а
7. в
8. а
9. 100
10. 10
11. б
12. 0
13. б
14. а
15. 4
Объяснение:
Спасибо
Ответ разместил: Гость
свалка=нарисовать вал ка вместе за ручки
пестициды=пест рядом недалеко припесать циды=пест циды
Ответ разместил: Гость
1) не знаю)
2)морепродукты,насекомые
3)не заню)
4)глина
5) паровая машина
6)радио волны
Другие вопросы по: Обществознание
03. 03.2019 05:05
03.2019 05:05
Ответов: 2
16.03.2019 19:40
Ответов: 3
17.03.2019 22:50
Ответов: 2
19.03.2019 09:17
Ответов: 3
29.03.2019 01:40
Ответов: 3
31.03.2019 17:00
Ответов: 3
Популярные вопросы
Ответов: 2
27.02.2019 15:20
Ответов: 3
02. 03.2019 11:10
03.2019 11:10
Ответов: 3
02.03.2019 18:50
Ответов: 2
02.03.2019 22:10
Ответов: 3
03. 03.2019 10:00
03.2019 10:00
Ответов: 1
03.03.2019 23:30
Ответов: 1
04.03.2019 11:30
Ответов: 3
04. 03.2019 12:30
03.2019 12:30
Ответов: 3
07.03.2019 22:50
Ответов: 2
Закрепление нового. Цель: организовать деятельность с применением новых знания, распознавать целое и части. | Работа по учебнику. Анализируют записи в таблице, формулируют вопросы. Работа в тетрадях. | Организует работу с учебником, деятельность по наблюдению за внешним видом числа 6, организация работы в тетрадях. | Работа в учебнике. Во второй строчке уменьшаемое подчеркните красным цветом, вычитаемое – зеленым. Чему равно значение разности? Третья строчка : чему равно уменьшаемое, значение разности? Что надо найти? Как найти вычитаемое? Записать. 4 строчка – аналогично. | Знать названия компонентов вычитания. Уметь работать с книгой, в тетради. Применять новые термины: уменьшаемое, вычитаемое, значение разности. | Регулятивные: планирование, прогнозирование, умение корректировать выполнение задания. Познавательные: решение проблемы, выдвижение гипотез и их обоснование. Коммуникативные: инициативное сотрудничество в поиске и выборе информации; формировать готовность к сотрудничеству с другими детьми. | Контролирующее задание. Цель: выявить умение записывать выражения и находить их значения, используя новые термины; распознавать целое и части. | Выделяют проблему, как называются числа при вычитании. Устные ответы. Работа в парах. | Формулирует задание. | Назовите компоненты вычитания.Записать под диктовку, найти значения выражений: уменьшаемое 4, вычитаемое – 2; разность чисел 6 и 1; уменьшаемое -6, вычитаемое – 3; разность чисел 3 и 1. Работа в учебнике. С. 63 № 6. Найти признак разбиения и составить выражения. Работаем в паре. Самопроверка. 2+4; 3+3; 2+2+2. № 8 – найти значения выражений и раскрасить соответствующим цветом. | Знать названия чисел при вычитании, уметь записывать выражения и находить их значения. | Регулятивные: контроль, оценка, коррекция.Понимание цели выполняемых действий. Познавательные: умение структурировать знания. Коммуникативные: формировать готовность к сотрудничеству с другими детьми. Личностные: умение высказывать свое мнение, выражать свои эмоции. | Рефлексия учебной деятельности. Цель: мобилизовать учащихся на рефлексию своего поведения, мотивацию способов деятельности, общения. | Определяют результаты урока, проводят рефлексию хода урока.Самооценка. | Создание ситуации для осмысления всей работы на уроке. | Назовите компоненты вычитания. Где можно применить полученные знания? Оцените свои достижения на уроке: закрасьте флажок красным – все отлично получилось; желтым – все хорошо получилось; Зленым – только часть заданий выполнена так, как хотелось. Вы сегодня хорошо потрудились, скажите друг другу спасибо. | Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли. Познавательные: рефлексия. Личностные: положительное отношение к учебной деятельности, самооценка. Регулятивные: умение проговаривать последовательность действий на уроке. |
|
Этапы урока, время |
Деятельность педагога |
Деятельность учащихся |
Методы, приёмы, средства |
|||||||||
|
Мотивация, самоопределение учебной деятельности (мин. |
— Здравствуйте, ребята!
— Долгожданный дан звонок – |
— Приветствуют, учителя |
|
|||||||||
|
Актуализация и фиксирование индивидуального затруднения в пробном действии (мин.) |
Устный счёт. Повторение. 1. Найдите закономерность и продолжите ряд чисел:
– Оцените свою работу. — Откройте тетради и запишите сегодняшнее число. |
42, 51, 61 43, 55, 69 82, 78, 81
|
|
|||||||||
|
Этап выявления места и причины затруднений (мин. |
Математический диктант. – Записывает только ответы, в строчку через клеточку.
— Молодцы!
– Назовите компоненты и результат действия сложения. – Назовите компоненты и результат действия вычитания? – Назовите компоненты и результат действия умножения? – Что бы вы хотели узнать сегодня на уроке?
|
40+16=56
80-7=73
63+8=71 6*3=18
75-21=54 8*4=32 12/4=3
— Называют
— Называют
— Называют
— Компоненты и результат действия деления
|
|
|||||||||
|
Этап построения выхода из создавшейся ситуации (мин. |
– Верно, сегодня мы узнаем название компонентов и результата действия деления. — Сейчас мы и познакомимся с названием компонентов и результата действия деления. |
— Слушают |
|
|||||||||
|
Реализация построенного проекта (мин.) |
– Прочитайте выражение: 6 : 2 = 3 . – А как бы вы назвали эти числа? – Первый компонент – первое число при делении, что мы с ним делаем? – Как можно его назвать? делимое – Второй компонент указывает на сколько разделили? – Как можно его назвать? – Результат действия деления – это значение части? – Как можно его назвать?
– Повторим и запомним. – Как называется число, на которое делим? – Как называется результат действия деления? – Как называется само выражение? – Давайте вместе прочитаем запись, используя новые термины, хором. – А как можно прочитать по другому? – Оцените свою работу. – Молодцы! Физминутка |
— 6 разделить на 2, получится 3
— Делим
— Делимое
— Делитель
— Частное — Делимое
— Делитель — Частное — Частное — Делимое 6, делитель 2, частное 3
— Частное чисел 6 и 2 равно 3 |
|
|||||||||
|
Этап первичного закрепления с проговариванием во внешней речи (мин. |
– Молодцы, для закрепления новых терминов выполним следующее задание – Прочитайте выражение. 16 : 2 – Чему равно его значение? – Вспомните названия компонентов действия деления. – Прочитайте по – разному. – Запишите в свои тетради числовые выражения: делимое 10, делитель 5. Что надо найти? – Чему равно частное? – Прочитайте по-другому. – Запишите примеры: делимое 18, делитель 6. – Прочитайте по-другому. 2. Работа по учебнику.
– Откройте учебники на стр. – Запишите в свои тетради числовые выражения во 2 столбик самостоятельно. 6:3=2 – Прочитайте по-другому. 12:6=2 – Оцените свою работу. |
— 8
— Частное — Частное равно 2. 10:5=2 — Частное чисел 10 и 2 равно 5 — 18:6=3
|
|
|||||||||
|
Этап самостоятельной работы с проверкой по эталону (мин. |
– Возьмите карточки, которые лежат у вас на столе. – Работая в парах, по памятке решите задачу. Для освещения космического корабля потребовалось 12 ламп. Сколько отсеков на корабле, если в каждом отсеке по 4 лампы? 1 вариант.
2 вариант 12 : 4 = 3 ( отс.) – Прочитайте решение задачи, называя компоненты действия деления. Ответ: на корабле 3 отсека. |
— Читают
— Решают |
|
|||||||||
|
Этап включения в систему знания и повторения (мин. |
– Расскажите мне по схеме, что вам дал сегодняшний урок математики?
|
— Отвечают |
|
|||||||||
|
Этап рефлексии учебной деятельности на уроке (мин. |
Домашняя работа. |
|
|
Тесты по математике для 2 класса. | Учителю начальных классов
Изображение взято из открытого источникаИзображение взято из открытого источника
Тест по математике для 2 класса. ВХОДЯЩИЕ
1.Математика- это наука о…
а) числах б) буквах в) растениях
2.Назовите однозначные числа
а) 1, 2, 8 б) 11, 3, 25 в) 26, 88, 2
3.Назовите двузначные числа
а) 25, 37, 90 б) 1, 34, 5 в) 2, 7, 9
4. Что называют десятком
а) числа от 11-100 б) круглые числа от 10 до 100 в) все числа
5.Найдите правильный ответ к задаче: На экскурсию в зоопарк пошли 27 учеников из 1 «А» класса, а из 2 «В» класса на 3 ученика больше. Сколько учеников пошло на экскурсию в зоопарк из 2 «В» класса?
Сколько учеников пошло на экскурсию в зоопарк из 2 «В» класса?
а) 30 б) 24 в) 20
6. На сколько число 7 меньше 11?
а) на 18 б) на 5 в) на 4
7. На сколько число 16 больше 9?
а) на 25 б) на 6 в) на 7
8. Назовите компоненты сложения:
а) уменьшаемое, вычитаемое, разность б) слагаемое, уменьшаемое, сумма
в) слагаемое, слагаемое, сумма
9.Назовите компоненты вычитания:
а) уменьшаемое, вычитаемое, разность б) слагаемое, уменьшаемое, сумма
в) слагаемое, слагаемое, сумма
10. Дима прочитал 14 страниц книги, а Юля на 8 страниц меньше. Сколько страниц прочитала Юля?
а) 7 б) 6 в) 5
11.Число 65 состоит
а) из 5 десятков 6 единиц б) из 6 десятков в) из 6 десятков 5 единиц
12. Сколько сантиметров в 1 метре?
а)1 б) 10 в) 100
13.Сколько сантиметров в 1 дециметре?
а) 1 б) 10 в) 100
14. Таня съела 8 слив, а Оля на 7 больше. Сколько слив съела Оля?
а) 24 б) 15 в) 13
15. Отрезок – это… а) линия, которая имеет начало, но не имеет конца
Отрезок – это… а) линия, которая имеет начало, но не имеет конца
б) линия, которая имеет и конец, и начало
в) линия, которая не имеет ни начала, ни конца
16.При сложении двузначных чисел с чем складывают единицы?
а) с единицами б) с десятками в) не знаю
17.При вычитании двузначных чисел от чего вычитают десятки
а) от единиц б) от десятков в) не знаю
18.На сколько частей разделят отрезок две точки?
а) на 2 б) на 3 в) на 5
19.Столяр должен отстругать 38 досок. За один день он отстругал 30 досок. Сколько еще досок должен отстругать столяр?
а)38 б) 30 в) 8
20. Число 30 больше, меньше или равно числа 50
а) больше б) равно в) меньше
21. Что нужно сделать, чтобы проверить сложение?
нужно от суммы чисел отнять одно из слагаемых
22.Что нужно сделать, чтобы проверить вычитание чисел?
нужно к разности прибавить вычитаемое
23. Что называется периметром многоугольника
сумма длин всех сторон многоугольника
24. Мастер сделал 9 кроваток, а люлек – на 2 больше. Сколько люлек сделал мастер?
Мастер сделал 9 кроваток, а люлек – на 2 больше. Сколько люлек сделал мастер?
11
25. В одной тарелке 9 булочек, в другой-3. Сколько всего булочек в двух тарелках?
21
КЛЮЧИ
1-а 2-а 3-а 4-б 5-а 6-б 7-в 8-в 9-а 10-б 11-в 12-в 13-б 14-б 15-б 16-а 17-б 18-б 19-в 20-б
21- нужно от суммы чисел отнять одно из слагаемых
22- нужно к разности прибавить вычитаемое
23- сумма длин всех сторон многоугольника
24- 11
25 — 21
Вычитание — объяснение и примеры
Как и сложение, вычитание — одна из самых старых и самых простых арифметических операций. Слово «вычитание» образовано от двух слов , « sub » и « tract », которые означают, соответственно, ниже или ниже и тянуть или уносить. Следовательно, вычитание означает унесение нижней части.
Вычитание известно математикам более 6000 лет. Немецкие математики впервые использовали символ вычитания в качестве отметок на бочках. Затем он используется в качестве рабочего символа в 1500-х годах. Позже, в 1557 году, это стало обычным явлением, когда Роберт Рекорд, известный врач и математик, использовал его в точильном камне Витте.
Затем он используется в качестве рабочего символа в 1500-х годах. Позже, в 1557 году, это стало обычным явлением, когда Роберт Рекорд, известный врач и математик, использовал его в точильном камне Витте.
Определение вычитания
В 1200-х годах метод вычитания назывался заимствованием или декомпозицией. После 1600 года математики ввели термин вычитание и определили его как математическую операцию, при которой сумма вычитается из общей суммы. Это также разница между двумя суммами.
Вычитание обозначается дефисом (-).
Например, в предложении вычитания 20 — 5 = 15, 5 вычитается из 20, остается 15. Предложение вычитания состоит из четырех основных частей: вычитание, уменьшение, знак равенства и разность.
Понимание частей предложения вычитания полезно, потому что оно позволяет учащимся усвоить ключевые принципы вычитания и разработать стратегии для решения задач вычитания.
Части вычитания
Минуэнд
Минус в предложении вычитания — это начальная сумма, из которой вычитаются другие суммы. Например, в предложении вычитания: 12-8 = 4, уменьшаемое значение равно 12.
Например, в предложении вычитания: 12-8 = 4, уменьшаемое значение равно 12.
Вычитающее
Это число отнимается от стартовой суммы. В предложении вычитания: 12-8 = 12, вычитаемое равно 8. В предложении вычитания может быть несколько вычитаний, в зависимости от сложности уравнения.
Знак равенства
Знак равенства, являющийся третьей частью любого предложения вычитания, означает, что две стороны уравнения эквивалентны.Знак равенства обозначается « = » и вставляется между вычитаемыми значениями.
Разница
В предложении с вычитанием разница — это ответ или результат операции. Например, 12 — 8 = 4; разница в данном случае составляет 4.
Свойства вычитания
Свойство identity указывает, что любое число минус или плюс ноль является самим числом. Например,
4 — 0 = 4.
В этом случае рекомендуется напомнить учащимся при вычитании больших групп чисел, что ноль не влияет на другие числа в уравнении.
Сложение и вычитание обычно противоположны друг другу. Например,
12 + 5 — 5 = 12.
Сложение и вычитание одной и той же суммы равносильно отмене двух сумм. По этой причине учащимся рекомендуется определять числа, которые отменяют каждое из них, особенно когда они имеют дело со сложением и вычитанием больших групп чисел.
Коммутативное свойство утверждает, что изменение чисел в математическом уравнении не влияет на окончательный ответ.Свойство коммутативности не применяется к вычитанию, потому что 5-2 не то же самое, что 2-5.
Свойство ассоциативности применяется к уравнениям, в которых скобки, фигурные скобки и круглые скобки используются для группировки чисел. Другими словами, вы можете перемещать круглые скобки по разным группам, не меняя окончательный ответ.
Это свойство также не применимо к вычитанию, потому что: (3-4) — 2 не эквивалентно 3 — (4-2). Это показывает, что вы не можете перемещать скобки при работе с уравнением вычитания.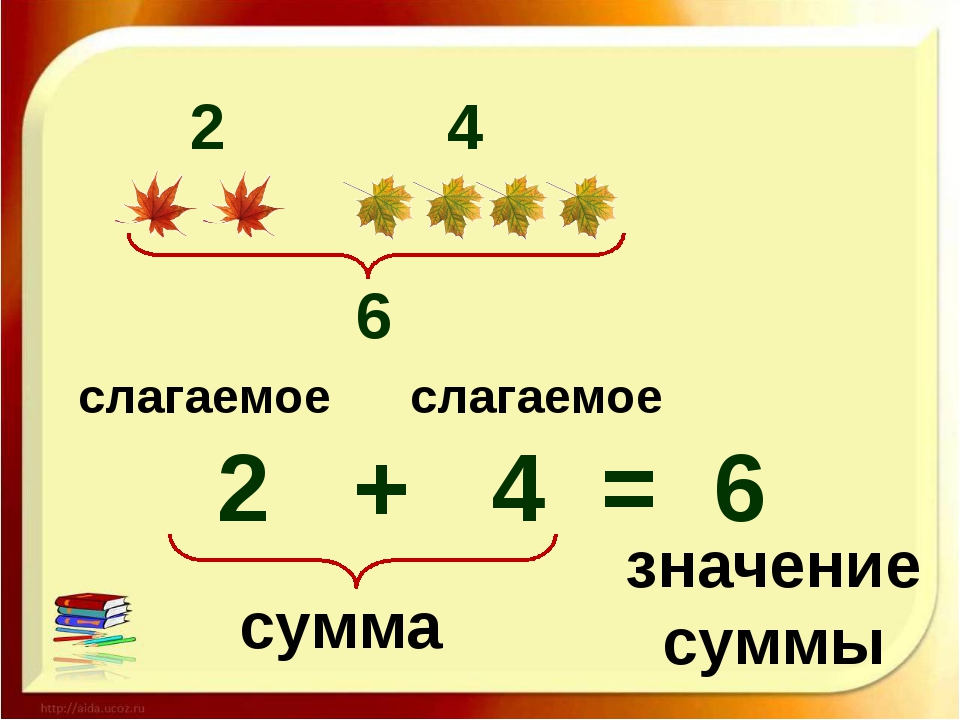
Пример 1
У Сэма 99 кексов. Если он отдал 32 Нине и 49 Джули, сколько кексов у него осталось?
Решение
Общее количество кексов = 99
Нина берет = 32
Джули берет = 49
Количество кексов осталось = 99-32-49 = 18
Пример 2
В 2012 году в компании работало 1000 сотрудников. В связи с рецессией компания увольняет 230 сотрудников в 2015 году и 220 сотрудников в 2017 году.Если в этот период компания не нанимает новых сотрудников, определите количество сотрудников до конца 2017 года.
Решение
Всего сотрудников в 2012 году = 1000
Компания увольняет 230 сотрудников в 2015 году,
Осталось сотрудников = 1000 — 230 = 770
Компания уволила 220 сотрудников в 2017 году,
Осталось сотрудников = 770 — 220 = 550
Пример 3
Джеймс, Майк и Карран имеют банковские счета в Центральном банке. У Майка на 500 долларов больше, чем у Джеймса, а у Каррана на 300 долларов меньше, чем у Джеймса. Если у Майка на счету 1200 долларов, сколько у Куррана?
У Майка на 500 долларов больше, чем у Джеймса, а у Каррана на 300 долларов меньше, чем у Джеймса. Если у Майка на счету 1200 долларов, сколько у Куррана?
Решение
Майк = Джеймс + $ 500
Карран = Джеймс — 300 долларов
Джеймс = Карран + 300 долларов
Майк = Курран + 300 долларов + 500 долларов
Карран = Майк — 300–500 долларов
Карран = Майк — 800 долларов
Курран = 1200 — 800 долларов
Курран = 400 $
Практические вопросы
- Из 568 детей села 354 ходят в школу.Сколько детей не ходят в школу?
- У человека было 5680 долларов. Если он потратил 3456 долларов из общей суммы, сколько денег у него останется?
- Насколько 3689 меньше 6789?
- Мелвин зарабатывает 6777 долларов в месяц. Предположим, она экономит 577 долларов в месяц. Рассчитать ее ежемесячные расходы?
- Телефон стоит 290 долларов, а часы на 78 долларов меньше телефона.
 Сколько стоят часы?
Сколько стоят часы? - В хозяйственном магазине было 20000 мешков цемента. Если было продано 3450 пакетов, сколько пакетов осталось в оборудовании?
- Женщина хочет купить платье по цене 205 долларов, но у нее есть только 156 долларов.Сколько еще денег ей нужно, чтобы купить платье?
- Мужчина отправился в путь длиной 5067 км на машине. Из общего пути он преодолел 3589 км на поезде, а оставшиеся 20 км — на мотоцикле. Сколько км он проехал на машине?
- Разница между двумя числами составляет 4509. Если меньшее число — 68888, вычислить значение большего числа?
- В четвертом классе школы 600 учеников. Из общего числа 200 студентов имеют возраст от 9 до 11 лет, а остальные — от 12 до 13 лет.Посчитать количество учеников с разницей в возрасте от 12 до 13 лет?
Что такое вычитание в математике? — Определение, методы и примеры — Видео и стенограмма урока
Сложение против вычитания
Сложение и вычитание тесно связаны. Хотя сложение противоположно вычитанию, верно и то, что любую задачу сложения можно переписать как задачу вычитания.Например, задачу 3 + 2 = 5 можно переписать как задачу вычитания 5 — 3 = 2 или 5 — 2 = 3. Обратите внимание, что сумма 5 в задаче сложения стала уменьшаемой, а другие числа стали вычитаемым и разница.
Хотя сложение противоположно вычитанию, верно и то, что любую задачу сложения можно переписать как задачу вычитания.Например, задачу 3 + 2 = 5 можно переписать как задачу вычитания 5 — 3 = 2 или 5 — 2 = 3. Обратите внимание, что сумма 5 в задаче сложения стала уменьшаемой, а другие числа стали вычитаемым и разница.
Кроме того, вы, вероятно, узнали что-то вроде следующего: если 3 + 2 = 5, то 2 + 3 = 5. Другими словами, вы можете изменить порядок добавляемых чисел и получить тот же ответ. Этого нельзя сделать вычитанием. Например, 5-3 и 3-5 не равны одному и тому же значению.
Методы вычитания
Существуют различные методы вычитания. Один из способов — использовать диаграмму, показывающую, с чего вы начинаете, что отбираете и что у вас остается.
Например, проблему 5 — 3 можно описать с помощью этой диаграммы:
Другой способ описания и помощи при вычитании — использование числовой прямой.
Чтобы указать задачу 5 — 3, нарисована стрелка, начиная с цифры 5, перемещаясь на три единицы в направлении меньших чисел и заканчивая конечной разницей 2.
При вычитании чисел, состоящих из двух или более цифр, важно записывать числа одно над другим, чтобы выстраивались одинаковые разрядные значения, как показано в задаче 37-25.
Затем вы вычитаете, начиная с самых крайних правых цифр. Итак, в этой задаче вы должны начать с 7–5 и поместить разницу 2 под числами. Затем вы должны вычесть 3–2 и поместить разницу 1 под этими числами.Это дает вам решение 37 — 25 = 12.
При вычитании чисел с двумя или более цифрами таким образом вы можете обнаружить, что уменьшаемое значение недостаточно велико, чтобы вычесть вычитаемое. В этом случае вам придется брать деньги из ближайшего ненулевого значения слева. Чтобы одолжить , вы берете один из ближайшего уменьшаемого значения и считаете его как десять, чтобы добавить к другому уменьшаемому справа. Это сделает число достаточно большим, чтобы вычесть из него.
Чтобы одолжить , вы берете один из ближайшего уменьшаемого значения и считаете его как десять, чтобы добавить к другому уменьшаемому справа. Это сделает число достаточно большим, чтобы вычесть из него.
Часто нам дают имена для вещей, которые мы вычитаем.Например, 10 щенков — 4 щенка = 6 щенков. В этом примере обратите внимание, что во всех трех частях задачи вычитания использовалась одна и та же единица — щенки. Если в задаче на вычитание дается единица, то все части задачи должны иметь одну и ту же единицу.
Проверка ответа
Ответ на задачу вычитания можно легко проверить с помощью сложения. Например, 37 — 25 = 12. Чтобы проверить этот ответ, сложите вычитаемое 25 и разность 12. Если вычитание было правильным, эта сумма будет равна исходному вычитаемому 37.Если бы мы сложили 25 + 12, ответ был бы 37, и это говорит нам, что мы вычитали правильно.
Повседневные примеры вычитания
Если вы не уверены, требует ли задача вычитания, вам могут помочь определенные слова или фразы, использованные в задаче. Помимо слов «минус», «разница» или «убрать», для обозначения вычитания часто используются другие фразы: сколько еще, сколько осталось и сколько еще. Кроме того, когда вам нужно узнать, насколько значение увеличилось или уменьшилось, часто используется вычитание.Рассмотрим следующие примеры.
Помимо слов «минус», «разница» или «убрать», для обозначения вычитания часто используются другие фразы: сколько еще, сколько осталось и сколько еще. Кроме того, когда вам нужно узнать, насколько значение увеличилось или уменьшилось, часто используется вычитание.Рассмотрим следующие примеры.
- Вы покупаете продуктов на 13,42 доллара и отдаете кассиру 15 долларов. Сколько сдачи вы должны получить? Чтобы найти сдачу в денежной транзакции, вы должны вычесть. 15 долларов США — 13,42 доллара США = 1,58 доллара США.
- Вы собираетесь в путешествие и должны проехать 500 миль. Если вы уже проехали 150 миль, сколько еще миль вам нужно проехать? Фраза «сколько еще» означает, что вы должны вычесть, чтобы получить ответ. 500 миль — 150 миль = 350 миль.
- Вы накопили 46 долларов в банке.У вашего друга в банке есть 63 доллара. Сколько еще денег скопил ваш друг? Фраза «сколько еще» означает вычитание. 63 — 46 долларов = 17 долларов.
- Если ваш рост 66 дюймов, а рост вашей сестры 61 дюйм, какая разница в вашем росте? Ключевое слово здесь — «разница».
 66 дюймов — 61 дюйм = 5 дюймов.
66 дюймов — 61 дюйм = 5 дюймов. - Цена на газ упала с 3,89 доллара за галлон до 3,55 доллара за галлон. Насколько изменилась цена? В этой задаче вы пытаетесь выяснить, насколько изменилась стоимость галлона газа.3,89 доллара США — 3,55 доллара США = 0,34 доллара США.
Краткое содержание урока
Вычитание — это обычная математическая операция, которая означает, что вы убираете из некоторой группы или объектов. Сумма, оставшаяся после вычитания, будет меньше. Три части любой задачи на вычитание — это minuend , часть, с которой вы начинаете; вычитает , часть убирается; и разность , оставшаяся часть.
Диаграммы могут использоваться для упрощения задач на вычитание.Для задач с двумя цифрами вы должны выстроить одинаковые разряды и вычесть справа налево. Возможно, вам также придется занять. В задачах со словами часто используются определенные фразы, указывающие на вычитание. Вычитание также указывается каждый раз, когда вам нужно узнать, насколько изменилось значение.
Результаты обучения
После этого урока вы должны уметь:
- Определить вычитание
- Опишите три части задачи на вычитание
- Объясните, как писать и решать задачи на вычитание
- Вспомните повседневные примеры вычитания и ключевые слова, используемые в задачах на вычитание
Термины для уравнений сложения, вычитания, умножения и деления — математика для 3-го класса
Выучите термины для уравнений сложения, вычитания, умножения и деления
Итак, вы научились решать уравнения сложения, вычитания, умножения и деления.000
Давайте рассмотрим терминов для каждого из них.
Совет: Термины — это имен различных частей уравнения.
Условия дополнения
Слагаемые — это числа, которые складываются вместе.
Сумма — это ответ, который вы получите, сложив числа.
Мы пишем плюс ( +) между двумя слагаемыми и знак равенства перед суммой.
Совет: Знак равенства (=) означает, что элементы слева и справа от него равны.
Условия вычитания
Minuend — это число, из которого вычитается. Это большее число.
Subtrahend — это число, которое убирается из убываемого. Это меньшее число.
Вычитаемое всегда предшествует вычитаемому.
Совет для запоминания:
Разница — это ответ, который мы получаем в уравнении вычитания.
Мы используем знак минус (-) между минусом и вычитаемым.
Запишем знак равенства перед разностью.
Условия умножения
Умножаемое — это число, которое нужно умножить.
Умножитель — это число, указывающее, сколько раз следует умножить множимое.
Множаемое и множитель также называются коэффициентами .
Множитель часто записывается первым, но положение этих чисел не имеет особого значения.Это называется коммутативным свойством умножения.
Ответ в уравнении умножения называется произведением .
Знак умножения ( ×) записывается между двумя множителями. Его также называют знаком раз.
Термины для подкласса
Дивиденды — это делимое число.
Делитель — это число, указывающее, сколько раз следует разделить дивиденд.Он отвечает на вопрос «На сколько равных групп делится число?».
Ответ, который мы получаем в уравнении деления, называется частным .
Между делимым и делителем ставится знак деления (÷). Это короткая горизонтальная линия с точками над и под ней.
Совет: Вы также можете увидеть /, используемое как знак деления. То же, что и ÷.
Смотри и учись
Отличная работа по изучению этих терминов. 000
000
Теперь попробуйте практиковаться, чтобы убедиться, что вы помните, что они означают.
Условия вычитания
Условия вычитанияВычитание натуральных чисел | |
| Операции с натуральными числами I | |
1.Вычитание натуральных чисел. Условия вычитания. | |
— Вычитание
противоположная операция сложения. | |
| font=’Monospaced,PLAIN,12′ tooltip.font=’Monospaced,PLAIN,12′ Explanation.font=’Monospaced,PLAIN,12′»/> 2,0)(-4,0)(-4,3)(-6.2,3)(-6.2,0)'»/> ./../imagenes_comunes/boton_adelante2*(p>1)’ expresion='(5,2)’ text='[b2]’ font=’Helvetica,PLAIN,30′ decimals=’0′ fixed=’yes’ size=’0′»/> 905 905 905 905 905 905 905 905 905 905 905 905 905 905 905 905 905 905 виртуальный де Java J2RE. | Проверить если вычитание правильное, мы складываем вычитаемое и разность.Результат должен быть минимальным. |
| Эдуардо Барберо Загон | ||
Министерство образования Испании. Год 2007 Год 2007 | ||
За исключением случаев, когда иное
отметил, что эта работа находится под лицензией Creative
Стандартная лицензия
Вычитание
Вычитание не следует определять как «забрать».Итак, возникает вопрос: если вычитание — это не отнятие, то что это такое?
Ответ на самом деле очень прост, когда мы связываем вычитание со сложением:
Вычитание — это поиск недостающего слагаемого в операторе сложения.
Я знаю. Звучит не так просто, но, надеюсь, следующее обсуждение прояснит это.
Поскольку вычитание основано на сложении, давайте сначала рассмотрим некоторые основы сложения.
У нас есть оператор сложения, 7 + 3 = 10.
Теперь предположим, что одно из дополнений неизвестно, например это
1) 7 + _ = 10
Какое число 10-7?
Ответ: это число, которое вы добавляете к 7, чтобы получить 10, что, конечно же, равно 3.
Вы используете вычитание, чтобы найти неизвестное слагаемое, когда вы знаете одно слагаемое и сумму.
Когда мы говорим о вычитании, мы меняем терминологию (по какой-то причине), что нечаянно помогает скрыть простую взаимосвязь между сложением и вычитанием.
Как показано выше, число, которое является «суммой» в добавлении, становится «уменьшаемым» при вычитании.
Кроме того, «слагаемые» становятся «вычитанием» и «разницей» при вычитании.
Что с этим?
Было бы намного проще сказать:
- Когда вы знаете два слагаемых, вы складываете их, чтобы найти сумму.
- Когда вы знаете одно слагаемое и сумму, вы вычитаете, чтобы найти другое слагаемое.
(Это один из многих случаев в математике, где используемая нами терминология настолько изолирована от очень небольших сегментов контента — «разрозненных»), что мы стреляем себе в коллективные ноги, когда дело доходит до обучения основным концепциям. )
)
Есть еще один способ определения вычитания, который означает то же самое, что и определение «недостающее слагаемое».
Вычитание — это нахождение разницы между двумя числами.
«Разница» в вычитании — это по определению одно из слагаемых в операторе сложения — это слагаемое, о котором мы не знаем. Это число, которое вы добавляете к известному слагаемому, чтобы получить известную сумму.
Итак, что это говорит об обучении концепции вычитания?
Один из способов представить себе вычитание — это «поиск недостающей части числа», где «число» — это уменьшаемое, то есть сумма, а «недостающая часть» — это «неизвестное слагаемое».”
Чтобы понять это определение, учащиеся должны понимать, что каждое число состоит из других чисел. Вычитание — это просто нахождение одного из чисел, составляющих другое число, уменьшаемого или суммы.
Что значит сказать, что числа состоят из других чисел? Это фундаментальное свойство чисел. Это связано с тем, что называется «мощностью» числа. А что такое мощность?
А что такое мощность?
Если вы подсчитываете группу из 8 объектов, каждый счет от 1 до 8 означает, что вы определили большую группу.
Когда вы указываете на первый объект и говорите «1», в группе будет только 1 элемент. Когда вы указываете на второй объект и говорите «2», вы не маркируете этот элемент, а обозначаете размер группы, которая содержит этот элемент, и первую, которую вы посчитали. Когда вы считаете «3», вы не маркируете этот элемент, вы описываете размер группы, которая содержит этот элемент, и двух, которые вы считали ранее. И так далее.
Другими словами, при каждом подсчете не отмечается элемент, на который вы указываете при подсчете.Он отмечает размер группы, в которую входят все элементы, которые вы подсчитали до этого момента. Это идея, которую мы называем «мощность».
Это приводит к такому выводу. У вас не может быть группы из 8 человек, если у вас нет группы из 7. И вы не можете иметь группу из 7 человек, если у вас нет группы из 6 человек, и так далее. Другими словами, все целые числа (за исключением 0 и 1) состоят из других целых чисел.
Другими словами, все целые числа (за исключением 0 и 1) состоят из других целых чисел.
Это фундаментальная концепция, которую студенты должны усвоить, чтобы понимать сложение и вычитание.Конечно, нет причин учить их называть это «мощность». Им просто нужно усвоить и использовать концепцию.
Эту тему обычно называют проблемой «композиции и разложения чисел».
Теперь, как это связано со сложением и вычитанием?
Когда вы складываете, вы знаете «количество» (мощность) двух разных, не пересекающихся групп.
Один из способов добавить их — сложить две группы и пересчитать их все, начиная с 1 и включая все элементы в обеих группах.Но во многих ситуациях это большая работа. Вот почему было изобретено сложение.
Например, вот два ящика.
В каждой коробке есть яблоки, и число в каждой коробке удобно написано снаружи коробки. (Либо вы подсчитали эти группы заранее, либо кто-то еще подсчитал их и записал числа на коробках за вас. ) В одной коробке 9 яблок, а в другой — 6 яблок.По какой-то причине мы хотим знать, сколько яблок в двух ящиках вместе взятых.
) В одной коробке 9 яблок, а в другой — 6 яблок.По какой-то причине мы хотим знать, сколько яблок в двух ящиках вместе взятых.
Один из способов сделать это — сложить эти две группы и пересчитать их все. Другими словами, мы находим мощность объединенной группы.
Или, если вы уже «запомнили» тот факт, что 9 + 6 равно 15, или вы узнали стратегию получения суммы, вы можете использовать сложение.
Все, что вы делаете, — это «мысленно» объединяете две группы (но не объединяете их физически, о чем мы поговорим позже).Мы знаем, что после тысяч лет повторения людьми этого процесса результат всегда равен 15.
Наши предки сделали всю работу за нас. Все, что нам нужно сделать, это вспомнить то, чему они научились на протяжении веков опыта. 9 и 6 больше всегда 15, независимо от того, какие группы представляют числа. И нам не нужно пересчитывать все предметы, чтобы это выяснить.
Когда мы слушаем наших предков и вспоминаем этот факт, мы знаем, что всего в двух коробках всего 15 яблок. Никакой работы, только небольшое воспоминание по памяти.
Никакой работы, только небольшое воспоминание по памяти.
Теперь давайте изменим эту ситуацию на вычитание.
Здесь мы не знаем, сколько яблок во второй коробке, но мы знаем, что их 15 в двух коробках вместе взятых. Пишем это так:
9 + _ = 15
Здесь мы используем вычитание. Мы знаем, что число в каждом квадрате является добавлением, и вместе они составляют число в сумме, равное 15.
Мы также знаем, что в число «15» встроены другие числа — оно состоит из других чисел (из-за количества элементов). В этом случае мы знаем, что один из «компонентов» числа 15 равен 9. Нам нужно знать, что это за другой компонент. Это номер во втором поле.
Чтобы найти число во втором поле (неизвестный компонент 15?), Мы вычитаем. Запишем вычитание так:
15 — 9 = _
Другими словами, мы находим недостающее слагаемое, число во втором поле.Чтобы решить задачу вычитания, мы задаем вопрос (мысленно) «какое число мы прибавляем к 9, чтобы получить 15?»
Опять же, нам не нужно делать никакой работы. Мы просто полагаемся на то, что передали нам наши предки. Ответ на этот вопрос — 6, независимо от того, к какому типу относятся числа.
Мы просто полагаемся на то, что передали нам наши предки. Ответ на этот вопрос — 6, независимо от того, к какому типу относятся числа.
Итак, у меня возникает вопрос — почему в мире так много умных, образованных людей, по крайней мере, за последние 100 с лишним лет, определили вычитание как «отнятие»? В этом примере нет ничего, что указывало бы на процесс «удаления», если только вы не занимаетесь какой-либо умственной гимнастикой (что не является хорошей идеей для обучения детей).
Это немного странно, если посмотреть на это объективно. Настоящий ответ сложен, но простой ответ — «это удобно».
Основная причина в том, что вычитание — это абстрактный процесс, как и большинство математических тем, поэтому мы обычно обучаем его, «подкрепляя его» опытом с физическими объектами, такими как строительные блоки. У нас дети «моделируют» математические операции.
Но у этого подхода есть огромная обратная сторона.Проблема в том, что эта единственная ситуация, которую легко смоделировать, не передает всей степени изучаемой концепции. Другой способ сказать это: дети учатся на том, что мы не говорим или не делаем, столько же, сколько они учатся на том, что мы говорим и делаем.
Другой способ сказать это: дети учатся на том, что мы не говорим или не делаем, столько же, сколько они учатся на том, что мы говорим и делаем.
Вычитание обучения — классический случай этого.
Вычитание используется в самых разных ситуациях. Когда мы учим, что означает вычитание, используя единственное представление, например «убирать» вещи, дети подсознательно ограничивают свое внутреннее определение этими ограниченными ситуациями.
Они делают то, что называется «недообобщением». Это означает, что они считают вычитание более ограниченным понятием, чем оно есть на самом деле. Когда они узнают, что вычитание «означает» только «отнять», им трудно справиться с тем фактом, что в подавляющем большинстве ситуаций, в которых используется вычитание, ничего «не отнимается».
Если мы хотим преодолеть эту проблему, мы должны разработать способы представления концепции вычитания, чтобы она точно и полностью представляла диапазон ситуаций, к которым ее можно применить. Это единственный способ дать детям полное представление о концепции вычитания.
Это единственный способ дать детям полное представление о концепции вычитания.
Смотрите других в этой серии:
- Вычитание не означает «убрать»
- Что такое вычитание?
- Обучение вычитанию на числовой прямой
- Что такое отрицательное число?
Нажмите ниже, чтобы увидеть другие ресурсы
Вычитание — определение, примеры | Вычитание в числовой строке
Вычитание — это процесс удаления одного числа у другого.Это основная арифметическая операция, которая обозначается символом вычитания (-) и является методом вычисления разницы между двумя числами.
Что такое вычитание?
Вычитание — это операция, используемая для нахождения разницы между числами. Когда у вас есть группа объектов и вы убираете из нее несколько объектов, группа становится меньше. Например, вы купили 9 кексов на день рождения, а ваши друзья съели 7 кексов. Осталось 2 кекса.Это можно записать в виде выражения вычитания: 9-7 = 2 и читается как «девять минус семь равно двум». Когда мы вычитаем 7 из 9, (9-7) получаем 2. Здесь мы выполнили операцию вычитания двух чисел 9 и 7, чтобы получить разницу 2.
Когда мы вычитаем 7 из 9, (9-7) получаем 2. Здесь мы выполнили операцию вычитания двух чисел 9 и 7, чтобы получить разницу 2.
Символ вычитания
В математике есть разные символы. Символ вычитания — один из важных математических символов, которые мы используем при выполнении вычитания. В предыдущем разделе мы читали о вычитании двух чисел 9 и 7.Если мы наблюдаем это вычитание: (9 — 7 = 2), символ (-) соединяет два числа и завершает данное выражение. Этот символ также известен как знак минус.
Формула вычитания
Когда мы вычитаем два числа, мы используем некоторые термины, которые используются в выражении вычитания:
- Minuend: число, из которого вычитается другое число.
- Subtrahend: число, которое нужно вычесть из уменьшаемого.
- Разница: конечный результат после вычитания минусом.
Формула вычитания записывается как: Minuend — Subtrahend = Difference
Давайте разберемся с формулой вычитания или математическим уравнением вычитания на примере.
Здесь 9 — уменьшение, 7 — вычитание, а 2 — разница.
Как решить задачи на вычитание?
При решении задач на вычитание однозначные числа можно вычитать простым способом, но для больших чисел мы разбиваем числа на столбцы, используя соответствующие им разряды, такие как Единицы, Десятки, Сотни, Тысячи и т. Д.При решении таких проблем мы можем столкнуться с некоторыми случаями с заимствованием, а некоторые без заимствования. Вычитание с заимствованием также известно как вычитание с перегруппировкой. Когда minuend меньше вычитаемого, мы используем метод перегруппировки. При перегруппировке мы заимствуем 1 число из предыдущего столбца, чтобы уменьшить значение больше, чем вычитаемое. Давайте разберемся в этом с помощью нескольких примеров.
Вычитание без перегруппировки
Пример: вычтем 25632 из 48756.
Примечание. При вычитании мы всегда вычитаем меньшее число из большего числа, чтобы получить правильный ответ.
Решение: Следуйте приведенным ниже инструкциям и попытайтесь связать их со следующим рисунком.
Шаг 1: Начните с цифры в единицах. (6 — 2 = 4)
Шаг 2: Перейти к разряду десятков. (5 — 3 = 2)
Шаг 3: Теперь вычтите цифры в разряде сотен. (7-6 = 1)
Шаг 4: Теперь вычтите цифры в разряде тысяч.(8 — 5 = 3)
Шаг 5: Наконец, вычтите цифры в разряде десяти тысяч. (4 — 2 = 2)
Шаг 6: Следовательно, разница между двумя данными числами составляет: 48756 — 25632 = 23124.
Вычитание с перегруппировкой
Пример: вычтем 3678 из 8162.
Решение: Следуйте приведенным ниже инструкциям и попытайтесь связать их со следующим рисунком.
Нам нужно решить: 8162 — 3678
Шаг 1: Начните вычитание цифр с единицы.Мы видим, что 8 больше 2. Итак, мы возьмем 1 из столбца десятков, в результате чего получится 12. Теперь 12 — 8 = 4 единицы.
Итак, мы возьмем 1 из столбца десятков, в результате чего получится 12. Теперь 12 — 8 = 4 единицы.
Шаг 2: После присвоения 1 столбцу единиц на предыдущем шаге 6 становится 5. Теперь давайте вычтем цифры в разряде десятков (5-7). Здесь 7 больше 5, поэтому мы возьмем 1 из столбца сотен. Это будет 15. Итак, 15-7 = 8 десятков.
Шаг 3: На шаге 2 мы присвоили 1 столбцу десятков, поэтому у нас осталось 0 в разряде сотен.Чтобы вычесть цифры в разряде сотен, то есть (0-6), мы возьмем 1 из столбца тысяч. Это будет 10. Итак, 10 — 6 = 4 сотни.
Шаг 4: Теперь вычтем цифры в разряде тысяч. После присвоения 1 столбцу сотен мы получаем 7. Итак, 7 — 3 = 4
Шаг 5: Следовательно, разница между двумя данными числами составляет: 8162 — 3678 = 4484
Вычитание по числовой строке
Числовая линия — это наглядное пособие, которое помогает нам понять вычитание, потому что она позволяет нам перемещаться вперед и назад по каждому числу. Чтобы понять, как это работает, давайте исследуем вычитание с помощью числовой прямой. Вычтем 4 из 9, используя числовую прямую. Начнем с отметки цифры 9 на числовой строке. Когда мы вычитаем с помощью числовой линии, мы считаем, перемещая по одному числу влево. Поскольку мы вычитаем 4 из 9, мы переместимся 4 раза влево. Число, на которое вы приземлитесь после 4 прыжков назад, и есть ответ. Таким образом, 9-4 = 5.
Чтобы понять, как это работает, давайте исследуем вычитание с помощью числовой прямой. Вычтем 4 из 9, используя числовую прямую. Начнем с отметки цифры 9 на числовой строке. Когда мы вычитаем с помощью числовой линии, мы считаем, перемещая по одному числу влево. Поскольку мы вычитаем 4 из 9, мы переместимся 4 раза влево. Число, на которое вы приземлитесь после 4 прыжков назад, и есть ответ. Таким образом, 9-4 = 5.
Задачи со словами на вычитание в реальной жизни
Концепция вычитания часто используется в нашей повседневной деятельности.Давайте разберемся, как решать реальные задачи на вычитание слов с помощью интересного примера.
Пример: футбольный матч собрал 4535 зрителей. После первых иннингов стадион покинули 2332 зрителя. Найдите количество оставшихся зрителей.
Решение:
Дано:
Общее количество зрителей, присутствовавших в первой иннингсе = 4535; Количество зрителей, покинувших стадион после первой подачи = 2332
. Здесь 4535 — вычитаемое, а 2332 — вычитаемое.
Здесь 4535 — вычитаемое, а 2332 — вычитаемое.
Чт В Т О
4 5 3 5
-2 3 3 2
2 2 0 3
Следовательно, количество оставшихся зрителей = 2203.
Важные примечания по вычитанию:
Вот несколько важных примечаний, которым вы можете следовать при выполнении вычитания в повседневной жизни.
- Любую задачу на вычитание можно преобразовать в задачу сложения и наоборот.
- Вычитание 0 из любого числа дает само число в качестве разницы.
- Когда 1 вычитается из любого числа, разница равна предшествующему числу.
- Такие слова, как «Минус», «Меньше», «Разница», «Уменьшение», «Убрать» и «Вычесть» означают, что вам нужно вычесть одно число из другого.
Темы, связанные с вычитанием
Прочтите эти интересные статьи, чтобы узнать о вычитании и связанных с ним темах.
Часто задаваемые вопросы о вычитании
Где мы используем вычитание?
В нашей повседневной жизни используется вычитание. Например, если мы хотим узнать, сколько денег мы потратили на купленные товары, или сколько денег осталось у нас, или, если мы хотим подсчитать время, оставшееся до завершения задачи, мы используем вычитание.
Например, если мы хотим узнать, сколько денег мы потратили на купленные товары, или сколько денег осталось у нас, или, если мы хотим подсчитать время, оставшееся до завершения задачи, мы используем вычитание.
Какие типы вычитания?
Под типами вычитания подразумеваются различные методы, используемые при вычитании. Например, вычитание с перегруппировкой и без нее, вычитание с использованием числовых диаграмм, вычитание с использованием числовой прямой, вычитание маленьких чисел с помощью пальцев и т. Д.
Что такое стратегии вычитания?
Стратегии вычитания — это разные способы обучения вычитанию. Например, используя числовую линию, с помощью таблицы значений мест, разделяя десятки и единицы, а затем вычитая их по отдельности, и многие другие.
Приведите примеры вычитания.
Существуют различные примеры вычитания из реальной жизни. Например, если у вас есть 5 яблок, и ваш друг съел 3 яблока. Используя вычитание, мы можем узнать количество оставшихся яблок: 5 — 3 = 2. Итак, у вас осталось 2 яблока. Точно так же, если в классе 16 учеников, из которых 9 девочки, то мы можем узнать количество мальчиков в классе, вычтя 9 из 16. (16 — 9 = 7). Итак, мы знаем, что в классе 7 мальчиков.
Итак, у вас осталось 2 яблока. Точно так же, если в классе 16 учеников, из которых 9 девочки, то мы можем узнать количество мальчиков в классе, вычтя 9 из 16. (16 — 9 = 7). Итак, мы знаем, что в классе 7 мальчиков.
Какие три части вычитания?
Три части вычитания называются следующим образом:
- Minuend: Число, из которого мы вычитаем другое число, известно как minuend.
- Subtrahend: число, которое вычитается из уменьшаемого, известно как вычитаемое.
- Разница: окончательный результат, полученный после выполнения вычитания, называется разницей.
Основные математические определения
| На этой странице мы собрали несколько основных определений. Для получения дополнительных определений, объяснений и т. Д. Воспользуйтесь поиском выше. |
| Или найдите свое слово в: |
| Иллюстрированный математический словарь |
Основные операции
В базовой математике есть много способов сказать одно и то же:
Символ | Использованных слов |
|---|---|
+ | Сложение, Сложение, Сумма, Плюс, Увеличение, Итого |
— | Вычитание, Вычитание, Минус, Меньше, Разница, Уменьшение, Убрать, Вычесть |
× | Умножение, умножение, произведение, на, раз, партии из |
÷ | Деление, деление, частное, входит, сколько раз |
Дополнение есть.
 ..
..… объединение двух или более чисел (или вещей), чтобы получить новую сумму.
Суммируемые числа называются « слагаемых »:
Вычитание …
… отбирая одно число от другого.
Minuend — Subtrahend = Разница
Minuend : число, из которого нужно вычесть.
Subtrahend : Число, которое нужно вычесть.
Разница : результат вычитания одного числа из другого.
Умножение …
… (в простейшем виде) повторное сложение .
Здесь мы видим, что 6 + 6 + 6 (три шестерки) составляют 18:
Также можно сказать, что 3 + 3 + 3 + 3 + 3 + 3 (шесть троек) составляют 18
Но мы также можем умножать на дроби или десятичные дроби, что выходит за рамки простой идеи повторного сложения:
Пример: 3.5 × 5 = 17,5
, что составляет 3,5 лота из 5 или 5 лотов из 3,5
Подразделение…
… разделение на равные части или группы. Это результат «честного обмена».
Это результат «честного обмена».
Division есть свои особые слова, которые нужно запомнить.
Давайте возьмем простой вопрос: 22 разделить на 5 . Ответ: 4 , осталось 2 .
Здесь мы видим важные слова:
Что также может быть в этой форме:
Дробь равна…
… часть целого.
Верхняя часть (числитель) говорит , сколько деталей у нас .
В нижней части (знаменатель) указано , на сколько частей делится целое на .
Подробнее см. Дроби.
Десятичное число …
… число который содержит десятичную точку.
Подробнее см. Десятичные дроби.
Процент есть…
… частей на 100. Символ%
Пример: 25% означает 25 на 100 (25% этого поля — зеленое)
Подробнее см. Проценты.
Среднее (Среднее) составляет …
… сумма , деленная на количество .


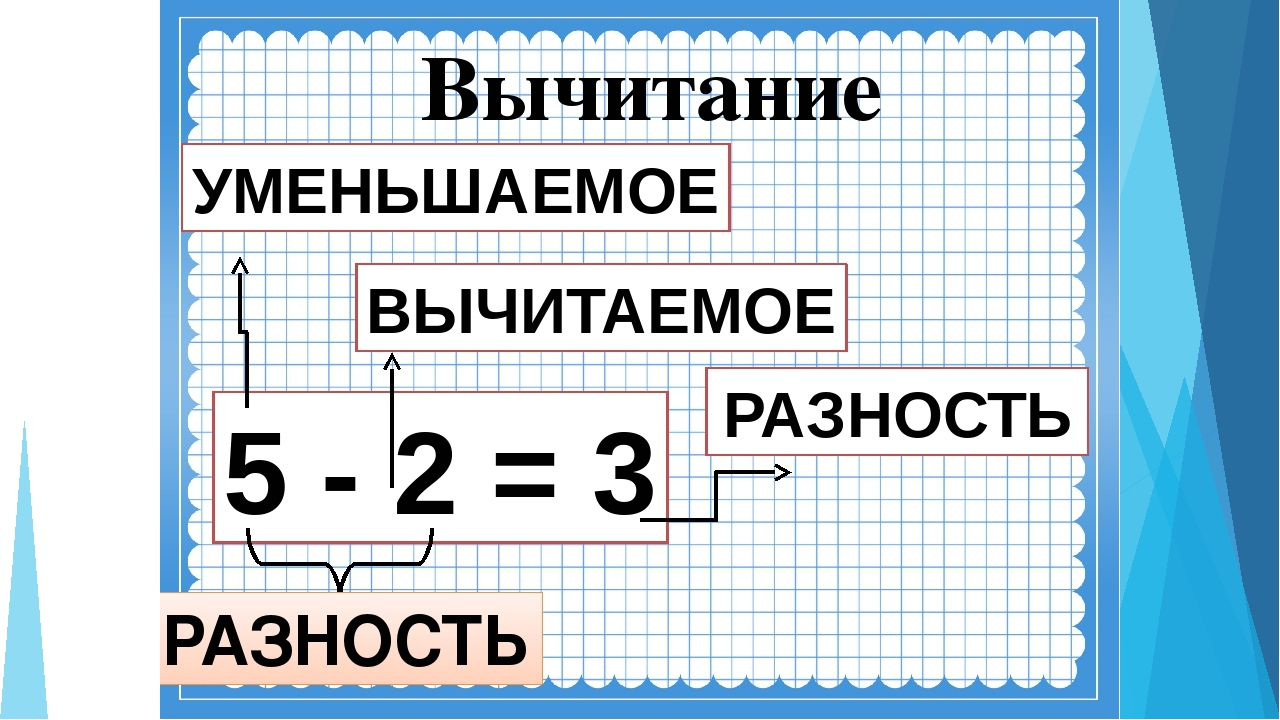 Откройте с. 62, № 2. Что известно в таблице? В первой строчке назовите уменьшаемое, вычитаемое. Что надо найти? Записать.
Откройте с. 62, № 2. Что известно в таблице? В первой строчке назовите уменьшаемое, вычитаемое. Что надо найти? Записать.

 )
)

 )
)

 )
)
 Как называется число, которое делим?
Как называется число, которое делим?
 )
)
 62, №1.
62, №1.
 )
)
 )
)
 )
)
 Сколько стоят часы?
Сколько стоят часы?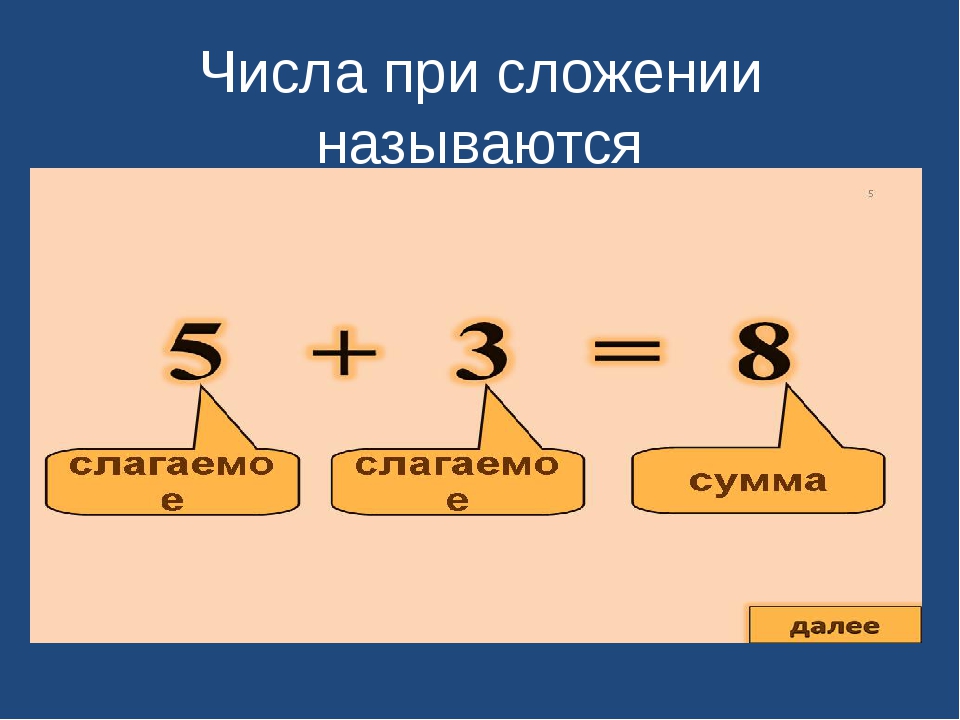 66 дюймов — 61 дюйм = 5 дюймов.
66 дюймов — 61 дюйм = 5 дюймов.
