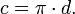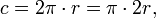Окружность длина окружности – ( )

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Основные определения и свойства

Фигура	Рисунок	Определения и свойства
Окружность		Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга		Часть окружности, расположенная между двумя точками окружности
Круг		Конечная часть плоскости, ограниченная окружностью
Сектор		Часть круга, ограниченная двумя радиусами
Сегмент		Часть круга, ограниченная хордой
Правильный многоугольник		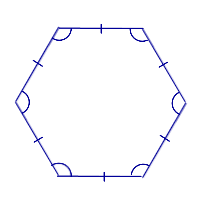Выпуклый многоугольник, у которого все стороны равны и все углы равны
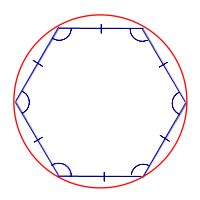		Около любого правильного многоугольника можно описать окружность

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Дуга

Часть окружности, расположенная между двумя точками окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Сектор

Часть круга, ограниченная двумя радиусами

Сегмент

Часть круга, ограниченная хордой

Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны Около любого правильного многоугольника можно описать окружность

      Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

      Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

      Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.

      Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.

      Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

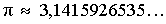
      Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.

Формулы для площади круга и его частей

Формулы для длины окружности и её дуг

Площадь круга

      Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный   n – угольник (рис. 1).

      Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.

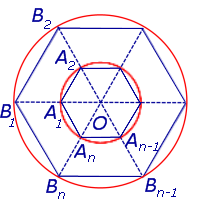
Рис.1

      Площадь правильного n – угольника, вписанного в окружность радиуса R, равна

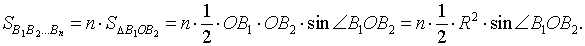
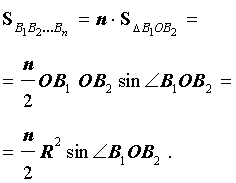
      Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна

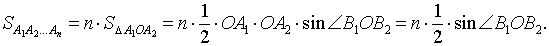
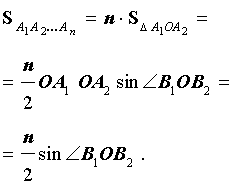
      Следовательно,

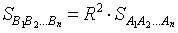
      Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу   πR².

      Таким образом, площадь круга радиуса R, обозначаемая S, равна

S = πR².

Длина окружности

      Рассмотрим правильный   n – угольник   B₁B₂…B_n , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).

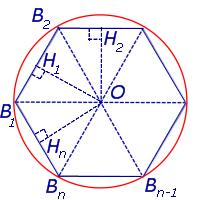
Рис.2

      Поскольку площадь n – угольника   B₁B₂…B_n   равна

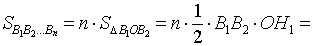
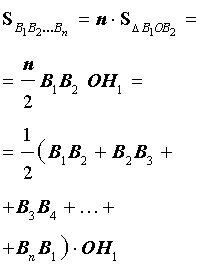
то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:

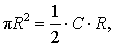
откуда вытекает формула для длины окружности радиуса R:

C = 2πR.

      Следствие. Длина окружности радиуса 1 равна   2π.

Длина дуги

      Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

Рис.3

      В случае, когда величина α выражена в градусах, справедлива пропорция

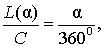
из которой вытекает равенство:

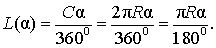
      В случае, когда величина α выражена в радианах, справедлива пропорция

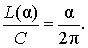
из которой вытекает равенство:

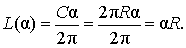
Площадь сектора

      Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

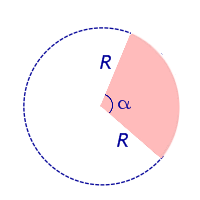
Рис.4

      В случае, когда величина α выражена в градусах, справедлива пропорция

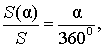
из которой вытекает равенство:

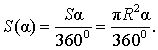
      В случае, когда величина α выражена в радианах, справедлива пропорция

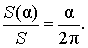
из которой вытекает равенство:

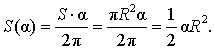
Площадь сегмента

      Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

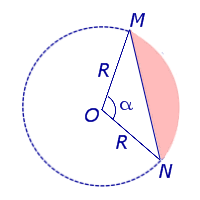
Рис.5

      Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем

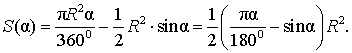
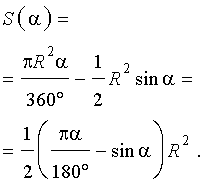
      Следовательно,

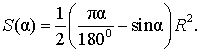
      В случае, когда величина α выражена в в радианах, получаем

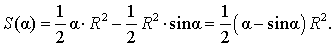
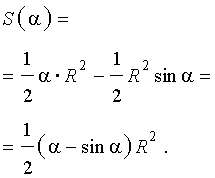
      Следовательно,

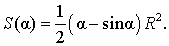
      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

www.resolventa.ru

Длина окружности. Площадь круга (Вольфсон Г.И.). Видеоурок. Математика 6 Класс

Как вы знаете, многие предметы имеют форму круга. Чем это обусловлено?

Возьмем, к примеру, колесо. Понятно, что круглое колесо катится гораздо лучше, чем, например, квадратное. Или, скажем, стакан круглой формы удобнее держать в руке, чем стакан прямоугольной формы. Поэтому в какой-то момент человечество стало использовать круглые предметы. Но если вы используете круглые предметы, нужно научиться их измерять. Например, вам нужно знать длину окружности стакана, чтобы понять, сколько материала пойдет на его изготовление, или вам нужно знать площадь колеса, чтобы, например, определять, какой должен быть объем исходных материалов, чтобы его сделать.

Поэтому сегодня мы обсудим, как же учились находить длину окружности и площадь круга, и решим некоторые задачи, связанные с этим.

Вначале вспомним, что такое окружность и круг.

Окружность – множество всех точек на плоскости, равноудаленных от данной точки.

Т. е. есть некоторая точка, мы задаем какое-то расстояние –

радиус окружности – и берем все точки, которые находятся от исходной на данном расстоянии (см. Рис. 1).

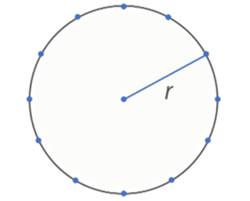
Рис. 1. Окружность

А теперь вспомним еще два важных понятия (см. Рис. 2).

Хордой называется такой отрезок, которые соединяет любые две точки, лежащие на окружности.

Диаметр – это такая хорда, которая проходит через центр окружности. Соответственно, как следствие, нетрудно догадаться, что диаметр равен двум радиусам.

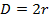
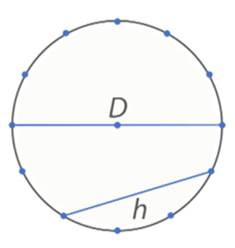
Рис. 2. Хорда и диаметр

Круг – это все точки на плоскости, которые лежат внутри окружности, а также сама окружность (см. Рис. 3).

Рис. 3. Круг

Теперь, когда мы вспомнили все важные определения, мы можем подумать, как же нам измерить длину окружности.

Один из способов, который был предложен, таков: возьмем, например, стакан, у которого дно будет круглой формы, и обмотаем нитку вокруг дна этого стакана. Теперь мы можем сделать засечку там, где конец нитки совпал с ее началом, затем размотать эту нитку и замерить ее длину линейкой. Естественно, измерение будет не совсем точным, оно будет зависеть от точности наших прикладываний, от точности линейки и т. п. Тем не менее мы примерно сможем измерить длину окружности (см. Рис. 4).

Рис. 4. Способ измерения длины окружности

Конечно же, чем дальше человечество продвигалось по своим научным взысканиям, тем более точно оно могло измерить эту самую длину окружности.

Еще в древности люди заметили, что если вы увеличите радиус окружности, например в два раза, то и длина этой окружности увеличится в два раза. Если уменьшить радиус в три раза, то и длина уменьшится в три раза. Иначе говоря: длина окружности и ее радиус пропорциональны друг другу. То есть их отношение – это постоянное число (см. Рис. 5).

Рис. 5. Иллюстрация пропорциональности длины окружности и радиуса

Так как отношение длины окружности к радиусу – постоянное число, то и отношение длины к диаметру – постоянное число.

Итак, пусть длина окружности 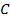, а диаметр окружности – 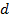. Так как отношение длины к диаметру всегда постоянное, то его можно примерно посчитать. Проделав это, вы примерно получите число  Так как число, которое равно отношению длины окружности к ее диаметру, не могли посчитать точно, его обозначили специальной буквой, буквой

 (буква греческого алфавита).

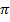
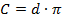
На самом деле сейчас, когда в использование вошли мощные компьютеры, можно посчитать и тысячу, и даже миллионы знаков после запятой у числа 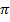. Это сделано, чтобы можно было более точно посчитать длину окружности. Для практических нужд нам достаточно знать первые несколько знаков: 3,14.

Кстати, есть специальные правила, которые позволяют запоминать число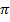

. Одно из правил – стихотворение:

Если очень постараться,

То запомнишь все как есть.

Три, четырнадцать, пятнадцать,

Девяносто два и шесть.

Есть и другое довольно забавное правило, которое тоже позволяет запомнить первые несколько знаков от числа .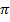

Это я знаю и помню прекрасно:

Пи многие знаки мне лишни, напрасны

 

Если посчитать количество букв в каждом слове, мы получим число 3,14159265358.

Таким образом, мы выписали еще более длинный ряд. На самом деле есть стихотворения еще более длинные, которые позволяют запоминать число π. Некоторые даже проводят соответствующее чемпионаты, есть, например, чемпионат мира по тому, кто больше запомнит знаков у числа π.

Вернемся к нашей теме.

Используя эту формулу, мы можем посчитать длину любой окружности практически точно, потому что диаметр мы можем просто измерить линейкой, и если мы умножим его число π, то мы получим длину. С другой стороны, число π мы знаем не совсем точно, но для наших приблизительных вычислений достаточно взять его с точностью до сотых или до тысячных, после чего, перемножив, получить искомое число длины. Не забывайте: если вы подставите вместо числа π, например, 3,14, или 3,1415, то длина у вас получится приблизительной, так что знак равенства в этом случае поставить не можем, а можем поставить лишь знак примерного равенства 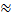. Если же вы хотите точное равенство, то оставляйте в ответе букву π, это и будет правильным ответом.

Рассмотрим конкретные примеры, на которых это работает.

Пример 1

Дана окружность с радиусом 2 сантиметра. Чему равна ее длина?

Решение:

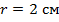
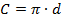
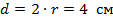
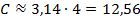
Ответ: 12,56 см.

Как видите, тут мы использовали знак приблизительного равенства.

 

Пример 2

Диаметр окружности равен 3 см, чему равна длина этой окружности?

Решение:

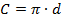
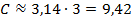
Ответ: 9,42 см.

Можно было записать ответ в виде: .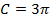

В этом случае мы можем поставить знак равенства, ведь значение абсолютно точное. Другой вопрос, что для практических целей оно не совсем удобно. Но так как математика – точная наука, то точным ответом будет .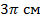

Между прочим, формулу 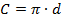 можно преобразовать. Если вспомнить, что диаметр – это удвоенный радиус, мы можем записать формулу в виде

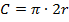
Или:

.

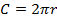Разберемся, как наши предки искали площадь круга. Есть один метод для вычисления приблизительной площади.

Рассмотрим круг, заметим, что площадь этого круга, меньше, чем площадь квадрата, который описывает этот круг. Причем площадь этого квадрата мы легко можем посчитать – это квадрат его стороны.

С другой стороны, мы можем немного приблизить нашу фигуру к кругу, если вырезать квадратные уголки со сторон вершин квадрата. Остается фигура, которая по площади ближе к кругу. Аналогичным образом мы можем продолжать до бесконечности (см. Рис. 6).

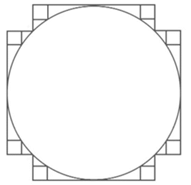
Рис. 6. Приблизительное вычисление площади круга

Естественно, что точно так же мы можем сделать, если мы нарисуем квадрат внутри круга, после чего добавим такие прямоугольники со всех сторон и т. д., пока мы сколь угодно близко не приблизимся к площади искомого круга (см. Рис. 7).

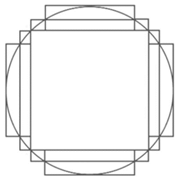
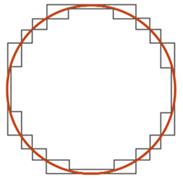
Рис. 7. Приблизительное вычисление площади круга

Площадь круга мы можем оценить как сверху (площадь круга будем меньше, чем площадь фигуры, которая описывает круг), так и снизу (площадь круга больше, чем площадь фигуры, вписанной в эту окружность). Соответственно, если прямоугольников, которыми мы измеряем, будет довольно много, то мы сможем приблизительно оценить площадь круга.

В девятом классе вы докажете формулу, что на самом деле площадь круга 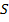 вычисляется так: .

Пример 1

Найдите площадь круга, если его радиус равен 1 см.

Решение:

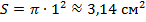
Можно записать отв

interneturok.ru

Формула длины окружности через радиус или диаметр

Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Диаметр окружности — отрезок, соединяющий две любые точки расположенные на линии окружности и проходящий через её центр. Диаметр, в два раза больше радиуса

---

r — радиус окружности

D — диаметр окружности

π ≈ 3.14

 

Формула длины окружности через радиус или диаметр, (L):

 

---

Калькулятор для расчета длины окружности через радиус

---

---

Калькулятор для расчета длины окружности через диаметр

---

 

S — площадь круга

O — центр круга

π ≈ 3.14

 

Формула длины окружности через площадь, (L):

 

---

Калькулятор для расчета длины окружности через площадь

---

 

Формулы для окружности и круга:

Подробности

Автор: Сергей Кондратов

Опубликовано: 07 сентября 2011

Обновлено: 09 октября 2017

www-formula.ru

Окружность. Длина окружности. Касательная, дуга

Общие определения

Окружность — это множество точек, которое располагается на одинаковом расстоянии от ее центра, представленного точкой.

Для любой точки L, лежащей на окружности, действует равенство OL=R. (Длина отрезка OL равняется радиусу окружности).

Отрезок, который соединяет две точки окружности, является ее хордой.

Хорда, проходящая прямо через центр окружности, является диаметром этой окружности (D). Диаметр можно вычислить по формуле: D=2R

Длина окружности вычисляется по формуле: C=2\pi R

Площадь круга: S=\pi R^{2}

Дугой окружности называется та ее часть, которая располагается между двух ее точек. Эти две точки и определяют две дуги окружности. Хорда CD стягивает две дуги: CMD и CLD. Одинаковые хорды стягивают одинаковые дуги.

Центральным углом называется такой угол, который находится между двух радиусов.

Длину дуги можно найти по формуле:

1. Используя градусную меру: CD = \frac{\pi R \alpha ^{\circ}}{180^{\circ}}
2. Используя радианную меру: CD = \alpha R

Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.

В случае, если хорды AB и CD окружности имеют пересечение в точке N, то произведения отрезков хорд, разделенные точкой N, равны между собой.

AN\cdot NB = CN \cdot ND

Касательная к окружности

Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.

Если же у прямой есть две общие точки, ее называют секущей.

Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.

Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.

AC = CB

Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть.

AC^{2} = CD \cdot BC

Можно сделать вывод: произведение целого отрезка первой секущей на его внешнюю часть равняется произведению целого отрезка второй секущей на его внешнюю часть.

AC \cdot BC = EC \cdot DC

Углы в окружности

Градусные меры центрального угла и дуги, на которую тот опирается, равны.

\angle COD = \cup CD = \alpha ^{\circ}

Вписанный угол — это угол, вершина которого находится на окружности, а стороны содержат хорды.

Вычислить его можно, узнав величину дуги, так как он равен половине этой дуги.

\angle AOB = 2 \angle ADB

Опирающийся на диаметр, вписанный угол, прямой.

\angle CBD = \angle CED = \angle CAD = 90^ {\circ}

Вписанные углы, которые опираются на одну дугу, тождественны.

\angle ADB = \angle AEB = \angle AFB

Опирающиеся на одну хорду вписанные углы тождественны или их сумма равняется 180^ {\circ}.

\angle ADB + \angle AKB = 180^ {\circ}

\angle ADB = \angle AEB = \angle AFB

На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.

Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.

\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left ( \cup DmC + \cup AlB \right )

Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.

\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left ( \cup DmC — \cup AlB \right )

Вписанная окружность

Вписанная окружность — это окружность, касающаяся сторон многоугольника.

В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.

Окружность может быть вписанной не в каждый многоугольник.

Площадь многоугольника с вписанной окружностью находится по формуле:

S = pr,

где:

p — полупериметр многоугольника,

r — радиус вписанной окружности.

Отсюда следует, что радиус вписанной окружности равен:

r = \frac{S}{p}

Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.

AB + DC = AD + BC

В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.

Радиус вписанной окружности вычисляется по формуле:

r = \frac{S}{p},

где p = \frac{a + b + c}{2}

Описанная окружность

Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника.

В точке пересечения серединных перпендикуляров сторон этой фигуры будет находиться центр описанной окружности.

Радиус можно найти, вычислив его как радиус окружности, которая описана около треугольника, определенного любыми 3-мя вершинами многоугольника.

Есть следующее условие: окружность возможно описать около четырехугольника только, если сумма его противоположных углов равна 180^{ \circ}.

\angle A + \angle C = \angle B + \angle D = 180^ {\circ}

Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.

Радиус описанной окружности можно вычислить по формулам:

R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}

R = \frac{abc}{4 S}

где:

a, b, c — длины сторон треугольника,

S — площадь треугольника.

Теорема Птолемея

Под конец, рассмотрим теорему Птолемея.

Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.

AC \cdot BD = AB \cdot CD + BC \cdot AD

academyege.ru

Формула расчета длины окружности

Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.

Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.

Определение длины окружности

 

 

Произвести расчёт окружности можно по следующей формуле:

L = πD = 2πr

 

r – радиус окружности

D – диаметр окружности

L – длина окружности

π – 3.14

Задача:

Вычислить длину окружности, имеющей радиус 10 сантиметров.

Решение:

Формула для вычисления дины окружности имеет вид:

L = πD = 2πr

где L – длина окружности, π – 3,14, r – радиус окружности, D – диаметр окружности.

Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:

L = 2 × 3,14 × 5 = 31,4 сантиметра

 

Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.

С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.

По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).

Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.

Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.

Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.

simple-math.ru

Длина окружности — это… Что такое Длина окружности?



Длина окружности

Длинна окружности = π × диаметр

Длина окружности — это длина закрытой кривой. Определение окружности в статье Окружность.

Длина окружности вычисляется из диаметра по формуле::

Или из половины диаметра, радиуса:

где r — это радиус, d — диаметр круга, а π (греческая буква пи), которая является математической постоянной, отношением длины окружности к ее диаметру (значение пи, первые цифры: 3.141 592 653 589 793).

Wikimedia Foundation. 2010.

• Длина Дебая
• Длина дебая

Смотреть что такое «Длина окружности» в других словарях:

• длина окружности резервуара — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN tank circumference …   Справочник технического переводчика

• длина окружности совокупность известных операций — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN circuit …   Справочник технического переводчика

• ДЛИНА — ДЛИНА, длины, мн. нет, жен. Протяжение линии, плоскости, тела в том направлении, в котором две крайние точки (линии, плоскости, тела) лежат на наибольшем расстоянии одна от другой. Предметы измеряются в длину, ширину и высоту. Длина стола. Меры… …   Толковый словарь Ушакова

• длина — ы/, только ед., ж. 1) Протяжение в том направлении, в котором две крайние точки линии, плоскости, тела лежат на наибольшем расстоянии друг от друга. Мера длины. Лыжи длиной в два метра. Измерить площадку в длину и в ширину. Синонимы: расстоя/ние… …   Популярный словарь русского языка

• Длина кривой — (или, что то же, длина дуги кривой) в метрическом пространстве числовая характеристика протяжённости этой кривой[1]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление). Если длина кривой… …   Википедия

• Длина шкалы — Расстояние между крайними отметками шкалы, отсчитанное по дуге окружности или по прямой линии, проходящей через середины наименьших отметок Источник: ГОСТ 2405 88: Манометры, вакуумметры, мановакуумметр …   Словарь-справочник терминов нормативно-технической документации

• Длина дуги — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… …   Википедия

• Длина дуги кривой — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… …   Википедия

• длина — 3.1 длина (length) l: Наибольший линейный размер лицевой грани измеряемого образца. Источник: ГОСТ Р ЕН 822 2008: Изделия теплоизоляционные, применяемые в строительстве. Методы измерения длины и ширины …   Словарь-справочник терминов нормативно-технической документации

• Длина —         числовая характеристика протяжённости линий. В разных случаях понятие Д. определяется различно. 1) Д. отрезка прямой расстояние между его концами, измеренное каким либо отрезком, принятым за единицу Д. 2) Д. ломаной сумма Д. её звеньев.… …   Большая советская энциклопедия

dic.academic.ru

Окружность и ее свойства. Длина окружности. :: SYL.ru

Окружность в математике является фигурой одной из самых главных и важных. Она необходима для множества расчетов. Знания свойств этой фигуры из школьной программы непременно пригодятся в жизни. Длина окружности требуется при расчете многих материалов с круглым сечением. Заниматься чертежами, строить заборчик возле клумбы – для этого понадобится знание геометрической фигуры и ее свойств.

Понятие окружности и ее основные элементы

Фигура на плоскости, состоящая из многочисленных точек, расположенных на равном расстоянии от центральной, называется окружностью. Отрезок, выходящий из центра и соединяющий его с одной из точек, образующих окружность, называется радиусом. Хордой является отрезок, который соединяет пару точек, расположенных по периметру круга, между собой. Если она расположена так, что проходит через центральную точку, то одновременно является диаметром.

Длина радиуса окружности равна длине диаметра, уменьшенной вдвое. Пара несовпадающих точек, находящихся на окружности, делят ее на две дуги. Если отрезок с концами в этих точках проходит через центральную точку (тем самым являясь диаметром), то образуемые дуги будут являться полуокружностями.

Длина окружности

Расчет периметра окружности определяется несколькими способами: через диаметр или через радиус. На практике было выявлено, что длина окружности (l) при делении на ее же диаметр (d) всегда дает одно число. Это число π, которое ровняется 3,141692666… Расчет производится по формуле: π= l/ d. Преобразуя ее, получается длина окружности. Формула такова: l=πd.

Для нахождения радиуса применим следующую формулу: d=2r. Это стало возможным, благодаря делению. Ведь радиус — это половина диаметра. Как только получили вышеуказанные значения, можно вычислить, чему же ровна длина окружности, по формуле следующего вида: l=2πr.

Основные свойства

Площадь круга всегда больше, если сравнивать ее с площадями иных замкнутых кривых. Касательная — это прямая, которая соприкасается с окружностью только в одной точке. Если прямая пересекает ее в двух местах, то она является секущей. Точка, в которой 2 различные окружности соприкасаются друг с другом, всегда находится на прямой, проходящей через их центральные точки. Пересекающимися на плоскости являются такие окружности, которые имеют 2 общие точки. Угол между ними рассчитывается как угол, образованный касательными к точкам соприкосновения.

Если через точку, не являющейся точкой окружности, провести две секущиеся к ней прямые, то образованный ими угол будет равен разности длин дуг, уменьшенной вдвое. Данное правило действует и в противоположном случае, когда речь идет о двух хордах. Две пересекающиеся хорды образуют угол, равный сумме длин дуг, уменьшенной в два раза. Дуги в такой ситуации выбирают в данном углу и углу, расположенному напротив. Оптическое свойство окружности гласит следующее: лучи света, отраженные от зеркал, расставленных по периметру круга, собираются обратно в его центр. В данном случае источник света должен быть установлен в центральной точке круга.

www.syl.ru

No related posts.