Определить заряд каждого конденсатора – Как найти напряжение и заряд на каждом из конденсаторов…

Формула заряда конденсатора, q

По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.

Формула заряда конденсатора

Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:

   

где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.

Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.

Заряд на пластинах плоского конденсатора равен:

   

где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.

Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:

   

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

Заряд на обкладках сферического конденсатора найдем как:

   

где – радиусы обкладок конденсатора.

Заряд конденсатора связан с энергией поля (W) внутри него:

   

Из формулы (6) следует, что заряд можно выразить как:

   

Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).

   

Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.

При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.

   

Примеры решения задач по теме «Заряд конденсатора»

ru.solverbook.com

Конденсаторы — задачи

 В задачах с присутствием конденсаторов очень часто нужно уметь находить емкость последовательного и параллельного соединения емкостей. С параллельным соединением емкостей все просто: при параллельном соединении емкости складываются. Почему это так? Дело в том, что при параллельном соединении на всех конденсаторах одинаковое напряжение, а их заряды пропорциональны емкостям:

 

и т.д.

 

Общий заряд на конденсаторах: 

 

Тогда емкость системы конденсаторов: .

 

С последовательным соединением все сложнее. Кстати, когда готовила эту статью, наткнулась на такой вот перл, который не могла не процитировать:

Заряды при последовательном соединении одинаковы на всех конденсаторах:

и т.д.

Тогда напряжение между крайними точками равно:

Емкость всей системы:  , или 

1. Разность потенциалов между точками А и В   В. Емкость конденсаторов соответственно равна  

мкФ и   мкФ. Определите заряды   и   и разности потенциалов   и    на обкладках первого и второго конденсаторов.

Задача 1

Определим общую емкость такого соединения: ,

 

мкФ (сразу считаем в микрофарадах, чтобы не расписывать степени десятки)

 

Тогда заряд равен:

 

мкКл.

 

Заряды при последовательном соединении на всех конденсаторах одинаковые, значит для первого:

 

, для второго .

 

Напряжения на конденсаторах:

 

В,   В.

 

Ответ: 18 мкКл, 6 В, 3 В.

2. Определите емкость батареи конденсаторов, изображенной на рисунке. Емкость каждого конденсатора  мкФ.

 

Задача 2

 

Емкости  и , поскольку они соединены параллельно, необходимо сложить:  мкФ. Тогда получим последовательное соединение трех одинаковых емкостей и , емкость которой вдвое больше. При последовательном соединении емкостей их эквивалентная емкость вычисляется по формуле: . Тогда получим: ,   мкФ.

 

Ответ: 286 нФ

3. Емкость батареи конденсаторов, образованной двумя последовательно включенными конденсаторами, 100 пФ, а заряд 20 нКл. Определите емкость второго конденсатора, а также разность потенциалов на обкладках каждого из них, если пФ.

Воспользуемся . Тогда  (считаем в пикофарадах)

 

Отсюда , ,  пФ.

 

При последовательном соединении заряд на конденсаторах равный:  нКл.

 

Напряжения также получатся одинаковыми:

 

В,   В.

 

Ответ: В,  нКл.

4. Наибольшая емкость конденсатора 60 мкФ. Какой заряд он накопит при подключении источника постоянного напряжения 60В?

Так как , то  мКл.

 

Ответ: 0,36 мКл

5. При введении в пространство между пластинами воздушного конденсатора твердого диэлектрика напряжение на конденсаторе уменьшилось с 400 до 100 В. Какова диэлектрическая проницаемость диэлектрика?

Рассмотрим сначала конденсатор до введения диэлектрика: ,  . Заряд остался тем же при введении  диэлектрика, а напряжение изменилось: .

Тогда  , или 

 

Емкость конденсатора, как известно, зависит от площади пластин и расстояния между ними, а также от диэлектрика:

 

 

В первом случае, без диэлектрика: , а во втором 

 

Найдем и в этом случае отношение емкостей:  , или 

 

Ответ:  Кл*Кл/Н*м*м

6. Площадь пластин конденсатора равна 520 см кв. На каком расстоянии нужно разместить пластины в воздухе, чтобы емкость конденсатора была равна 50 пФ?

Емкость конденсатора без диэлектрика:

 

 

Площадь нужно выразить в кв. метрах: 

 

Электрическая постоянная .

 

Выразим из первого выражения нужную нам величину:  м, или 9,2 мм.

 

Ответ: 9,2 мм

7. Конденсатору емкостью 20 мкФ сообщили заряд 5 мкКл. Какова энергия заряженного конденсатора?

Энергию электрического поля, накопленную конденсатором, можно вычислить по формуле:

 

– и в этой задаче как раз хорошо будет воспользоваться второй записью.

 

Тогда:  мкДж

8. Расстояние между пластинами плоского конденсатора с диэлектриком из бумаги, пропитанной парафином, равно 2 мм, а напряжение 200 В. Найти плотность энергии поля.

Чтобы найти плотность энергии, нужно сначала определить энергию поля, а потом посчитать, в каком объеме она сосредоточена.

 

, с другой стороны, емкость , тогда . Объем пространства между пластинами конденсатора – это произведение площади пластин на расстояние между ними:  . Тогда плотность энергии поля равна  

 

Посмотрим в справочнике, какова диэлектрическая проницаемость бумаги с парафином, выразим расстояние между пластинами в метрах, и подставим цифры:

 

мДж

easy-physic.ru

Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»

Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»

«Физика — 10 класс»

«Электроёмкость» — последняя тема раздела «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: закон сохранения электрического заряда, понятия напряжённости поля и потенциала, сведения о поведении проводников в электростатическом поле, о напряжённости поля в диэлектриках, о законе сохранения энергии применительно к электростатическим явлениям. Основной формулой при решении задач на электроёмкость является формула (14.22).

Задача 1.

Электроёмкость конденсатора, подключённого к источнику постоянного напряжения U = 1000 В, равна C₁ = 5 пФ. Расстояние между его обкладками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля.

Р е ш е н и е.

Согласно формуле (14.22) заряд конденсатора q = CU. Отсюда изменение заряда Δq — (С₂ — C)U = (nC₁ — C₁)U = (п — 1)С₁U = 10^-8 Кл.

Изменение энергии электрического поля

Задача 2.

Заряд конденсатора q = 3 • 10^-8 Кл. Ёмкость конденсатора С = 10 пФ. Определите скорость, которую приобретает электрон, пролетая в конденсаторе путь от одной пластины к другой. Начальная скорость электрона равна нулю. Удельный заряд электрона

Р е ш е н и е.

Начальная кинетическая энергия электрона равна нулю, а конечная равна Применим закон сохранения энергии где А — работа электрического поля конденсатора:

Следовательно,

Окончательно

Задача 3.

Четыре конденсатора ёмкостями С₁ = С₂ = = 1 мкФ, С₃ = 3 мкФ, С₄ = 2 мкФ соединены, как показано на рисунке 14.46. К точкам А и В подводится напряжение U = 140 В. Определите заряд q1 и напряжение U1, на каждом из конденсаторов.

Р е ш е н и е.

Для определения заряда и напряжения прежде всего найдём ёмкость батареи конденсаторов. Эквивалентная ёмкость второго и третьего конденсаторов С_2,3 = С₂ + С₃, а эквивалентную ёмкость всей батареи конденсаторов, представляющей собой три последовательно соединённых конденсатора ёмкостями С₁, С_2,3, С₄, найдём из соотношения

1/Cэкв = 1 /С₁ + 1/С_2,3 + 1 /С₄, Сэкв = (4/7) • 10^-6 Ф.

Заряды на этих конденсаторах одинаковы:

q₁ = q_2,3 = q₄ = Сэкв = 8 • 10^-5 Кл.

Следовательно, заряд первого конденсатора q₁ = 8 • 10^-5 Кл, а разность потенциалов между его обкладками, или напряжение, U₁ = q₁/С₁ = 80 В.

Для четвёртого конденсатора аналогично имеем q₄ = 8 • 10^-5 Кл, U₄ = q₄/C₄ = 40 В.

Найдём напряжение на втором и третьем конденсаторах: U₂ = U₃ = q_2,3/C_2,3 = 20 В.

Таким образом, на втором конденсаторе заряд q₂ = C₂U₂ = 2 • 10-5 Кл, а на третьем конденсаторе q₃ = C₃U₃ = 6 • 10^-5 Кл. Отметим, что q_2,3 = q₂ + g₃.

Задача 4.

Определите эквивалентную электрическую ёмкость в цепи, изображённой на рисунке (14.47 а), если ёмкости конденсаторов известны.

Р е ш е н и е.

Часто при решении задач, в которых требуется определить эквивалентную электрическую ёмкость, соединение конденсаторов не очевидно. В этом случае если удаётся определить точки цепи, в которых потенциалы равны, то можно соединить эти точки или исключить конденсаторы, присоединённые к этим точкам, так как они не могут накапливать заряд (Δφ = 0) и, следовательно, не играют роли при распределении зарядов.

В приведённой на рисунке (14.47, а) схеме нет очевидного параллельного или последовательного соединения конденсаторов, так как в общем случае φ_A ≠ φ_B в и к конденсаторам С1 и С2 приложены разные напряжения. Однако заметим, что в силу симметрии и равенства ёмкостей соответствующих конденсаторов потенциалы точек А и В равны. Следовательно, можно, например, соединить точки А и В. Схема преобразуется к виду, изображённому на рисунке (14.47, б). Тогда конденсаторы С1, так же как и конденсаторы С2, будут соединены параллельно и С_экв определим по формуле 1/С_экв = 1/2С₁ + 1/2С₂, откуда

Можно также просто не учитывать присутствие в схеме конденсатора СЗ, так как заряд на нём равен нулю. Тогда схема преобразуется к виду, изображённому на рисунке (14.47, в). Конденсаторы С1 и С2 соединены последовательно, следовательно,

Эквивалентные конденсаторы с С’_экв соединены параллельно, так что окончательно получим такое же выражение для эквивалентной ёмкости:

Задача 5.

Энергия плоского воздушного конденсатора W₁ = 2 • 10^-7 Дж. Определите энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью ε = 2, если:

1) конденсатор отключён от источника питания;

2) конденсатор подключён к источнику питания.

Р е ш е н и е.

1) Так как конденсатор отключён от источника питания, то его заряд q₀ остаётся постоянным. Энергия конденсатора до заполнения его диэлектриком после заполнения где С₂ = εС₁.

Тогда

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Электростатика — Физика, учебник для 10 класса — Класс!ная физика

Что такое электродинамика — Электрический заряд и элементарные частицы. Закон сохранения заряд — Закон Кулона. Единица электрического заряда — Примеры решения задач по теме «Закон Кулона» — Близкодействие и действие на расстоянии — Электрическое поле — Напряжённость электрического поля. Силовые линии — Поле точечного заряда и заряженного шара. Принцип суперпозиции полей — Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» — Проводники в электростатическом поле — Диэлектрики в электростатическом поле — Потенциальная энергия заряженного тела в однородном электростатическом поле — Потенциал электростатического поля и разность потенциалов — Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности — Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» — Электроёмкость. Единицы электроёмкости. Конденсатор — Энергия заряженного конденсатора. Применение конденсаторов — Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»

class-fizika.ru

Заряд и разряд конденсатора. Определить заряд и напряжение каждого конденсатора

Пр. 1. конденсаторы

ПРАКТИЧАСКАЯ РАБОТА №1

«Расчет эквивалентной емкости при смешанном соединении конденсаторов, а также распределения зарядов и напряжений»

На рисунке 1 дана схема соединения конденсаторов. Значение емкостей конденсаторов и значение одного из напряжений или зарядов для своего варианта взять из таблицы 1.

Вычислить эквивалентную емкость батареи конденсаторов; напряжение сети, напряжение на каждом конденсаторе; общий заряд и заряд на каждом конденсаторе; энергию, накопленную батареей, а также потенциал заданной точки.

Рисунок 1

Таблица 1

№ вар.	Емкость конденсатора, мкФ						Напряжение, заряд		Точка, потенциал которой следует вычислить
	С1	С2	С3	С4	С5
1	120	280	16	80	70	U=20 В		Б
2	600	200	150	400	200	Q3=72∙10-4 Кл		Б
3	24	12	2	16	14	U5=25 В		А
4	30	20	12	20	16	Q4=4∙10-4 Кл		Б
5	10	15	24	6	9	U1=15 В		А
6	12	6	5	9	9	Q2=282∙10-6 Кл		А
7	30	15	10	65	15	Q5=6∙10-4 Кл		А
8	18	9	12	15	21	U2=84 В		Б
9	140	60	6	30	18	U3=50 В		А
10	150	50	37,5	30	20	Q1=3∙10-4 Кл		Б
11	200	300	40	160	100	U=40 В		Б
12	540	150	90	380	120	Q3=54∙10-4 Кл		А
13	46	26	8	34	28	U5=45 В		Б
14	60	45	25	40	30	Q4=8∙10-4 Кл		А
15	30	25	46	20	18	U1=30 В		Б
16	25	15	10	20	15	Q2=564∙10-6 Кл		Б
17	60	30	45	120

xn—-7sbeb3bupph.xn--p1ai

Заряд конденсатора, теория и примеры задач

Определение и заряд конденсатора

Возможность конденсатора накопить электрический заряд зависит от главной характеристики конденсатора – емкости (C).

По своему назначению конденсатор можно уподобить батарейке. Однако существует принципиальное отличие в принципах работы этих элементов. Отличаются, также максимальные емкости и скорости зарядки и разряда конденсатора и батарейки.

Если к конденсатору присоединить источник напряжения (рис.1), то на одной из пластин конденсатора станут накапливаться отрицательные заряды (электроны), на другой положительные частицы (положительные ионы). Между обкладками конденсатора находится диэлектрик, вследствие этого, заряды не могут перебраться на противоположную пластину. Однако заметим, что электроны двигаются от источника тока до пластины конденсатора.

При первоначальном соединении конденсатора и источника тока на обкладках конденсатора много свободного места. Это означает, что сопротивление току этот момент времени минимально, сам ток максимален. В ходе зарядки конденсатора сила тока в цепи постепенно падает, до того момента пока не закончится свободное место на обкладках. При полной зарядке конденсатора ток в цепи прекратится.

Время, которое затрачивается на зарядку конденсатора от нулевого заряда (максимального тока) до полностью заряженного конденсатора (минимальная или нулевая сила тока) называют переходным периодом заряда конденсатора. На практике процесс зарядки конденсатора считают законченным, если сила тока уменьшилась до 1% от начальной величины.

Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:

   

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Пример решения задачи на определение заряда батареи конденсаторов

Конденсаторы соединены в батарею по схеме изображенной на рисунке. Определить какой заряд необходимо сообщить батарее, чтобы зарядить ее до напряжения 500 Вольт. Емкость конденсаторов: С₁=4×10^-6 Ф; С₂=6×10^-6 Ф; С₃=8×10^-6 Ф; С₄=12×10^-6 Ф.

Дано: С₁=4×10^-6 Ф; С₂=6×10^-6 Ф; С₃=8×10^-6 Ф; С₄=12×10^-6 Ф; U=500 В
Найти: q — ?

Решение:

Емкость батареи конденсаторов определим из соотношения , откуда

Заряд батареи конденсаторов определим по формуле , тогда

Кл

Ответ: батареи конденсаторов необходимо сообщить заряд 1,235×10^-3 Кулон

Поделитесь с друзьями:

zadachi-po-fizike.electrichelp.ru

Электроемкость. Конденсатор . Видеоурок. Физика 10 Класс

На этом уроке мы начнем изучение нового прибора – конденсатора – и новой физической величины – электроемкости. Исходя из опытов, мы рассмотрим количественную неодинаковость электризации разных тел одинаковыми зарядами, познакомимся с прибором для накопления зарядов и его основными характеристиками.

Тема: Основы электродинамики
Урок: Электроёмкость. Конденсаторы

На предыдущих уроках мы знакомились с элементарными электрическими понятиями и принципами, в частности, мы говорили об электризации – явлении перераспределения заряда. Разговор о более глубоком исследовании этого явления начнем с опыта.

Изначально пусть нам даны две разные по размеру изолированные банки, подключенные к электроскопу (рис. 1):

Рис. 1

Теперь к каждой из банок поднесли одинаково заряженное тело. Естественно, с каждой банкой произойдет процесс электризации, и стрелки обоих электроскопов разойдутся. Однако оказалось, что электроскоп большей банки показал меньшее отклонение (рис. 2):

Рис. 2

Данный опыт доказывает, что различные тела электризуются одним и тем же зарядом по-разному (конкретно большая банка одним и тем же зарядом зарядилась до меньшего потенциала). И существует некоторая величина, которая показывает способность тела накапливать электрический заряд. Собственно, о ней и пойдет речь.

Определение. Электроемкость (емкость) – величина, равная отношению заряда переданного проводнику к потенциалу этого проводника.

Здесь:  – емкость;  – переданный заряд;  – потенциал, до которого зарядился проводник.

Теперь непосредственно познакомимся со специализированными приборами для накопления зарядов.

Определение. Конденсатор – набор проводников, служащий для накопления электрического заряда. Конденсаторы состоят из двух проводников и разделяющего их диэлектрика, причем толщина диэлектрического слоя много меньше размеров проводников (рис. 3).

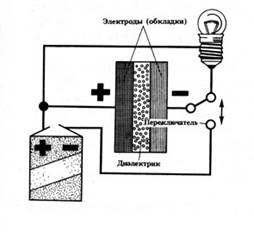
Рис. 3. Схематическое изображение конденсатора (Источник)

Особое внимание мы будем уделять так называемым плоским конденсаторам (слой диэлектрика расположен между двумя плоскими пластинами проводника). На электрической схеме конденсатор обозначается следующим образом (рис. 4): 

Рис. 4. Условное обозначение конденсатора на электрической схеме

Емкость конденсатора определяется так же, как и любая другая электроемкость, однако с небольшим отличием (так как речь идет о системе проводников, а не о отдельно взятом проводнике, в формуле фигурирует не потенциал, а разность потенциалов или напряжение)

Здесь: &n

interneturok.ru