Параллелепипед — Википедия
Материал из Википедии — свободной энциклопедии
Параллелепи́пед (др.-греч. παραλληλ-επίπεδον[1] от др.-греч. παρ-άλληλος — «параллельный» и др.-греч. ἐπί-πεδον — «плоскость») — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них — параллелограмм.
Прямоугольный параллелепипедРазличается несколько типов параллелепипедов:
- Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
- Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани прямоугольники.
- Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
- Ромбоэдр — параллелепипед, грани которого являются равными ромбами.
- Куб — параллелепипед, грани которого являются квадратами.
Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.
- Параллелепипед симметричен относительно середины его диагонали.
- Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
- Противолежащие грани параллелепипеда параллельны и равны.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Прямой параллелепипед[править | править код]
Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота
Площадь полной поверхности Sп=Sб+2S о, где Sо — площадь основания
Объём V=Sо*h
Прямоугольный параллелепипед[править | править код]
Площадь боковой поверхности Sб=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда
Площадь полной поверхности Sп=2(ab+bc+ac)
Объём V=abc, где a, b, c — измерения прямоугольного параллелепипеда.
Куб[править | править код]
Площадь поверхности: S=6a2{\displaystyle S=6a^{2}}
Объём: V=a3{\displaystyle V=a^{3}}, где a{\displaystyle a} — ребро куба.
Произвольный параллелепипед[править | править код]
Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры. Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения[2]:215.
В математическом анализе под n-мерным прямоугольным параллелепипедом B{\displaystyle B} понимают множество точек x=(x1,…,xn){\displaystyle x=(x_{1},\ldots ,x_{n})} вида B={x|a1⩽x1⩽b1,…,an⩽xn⩽bn}{\displaystyle B=\{x|a_{1}\leqslant x_{1}\leqslant b_{1},\ldots ,a_{n}\leqslant x_{n}\leqslant b_{n}\}}
ru.wikipedia.org
Прямоугольный параллелепипед. Видеоурок. Геометрия 10 Класс
На этом уроке все желающие смогут изучить тему «Прямоугольный параллелепипед». В начале урока мы повторим, что такое произвольный и прямой параллелепипеды, вспомним свойства их противоположных граней и диагоналей параллелепипеда. Затем рассмотрим, что такое прямоугольный параллелепипед, и обсудим его основные свойства.
Тема: Перпендикулярность прямых и плоскостей
Урок: Прямоугольный параллелепипед
Поверхность, составленная из двух равных параллелограммов АВСD и А1В1С1D1 и четырех параллелограммов АВВ1А1, ВСС1В1, СDD1С1, DАА1D1, называется параллелепипедом (рис. 1).
Рис. 1 Параллелепипед
То есть: имеем два равных параллелограмма АВСD и А1В1С1D1 (основания), они лежат в параллельных плоскостях так, что боковые ребра АА1, ВВ1, DD1, СС1 параллельны. Таким образом, составленная из параллелограммов поверхность называется параллелепипедом.
Таким образом, поверхность параллелепипеда — это сумма всех параллелограммов, из которых составлен параллелепипед.
1. Противоположные грани параллелепипеда параллельны и равны.
(фигуры равны, то есть их можно совместить наложением)
Например:
АВСD = А1В1С1D1 (равные параллелограммы по определению),
АА1В1В = DD1С1С (так как АА1В1В и DD1С1С – противоположные грани параллелепипеда),
АА1D1D = ВВ1С1С (так как АА1D1D и ВВ1С1С – противоположные грани параллелепипеда).
2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Диагонали параллелепипеда АС1, В1D, А1С, D1В пересекаются в одной точке О, и каждая диагональ делится этой точкой пополам (рис. 2).
Рис. 2 Диагонали параллелепипеда пересекаются и деляться точкой пересечения пополам.
3. Имеются три четверки равных и параллельных ребер параллелепипеда: 1 – АВ, А1В1, D1C1, DC, 2 – AD, A1D1, B1C1, BC, 3 – АА1, ВВ1, СС1, DD1.
Определение. Параллелепипед называется прямым, если его боковые ребра перпендикулярны основаниям.
Пусть боковое ребро АА1 перпендикулярно основанию (рис. 3). Это означает, что прямая АА1 перпендикулярна прямым АD и АВ, которые лежат в плоскости основания. А, значит, в боковых гранях лежат прямоугольники. А в основаниях лежат произвольные параллелограммы. Обозначим, ∠BAD = φ, угол φ может быть любым.
Рис. 3 Прямой параллелепипед
Итак, прямой параллелепипед — это параллелепипед, в котором боковые ребра перпендикулярны основаниям параллелепипеда.
Определение. Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию. Основания являются прямоугольниками.
Параллелепип
interneturok.ru
Прямоугольный параллелепипед — Википедия
Материал из Википедии — свободной энциклопедии
Прямоугольный параллелепипедПрямоуго́льный параллелепи́пед (кубоид) — многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником.
Противолежащие грани параллелепипеда равны. Рёбра параллелепипеда, сходящиеся в одной вершине взаимно перпендикулярны.
Примерами тел, имеющих форму прямоугольного параллелепипеда служат классная комната, кирпич, спичечный коробок или системный блок компьютера.
Длины трёх рёбер прямоугольного параллелепипеда, принадлежащих одной вершине, иногда называют измерениями. Например, распространённый спичечный коробок имеет измерения 15, 35, 50 мм.
Правильным или квадратным параллелепипедом называют параллелепипед, у которого два измерения равны, у такого параллелепипеда две противолежащие грани представляют собой квадраты.
Объём прямоугольного параллелепипеда можно найти по формуле:
- V=abc,{\displaystyle V=abc,}
где a,b,c{\displaystyle a,b,c} — его измерения.
Квадрат длины диагонали d{\displaystyle d} прямоугольного параллелепипеда равен сумме квадратов трёх его измерений:
- d2=a2+b2+c2,{\displaystyle d^{2}=a^{2}+b^{2}+c^{2},}
соответственно, длина диагонали равна:
- d=a2+b2+c2.{\displaystyle d={\sqrt {a^{2}+b^{2}+c^{2}}}.}
Площадь поверхности прямоугольного параллелепипеда равна
- S=2(ab+bc+ac).{\displaystyle S=2(ab+bc+ac).}
Прямоугольный параллелепипед с равными измерениями называется кубом. Все шесть граней куба — равные квадраты.
ru.wikipedia.org
Параллелепипед, куб. Площади поверхностей. Объём
Напомним, что призма, в основании которой лежит параллелограмм, называется параллелепипедом.
Стороны параллелограммов называются рёбрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра.
Например, грани и – противолежащие.
Грани, имеющие общее ребро, называются смежными. Например, грани и – смежные, ребро у них общее.
Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, – его боковыми рёбрами.
В нашем случае у параллелепипеда грани и – его основания. Остальные же грани являются боковыми гранями.
Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий, противолежащие вершины, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.
Объединение боковых граней называется боковой поверхностью параллелепипеда, а объединение всех граней называется полной поверхностью параллелепипеда. Тогда площадью боковой поверхности параллелепипеда называется сумма площадей его боковых граней.
А площадью полной поверхности параллелепипеда называется сумма площадей всех его граней.
Параллелепипед обладает следующими свойствами:
1. Противолежащие грани параллелепипеда равны и лежат в параллельных плоскостях.
2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Объём параллелепипеда равен произведению площади основания на высоту.
Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Куб – это прямоугольный параллелепипед, все рёбра которого равны, то есть все грани которого – равные квадраты.
Диагональ куба с ребром равна .
Объём куба равен , где – ребро куба.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача первая. В основании прямого параллелепипеда лежит параллелограмм с основаниями см и см и острым углом . Боковое ребро параллелепипеда равно см. Найдите площадь полной поверхности параллелепипеда.
Решение.
Задача вторая. Все грани параллелепипеда – ромбы с диагоналями см и см. Найдите площадь полной поверхности параллелепипеда.
Решение.
Задача
третья. Найдите меньшую диагональ прямого параллелепипеда
высотой см
со сторонами основания см
и см
и углом между ними .
Решение.
Задача четвёртая. В прямоугольном параллелепипеде ребро см, см. Найдите расстояние между диагональю параллелепипеда и ребром .
Решение.
Задача пятая. Две стороны основания параллелепипеда равны см и см, угол между ними . Боковое ребро равно см и наклонено к основанию под углом . Найдите объём параллелепипеда.
Решение.
Задача шестая. Все грани параллелепипеда – ромбы с периметром равным и острым углом . Найдите объём параллелепипеда. В ответ запишите значение .
Решение.
videouroki.net
5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде
Видеоурок 1: Параллелепипед
Видеоурок 2: Прямоугольный параллелепипед
Лекция: Параллелепипед; куб; симметрии в кубе, в параллелепипеде
Параллелепипед
Основной тип объемной фигуры мы выучили. Однако в зависимости от вида многоугольника, который лежит в основании, призма может видоизменяться.
Призма, в основании которой лежит параллелограмм, называется параллелепипедом.
Все, что мы изучали ранее о призме, можно использовать и при изучении параллелепипеда.
Параллелепипед имеет 6 граней, две из которых являются основаниями. У параллелепипеда все противолежащие грани равны между собой.
Параллелепипеды могут быть прямоугольными (те, у которых угол между всеми соседними ребрами прямой), а так же наклонными (те, у которых угол между соседними ребрами отличается от прямого).
Любой параллелепипед имеет вершины. Вершинами параллелепипеда являются вершины соответствующих граней.
В качестве оснований призмы можно выбрать любые параллельные грани.
Если грани параллелепипеда имеют одно общее ребро, то они называются смежными, если же таковых не имеется, то грани противоположные.
Любой отрезок, который соединяет вершины противоположных граней, называется диагональю этой призмы.
Любые три ребра, которые имеют общую вершину, называются характеристиками параллелепипеда, то есть являются его длиной, шириной и высотой.
Свойства:
- Какой бы параллелепипед Вы не построили бы, он должен иметь симметрию относительно любой диагонали данной фигуры.
- Если построить несколько диагоналей, то они пересекутся в точке, которая поделит их на две равные части.
- Любые две грани, которые лежат друг против друга, имеют одинаковую длину, и обязательно параллельны.
- Сумма квадратов длины, ширины и высоты равна квадрату диагонали.
Формулы полной поверхности и объема прямоугольного параллелепипеда:
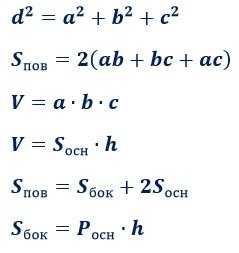
Куб
Частным случаем параллелепипеда является куб. С ним все намного проще: куб – это параллелепипед, у которого все грани являются квадратами. Причем все соседние ребра перпендикулярные друг другу.
Все свойства, которые изучались для призмы и для параллелепипеда, справедливы и для куба.
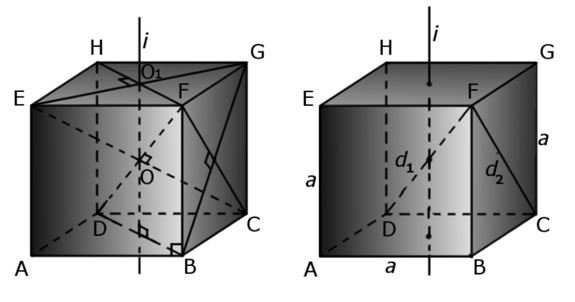
У куба все грани являются правильными четырехугольниками, которые лежат под углом 90 градусов друг к другу. При этом стоит помнить, что для того, чтобы найти площадь одной грани, необходимо воспользоваться формулой площади квадрата S = a2. Мы знаем, что куб состоит из 6 граней, а это значит, что для нахождения площади поверхности куба, достаточно просто площадь одной грани умножить на 6. Sобщ = 6a2
Если некоторый отрезок проходит через центр куба (место, где пересекаются все диагонали куба), через центры параллельных граней, то он будет называться осью данного куба.
С легкостью можно найти диагональ куба. Для этого достаточно воспользоваться формулой:
Объем куба можно определить по известной длине стороны или же по диагоналям:
Если провести сечение через диагонали, через центр куба, или же просто взять его ось или диагонали, то куб всегда будет симметричен относительно всего перечисленного.
cknow.ru
Параллелепипед [wiki.eduVdom.com]
Призма называется параллелепипедом, если её основания — параллелограммы. См.Рис.1.
Рис.1
Свойства параллелепипеда:
Противоположные грани параллелепипеда параллельны (т.е. лежат в параллельных плоскостях) и равны.
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Параллелепипед является многогранником.
Смежные грани параллелепипеда – две грани, имеющие общее ребро.
Противоположные грани параллелепипеда – грани, не имеющих общих рёбер.
Противоположные вершины параллелепипеда – две вершины, не принадлежащие одной грани.
Диагональ параллелепипеда – отрезок, который соединяет противоположные вершины.
Если боковые ребра перпендикулярны плоскостям оснований, то параллелепипед называется прямым.
Прямой параллелепипед, основания которого – прямоугольники, называется прямоугольным. Призма, все грани которой — квадраты, называется кубом.
Параллелепипед – призма, у которой основаниями служат параллелограммы.
Прямой параллелепипед – параллелепипед, у которого боковые ребра перпендикулярны плоскости основания.
Прямоугольный параллелепипед – это прямой параллелепипед, основаниями которого являются прямоугольники.
Куб – прямоугольный параллелепипед с равными ребрами.
Параллелепипедом называется призма, основание которой – параллелограмм; таким образом, параллелепипед имеет шесть граней и все они — параллелограммы.
Противоположные грани попарно равны и параллельны. Параллелепипед имеет четыре диагонали; все они пересекаются в одной точке и делятся в ней пополам. За основание может быть принята любая грань; объем равен произведению площади основания на высоту: V = Sh.
Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым.
Прямой параллелепипед, у которого все шесть граней — прямоугольники, называется прямоугольным.
См.
Рис.2
Объем (V) прямого параллелепипеда равен произведению площади основания (S) на высоту (h): V = Sh .
Для прямоугольного параллелепипеда, кроме того, имеет место формула V=abc , где a,b,c — ребра.
Диагональ (d) прямоугольного параллелепипеда связана с его ребрами соотношением d2 = а2 + b2 + c2 .
Прямоугольный параллелепипед – параллелепипед, у которого боковые рёбра перпендикулярны основаниям, а основания прямоугольниками.
Свойства прямоугольного параллелепипеда:
В прямоугольном параллелепипеде все шесть граней – прямоугольники.
Все двугранные углы прямоугольного параллелепипеда прямые.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений (длин трёх рёбер, имеющих общую вершину).
Диагонали прямоугольного параллелепипеда равны.
Прямоугольный параллелепипед, все грани которого — квадраты, называется кубом. Все ребра куба равны; объем (V) куба выражается формулой V=a3, где a — ребро куба.
Пример №1
Пример №2
wiki.eduvdom.com
Прямоугольный параллелепипед — урок. Математика, 5 класс.

Вокруг нас мы часто встречаем предметы, имеющие форму коробки.
Они могут быть сделаны из разного материала и окрашены в разные цвета, но по форме они напоминают друг друга: коробки, шкафы, здания и т. п.
Все эти предметы напоминают геометрическое тело — прямоугольный параллелепипед.
Поверхность его состоит из \(6\) прямоугольников, которые называются гранями прямоугольного параллелепипеда.
Две грани называются противоположными, если у них нет общего ребра. Каждые две противолежащие грани равны.
Грани можно назвать в зависимости от того, как мы видим прямоугольный параллелепипед:
та грань, которая обращена к нам, называется передней;
точно такая же грань имеется сзади — это задняя грань;
боковые грани также являются равными прямоугольниками;
та грань, которая находится сверху, называется верхней;
а грань, на которой фигура стоит, называется нижней, или основанием, и эти две грани равны.
Стороны граней называются рёбрами, а вершины граней — вершинами параллелепипеда.
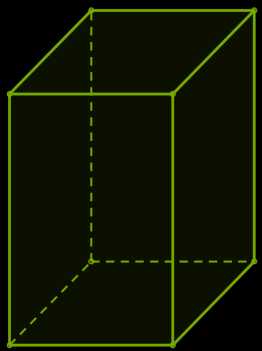
У прямоугольного параллелепипеда всего \(6\) граней (передняя, задняя, нижняя, верхняя и две боковые), \(12\) рёбер и \(8\) вершин.
Рёбра, которые имеют общую вершину, называют измерениями прямоугольного параллелепипеда (на нижнем рисунке — красные рёбра).

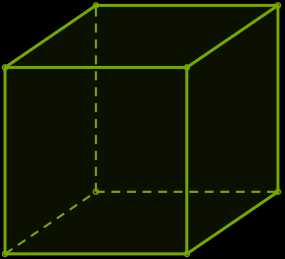
Куб — это прямоугольный параллелепипед, у которого все измерения равны, то есть поверхность куба состоит из \(6\) равных квадратов.
www.yaklass.ru

