Параллельное или последовательное соединение: Последовательное и параллельное соединение

Последовательное и параллельное соединение

В данной статье речь пойдет о последовательном и параллельном соединении проводников. На примерах будут рассмотрены данные соединения и как при таких соединениях будут изменяться такие величины как:

• ток;
• напряжение;
• сопротивление.

В таблице 1.8 [Л2, с.24] приведены схемы и формулы по определению сопротивлений, токов и напряжений при параллельном и последовательном соединении.

Последовательное соединение

Последовательным соединением называются те участки цепи, по которым всегда проходят одинаковые токи.

При последовательном соединении:

• сила тока во всех проводниках одинакова;
• напряжение на всём соединении равно сумме напряжений на отдельных проводниках;
• сопротивление всего соединения равно сумме сопротивлений отдельных проводников.

Пример 1

Последовательно подключены две лампы накаливания одинаковой мощности Рл1=Рл2=100 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляет Rл1=Rл2=122 Ом. Номинальное напряжение для ламп равно 220 B. На рис.1 показано последовательное включение ламп.

Решение

Составляем схему замещения, выражая каждую из входящих элементов цепи (в данном случае лампы накаливания) в виде сопротивлений.

1. Определяем ток протекающей по участкам цепи:

Iн = Uн/Rл1+ Rл2 = 220/122+122 = 0,9 A

2. Определяем напряжение на каждой из ламп накаливания, так как мощность ламп у нас одинаковая, то и напряжение для каждой из ламп будет одинаково:

Uл1=Uл2 = Iн*R = 0,9*122 = 110 B

Как мы видим напряжение источника (в данном примере 220 В) разделиться поровну, между обоими последовательно включенными лампами. При этом лампы будут ели светит, их накал будет неполным.

Для того чтобы лампы горели с полным накалом, нужно увеличить напряжение источника с 220В до 440В, при этом на каждой из ламп установиться номинальное (рабочее) напряжение равное 220В.

Пример 2

Последовательно подключены две лампы накаливания мощность Рл1 = 100 Вт и Рл2 = 75 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляют Rл1= 122 Ом для стоваттной лампы и Rл2= 153 Ом для семидесяти пяти ватной лампы.

Решение

1. Определяем ток протекающей по участкам цепи:

Iн = Uн/Rл1+ Rл2 = 220/100+75 = 0,8 A

2. Определяем напряжение на каждой из ламп накаливания:

Uл1= Iн*Rл1 = 0,8*122 = 98 B
Uл2= Iн*Rл2 = 0,8*153 = 122 B

Исходя из результатов расчетов, более мощная лампа 100 Вт получает при этом меньшее напряжение. Но ток в двух последовательно включенных даже разных лампах остается одинаковым. Например, если одна из ламп перегорит (порвется ее нить накаливания), погаснут обе лампы.

Данное соединение лампочек, например, используется в трамвайном вагоне для освещения салона.

Параллельное соединение

Параллельное соединение – это соединение, при котором начала всех проводников присоединяются к одной точке цепи, а их концы к другой.

Точки цепи, к которым сходится несколько проводов, называют узлами. Участки цепи, соединяющие между собой узлы, называют ветвями.

При параллельном соединении:

• напряжение на всех проводниках одинаково;
• сила тока в месте соединения проводников равна сумме токов в отдельных проводниках;
• величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.

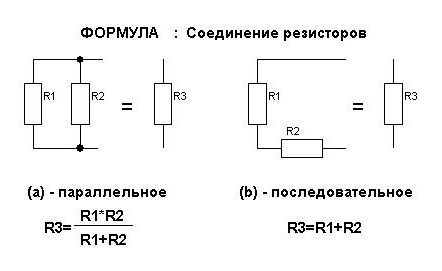
Пример 3

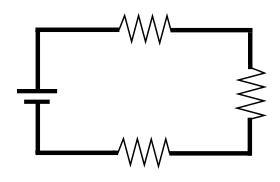
Определить токи и напряжения всех участков цепи (рис.5), если известно:

• Номинальное напряжение сети Uн = 220В;
• Сопротивление нити в лампах HL1 и HL2 составляют Rл1 = Rл2 = 122 Ом.
• Сопротивление нити в лампе HL3 составляют Rл3 = 153 Ом.

Решение

Составляем схему замещения для схемы, представленной на рис.5.

1. Определяем проводимость всей цепи [Л1, с.47] и согласно таблицы 1.8:

2. Определяем сопротивление всей цепи [Л1, с.47]:

3. Определяем силу тока цепи по закону Ома:

4. Определяем токи для каждой цепи [Л1, с.47]:

5. Выполним проверку, согласно которой, сила тока в месте соединения проводников равна сумме токов в отдельных проводниках:

Iл1+ Iл2+ Iл3=Iобщ.=1,8+1,8+1,44=5,04=5,04 (условие выполняется)

Смешанное соединение

Смешанным соединением – называется последовательно-параллельное соединение сопротивлений или участков цепи.

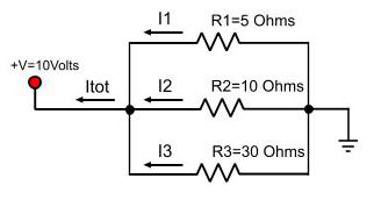
Пример 4

Определить токи и напряжения всех участков цепи (рис.7), если известно:

• Номинальное напряжение сети Uн = 220В;
• Сопротивление нити в лампах HL1, HL2, HL3 составляют Rл1 = Rл2 = Rл3 = 122 Ом.
• Сопротивление нити в лампе HL4 составляют Rл4 = 153 Ом.
• Результаты расчетов для участка цепи ВС (параллельное соединение проводников) применим из примера 3:
  Сопротивление цепи ВС составляет Rвс = 43,668 Ом.

Решение

Составляем схему замещения для схемы, представленной на рис.7.

1. Определяем сопротивление всей цепи:

Rобщ = Rав+Rвс = Rл1+Rвс = 122+43,688 = 165,688 Ом

2. Определяем силу тока цепи, согласно закона Ома:

3. Определяем напряжение на первом сопротивлении:

Uав=Uл1= Iобщ*Rл1 = 1,33*122 = 162 B

4. Определяем напряжение на участке ВС:

Uвс= Iобщ*Rвс = 1,33*43,688 = 58,1 B

5. Определяем токи для каждой цепи участка ВС:

6. Выполним проверку для участка цепи ВС:

Iл2+ Iл3+ Iл4= Iобщ.=0,48+0,48+0,38=1,33=1,33 (условие выполняется)

Литература:

1. Общая электротехника с основами электроники, В.С. Попов, 1972 г.
2. Справочная книга электрика. В.И. Григорьева. 2004 г.

Последовательное и параллельное соединение — Википедия

Материал из Википедии — свободной энциклопедии

Последовательное соединение проводников. Параллельное соединение проводников.

Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.

При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.

При параллельном соединении падение напряжения между двумя узлами

, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включённых проводников.

Последовательное соединение

При последовательном соединении проводников сила тока в любых частях цепи одна и та же: I = I 1 = I 2 = ⋯ = I n {\displaystyle I\mathrm {=} I_{1}=I_{2}=\cdots =I_{n}} (так как сила тока определяется количеством электронов, проходящим через поперечное сечение проводника, и если в цепи нет узлов, то все электроны в ней будут течь по одному проводнику).

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника питания, равно сумме напряжений на отдельных участках цепи: U = U 1 + U 2 + ⋯ + U n {\displaystyle U\mathrm {=} U_{1}+U_{2}+\cdots +U_{n}} .

Резисторы

R = R 1 + R 2 + ⋯ + R n {\displaystyle R=R_{1}+R_{2}+\cdots +R_{n}}

Катушка индуктивности

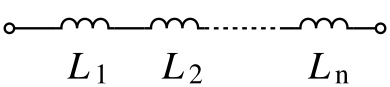
L = L 1 + L 2 + ⋯ + L n {\displaystyle L=L_{1}+L_{2}+\cdots +L_{n}}

Электрический конденсатор

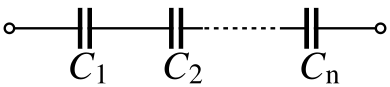
1 C = 1 C 1 + 1 C 2 + ⋯ + 1 C n {\displaystyle {\frac {1}{C}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}+\cdots +{\frac {1}{C_{n}}}} .

Мемристоры

M = M 1 + M 2 + ⋯ + M n {\displaystyle M=M_{1}+M_{2}+\cdots +M_{n}}

Выключатели

Цепь замкнута, когда замкнуты все выключатели. Цепь разомкнута, когда разомкнут хотя бы один выключатель. (См.также Логическая операция И).

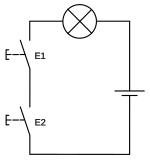
Параллельное соединение

Сила тока в неразветвлённой части цепи равна сумме сил тока в отдельных параллельно соединённых проводниках: I = I 1 + I 2 + ⋯ + I n {\displaystyle I\mathrm {=} I_{1}+I_{2}+\cdots +I_{n}}

Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же: U = U 1 = U 2 = ⋯ = U n {\displaystyle U\mathrm {=} U_{1}=U_{2}=\cdots =U_{n}}

Резисторы

При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость 1 R {\displaystyle {\frac {1}{R}}} складывается из проводимостей каждого резистора 1 R i {\displaystyle {\frac {1}{R_{i}}}} )

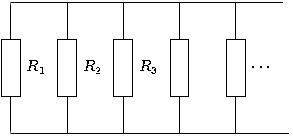
Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее (искомое) сопротивление.

Доказательство

Для двух параллельно соединённых резисторов их общее сопротивление равно: R = R 1 R 2 R 1 + R 2 {\displaystyle R={\frac {R_{1}R_{2}}{R_{1}+R_{2}}}} .

Если R 1 = R 2 = R 3 = . . . = R n {\displaystyle R_{1}=R_{2}=R_{3}=…=R_{n}} , то общее сопротивление равно: R = R 1 n {\displaystyle R={\frac {R_{1}}{n}}} .

При параллельном соединении резисторов их общее сопротивление будет меньше наименьшего из сопротивлений.

Катушка индуктивности

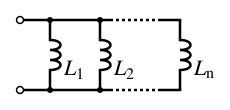
1 L t o t a l = 1 L 1 + 1 L 2 + ⋯ + 1 L n {\displaystyle {\frac {1}{L_{\mathrm {total} }}}={\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}}

Электрический конденсатор

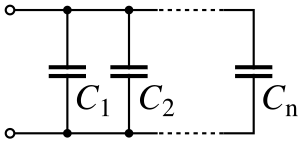
C t o t a l = C 1 + C 2 + ⋯ + C n {\displaystyle C_{\mathrm {total} }=C_{1}+C_{2}+\cdots +C_{n}} .

Мемристоры

M t o t a l = M 1 ‖ M 2 ‖ ⋯ ‖ M n = ( M 1 − 1 + M 2 − 1 + ⋯ + M n − 1 ) − 1 {\displaystyle M_{total}=M_{1}\|M_{2}\|\cdots \|M_{n}=\left(M_{1}^{-1}+M_{2}^{-1}+\cdots +M_{n}^{-1}\right)^{-1}}

Выключатели

Цепь замкнута, когда замкнут хотя бы один из выключателей.

Примеры использования

• Батареи гальванических элементов или аккумуляторов, в которых отдельные химические источники тока соединены последовательно (для увеличения напряжения) или параллельно (для увеличения тока).
• Регулировка мощности электрического устройства, состоящего из нескольких одинаковых потребителей электроэнергии, путём их переключения с параллельного на последовательное соединение. Таким способом регулируется мощность конфорки электрической плиты, состоящей из нескольких спиралей; мощность (скорость движения) электровоза, имеющего несколько тяговых двигателей.
• Делитель напряжения
• Балласт
• Шунт

См. также

Литература

• Перышкин А. В. Учебник для общеобразовательных учреждений 10 класс. М.: 2011. С.121
• Перышкин А. В. Учебник для общеобразовательных учреждений 8 класс № 42

Ссылки

Последовательное и параллельное соединение резисторов.

Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.

Последовательное соединение резисторов.

Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:

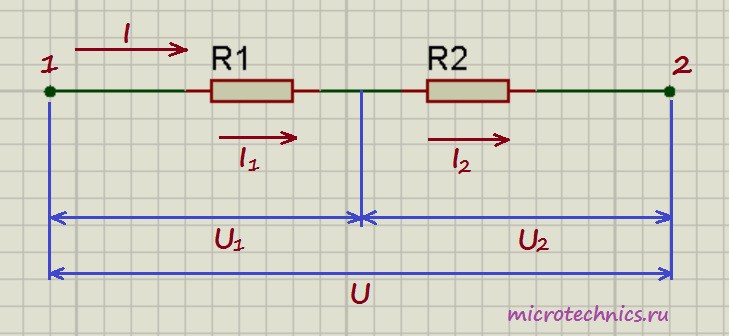
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:

I = I_1 = I_2

А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:

U = U_1 + U_2

В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:

U_1 = I_1R_1 = IR_1

U_2 = I_2R_2 = IR_2

Тогда для вычисления общего напряжения можно будет использовать следующее выражение:

U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)

Но для общего напряжение также справедлив закон Ома:

U = IR_0

Здесь R_0 – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:

R_0 = R_1 + R_2

Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.

Например для следующей цепи:

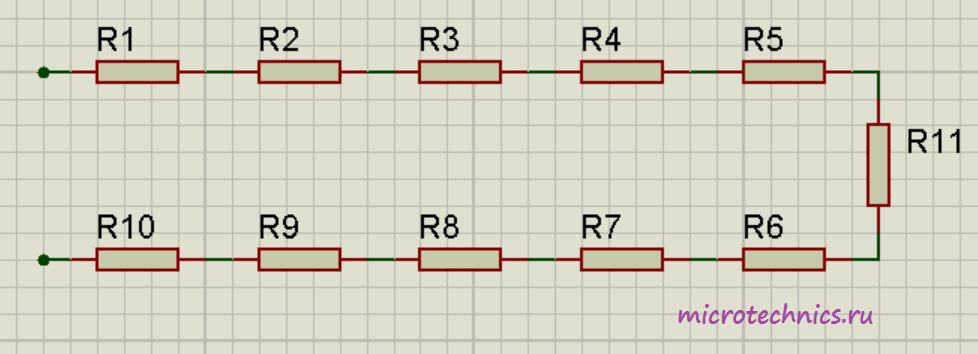
Общее сопротивление будет равно:

R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_{10}

Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном  соединении все сопротивления равны (R_1 = R_2 = … = R), то общее сопротивление цепи составит:

R_0 = nR

В данной формуле n равно количеству элементов цепи. С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.

Параллельное соединение резисторов.

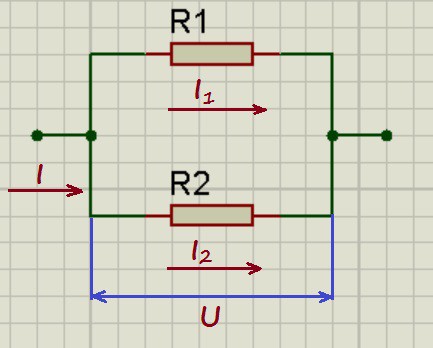
При параллельном соединении напряжения на проводниках равны:

U_1 = U_2 = U

А для токов справедливо следующее выражение:

I = I_1 + I_2

То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:

I_1 = \frac{U_1}{R_1} = \frac{U}{R_1}

I_2 = \frac{U_2}{R_2} = \frac{U}{R_2}

Подставим эти выражения в формулу общего тока:

I = \frac{U}{R_1} + \frac{U}{R_2} = U\medspace (\frac{1}{R1} + \frac{1}{R2})

А по закону Ома ток:

I = \frac{U}{R_0}

Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:

\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2}

Данную формулу можно записать и несколько иначе:

R_0 = \frac{R_1R_2}{R_1 + R_2}

Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:

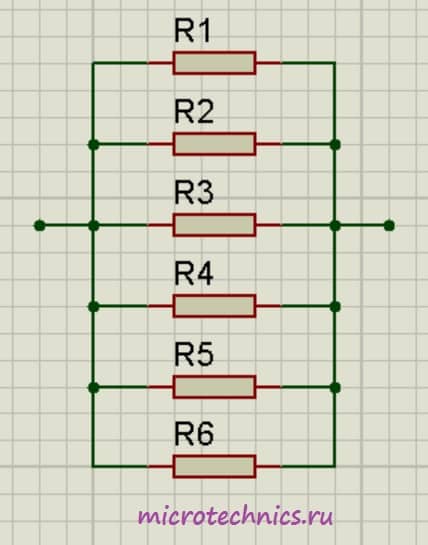
\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_5} + \frac{1}{R_6}

Смешанное соединение резисторов.

Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:

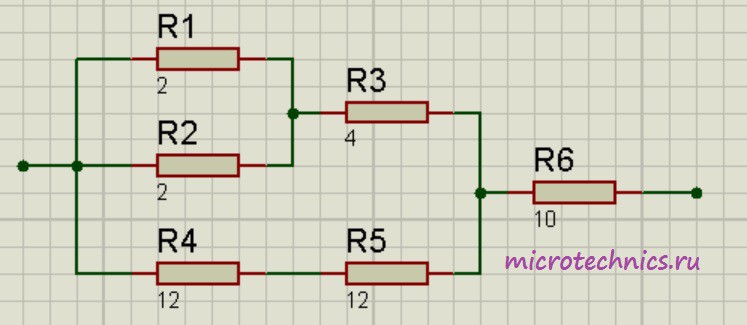
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов R_1 и R_2 – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_{1-2}:

R_{1-2} = \frac{R1\cdot R2}{R1 + R2} = 1

Теперь у нас образовались две группы последовательно соединенных резисторов:

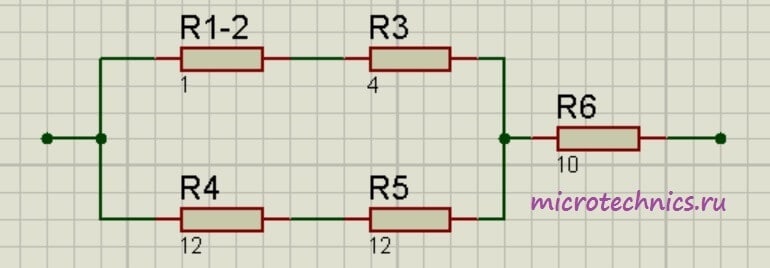
Заменим эти две группы двумя резисторами, сопротивление которых равно:

R_{1-2-3} = R_{1-2} + R_3 = 5

R_{4-5} = R_4 + R_5 = 24

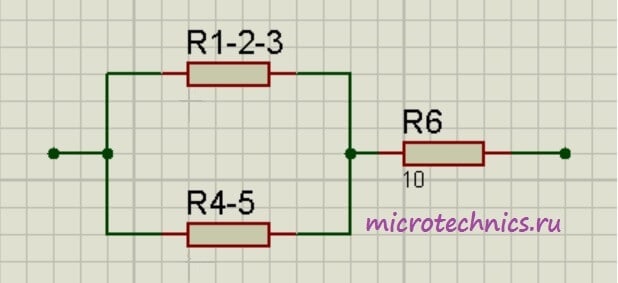
Как видите, схема стала уже совсем простой 🙂 Заменим группу параллельно соединенных резисторов R_{1-2-3} и R_{4-5}  одним резистором R_{1-2-3-4-5}:

R_{1-2-3-4-5}\enspace = \frac{R_{1-2-3}\medspace\cdot R_{4-5}}{R_{1-2-3} + R_{4-5}} = \frac{5\cdot24}{5 + 24} = 4.14

И в итоге у нас на схеме осталось только два резистора соединенных последовательно:

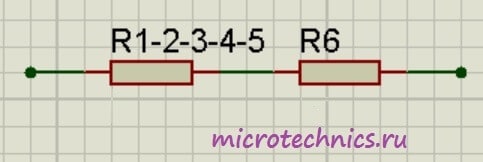
Общее сопротивление цепи получилось равным:

R_0 = R_{1-2-3-4-5}\medspace +\medspace R_6 = 4.14 + 10 = 14.14

Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов!

Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!

Параллельное и последовательное соединение. Последовательное и параллельное соединения проводников

В физике изучается тема про параллельное и последовательное соединение, причем это могут быть не только проводники, но и конденсаторы. Здесь важно не запутаться в том, как выглядит каждое из них на схеме. А уже потом применять конкретные формулы. Их, кстати, нужно помнить наизусть.

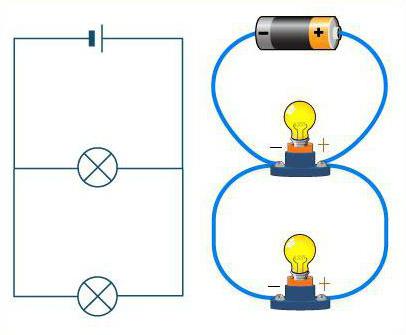
Как различить эти два соединения?

Внимательно посмотрите на схему. Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.

Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.

Формулы для силы тока

О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину силы тока в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.

Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:

I _общ = I ₁ = I ₂

Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.

Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при параллельном соединении проводников:

I _общ = I ₁ + I ₂

Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.

Формулы для напряжения

Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе. Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.

Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:

U _общ = U ₁ + U ₂, где U — обозначение, принятое для электрического напряжения.

Другая ситуация складывается, если рассматривается параллельное соединение резисторов. Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек. Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:

U _общ = U ₁ = U ₂

Формулы для электрического сопротивления

Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления. То есть U = I * R, где R — сопротивление.

Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:

• последовательно, значит, нужно равенство для напряжения — I_общ * R_общ = I₁ * R₁ + I₂ * R_2;
• параллельно необходимо пользоваться формулой для силы тока — U_общ / R_общ = U₁ / R₁ + U₂ / R₂ .

Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны. Значит, их можно сократить. То есть получаются такие выражения:

1. R _общ = R ₁ + R ₂ (для последовательного соединения проводников).
2. 1 / R _общ = 1 / R ₁ + 1 / R ₂ (при параллельном соединении).

При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.

Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.

Работа тока

Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу. Она записывается так: А = I * U * t, где А — работа тока, t — время его прохождения по проводнику.

Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U ₁ + U ₂) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.

Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А ₁ + А ₂.

Мощность тока

При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I. После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р ₁ + Р ₂.

То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.

Как влияет соединение проводников на ремонт новогодней гирлянды?

Сразу же после того, как перегорит одна из лампочек, станет ясно, как они были соединены. При последовательном соединении не будет светиться ни одна из них. Это объясняется тем, что пришедшая в негодность лампа создает разрыв в цепи. Поэтому нужно проверить все, чтобы определить, какая перегорела, заменить ее — и гирлянда станет работать.

Если в ней используется параллельное соединение, то она не перестает работать при неисправности одной из лампочек. Ведь цепь не будет полностью разорвана, а только одна параллельная часть. Чтобы отремонтировать такую гирлянду, не нужно проверять все элементы цепи, а только те, которые не светятся.

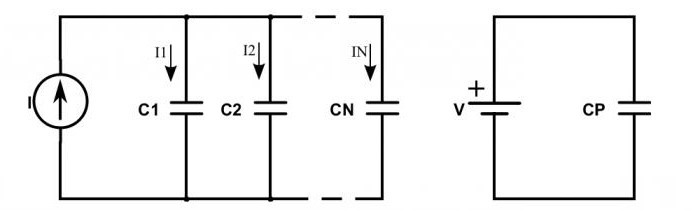
Что происходит с цепью, если в нее включены не резисторы, а конденсаторы?

При их последовательном соединении наблюдается такая ситуация: заряды от плюсов источника питания поступают только на внешние обкладки крайних конденсаторов. Те, что находятся между ними, просто передают этот заряд по цепочке. Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:

q _общ = q ₁ = q ₂.

Для того чтобы определить напряжение на каждом конденсаторе, потребуется знание формулы: U = q / С. В ней С — емкость конденсатора.

Общее напряжение подчиняется тому же закону, который справедлив для резисторов. Поэтому, заменив в формуле емкости напряжение на сумму, мы получим, что общую емкость приборов нужно вычислять по формуле:

С = q / (U ₁ + U ₂).

Упростить эту формулу можно, перевернув дроби и заменив отношение напряжения к заряду емкостью. Получается такое равенство: 1 / С = 1 / С ₁ + 1 / С ₂.

Несколько по-другому выглядит ситуация, когда соединение конденсаторов — параллельное. Тогда общий заряд определяется суммой всех зарядов, которые накапливаются на обкладках всех приборов. А значение напряжения по-прежнему определяется по общим законам. Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:

С = (q 1 + q 2 ) / U.

То есть эта величина считается, как сумма каждого из использованных в соединении приборов:

С = С ₁ + С _2.

Как определить общее сопротивление произвольного соединения проводников?

То есть такого, в котором последовательные участки сменяют параллельные, и наоборот. Для них по-прежнему справедливы все описанные законы. Только применять их нужно поэтапно.

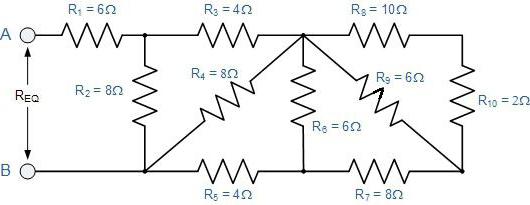
Сперва полагается мысленно развернуть схему. Если представить ее сложно, то нужно нарисовать то, что получается. Объяснение станет понятнее, если рассмотреть его на конкретном примере (см. рисунок).

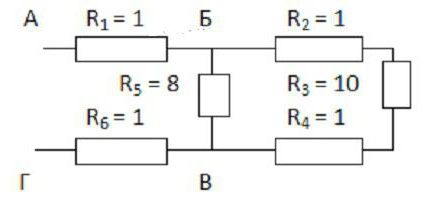
Ее удобно начать рисовать с точек Б и В. Их необходимо поставить на некотором удалении друг от друга и от краев листа. Слева к точке Б подходит один провод, а вправо направлены уже два. Точка В, напротив, слева имеет два ответвления, а после нее расположен один провод.

Теперь необходимо заполнить пространство между этими точками. По верхнему проводу нужно расположить три резистора с коэффициентами 2, 3 и 4, а снизу пойдет тот, у которого индекс равен 5. Первые три соединены последовательно. С пятым резистором они параллельны.

Оставшиеся два резистора (первый и шестой) включены последовательно с рассмотренным участком БВ. Поэтому рисунок можно просто дополнить двумя прямоугольниками по обе стороны от выбранных точек. Осталось применить формулы для расчета сопротивления:

• сначала ту, которая приведена для последовательного соединения;
• потом для параллельного;
• и снова для последовательного.

Подобным образом можно развернуть любую, даже очень сложную схему.

Задача на последовательное соединение проводников

Условие. В цепи друг за другом подсоединены две лампы и резистор. Общее напряжение равно 110 В, а сила тока 12 А. Чему равно сопротивление резистора, если каждая лампа рассчитана на напряжение в 40 В?

Решение. Поскольку рассматривается последовательное соединение, формулы его законов известны. Нужно только правильно их применить. Начать с того, чтобы выяснить значение напряжения, которое приходится на резистор. Для этого из общего нужно вычесть два раза напряжение одной лампы. Получается 30 В.

Теперь, когда известны две величины, U и I (вторая из них дана в условии, так как общий ток равен току в каждом последовательном потребителе), можно сосчитать сопротивление резистора по закону Ома. Оно оказывается равным 2,5 Ом.

Ответ. Сопротивление резистора равно 2,5 Ом.

Условие. Имеются три конденсатора с емкостями 20, 25 и 30 мкФ. Определите их общую емкость при последовательном и параллельном соединении.

Решение. Проще начать с параллельного подключения. В этой ситуации все три значения нужно просто сложить. Таким образом, общая емкость оказывается равной 75 мкФ.

Несколько сложнее расчеты будут при последовательном соединении этих конденсаторов. Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.

Ответ. Общая емкость при последовательном соединении 8 мкФ, при параллельном — 75 мкФ.

Последовательное и параллельное соединение источников питания |

Что такое источник питания

Источник питания – это специальное устройство, которое может генерировать ЭДС. К источникам питания постоянного тока можно отнести аккумуляторы, батарейки, различные генераторы постоянного тока (лабораторный блок питания), элементы Пельтье и тд. То есть это все те устройства, которые создают ЭДС.

Источник питания на примере гидравлики

Давайте рассмотрим водобашню, в которой есть автоматическая подача воды. То есть сколько бы мы не потребляли воды из башни, ее уровень воды будет неизменным.

Схематически это будет выглядеть вот так:

Башню с автоматической подачей воды можно считать источником питания. В химических же источниках питания происходит разряд, что ведет к тому, что уровень напряжения понижается при длительной работе. А что такое напряжение по аналогии с гидравликой? Это тот же самый уровень воды)

Давайте отпилим у водобашни верхнюю часть для наглядности. У нас получится цилиндр, который заполнен водой. Возьмем за точку отсчета уровень земли. Пусть он у нас будет равняться нулю.

Теперь вопрос на засыпку. В каком случае давление на дно будет больше? Когда в башне немного воды

либо когда башня полностью залита водой так, что даже вода выходит за ее края

Разумеется, когда башня наполнена только наполовину водой, на дне башни давление меньше, чем тогда, когда в башне воды под завязку.

Думаю, не надо объяснять, что если в башне вообще нет воды, то никакого давления на дне башни не будет.

 

По тому же самому принципу работает батарейка или аккумулятор

На электрических схемах ее обозначение выглядит примерно вот так:

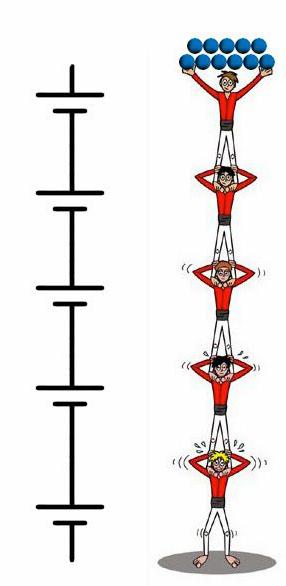
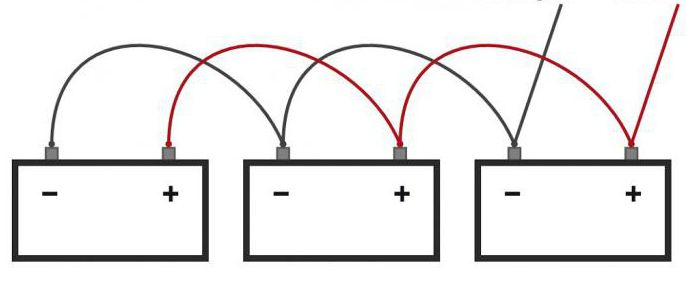
Также, чтобы получить необходимое напряжение, одноэлементные источники питания соединяют последовательно. На схеме это выглядит вот так:

Любой аккумулятор или источник постоянного тока имеет два полюса: “плюс” и “минус”. Минус – это уровень земли, как в нашем примере с водобашней, а плюс – это напряжение, по аналогии с гидравликой это и будет тот самый уровень воды.

Последовательное соединение источников питания

Теперь давайте представим вот такую ситуацию. Что будет, если в нашей обрезанной водобашне полной воды добавим еще одну такую же сверху полную воды? Схематически это будет выглядеть примерно вот так:

Как вы думаете, уменьшится давление на землю, или увеличится? Понятное дело, что увеличится! Да еще и ровно в два раза! Почему так произошло? Уровень воды стал выше, следовательно, давление на дно увеличилось.

Если “минус” одной батарейки соединить с “плюсом” другой батарейки, то их общее напряжение суммируется.

Полностью заряженная батарейка будет выглядеть как башня, полностью залитая водой с учетом того, что работает насос автоматической подачи воды. По аналогии, насос – это ЭДС.

Наполовину разряженная батарейка будет уже выглядеть примерно вот так:

Можно сказать, насос уже не справляется.

Батарейка посаженная в “ноль” будет выглядеть вот так:

Насос автоматической подачи воды сломался.

Естественно, что если вы соедините полностью заряженную и наполовину дохлую батарейку последовательно, то их общее напряжение будет выглядеть примерно вот так:

Давайте все это продемонстрируем на практике. Итак, у нас есть 2 литий-ионных аккумулятора. Я их пометил цифрами 1 и 2. С плюса каждого аккумулятора я вывел красный провод, а с минуса – черный.

Давайте замеряем напряжение аккумулятора под №1 с помощью мультиметра. Как это сделать, я еще писал в статье Как измерить ток и напряжение мультиметром.

На первом аккумуляторе у нас напряжение 3,66 Вольт. Это типичное значение литий-ионного аккумулятора.

Таким же способом замеряем напряжение на аккумуляторе №2

О, как совпало). Те же самые 3,66 Вольт.

Для того, чтобы соединить последовательно эти аккумуляторы, нам надо сделать что-то подобное:

Также как и в башнях, нам надо соединить основание одной башни с верхушкой другой башни. В источниках питания, типа аккумуляторов или батареек, нам надо соединить минус одной батарейки с плюсом другой. Так мы и сделаем. Соединяем плюс одной батарейки с минусом другой и получаем… сумму напряжений каждой батарейки! Как вы помните, на первой батарейке у нас было напряжение 3,66 В, на второй тоже 3,66 В. 3,66+3,6=7,32 В.

Мультиметр показывает 7,33 В. 0,01В спишем на погрешность измерений.

Это свойство прокатывает не только с двумя аккумуляторами, но также с их бесконечным множеством. Думаю, не стоит говорить, что если выставить в ряд штук 100 таких аккумуляторов, соединить последовательно и коснуться крайних полюсов голыми руками, то все это может завершиться даже летальным исходом.

Параллельное соединение источников питания

Но что будет, если источники питания соединить параллельно? Давайте же рассмотрим это с точки зрения той же самой гидравлики. Имеем те же самые башни, в которых воды до самых краев:

Нет, здесь мы не будет извращаться. Мы просто соединим наши башни у самого основания трубой:

Давление на дно у каждой башни изменится? Думаю, нет. Оно останется таким же, как в одной из башен. А что поменялось? Поменялся просто объем воды. Ее стало в 2 раза больше.

Но вы можете сказать, что в первом случае у нас тоже воды стало в 2 раза больше!

Да, все оно так, но здесь важное значение имеет именно то, что давление на дно башни изменилось и стало также в два раза больше. Если сделать врезку одинакового диаметра прямо у подножия водобашни, то  в случае, когда водобашни стоят одна на другой сила потока воды будет в два раза быстрее, чем если бы мы делали точно такую же врезку на картинке, где мы соединяли водобашни трубой. Более подробно эту мысль я еще озвучивал в статье про Закон Ома.

Если всю эту мысль спроецировать на наши источники питания, то получается, что при последовательном соединении у нас суммировалась напряжение, а при параллельном должна суммироваться сила тока. Но это не значит, что нагрузка, которая кушала, к примеру, 1 Ампер, после того, как мы ее цепанем к двум параллельным источникам питания, будет кушать 2 Ампера. При параллельном соединении у нас напряжение остается таким же, а вот емкость батарей увеличивается. Но нагрузка все равно будет кушать тот же самый 1 Ампер, иначе бы все это противоречило закону Ома.

Настало время все это рассмотреть на реальном примере. Итак, замеры мы уже делали. Осталось соединить два источника питания параллельно, в нашем случае это аккумуляторы li-ion:

Как вы видите, напряжение не изменилось.

При параллельном соединении источников питания должно соблюдаться условие, что на них должно быть одинаковое напряжение.

Вот сами подумайте, что может произойти, если одна из башен будет пустая?

Думаю, нетрудно догадаться, что вода из одной башни будет перетекать в другую башню, пока их уровень не выровняется (закон сообщающихся сосудов), если у одной башни сломался насос и она пустая.

То же самое и с источниками питания. Нельзя соединять источники питания разных напряжений параллельно. Это чревато тем, что вы убьете здоровые аккумуляторы, а дохлые так и останутся дохлыми или чуток зарядятся. Если разница между напряжениями аккумулятора большая, то в такой цепи может течь бешеная сила тока, которая вызовет нагрев и даже возгорание аккумуляторов.

Нельзя соединять источники питания разных напряжений параллельно

Последовательно-параллельное соединение источников питания

А кто вам мешает соединять аккумуляторы или батарейки сразу и последовательно и параллельно? Но разве так можно? Можно). На примере с водобашнями это может выглядеть вот так:

Здесь мы видим две башни, каждая из которых состоит их двух башенок, и эти две большие башни соединены с помощью трубы.

Очень часто последовательно-параллельное соединение используется в электротранспорте. Недавно я делал батарею для своего электровелосипеда из li-ion аккумуляторов 18650. Для моего электробайка требовалось напряжение в 36 Вольт. Итак, теперь включаем логику. Один аккумулятор выдает 3,6 Вольт. Чтобы получить 36 Вольт, мне надо соединить 10 аккумуляторов последовательно.

Чтобы было проще для понимания, я их нарисую не по ГОСТу:

Ура! Я получил 36 Вольт для своего электровелосипеда. Но вот проблема в том, что один такой аккумулятор может отдать в нагрузку силу тока 2800 миллиАмпер в течение 1 часа или 2,8 Ампер в течение 1 часа. Такой параметр указывается на аккумуляторах как mAh. Об этом я подробно писал в этой статье “Как измерить ток и напряжение мультиметром“.

То, что я все аккумуляторы соединил последовательно, не означает, что их емкость возросла в 10 раз. В 10 раз возросло только напряжение, так как я их соединил последовательно. То есть общая сумма получилась 36 Вольт и все те же самые 2800 mAh как и у одного аккумулятора.

Поэтому, чтобы увеличить емкость, я должен в параллель этой ветви соединить точно такую же ветвь из аккумуляторов, иначе мой электровелосипед не проедет и пару тройку километров. Я ведь хочу кататься весь день!

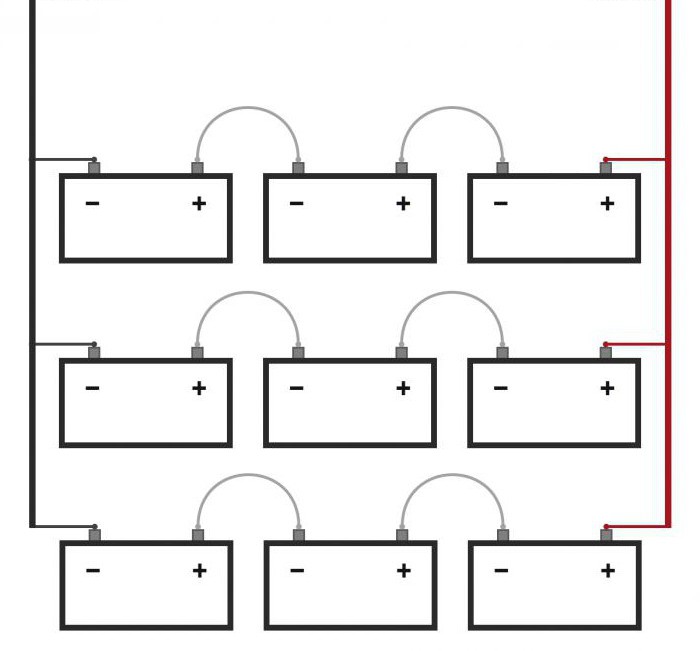
Сказано – сделано. Цепляем еще одну ветвь в 36 Вольт. Вы ведь не забыли правило, что при параллельном соединении у нас напряжение должно быть одинаково? В результате мы получаем что-то типа этого:

Итого, мы получили те же самые пресловутые 36 Вольт, но вот емкость увеличилась в два раза. 2800 mAh +2800 mAh = 5600 mAh. Ну вот, с такой батареей можно проехать уже чуть дальше. Но мне этого тоже показалось мало, поэтому я добавил еще 2 ветви. В результате моя самопальная батарея для электровелосипеда схематически, по идее, должна выглядеть вот так:

Пару слов о BMS (Battery Management System)

Дело в том, что для того, чтобы управлять зарядом, предохранять от короткого замыкания и управлять силой выдаваемого тока к такой батарее надо приделать плату BMS (Battery Managment System). Самые простые выглядят вот так:

 

Чуть получше и дороже:

10S 36V на BMS говорит нам о том, что эта BMS рассчитана для 10 аккумуляторов, включенных последовательно. Если на каждом аккумуляторе будет по 3,6 В, следовательно, 10х3,6=36 Вольт что и написано на самой BMS.

Discharge current  – ток разрядки, то есть максимальный выдаваемый ток

Charge current – ток зарядки, то есть максимальный ток заряда

Внутри такой платы имеется все, чтобы полностью управлять состоянием батареи.

Схемы подключения таких BMS выглядят примерно вот так:

Как вы видите, у нас BMS вроде как должна заряжать только 10 банок в ряд. Но в нашей самопальной батарее их 40. Что же делать? Почему бы вместо одной банки не поставить в параллель 4 банки и не обмануть BMS?

Получается, схема с BMS 10s4p под плату с BMS будет выглядеть вот так:

В сообществе электронщиков и самоделкиных такая батарея называется 10S4P. Расшифровывается очень просто:

S – serial – с англ.  – последовательный.

P – parallel – параллельный.

В нашем случае 10 аккумуляторов последовательно и 4 в параллель – 10S4P. Все до боли просто)

А вот выглядит моя самопальная батарея для электровелосипеда пока что без модуля BMS.

Параллельное и последовательное соединение :: SYL.ru

Ток в цепи протекает по проводникам к нагрузке от источника. Чаще всего в качестве таких элементов используют медь. Цепь может иметь несколько электрических приемников. Их сопротивления разнятся. В схеме электроприборов проводники могут иметь параллельное или последовательное соединение. Встречаются также смешанные его типы. Отличие каждого из них следует знать перед выбором структуры электроцепи.

Проводники и элементы цепи

Ток идет через проводники. Он следует от источника к нагрузке. При этом проводник обязан легко высвобождать электроны.

Проводник, имеющий сопротивление, называется резистором. Напряжение этого элемента — это разность потенциалов между концами резистора, которое согласовывается с направлением протекания питания.

Последовательное и параллельное соединение проводников характеризуется одним общим принципом. Ток течет в цепи от плюса (его называют источником) к минусу, где потенциал становится все меньшим, убывает. На электрических схемах сопротивление проводов считается равным нулю, так как оно пренебрежительно мало.

Поэтому, просчитывая последовательное или параллельное соединение, прибегают к идеализации. Это упрощает их изучение. В реальных цепях потенциал постепенно уменьшается при передвижении по проводу и элементам, имеющим параллельное или последовательное соединение.

Последовательное соединение проводников

При наличии последовательного сочетания проводников сопротивления включаются одно за другим. При таком положении сила тока во всех элементах цепи одинакова. Последовательно соединенные проводники создают на участке напряжение, которое равно их сумме на всех элементах.

Заряды не имеют возможности накапливаться в узлах цепи. Это бы привело к изменению напряжения электрического поля и силы тока.

При наличии постоянного напряжения ток будет зависеть от сопротивления цепи. Поэтому при последовательном соединении сопротивление будет меняться из-за перемены одной нагрузки.

Последовательное соединение проводников имеет недостаток. При поломке одного из элементов схемы будет прервана работа всех остальных ее составляющих. Например, как в гирлянде. Если в ней перегорит одна лампочка, все изделие не будет работать.

Последовательное соединение сопротивлений

Если проводники были подсоединены в цепи последовательно, их сопротивление в каждой точке будет одинаковым. Сопротивление в сумме всех элементов схемы будет равняться сумме уменьшения напряжений на участках цепи.

Это может подтвердить опыт. Последовательное соединение сопротивлений подсчитывается при помощи приборов и математической проверки. Например, берутся три постоянных сопротивления известной величины. Их последовательно соединяют и подключают к питанию в 60 В.

После этого подсчитывают предполагаемые показатели приборов, если замкнуть цепь. По закону Ома находится ток в цепи, что позволит определить падение напряжения на всех ее участках. После этого суммируются полученные результаты и получается общая величина снижения сопротивления во внешней цепи. Последовательное соединение сопротивлений можно подтвердить примерно. Если не брать во внимание внутреннее сопротивление, создающееся источником энергии, то падение напряжения будет меньше, чем сумма сопротивлений. По приборам можно убедиться, что равенство приблизительно соблюдается.

Параллельное соединение проводников

При последовательном и параллельном соединении проводников в цепи применяют резисторы. Параллельное соединение проводников представляет собой систему, в которой одни концы всех резисторов сходятся в один общий узел, а другие — в другой узел. В этих местах схемы сходятся более двух проводников.

При таком соединении к элементам прикладывается одинаковое напряжение. Параллельные участки цепи называются ветвями. Они проходят между двумя узлами. Параллельное и последовательное соединение имеют свои свойства.

Если в электросхеме есть ветви, то напряжение на каждой из них будет одинаковым. Оно равняется напряжению на неразветвленном участке. В этом месте сила тока будет рассчитываться как сумма ее в каждой ветви.

Величина, равная сумме показателей, обратных сопротивлениям разветвлений, будет обратна и сопротивлению участка параллельного соединения.

Параллельное соединение сопротивлений

Параллельное и последовательное соединение отличаются расчетом сопротивлений ее элементов. При параллельном соединении ток разветвляется. Это увеличивает проводимость цепи (уменьшает общее сопротивление), которая будет равна сумме проводимости ветвей.

Если несколько резисторов, имеющих одинаковую величину, соединены параллельно, то суммарное сопротивление цепи будет меньше одного резистора во столько раз, сколько их включено в схему.

Последовательное и параллельное соединение проводников имеют ряд особенностей. В параллельном подключении ток обратно пропорционален сопротивлению. Токи в резисторах не зависят друг от друга. Поэтому выключение одного из них не отразится на работе остальных. Поэтому множество электроприборов имеют именно этот тип соединения элементов цепи.

Смешанное

Параллельное и последовательное соединение проводников может комбинироваться в одной и той же схеме. Например, элементы, подключенные между собой параллельно, могут быть соединены последовательно с другим резистором или их группой. Это смешанное соединение. Общее сопротивление цепей вычисляется путем отдельного суммирования значений для параллельно подключенного блока и для последовательного соединения.

Причем сначала вычисляются эквивалентные сопротивления последовательно подключенных элементов, а потом уже рассчитывается общее сопротивление параллельных участков цепи. Последовательное соединение в вычислениях является приоритетнее. Такие типы электросхем довольно часто встречаются в различных приборах и оборудовании.

Ознакомившись с видами соединения элементов цепи, можно понять принцип организации схем различных электрических приборов. Параллельное и последовательное соединение обладают рядом особенностей расчета и функционирования всей системы. Зная их, можно правильно применять каждый из представленных видов для подключения элементов электрических цепей.

Соединения проводников — материалы для подготовки к ЕГЭ по Физике

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: параллельное и последовательное соединение проводников, смешанное соединение проводников.

Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.

Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.

Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1):

Рис. 1. Резистор

Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.

Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.

Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2):

Рис. 2.

Стационарное поле совершает при этом положительную работу .

Так как и , то и , т. е. .

Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .

Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3):

Рис. 3.

Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным. В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.

Последовательное соединение

При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.

Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.

Рис. 4. Последовательное соединение

Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.

1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.

2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике.

Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:

Можно и более формально, без всяких словесных объяснений:

3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.

Пусть — сопротивление участка . По закону Ома имеем:

что и требовалось.

Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .

Сопротивления проводников равны:

Эти два проводника образуют единый проводник длиной и сопротивлением

Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.

Параллельное соединение

При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.

Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).

Рис. 5. Параллельное соединение

Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от к (по направлению тока) называется неразветвлённой частью цепи.

Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.

1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:

Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.

2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .

Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:

что и требовалось.

3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:

Сокращая на , получим:

(1)

что и требовалось.

Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:

Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.

Из соотношения (1) можно найти :

(2)

К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением

(3)

Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:

откуда

Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.

Смешанное соединение

Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.

Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.

Рассмотрим пример смешанного соединения проводников (рис. 6).

Рис. 6. Смешанное соединение

Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.

Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :

Ом.

Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:

Ом.

Сопротивление цепи:

Ом.

Теперь находим силу тока в цепи:

A.

Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:

B;

B.

(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)

Оба резистора и находятся под напряжением , поэтому:

A;

A.

(В сумме имеем А, как и должно быть при параллельном соединении.)

Сила тока в резисторах и одинакова, так как они соединены последовательно:

А.

Стало быть, через резистор течёт ток A.

Параллельно и последовательно подключенные конденсаторы

Параллельно подключенные конденсаторы

Конденсаторы могут быть подключены параллельно:

Эквивалентная емкость для параллельно подключенных конденсаторов может быть рассчитана как

C = C ₁ + C ₂ +. , + C _n (1)

где

C = эквивалентная емкость для параллельно соединенной цепи (Фарад, Ф, мкФ)

C _1..n = емкостные конденсаторы (Фарад, Ф, мкФ)

Обычно в качестве единицы измерения емкости используют мкФ .

Конденсаторы серии

Конденсаторы могут быть подключены последовательно:

Эквивалентная емкость для последовательно подключенных конденсаторов может быть рассчитана как

1 / C = 1 / C ₁ + 1 / C ₂ +. , + 1 / C _n (2)

Для особого случая с двумя последовательно включенными конденсаторами — емкость может быть выражена как

1 / C = ( C ₁ + C ₂ ) / (C ₁ C ₂ ) (2b)

— или преобразовано в

C = C ₁ C ₂ / (C ₁ + C ₂ ) (2c)

Пример — конденсаторы, подключенные параллельно и последовательно

Эквивалентная емкость двух конденсаторов с емкостью 10 мкФ и 20 мкФ может быть рассчитана как

параллельно

C = (10 мкФ) + (20 мкФ)

= 30 (мкФ)

последовательно

1 / C = 1 / (10 мкФ) + 1 / (20 мкФ)

= 0.15 (1 / мкФ)

или

C = 1 / 0,15 (1 / мкФ)

= 6,7 (мкФ)

Конденсаторы серии

Три конденсатора C ₁ = 3 мкФ, C ₂ = 6 мкФ и C ₃ = 12 мкФ подключены последовательно, как показано на рисунке выше. Напряжение питания цепи составляет 230 В.

Емкость эквивалентной схемы может быть рассчитана с помощью (2)

1 / C = 1 / ( 3 мкФ ) + 1 / (6 мкФ ) + 1/ ( 12 мкФ )

= (4 + 2 + 1) / 12

= 0.58 1 / мкФ

— или преобразованное

C = 12 / (4 + 2 + 1)

= 1,7 мкФ

Общий заряд в цепи может рассчитывается с помощью

Q = UC

, где

Q = заряд (кулон, Кл)

U = электрический потенциал (В)

— или со значениями

Q = (230 В) (1.7 10 ^-6 F)

= 3,91 10 ^-4 C

= 391 мкКл

Поскольку конденсаторы соединены последовательно — заряд 391 мкКл на каждом из них.

Можно рассчитать напряжение на конденсаторе 1

U ₁ = Q / C ₁

= (391 мкКл) / (3 мкФ)

= 130 В

Напряжение на конденсаторе 2 можно рассчитать

U ₂ = Q / C ₂

= (391 мкКл) / (6 мкФ)

= 65 В

Напряжение на конденсаторе 3 можно рассчитать

U ₃ = Q / C ₃

= (391 мкКл) / (12 мкФ)

= 33 В

Емкость двух коаксиальных Цилиндры

Емкость двух коаксиальных цилиндров, как показано на рисунке, можно рассчитать как

C = 2 π ε _o ε _r л / л (r ₂ / r ₁ )(3)

, где

ε _o = абсолютная диэлектрическая проницаемость, диэлектрическая проницаемость вакуума (8.85 10 ^-12 Ф / м, Фарад / м)

ε _r = относительная диэлектрическая проницаемость

l = длина цилиндров

r ₂ = радиус внутреннего цилиндра

r ₁ = радиус внешнего цилиндра

.

Последовательный и параллельный

Два основных типа связи: последовательный и параллельный . Они настолько распространены, что даже кабели носят название последовательный кабель и параллельный кабель . Поскольку электричество ведет себя согласно законам физики, оно невозможно заставить электрический сигнал идти быстрее. Есть два способы быстрее переносить данные из одного места в другое. Первый — раздавить биты данных плотнее вместе (оставляйте меньшее расстояние между ними, когда они по проводу).Второй способ — одновременная передача большего количества битов.

Имейте в виду, что приведенная ниже информация является очень общей и не совсем верной. с инженерной точки зрения. Мы просто фокусируемся на том, чтобы вы здесь поняли концепции .

СЕРИЙНЫЙ

Когда информация отправляется по одному проводу, один бит данных в свое время его называли серийным . Каждый компьютер на земле есть какая-то форма последовательной связи разъем на нем, будь то внутри или снаружи.Большинство людей знакомы с D-образным 9-контактным разъемом на задняя часть своего компьютера. Это разъем серийный . Типичный 9-контактный D-образный разъем на задней панели компьютер использует 2 витка провода (по 1 в каждом направлении) для данных связь, плюс дополнительные провода контролировать поток информации. Однако в любом направлении данные все еще течет по единственному проводу.

ПАРАЛЛЕЛЬ

Вместо сжатия битов передаются биты по нескольким проводам одновременно. В случае 25-контактного параллельного порта вы иметь восемь проводов для передачи данных, чтобы можно было отправлять восемь битов одновременно. Поскольку имеется 8 проводов для передачи данных, передача данных прекращается. в восемь раз быстрее, чем последовательное соединение.

---

Добавьте эту страницу в закладки и ПОДЕЛИТЬСЯ:

,

Электрическое сопротивление в последовательных и параллельных сетях

Последовательное соединение

Общее сопротивление для резисторов, подключенных последовательно, можно рассчитать как

R = R ₁ + R ₂ + …. + R _n (1)

где

R = сопротивление (Ом, Ом)

• Резисторы — стандартные значения

Пример — Резисторы в серии

Три резистора 33 Ом , 33 Ом и 47 Ом соединены последовательно.Общее сопротивление можно рассчитать как

R = ( 33 Ом) + ( 33 Ом) + ( 47 Ом)

= 113 Ом

• Резисторы — Цветовые коды Калькулятор

Параллельное соединение

Общее сопротивление для резисторов, подключенных параллельно, можно рассчитать как

1 / R = 1 / R ₁ + 1 / R ₂ +…. + 1 / R _n (2)

Эквивалентное сопротивление двух параллельно подключенных резисторов можно выразить как

R = R ₁ R ₂ / (R ₁ + R ₂ ) ₍₃₎

Пример — параллельные резисторы

Три резистора 33 Ом , 33 Ом и 47 Ом подключены параллельно. Общее сопротивление можно рассчитать как

1 / R = 1 / ( 33 Ом ) + 1 / ( 33 Ом ) + 1 / (47 Ом )

= 0.082 (1 / Ом)

R = 1 / (0,082 Ом)

= 12,2 Ом

Если напряжение батареи 12 В — ток в цепи можно рассчитать с помощью закон

I = U / R

= (12 В) / (12,2 Ом)

= 0,98 ампер

Можно рассчитать ток через каждый резистор

I ₁ = U / R ₁ = (12 В) / (33 Ом) = 0.36 ампер

I ₂ = U / R ₂ = (12 В) / (33 Ом) = 0,36 ампер

I ₃ = U / R ₃ = (12 В) / (47 Ом) = 0,26 ампера

Резисторы, подключенные параллельно — Calculator

Сложите сопротивления до пяти параллельно подключенных резисторов и (необязательно) напряжение цепи.

Общее сопротивление и ток, а также отдельные токи во всех резисторах будут рассчитаны:

R ₁ (Ом) I ₁ (ампер)

R ₂ (Ом) I ₂ (ампер)

R ₃ (ом) I ₃ (ампер)

R ₄ (ом ) I ₄ (ампер)

R ₅ (Ом) I ₅ (ампер)

Напряжение (В)

R (Ом) I (амперы)

,

В чем разница между последовательным и параллельным портом?

И последовательные, и параллельные порты являются примерами компьютерных технологий, которые когда-то были передовыми; На протяжении большей части истории персональных компьютеров как последовательный, так и параллельный порт были наиболее распространенными средствами передачи данных и связи. С развитием технологий последовательный и параллельный порт в значительной степени были заменены использованием портов USB, и все меньше новых устройств разработано для включения последовательного или параллельного порта.Старые персональные компьютеры с последовательным и параллельным портами часто требуют переходного кабеля для использования периферийных устройств последнего поколения. Возможно, основное различие между последовательным и параллельным портами заключается в способе передачи информации: параллельный порт может передавать информацию только с жесткого диска, а последовательный порт может передавать информацию как на жесткий диск, так и с него.

Для параллельных портов используется 25-контактный разъем, а для последовательных портов — 9-контактный адаптер.

Параллельные порты

Из этих двух параллельный порт — это более старая конструкция порта, впервые использовавшаяся в начале 1970-х годов, позволяющая подключать принтеры непосредственно к мэйнфрейму и выполнять заказы на печать путем ввода раздела кода через командную станцию.Параллельный порт позволяет одностороннюю передачу данных от источника к вторичному устройству, например к принтеру. В некоторых кругах параллельный порт стал широко известен как порт принтера, поскольку эта функция изначально была наиболее распространенным приложением устройства. Ранние внешние модемы и устройства хранения данных являются парой примеров более широкого использования параллельных портов. С начала 21 века параллельный порт в значительной степени был заменен портом USB, хотя некоторые вспомогательные устройства все еще допускают подключение обоими способами.

Последовательные порты можно найти на старых ноутбуках, но, как правило, они не входят в комплект нового устройства, так как они были заменены портами USB.

Параллельные порты обычно имеют как минимум 25-контактные разъемы, составляющие фактическую соединительную часть устройства.Эти 25 контактов будут соответствовать концу устройства, к которому подключается порт, и именно через контакты передается информация. Каждый контактный разъем выполняет разные функции.

Параллельные порты впервые были использованы в 1970-х годах для подключения компьютерных принтеров.

Последовательные порты

Одно из ключевых различий между последовательным и параллельным портами заключается в том, что последовательный порт позволяет передавать данные на жесткий диск с удаленного устройства или с жесткого диска на удаленное устройство, в отличие от параллельного порта только для исходящей связи. ; последовательный порт может также называться коммуникационным портом или двунаправленным портом.Этот процесс двусторонней связи позволяет подключать рабочие станции к более крупным терминалам, а также к широкому спектру периферийных устройств, таких как внешние жесткие диски или смартфоны. Однако известно, что последовательные порты работают медленнее, чем параллельные, поскольку они могут передавать информацию в двух направлениях одновременно.

Последовательный порт обычно состоит из девяти- или 25-контактных разъемов; некоторые из разъемов 25-контактного порта не используются регулярно.Первоначально считалось, что девятиконтактный порт более компактен и экономичен, но часто он был недостаточно эффективным для выполнения своей задачи.

И последовательные, и параллельные порты в основном были заменены использованием портов USB. ,