Признаки и свойства параллельных прямых
Признаки параллельных прямых
1. Если две прямые параллельны третьей прямой, то они являются параллельными:
Если a||c и b||c, то a||b.
2. Если две прямые перпендикулярны третьей прямой, то они параллельны:
Если a⊥c и b⊥c, то a||b.
Остальные признаки параллельности прямых основаны на углах, образующихся при пересечении двух прямых третьей.
3. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны:
Если ∠1 + ∠2 = 180°, то a||b.
4. Если соответственные углы равны, то прямые параллельны:
Если ∠2 = ∠4, то a||b.
5. Если внутренние накрест лежащие углы равны, то прямые параллельны:
Если ∠1 = ∠3, то a||b.
Свойства параллельных прямых
Утверждения, обратные признакам параллельности прямых, являются их свойствами. Они основаны на свойствах углов, образованных пересечением двух параллельных прямых третьей прямой.
1. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°:
Если a||b, то ∠1 + ∠2 = 180°.
2. При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны:
Если a||b, то ∠2 = ∠4.
3. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы равны:
Если a||b, то ∠1 = ∠3.
Следующее свойство является частным случаем для каждого предыдущего:
4. Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:
Если a||b и c⊥a, то c⊥b.
Пятое свойство – это аксиома параллельности прямых:
5. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой:
naobumium.info
Признаки параллельности прямых | Треугольники
Признаки параллельности прямых:
1) Если внутренние накрест лежащие углы равны, то прямые параллельны.
2) Если соответственные углы равны, то прямые параллельны.
3) Если сумма внутренних односторонних углов равна 180, то то прямые параллельны.
4) Если две прямые параллельны третьей прямой, то они параллельны между собой.
5) Если две прямые перпендикулярны третьей прямой, то они параллельны между собой.
Виды углов
www.treugolniki.ru
Признаки параллельности двух прямых / Параллельные прямые / Справочник по геометрии 7-9 класс
Рассмотрим две прямые и , которые пересекает в двух точках третья прямая (Рис.1). Прямая называется секущей по отношению к прямым и .
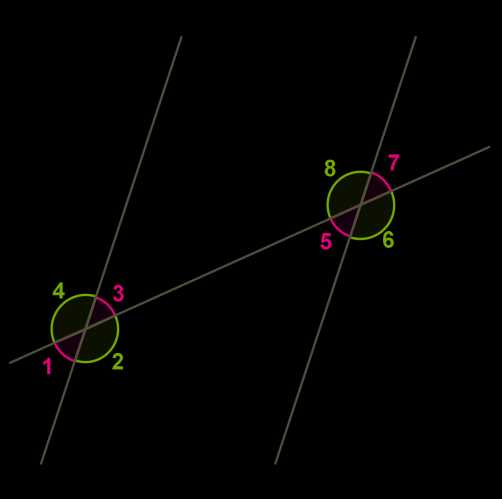
При пересечении прямых и секущей образуется восемь углов, которые обозначены цифрами на Рис.2.
Некоторые пары из этих углов имеют специальные названия:
накрест лежащие углы: 3 и 5, 4 и 6;
односторонние углы: 4 и 5, 3 и 6;
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
Признаки параллельности двух прямых
1. Теорема
| Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. |
Дано: прямые и , АВ — секущая, 1 и 2 — накрест лежащие, 1 = 2 (Рис.3).
Доказать: .
Доказательство:
1 случай
Предположим, что 1 = 2 = 900, т.е. эти углы прямые, получим АВ и АВ (Рис.4), следовательно, (т.к. две прямые перпендикулярные к третьей прямой не пересекаются, т.е. параллельны).
2 случай
Предположим, что 1 и 2 — не прямые. Из середины О отрезка АВ проведем перпендикуляр ОН к прямой и продолжим его до пересечения с прямой , точку пересечения ОН с прямой обозначим Н1 (Рис. 5).
Получим ОНА = ОН1В по 2 признаку равенства треугольников (углы
3 и 4 вертикальные, т.к. получены при пересечении двух прямых АВ и НН1, а вертикальные углы равны друг другу, т.е. 3 = 4, АО = ОВ, т.к. О — середина АВ, 1 = 2 по условию), следовательно, 5 =6, значит, 6 — прямой, также как и 5 (т.к по построению ОН ).Получаем, НН1 и НН1, значит (т.к. две прямые перпендикулярные к третьей прямой не пересекаются, т.е. параллельны). Что и требовалось доказать.
2. Теорема
| Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. |
Дано: прямые и , АВ — секущая, 1 и 2 — соответственные, 1 = 2 (Рис.6).
Доказать: .
Доказательство:
По условию 1 = 2 и 2 = 3, т.к.они вертикальные, откуда 1 = 3, при этом углы 1 и 3 накрест лежащие, следовательно, (см. теорему 1). Что и требовалось доказать.
3. Теорема
| Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны. |
Дано: прямые и , АВ — секущая, 1 и 2 — односторонние, 1 + 2 = 1800 (Рис.7).
Доказать: .
Доказательство:
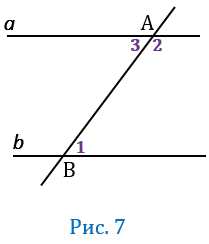
Углы 3 и 2 — смежные, значит по свойству смежных углов 3 + 2 = 1800, откуда 3 = 1800 — 2, при этом 1 + 2 = 1800, откуда 1 = 1800 — 2, тогда 1 = 3, а углы 1 и 3 накрест лежащие, следовательно, (см. теорему 1). Что и требовалось доказать.
budu5.com
1. Определение и доказательства признаков параллельности прямых в плоскости
Две прямые, лежащие на одной плоскости, либо имеют только одну общую точку, либо не имеют ни одной общей точки.
В первом случае говорят, что прямые пересекаются, во втором случае — прямые не пересекаются.
На плоскости две прямые \(a\) и \(b\), которые не пересекаются, называются параллельными и обозначаются a∥b.
Обрати внимание!
Если рассмотреть прямые, которые не лежат в одной плоскости, то возможна ситуация, что прямые не пересекаются, но они и не параллельны.
Один из признаков параллельности прямых на плоскости гласит:
1. признак. Если две прямые на плоскости перпендикулярны одной и той же прямой, то они параллельны.
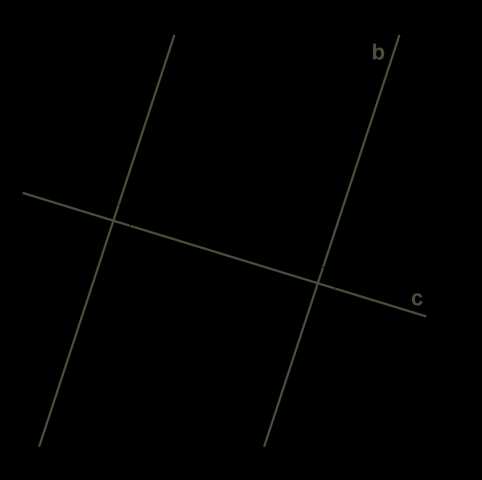
Этот признак легко доказать, если вспомнить, что к прямой в плоскости из любой точки можно провести только один перпендикуляр.
Допустим, что прямые, перпендикулярные одной и той же прямой, не параллельны, то есть имеют общую точку.
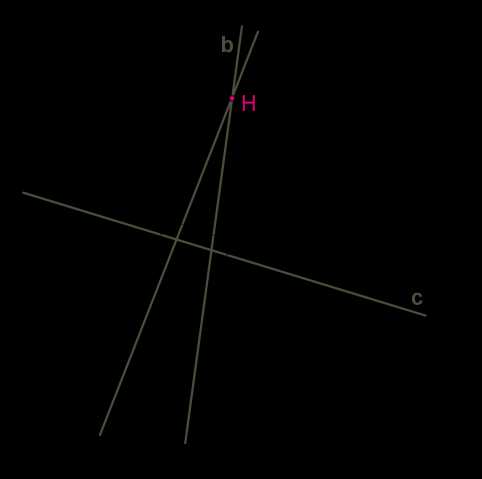
Получается противоречие — из одной точки \(H\) к прямой \(c\) проведены два перпендикуляра. Такое невозможно, поэтому две прямые на плоскости, перпендикулярные одной и той же прямой, параллельны.
Для рассмотрения других признаков надо ознакомиться с некоторыми видами углов:
1) вспомним, что нам известны названия и свойства углов, которые образуют две пересекающиеся прямые.
Вертикальные углы равны: ∡1=∡3;∡2=∡4.
Сумма смежных углов 1800:∡1+∡2=∡2+∡3=∡3+∡4=∡4+∡1=1800.
2) Если две прямые пересекает третья прямая, то углы называются так:
накрест лежащие углы: ∡3 и ∡5;∡2 и ∡8;
соответственные углы: ∡1 и ∡5;∡4 и ∡8;∡2 и ∡6;∡3 и ∡7;
односторонние углы: ∡3и∡8;∡2и∡5.
Эти углы помогут определить параллельность прямых \(a\) и \(b\). Итак, другой признак параллельности прямых на плоскости гласит:
2. признак. Если при пересечении двух прямых третьей секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна \(180°\) — то прямые параллельны.
Докажем этот признак.
Сначала докажем: если прямые \(a\) и \(b\) пересекает прямая \(c\), и накрест лежащие углы равны, то прямые \(a\) и \(b\) параллельны.
Например, если ∡3=∡5, то a∥b.
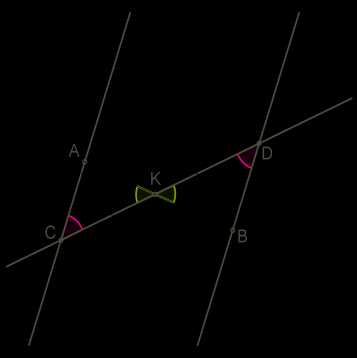
1) Отметим точки \(C\) и \(D\), в которых прямые \(a\) и \(b\) пересекает прямая \(c\). Через серединную точку \(K\) этого отрезка проведём перпендикуляр \(AB\) к прямой \(a\).
2) ∡CKA \(=\) ∡DKB как вертикальные углы, ∡3 \(=\) ∡5 \(=\) α, \(CK = KD\) — значит, ΔCKA \(=\) ΔDKB по признаку о стороне и двум прилежащим к ней углам.
3) Очевидно, если ΔCKA прямоугольный, то и ΔDKB прямоугольный, и \(AB\) перпендикулярен к прямой \(b\).
4) Согласно первому доказанному признаку прямые, перпендикулярные одной и той же прямой, параллельны.
5) В случае, когда равны соответственные углы, имеем в виду, что вертикальные углы равны, и доказываем, как в пунктах 1) — 4).
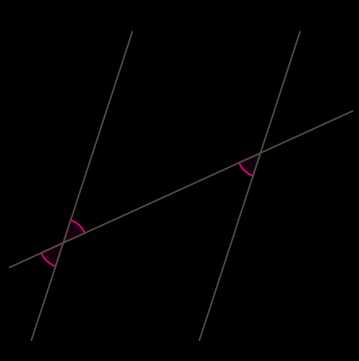
6) В случае, когда сумма односторонних углов равна 180°, имеем в виду, что сумма смежных углов тоже равна \(180°\), и используем в доказательстве пункты 1) — 4).
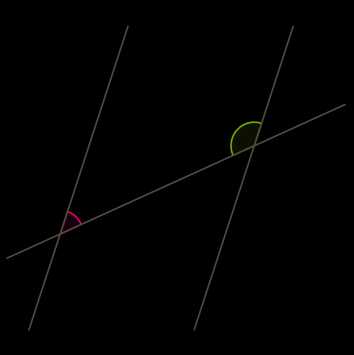
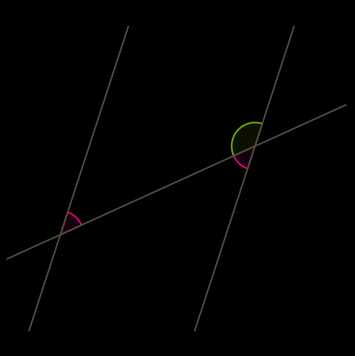
3. Признак параллельных прямых действует и как свойство параллельных прямых.
При пересечении двух параллельных прямых третьей секущей:
— накрест лежащие углы равны,
— соответственные углы равны,
— сумма односторонних углов равна \(180°\).
О других свойствах параллельных прямых — в следующем пункте теории.
www.yaklass.ru
Параллельные прямые — Википедия
Материал из Википедии — свободной энциклопедии
Паралле́льные прямы́е (от греч. παράλληλος, буквально — идущий рядом) — в планиметрии прямые, которые не пересекаются, сколько бы их ни продолжали в обе стороны.
На чертежах параллельные линии выделяются одинаково направленными стрелками.В евклидовой геометрии параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются
Параллельность прямых m{\displaystyle m} и n{\displaystyle n} обычно обозначается:
- m∥n{\displaystyle m\parallel n}
Свойства[править | править код]
- Через любую точку, не лежащую на прямой, можно провести прямую, параллельную данной, и притом только одну. Последняя часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского (см. ниже).
- Если прямая пересекает одну из параллельных прямых, то она пересекает и другую (такая прямая называется секущей). При этом образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
- Соответственные углы равны (Рис.1).
- Накрест лежащие углы равны (Рис.2).
- Внутренние односторонние углы в сумме составляют 180° (Рис.3).
- Если считать совпадающие прямые параллельными, то параллельность будет бинарным отношением эквивалентности, которое разбивает всё множество прямых на классы параллельных между собой прямых.
- Множество точек плоскости, расположенных на некотором фиксированном расстоянии от данной прямой, по одну сторону от неё, есть прямая, параллельная данной.
Построение параллельных прямых[править | править код]
В стереометрии[править | править код]
В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.
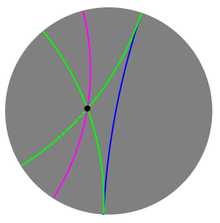Параллельные прямые в модели Пуанкаре: две зелёные прямые равнобежны (асимптотически параллельны) синей прямой, а фиолетовая ультрапараллельна к нейВ геометрии Лобачевского в плоскости через точку C{\displaystyle C} вне данной прямой AB{\displaystyle AB} проходит бесконечное множество прямых, не пересекающих AB{\displaystyle AB}. Прямая CE{\displaystyle CE} называется равнобежной прямой AB{\displaystyle AB} в направлении от A{\displaystyle A} к B{\displaystyle B}, если:
- точки B{\displaystyle B} и E{\displaystyle E} лежат по одну сторону от прямой AC{\displaystyle AC};
- прямая CE{\displaystyle CE} не пересекает прямую AB{\displaystyle AB}, но всякий луч, проходящий внутри угла ACE{\displaystyle ACE}, пересекает луч AB{\displaystyle AB}.
Аналогично определяется прямая, равнобежная AB{\displaystyle AB} в направлении от B{\displaystyle B} к A{\displaystyle A}.
Равнобежные прямые называются также асимптотически параллельными или просто параллельными. Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися[5].
Свойства[править | править код]
Расходящиеся параллельные прямые имеют единственный общий перпендикуляр. Этот перпендикуляр соединяет ближайшую пару точек на этих прямых.
Несмотря на то, что асимптотически параллельные прямые не пересекаются, на любой паре асимптотически параллельных прямых можно выбрать произвольно близкие точки.
ru.wikipedia.org
Признаки параллельности двух прямых. Свойства параллельных прямых [wiki.eduVdom.com]
Признаки параллельности двух прямых
Рис.1
Теорема 1. Если при пересечении двух прямых секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна 180°, то
прямые параллельны (рис.1).
Доказательство. Ограничимся доказательством случая 1.
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.
Следствие 1. Две различные прямые на плоскости, перпендикулярные одной и той же прямой, параллельны (рис.2).
Рис.2
Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное)
тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду). Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.
Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.
Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).
Рис.3
Затем проводим через точку М прямую b перпендикулярно прямой р. Прямая b параллельна прямой а согласно следствию из теоремы 1.
Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной.
Основное свойство параллельных прямых состоит в следующем.
Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис.4).
Рис.4
2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).
Рис.5
Справедлива и следующая теорема.
Теорема 2. Если две параллельные прямые пересечены секущей, то:
накрест лежащие углы равны;
соответственные углы равны;
сумма односторонних углов равна 180°.
Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).
Рис.2
Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.
Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.
Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.
Решение. Пусть условию отвечает рисунок 6.
Рис.6
Углы 1 и 2 внутренние односторонние, их сумма равна 180°, т. е.
∠ l + ∠ 2 = 180°. (1)
Обозначим градусную меру угла 1 через х. По условию ∠ 2 — х = 30°, или ∠ 2 = 30° + x.
Подставим в равенство (1) значения углов 1 и 2, получим
х + 30° + х = 180°.
Решая это уравнение, получим х = 75°, т. е.
∠ 1 = 75°, a ∠ 2 = 180° — 75° = 105°.
Пример 2. Две параллельные прямые пересечены третьей. Известно, что сумма двух внутренних накрест лежащих углов равна 150°. Чему равны эти углы и остальные шесть?
Решение. Пусть условию задачи соответствует рисунок 7.
Рис.7
Углы 1 и 2 внутренние накрест лежащие, следовательно, они равны. Сумма этих углов по условию задачи равна 150°, тогда ∠ 1 = ∠ 2 = 75°.
Найдем остальные углы (рис. 8):
Рис.8
∠ 1 = ∠ 3 = 75° и ∠ 2 = ∠ 7 = 75° (вертикальные). Углы 4 и 5, 6 и 8 равны как вертикальные, a ∠ 5 = ∠ 6 как внутренние накрест лежащие. Все перечисленные углы 4, 5, 6 и 8 равны между собой и равны по 105°, так как ∠ 4 + ∠ 3 = 180°, a ∠ 4 = 180° — ∠ 3.
Получили четыре угла по 75°, четыре угла по 105°.
wiki.eduvdom.com
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
При пересечении двух прямых третьей прямой образуются углы, названия которых приведены в следующей таблице.
Углы, образующиеся при пересечении двух прямых третьей прямой
Перечисленные в таблице углы используются в формулировках признаков параллельности двух прямых.
Определение. Две прямые на плоскости называются параллельными, если они не имеют общих точек.
Замечание. Два отрезка называются параллельными, если они лежат на параллельных прямых.
Признаки параллельности двух прямых
Признак параллельности: Прямые параллельны тогда и только тогда, |
Признак параллельности: Прямые параллельны тогда и только тогда, |
Признак параллельности: Прямые параллельны тогда и только тогда, |
Признак параллельности: Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180° |
Признак параллельности: Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180° |
Следствие
| Рисунок | Признак параллельности |
| Две прямые, перпендикулярные к третьей прямой, параллельны |
Признак параллельности: Две прямые, перпендикулярные к третьей прямой, параллельны |
Переход свойства параллельности прямых
| Рисунок | Признак параллельности |
| Если прямая a параллельна прямой b, а прямая b параллельна прямой c, то прямая a параллельна прямой c |
Признак параллельности: Если прямая a параллельна прямой b, |
Задача. Доказать, что биссектрисы внутренних односторонних углов, полученных при пересечении двух параллельных прямых третьей прямой, перпендикулярны.
Решение. Решение этой задачи почти дословно совпадает с решением задачи из раздела нашего справочника «Углы на плоскости» и предоставляется читателю в качестве несложного самостоятельного упражнения.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
www.resolventa.ru
