Переход от десятичного логарифма к натуральному – Логарифмы / math4school.ru

Логарифмы / math5school.ru

Формулы перехода от десятичного к натуральному логарифму и наоборот

 

Определение логарифма

Логарифмом положительного числа b по основанию а (a > 0, a ≠ 1) называется такой показатель степени c, в которую нужно возвести число а, чтобы получить число b.

Записывают: с = log_a b, что означает a ^c= b. 

Из определения логарифма следует справедливость равенства: 

a ^log_a b = b, (а > 0, b > 0, a ≠ 1),

называемого основным логарифмическим тождеством.

В записи log_a b число а – основание логарифма, b – логарифмируемое число.

Из определения логарифмов вытекают следующие важные равенства:

log_a 1 = 0,

log_a а = 1.

Первое следует из того, что

a ⁰ = 1, а второе – из того, что a ¹ = а. Вообще имеет место равенство

log_a a ^r = r.

 

Свойства логарифмов

Для положительных действительных чисел a (a ≠ 1), b, c справедливы следующие соотношения:

log_a (b · c) = log_a b + log_a c

log_a (b ⁄ c) = log_a b – log_a c

log_a b ^p = p · log_a b

log_a ^q b = 1/q · log_a b

log_a ^q b ^p = p/q · log_a b

log_a ^pr b ^ps = log_a ^r b ^s

log_a b = log_c b ⁄ log

c a  (c ≠ 1)

log_a b = 1 ⁄ log_b a  (b ≠ 1)

log_a b · log_b c = log_a c

c ^log_a b = b ^log_a c

Замечание 1. Если а > 0, a ≠ 1, числа b и c отличны от 0 и имеют одинаковые знаки, то

log_a (b · c) = log_a |b| + log_a |c|

log_a (b ⁄ c) = log_a |b| – log_a |c| .

Замечание 2. Если p и q – чётные числа, а > 0, a ≠ 1 и b ≠ 0, то

log_a b ^p = p · log_a |b|

log_a ^pr b ^ps

 = log_a ^r |b ^s|

log_a ^q b ^p = p/q · log_a |b| .

Для любых положительных, отличных от 1 чисел a и b верно:

log_a b > 0  тогда и только тогда, когда  a > 1  и  b > 1  или  0 < a < 1  и  0 < b < 1;

log_a b < 0  тогда и только тогда, когда  a > 0  и  0 < b < 1  или  0 < a < 1  и  b > 1.

 

Десятичный логарифм

Десятичным логарифмом называется логарифм, основание которого равно 10.

Обозначаются символом lg:

log₁₀ b = lg b.

Десятичные логарифмы до изобретения в 70-х годах прошлого века компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня.

Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже – с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми.

В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: log, Log, Log10, причём следует иметь в виду, что первые два варианта могут относиться и к натуральному логарифму.

 

Таблица десятичных логарифмов целых чисел от 0 до 99

Десятки	Единицы
	0	1	2	3	4	5	6	7	8	9
0	–	0	0,30103	0,47712	0,60206	0,69897	0,77815	0,84510	0,90309	0,95424
1	1	1,04139	1,07918	1,11394	1,14613	1,17609	1,20412	1,23045	1,25527	1,27875
2	1,30103	1,32222	1,34242	1,36173	1,38021	1,39794	1,41497	1,43136	1,44716	1,46240
3	1,47712	1,49136	1,50515	1,51851	1,53148	1,54407	1,55630	1,56820	1,57978	1,59106
4	1,60206	1,61278	1,62325	1,63347	1,64345	1,65321	1,66276	1,67210	1,68124	1,69020
5	1,69897	1,70757	1,71600	1,72428	1,73239	1,74036	1,74819	1,75587	1,76343	1,77085
6	1,77815	1,78533	1,79239	1,79934	1,80618	1,81291	1,81954	1,82607	1,83251	1,83885
7	1,84510	1,85126	1,85733	1,86332	1,86923	1,87506	1,88081	1,88649	1,89209	1,89763
8	1,90309	1,90849	1,91381	1,91908	1,92428	1,92942	1,93450	1,93952	1,94448	1,94939
9	1,95424	1,95904	1,96379	1,96848	1,97313	1,97772	1,98227	1,98677	1,99123	1,99564

 

Натуральный логарифм

Натуральным логарифмом называется логарифм, основание которого равно  числу е, математической константе, являющейся иррациональным числом, к которому стремится последовательность

а_n = (1 + 1/n)ⁿ при n → +∞.

Иногда число e называют числом Эйлера или числом Непера. Значение числа е с первыми пятнадцатью цифрами после запятой следующее: 

е = 2,718281828459045… .

Натуральный логарифм обозначаются символом ln:

log_e b = ln b.

Натуральные логарифмы являются самыми удобными при проведении различного рода операций, связанных с анализом функций.

 

Таблица натуральных логарифмов целых чисел от 0 до 99

Десятки	Единицы
	0	1	2	3	4	5	6	7	8	9
0	–	0	0,69315	1,09861	1,38629	1,60944	1,79176	1,94591	2,07944	2,19722
1	2,30259	2,39790	2,48491	2,56495	2,63906	2,70805	2,77259	2,83321	2,89037	2,94444
2	2,99573	3,04452	3,09104	3,13549	3,17805	3,21888	3,25810	3,29584	3,33220	3,36730
3	3,40120	3,43399	3,46574	3,49651	3,52636	3,55535	3,58352	3,61092	3,63759	3,66356
4	3,68888	3,71357	3,73767	3,76120	3,78419	3,80666	3,82864	3,85015	3,87120	3,89182
5	3,91202	3,93183	3,95124	3,97029	3,98898	4,00733	4,02535	4,04305	4,06044	4,07754
6	4,09434	4,11087	4,12713	4,14313	4,15888	4,17439	4,18965	4,20469	4,21951	4,23411
7	4,24850	4,26268	4,27667	4,29046	4,30407	4,31749	4,33073	4,34381	4,35671	4,36945
8	4,38203	4,39445	4,40672	4,41884	4,43082	4,44265	4,45435	4,46591	4,47734	4,48864
9	4,49981	4,51086	4,52179	4,5326	4,54329	4,55388	4,56435	4,57471	4,58497	4,59512

 

Формулы перехода от десятичного к натуральному логарифму и наоборот

Так как lg е = 1 / ln 10 ≈ 0,4343, то lg b ≈ 0,4343 · ln b;

так как ln 10 = 1 / lg e ≈ 2,3026, то ln b ≈ 2,3026 · lg b.

math4school.ru

Таблица и формула для перехода от десятичных логарифмов к натуральным.

Таблица и формула для перехода от десятичных логарифмов к натуральным. Если Вам известен десятичный логарифм какого-то числа Х (равный lg(X)), то натуральный логарифм этого числа (равный ln(X)) будет равен, согласно основным свойствам логарифмов : ln(X)=In10*lg(X)=(1/Ig(e))*lg(X)=(1/M)*lg(X), т.е. натуральный логарифм числа, равен десятичному логарифму этого числа умноженному на «число 1/М»=1/Ig(e). Для быстрых оценок приводим табличку: Таблица для перехода от десятичных логарифмов к натуральным (таблица умножения на «число 1/М» (у англосаксов это «число 1/A») = In 10 = 2,3025851). Таблица для перехода от десятичных логарифмов к натуральным (таблица умножения на «число 1/М» (у англосаксов это «число 1/A») = In 10 = 2,3025851).   0 10 20 30 40 50 60 70 80 90 0 0,0000 23,026 46,052 69,078 92,103 115,129 138,155 161,181 184,207 207,233 1 2,3026 25,328 48,354 71,380 94,406 117,431 140,458 163,484 186,509 209,535 2 4,6052 27,631 50,657 73,683 96,709 119,734 142,760 165,786 188,812 211,838 3 6,9078 29,934 52,959 75,985 99,011 122,037 145,062 166,089 191,115 214,140 4 9,2103 32,236 55,262 78,288 101,314 124,340 147,365 170,391 193,417 216,443 5 11,513 34,539 57,565 80,590 103,616 126,642 149,668 172,694 195,720 218,746 6 13,816 36,841 59,867 82,893 105,919 128,945 151,971 174,997 198,022 221,048 7 16,118 39,144 62,170 85,196 108,221 131,247 154,273 177,299 200,325 223,351 8 18,421 41,447 64,472 87,498 110,524 133,550 156,576 179,602 202,627 225,653 9 20,723 43,749 66,775 89,801 112,827 135,853 158,878 181,904 204,930 227,956

tehtab.ru

Десятичный логарифм — Википедия

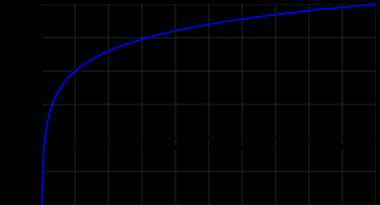График десятичного логарифма

Десятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа b{\displaystyle b} есть решение уравнения 10x=b.{\displaystyle 10^{x}=b.}

Вещественный десятичный логарифм числа b{\displaystyle b} существует, если b>0{\displaystyle b>0} (комплексный десятичный логарифм существует для всех b≠0{\displaystyle b\neq 0}). Международный стандарт ISO 31-11 обозначает его lgb{\displaystyle \lg \,b}. Примеры:

lg1=0;lg10=1;lg100=2{\displaystyle \lg \,1=0;\,\lg \,10=1;\,\lg \,100=2}

lg1000000=6;lg0,1=−1;lg0,001=−3{\displaystyle \lg \,1000000=6;\,\lg \,0{,}1=-1;\,\lg \,0{,}001=-3}

В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: log,Log,Log10{\displaystyle \operatorname {log} ,\operatorname {Log} ,\operatorname {Log10} }, причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.

В нижеследующей таблице предполагается, что все значения положительны^[1]:

Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные переменные, например:

lg⁡|xy|=lg⁡(|x|)+lg⁡(|y|),{\displaystyle \lg |xy|=\lg(|x|)+\lg(|y|),}

lg|xy|=lg⁡(|x|)−lg⁡(|y|),{\displaystyle \lg \!\left|{\frac {x}{y}}\right|=\lg(|x|)-\lg(|y|),}

Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:

lg⁡(x1x2…xn)=lg⁡(x1)+lg⁡(x2)+⋯+lg⁡(xn){\displaystyle \lg(x_{1}x_{2}\dots x_{n})=\lg(x_{1})+\lg(x_{2})+\dots +\lg(x_{n})}

Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел x,y{\displaystyle x,y} с помощью логарифмических таблиц^[⇨] производилось по следующему алгоритму:

1. Найти в таблицах логарифмы чисел x,y{\displaystyle x,y}.
2. Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения x⋅y{\displaystyle x\cdot y}.
3. По логарифму произведения найти в таблицах само произведение.

Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично производились возведение в степень и извлечение корня.

Связь десятичного и натурального логарифмов^[2]:

ln⁡x≈2,30259 lg⁡x;lg⁡x≈0,43429 ln⁡x{\displaystyle \ln x\approx 2{,}30259\ \lg x;\quad \lg x\approx 0{,}43429\ \ln x}

Знак логарифма зависит от логарифмируемого числа: если оно больше 1, логарифм положителен, если оно между 0 и 1, то отрицателен. Пример:

lg0,012=lg(10−2×1,2)=−2+lg1,2≈−2+0,079181=−1,920819{\displaystyle \lg \,0{,}012=\lg \,(10^{-2}\times 1{,}2)=-2+\lg \,1{,}2\approx -2+0{,}079181=-1{,}920819}

Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть (характеристика) надчёркивалась сверху:

lg0,012≈−2+0,079181=2¯,079181{\displaystyle \lg \,0{,}012\approx -2+0{,}079181={\bar {2}}{,}079181}

Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.

Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: y=lgx.{\displaystyle y=\lg \,x.} Она определена при всех x>0.{\displaystyle x>0.} Область значений: E(y)=(−∞;+∞){\displaystyle E(y)=(-\infty ;+\infty )}. График этой кривой часто называется логарифмикой^[3].

Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:

ddxlgx=lgex{\displaystyle {\frac {d}{dx}}\lg \,x={\frac {\lg \,e}{x}}}

Ось ординат (x=0){\displaystyle (x=0)} является вертикальной асимптотой, поскольку:

limx→0+0lgx=−∞{\displaystyle \lim _{x\to 0+0}\lg \,x=-\infty }

Логарифмы по основанию 10 до изобретения в 1970-е годы компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня. Но десятичные логарифмы обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа x{\displaystyle x} (характеристику логарифма) [lg⁡x]{\displaystyle [\lg x]} легко определить.

• Если x⩾1{\displaystyle x\geqslant 1}, то [lg⁡x]{\displaystyle [\lg x]} на 1 меньше числа цифр в целой части числа x{\displaystyle x}. Например, сразу очевидно, что lg⁡345{\displaystyle \lg 345} находится в промежутке (2,3){\displaystyle (2,3)}.
• Если 0<x<1{\displaystyle 0<x<1}, то ближайшее к lg⁡x{\displaystyle \lg x} целое в меньшую сторону равно общему числу нулей в x{\displaystyle x} перед первой ненулевой цифрой (включая ноль перед запятой), взятому со знаком минус. Например, lg⁡0,0014{\displaystyle \lg 0{,}0014} находится в интервале (−3,−2){\displaystyle (-3,-2)}.

Кроме того, при переносе десятичной запятой в числе на n{\displaystyle n} разрядов значение десятичного логарифма этого числа изменяется на n.{\displaystyle n.} Например:

lg⁡8314,63=lg⁡8,31463+3{\displaystyle \lg 8314{,}63=\lg 8{,}31463+3}

Отсюда следует, что для вычисления десятичных логарифмов достаточно составить таблицу логарифмов для чисел в диапазоне от 1{\displaystyle 1} до 10{\displaystyle 10}^[4]. Такие таблицы, начиная с XVII века, выпускались большим тиражом и служили незаменимым расчётным инструментом учёных и инженеров.

Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным^[5]. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал.

Десятичные логарифмы для чисел вида 5 × 10^C

Число	Логарифм	Характеристика	Мантисса	Запись
n	lg(n)	C	M = lg(n) − C
5 000 000	6.698 970…	6	0.698 970…	6.698 970…
50	1.698 970…	1	0.698 970…	1.698 970…
5	0.698 970…	0	0.698 970…	0.698 970…
0.5	−0.301 029…	−1	0.698 970…	1.698 970…
0.000 005	−5.301 029…	−6	0.698 970…	6.698 970…

Обратите внимание, что у всех приведенных в таблице чисел n{\displaystyle n} одна и та же мантисса M{\displaystyle M}, поскольку:

lg⁡(n)=lg⁡(x×10C)=lg⁡(x)+lg⁡(10C)=lg⁡(x)+C{\displaystyle \lg(n)=\lg \left(x\times 10^{C}\right)=\lg(x)+\lg \left(10^{C}\right)=\lg(x)+C},

где 1<x<10{\displaystyle 1<x<10} — значащая часть числа n{\displaystyle n}.

Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже — с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми. Но в этих и в последующих изданиях таблиц обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги (1783) появилось только в 1852 году в Берлине (таблицы Бремикера)^[6].

В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого^[7]. В СССР выпускались несколько сборников таблиц логарифмов^[8]:

1. Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
2. Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.

Теория логарифмов

История логарифмов

• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. I. Арифметика. Алгебра. Анализ. — 432 с.
• Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
• Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
• Успенский Я. В. Очерк истории логарифмов. — Петроград: Научное книгоиздательство, 1923. — 78 с.

1. ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187..
2. ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189..
3. ↑ Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
4. ↑ Элементарная математика, 1976, с. 94—100.
5. ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 406..
6. ↑ История математики, том II, 1970, с. 62..
7. ↑ Гнеденко Б. В. Очерки по истории математики в России, издание 2-е.. — М.: КомКнига, 2005. — С. 66.. — 296 с. — ISBN 5-484-00123-4.
8. ↑ Логарифмические таблицы //Большая советская энциклопедия.

ru.wikipedia.org

Таблица и формула для перехода от натуральных логарифмов к десятичным.

Таблица и формула для перехода от натуральных логарифмов к десятичным Если Вам известен натуральный логарифм какого-то числа Х (равный ln(X)), то десятичный логарифм этого числа (равный lg(X)) будет равен, согласно основным свойствам логарифмов : lg(X)=lg(e)*ln(X)=M*ln(X), т.е. десятичный логарифм числа, равен натуральному логарифму этого числа умноженному на число М=lg(e). Для быстрых оценок приводим табличку: Таблица для перехода от натуральных логарифмов к десятичным (таблица умножения на «число М» (у англосаксов это «число A») = lg е = 0,4342945…) Таблица для перехода от натуральных логарифмов к десятичным (таблица умножения на «число М» (у англосаксов это «число A») = lg е = 0,4342945…)   0 10 20 30 40 50 60 70 80 90 0 0,0000 4,3430 8,6859 13,0288 17,3718 21,7147 26,0577 30,4006 34,7436 39,0865 1 0,4343 4,7772 9,1202 13,4631 17,8061 22,1490 26,4920 30,8349 35,1779 39,5208 2 0,8686 5,2115 9,5545 13,8974 18,2404 22,5833 26,9263 31,2692 35,6122 39,9551 3 1,3029 5,6458 9,9888 14,3317 18,6747 23,0176 27,3606 31,7035 36,0464 40,3894 4 1,7372 6,0801 10,4231 14,7660 19,1090 23,4519 27,7948 32,1378 36,4807 40,8237 5 2,1715 6,5144 10,8574 15,2003 19,5433 23,8862 28,2291 32,5721 36,9150 41,2580 6 2,6058 6,9487 11,2917 15,6346 19,9775 24,3205 28,6634 33,0064 37,3493 41,6923 7 3,0401 7,3830 11,7260 16,0689 20,4118 24,7548 29,0977 33,4407 37,7836 42,1266 8 3,4744 7,8173 12,1602 16,5032 20,8461 25,1891 29,5320 33,8750 38,2179 42,5609 9 3,9086 8.2516 12,5945 16,9375 21,2804 25,6234 29,9663 34,3093 38,6522 42,9952

tehtab.ru

Десятичные и натуральные логарифмы

При решении логарифмов пока мы с вами сталкивались лишь с логарифмами, у которых были одинаковые основания.

Однако, зачастую приходится искать значения выражений, которые составлены из логарифмов по разным основаниям.

…

Заметим, что действия с логарифмами возможны только при одинаковых основаниях!

Тогда как поступают, если основания у логарифмов разные? Что нужно сделать, чтобы найти значения таких выражений? Так вот для этого вводятся десятичные и натуральные логарифмы, а также формула перехода от логарифма по одному основанию к логарифму по другому основанию.

Среди различных оснований для вычисления логарифмов чаще всего используется число 10. Логарифмы по такому основанию называют десятичными. Другими словами, десятичный логарифм числа  есть решение уравнения

 Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: , читают «десятичный логарифм числа ».

Что же касается натурального логарифма числа, то так называют логарифм этого числа по основанию , где  – иррациональное число, приближённо

Натуральный логарифм также имеет особое обозначение: , читают так: «натуральный логарифм числа ».

Кстати, иррациональное число е играет важную роль в математике и её приложениях. Число е можно представить как сумму:

……           

Все свойства, которые мы рассматривали для логарифмов по произвольному основанию, справедливы для десятичного и натурального логарифмов.

1., .                                                       1., .

2. .                                                                        2. .

 3. .                                                                          3. .

4. , , .                            4. , , .

5. , , .                              5. , , .

6. , , .                                    6. , , .

7. , , .                                   7. , , .

А теперь давайте разберёмся, как вычисляют десятичный и натуральный логарифмы. Проще всего значение логарифма можно найти с помощью инженерного калькулятора.

Итак, на инженерном калькуляторе для вычисления значения десятичного логарифма есть кнопка «log», для натурального логарифма – кнопка «ln».

Давайте посмотрим, как находят значения следующих логарифмов при помощи инженерного калькулятора: ; .

Найдём значение десятичного логарифма числа .

Для этого наберём число  и нажмём кнопку «log». Видим, на табло у нас высветились следующие цифры: …

На практике, конечно, мы округлим это число до нужного разряда.

Теперь найдём значение . Для этого наберём 15 и нажмём кнопку «ln». На табло у нас высветились следующие цифры: ….

Ранее мы с вами уже говорили, что с появлением логарифмов многие учёные занялись составлением логарифмических таблиц. Так, например, первые таблицы десятичных логарифмов для чисел от 1 до 1000 опубликовал в 1617 году оксфордский профессор математики Генри Бригс, с восемью (позже — с четырнадцатью) знаками.

Давайте рассмотрим принцип использования такой таблицы на примере двузначной таблицы десятичных логарифмов. На экране вы видите таблицу, в которой указаны значения десятичных логарифмов чисел от 1 до .

 

Левый столбец таблицы отвечает за число целых, а верхняя строка – за число десятых. Давайте найдём значение .

Итак, значение этого логарифма будет расположено на пересечении строки с числом 7 целых и столбца с числом 3 десятых. Как видим, значение нашего логарифма совпало с ранее найденным нами при помощи инженерного калькулятора, оно  .

А теперь найдём значение  при помощи таблицы натуральных логарифмов российского математика Брадиса.

На экране вы видите таблицу, в которой указаны значения натуральных логарифмов чисел от 1 до 99. Здесь левый столбец таблицы отвечает за число десятков, а верхняя строка – за число единиц.

Итак, значение  будет расположено на пересечении строки с числом 1 и столбца с числом 5. Как видим, значение нашего логарифма совпало с ранее найденным нами при помощи инженерного калькулятора, оно приближённо равно .

А как же быть с вычислением логарифмов по другим основаниям? Ведь при помощи инженерного калькулятора и таблиц логарифмов мы вычисляли только значения десятичных и натуральных логарифмов. Оказывается, достаточно знать значения только десятичных и натуральных логарифмов чисел, чтобы находить логарифмы чисел по любому основанию. Для этого используют формулу перехода от логарифма по одному основанию к логарифму по другому основанию.

Сейчас мы её с вами выведем. Итак, пусть .

Перейдём к показательной форме записи этого равенства, то есть получим .

Теперь прологарифмируем это равенство по основанию с. Другими словами, найдём логарифмы с основанием  обеих частей этого равенства. Получим:.

Применим к левой части равенства свойство логарифма степени, получим  .

Теперь разделим обе части равенства на . Получим .

Так как , то имеем .

Получившееся равенство и есть формула перехода от логарифма по одному основанию к логарифму по другому основанию.

Отметим, что эта формула верна, если выполняются следующие условия:

, , , , .

Из формулы перехода от логарифма по одному основанию к логарифму по другому основанию следует формула .

Также из формулы перехода от логарифма по одному основанию к логарифму по другому основанию при  и при  получаются формулы перехода к десятичным и натуральным логарифмам.

 и

А теперь давайте приступим к практической части нашего урока.

Задание 1. Найдите значение .

Решение.

Исходя из формулы  , имеем логарифм

При помощи калькулятора вычислим значения десятичного  – оно  

и   .

Подставим найденные значения в формулу перехода. Получим, что  .

Задание 2. Пусть , . Выразите через   и   число  .

Решение.

videouroki.net

Таблица логарифмов, формулы и примеры

Определения и таблица логарифмов

Иногда при расчетах необходимо знать значения логарифмов некоторых величин, но их нельзя вычислить точно. Было составлено ряд таблиц для упрощения вычислений.

Таблица натуральных логарифмов

Единицы Десятки	0	1	2	3	4	5	6	7	8	9
0	–	0	0,6931	1,0986	1,3863	1,6094	1,7918	1,9459	2,0794	2,1972
1	2,3026	2,3979	2,4849	2,5649	2,6391	2,7081	2,7726	2,8332	2,8904	2,9444
2	2,9957	3,0445	3,091	3,1355	3,1781	3,2189	3,2581	3,2958	3,3322	3,3673
3	3,4012	3,434	3,4657	3,4965	3,5264	3,5553	3,5835	3,6109	3,6376	3,6636
4	3,6889	3,7136	3,7377	3,7612	3,7842	3,8067	3,8286	3,8501	3,8712	3,8918
5	3,912	3,9318	3,9512	3,9703	3,989	4,0073	4,0254	4,0431	4,0604	4,0775
6	4,0943	4,1109	4,1271	4,1431	4,1589	4,1744	4,1897	4,2047	4,2195	4,2341
7	4,2485	4,2627	4,2767	4,2905	4,3041	4,3175	4,3307	4,3438	4,3567	4,3694
8	4,382	4,3944	4,4067	4,4188	4,4308	4,4427	4,4543	4,4659	4,4773	4,4886
9	4,4998	4,5109	4,5218	4,5326	4,5433	4,5539	4,5643	4,5747	4,5850	4,5951
10	4,6052	4,6151	4,625	4,6347	4,6444	4,654	4,6634	4,6728	4,6821	4,6913

Таблица и формула перехода от натуральных логарифмов к десятичным

Если известен натуральный логарифм некоторого числа , то десятичный логарифм этого числа, согласно свойствам логарифма, будет равен

   

где .

Итак, десятичный логарифм числа равен произведению натурального логарифма этого же числа и числа .

Десятки Единицы	0	1	2	3	4	5	6	7	8	9
0	0,0000	4,3430	8,6859	13,0288	17,3718	21,7147	26,0577	30,4006	34,7436	39,0865
1	0,4343	4,7772	9,1202	13,4631	17,8061	22,1490	26,4920	30,8349	35,1779	39,5208
2	0,8686	5,2115	9,5545	13,8974	18,2404	22,5833	26,9263	31,2692	35,6122	39,9551
3	1,3029	5,6458	9,9888	14,3317	18,6747	23,0176	27,3606	31,7035	36,0464	40,3894
4	1,7372	6,0801	10,4231	14,7660	19,1090	23,4519	27,7948	32,1378	36,4807	40,8237
5	2,1715	6,5144	10,8574	15,2003	19,5433	23,8862	28,2291	32,5721	36,9150	41,2580
6	2,6058	6,9487	11,2917	15,6346	19,9775	24,3205	28,6634	33,0064	37,3493	41,6923
7	3,0401	7,3830	11,7260	16,0689	20,4118	24,7548	29,0977	33,4407	37,7836	42,1266
8	3,4744	7,8173	12,1602	16,5032	20,8461	25,1891	29,5320	33,8750	38,2179	42,5609
9	3,9086	8.2516	12,5945	16,9375	21,2804	25,6234	29,9663	34,3093	38,6522	42,9952

Таблица и формула для перехода от десятичных логарифмов к натуральным.

Пусть известно значение десятичного логарифма некоторого положительного числа , тогда натуральный логарифм этого числа можно вычислить по формуле

   

то есть натуральный логарифм числа равен произведению десятичного логарифма этого числа и числа, обратного к числу :

   

Десятки Единицы	0	1	2	3	4	5	6	7	8	9
0	0,0000	23,026	46,052	69,078	92,103	115,129	138,155	161,181	184,207	207,233
1	2,3026	25,328	48,354	71,380	94,406	117,431	140,458	163,484	186,509	209,535
2	4,6052	27,631	50,657	73,683	96,709	119,734	142,760	165,786	188,812	211,838
3	6,9078	29,934	52,959	75,985	99,011	122,037	145,062	166,089	191,115	214,140
4	9,2103	32,236	55,262	78,288	101,314	124,340	147,365	170,391	193,417	216,443
5	11,513	34,539	57,565	80,590	103,616	126,642	149,668	172,694	195,720	218,746
6	13,816	36,841	59,867	82,893	105,919	128,945	151,971	174,997	198,022	221,048
7	16,118	39,144	62,170	85,196	108,221	131,247	154,273	177,299	200,325	223,351
8	18,421	41,447	64,472	87,498	110,524	133,550	156,576	179,602	202,627	225,653
9	20,723	43,749	66,775	89,801	112,827	135,853	158,878	181,904	204,930	227,956

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Натуральные логарифмы чисел (Таблица)

I. Таблица натуральные логарифмы чисел ¹⁾

¹⁾Натуральный логарифм числа, не содержащегося среди аргументов таблицы, находится следующим образом. Пусть ищется ln 753. Имеем: ln 753 = ln (7,53 • 10²) = ln 7,53 4- 2 ln 10. Первое слагаемое находим по таблице натуральных логарифмов, второе — по таблице III. Получаем: ln 753 = 2,0189 + 4,6052 = 6,6241. Таким же образом находим ln 0,00753 = ln (7,53 • 10″³) = 2,0189 — 6,9078 = -4,8889.

N	0	1	2	3	4	5	6	7	8	9
1,0	0,0000	0,0100	0,0198	0,0296	0,0392	0,0488	0,0583	0,0677	0,0770	0,0862
1,1	0,0953	0,1044	0,1133	0,1222	0,1310	0,1398	0,1484	0,1570	0,1655	0,1740
1,2	0,1823	0,1906	0,1989	0,2070	0,2151	0,2231	0,2311	0,2390	0,2469	0,2546
1,3	0,2624	0,2700	0,2776	0,2852	0,2927	0,3001	0,3075	0,3148	0,3221	0,3293
1,4	0,3365	0,3436	0,3507	0,3577	0,3646	0,3716	0,3784	0,3853	0,3920	0,3988
1,5	0,4055	0,4121	0,4187	0,4253	0,4318	0,4383	0,4447	0,4511	0,4574	0,4637
1,6	0,4700	0,4762	0,4824	0,4886	0,4947	0,5008	0,5068	0,5128	0,5188	0,5247
1,7	0,5306	0,5365	0,5423	0,5481	0,5539	0,5596	0,5653	0,5710	0,5766	0,5822
1,8	0,5878	0,5933	0,5988	0,6043	0,6098	0,6152	0,6206	0,6259	0,6313	0,6366
1,9	0,6419	0,6471	0,6523	0,6575	0,6627	0,6678	0,6729	0,6780	0,6831	0,6881
2,0	0,6931	0,6981	0,7031	0,7080	0,7129	0,7178	0,7227	0,7275	0,7324	0,7372
2,1	0,7419	0,7467	0,7514	0,7561	0,7608	0,7655	0,7701	0,7747	0,7793	0,7839
2,2	0,7885	0,7930	0,7975	0,8020	0,8065	0,8109	0,8154	0,8198	0,8242	0,8286
2,3	0,8329	0,8372	0,8416	0,8459	0,8502	0,8544	0,8587	0,8629	0,8671	0,8713
2,4	0,8755	0,8796	0,8838	0,8879	0,8920	0,8961	0,9002	0,9042	0,9083	0,9123
2,5	0,9163	0,9203	0,9243	0,9282	0,9322	0,9361	0,9400	0,9439	0,9478	0,9517
2,6	0,9555	0,9594	0,9632	0,9670	0,9708	0,9746	0,9783	0,9821	0,9858	0,9895
2,7	0,9933	0,9969	1,0006	1,0043	1,0080	1,0116	1,0152	1,0188	1,0225	1,0260
2,8	1,0296	1,0332	1,0367	1,0403	1,0438	1,0473	1,0508	1,0543	1,0578	1,0613
2,9	1,0647	1,0682	1,0716	1,0750	1,0784	1,0818	1,0852	1,0886	1,0919	1,0953
3,0	1,0986	1,1019	1,1053	1,1086	1,1119	1,1151	1,1184	1,1217	1,1249	1,1282
3,1	1,1314	1,1346	1,1378	1,1410	1,1442	1,1474	1,1506	1,1537	1,1569	1,1600
3,2	1,1632	1,1663	1,1694	1,1725	1,1756	1,1787	1,1817	1,1848	1,1878	1,1909
3,3	1,1939	1,1969	1,2000	1,2030	1,2060	1,2090	1,2119	1,2149	1,2179	1,2208
3,4	1,2238	1,2267	1,2296	1,2326	1,2355	1,2384	1,2413	1,2442	1,2470	1,2499
3,5	1,2528	1,2556	1,2585	1,2613	1,2641	1,2669	1,2698	1,2726	1,2754	1,2782
3,6	1,2809	1,2837	1,2865	1,2892	1,2920	1,2947	1,2975	1,3002	1,3029	1,3056
3,7	1,3083	1,3110	1,3137	1,3164	1,3191	1,3218	1,3244	1,3271	1,3297	1,3324
3,8	1,3350	1,3376	1,3403	1,3429	1,3455	1,3481	1,3507	1,3533	1,3558	1,3584
3,9	1,3610	1,3635	1,3661	1,3686	1,3712	1,3737	1,3762	1,3788	1,3813	1,3838
4,0	1,3863	1,3888	1,3913	1,3938	1,3962	1,3987	1,4012	1,4036	1,4061	1,4085
4,1	1,4110	1,4134	1,4159	1,4183	1,4207	1,4231	1,4255	1,4279	1,4303	1,4327
4,2	1,4351	1,4375	1,4398	1,4422	1,4446	1,4469	1,4493	1,4516	1,4540	1,4563
4,3	1,4586	1,4609	1,4633	1,4656	1,4679	1,4702	1,4725	1,4748	1,4770	1,4793
4,4	1,4816	1,4839	1,4861	1,4884	1,4907	1,4929	1,4951	1,4974	1,4996	1,5019
4,5	1,5041	1,5063	1,5085	1,5107	1,5129	1,5151	1,5173	1,5195	1,5217	1,5239
4,6	1,5261	1,5282	1,5304	1,5326	1,5347	1,5369	1,5390	1,5412	1,5433	1,5454
4,7	1,5476	1,5497	1,5518	1,5539	1,5560	1,5581	1,5602	1,5623	1,5644	1,5665
4,8	1,5686	1,5707	1,5728	1,5748	1,5769	1,5790	1,5810	1,5831	1,5851	1,5872
4,9	1,5892	1,5913	1,5933	1,5953	1,5974	1,5994	1,6014	1,6034	1,6054	1,6074
5,0	1,6094	1,6114	1,6134	1,6154	1,6174	1,6194	1,6214	1,6233	1,6253	1,6273
5,1	1,6292	1,6312	1,6332	1,6351	1,6371	1,6390	1,6409	1,6429	1,6448	1,6467
5,2	1,6487	1,6506	1,6525	1,6544	1,6563	1,6582	1,6601	1,6620	1,6639	1,6658
5,3	1,6677	1,6696	1,6715	1,6734	1,6752	1,6771	1,6790	1,6808	1,6827	1,6845
5,4	1,6864	1,6882	1,6901	1,6919	1,6938	1,6956	1,6974	1,6993	1,7011	1,7029
5,5	1,7047	1,7066	1,7084	1,7102	1,7120	1,7138	1,7156	1,7174	1,7192	1,7210
5,6	1,7228	1,7246	1,7263	1,7281	1,7299	1,7317	1,7334	1,7352	1,7370	1,7387
5,7	1,7405	1,7422	1,7440	1,7457	1,7475	1,7492	1,7509	1,7527	1,7544	1,7561
5,8	1,7579	1,7596	1,7613	1,7630	1,7647	1,7664	1,7681	1,7699	1,7716	1,7733
5,9	1,7750	1,7766	1,7783	1,7800	1,7817	1,7834	1,7851	1,7867	1,7884	1,7901
6,0	1,7918	1,7934	1,7951	1,7967	1,7984	1,8001	1,8017	1,8034	1,8050	1,8066
6,1	1,8083	1,8099	1,8116	1,8132	1,8148	1,8165	1,8181	1,8197	1,8213	1,8229
6,2	1,8245	1,8262	1,8278	1,8294	1,8310	1,8326	1,8342	1,8358	1,8374	1,8390
6,3	1,8405	1,8421	1,8437	1,8453	1,8469	1,8485	1,8500	1,8516	1,8532	1,8547
6,4	1,8563	1,8579	1,8594	1,8610	1,8625	1,8641	1,8656	1,8672	1,8687	1,8703
6,5	1,8718	1,8733	1,8749	1,8764	1,8779	1,8795	1,8810	1,8825	1,8840	1,8856
6,6	1,8871	1,8886	1,8901	1,8916	1,8931	1,8946	1,8961	1,8976	1,8991	1,9006
6,7	1,9021	1,9036	1,9051	1,9066	1,9081	1,9095	1,9110	1,9125	1,9140	1,9155
6,8	1,9169	1,9184	1,9199	1,9213	1,9228	1,9242	1,9257	1,9272	1,9286	1,9301
6,9	1,9315	1,9330	1,9344	1,9359	1,9373	1,9387	1,9402	1,9416	1,9430	1,9445
7,0	1,9459	1,9473	1,9488	1,9502	1,9516	1,9530	1,9544	1,9559	1,9573	1,9587
7,1	1,9601	1,9615	1,9629	1,9643	1,9657	1,9671	1,9685	1,9699	1,9713	1,9727
7,2	1,9741	1,9755	1,9769	1,9782	1,9796	1,9810	1,9824	1,9838	1,9851	1,9865
7,3	1,9879	1,9892	1,9906	1,9920	1,9933	1,9947	1,9961	1,9974	1,9988	2,0001
7,4	2,0015	2,0028	2,0042	2,0055	2,0069	2,0082	2,0096	2,0109	2,0122	2,0136
7,5	2,0149	2,0162	2,0176	2,0189	2,0202	2,0215	2,0229	2,0242	2,0255	2,0268
7,6	2,0281	2,0295	2,0308	2,0321	2,0334	2,0347	2,0360	2,0373	2,0386	2,0399
7,7	2,0412	2,0425	2,0438	2,0451	2,0464	2,0477	2,0490	2,0503	2,0516	2,0528
7,8	2,0541	2,0554	2,0567	2,0580	2,0592	2,0605	2,0618	2,0631	2,0643	2,0656
7,9	2,0669	2,0681	2,0694	2,0707	2,0719	2,0732	2,0744	2,0757	2,0769	2,0782
8,0	2,0794	2,0807	2,0819	2,0832	2,0844	2,0857	2,0869	2,0882	2,0894	2,0906
8,1	2,0919	2,0931	2,0943	2,0956	2,0968	2,0980	2,0992	2,1005	2,1017	2,1029
8,2	2,1041	2,1054	2,1066	2,1078	2,1090	2,1102	2,1114	2,1126	2,1138	2,1150
8,3	2,1163	2,1175	2,1187	2,1199	2,1211	2,1223	2,1235	2,1247	2,1258	2,1270
8,4	2,1282	2,1294	2,1306	2,1318	2,1330	2,1342	2,1353	2,1365	2,1377	2,1389
8,5	2,1401	2,1412	2,1424	2,1436	2,1448	2,1459	2,1471	2,1483	2,1494	2,1506
8,6	2,1518	2,1529	2,1541	2,1552	2,1564	2,1576	2,1587	2,1599	2,1610	2,1622
8,7	2,1633	2,1645	2,1656	2,1668	2,1679	2,1691	2,1702	2,1713	2,1725	2,1736
8,8	2,1748	2,1759	2,1770	2,1782	2,1793	2,1804	2,1815	2,1827	2,1838	2,1849
8,9	2,1861	2,1872	2,1883	2,1894	2,1905	2,1917	2,1928	2,1939	2,1950	2,1961
9,0	2,1972	2,1983	2,1994	2,2006	2,2017	2,2028	2,2039	2,2050	2,2061	2,2072
9,1	2,2083	2,2094	2,2105	2,2116	2,2127	2,2138	2,2148	2,2159	2,2170	2,2181
9,2	2,2192	2,2203	2,2214	2,2225	2,2235	2,2246	2,2257	2,2268	2,2279	2,2289
9,3	2,2300	2,2311	2,2322	2,2332	2,2343	2,2354	2,2364	2,2375	2,2386	2,2396
9,4	2,2407	2,2418	2,2428	2,2439	2,2450	2,2460	2,2471	2,2481	2,2492	2,2502
9,5	2,2513	2,2523	2,2534	2,2544	2,2555	2,2565	2,2576	2,2586	2,2597	2,2607
9,6	2,2618	2,2628	2,2638	2,2649	2,2659	2,2670	2,2680	2,2690	2,2701	2,2711
9,7	2,2721	2,2732	2,2742	2,2752	2,2762	2,2773	2,2783	2,2793	2,2803	2,2814
9,8	2,2824	2,2834	2,2844	2,2854	2,2865	2,2875	2,2885	2,2895	2,2905	2,2915
9,9	2,2925	2,2935	2,2946	2,2956	2,2966	2,2976	2,2986	2,2996	2,3006	2,3016

 

II. Таблица для перехода от натуральных логарифмов к десятичным 

(таблица умножения на М = log е = 0,4342945…)

	0	10	20	30	40	50	60	70	80	90
0	0,0000	4,3430	8,6859	13,0288	17,3718	21,7147	26,0577	30,4006	34,7436	39,0865
1	0,4343	4,7772	9,1202	13,4631	17,8061	22,1490	26,4920	30,8349	35,1779	39,5208
2	0,8686	5,2115	9,5545	13,8974	18,2404	22,5833	26,9263	31,2692	35,6122	39,9551
3	1,3029	5,6458	9,9888	14,3317	18,6747	23,0176	27,3606	31,7035	36,0464	40,3894
4	1,7372	6,0801	10,4231	14,7660	19,1090	23,4519	27,7948	32,1378	36,4807	40,8237
5	2,1715	6,5144	10,8574	15,2003	19,5433	23,8862	28,2291	32,5721	36,9150	41,2580
6	2,6058	6,9487	11,2917	15,6346	19,9775	24,3205	28,6634	33,0064	37,3493	41,6923
7	3,0401	7,3830	11,7260	16,0689	20,4118	24,7548	29,0977	33,4407	37,7836	42,1266
8	3,4744	7,8173	12,1602	16,5032	20,8461	25,1891	29,5320	33,8750	38,2179	42,5609
9	3,9086	8.2516	12,5945	16,9375	21,2804	25,6234	29,9663	34,3093	38,6522	42,9952

 

III. Таблица для перехода от десятичных логарифмов к натуральным

(таблица умножения на i = In 10 = 2,302585)

	0	10	20	30	40	50	60	70	80	90
0	0,0000	23,026	46,052	69,078	92,103	115,129	138,155	161,181	184,207	207,233
1	2,3026	25,328	48,354	71,380	94,406	117,431	140,458	163,484	186,509	209,535
2	4,6052	27,631	50,657	73,683	96,709	119,734	142,760	165,786	188,812	211,838
3	6,9078	29,934	52,959	75,985	99,011	122,037	145,062	166,089	191,115	214,140
4	9,2103	32,236	55,262	78,288	101,314	124,340	147,365	170,391	193,417	216,443
5	11,513	34,539	57,565	80,590	103,616	126,642	149,668	172,694	195,720	218,746
6	13,816	36,841	59,867	82,893	105,919	128,945	151,971	174,997	198,022	221,048
7	16,118	39,144	62,170	85,196	108,221	131,247	154,273	177,299	200,325	223,351
8	18,421	41,447	64,472	87,498	110,524	133,550	156,576	179,602	202,627	225,653
9	20,723	43,749	66,775	89,801	112,827	135,853	158,878	181,904	204,930	227,956

_______________

Источник информации: Справочник по высшей математике / М. Я. Выгодский. — М.: ACT: Астрель, 2006.

infotables.ru