Законы регулирования: П, ПИ, ПИД
П-закон регулирования
Руководствуясь таблицей 1 можно утверждать, что наибольшее быстродействие обеспечивает П-закон управления, — исходя из соотношения tp / Td.
Однако, если коэффициент усиления П-регулятора Кр мал (чаще всего это наблюдается в системах с запаздыванием), то такой регулятор не обеспечивает высокой точности регулирования, т.к. в этом случае велика величина статической ошибки.
Если Кр > 10, то П-регулятор приемлем, а если Если Кр < 10, то требуется введение в закон управления интегральной составляющей.
ПИ-закон регулирования
Наиболее распространенным на практике является ПИ-регулятор, который обладает следующими достоинствами:
- Обеспечивает нулевую статическую ошибку регулирования.
- Достаточно прост в настройке, т.к. настраиваются только два параметра, а именно коэффициент усиления Кр и постоянная времени интегрирования Ti. В таком регуляторе имеется возможность оптимизации величины отношения Кр/Ti—min, что обеспечивает управление с минимально возможной среднеквадратичной ошибкой регулирования.

- Малая чувствительность к шумам в канале измерения (в отличие от ПИД-регулятора).
ПИД-закон регулирования
Для наиболее ответственных контуров регулирования можно рекомендовать использование ПИД-регулятора, обеспечивающего наиболее высокое быстродействие в системе.
Однако следует учитывать, что это условие выполняется только при его оптимальных настройках (настраиваются три параметра).
С увеличением запаздывания в системе резко возрастают отрицательные фазовые сдвиги, что снижает эффект действия дифференциальной составляющей регулятора. Поэтому качество работы ПИД-регулятора для систем с большим запаздыванием становится сравнимо с качеством работы ПИ-регулятора.
Кроме этого, наличие шумов в канале измерения в системе с ПИД-регулятором приводит к значительным случайным колебаниям управляющего сигнала регулятора, что увеличивает дисперсию ошибки регулирования и износ исполнительного механизма.
Таким образом, ПИД-регулятор следует выбирать для систем регулирования, с относительно малым уровнем шумов и величиной запаздывания в объекте управления. Примерами таких систем является системы регулирования температуры.
Примерами таких систем является системы регулирования температуры.
ПИД регуляторы позволяют для объектов постоянной времени обьекта (инерционностью) Тис малым транспортным запаздыванием Td<0,2T обеспечить хорошее качество регулирования: рассогласование регулирования E < 1% (от заданной точки), достаточное малое время выхода на режим и невысокую чувствительность к внешним возмущениям. Иногда (в некоторых обьектах регулирования с существенным транспортным запаздыванием), при Td>0,2T ПИД регулятор обладает плохим качеством регулирования. В этом случае хорошие качественные показатели обеспечивают системы управления с моделью объекта.
Следует иметь в виду, что при неточном задании коэффициентов настройки ПИД регулятор может иметь худшие показатели, чем двухпозиционный регулятор и даже перейти в режим автоколебаний. Для типовых П-, ПИ-, ПИД регуляторов известны простейшие аналитические и табличные методы настройки (например методики Циглера-Никольса).
Вопросы настройки П-, ПИ-, ПД-, ПИД-регуляторов расмотрены в разделе Методы настройки регуляторов.
Энергетическое образование
2. Пропорциональное регулирование (П-закон)
Простейший регулятор – пропорциональный или П-регулятор – это простой усилитель с передаточной функцией $C(s)=K$. Его выход – это ошибка управления $e(t)$, умноженная на коэффициент $K$. С помощью П-регулятора можно управлять любым устойчивым объектом, однако он дает относительно медленные переходные процессы и ненулевую статическую ошибку.
Переходный процесс в контуре с П-регулятором при разных K показан на рисунке ниже.
Изменение переменной y(t) во времени при подаче единичного скачка r(t) на вход системы при разных K.При малых система имеет малое перерегулирование, но большую статическую погрешность (при $K=1$ погрешность составляет 50%). С ростом $K$ погрешность уменьшается, но возрастает перерегулирование.
При цифровой реализации П-закона регулирования выходной сигнал регулятора $Y_i$ пропорционален величине рассогласования $E_i$, т.е.
где $X_p$ – полоса пропорциональности, в пределах которой справедлива эта формула; $E_i$ – разность между заданным $Т_уст$ и текущей $Т_i$ значениями измеряемой величины или рассогласование.
Полоса пропорциональности $X_p$, как и отклонение $E$, выражается в единицах контролируемого параметра. Чем шире полоса пропорциональности $X_p$, тем меньше величина выходного сигнала $Y$ при одном и том же отклонении $E$. Вне полосы пропорциональности выходной сигнал $Y$ равен 0 или 100 %.
При действии П-закона совместно с реле регулятор выдает импульсы, в которых присутствует только пропорциональная составляющая величины выходного сигнала.
Выходной сигнал П-регулятора и длительность управляющих импульсов при различных значениях $X_p$ и $E=10$. Зависимость выходного сигнала П-регулятора от рассогласования при различных значениях $X_p$.
Зависимость выходного сигнала П-регулятора от рассогласования при различных значениях $X_p$.Законы регулирования в автоматике с примерами
Закон регулирования — это зависимость перемещения регулирующего органа от отклонения регулируемой переменной. Качество регулирования обеспечивается выбором закона регулирования. Наибольшее распространение получили следующие пять основных законов регулирования: двухпозиционный, пропорциональный, интегральный, дифференциальный и пропорционально-интегрально-дифференциальный (ПИД).
Система ручного регулирования уровняОбратите внимание на теорию автоматического регулирования и на приборы для регулирования.
Двухпозиционный закон регулирования — это «Двухпозиционное регулирование», которое называют еще «Старт-стопное регулирование». Чтобы моделировать двухпозиционный режим регулирования, оператор на рисунке выше устанавливал бы регулирующий клапан в одно из двух крайних положений: или полностью открыт, или полностью закрыт, то есть «включено» или «выключено».
Чтобы моделировать пропорциональный закон регулирования, оператор непрерывно устанавливал бы регулирующий клапан в положение, отвечающее произошедшему на данный момент изменению уровня. Так, например, если уровень понизился немного, оператор откроет клапан немного; если уровень понизился еще больше, оператор увеличит степень открытия клапана. Наоборот, если уровень несколько повысится, оператор уменьшит степень открытия клапана на соответствующую величину. Таким образом, моделируя пропорциональное регулирование, оператор непрерывно в соответствии с изменением уровня изменяет положение клапана. Регулирование уровня при этом будет выполняться более эффективно, чем при простом открытии и закрытии клапана. Когда изменения уровня прекращаются, оператор прекращает позиционирование клапана.
Так как при пропорциональном регулировании выходной корректирующий сигнал вырабатывается на изменения регулируемой переменной процесса, пропорциональный регулятор не дает выходного управляющего сигнала, если регулируемая переменная процесса не изменяется. Например, когда уровень в резервуаре изменяется, оператор открывает или закрывает клапан пропорционально этим изменениям. Когда изменения уровня прекращаются, оператор останавливает позиционирование клапана. При этом уровень установится на некоторой отметке, но это может не быть заданное значение уровня. Это означает, что при пропорциональном регулировании может быть смещение регулируемой переменной процесса или ошибка регулирования. В определенных системах это вполне приемлемо. Если же смещение регулируемой переменной не допускается, надо применить другой закон регулирования: интегральный, при котором обеспечивается возвращение регулируемой переменной к уставке.
Чтобы моделировать закон интегрального регулирования, оператор продолжает открывать или закрывать клапан так долго пока уровень отклоняется от уставки в независимости от того происходят ли при этом произвольные изменения уровня или не происходят. Так, например, если уровень немного понизился, оператор приоткроет клапан немного. Затем, даже если уровень перестал изменяться, оператор продолжит открывать клапан пока уровень не возвратится к заданному значению (уставке).
Так, например, если уровень немного понизился, оператор приоткроет клапан немного. Затем, даже если уровень перестал изменяться, оператор продолжит открывать клапан пока уровень не возвратится к заданному значению (уставке).
Рисунок выше иллюстрирует процесс, который может требовать применения другого закона регулирования. Этот процесс — тот же самый процесс поддержания уровня из первого примера, отличающийся лишь тем, что емкость резервуара много больше, в то время как питательная труба остается той же самой. Это означает, что, когда оператор открывает или закрывает клапан как прежде, оказывается меньшее непосредственное влияние на уровень в резервуаре. При увеличения уровня, пропорциональное регулирование могло бы отработать воздействия, направленные на снижение уровня, но действие не было бы достаточно быстрым, чтобы поддерживать уровень внутри желательных ограничений.
Закон дифференциального регулирования используется, чтобы предотвратить чрезмерное отклонение регулируемой переменной от уставки, вырабатывая корректирующее воздействие пропорциональное скорости отклонения. Так, моделируя дифференциальный закон регулирования, оператор изменяет степень открытия регулирующего клапана в соответствии со скоростью возрастания отклонения уровня от уставки. Например, если уровень начал понижаться, оператор быстро увеличит степень открытия приточного клапана (при чем эти изменения положения клапана большие, чем при чисто пропорциональном законе регулирования), чтобы замедлить скорость изменения уровня и, в конечном счете, стабилизировать уровень. Если уровень начал быстро понижаться, оператор должен быстро и значительно открыть клапан, чтобы замедлить скорость падения уровня и потом его стабилизировать.
Так, моделируя дифференциальный закон регулирования, оператор изменяет степень открытия регулирующего клапана в соответствии со скоростью возрастания отклонения уровня от уставки. Например, если уровень начал понижаться, оператор быстро увеличит степень открытия приточного клапана (при чем эти изменения положения клапана большие, чем при чисто пропорциональном законе регулирования), чтобы замедлить скорость изменения уровня и, в конечном счете, стабилизировать уровень. Если уровень начал быстро понижаться, оператор должен быстро и значительно открыть клапан, чтобы замедлить скорость падения уровня и потом его стабилизировать.
Последним мы рассмотрим пропорционально-интегрально-дифференциальный закон регулирования. Чтобы воспроизвести этот закон регулирования, оператор изменяет положение регулирующего клапана в зависимости от величины отклонения, скорости изменения и продолжительности рассогласования. Другими словами, оператор в этом случае объединяет пропорциональный, интегральный и дифференциальный законы регулирования.
ПИД-регулятор, что это такое
Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью.
ПИД (от англ. P-proportional, I-integral, D-derivative) — регулятором называется устройство, применяемое в контурах управления, оснащенных звеном обратной связи. Данные регуляторы используют для формирования сигнала управления в автоматических системах, где необходимо достичь высоких требований к качеству и точности переходных процессов.
Управляющий сигнал ПИД-регулятора получается в результате сложения трех составляющих: первая пропорциональна величине сигнала рассогласования, вторая — интегралу сигнала рассогласования, третья — его производной. Если какой-то из этих трех компонентов не включен в процесс сложения, то регулятор будет уже не ПИД, а просто пропорциональным, пропорционально-дифференцирующим или пропорционально-интегрирующим.
Первый компонент — пропорциональный
Выходной сигнал дает пропорциональная составляющая. Сигнал этот приводит к противодействию текущему отклонению входной величины, подлежащей регулированию, от установленного значения. Чем больше отклонение — тем больше и сигнал. Когда на входе значение регулируемой величины равно заданному, то выходной сигнал становится равным нулю.
Сигнал этот приводит к противодействию текущему отклонению входной величины, подлежащей регулированию, от установленного значения. Чем больше отклонение — тем больше и сигнал. Когда на входе значение регулируемой величины равно заданному, то выходной сигнал становится равным нулю.
Если оставить только эту пропорциональную составляющую, и использовать только ее, то значение величины, подлежащей регулированию, не стабилизируется на правильном значении никогда. Всегда есть статическая ошибка, равная такому значению отклонения регулируемой величины, что выходной сигнал стабилизируется на этом значении.
К примеру, терморегулятор управляет мощностью нагревательного прибора. Выходной сигнал уменьшается по мере приближения требуемой температуры объекта, и сигнал управления стабилизирует мощность на уровне тепловых потерь. В итоге заданного значения температура так и не достигнет, ибо нагревательный прибор в просто должен будет быть выключен, и начнет остывать (мощность равна нулю).
Больше коэффициент усиления между входом и выходом — меньше статическая ошибка, но если коэффициент усиления (по сути — коэффициент пропорциональности) будет слишком большим, то при условии наличия задержек в системе (а они зачастую неизбежны), в ней вскоре начнутся автоколебания, а если увеличить коэффициент еще больше — система попросту утратит устойчивость.
Или пример позиционирования двигателя с редуктором. При малом коэффициенте нужное положение рабочего органа достигается слишком медленно. Увеличить коэффициент — реакция получится более быстрая. Но если увеличивать коэффициент дальше, то двигатель «перелетит» правильную позицию, и система не перейдет быстро к требуемому положению, как хотелось бы ожидать. Если теперь увеличивать коэффициент пропорциональности дальше, то начнутся осцилляции около нужной точки — результат снова не будет достигнут…
Второй компонент — интегрирующий
Интеграл по времени от величины рассогласования — есть основная часть интегрирующей составляющей. Она пропорциональна этому интегралу. Интегрирующий компонент используется как раз для исключения статической ошибки, поскольку регулятор со временем учитывает статическую погрешность.
Она пропорциональна этому интегралу. Интегрирующий компонент используется как раз для исключения статической ошибки, поскольку регулятор со временем учитывает статическую погрешность.
В отсутствие внешних возмущений, через какое-то время подлежащая регулированию величина будет стабилизирована на правильном значении, когда пропорциональная составляющая окажется равной нулю, и точность выхода будет целиком обеспечена интегрирующей составляющей. Но интегрирующая составляющая тоже может породить осцилляции около точки позиционирования, если коэффициент не подобран правильно.
Третий компонент — дифференцирующий
Темпу изменения отклонения величины, подлежащей регулированию, пропорциональна третья — дифференцирующая составляющая. Она необходима для того, чтобы противодействовать отклонениям (вызванным внешними воздействиями или задержками) от правильного положения, прогнозируемого в будущем.
Теория работы ПИД-регулятора
Как вы уже поняли, ПИД-регуляторы применяют для поддержания заданного значения х0 некоторой одной величины, благодаря изменению значения u другой величины. Есть уставка или заданное значение х0, и есть разность или невязка (рассогласование) е = х0-х. Если система линейна и стационарна (практически это вряд ли возможно), то для задания u справедливы нижеследующие формулы:
Есть уставка или заданное значение х0, и есть разность или невязка (рассогласование) е = х0-х. Если система линейна и стационарна (практически это вряд ли возможно), то для задания u справедливы нижеследующие формулы:
В этой формуле вы видите коэффициенты пропорциональности для каждого из трех слагаемых.
Практически в ПИД-регуляторах используют для настройки другую формулу, где коэффициент усиления применен сразу ко всем компонентам:
Практическая сторона ПИД-регулирования
Практически теоретический анализ ПИД-регулируемых систем редко применяют. Сложность состоит в том, что характеристики объекта управления неизвестны, и система практически всегда нестационарна и нелинейна.
Реально работающие ПИД-регуляторы всегда имеют ограничение рабочего диапазона снизу и сверху, это принципиально объясняет их нелинейность. Настройка поэтому практически всегда и везде производится экспериментальным путем, когда объект управления подключен к системе управления.
Использование величины, формируемой программным алгоритмом управления, обладает рядом специфических нюансов. Если речь, например, о регулировке температуры, то часто требуется все же не одно, а сразу два устройства: первое управляет нагревом, второе — охлаждением. Первое подает разогретый теплоноситель, второе — хладагент. Три варианта практических решений может быть рассмотрено.
Первый — близок к теоретическому описанию, когда выход — аналоговая и непрерывная величина. Второй — выход в форме набора импульсов, например для управления шаговым двигателем. Третий — ШИМ-управление, когда выход с регулятора служит для задания ширины импульсов.
Сегодня системы автоматизации практически все строятся на основе ПЛК, и ПИД-регуляторы представляют собой специальные модули, добавляемые к управляющему контроллеру или вообще реализуемые программно путем загрузки библиотек. Для правильной настройки коэффициентов усиления в таких контроллерах, их разработчики предоставляют специальное ПО.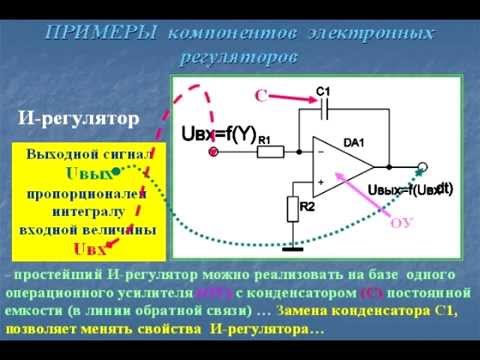
Ранее ЭлектроВести писали, что Президент Украины подписал закон, который выполняет решение Конституционного суда и регулирует деятельность НКРЭКУ.
По материалам: electrik.info.
принцип действия, схема и т.д.
П-регулирование, оно же пропорциональное регулирование — это способ регулирования, основанный на законе пропорционального регулирования, при котором характеристики выходного сигнала пропорциональны характеристикам входного сигнала.
Другими словами, если вход пропорционального регулятора возрастет на некоторую величину, вывод регулятора увеличится на некоторую соответствующую величину и, если вход уменьшится, выход тоже уменьшится на соответствующую величину.
Обратите внимание на теорию автоматического регулирования и на приборы для регулирования.
Закон П-регулирования
Пропорциональный закон регулирования — это процесс регулирования, при котором относительное изменение регулирующего воздействия (выходного сигнала регулятора) пропорционально относительному отклонению регулируемой величины.
Принцип работы П-регулирования
При пропорциональном регулировании ступенчатый сигнал на вводе приводит к ступенчатому изменению сигнала на выходе, а линейно изменяющийся сигнал на входе дает линейно изменяющийся сигнал на выходе. Иначе говоря, в пропорциональном регуляторе относительное изменение выходного сигнала (регулирующего воздействия) пропорционально относительному отклонению регулируемой величины (входного сигнала регулятора). Это позволяет устранить зону нечувствительности, характерную для двухпозиционного регулирования.
Простая система автоматического регулированияКогда уровень воды в резервуаре изменяется, первичный чувствительный элемент (1) преобразовывает изменение в механическое движение. Механическое движение измеряется измерительным элементом (2) и преобразовывается в пневматический сигнал. Пневматический сигнал передается регулирующему элементу (регулятору) (3), который измеряет сигнал, сравнивает его с уставкой, вычисляет разность и вырабатывает сигнал управления (корректирующее воздействие), передаваемый к конечному элементу системы регулирования (4).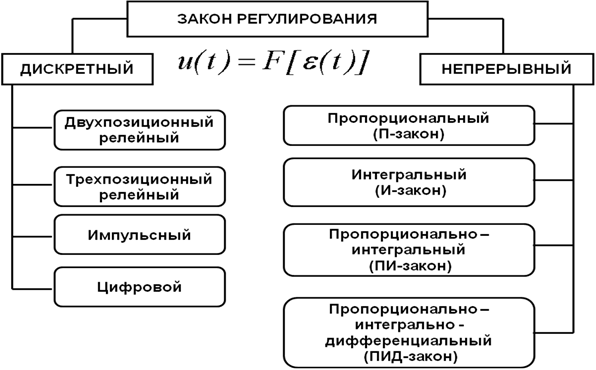 Конечный элемент регулирования (в нашем примере пневматический регулирующий клапан) перемещается согласно выходному сигналу регулятора, изменяя приток воды в резервуар.
Конечный элемент регулирования (в нашем примере пневматический регулирующий клапан) перемещается согласно выходному сигналу регулятора, изменяя приток воды в резервуар.
7.2 Законы регулирования.
К числу реализуемых законов регулирования в теплоэнергетике относят:
— пропорциональный закон регулирования, П – закон;
— интегральный закон, И – закон;
— пропорционально — -интегральный закон, ПИ – закон;
— пропорционально – дифференциальный закон, ПД – закон;
— пропорционально – интегрально — дифференциальный закон, ПИД — закон;
Действие регулятора всегда направленно в сторону противоположную отклонению регулируемого параметра, поэтому в уравнениях, описывающих законы регулирования, регулирующее воздействие в сторону объекта регулирования всегда со знаком действия, противоположным отклонению регулируемой величины.
Пропорциональный закон регулирования, П — закон.
Уравнение закона регулирования (7-1)
В этом случае каждому значению входного параметра соответствует определенное положение регулировочного органа. Регулятор, реализующий П-закон регулирования, называется П-регулятором.
Передаточная функция регулятора . (7-2)
Статическая характеристика пропорционального регулирования (Рис. 7.2)
Рис. 7.2 Статическая характеристика.
— коэффициент передачи (усиления) регулятора
Для замкнутой АСР, состоящей из ОР и П — регулятора, характерно наличие остаточного отклонения регулируемой величины или ошибки, по окончанию процесса регулирования.
-коэффициент неравномерности или статизм регулирования для П – регулятора, определяет величину погрешности регулирования в установившихся процессах.
Динамическая характеристика П — регулятора. (Рис. 7.3)
Рис. 7.3 Динамическая характеристика П-регулятора.
Динамическая характеристика АСР с П-регулятором (Рис. 7.4).
Рис. 7.4 Переходные процессы в АСР с П-регулятором при управляющем (1) и возмущающем (2) воздействии.
Настроечным параметром П – регулятора является — его коэффициент неравномерности. При настройке устанавливают допустимые отклонение регулируемого параметра от заданного значения в статике – погрешность регулирования.
Достоинство П — регуляторов – динамичность; регулятор вступает в действие сразу после получения сигнала на его вход .Недостатком регулятора является наличие ошибки регулирования в статике. От ошибки не избавится, так как статическая характеристика П- регулятора имеет наклон, величина которого зависит от коэффициента неравномерности .
Интегральный закон регулирования, И – закон.
Уравнение закона регулирования (7-3)
Проинтегрировав уравнение (7.3) получим
,
где — коэффициент передачи, характеризующий скорость нарастания сигнала на выходе после нанесения воздействия.
Передаточная функция интегрального (И) регулятора
(7-4)
Другая формула записи И- закона регулирования
(7-5)
Передаточная функция интегрального (И) регулятора
, (7-6)
— условный коэффициент передачи И- регулятора,
— условная постоянная времени интегрирования.
Скоростная характеристика И – регулятора
Рис. 7.5 Скоростная характеристика И-регулятора
Чем больше , тем больше угол наклонапри одинаковой величине воздействия.
Статическая характеристика регулятора (рис.7.6)
Рис. 7.6 Статическая характеристика И-регулятора
Достоинство И- регулятора — отсутствие статической погрешности регулирования.
Динамическая характеристика И-регулятора (Рис.7.7).
Рис. 7.7 Динамическая характеристика И-регулятора
Чем больше по величине сигнал на входе регулятора, тем выше скорость перемещения регулировочного органа при одном и том же воздействии. Чем больше , тем больше скорость перемещения регулировочного органа.
Пропорционально — интегральный закон регулирования. ПИ – закон.
Преимущества П — регулятора (его динамичность) и И — регулятора (отсутствие в статике погрешности регулирования) объединены в ПИ – законе и соответственно в ПИ-регуляторе, когда регулировочные органы перемещаются со скоростью, пропорциональной величине и скорости изменения входного сигнала поступающего на ПИ – регулятор.
Уравнение
(7-7)
Проинтегрировав уравнение (7.7), получим (7.8)
(7-8)
Передаточная функция для ПИ-регулятора.
(7-9)
Динамическая характеристика ПИ-регулятора.
Рис. 7.5 Динамическая характеристика ПИ-регулятора
В замкнутой одноконтурной АСР, состоящей из ОР и ПИ-регулятора отсутствует остаточная погрешность регулируемого параметра. В то же время при установившемся значении регулируемого параметра регулирующий орган может занимать различные положения.
Параметры настройки ПИ – регулятора: и..
Пропорционально-дифференциальный закон регулирования, ПД – закон.
П, И, ПИ-регуляторы реагируют только на возникшие нарушения технологического процесса. Если же регулируемая величина в какой то момент времени начинает быстро отклонятся от заданного значения, то это значит, что на ОР поступило значительное воздействие и что отклонениев результате этого может быть так же значительным.
В этом случае целесообразно, чтобы регулятор вырабатывал регулирующее воздействие пропорционально скорости отклонения от.
С этой целью в состав АСР вводят дифференциатор- устройство, позволяющее формировать в законе регулирования сигнал, пропорциональный скорости изменения регулируемой величины (Рис. 7.9).
Рис. 7.9 структурная схема ПД-регулятора
Д-р – дифференциатор, Р-р – П—регулятор
Закон регулирования:
а) для идеального дифференциатора
(7-10)
Передаточная функция ПД — регулятора
(7-11)
б) для реального дифференциатора
(7-12)
Передаточная функция реального дифференциатора
(7-13)
Здесь — коэффициент передачи собственно регулятора,
— коэффицент усиления дифференциатора,
— постоянная времени дифференциатора – время действия дифференциатора.
При отклонении регулируемого параметра на выходе регулятора мгновенно появляется сигнал от действия дифференцирующего устройства и затем сигнал от пропорциональной его составляющей.
В установившемся движении АСР сигнал от дифференциатора спадает до нуля и остается сигнал П — составляющей, равный .
Динамическая характеристика ПД-регулятора (Рис.7.10)
Основные законы регулирования. П & И
Задача системы регулирования – преобразовать возмущение в регулирующее воздействие.
То есть мы можем записать, что: y(t)=K·x(t)
Вот этот коэффициент К – это коэффициент, который может быть просто числом, а может быть выражением. Поэтому говорят, что К – это не коэффициент, а оператор и обозначают его W(t). Мало того, этому оператору присвоено имя передаточная функция.
Изобразим:
где, Wоб(t) – передаточная функция самого объекта управления, Wр(t) – передаточная функция регулятора.
Существуют понятия линейная система или нелинейная, непрерывная или дискретная. В большинстве случаев у нас системы нелинейные, т.е. W≠K, и цифровые, т.е. дискретные.
Регуляторы бывают разные:
П-регулятор: Данный регулятор представляет собой регулятор, работающий по следующей формуле:
М=Кр(Хзад.—Хизм.)
М – это воздействие регулятора на объект, целью которого является компенсация изменения регулируемой величины, возникающей из-за нанесения возмущения (Хзад — Хизм), перед тем, как нанести управляющее воздействие.
Схема работы такого регулятора:
Таким образом, видно, что для того, чтобы скомпенсировать ∆Х=6°С, необходимо переместить регулирующий орган в положение 5 В выходного сигнала.
Вычислим Кр:
Кр=5/6
Формула П-регулятора при этом будет:
M(t)=(5/6)·(Хзад.- Хизм.)(t)
Таким образом, можно приблизительно определить Кр пропорционального регулятора.
Достоинство данного регулятора – скорость.
Недостатки: ошибка (очень важный параметр) после окончания регулирования – статическая ошибка. Она возникает из-за того, что П-регулятор дает команду только тогда, когда M(t2)-M(t1)≠0, т.е. если после нанесения регулирования M(t2)=M(t1), то регулятор больше пересчитываться не будет. Физически это происходит из-за неидеальности исполнительных механизмов, каналов измерения, а также инерционности объектов, которую П-регулятор учесть не может.
И-регулятор: Данный регулятор учитывает все те проблемы, которые возникли при П-регулировании.
Если мы проинтегрируем во времени (сложим) все (Хзад.-Хизм.) и пропорционально ∫(Хзад.-Хизм.)dt выдадим управляющее воздействие, то такая система успокоится только тогда, когда не от чего будет брать ∫, то есть тогда, когда Хзад.-Хизм.= 0. В этом случае будут учитываться и люфты, и погрешности измерений, а также и инерционность объектов.
Однако, обратим внимание на формулу И-регулятора:
где, Ки – коэффициент пропорциональности интегрирующей составляющей.
Обычно рассматривают величину, обратно-пропорциональную Ки, Ти=1/Ки – постоянная времени интегрирования.
Так вот ∫ изменяется очень медленно, по мере накопления ошибки регулирования, то есть данный регулятор имеет существенный недостаток – это медленная скорость приведения регулируемого параметра к заданному значению.
Недостатки П и И регуляторов компенсируются путем соединения их в один ПИ-регулятор.
Совместим формулу П-регулятора с формулой И-регулятора:
Данный ПИ-регулятор работает следующим образом: при возникновении сигнала рассогласования (Хзад.- Хизм.≠0) сразу вступает в работу П-составляющая и происходит перемещение исполнительного механизма пропорционально Кр(Хзад.- Хизм.). После этого вступает в работу И-составляющая, которая перемещает исполнительный механизм по закону (1/Ти )·∫(Хзад.- Хизм.)dt до тех пор, пока Хзад. не сравняется с Хизм..
Например: если t воды в чайнике изменилась от заданной t на 20°С, то П-составляющая подвинет ручку конфорки на 18°С, а И-составляющая уберет оставшихся 2°С разницы.
В настоящее время большинство инженерных систем управляются ПИ-регулятором.
Литература:
1. В. А. БЕСЕКЕРСКИЙ, А. Н. ГЕРАСИМОВ, Л. Ф. ПОРФИРЬЕВ, Е. А. ФАБРИКАНТ, С. М. ФЕДОРОВ, В. И. ЦВЕТКОВ. Сборник задач по теории автоматического регулирования и управления
2. Айзерман М. А. Лекции по ТАУ. Гостехиздат, 1966г.
3. Иващенко Н. Н. Автоматическое регулирование. Машгиз.1958г.
4. 8. Школа автоматчиков. УРОК №5. Основы автоматизации
4. Автоматизация производства и промышленная электроника. Энциклопедия. Под ред. А. И. Берга. и В. А. Трапезника. М.1962-1965г
— NI
Основная идея ПИД-регулятора заключается в считывании показаний датчика, затем вычислении желаемого выходного сигнала привода путем вычисления пропорционального, интегрального и производного откликов и суммирования этих трех компонентов для вычисления выходного сигнала. Прежде чем мы начнем определять параметры ПИД-регулятора, мы увидим, что такое замкнутая система, и некоторые термины, связанные с ней.
Система с замкнутым контуром
В типичной системе управления технологическая переменная — это системный параметр, который необходимо контролировать, например температура (ºC), давление (psi) или расход (литры / минуту).Датчик используется для измерения переменной процесса и обеспечения обратной связи с системой управления. Уставка — это желаемое или командное значение для переменной процесса, например 100 градусов Цельсия в случае системы контроля температуры. В любой данный момент разница между переменной процесса и уставкой используется алгоритмом системы управления (компенсатор) для определения желаемой выходной мощности привода для управления системой (установкой). Например, если измеряемая температура технологической переменной составляет 100 ºC, а желаемая уставка температуры составляет 120 ºC, то выход исполнительного механизма , заданный алгоритмом управления, может приводить в действие нагреватель.Приведение в действие исполнительного механизма для включения нагревателя приводит к нагреванию системы и увеличению температуры технологической переменной. Это называется системой управления с обратной связью, потому что процесс считывания показаний датчиков для обеспечения постоянной обратной связи и вычисления желаемой выходной мощности привода повторяется непрерывно и с фиксированной скоростью цикла, как показано на рисунке 1.
Во многих случаях выходной сигнал привода равен не единственный сигнал, влияющий на систему. Например, в температурной камере может быть источник холодного воздуха, который иногда дует в камеру и нарушает температуру.Такой термин обозначается как нарушение . Обычно мы стараемся спроектировать систему управления, чтобы минимизировать влияние возмущений на переменную процесса.
Рисунок 1: Блок-схема типичной замкнутой системы.
Определение терминологии
Процесс разработки средств управления начинается с определения требований к рабочим характеристикам. Производительность системы управления часто измеряется путем применения ступенчатой функции в качестве переменной команды задания уставки, а затем измерения реакции переменной процесса.Обычно отклик количественно оценивается путем измерения определенных характеристик формы волны. Время нарастания — это время, необходимое системе для перехода от 10% до 90% от установившегося или конечного значения. Процент превышения — это величина, на которую переменная процесса превышает конечное значение, выраженное в процентах от конечного значения. Время установления — это время, необходимое для того, чтобы переменная процесса установилась в пределах определенного процента (обычно 5%) от окончательного значения. Ошибка устойчивого состояния — это окончательная разница между переменной процесса и уставкой.Обратите внимание, что точное определение этих количеств будет варьироваться в зависимости от отрасли и академических кругов.
Рисунок 2: Реакция типичной замкнутой системы ПИД-регулирования.
После использования одной или всех этих величин для определения требований к характеристикам системы управления полезно определить условия наихудшего случая, при которых ожидается, что система управления будет соответствовать этим проектным требованиям. Часто в системе возникает сбой, который влияет на параметр процесса или на измерение параметра процесса.Важно разработать систему управления, которая удовлетворительно работает в наихудших условиях. Мера того, насколько хорошо система управления способна преодолевать эффекты возмущений, называется отклонением возмущений системы управления.
В некоторых случаях реакция системы на заданный управляющий выход может изменяться со временем или в зависимости от некоторой переменной. Нелинейная система — это система, в которой параметры управления, которые дают желаемый отклик в одной рабочей точке, могут не давать удовлетворительного отклика в другой рабочей точке.Например, камера, частично заполненная жидкостью, будет гораздо быстрее реагировать на мощность нагревателя, когда она почти пуста, чем когда она почти заполнена жидкостью. Мера того, насколько хорошо система управления будет выдерживать возмущения и нелинейности, называется устойчивостью системы управления.
Некоторые системы демонстрируют нежелательное поведение, называемое deadtime . Мертвое время — это задержка между изменением переменной процесса и моментом, когда это изменение можно наблюдать.Например, если датчик температуры расположен далеко от впускного клапана холодной воды, он не будет сразу измерять изменение температуры, если клапан открывается или закрывается. Мертвое время также может быть вызвано системой или выходным приводом, который медленно реагирует на команду управления, например, клапан, который медленно открывается или закрывается. Обычным источником простоя на химических предприятиях является задержка, вызванная потоком жидкости по трубам.
Цикл цикла также является важным параметром замкнутой системы.Интервал времени между вызовами алгоритма управления — это время цикла цикла. Системы, которые быстро меняются или имеют сложное поведение, требуют более высокой скорости контура управления.
Рисунок 3: Реакция замкнутой системы с мертвым временем.
После определения требований к рабочим характеристикам пора проверить систему и выбрать подходящую схему управления. В подавляющем большинстве приложений ПИД-регулирование обеспечивает требуемые результаты
9.2: P, I, D, PI, PD и ПИД-регулирование
Как и многие инженерные системы, ПИД-регуляторы можно моделировать в Excel с помощью численных методов, таких как метод Эйлера. Сначала начните с начального значения данного параметра. Определите изменение этого параметра на определенном временном шаге, суммируя три контроллера P, I и D на этом этапе, которые находятся с использованием уравнений, перечисленных в разделе P, I, D, PI, PD, PID Control выше. . Возьмите это изменение, умножьте его на выбранный временной шаг и добавьте его к предыдущему значению интересующего параметра.Для получения более подробной информации см. Численное решение ОДУ в Excel. Пример проблемы химической инженерии, в которой используется этот метод, можно увидеть в Примере 4 ниже.
Устранение неполадок при моделировании ПИД-регулирования в Excel
При настройке электронной таблицы Excel для моделирования ПИД-регулятора вы можете получить сообщение об ошибке о том, что вы создали циклическую ссылку. Допустим, вы контролируете расход одного реагента (\ (B \)) в реактор, который зависит от концентрации другого реагента (\ (A \)) уже внутри реактора.Ваши уравнения ПИД-регулятора выглядят следующим образом:
\ [FB = 1 + K_ {c} \ left [\ left (A-A _ {\ mathrm {set}} \ right) + \ frac {1} {\ tau_ {i}} \ int \ left (A- A _ {\ mathrm {set}} \ right) d t + \ tau_ {d} \ frac {d \ left (A-A _ {\ mathrm {set}} \ right)} {dt} \ right] \ nonumber \]
и
\ [x_ {i} = \ frac {d \ left (A-A _ {\ mathrm {set}} \ right)} {d t} \ nonumber \]
После того, как вы настроили столбцы для \ (A — A_ {set} \), \ (d (A — A_ {set}) / dt \), \ (x_i \) и ячеек для ваших параметров, таких как \ (K_c \), \ (\ tau_i \) и \ (\ tau_d \), вам нужно будет настроить свой столбец PID с вашим уравнением PID в нем.После ввода уравнения в первую ячейку столбца PID может появиться сообщение об ошибке «Циркулярная ссылка» при попытке перетащить уравнение в другие ячейки столбца.
Вы можете сделать две вещи:
- Вероятно, вам нужно начать уравнение PID во второй или третьей ячейке столбца PID. Введите разумные значения в первую пару ячеек перед тем, как начать уравнение ПИД, и вы обнаружите, что эти значения не должны влиять на конечный результат вашего контроллера.
- Вы также можете попробовать уменьшить размер шага (\ (Δt \)).
Сводные таблицы
Краткое изложение преимуществ и недостатков трех элементов управления показано ниже и показано в таблице 1.
Таблица 1. Преимущества и недостатки средств управления
Руководство по типичному использованию различных контроллеров показано ниже в Таблице 2.
Таблица 2. Типичное применение контроллеров P, I, D, PI и PID
Краткое изложение определений терминов и символов показано ниже в Таблице 3.
Таблица 3. Определения терминов и символов.
Пример \ (\ PageIndex {1} \)
КомпанияHypothetical Industries только что назначила вас ответственным за один из своих реакторов периодического действия. Ваша задача — придумать способ поддержания заданного уровня внутри реактора. Ваш босс хочет использовать какой-нибудь регулятор регулятора, но он не совсем уверен, какой из них использовать. Помогите своему боссу найти контроллер подходящего типа. Чрезвычайно важно, чтобы уровень внутри реактора находился на заданном уровне.Большие колебания и ошибки недопустимы.
Решение
Вы хотели бы использовать ПИД-регулятор. Благодаря действию P-регулятора система очень быстро отреагирует на изменение. Благодаря действию I control система может вернуться к заданному значению. Наконец, поскольку для системы очень важно оставаться на постоянном заданном значении, D-контроль будет измерять изменение ошибки и помогать соответствующим образом отрегулировать систему.
Пример \ (\ PageIndex {2} \)
Вы возвращаетесь в старшую школу и замечаете духовку на своем старом уроке химии.Духовка используется для удаления воды из растворов. Используя свои знания из ChE 466, вы начинаете задаваться вопросом, какой тип контроллера использует духовка для поддержания заданной температуры. Вы замечаете, что некоторые старшеклассники хотят учиться, и решаете поделиться с ними своими знаниями в надежде вдохновить их стать инженерами-химиками. Объясните им тип контроллера, который, скорее всего, находится в духовке, и как этот контроллер работает.
Решение
Поскольку печь используется только для удаления воды из раствора, колебания, погрешности и запаздывание между заданной точкой и фактической температурой допустимы.Поэтому самым простым и простым в использовании контроллером будет контроллер включения-выключения. Контроллер включения-выключения включает механизм нагрева, когда температура в духовке ниже заданной температуры. Если температура духовки поднимется выше установленной, контроллер отключит нагревательный механизм.
Пример \ (\ PageIndex {3} \)
Воспользовавшись вашим советом, начальник компании Hypothetical Industries решает установить ПИД-регулятор для контроля уровня в реакторе периодического действия.При первом запуске реактора контроллер сначала получил ступенчатый вход. Когда реактор переходит в устойчивое состояние, уровень в реакторе имеет тенденцию колебаться, посылая импульсные входы в контроллер. Для импульсного входа предоставьте графическое представление выхода ПИД-регулятора.
Рисунок 8. Импульсный вход.Решение
Выход ПИД-регулятора будет представлять собой комбинацию выходов регуляторов только P, I и D. Аналогично выходу П-регулятора для ступенчатого входа, выход П-регулятора для импульсного входа будет точно напоминать вход.
Рисунок 9. Выход П-регулятора для импульсного входа.Выход I-контроллера представляет собой область под графиком входов. В отличие от пошагового входа, площадь под графиком импульсного входа уменьшалась до нуля после прохождения импульса. Следовательно, вместо того, чтобы постоянно увеличиваться, выходной график I-контроллера в конце концов выровняется.
Рисунок 10. Выход I-контроллера для импульсного входа.Выход D-контроллера представляет собой производную входного графика. Производная на первом разрыве графика будет положительной бесконечностью.Производная второго разрыва вниз — отрицательная бесконечность.
Рисунок 11. Выход D-контроллера для импульсного входа.Комбинируя качественные характеристики всех трех графиков, можно определить выход ПИД-регулятора для импульсного входа.
Рисунок 12. Выход ПИД-регулятора для импульсного входа.Пример \ (\ PageIndex {3} \)
При определении устойчивости ПИД-регулятора возможны различные виды помех. Эти различные нарушения используются для имитации изменений, которые могут произойти в вашей системе.Для реактора CSTR вы решаете нагреть свою систему, чтобы учесть холодную погоду. Нарушение температуры на входе — это нарушение линейного изменения, как показано на рисунке №. Если контроллер реагирует на температуру на входе, каким будет выход ПИД-регулятора?
Рисунок 13. Ввод рампы.Решение
Используя контроллер только с контроллером p-only, мы увидим пропорциональное изменение на выходе контроллера, соответствующее изменению входной переменной.См. Рисунок 14 ниже
Рисунок 14. Выход П-регулятора для входа рампы.Используя I-only контроллер, мы увидим контроллер, соответствующий области под графиком, которая в этом случае, кажется, экспоненциально увеличивается с геометрической формой рампы.
Рисунок 15. Выход I-контроллера для входа рампы.Используя контроллер D-only, мы увидим ступенчатую реакцию на возмущение рампы. Это связано с тем, что D-составляющая соответствует производной, а вход рампы показывает постоянный наклон (в данном случае положительный), который отличается от наклона начального условия (обычно нулевой).См. Рисунок 16.
Рисунок 16. Выход D-контроллера для входа рампы.При использовании ПИД-регулятора все три компонента начинают действовать на выходе регулятора. Как и следовало ожидать, результатом будет простое добавление трех отдельных графов компонентов.
Рисунок 17. Выход D-контроллера для входа рампы.Пример \ (\ PageIndex {6} \)
Ниже приводится P&ID процесса A + B -> C.
Рисунок 18. P&ID для процесса реакции.Каково выражение ПИД-регулятора на V3, регулирующем объем в TK001 до заданного значения 50 литров? Примечание. ПИД-регулятор использует LC1 для измерения объема.
Решение
Общее уравнение для ПИД-регулятора:
\ [c (t) = K_ {c} \ left [e (t) + \ frac {1} {T_ {i}} \ int e (t) d t + T_ {d} \ frac {de} { dt} \ right] + C \ nonumber \]
где
- \ (c (t) \) = выход контроллера
- \ (K_c \) = коэффициент усиления контроллера
- \ (e (t) \) = ошибка
- \ (T_i \) = время интегрирования
- \ (T_d \) = производная постоянная времени
- \ (C \) = начальное значение контроллера
Следовательно, для этого примера решение:
\ [F _ {\ mathrm {out}} = offse t + K_ {c} \ left [\ left (V_ {1} -V _ {\ mathrm {set}} \ right) + \ frac {1} {T_ { i}} \ int \ left (V_ {1} -V _ {\ mathrm {set}} \ right) d t + T_ {d} \ frac {d \ left (V_ {1} -V _ {\ mathrm {vet} } \ right)} {dt} \ right].\ nonumber \]
Пример \ (\ PageIndex {6} \)
В этой задаче будут определены дифференциальные уравнения, описывающие конкретную систему первого порядка с ПИД-регулятором. Это сделано, чтобы показать, как четко определенные системы могут быть смоделированы или объяснены математически. В качестве дополнения к этой проблеме посетите Constructing Block Diagrams. Обратите внимание, что это пример решения с использованием интегро-дифференциальных операторов, а не преобразований Лапласа. Здесь мы установили \ (K_p = 1 \).{t} d \ tau + \ tau_ {D} \ frac {d} {d t} \ right] \ nonumber \]
Решение: Используйте Построение блок-схем в качестве справочного материала при решении этой проблемы.
Система определения уравнений,
- Процесс: τ p Y ‘( т ) + Y ( т ) = X ( т )
- Контроллер: X ( т ) = G ε ( т )
- Компаратор: ε ( т ) = R ( т ) — M ( т )
- Размер: M ( т ) = Y ( т )
Когда эти уравнения объединяются в одно уравнение, получается следующее уравнение. {\ prime} (t) + R (t) \]
Вышеупомянутое уравнение затем можно решить вручную или с помощью такой программы, как Mathematica.При использовании компьютерной программы можно выбрать различные значения для параметров управления K c , τ I , τ D , а реакцию на изменение в системе можно оценить графически.
Упражнение \ (\ PageIndex {1} \)
Какой тип контроллера отображается в приведенном ниже уравнении?
\ [c (t) = K_ {c} \ left [e (t) + \ frac {1} {T_ {i}} \ int e (t) d t \ right] \ nonumber \]
- Прямая связь
- PID
- Производная
- Пропорционально-интегральный
- Ответ
д
Упражнение \ (\ PageIndex {2} \)
Какой тип контроллера повышает стабильность системы, поддерживая постоянные настройки?
- Производная
- Пропорциональный
- Вкл / Выкл
- Интегральный
- Ответ
а
Упражнение \ (\ PageIndex {3} \)
Какой тип контроллера увеличивает скорость отклика для достижения желаемой уставки быстрее всего при устранении смещения?
- Вкл / Выкл
- Пропорциональный
- Интегральный
- Пропорционально-интегральный
- Ответ
д
Лаборатория микробиологии обнаружила новый смертельно опасный штамм бактерий P.Вулфи, в городском водопроводе. Чтобы стерилизовать воду, бактерии необходимо уничтожить нагреванием при температуре 105 градусов Цельсия. Однако это выше точки кипения воды при 1 атм, и бактерии чувствительны к нагреванию только в жидкости из-за образования спор в газе или паре. Для выполнения этой стерилизации было предложено использовать автоклав, чтобы поддерживать воду в жидком состоянии, поддерживая ее под давлением 5 атм при нагревании в течение 30 секунд. Автоклав может выдерживать давление только до 7 атм перед взрывом, поэтому для обеспечения того, чтобы процесс выполнялся в соответствии с желаемыми характеристиками, модель ПИД-регулятора должна быть создана в Excel.См. Рисунок 18 для визуального представления системы.
Рисунок 18: Автоклава с ПИД-регулированием температуры и давленияЩелкните по этой ссылке, чтобы просмотреть разработанное решение Excel
.Пояснение:
Для моделирования реальной ситуации изменения давления в системе в столбце B вызывается уравнение для генерации случайных колебаний давления. Pset — это просто желаемая спецификация. Ошибка — это разница между установленным давлением и измеренным сигналом. du / dt — это сумма членов P, I и D.Уравнения, используемые для расчета каждого из них, можно найти в статье, они учитывают ошибку, связанную с каждым временным шагом. dU / dt — это параметр, который варьируется для корректировки разницы между измеренным давлением и желаемым давлением.
Правила настройки ПИД-регулятора
Этот пост написал Грег Макмиллан, отраслевой консультант, автор множества книг по управлению технологическими процессами, обладатель премии ISA Life Achievement Award 2010 и бывший старший научный сотрудник Solutia Inc.(теперь Eastman Chemical).
Практически каждый поставщик систем автоматизации, консультант, профессор теории управления и пользователь имеет свой любимый набор правил настройки ПИД-регулятора. Многие из этих экспертов уверены, что их набор самый лучший. В справочнике по настройке более 500 страниц правил. Энтузиазм и огромное количество правил являются свидетельством важности настройки и большого разнообразия динамики приложений, требований и сложностей. Хорошая новость в том, что эти методы сходятся для достижения общей цели.
Добавление функций ПИД-регулятора, таких как опережение уставки, динамический сброс и пределы выходной скорости, а также интеллектуальная приостановка интегрального действия, позволяют использовать настройку подавления помех для достижения других системных требований, таких как максимизация отклика уставки, координирование контуров, расширение срок службы уплотнения клапана и минимизация сбоев в работе и других контурах управления.
Возможная производительность
Целью контура управления является отклонение нежелательных изменений, игнорирование посторонних изменений и достижение желаемых изменений, таких как новые заданные значения.ПИД-регулирование обеспечивает наилучшее подавление неизмеряемых помех (регулирующее управление) при правильной настройке. Добавление простого блока мертвого времени в путь внешнего сброса может улучшить возможности регулирования ПИД-регулятора больше, чем другие контроллеры со встроенным интеллектом для динамики процесса, таким как управление с прогнозированием модели. На заводах неизвестные и посторонние изменения — реальность, и PID — лучший инструмент, если он правильно настроен. Время тестирования для самых сложных петель было значительно сокращено.Были разработаны простые уравнения для оценки настройки и результирующей производительности для унифицированного подхода. (Вывод уравнений и простой метод настройки находятся в онлайн-версии.)
Требования к контролю
Основным требованием к PID является предотвращение срабатывания контрольно-измерительной системы безопасности или предохранительного устройства и предотвращение нарушения окружающей среды (RCRA pH), помпажа компрессора и останова из-за отклонения от процесса. Пиковая погрешность (максимальное отклонение от заданного значения) является наиболее подходящей метрикой.Самым серьезным нарушением является неизмеряемое ступенчатое возмущение, которое может вызвать ошибку разомкнутого контура ( E o ), если ПИД-регулятор был в ручном режиме или не существовал. Доля ошибки разомкнутого контура, наблюдаемая при управлении с обратной связью, больше зависит от коэффициента усиления регулятора, чем от времени интегрирования, поскольку пропорциональный режим обеспечивает начальную реакцию, важную для минимизации пиковой ошибки. Уравнение (1) показывает, если произведение коэффициента усиления контроллера ( K c ) и коэффициента усиления разомкнутого контура ( K o ) намного больше единицы, пиковая ошибка ( E x ) равна значительно меньше, чем ошибка разомкнутого контура.Коэффициент усиления разомкнутого контура ( K o ) является произведением конечного элемента, процесса и усиления измерения и представляет собой процентное изменение переменной процесса, деленное на процентное изменение выходного сигнала контроллера для изменения уставки. Для большинства контуров регулирования температуры и давления в резервуаре и колонне скорость изменения процесса намного ниже, чем мертвое время. Следовательно, коэффициент усиления регулятора может быть установлен достаточно большим, когда знаменатель становится просто обратным произведению коэффициентов усиления.И наоборот, для контуров, в которых преобладает мертвое время, знаменатель приближается к единице, а пиковая ошибка — это, по сути, ошибка разомкнутого контура. Пиковая погрешность имеет решающее значение для качества продукта при окончательной обработке расплавов, твердых частиц или пасты, например, в экструдерах, линиях для производства листов и прядильных линиях. Пиковые погрешности проявляются в виде бракованного продукта из-за цвета, консистенции, оптической прозрачности, толщины, размера, формы и, в случае еды, вкусовых качеств. К сожалению, в этих системах преобладают задержки при транспортировке. Пиковые ошибки и сбои в исходных процессах должны быть сведены к минимуму.Наиболее широко цитируемым показателем является интегрированная абсолютная ошибка (IAE), которая представляет собой область между переменной процесса и уставкой. Для неосциллирующего отклика IAE и интегрированная ошибка (IE) одинаковы. Поскольку пропорциональное и интегральное действие важны для минимизации этой ошибки, уравнение (2) показывает, что IE увеличивается по мере увеличения времени интегрирования ( T i ) и уменьшения коэффициента усиления регулятора. Уравнение (2) также показывает, как IE увеличивается со временем выполнения контроллера ( Δt x ) и временем фильтрации сигнала ( τ f ).Эквивалентное мертвое время из этих условий также снижает минимально допустимое время интегрирования и максимально допустимое усиление контроллера, что еще больше ухудшает максимально возможные характеристики. Во многих случаях первоначальная настройка контроллера происходит медленнее, чем разрешено, и остается неизменной, поэтому единственное наблюдаемое ухудшение связано с этими членами в числителе уравнения (2). Исследования влияния динамики систем автоматизации и инноваций могут привести к противоречивым результатам из-за отсутствия признания влияния настройки на исходный случай и эффективность сравнительного случая.Другими словами, вы можете легко доказать все, что захотите, настроив контроллер. IE указывает на количество продукта, не отвечающего техническим требованиям, которое может привести к снижению выхода и более высокому соотношению затрат на сырье или переработку вторичного сырья к продукту. Если некондиционный продукт не может быть переработан или скорость подачи не может быть увеличена, происходит потеря производительности. Если некондиционный не подлежит восстановлению, существует стоимость обработки отходов. Контроллер, настроенный на максимальную производительность, будет иметь реакцию замкнутого контура на неизмеряемое возмущение, которое напоминает два прямоугольных треугольника, поставленных спиной к спине.Основание каждого треугольника — это полное мертвое время контура, а высота — это пиковая ошибка. Если время интегрирования (время сброса) слишком велико, возврат к заданному значению будет медленнее. Если коэффициент усиления регулятора слишком мал, пиковая ошибка увеличивается, а прямоугольный треугольник больше для возврата к заданному значению.
Динамика процесса
Основные типы динамики процесса различаются по конечному пути отклика разомкнутого контура на изменение выходного сигнала ручного регулятора при отсутствии возмущений.(В онлайн-версии показаны три основных типа откликов и связанные с ними динамические составляющие.) Если отклик переходит в новое установившееся состояние, процесс саморегулируется с постоянной времени разомкнутого контура ( τ o ), которая является наибольшей постоянной времени в контуре. Температура и концентрация потока и непрерывной работы являются саморегулирующимися процессами. Если реакция продолжает расти, процесс интегрируется. Уровень, давление в колонне и сосуде, рабочая температура партии и концентрация являются интегрирующими процессами.Если реакция ускоряется, достигая точки невозврата, процесс имеет положительную обратную связь, ведущую к побегу. Периодическая или постоянная температура в сильно экзотермических реакторах (например, полимеризация) может стать неуправляемым процессом. Продолжительные испытания без обратной связи не разрешены, а изменения уставки ограничены. Следовательно, ускорение редко наблюдается намеренно.
Единый подход
Три основных типа откликов имеют начальный период отсутствия отклика, который представляет собой полное мертвое время контура ( θ o ), за которым следует наклон перед замедлением (точка перегиба) саморегулирующегося отклика и ускорение. беглого ответа.Процентная скорость линейного изменения, разделенная на процентное изменение выходного сигнала контроллера, представляет собой интегрирующее усиление процесса ( K i ) с единицами измерения% / сек /%, которое уменьшается до 1 / сек. В течение как минимум 10 лет медленные саморегулирующиеся процессы с длительным временем до замедления показали, что они эффективно идентифицируются и настраиваются как процессы «почти интегрированные» или «псевдоинтегрирующие», что приводит к «методу быстрой настройки», в котором используется только мертвое время и необходимо определить начальную скорость нарастания. Время проверки настройки для этих процессов, «близких к интеграции», можно сократить более чем на 90%, если не дожидаться установившегося состояния.Недавно этот метод был расширен на неуправляемые процессы и саморегулирующиеся процессы с преобладанием мертвого времени за счет использования блока мертвого времени для вычисления скорости нарастания в течение интервала мертвого времени. Кроме того, было обнаружено, что другие правила настройки дают такое же уравнение для усиления контроллера, когда целью производительности было максимальное подавление неизмеренных помех. Например, использование постоянной времени замкнутого контура ( λ ), равной полному мертвому времени контура при настройке лямбда, дает тот же результат, что и методы предельных колебаний и кривой реакции Циглера-Николса (ZN), если усиление ZN уменьшается вдвое. для плавности и прочности.Уравнение (3) показывает, что коэффициент усиления регулятора равен половине обратного произведения интегрирования коэффициента усиления процесса и мертвого времени. Специалисты понимают, что слишком большое усиление регулятора вызовет относительно быстрые колебания и может спровоцировать нестабильность (нарастающие колебания). Для процесса интеграции не осознается, что слишком малое усиление контроллера может вызвать чрезвычайно медленные колебания, которые требуют больше времени для затухания при уменьшении усиления. Также нереализованным для процесса разгона является то, что усиление регулятора, установленное ниже значения, обратного усилению разомкнутого контура, вызывает ускорение повышения температуры до точки невозврата.Есть окно допустимых коэффициентов усиления контроллера. Также понимается, что слишком малое время интегрирования вызовет перерегулирование и может привести к циклу сброса. Практически полностью не осознается, что слишком медленное время интегрирования приведет к устойчивому превышению заданного значения, которое становится больше и устойчивее по мере увеличения времени интегрирования для процессов интеграции. Следовательно, существует окно допустимых интегральных времен. Уравнение 4a обеспечивает правильный размер интегрального времени для интегрирования процессов. Если мы подставим уравнение 3 в уравнение 4a, мы получим уравнение 4b, которое является общим выражением времени интегрирования для максимального подавления помех.Уравнение 4a чрезвычайно важно, потому что большинство интегрирующих процессов имеют коэффициент усиления регулятора в 5-10 раз меньше допустимого. Коэффициент в уравнении 4b может быть уменьшен для саморегулирующихся процессов, поскольку мертвое время становится больше постоянной времени разомкнутого контура ( τ o ), оцененной уравнением 5. Настройка, используемая для максимального отклонения нагрузки, может использоваться для эффективного и плавный отклик уставки, если изменение уставки проходит через опережение-запаздывание. Время запаздывания устанавливается равным времени интегрирования, а время опережения устанавливается приблизительно равным ¼ времени запаздывания.Для запуска, смены сорта и оптимизации непрерывных процессов и пакетных операций важен отклик заданного значения. Сведение к минимуму времени достижения новой уставки (времени нарастания) во многих случаях может максимизировать эффективность и производительность процесса. Время нарастания ( T r ) при отсутствии насыщения выхода, без упреждающего задания уставки и без специальной логики является обратным произведению интегрирующего усиления процесса и усиления контроллера плюс общее мертвое время контура. Уравнение 6 не зависит от изменения уставки.
Осложнения, простые решения
Быстрые изменения на выходе контроллера могут вызвать колебания от медленного вторичного контура или медленного конечного элемента управления. Проблема коварна в том, что колебания могут развиваться только при больших возмущениях или больших изменениях уставки. Включение опции ограничения динамического сброса и своевременной внешней обратной связи сброса вторичного контура или переменной процесса конечного элемента управления предотвратит изменение выходного сигнала первичного ПИД-регулятора быстрее, чем может реагировать вторичный или конечный элемент управления, предотвращая колебания.Агрессивная настройка контроллера также может нарушить работу, нарушить работу других контуров и вызвать постоянное пересечение точки разделения диапазона. Пределы скорости могут быть добавлены к блоку аналогового вывода, включена опция ограничения динамического сброса и переменная процесса блока, используемая в качестве внешнего сброса, чтобы обеспечить подавление направленного движения для сглаживания реакции по мере необходимости без перенастройки. Различный отклик контуров с обратной связью может снизить координацию, что особенно важно для объединения и упрощения идентификации моделей для усовершенствованных систем управления технологическим процессом, которые манипулируют этими контурами.Нелинейность процесса может привести к более быстрой реакции в одном направлении. Пределы направленной выходной скорости и опция ограничения динамического сброса могут использоваться для выравнивания постоянных времени замкнутого контура без перенастройки. Пределы разрешения конечного элемента управления (прилипание-проскальзывание) и зона нечувствительности (люфт) могут вызвать предельный цикл, если в контуре присутствуют один, два или более интегратора соответственно. Интегратор может быть в процессе или во вторичном или первичном ПИД-регуляторе через интегральный режим. Увеличение времени интегрирования замедлит период цикла, но не может устранить колебания.Однако полная приостановка интегрального действия, когда нет значительного изменения переменной процесса и когда процесс близок к заданному значению, может остановить предельный цикл. Пределы выходной скорости также можно использовать для предотвращения колебаний на выходе контроллера из-за шума измерения, превышающего зону нечувствительности или предел разрешения регулирующего клапана, предотвращающего дизеринг, что дополнительно снижает износ клапана.
Итог
Контроллерымогут быть настроены на максимальное подавление помех унифицированным методом для основных типов процессов.Опции ПИД-регулирования в сегодняшней РСУ, такие как опережение уставки, ограничения направленной выходной скорости, предел динамического сброса и интеллектуальная приостановка интегрального действия, могут устранить колебания без перенастройки. Меньшее количество колебаний снижает изменчивость процесса, позволяет лучше распознавать тенденции, упрощает определение динамики и обеспечивает увеличение срока службы сальника клапана.
Поскольку ПИД-регулятор является ключевой частью почти каждого контура управления и обладает значительными неиспользованными возможностями, предлагаются приложения, чтобы помочь пользователям максимально эффективно использовать свои ПИД-регуляторы.Приложения также предлагают понимание и понимание, которые полезны не только при настройке контроллеров. Приложения призваны помочь пользователям разобраться в значительной сложности, представленной в литературе, и понять суть возможностей управления процессом, используя полученные знания.
Об авторе
Грегори К. Макмиллан, CAP, старший научный сотрудник на пенсии из Solutia / Monsanto, где он работал в области инженерных технологий над улучшением управления процессами.Грег также был аффилированным профессором Вашингтонского университета в Сент-Луисе. Грег является членом ISA и получил награду ISA Kermit Fischer Environmental Award за контроль pH в 1991 году, награда журнала Control «Инженер года» для перерабатывающей промышленности в 1994 году была введена в Зал славы автоматизации процессов журнала Control в 2001 г., журнал InTech назвал в 2003 г. одним из самых влиятельных новаторов в области автоматизации и получил премию ISA Life Achievement Award в 2010 г.Грег является автором множества книг по управлению технологическими процессами, в том числе Advances in Reactor Measurement and Control и Essentials of Modern Measurements and Final Elements in the Process Industry . Грег ведет ежемесячный обозреватель Control Talk в журнале Control с 2002 года. В настоящее время Грег работает консультантом по моделированию и управлению в отделе технологий моделирования процессов в компании Emerson Automation Solutions, специализируясь на использовании виртуального оборудования для изучения новых возможностей. .Он тратит большую часть своего времени на написание, обучение и руководство программой наставничества ISA, которую он основал в 2011 году.
Связаться с Грегом:
Версия этой статьи также была опубликована в журнале InTech.
ПИД-регулятор: типы, что это такое и как работает
ПИД-регулятор — это прибор, используемый в промышленных системах управления для регулирования температуры, расхода, давления, скорости и других переменных процесса.Контроллеры PID (пропорциональная интегральная производная) используют механизм обратной связи контура управления для управления переменными процесса и являются наиболее точным и стабильным контроллером.
ПИД-регулирование — это хорошо зарекомендовавший себя способ привести систему к целевому положению или уровню. Это практически повсеместно используется в качестве средства контроля температуры и находит применение в бесчисленных химических и научных процессах, а также в автоматизации.ПИД-регулирование использует обратную связь управления с обратной связью, чтобы поддерживать фактический выходной сигнал процесса как можно ближе к целевому или заданному выходному значению.
Что такое ПИД-регулятор температуры?
ПИД-регулятор температуры, как следует из его названия, представляет собой инструмент, используемый для управления температурой, в основном без значительного участия оператора.ПИД-регулятор в системе контроля температуры принимает датчик температуры, такой как термопара или RD, в качестве входного сигнала и сравнивает фактическую температуру с желаемой контрольной температурой или заданным значением. Затем он предоставит вывод для элемента управления.
Что такое цифровой ПИД-регулятор?
Цифровой ПИД-регулятор считывает сигнал датчика, обычно с термопары или RTD, и связывает измерения с техническими единицами измерения, такими как градусы Фаренгейта или Цельсия, которые затем отображаются в цифровом формате.
История ПИД-регулятора
Первая эволюция ПИД-регулятора была разработана в 1911 году Элмером Сперри. Однако только в 1933 году компания Taylor Instrumental Company (TIC) представила первый пневматический контроллер с полностью настраиваемым пропорциональным контроллером. Несколько лет спустя инженеры по управлению устранили ошибку установившегося состояния, обнаруженную в пропорциональных контроллерах, установив точку на какое-то искусственное значение, пока ошибка не была равна нулю.Этот сброс «интегрировал» ошибку и получил название пропорционально-интегрального регулятора. Затем, в 1940 году, компания TIC разработала первый пневматический контроллер ПИД-регулятора с производным действием, который уменьшил проблемы с перерегулированием. Однако только в 1942 году, когда были введены правила настройки Циглера и Николса, инженеры смогли найти и установить соответствующие параметры ПИД-регуляторов. К середине 1950-х годов автоматические ПИД-регуляторы получили широкое распространение в промышленности.
- Продолжайте читать: Как работают ПИД-регуляторы
Техника управления | Понимание основ ПИД-регулирования и настройки контура
«Контур управления» — это механизм обратной связи, который пытается исправить расхождения между измеренным параметром процесса и желаемой уставкой.Компьютер специального назначения, известный как «контроллер», прилагает необходимые корректирующие усилия с помощью исполнительного механизма, который может управлять переменной процесса вверх или вниз. Домашняя печь использует базовый контроллер обратной связи для увеличения или уменьшения нагрева, если температура, измеренная термостатом, слишком низкая или слишком высокая.
Для промышленного применения контроллер пропорционально-интегрально-производной (ПИД) отслеживает ошибку между переменной процесса и уставкой, интеграл недавних ошибок и производную сигнала ошибки.Он вычисляет следующее корректирующее усилие на основе взвешенной суммы этих трех членов, затем применяет результаты к процессу и ожидает следующего измерения. Он повторяет этот цикл измерения-решения-срабатывания до тех пор, пока ошибка не будет устранена. [подзаголовок]
Основы PID
ПИД-регулятор, использующий идеальную форму или стандартную форму ПИД-алгоритма Международного общества автоматизации (ISA), вычисляет свой выходной CO (t) в соответствии с формулой, показанной на рисунке 1. PV (t) — это переменная процесса, измеренная в момент времени t, а ошибка e (t) — это разница между переменной процесса и уставкой.Формула PID взвешивает пропорциональный член с коэффициентом P, интегральный член с коэффициентом P / T I и производный член с коэффициентом P . T D где P — коэффициент усиления регулятора, T I — время интегрирования, а T D — время производной.
Эта терминология требует пояснений. «Усиление» относится к проценту, на который сигнал ошибки будет увеличиваться или уменьшаться по мере того, как он проходит через контроллер на пути к тому, чтобы стать частью выходного сигнала контроллера.ПИД-регулятор с высоким коэффициентом усиления будет иметь тенденцию создавать особенно агрессивные корректирующие усилия.
«Время интегрирования» относится к гипотетической последовательности событий, в которой ошибка начинается с нуля, а затем резко перескакивает на фиксированное значение. Такая ошибка вызовет мгновенный отклик пропорционального члена контроллера и отклик интегрального члена, который начинается с нуля и постоянно увеличивается. Время, необходимое для того, чтобы интегральный член догнал неизменный пропорциональный член, — это время интегрирования T I .ПИД-регулятор с большим временем интегрирования более склонен к пропорциональному действию, чем к интегральному действию.
Аналогично, «время производной» T D является мерой относительного влияния члена производной в формуле PID. Если бы ошибка начиналась с нуля и начинала увеличиваться с фиксированной скоростью, пропорциональный член начинался бы с нуля, в то время как производный член принимал бы фиксированное значение. Затем пропорциональный член будет неуклонно увеличиваться, пока не догонит производный член в конце производного времени.ПИД-регулятор с большим временем производной более склонен к производному действию, чем к пропорциональному действию.
Историческая справка
Первые контроллеры с обратной связью включали только пропорциональный член. По математическим причинам, которые стали очевидными позже, контроллер только для P имеет тенденцию уменьшать ошибку до небольшого, но ненулевого значения, а затем прекращает работу. Операторы, наблюдающие это явление, будут вручную увеличивать выходную мощность контроллера до тех пор, пока не будут устранены последние признаки ошибки.Они назвали эту операцию «перезагрузкой» контроллера.
Когда был введен интегральный член, операторы заметили, что он будет выполнять операцию сброса автоматически. То есть контроллер будет увеличивать свое пропорциональное действие ровно настолько, чтобы полностью устранить ошибку. Следовательно, интегральное действие первоначально называлось «автоматический сброс» и остается таковым на некоторых ПИД-регуляторах по сей день. Вскоре после этого был изобретен производный термин, который достаточно точно описали как «контроль скорости».«
Хитрый бизнес
Настройка контура — это искусство выбора значений для параметров настройки P, T I и T D , чтобы контроллер мог быстро устранить ошибку, не вызывая чрезмерных колебаний переменной процесса. Легче сказать, чем сделать.
Рассмотрим, например, круиз-контроллер автомобиля. Он может разогнать автомобиль до желаемой крейсерской скорости, но не мгновенно. Инерция автомобиля вызывает задержку между моментом, когда контроллер задействует акселератор, и моментом, когда скорость автомобиля достигает заданного значения.Насколько хорошо работает ПИД-регулятор, во многом зависит от таких задержек.
Предположим, что перегруженный автомобиль с малоразмерным двигателем внезапно трогается с крутого холма. Возникающая в результате ошибка между фактической и желаемой скоростью автомобиля приведет к немедленному срабатыванию производных и пропорциональных действий контроллера. Контроллер начнет разгонять машину, но только настолько быстро, насколько позволяет задержка.
Через некоторое время интегральное действие также начнет вносить вклад в выходной сигнал контроллера и в конечном итоге станет доминировать над ним, потому что ошибка уменьшается так медленно, когда время задержки велико, и постоянная ошибка — это то, что движет интегральным действием.Но когда именно это произойдет и насколько доминирующим станет интегральное действие после этого, будет зависеть от серьезности запаздывания и относительных размеров интегрального и производного времен контроллера.
Этот простой пример демонстрирует фундаментальный принцип настройки ПИД-регулятора. Лучший выбор для каждого из параметров настройки P, T I и T D зависит от значений двух других, а также от поведения управляемого процесса. Более того, изменение настройки любого одного элемента влияет на производительность других, потому что измененный контроллер влияет на процесс, а процесс, в свою очередь, влияет на контроллер.
тюнинг Ziegler-Nichols
Как может инженер по регулированию, проектирующий контур ПИД-регулирования, определить значения P, T I и T D , которые лучше всего подходят для конкретного приложения? Джон Г. Зиглер и Натаниэль Б. Николс из Taylor Instruments (ныне часть ABB) обратились к этому вопросу в 1942 году, когда они опубликовали два метода настройки контура, которые остаются популярными по сей день.
Их метод разомкнутого контура основан на результатах ударного или пошагового теста, для которого контроллер отключается и вручную принудительно увеличивает свой выходной сигнал.Полосовая диаграмма последующей траектории переменной процесса известна как «кривая реакции» (см. Рисунок 2).
Наклонная линия, касательная к кривой реакции в ее самой крутой точке, показывает, насколько быстро процесс отреагировал на скачкообразное изменение выходного сигнала контроллера. Обратная величина наклона этой прямой — это постоянная времени процесса T, которая измеряет серьезность запаздывания.
Кривая реакции также показывает, сколько времени потребовалось процессу, чтобы продемонстрировать свою первоначальную реакцию на шаг (мертвое время d), и насколько увеличилась переменная процесса относительно размера шага (коэффициент усиления процесса K).Методом проб и ошибок Зиглер и Николс определили, что наилучшие настройки для параметров настройки P, T I и T D могут быть вычислены из T, d и K, как показано уравнением:
После того, как эти настройки параметров были загружены в формулу ПИД и контроллер вернулся в автоматический режим, контроллер должен иметь возможность устранять будущие ошибки, не вызывая чрезмерных колебаний переменной процесса.
Циглер и Николс также описали технику настройки с обратной связью, которая выполняется с контроллером в автоматическом режиме, но с отключенными интегральными и производными действиями.Коэффициент усиления контроллера увеличивается до тех пор, пока даже малейшая ошибка не вызовет устойчивые колебания технологической переменной (см. Рисунок 3).
Наименьшее усиление регулятора, которое может вызвать такие колебания, называется «предельным усилением» P u . Период этих колебаний называется «конечным периодом» Ту. Соответствующие параметры настройки могут быть вычислены из этих двух значений в соответствии со следующими правилами:
Предупреждения
К сожалению, настройка контура ПИД-регулятора на самом деле не так проста.В разных ПИД-регуляторах используются разные версии формулы ПИД, и каждый должен быть настроен согласно соответствующему набору правил. Правила также меняются, когда:
- Производные и / или интегральные действия отключены.
- Сам процесс по своей природе является колебательным.
- Процесс ведет себя так, как если бы он содержал свой собственный интегральный член (как в случае с контролем уровня).
- Мертвое время d очень мало или значительно больше постоянной времени T.
Кроме того, Циглер и Николс имели в виду конкретную цель производительности замкнутого контура, когда они остановились на своих конкретных правилах настройки. Они решили допустить некоторые колебания переменной процесса, пока каждый последующий пик был не более чем на 0,25 размера своего предшественника, что называется «четвертьволновым затуханием». Для приложений, требующих еще меньших колебаний, требуется дополнительная настройка параметров настройки.
Вот где настройка петли становится искусством.Чтобы найти правильную комбинацию P, T I и T D , требуется больше, чем немного опыта, а иногда и большая удача.
Вэнс ВанДорен, доктор философии, PE , является специалистом по контенту Control Engineering . Свяжитесь с ним по адресу [email protected]. Отредактировал Джек Смит, менеджер по контенту, CFE Media, Control Engineering , [email protected].
ПОДРОБНЕЕ
Ключевые концепции
- ПИД-регулятор с высоким коэффициентом усиления имеет тенденцию вызывать особенно агрессивные корректирующие усилия.
- Настройка контура — это искусство выбора значений для параметров настройки, которые позволяют контроллеру быстро устранять ошибку, не вызывая чрезмерных колебаний переменных процесса.
- Различные контроллеры PID используют разные версии формулы PID, и каждый должен быть настроен в соответствии с соответствующим набором правил.
Рассмотрим это
Оптимально ли настроены контуры ПИД-регулирования на вашем предприятии?
ОНЛАЙН экстра
См. Соответствующие статьи ниже, предлагающие дополнительную информацию о ПИД-регулировании и настройке контура.
ПИД-регулирование и производная по измерениям — Control Guru
Подобно ПИ-регулятору, пропорционально-интегрально-производный (ПИД) регулятор вычисляет выходной сигнал регулятора (СО) для конечного элемента управления каждый раз выборки T.
ПИД-регулятор является трехрежимным. То есть его активность и производительность основаны на значениях, выбранных для трех параметров настройки, каждый из которых номинально связан с пропорциональным, интегральным и производным членами.
Как мы обсуждали ранее, ПИ-регулятор представляет собой достаточно простое уравнение с двумя регулируемыми параметрами настройки. Количество различных способов, которыми коммерческие поставщики могут реализовать форму PI, довольно ограничено, и все они обеспечивают одинаковую производительность при правильной настройке.
С добавлением третьего регулируемого параметра настройки количество перестановок алгоритма заметно увеличивается. И есть даже разные формы самого уравнения ПИД. Это создает дополнительные проблемы при проектировании и настройке контроллера.
Здесь мы сосредоточимся на том, что такое производная, как она вычисляется и что она означает для управления. Мы также исследуем, почему производная от измерения широко рекомендуется в производственной практике.
В этой статье мы сужаем наш мир и сосредотачиваемся на зависимой, идеальной форме контроллера. В следующих статьях мы вернемся и поговорим о различных формах алгоритмов, методах проектирования и настройки, ограничениях алгоритмов и других практических вопросах.
Форма зависимого идеального ПИД-регулятора
Популярный способ, которым производители выражают зависимый идеальный ПИД-регулятор:
Где:
CO = выходной сигнал контроллера (выход провода)
CO смещение = смещение контроллера; устанавливается плавным переключением
e (t) = ошибка регулятора тока, определяемая как SP — PV
SP = уставка
PV = измеряемая переменная процесса (входной провод)
Kc = усиление регулятора, параметр настройки
T i = время сброса, параметр настройки
T d = время производной, параметр настройки
Первые три члена справа от знака равенства идентичны ПИ-регулятору, который мы уже подробно исследовали.
Режим производной ПИД-регулятора — это дополнительный и отдельный член, добавляемый в конец уравнения, который учитывает производную (или скорость изменения) ошибки, поскольку она изменяется во времени.
Вклад производного члена
Пропорциональный член учитывает , как далеко PV от SP в любой момент времени. Его вклад в СО основан на размере e (t) только в момент времени t. По мере того, как e (t) увеличивается или уменьшается, влияние пропорционального члена немедленно и пропорционально увеличивается или уменьшается.
Интегральный член указывает на , как долго и как далеко PV был удален от SP. Интегральный член непрерывно суммирует e (t). Таким образом, даже небольшая ошибка, если она сохраняется, будет иметь общую сумму, которая со временем будет расти, и влияние интегрального члена также будет расти.
Производная описывает крутизну кривой. Точнее, производная описывает наклон или скорость изменения кривой сигнала в определенный момент времени. Соответственно, член производной в приведенном выше уравнении PID учитывает , насколько быстро , или скорость, с которой ошибка (или PV, как мы обсудим далее) изменяется в текущий момент.
Производная на PV противоположна, но равна
Хотя пропорциональные и интегральные члены уравнения PID определяются ошибкой контроллера, e (t), вычисление производной во многих коммерческих реализациях должно основываться на самом значении PV.
Производная e (t) математически идентична отрицательной производной PV везде, кроме случаев изменения уставки. А при изменении уставки производная по ошибке приводит к нежелательному управляющему действию, называемому , производным выбросом .
| Математическое примечание: математическое обоснование того, что «производная e (t) равна отрицательной производной от PV, когда SP является постоянным», предполагает, что, поскольку e (t) = SP — PV, следующее уравнение следует. То есть производная ошибки равна производной уставки минус переменная процесса. Производная постоянной равна нулю, поэтому, когда SP является постоянным, математически производная (или крутизна, или скорость изменения) ошибки контроллера равна производной (или крутизна или скорость изменения) измеряемой переменной процесса, PV, за исключением противоположного знака. |
Рисунки ниже (щелкните, чтобы увеличить) наглядно демонстрируют, что производная e (t) является отрицательной величиной производной PV.
Верхний график показывает измеренную кривую PV после шага уставки. На нижнем графике показана кривая e (t) = SP — PV для того же события.
Если мы сравним два графика после шага SP в момент времени t = 10, мы увидим, что кривая PV на верхнем графике является точным отражением кривой e (t) на нижнем графике.Кривая PV поднимается, достигает пика и затем стабилизируется, в то время как в отраженном образце кривая e (t) опускается, спадает и затем стабилизируется.
Математически это «зеркальное отображение» форм кривых означает, что производные (или наклоны, или скорости изменения) одинаковы везде после шага SP, за исключением того, что они противоположны по знаку.
Производная от PV, используемая на практике
Хотя форма e (t) и PV противоположна, но одинакова везде после шага уставки, существует важное различие в момент изменения SP.Нижний график показывает вертикальный всплеск e (t) в этот момент. На графике PV нет соответствующего всплеска.
Производная (или наклон) вертикального всплеска в теоретическом мире приближается к бесконечности. В реальном мире это как минимум очень большое число. Если T d достаточно велик, чтобы придать какой-либо значимый вес производному члену, это огромное значение производной вызовет большие и внезапные манипуляции в CO. Эти большие манипуляции в CO, называемые производными , почти всегда нежелательны. .
Пока время выборки контура T задано правильно, кривая PV будет следовать постепенному и непрерывному отклику, избегая резких вертикальных всплесков, очевидных на кривой e (t).
Поскольку производная по e (t) идентична производной по PV во все времена, кроме случаев, когда SP изменяется, и когда уставка действительно изменяется, производная по ошибке предоставляет информацию, которую мы не хотим, чтобы наш контроллер использовал, мы заменяем « математическое примечание »в желтом поле выше, чтобы получить ПИД-регулятор с производной на контроллере измерения:
Производная от PV не «пинает»
Ниже мы показываем пример использования теплообменника при ПИД-регулировании с использованием зависимой, идеальной формы алгоритма и умеренных значений настройки, вычисленных в этой статье.
Первые шаги уставки слева на графике ниже (щелкните, чтобы увеличить) показывают производительность контура при использовании ПИД-регулятора с производной при ошибке. Шаги уставок вправо представляют идентичный сценарий, за исключением того, что используется ПИД-регулятор с производной по измерению.
«Удар», который доминирует на трассе CO при использовании производной по ошибке, довольно драматичен и несколько тревожит. Хотя он существует только в течение короткого времени и не влияет на производительность в этом примере, мы не должны предполагать, что это всегда будет так.В любом случае такое действие в конечном итоге скажется на механических конечных элементах управления.
Основываясь на предыдущем обсуждении, мы рекомендуем использовать производную по измеренной PV, если наш поставщик предоставляет такую возможность (к счастью, большинство из них). Значения настройки остаются одинаковыми для обоих алгоритмов.
Общие сведения о производном действии
Быстро меняющаяся PV имеет крутой наклон, что приводит к большой производной. Это верно независимо от того, началось ли динамическое событие только что или продолжается уже некоторое время.
На графике ниже (щелкните, чтобы увеличить) производная dPV / dt описывает наклон или «крутизну» PV во время реакции процесса.
В начале ответа наклон большой и положительный, когда кривая PV быстро увеличивается. Когда PV уменьшается, производная (наклон) отрицательна. И когда PV проходит через пик или впадину, наступает момент времени, когда производная равна нулю.
Чтобы понять влияние этой изменяющейся производной, предположим для обсуждения, что:
| ▪ | Коэффициент усиления регулятора Kc положительный. |
| ▪ | Время производной, T d (всегда положительное) достаточно велико, чтобы придать значимый вес производному члену. В конце концов, если T d очень мало, член производной имеет небольшое влияние, независимо от наклона PV. |
Отрицательный знак перед членом производной ПИД с производной на контроллере измерения (и с учетом приведенных выше предположений) означает, что влияние на СО от члена производной будет противоположно знаку наклона:
Таким образом, когда dPV / dt велико и положительно, член производной имеет большое влияние и стремится уменьшить CO.
И наоборот, когда dPV / dt отрицательно, член производной стремится увеличить CO.
Интересно отметить, что член производной не учитывает, движется ли PV к заданной точке или от нее (независимо от того, является ли e (t) положительным или отрицательным). Единственное, что нужно учитывать, это то, идет ли PV вверх или вниз и как быстро.
В результате производное действие направлено на подавление быстрых движений в ЛВ. Это может быть особенно полезной характеристикой при стремлении ослабить колебания в PV, которые имеют тенденцию усиливаться интегральным действием.К сожалению, как мы обсудим, потенциальная выгода имеет свою цену.
ОписаниеPID для инженеров-технологов: Часть 3 — Функции и опции
Поймите общие функции и опции, которые часто включаются в цифровые реализации блока PID.
В первой части этой серии статей, вышедшей в январе, были представлены основные уравнения для пропорционально-интегрально-производного (ПИД) регулирования (1) . В части 2, в феврале, были рассмотрены различные аспекты, относящиеся к параметрам настройки (2) .В этом заключительном выпуске серии объясняются функции и опции, обычно предоставляемые коммерческими системами управления технологическими процессами. Как типично для цифровых технологий, цифровые реализации уравнений ПИД-регулирования предоставляют больше функций и возможностей, чем их аналоговые предшественники (3) .
Формулировка обратной связи сброса
Взаимосвязи, которые составляют ПИ-регулятор, могут быть выражены уравнением для интегрального режима:
и уравнением для пропорционального режима:
, где M R — это выходное смещение контроллера, K C — коэффициент усиления контроллера, T I — время интегрирования, E — ошибка управления и M — выход контроллера.
Входными данными для вычислений интегрального режима является ошибка управления, E . Альтернативная форма, форма обратной связи сброса, имеет выход контроллера, M , как вход для вычислений интегрального режима.
Чтобы получить формулировку обратной связи сброса, выразите уравнение интегрального режима в дифференциальной форме:
Из уравнения пропорционального режима замените K C E на ( M — M R ):
и переставить уравнение.4 to:
Известный как запаздывание первого порядка, уравнение. 5 часто возникает в контексте управления технологическим процессом. Распространенным применением является экспоненциальный или запаздывающий фильтр, используемый для сглаживания (ослабления) шума, который сопровождает входные данные для управления процессом.
Рисунок 1 . В этой реализации обратной связи сброса ПИ-регулятора блок сброса получает смещение выхода контроллера, M R , путем фильтрации или сглаживания выходного сигнала контроллера, M , используя время сброса, T I , как постоянную времени в дифференциальном уравнении для запаздывания первого порядка.
На рисунке 1 изображена реализация ПИ-регулятора с обратной связью по сбросу. Лето реализует уравнение пропорционального режима. В тракте обратной связи, содержащем блок сброса, выход сумматора, M , является входом для блока сброса. Смещение выхода контроллера, M R , получается путем применения уравнения запаздывания первого порядка к выходу контроллера, M. Время сброса, T I , является постоянной времени для первого задержка заказа.
В первой части данной серии статей представлена вычислительная процедура, основанная на разностных уравнениях для ПИД-регулирования. Вкратце, для каждой итерации n, процедура: (1) начинается со значений переменной процесса, PV, на текущей и предыдущей итерациях; (2) вычислить скорость изменения PV ; (3) вычислить прогнозируемое значение PV ; (4) вычислить ошибку управления и прогнозируемую ошибку управления; (5) применить интегральное действие для получения нового значения смещения выхода контроллера; и (6) применить уравнение пропорциональности плюс смещения для получения выходного сигнала контроллера на итерации n, M n .
Шаг 5 этой процедуры использует уравнение разности для режима сброса для приблизительного интегрирования ошибки управления:
Чтобы использовать форму обратной связи сброса, требуется только одно изменение этой процедуры. Чтобы получить интегральное действие, уравнение. 6 заменяется уравнением разности для запаздывания первого порядка:
Большинство коммерческих цифровых систем управления технологическим процессом интегрируют ошибку управления, E (уравнение 6). Некоторые, но не все, коммерческие системы управления предоставляют возможность использования формы обратной связи сброса.
В аналоговом мире выполнение вычислений сброса путем интегрирования E нецелесообразно. Во всех пневматических и электронных контроллерах используется структура обратной связи сброса, показанная на рисунке 1, которую гораздо проще реализовать в аналоговой схеме.
Почему возникает интерес к обратной связи по сбросу? Функция, известная как внешний сброс (кратко описанная далее в этой статье), является уникальной для формы обратной связи сброса уравнения ПИД-регулирования.
Параллельный и последовательный
Два немного разных подхода, один обозначен как параллельный, а другой как последовательный, можно использовать для получения уравнения ПИД-регулирования.В таблице 1 представлены уравнения для производной на основе E. Вычисления производятся следующим образом:
- Вычислите ошибку управления, E .
- Вычислите прогнозируемую ошибку управления, Ê , используя следующее уравнение для производной на основе E (аналогичный подход можно использовать для производной на основе PV ):
- PI-регулирование использует E в как пропорциональные, так и интегральные члены. Чтобы получить ПИД-регулирование, уравнение ПИ-регулирования можно вычислить с помощью:
a.пропорциональный на основе Ê
b. интегральная на основе E (параллельная версия) или Ê (последовательная версия).
Единственное различие между двумя уравнениями ПИД заключается в вычислениях в интегральном режиме — параллельная версия основана на ошибке управления, E , а последовательная версия основана на прогнозируемой ошибке управления, Ê . Уравнение 6 содержит E n , что указывает на параллельную форму.Чтобы получить форму серии, замените E n на Ê n .
Вторая и третья строки таблицы 1 показывают, что алгебраическая замена E + T D dE / dt для прогнозируемой ошибки управления дает уравнения управления PID в терминах E . Эти два уравнения немного отличаются, но оба являются уравнениями ПИД.
Параллельная форма уравнения ПИД-регулирования содержит три различных члена: пропорциональный, интегральный и производный.По крайней мере, концептуально, каждый член может быть вычислен индивидуально (или параллельно), а затем добавлен для получения выходных данных контроллера.


