Правило выделения полного квадрата – Метод выделения полного квадрата — урок. Алгебра, 7 класс.

Выделение полного квадрата многочлена ℹ️ формулы выделения квадратов суммы и разности, преобразования и графики функций, правила, методы и примеры решения уравнений

Однако не все его знают. В результате этого объем вычислений увеличивается, а также допускаются ошибки. Он также применяется для нахождения корней уравнений и построения графиков.

Общая информация

Выделить полный квадрат из многочлена второй степени означает, что его следует привести к более читабельной формуле. Эта операция применяется в следующих случаях: интегрирование, дифференцирование, построение графиков и решение уравнений (чаще — в последних двух).

За основу взяты три формулы сокращенного умножения (разложение квадратного многочлена на множители), которые специалисты рекомендуют запомнить или выписать отдельно.

К ним относятся следующие соотношения:

1. Квадрат суммы: (y + z)^2 = y ² + 2yz + z ² .
2. Квадрат разности: (y — z)^2 = y ² — 2yz + z ² .
3. Разность квадратов: y ² — z ² = (y — z)(y + z).

Существует правило, позволяющее выполнить операцию упрощения многочлена ay ² + by + c второй степени путем разложения его на множители. Это означает, что его следует свести (преобразовать) к виду a * (y — y0)^2 + y0.

Универсальный алгоритм

Алгоритмом называется комплексное решение, состоящее из последовательного набора правил. Преобразование ay ² + by + c осуществляется следующим образом:

1. Привести к такому виду первое слагаемое на основании формулы (y + z)^2 = y ² + 2yz + z ² : [(a)^(½) * y]^2. Корень из коэффициента «а» следует указывать обязательно.
2. Второе слагаемое должно состоять из удвоенного произведения: by = [(2 * (a)^(½) * y)] * (b / [2 * (a)^(½)].
3. Третий свободный член находится по формуле z = (b / [2 * (a)^(½)].
4. Для равновесия следует отнять число, полученное в пункте 3.
5. Записать результат нужно таким образом: [(a)^(½) * y]^2 + [(2 * (a)^(½) * y)] * (b / [2 * (a)^(½)] + [(b / (2 * (a)^(½))]^2 — [(b / (2 * (a)^(½))]^2 + c.

Для квадрата разности алгоритм похожий. Формула выделения полного квадрата имеет такой вид: [(a)^(½) * y]^2 — [(2 * (a)^(½) * y)] * (b / [2 * (a)^(½)] + [(b / (2 * (a)^(½))]^2 — [(b / (2 * (a)^(½))]^2 + c. Соотношение также применяется математиками в алгебре, а также в различных дисциплинах с физико-математическим уклоном. Для этого нужно воспользоваться таким подробным объяснением правил решения:

1. Запись формулы: ay ² — c = ((a)^(½) * y — (c)^(½))((a)^(½) * y + (c)^(½)).
2. Коэффициент «с^(½)» должен быть равен целому числу.
3. Если условие во втором пункте не выполняется, то следует воспользоваться таким соотношением: с + a — a= с1 — a.
4. Записать выражение в таком виде: ay ² — c + a — a = ((a)^(½) * y — (c1)^(½))((a)^(½) * y + (c1)^(½)) — a.

Число «а» может быть положительным или отрицательным. Если его прибавить к «с», то должно получиться значение «с1».

При извлечении квадратного корня результат должен быть целым. Чтобы равенство не нарушалось, следует прибавить и отнять «а».

Алгоритм записан в общем виде. В теории он является сложным для понимания.

Однако при практическом применении некоторые неясности исчезают. Для начала нужно разобрать, где его нужно применять.

Сферы использования

Математики рекомендуют разобрать основные примеры выделения полного квадрата. Следует их систематизировать, поскольку это позволит оптимизировать процесс решения. Основной смысл заключается в применении соответствующих алгоритмов для экономии времени.

Некоторые считают, что шаблонами пользоваться нежелательно. Однако в этом есть и свои положительные стороны. Например, при поступлении в какое-либо высшее учебное заведение следует придерживаться общепринятых вариантов решения. При успешном зачислении в университет можно применить нестандартные подходы выполнения задания.

Шаблоны широко применяются не только в дисциплинах с физико-математическим уклоном, но и в программировании.

Распространенными заданиями с упрощением квадратного трехчлена являются:

• построение графиков квадратичной функции;
• решение уравнений;
• упрощение выражений.

Для нахождения решений следует подробно разобрать алгоритмы. Нет необходимости заучивать основные определения, формулы и правила. Их следует понимать, поскольку в философии есть такой закон: «переход количества в качество». Кроме того, программистами были созданы специальные онлайн-калькуляторы, позволяющие получить полный квадрат, разложить многочлен на множители и так далее.

Построение графиков

Графиком квадратичной функции z = a[y — c]^2 + d является кривая, которая называется параболой. Далее следует ввести следующие пояснения:

1. Коэффициенты «а» и «с» — некоторые числа. Последнее вычисляется по такой формуле: с = b / 2a.
2. Константа «d» является свободным членом.

Следует отметить, что расположение графика функции зависит от вышеописанных коэффициентов. Для построения параболы математики рекомендуют разобрать частные случаи:

1. Направление ветвей: вверх (a > 0) и вниз (a < 0).
2. Смещение вершины на величину «с»: по оси ОУ в положительную сторону (c > 0), по ОУ в отрицательном направлении (c < 0) и находится на ОХ (c = 0).
3. Смещение по ОХ: в сторону положительных значений на (b / 2a) и отрицательных — (-b / 2a).

Уравнение параболы всегда нужно приводить к правильному виду, поскольку график будет строить намного проще. Кроме того, его можно построить, зная частные случаи, и схематически.

Нахождение корней

Решить квадратное уравнение вида az ² + bz + с = 0 означает найти все его корни или доказать, что их нет. Его можно решать несколькими методами: нахождение дискриминанта, использование теоремы Виета или представление в виде квадрата.

При использовании первого метода нужно воспользоваться таким алгоритмом:

1. Упростить выражение (выведение общего множителя, раскрытие скобок и приведение подобных слагаемых).
2. Вычисление дискриминанта: D = (-b)^2 — 4ac.
3. Разобрать частные случаи, и выбрать ход решения, который зависит от значения D: при D > 0 решением уравнения являются два значения или корня (z1 = -b — D^(½) / 2a и z2 = -b + D^(½) / 2a; D = 0 — один корень (z = -b / 2a) и D < 0 — нет корней.
4. Подставить корни, полученные при решении, и проверить уравнение — значение в левой части должно быть равно нулю (0 = 0).

Вид квадратного уравнения зависит от коэффициентов a, b и c. Если а = 0, то старшая степень исчезает, и тождество превращается в обыкновенное линейное равенство (bz + c = 0) или функцию, графиком которой является прямая, а не парабола. При а = 1 его можно решить при помощи второго способа, который называется теоремой Виета (z1 + z2 = — b и z1 * z2 = с). Когда b = 0 (az ² + c = 0), то дискриминант можно не высчитывать. Решение находится следующим образом:

1. Нужно перенести свободный член «с» в правую сторону. Если с < 0, то решений нет. Когда значения c > 0, необходимо перейти ко второму шагу решения.
2. Разделить обе части на «а».
3. Вычислить корни по формулам (будут одинаковыми числами, но с разными знаками): z1 = -[c/a]^(½) z2 = [c/a]^(½).

Когда коэффициент с = 0 (az ² + bz = 0), то решить уравнение очень просто.

Для этого нужно произвести такие действия:

1. Сократить обе части на «a».
2. Вынести за скобку общий множитель: z (z + b/a) = 0.
3. Решить два уравнения: z1 = 0 и z2 + b/a = 0.
4. Проверить корни, подставив в исходное тождество.

Третий способ — выделение квадрата или использование формул сокращенного умножения. В этом случае нет необходимости использовать стандартный первый метод. Если построить график функции, то корнями будут являться его точки пересечения с осью абсцисс. Можно получить решения при помощи математических преобразований. Последний считается менее точным способом, поскольку корнями могут быть иррациональные числа, а не действительные.

Упрощение выражений

Бывают случаи, когда следует решить уравнение, упростив его. Например, чтобы решить равенство (2z ² — 5z + 7) + (z + 5)(z + 3) = 0, нужно раскрыть скобки, а затем привести подобные слагаемые. Этот способ называется методом математических преобразований.

В некоторых случаях следует возвести в квадрат, а затем привести подобные слагаемые. После этого необходимо опять воспользоваться формулами, сгруппировав элементы.

Этот шаг позволяет оптимизировать процесс вычислений. Например, нет необходимости подставлять численные значения в выражение z ² + 4z + 16 + z ² — 16. Его можно просто упростить: z ² + 8z + 16 + z ² — 16 = (z + 4)^2 + (z — 4)(z + 4) = (z + 4)(z + 4 + z — 4) = 2z (z + 4).

Пример решения

Необходимо решить квадратное уравнение z^2 + 20z + 50 = 6z + 5 несколькими способами, используя следующие методы: нахождение дискриминанта, формул разложения, теоремы Виета и построить график. Вычисление корней первым методом (через дискриминант) выглядит таким образом:

1. Упростить выражение: z^2 + 20z + 50 — 6z — 5 = z^2 + 14z + 45.
2. Вычислить дискриминант: D = 14^2 — 4 * 1 * 45 = 196 — 180 = 16 = 4^2.
3. Осуществить анализ второго пункта: если D = 16 > 0, то значит у уравнения два корня.
4. Первый корень: z1 = (-14 — 4) / 2 = -9.
5. Второе решение: z2 = (-14 + 4) / 2 = -5.
6. Проверка: (-9)^2 + (-9) * 14 + 45 = 81 — 126 + 45 = 0 и (-5)^2 + (-5) * 14 + 45 = 25 — 70 + 45 = 0.

Два корня подходят, поскольку равенство 0 = 0 соблюдается. Специалисты рекомендуют опускать проверку, поскольку задача решается несколькими способами.

Второй метод заключается в использовании теоремы Виета. Произвести поиск корней довольно просто, поскольку а = 1. Воспользовавшись формулами z1 + z2 = — 14 и z1 * z2 = 45, можно подобрать корни: z1 = -9 и z2 = -5.

Третий метод заключается в использовании формул разложения. Их разрешается применять несколько раз и в любом порядке. Алгоритм решения выглядит таким образом:

1. Разложить на множители (формула квадрат суммы): z^2 + 14z + 45 = z^2 + 14z + 45 + 4 — 4 = (z^2 + 14z + 49) — 4 = (z + 7)^2 — 4.
2. Использовать формулу разности квадратов двух чисел: (z + 7)^2 — 4 = (z + 7 — 2)(z + 7 — 2) = (z + 5)(z + 9).
3. Записать в виде уравнений: (z + 5) = 0 и (z + 9) = 0.
4. Корни: z1 = -5 и z2 = -9.

Использование графического метода позволит получить точные значения, поскольку во всех предыдущих способах они являются целыми числами. Необходимо записать уравнения параболы (можно воспользоваться вторым пунктом алгоритма третьего метода): (z + 7)^2 — 4. Анализ перед построением выглядит таким образом:

1. Ветви направлены вверх, поскольку a = 1 > 0.
2. Смещение вершины по ОУ на -4 в отрицательном направлении (с < 0), а по ОХ — на 7.

Для построения следует составить таблицу 1 зависимости функции y от аргумента z. По значениям также можно вычислить корни (все y = 0).

y	0	-3	0	5	21	45	77	117	165
z	-9	-6	-5	-4	-2	0	2	4	6

Таблица 1. Подготовка к построению.

После подготовки необходимо строить график. Это можно выполнить ручным методом или воспользоваться специализированным сайтом. Последним рекомендуется пользоваться только при проверке правильности решения.

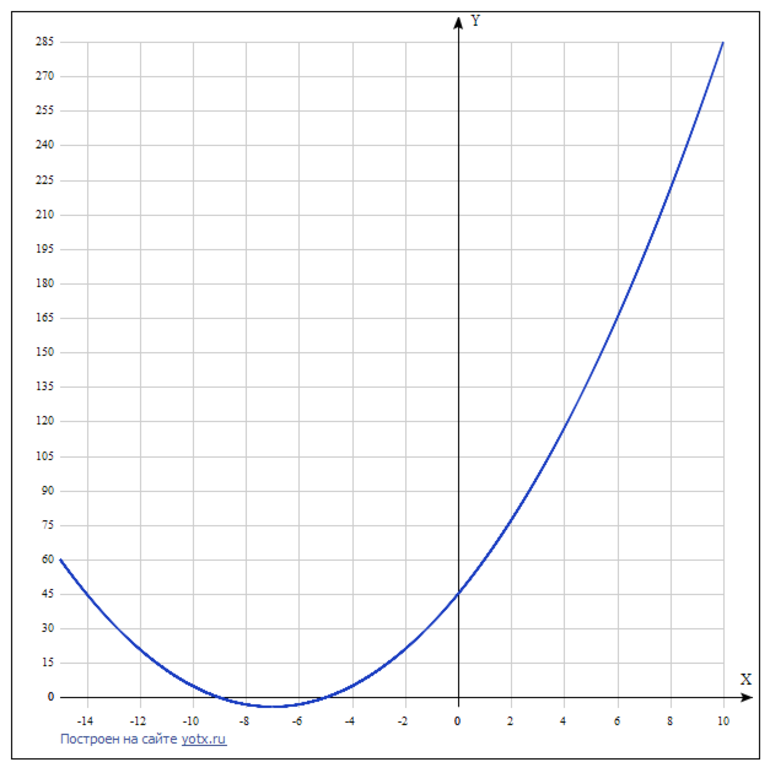
Рисунок 1. Графическое представление y = z^2 + 14 * z + 45.

На графике видно, что корнями уравнения являются числа -9 и -5. Они совпадают с полученными ранее значениями. Следовательно, решение является верным. Числа можно также подставить в исходное равенство.

Таким образом, при решении уравнений, упрощении выражений и построении графиков функций рекомендуется применять формулы сокращенного умножения. Это позволит сохранить много времени.

nauka.club

Выделить полный квадрат онлайн

Задача выделения полного квадрата заключается в преобразовании квадратного многочлена следующим образом:

где p и q неизвестные параметры которые требуется определить.

Для определения неизвестных параметров p и q, преобразуем приведенное выше равенство следующим образом:

и далее, раскроем скобки:

Для того, чтобы приведённое выше равенство соблюдалось, приравняем коэффициенты при одинаковых степенях:

В полученной системе уравнений, первое уравнение обозначает верное тождество при любых значениях параметра a, поэтому его можно исключить. Из второго уравнения выражаем параметр p и подставляем полученное выражение в третье уравнение системы:

Упрощаем третье уравнение системы и выражением из него значение параметра q:

Подставляем полученные значения p и q в самое первое уравнение и получаем формулу для выделения полного квадрата из квадратного многочлена:

Необходимость выделения полного квадрата часто возникает при решении задач интегрирования рациональных функций. Кроме того, выделив полный квадрат, можно получить формулу для решения квадратных уравнений.

Наш онлайн калькулятор выделяет полный квадрат для многочлена второй степени с описанием подробного хода решения на русском языке.

mathforyou.net

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

      Квадратным трёхчленом относительно переменной   x   называют многочлен

где a, b и c – произвольные вещественные числа, причем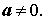

      Квадратным уравнением относительно переменной   x   называют уравнение

где a, b и c – произвольные вещественные числа, причем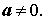

      Полным квадратным уравнением относительно переменной   x   называют уравнение

ax² + bx + c = 0,

где a, b и c – произвольные вещественные числа, отличные от нуля.

      Неполными квадратными уравнениями называют квадратные уравнения следующих типов:

Решение неполных квадратных уравнений

      Покажем, как решаются неполные квадратные уравнения на примерах.

      Пример 1. Решить уравнение

5x² = 0 .

      Решение.

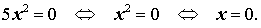
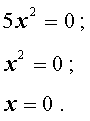
      Ответ: 0 .

      Пример 2. Решить уравнение

      Решение. Вынося в левой части уравнения (3) переменную   x   за скобки, перепишем уравнение в виде

      Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:

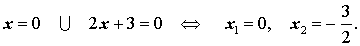
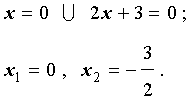
      Ответ: .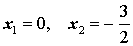

      Пример 3. Решить уравнение

2x² – 5 = 0 .

      Решение.

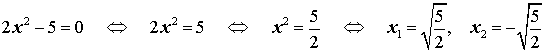
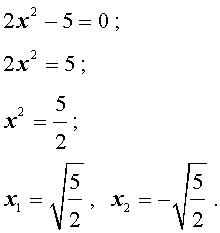
      Ответ: .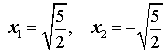

      Пример 4. Решить уравнение

      Решение. Поскольку левая часть уравнения (5) положительна при всех значениях переменной   x, а правая часть равна 0, то уравнение  решений не имеет.

      Ответ: .

Выделение полного квадрата

      Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:

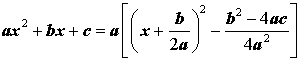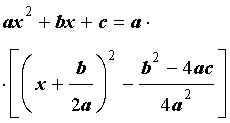(6)

      Для того, чтобы получить формулу (6), совершим следующие преобразования:

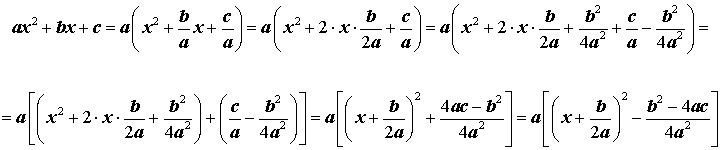
      Формула (6) получена.

Дискриминант

      Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой   D   и вычисляется по формуле:

      Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.

      Используя дискриминант, формулу (6) можно переписать в виде

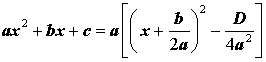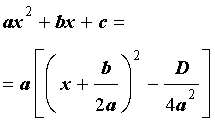(8)

Разложение квадратного трёхчлена на множители

      Утверждение. В случае, когда 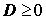, квадратный трёхчлен (1) разлагается на линейные множители. В случае, когда   D < 0, квадратный трехчлен нельзя разложить на линейные множители.

      Доказательство. В случае, когда   D = 0, формула (8) и является разложением квадратного трехчлена на линейные множители:

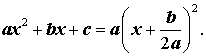(9)

      В случае, когда   D > 0, выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:

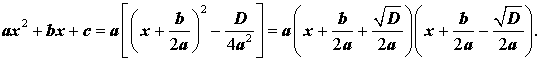
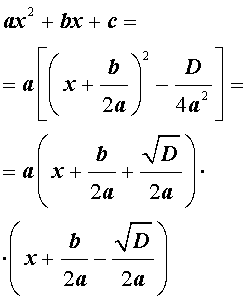
      Таким образом, в случае, когда   D > 0, разложение квадратного трехчлена (1) на линейные множители имеет вид

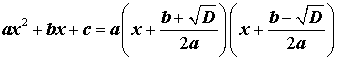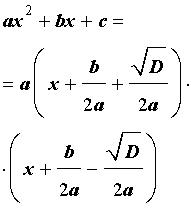(10)

      В случае, когда  D < 0, выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.

      Замечание. В случае, когда  D < 0, квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.

Формула для корней квадратного уравнения

      Из формул (9) и (10) вытекает формула для корней квадратного уравнения .

      Действительно, в случае, когда   D = 0, из формулы (9) получаем:

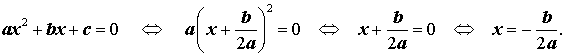
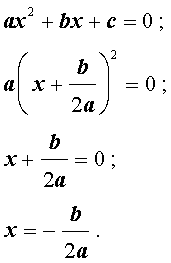
      Следовательно, в случае, когда   D = 0, уравнение (1) обладает единственным корнем, который вычисляется по формуле

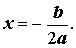(11)

      В случае, когда   D > 0, из формулы (10) получаем:

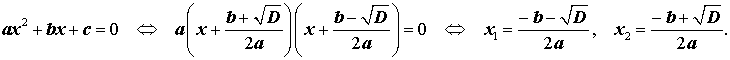
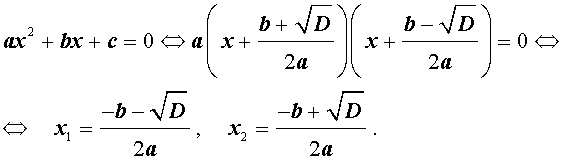
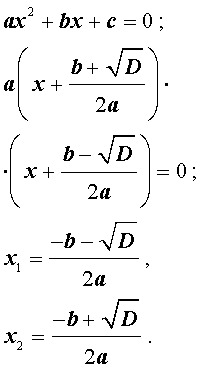
      Таким образом, в случае, когда   D > 0, уравнение (1) имеет два различных корня, которые вычисляются по формулам

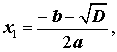	(12)
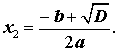	(13)

      Замечание 1. Формулы (12) и (13) часто объединяют в одну формулу и записывают так:

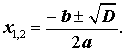(14)

      Замечание 2. В случае, когда   D = 0, обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда   D = 0, квадратное уравнение (1) имеет два совпавших корня, вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:

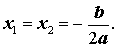(15)

      Замечание 3. В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.

      В случае, когда   D = 0, разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):

ax2 + bx + c = = a (x – x1)2.

(16)

      В случае, когда   D > 0, разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:

ax2 + bx + c = = a (x – x1) (x – x2) .

(17)

      Замечание 4. В случае, когда   D = 0, корни   x₁ и   x₂ совпадают, и формула (17) принимает вид (16).

Прямая и обратная теоремы Виета

      Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство

ax² + bx + c =
= a (x – x₁) (x – x₂) =
= a [x² – (x₁ + x₂) x + x₁x₂] =
= ax² – a(x₁ + x₂) x + ax₁x₂ .

      Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена

ax² + bx + c

равны соответствующим коэффициентам многочлена

ax² – a (x₁ + x₂) x + a x₁x₂ .

      Таким образом, справедливы равенства

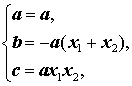
следствием которых являются формулы

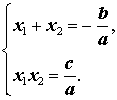(18)

      Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета).

      Словами прямая теорема Виета формулируется так: — «Если числа   x₁ и   x₂ являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».

      Обратная теорема Виета формулируется так: — «Если числа   x₁ и   x₂ являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».

      Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».

      Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

www.resolventa.ru

Выделение квадрата | Алгебра

Выделение квадрата двучлена в алгебре применяют в ходе преобразования многочленов.

Как выделить полный квадрат суммы или разности?

Начнём со случая, когда коэффициент при x² равен 1.

Полный квадрат суммы или разности состоит из трёх слагаемых, два из которых — квадраты:

   

Если нужны выделить полный квадрат из выражения типа

   

то

   

Отсюда следует, что b=p/2. Третье слагаемое,  b²,  должно равняться (p/2)². Прибавим его и отнимем, чтобы не изменить выражение.

В общем виде выделение квадрата можно записать так:

   

   

Первые три слагаемых можно свернуть как полный квадрат суммы (или разности, зависит от знака перед удвоенным произведением):

   

   

Примеры выделения полного квадрата.

   

Здесь a=x, 2ab=6x, следовательно, b=3. Прибавим к x²+2∙x∙3 квадрат тройки и тут же его вычтем, чтобы не данное выражение не изменилось:

   

В скобках получили полный квадрат разности. Его свернём по формуле. За скобками — -3²+23, упрощаем и получаем:

   

   

   

   

   

   

   

Шаг второй.

А как выделить полный квадрат, если перед x² стоит коэффициент, отличный от 1? В этом случае  надо вынести этот коэффициент за скобки, а дальше — аналогично.

Примеры.

Проще всего, если каждое из слагаемых делится нацело на коэффициент при  x².

   

   

   

   

Если перед x² стоит 2, 5, 10 или другое число, деление на которое приводит к появлению десятичной дроби, удобнее результат деления записывать именно в виде десятичной дроби.

   

   

   

   

Сложнее всего вычисления в случаях обыкновенных дробей.

   

   

   

   

   

   

   

В следующий раз рассмотрим, как с помощью выделения квадрата двучлена можно решить квадратное уравнение.

www.algebraclass.ru

Выделение полного квадрата Википедия

Квадра́тное уравне́ние — алгебраическое уравнение общего вида

ax2+bx+c=0,{\displaystyle ax^{2}+bx+c=0,}

где x{\displaystyle x} — неизвестное, a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c} — коэффициенты, причём a≠0.{\displaystyle \quad a\neq 0.}

Выражение ax2+bx+c{\displaystyle ax^{2}+bx+c} называют квадратным трёхчленом^[1].

Корень — это значение переменной x{\displaystyle x}, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное числовое равенство.

Элементы квадратного уравнения имеют собственные названия^[1]:

• a{\displaystyle a} называют первым или старшим коэффициентом,
• b{\displaystyle b} называют вторым, средним или коэффициентом при x{\displaystyle x},
• c{\displaystyle c} называют свободным членом.

Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице^[1]. Такое уравнение может быть получено делением всего выражения на старший коэффициент a{\displaystyle a}:

x2+px+q=0,p=

ru-wiki.ru

Выделение полного квадрата двучлена из квадратного трехчлена. Разложение многочлена на множители

Выделение полного квадрата двучлена из квадратного трехчлена

Пусть дан квадратный трехчлен
ах² + bх + с
и нужно преобразовать его к виду
a(x+m)² + n .
Для этого поступаем следующим образом: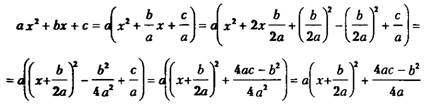

Приведем примеры на выделение полного квадрата.
Пример 1. х² — 4х + 1 = х² — 2·x·2 + 2² — 2² + 1 = (х-2)² — 4 + 1 =
= (х-2)² — 3.
Ответ: x² — 4х + 1 = (х-2)² — 3.
Пример 2.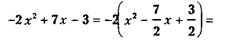


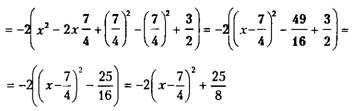
Ответ:

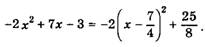
Разложение многочлена на множители

Разложением многочлена на множители называется преобразование многочлена в произведение двух или нескольких многочленов, среди которых могут быть и одночлены. Существует четыре основных способа разложения многочлена на множители.
Первый способ. Вынесение общего множителя за скобки.
Пример 1.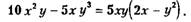

Второй способ. Способ группировки, который заключается в том, что объединяются в группы те члены, которые имеют общие множители, и выносится за скобки общий множитель каждой из групп. Если после такого преобразования окажется общий множитель у всех получившихся групп, то его выносят за скобки.
Пример 2.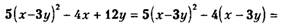


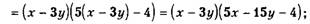
(x-3y) — общий множитель.
Третий способ. Применение формул сокращенного умножения.
Пример 3.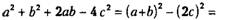


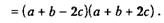
Четвертый способ. Разложение квадратного трехчлена на линейные множители, если известны его корни. Забегая вперед, заметим, что если квадратный трехчлен ах² + bх + с имеет действительные корни x1 и х2,то он может быть разложен на линейные множители следующим образом: ах² + bх + с = a(x-x1)(x — х2).
Пример 4.
х² — Зх — 4 = (х + 1)(х — 4), так как х² — Зх — 4 = 0 x1 = -1. x2 = 4 .

math-helper.ru

Квадратные уравнения: выделение полного квадрата

Квадратные уравнения можно решать еще до изучения темы «Квадратный корень»: выделение полного квадрата позволяет разложить квадратный трёхчлен на множители.

Рассмотрим на примерах, как можно использовать выделение квадрата двучлена для решения квадратных уравнений.

   

Выделим полный квадрат из трёхчлена, стоящего в левой части уравнения:

   

   

64 представим как квадрат 8:

   

Левую часть уравнения расложи на множители по формуле разности квадратов:

   

   

Получили уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:

   

   

Ответ: -6; 10.

   

Выделяем полный квадрат:

   

   

   

то есть быть раной нулю левая часть уравнения быть не может. Следовательно, данное уравнение не имеет корней.

Ответ: корней нет.

   

Разделим обе части уравнения почленно на число, стоящее перед x ²:

   

   

Выделим полный квадрат

   

   

   

   

   

   

   

Ответ: -1,5; -1.

С помощью выделения полного квадрата можно решать квадратные уравнения даже в курсе алгебры 7 класса при условии, что корни — рациональные числа.

Если корни — иррациональные числа, решить квадратное уравнение выделением квадрата двучлена также можно, но уже после введения понятия квадратного корня.

Пример.

   

Выделяем полный квадрат двучлена

   

   

Так как

   

   

   

   

Ответ:

   

Хотя выделение полного квадрата для решения квадратных уравнений в курсе алгебры используют редко, не стоит пренебрегать возможностью выработать соответствующий навык, который пригодится в будущем (например, в курсе математического анализа).

www.algebraclass.ru