Примеры на отрицательные и положительные числа – Сложение и вычитание отрицательных и положительных чисел. Решение примеров.

Сложение и вычитание отрицательных и положительных чисел. Решение примеров.

Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.

Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:

• Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.

\((-2)+(-3)=-5\)

• Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:

\((-8)+4=4-8=-4\)

\(9+(-4)=9-4=5\)

Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:

\(-9+9=0\)     \(7,1+(-7,1)=0\)

• При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.

\((-7)-(-6)=(-7)+6=(-1)\)

• Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.

\(7-9=-2\) так как \(9>7\)

• Также не стоит забывать минус на минус дает плюс:

\(7-(-9)=7+9=16\)

Задача 1. Вычислите:

 

1.  \(4+(-5)\)
2.  \(-36+15\)
3. \((-17)+(-45)\)
4. \(-9+(-1)\)

 

Решение:

 

1.  \(4+(-5)=4-5=-1\)
2.  \(-36+15=-21\)
3. \((-17)+(-45)\) \(=-17-45=-62\)
4. \(-9+(-1)=-9-1=-10\)

Задача 2. Вычислите:

1. \(3-(-6)\)
2.  \(-16-35\)
3. \(-27-(-5)\)
4.  \(-94-(-61)\)

Решение:

1.  \(3-(-6)=3+6=9\)
2. \(-16-35=-51\)
3.  \(-27-(-5)=-27+5=-22\)
4.  \(-94-(-61)=-94+61=-33\)

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

myalfaschool.ru

Карточки для самостоятельной работы по математике на тему «Все действия с положительными и отрицательными числами» (6 класс)

В-1 1) 0; 2) -84; 3) -58; 4) 4; 5) 18; 6) -90; 7) -19; 8) -16; 9) 56; 10) -78; 11) -55; 12) 0.

В-2. 1) 0; 2) -57; 3) 0; 4) -48; 5) 5; 6) -92; 7) -68; 8) -46; 9) 40; 10) -66; 11) -75; 12) 24.

В-3 1) 0; 2) -22; 3) 0; 4) -93; 5) -68; 6) 97; 7) -87; 8) -70; 9) -61; 10) 12; 11) -28; 12) 2.

В-4. 1) 3; 2) 0; 3) -62; 4) 0; 5) -42; 6) -94; 7) -42; 8) 14; 9) 61; 10) -33; 11) -73; 12) -60

В-5. .1) -51; 2) 11; 3) -87; 4) 73; 5) -73; 6) 2; 7) -95; 8) -96; 9) -38; 10) -52; 11) 0; 12) 0.

В-6. 1) 0; 2) -14; 3) -78; 4) -95; 5) 0; 6) -44; 7) 7; 8) -53; 9) 19; 10) -47; 11) -29; 12) 11.

В-7. 1) 0; 2) -61; 3) 0; 4) -86; 5) 98; 6) -13; 7) -35; 8) 3; 9) -42; 10) 15; 11) -69; 12) -99.

В-8 1) 0; 2) -7; 3) -98; 4) -84; 5) 48; 6) -58; 7) -27; 8) -99; 9) 4; 10) 68; 11) -60; 12) 0.

В-9 1) 0; 2) -78; 3) 57; 4) 16; 5) -57; 6) -49; 7) -51; 8) 3; 9) 0; 10) -58; 11) -43; 12) -57.

В-10. .1) -99; 2) 4; 3) -33; 4) 0; 5) 34; 6) 0; 7) -85; 8) -87; 9) 27; 10) -21; 11) -35; 12) -42.

В-11 1) -59; 2) -17; 3) 7; 4) 91; 5) 44; 6) 0; 7) -78; 8) 0; 9) -28; 10) -79; 11) -19; 12) -99

В-12 1) -83; 2) 13; 3) 0; 4) 0; 5) -48; 6) -71; 7) -64; 8) -99; 9) 2; 10) -42; 11) 64; 12) -47.

В-13 1) 0; 2) -85; 3) 23; 4) -65; 5) -65; 6) -95; 7) -99; 8) 5; 9) -46; 10) -68; 11) 0; 12) 45.

В-14 1) -55; 2) 0; 3) -65; 4) 52; 5) -49; 6) -44; 7) 0; 8) 4; 9) -72; 10) 11; 11) -63; 12) -89.

В-15 1) -64; 2) -86; 3) 51; 4) -63; 5) 0; 6) -59; 7) 3; 8) -96; 9) -91; 10) 15; 11) 0; 12) -41.

В-16 1) -88; 2) -89; 3) 0; 4) 0; 5) -45; 6) -83; 7) 2; 8) 15; 9) -13; 10) 69; 11) -40; 12) -64.

В-17 1) 11; 2) -4; 3) 0; 4) 36; 5) -70; 6) -58; 7) 3; 8) 0; 9) -88; 10) -32; 11) -99; 12) -35

В-18. 1) -83; 2) 87; 3) 0; 4) -56; 5) -99; 6) 0; 7) -79; 8) -57; 9) 16; 10) -68; 11) -88; 12) 5

В-19. 1) 2; 2) -47; 3) -96; 4) -26; 5) 63; 6) 0; 7) 0; 8) -64; 9) -51; 10) -85; 11) 24; 12) -35

В-20. 1) -53; 2) -77; 3) -50; 4) -29; 5) 11; 6) 79; 7) -27; 8) 0; 9) -93; 10) 4; 11) 0; 12) -80

В-21 1) 24,3; 2) -6,9; 3) 61,86; 4) -90,8; 5) -3; 6) -165; 7) -13,57; 8) -25,99; 9) -15,9; 10) -27; 11) 0,15; 12) -0,56.

В-22 1) -68,6; 2) -4; 3) 101,91; 4) 550; 5) -0,21; 6) -101,4; 7) 9,75; 8) -1,98; 9) -20; 10) 30,2; 11) -10,2; 12) -90,72.

В-23 1) -12; 2) -104,25; 3) 29,3; 4) 18,3; 5) 0,65; 6) -38,45; 7) 88,03; 8) -4; 9) -25,5; 10) -18,2; 11) -0,48; 12) -114.

В-24 1) -92,5; 2) -95,01; 3) 124,2; 4) 4,85; 5) -16,18; 6) -4; 7) -6; 8) -1,97; 9) 97,61; 10) -32,9; 11) -0,36; 12) 25,2.

В-25 1) 8,62; 2) -90,9; 3) 50,62; 4) -0,28; 5) -3; 6) -10,56; 7) -27,5; 8) -2; 9) -14,91; 10) 8,3; 11) -55; 12) 6,3.

В-26 1) -126,16; 2) 10,92; 3) -18; 4) 0,45; 5) -96; 6) -1,4; 7) -0,09; 8) -32,5; 9) 4,6; 10) 40,2; 11) -88,34; 12) -42,1.

В -27 1) 12,2; 2) 0,18; 3) -15,3; 4) 26,78; 5) -71; 6) -59,88; 7) -0,32; 8) -35,4; 9) -48; 10) -8; 11) -107,48; 12) -15,9.

В-28 1) -0,6; 2) 74,19; 3) 88,6; 4) 4,42; 5) -18; 6) -88; 7) -7,58; 8) 2,58; 9) -0,18; 10) -102,55; 11) 20,2; 12) -260.

В-29 1) -205; 2) 14,64; 3) -0,72; 4) 410; 5) -19,2; 6) 32,4; 7) -94,04; 8) -15; 9) -15,3; 10) -120,12; 11) 0,85; 12) 5,5.

В-30 .1) -149,49; 2) 37,48; 3) 96; 4) 13,43; 5) 0,32; 6) -0,24; 7) -14; 8) -480; 9) -7,5; 10) 56,4; 11) -6,4; 12) -77,08.

infourok.ru

Карточки для самостоятельной работы по математике на тему «Сложение и вычитание положительных и отрицательных чисел» (6 класс)

В-1.1 1) -92; 2) 100; 3) 30; 4) 49; 5) -18; 6) 62; 7) -77; 8) 5; 9) 0; 10) -38; 11) -88; 12) 0.

В -1.2 1) 0; 2) 64; 3) 0; 4) -84; 5) 72; 6) -35; 7) 100; 8) -38; 9) 1; 10) 80; 11) -20; 12) -90.

В-1.3 1) 5; 2) 62; 3) 35; 4) -82; 5) 100; 6) 0; 7) 0; 8) -22; 9) -16; 10) -98; 11) 14; 12) -52.

В-1.4 1) 2; 2) 0; 3) 10; 4) -3; 5) -24; 6) 80; 7) -48; 8) 78; 9) -65; 10) -94; 11) 100; 12) 0.

В -1.5. 1) 64; 2) 100; 3) 5; 4) -98; 5) 0; 6) 58; 7) -63; 8) -36; 9) 0; 10) -32; 11) -24; 12) 96.

В-1.6 1) 5; 2) -56; 3) 10; 4) -92; 5) -42; 6) 72; 7) 0; 8) -11; 9) 68; 10) 100; 11) -38; 12) 0.

В-1.7 1) 0; 2) -19; 3) 86; 4) -66; 5) 6; 6) 52; 7) -74; 8) 100; 9) -30; 10) -84; 11) 42; 12) 0.

В- 1.8 1) 0; 2) 34; 3) -42; 4) 0; 5) 32; 6) 56; 7) -24; 8) -94; 9) 100; 10) 2; 11) -58; 12) -72.

В-1.9 1) 0; 2) 34; 3) -42; 4) 0; 5) 32; 6) 56; 7) -24; 8) -94; 9) 100; 10) 2; 11) -58; 12) -72.

В-1.10. 1) 4; 2) 98; 3) 100; 4) -96; 5) 0; 6) 0; 7) -64; 8) 38; 9) -33; 10) -66; 11) 78; 12) -24.

В-1.11 1) 0; 2) 8; 3) 83; 4) -71; 5) -37; 6) 42; 7) 100; 8) 0; 9) -48; 10) -39; 11) -88; 12) 92.

В-1.12 1) 0; 2) 8; 3) 83; 4) -71; 5) -37; 6) 42; 7) 100; 8) 0; 9) -48; 10) -39; 11) -88; 12) 92.

В-1.13 1) 54; 2) -97; 3) 0; 4) 3; 5) -98; 6) 25; 7) 0; 8) -46; 9) 100; 10) -41; 11) -84; 12) 26.

В-1.14. 1) -90; 2) 0; 3) -36; 4) 3; 5) -74; 6) 66; 7) -11; 8) 0; 9) 100; 10) -32; 11) 22; 12) 77.

В -1.15. 1) -29; 2) 0; 3) 86; 4) 49; 5) -32; 6) 0; 7) -92; 8) -27; 9) 100; 10) 50; 11) -68; 12) 3.

В-1.16. 1) -25; 2) -37; 3) 76; 4) 0; 5) 32; 6) -24; 7) 0; 8) -92; 9) 6; 10) -63; 11) 45; 12) 100.

В-1.10. 1) 54; 2) -86; 3) 100; 4) -64; 5) 1; 6) 27; 7) 34; 8) 0; 9) 0; 10) -37; 11) -26; 12) -39.

В-1.18. 1) 58; 2) 85; 3) 100; 4) 52; 5) 6; 6) 0; 7) -30; 8) 0; 9) -52; 10) -14; 11) -82; 12) -26.

В-1 .19. 1) 86; 2) 42; 3) -37; 4) 100; 5) -57; 6) -86; 7) 0; 8) -51; 9) 46; 10) 5; 11) 0; 12) -58

В-1.20. 1) 100; 2) 30; 3) 25; 4) -69; 5) 78; 6) -55; 7) 7; 8) -94; 9) -88; 10) 0; 11) -45; 12) 0.

В-1.21. 1) 52,92; 2) -12,6; 3) 60; 4) 9,8; 5) 3; 6) 0; 7) -3,6; 8) -101,41; 9) -8,8; 10) -49,74; 11) 79,23; 12) 69,55.

В-1.22. 1) -125,7; 2) -23,42; 3) 4; 4) 5,95; 5) 28,9; 6) -20,3; 7) 97,41; 8) 0; 9) 13,92; 10) -137,68; 11) 50; 12) -10,2.

В-1.23. 1) -7,3; 2) 32,4; 3) -18,8; 4) -142,35; 5) -103,2; 6) 0; 7) 10,95; 8) 5,73; 9) 50; 10) 97,14; 11) 7; 12) -25,7.

В-1.24. 1) -106,2; 2) -65,18; 3) 80; 4) -12,58; 5) 3,48; 6) -2,1; 7) -47,6; 8) 3,9; 9) 99; 10) 77,71; 11) 0; 12) 85,99.

В-1.25. 1) -19,3; 2) 47,17; 3) 107,95; 4) -75,68; 5) 5,9; 6) -8,02; 7) -22,4; 8) 9; 9) 20; 10) 0; 11) -4,4; 12) 1,55.

В-1.26. 1) 30; 2) -26,7; 3) -24,72; 4) 6,52; 5) -10,4; 6) 9; 7) -288,1; 8) -77,38; 9) 0; 10) 5,83; 11) 4,41; 12) 21,3.

В-1.27. 1) 30; 2) -26,7; 3) -24,72; 4) 6,52; 5) -10,4; 6) 9; 7) -288,1; 8) -77,38; 9) 0; 10) 5,83; 11) 4,41; 12) 21,3.

В-1.28. 1) 60; 2) -62,6; 3) 96; 4) 3,83; 5) -53,36; 6) 7,09; 7) 12,54; 8) -122,8; 9) 67,3; 10) 0; 11) -3,4; 12) -166,18.

В-1.29. 1) 3; 2) -6,4; 3) 5,26; 4) -155,6; 5) -23,34; 6) -27,9; 7) 4,87; 8) 80; 9) 0; 10) 96,79; 11) 28,6; 12) -66,12.

В-1.30. 1) 63,1; 2) 0; 3) 95,93; 4) -152,4; 5) -14,8; 6) -71,1; 7) 3,82; 8) 40; 9) -94,37; 10) 8,94; 11) 4; 12) -13,7.

infourok.ru

Сложение и вычитание отрицательных и положительных чисел ℹ️ правило сложения чисел с разными знаками и действия с ними, как складывать и вычитать числа с разными знаками, онлайн-калькулятор

Впервые знакомство с отрицательными числами происходит в школьном курсе в 6 классе, иногда раньше. Число со знаком «+» называется положительным, противоположное — отрицательным.

Чтобы понять, что такое сложение и вычитание положительных и отрицательных чисел, достаточно воспользоваться координатной прямой. Например, сумма чисел -18 и 2. Сначала отмечаем на координатном отрезке число (-18), откладываем от него вправо, соответствующие масштабу, 2 единичных отрезка, и получаем на координатном луче число -16.

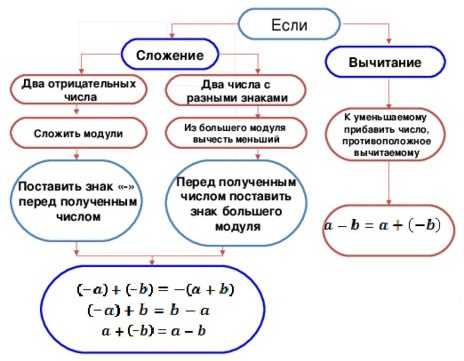
Правило сложения отрицательных чисел и чисел с разными знаками

Для суммирования двух отрицательных чисел, необходимо:

Например, сложение чисел -9 и -6 будет выглядеть следующим образом:

-9 + (-6) = -15

В данном случае, складываем модули 9 и 6, и перед получившимся натуральным числом 15 ставим знак «-«. 

Сложение рациональных или дробных чисел выполняется аналогичным способом:

-26,35 + (-25,35) = -(26,35 + 25,35) = -51,75

К 26,35 прибавляем 25,35 (т. е. мы складываем модули), в итоге получаем 51,75 с отрицательным значением. Перед ним ставим знак «минус».

Для суммирования натуральных чисел со знаками «+» и «-», надо:

• из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;

• перед полученным результатом поставить знак того слагаемого, которое имело большее значение.

Пример:

61,2 + (-31,5) = + (61,2 — 31,5) = 30,5

Модуль большего числа со знаком «+», соответственно, сумма получилась положительная:

-81 + 35 = -(81 — 35) = 46

Большее число со знаком «-», поэтому заменяем плюс на минус и получаем отрицательный ответ.

Как вычитать отрицательные и положительные числа

Для нахождения разности противоположных чисел, надо к уменьшаемому прибавить вычитаемое с противоположным знаком, то есть заменить разность суммой.

Наглядно данное действие лучше представить в виде формулы:

a — b = a + (-b)

То есть любое выражение, содержащее знаки сложения и вычитания, следует решать как сумму чисел.

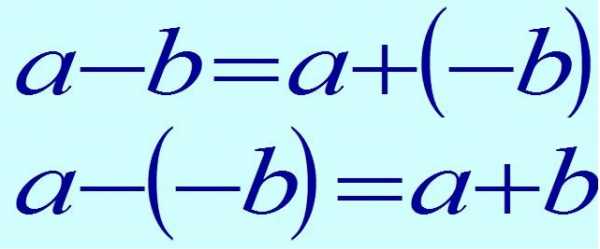
Примеры:

-20 — 14 = -20 + (-14) = -34;

-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.

Разность выражения будет положительной, если уменьшаемое больше вычитаемого, и отрицательной, если значение модуля уменьшаемого меньше вычитаемого. В случае, когда уменьшаемое и вычитаемое одинаковые, их разность будет равна нулю.

Примеры:

• 15 — 6 = 15 + (-6) = 9 — уменьшаемое 15, больше вычитаемого, поэтому ответ положительный;

•  -15 — 6 = -15 + (-6) = -21 — уменьшаемое -15, меньше вычитаемого, следовательно, ответ отрицательный. 

Если нужно отнять отрицательное число, то два знака «минус» подряд дают знак «плюс».

Пример:

10 — (-5) = 10 + 5 = 15;

— 10 — (-5) = -10 + 5 = 5 — 10 = -5.

 

Все вышеперечисленные действия возможно выполнить на калькуляторе. Для этого достаточно ввести сначала модуль числа, потом нажать кнопку изменения знака «+/-».

Например, чтобы задать число -81,73, надо в следующем порядке нажать кнопки: «8», «1», «,», «7». «3», «+/-». А решать пример с отрицательными числами следует в том же порядке, что и с положительными. 

Заключение

Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма. 

Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.

nauka.club

Отрицательные числа

Отрицательные числа — это числа со знаком минус (−), например −1, −2, −3. Читается как: минус один, минус два, минус три.

Примером применения отрицательных чисел является термометр, показывающий температуру тела, воздуха, почвы или воды. В зимнее время, когда на улице очень холодно, температура бывает отрицательной (или как говорят в народе «минусовой»).

Например, −10 градусов холода:

Обычные же числа, которые мы рассматривали ранее такие как 1, 2, 3 называют положительными. Положительные числа — это числа со знаком плюс (+).

При записи положительных чисел знак + не записывают, поэтому мы и видим привычные для нас числа 1, 2, 3. Но следует иметь ввиду, что эти положительные числа выглядят так: +1, +2, +3.

Координатная прямая

Координатная прямая это прямая линия, на которой располагаются все числа: и отрицательные и положительные. Выглядит следующим образом:

Здесь показаны только числа от −5 до 5. На самом деле координатная прямая бесконечна. На рисунке представлен лишь её небольшой фрагмент.

Числа на координатной прямой отмечают в виде точек. На рисунке жирная чёрная точка является началом отсчёта. Начало отсчёта начинается с нуля. Слева от начала отсчёта отмечают отрицательные числа, а справа — положительные.

Координатная прямая продолжается бесконечно по обе стороны. Бесконечность в математике обозначается символом ∞. Отрицательное направление будет обозначаться символом −∞, а положительное символом +∞. Тогда можно сказать, что на координатной прямой располагаются все числа от минус бесконечности до плюс бесконечности:

(−∞; +∞)

Каждая точка на координатной прямой имеет своё имя и координату. Имя — это любая латинская буква. Координата — это число, которое показывает положение точки на этой прямой. Проще говоря, координата это то самое число, которое мы хотим отметить на координатной прямой.

Например, точка А(2) читается как «точка А с координатой 2« и будет обозначаться на координатной прямой следующим образом:

Здесь A — это имя точки, 2 — координата точки A.

---

Пример 2. Точка B(4) читается как «точка B с координатой 4« и будет обозначаться на координатной прямой так:

Здесь B — это имя точки, 4 — координата точки B.

---

Пример 3. Точка M(−3) читается как «точка M с координатой минус три» и будет обозначаться на координатной прямой так:

Здесь M — это имя точки, −3 — координата точки M.

Точки можно обозначать любыми буквами. Но общепринято обозначать их большими латинскими буквами. Более того, начало отчёта, которое по другому называют началом координат принято обозначать большой латинской буквой O

 

Легко заметить, что отрицательные числа лежат левее относительно начала отсчёта, а положительные числа правее.

Существуют такие словосочетания как «чем левее, тем меньше» и «чем правее, тем больше». Наверное, вы уже догадались о чём идёт речь. При каждом шаге влево число будет уменьшаться в меньшую сторону. И при каждом шаге вправо число будет увеличиваться. Стрелка, направленная вправо, указывает на положительное направление отсчёта.

---

Сравнение отрицательных и положительных чисел

Правило 1. Любое отрицательное число меньше любого положительного числа.

Например, сравним два числа: −5 и 3. Минус пять меньше, чем три, несмотря на то, что пятёрка бросается в глаза в первую очередь, как цифра большая, чем три.

Связано это с тем, что −5 является отрицательным числом, а 3 — положительным. На координатной прямой можно увидеть, где располагаются числа −5 и 3

Видно, что −5 лежит левее, а 3 правее. А мы говорили, что «чем левее, тем меньше». И правило говорит, что любое отрицательное число меньше любого положительного числа. Отсюда следует, что

−5 < 3

«Минус пять меньше, чем три»

---

Правило 2. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой.

Например, сравним числа −4 и −1. Минус четыре меньше, чем минус единица.

Связано это опять же с тем, что на координатной прямой −4 располагается левее, чем −1

Видно, что −4 лежит левее, а −1 правее. А мы говорили, что «чем левее, тем меньше». И правило говорит, что из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Отсюда следует, что

−4 < −1

Минус четыре меньше, чем минус единица

---

Правило 3. Ноль больше любого отрицательного числа.

Например, сравним 0 и −3. Ноль больше, чем минус три. Связано это с тем, что на координатной прямой 0 располагается правее, чем −3

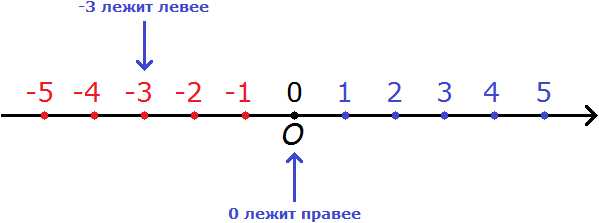
Видно, что 0 лежит правее, а −3 левее. А мы говорили, что «чем правее, тем больше». И правило говорит, что ноль больше любого отрицательного числа. Отсюда следует, что

0 > −3

Ноль больше, чем минус три

---

Правило 4. Ноль меньше любого положительного числа.

Например, сравним 0 и 4. Ноль меньше, чем 4. Это в принципе ясно и так. Но мы попробуем увидеть это воочию, опять же на координатной прямой:

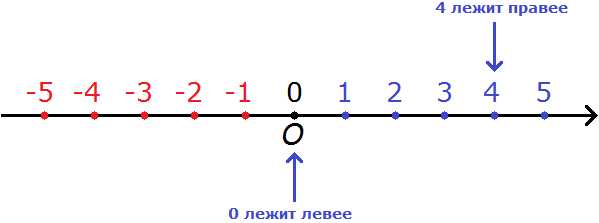
Видно, что на координатной прямой 0 располагается левее, а 4 правее. А мы говорили, что «чем левее, тем меньше». И правило говорит, что ноль меньше любого положительного числа. Отсюда следует, что

0 < 4

Ноль меньше, чем четыре

Задания для самостоятельного решения

Задание 1. Сравните числа −2 и 1

Задание 2. Сравните числа −5 и −2

Задание 3. Сравните числа −5 и −16

Задание 4. Сравните числа 15 и 20

Задание 5. Сравните числа −7 и 0

Задание 6. Сравните числа 5 и 0

Задание 7. Сравните числа 5 и 7

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

spacemath.xyz

«Отрицательные числа в изучении математики» (6 класс)

ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА.

1. История возникновения отрицательных чисел:

Впервые отрицательные числа появились в древнем Китае примерно 2100 лет тому назад. Там умели также складывать и вычитать положительные и отрицательные числа. Отрицательные числа трактовали как долг, а положительные как имущество. Таким же образом смотрели на эти числа и в Индии в VII столетии, но там уже были известны правила умножения и деления. Люди с некоторым недоверием относились к отрицательным числам, считая их не совсем реальными, истолкование их как имущество – долг вызвало недоумение: как можно «складывать» и «вычитать» имущество и долг.

Натуральные числа принято называть положительными целыми числами. Иногда перед положительными числами ставят знак «+».

Например: + 5=5 ; +7=7.

Два положительных или два отрицательных числа-это числа одного знака. Положительное и отрицательное число-это числа разных знаков.

С помощью знака «минус» записывается число, противоположное данному:

Число противоположное а, обозначают — а

Если а=15, то -а = -15;

Если а= -20, то –а = -(-20) = 20;

Если а =0, то –а = 0. Если положительные числа появились еще в древности, и стали использоваться для счета предметов, то отрицательные числа, изобретение недавнее: Отрицательные числа возникали при вычитании. Вначале они представлялись непонятными и бессмысленными, т.к наименьшим количеством было «ничто», то есть, как всегда привыкли считать это нуль. Что может быть меньше нуля?

XVII веке великий французский математик Рене Декарт предложил откладывать отрицательные числа на числовой оси влево от нуля. Отрицательные числа получили реальное истолкование. Их стали признавать наравне с положительными. Наступило полное числовое равноправие.

-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

О

Если перед числом стоит знак «+», его называют положительным.

Если «-», отрицательным.

Число «0» не является ни положительным , ни отрицательным.

На координатной прямой числа расположенные справа от нуля —положительные;

Числа расположенные слева от нуля — отрицательные.

2. Отрицательные числа.

На уроках математики мы уже познакомились с натуральными , дробными числами и действиями над ними. Однако в жизни мы уже встречались и с отрицательными числами. Примером может быть обыкновенный термометр:

Из рисунка можно наблюдать, что температура может быть как выше нуля, так и ниже нуля. Со знаком «+» и со знаком «-

Любое положительное число больше нуля : 5 > 0;

Любое отрицательное число меньше нуля: — 7 < 0;

Любое отрицательное число < положительного: — 7 < 5

3.Пример применения отрицательных чисел:

— в географии:

Самая большая положительная величина на Земле –вершина

Джомолунгма +8848 м.

Самая большая отрицательная величина—

Марианская впадина — 11034 м.

-в физике:

При растяжении пружины:

Если пружину растянуть, то измерение длины является положительным числом, а если сжать –отрицательным числом.

3. Правила умножения положительных и отрицательных чисел:

При умножении двух чисел с разными знаками в результате получается отрицательное число, модуль которого равен произведению модулей множителей.

«+» * «-» = «-»

«-» * «+» = «-»

При умножении двух чисел с одинаковыми знаками в результате получается положительное число, модуль которого равен произведению модулей множителей.

«-» * «-» = «+»

«+» * «+» = «+»

4.Сравнение отрицательных чисел:

-7 -6 -5 -4 -3 -2 -1 0 1

>

А В О

При сравнении целых отрицательных чисел, можно представить их на координатной прямой. Точка А с координатой -7 левее, чем точка В с координатой -3,

Поэтому: -7 < -3.

Из двух отрицательных чисел больше то, у которых модуль меньше.

5. Практические задачи:

Задача 1. Таня живет на пятом этаже многоэтажного дома, где имеется три подвала для парковки автомобилей (в лифте они указаны числами -1, -2, -3). Выйдя из своей квартиры, смогла бы Таня спуститься на лифте на семь этажей и какую кнопку ей следует нажать.

Ответ: Да, спуститься сможет. Нужно нажать на кнопку второго этажа подвала «-2»

Задача 2. Белые медведи выдерживают температуру до -80⁰ С, моржи – выше этой температуры на 45⁰ С, самые «морозостойкие» гуси и утки – ниже на 30⁰ С. Какую температуру выдерживают моржи и гуси, утки?

Решение: — 80 + 45 = — 35⁰ С выдерживают моржи; — 80 – 30 = — 110⁰ С выдерживают гуси, утки. Ответ: — 35⁰ С, — 110⁰ С.

Задание 3. Попробуйте в тексте найти положительные и отрицательные величины и сделайте выводы об их использовании в жизни.

Площадь Кунгурской Ледяной пещеры составляет 106,5 гектаров. Ее поверхность усеяна многочисленными карстовыми воронками, крупнейшие из которых достигают 50-60 метров в диаметре и 10-12 м в глубине.

В первом Бриллиантовом гроте пещеры зимой температура может достигать -15, -20 градусов, хотя в центре пещеры постоянная весна: +5 °C летом и зимой при 100% влажности.

В каменной нише Полярного грота скрывается массивная ледяная колонна, напоминающая застывший водопад. Ее еще описывал профессор М.Я. Киттара 165 лет назад.

Большое подземное озеро находится в гроте «Титанический» (площадь – 1300 кв.м., ширина 38 м, глубина достигает 3 м., температура воды постоянная +5 °C). В другом гроте – «Романтиков» экскурсанты могут любоваться небольшим озером с так называемым сифоном – подводным каналом, который опускается ниже уровня озера на 4-5 м.

(отрывок из книги Валентина Рапп «Путеводитель по Кунгуру и Ледяной пещере»)

Использованная литература:

1. Выгодский М.Я. Справочник по элементарной математике. – М.: Наука, 1972. – С. 130-136.

2. Едуш О.Ю. Математика. Подсказки на каждый день.

3. Лиман М.М. Школьникам о математике и математиках. – М.: Просвещение, 1981. – С. 26.

4. Новейший полный справочник школьника 5-11 классы. Том 1.– М.: Эксмо, 2014. – С. 224.

5. Рапп В.В. Путеводитель по Кунгуру и Ледяной пещере.– Пермь: Звезда, 1999. – С. 73-87.

6. История возникновения отрицательных чисел [Электронный ресурс]

7. История возникновения цифр. Применение отрицательных чисел.[Электронный ресурс]

infourok.ru

Сложение и вычитание отрицательных дробей.

Отрицательные дроби складываются и вычитаются также как и отрицательные числа, только по правилам сложения дробей. Мы можете добавлять только половинки к половинкам, четверти к четвертям или десятые к десятым и так далее. Вычитание отрицательных дробей следует тем же правилам. Для того чтобы сложить или вычесть две дроби нам нужно привести их к общему знаменателю. Если дробь отрицательная мы можем знак минус поставить в числитель и наоборот. Ниже расписано сложение \(-\frac{7}{6}+\frac{5}{7}\):

При сложении двух отрицательных дробей результат будет отрицательным. Когда мы вычитаем две отрицательные дроби, то мы к первой отрицательной дроби прибавляем положительную вторую, так как минус на минус дает плюс.

 

 

Рассмотрим сложение и вычитание следующих отрицательных дробей.

Задача 1. Вычислите \(\frac{1}{4}+(-\frac{3}{10})-(-\frac{1}{2}).\).

Решение. Приводим к наименьшему общему знаменателю:

\(\frac{1}{4}+(-\frac{3}{10})-(-\frac{1}{2})=\frac{5-3*2+10}{20}=\frac{9}{20}\)

Ответ: \(\frac{9}{20}\).

Задача 2. Вычислите \(\frac{1}{7}-(-\frac{5}{6})-(-\frac{1}{3})\).

Решение. Приводим к наименьшему общему знаменателю:

\(\frac{6-35+14}{42}=-\frac{15}{42}=-\frac{5}{14}\)

Ответ: \(-\frac{5}{14}\).

Задача 3. Вычислите \(\frac{1}{4}+\frac{5}{3}-(-\frac{1}{12})\).

Решение. Приводим к наименьшему общему знаменателю:

\(\frac{3+20+1}{12}=\frac{24}{12}=2.\)

Ответ: \(2.\).

Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.

 

 

 

 

 

 

 

 

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

myalfaschool.ru