Примеры на положительные и отрицательные числа: определение, примеры, какое число больше положительное или отрицательное

Сложение и вычитание отрицательных и положительных чисел. Решение примеров.

Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.

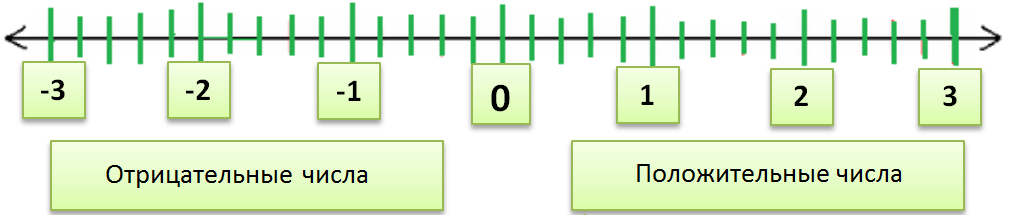
Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:

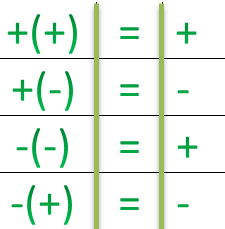
• Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.

\((-2)+(-3)=-5\)

• Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:

\((-8)+4=4-8=-4\)

\(9+(-4)=9-4=5\)

Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:

\(-9+9=0\)     \(7,1+(-7,1)=0\)

• При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.

\((-7)-(-6)=(-7)+6=(-1)\)

• Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.

\(7-9=-2\) так как \(9>7\)

• Также не стоит забывать минус на минус дает плюс:

\(7-(-9)=7+9=16\)

Задача 1. Вычислите:

 

1.  \(4+(-5)\)
2.  \(-36+15\)
3. \((-17)+(-45)\)
4. \(-9+(-1)\)

 

Решение:

 

1.  \(4+(-5)=4-5=-1\)
2.  \(-36+15=-21\)
3. \((-17)+(-45)\) \(=-17-45=-62\)
4. \(-9+(-1)=-9-1=-10\)

Задача 2. Вычислите:

1. \(3-(-6)\)
2.  \(-16-35\)
3. \(-27-(-5)\)
4.  \(-94-(-61)\)

Решение:

1.  \(3-(-6)=3+6=9\)
2. \(-16-35=-51\)
3.  \(-27-(-5)=-27+5=-22\)
4.  \(-94-(-61)=-94+61=-33\)

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Сложение и вычитание отрицательных и положительных чисел ℹ️ правило сложения чисел с разными знаками и действия с ними, как складывать и вычитать числа с разными знаками, онлайн-калькулятор

Впервые знакомство с отрицательными числами происходит в школьном курсе в 6 классе, иногда раньше. Число со знаком «+» называется положительным, противоположное — отрицательным.

Чтобы понять, что такое сложение и вычитание положительных и отрицательных чисел, достаточно воспользоваться координатной прямой. Например, сумма чисел -18 и 2. Сначала отмечаем на координатном отрезке число (-18), откладываем от него вправо, соответствующие масштабу, 2 единичных отрезка, и получаем на координатном луче число -16.

Правило сложения отрицательных чисел и чисел с разными знаками

Для суммирования двух отрицательных чисел, необходимо:

Например, сложение чисел -9 и -6 будет выглядеть следующим образом:

-9 + (-6) = -15

В данном случае, складываем модули 9 и 6, и перед получившимся натуральным числом 15 ставим знак «-«. 

Сложение рациональных или дробных чисел выполняется аналогичным способом:

-26,35 + (-25,35) = -(26,35 + 25,35) = -51,75

К 26,35 прибавляем 25,35 (т. е. мы складываем модули), в итоге получаем 51,75 с отрицательным значением. Перед ним ставим знак «минус».

Для суммирования натуральных чисел со знаками «+» и «-», надо:

• из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;

• перед полученным результатом поставить знак того слагаемого, которое имело большее значение.

Пример:

61,2 + (-31,5) = + (61,2 — 31,5) = 30,5

Модуль большего числа со знаком «+», соответственно, сумма получилась положительная:

-81 + 35 = -(81 — 35) = 46

Большее число со знаком «-», поэтому заменяем плюс на минус и получаем отрицательный ответ.

Как вычитать отрицательные и положительные числа

Для нахождения разности противоположных чисел, надо к уменьшаемому прибавить вычитаемое с противоположным знаком, то есть заменить разность суммой.

Наглядно данное действие лучше представить в виде формулы:

a — b = a + (-b)

То есть любое выражение, содержащее знаки сложения и вычитания, следует решать как сумму чисел.

Примеры:

-20 — 14 = -20 + (-14) = -34;

-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.

Разность выражения будет положительной, если уменьшаемое больше вычитаемого, и отрицательной, если значение модуля уменьшаемого меньше вычитаемого. В случае, когда уменьшаемое и вычитаемое одинаковые, их разность будет равна нулю.

Примеры:

• 15 — 6 = 15 + (-6) = 9 — уменьшаемое 15, больше вычитаемого, поэтому ответ положительный;

•  -15 — 6 = -15 + (-6) = -21 — уменьшаемое -15, меньше вычитаемого, следовательно, ответ отрицательный. 

Если нужно отнять отрицательное число, то два знака «минус» подряд дают знак «плюс».

Пример:

10 — (-5) = 10 + 5 = 15;

— 10 — (-5) = -10 + 5 = 5 — 10 = -5.

 

Все вышеперечисленные действия возможно выполнить на калькуляторе. Для этого достаточно ввести сначала модуль числа, потом нажать кнопку изменения знака «+/-».

Например, чтобы задать число -81,73, надо в следующем порядке нажать кнопки: «8», «1», «,», «7». «3», «+/-». А решать пример с отрицательными числами следует в том же порядке, что и с положительными. 

Заключение

Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма. 

Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.

Карточки для самостоятельной работы по математике на тему «Все действия с положительными и отрицательными числами» (6 класс)

В-1 1) 0; 2) -84; 3) -58; 4) 4; 5) 18; 6) -90; 7) -19; 8) -16; 9) 56; 10) -78; 11) -55; 12) 0.

В-2. 1) 0; 2) -57; 3) 0; 4) -48; 5) 5; 6) -92; 7) -68; 8) -46; 9) 40; 10) -66; 11) -75; 12) 24.

В-3 1) 0; 2) -22; 3) 0; 4) -93; 5) -68; 6) 97; 7) -87; 8) -70; 9) -61; 10) 12; 11) -28; 12) 2.

В-4. 1) 3; 2) 0; 3) -62; 4) 0; 5) -42; 6) -94; 7) -42; 8) 14; 9) 61; 10) -33; 11) -73; 12) -60

В-5. .1) -51; 2) 11; 3) -87; 4) 73; 5) -73; 6) 2; 7) -95; 8) -96; 9) -38; 10) -52; 11) 0; 12) 0.

В-6. 1) 0; 2) -14; 3) -78; 4) -95; 5) 0; 6) -44; 7) 7; 8) -53; 9) 19; 10) -47; 11) -29; 12) 11.

В-7. 1) 0; 2) -61; 3) 0; 4) -86; 5) 98; 6) -13; 7) -35; 8) 3; 9) -42; 10) 15; 11) -69; 12) -99.

В-8 1) 0; 2) -7; 3) -98; 4) -84; 5) 48; 6) -58; 7) -27; 8) -99; 9) 4; 10) 68; 11) -60; 12) 0.

В-9 1) 0; 2) -78; 3) 57; 4) 16; 5) -57; 6) -49; 7) -51; 8) 3; 9) 0; 10) -58; 11) -43; 12) -57.

В-10. .1) -99; 2) 4; 3) -33; 4) 0; 5) 34; 6) 0; 7) -85; 8) -87; 9) 27; 10) -21; 11) -35; 12) -42.

В-11 1) -59; 2) -17; 3) 7; 4) 91; 5) 44; 6) 0; 7) -78; 8) 0; 9) -28; 10) -79; 11) -19; 12) -99

В-12 1) -83; 2) 13; 3) 0; 4) 0; 5) -48; 6) -71; 7) -64; 8) -99; 9) 2; 10) -42; 11) 64; 12) -47.

В-13 1) 0; 2) -85; 3) 23; 4) -65; 5) -65; 6) -95; 7) -99; 8) 5; 9) -46; 10) -68; 11) 0; 12) 45.

В-14 1) -55; 2) 0; 3) -65; 4) 52; 5) -49; 6) -44; 7) 0; 8) 4; 9) -72; 10) 11; 11) -63; 12) -89.

В-15 1) -64; 2) -86; 3) 51; 4) -63; 5) 0; 6) -59; 7) 3; 8) -96; 9) -91; 10) 15; 11) 0; 12) -41.

В-16 1) -88; 2) -89; 3) 0; 4) 0; 5) -45; 6) -83; 7) 2; 8) 15; 9) -13; 10) 69; 11) -40; 12) -64.

В-17 1) 11; 2) -4; 3) 0; 4) 36; 5) -70; 6) -58; 7) 3; 8) 0; 9) -88; 10) -32; 11) -99; 12) -35

В-18. 1) -83; 2) 87; 3) 0; 4) -56; 5) -99; 6) 0; 7) -79; 8) -57; 9) 16; 10) -68; 11) -88; 12) 5

В-19. 1) 2; 2) -47; 3) -96; 4) -26; 5) 63; 6) 0; 7) 0; 8) -64; 9) -51; 10) -85; 11) 24; 12) -35

В-20. 1) -53; 2) -77; 3) -50; 4) -29; 5) 11; 6) 79; 7) -27; 8) 0; 9) -93; 10) 4; 11) 0; 12) -80

В-21 1) 24,3; 2) -6,9; 3) 61,86; 4) -90,8; 5) -3; 6) -165; 7) -13,57; 8) -25,99; 9) -15,9; 10) -27; 11) 0,15; 12) -0,56.

В-22 1) -68,6; 2) -4; 3) 101,91; 4) 550; 5) -0,21; 6) -101,4; 7) 9,75; 8) -1,98; 9) -20; 10) 30,2; 11) -10,2; 12) -90,72.

В-23 1) -12; 2) -104,25; 3) 29,3; 4) 18,3; 5) 0,65; 6) -38,45; 7) 88,03; 8) -4; 9) -25,5; 10) -18,2; 11) -0,48; 12) -114.

В-24 1) -92,5; 2) -95,01; 3) 124,2; 4) 4,85; 5) -16,18; 6) -4; 7) -6; 8) -1,97; 9) 97,61; 10) -32,9; 11) -0,36; 12) 25,2.

В-25 1) 8,62; 2) -90,9; 3) 50,62; 4) -0,28; 5) -3; 6) -10,56; 7) -27,5; 8) -2; 9) -14,91; 10) 8,3; 11) -55; 12) 6,3.

В-26 1) -126,16; 2) 10,92; 3) -18; 4) 0,45; 5) -96; 6) -1,4; 7) -0,09; 8) -32,5; 9) 4,6; 10) 40,2; 11) -88,34; 12) -42,1.

В -27 1) 12,2; 2) 0,18; 3) -15,3; 4) 26,78; 5) -71; 6) -59,88; 7) -0,32; 8) -35,4; 9) -48; 10) -8; 11) -107,48; 12) -15,9.

В-28 1) -0,6; 2) 74,19; 3) 88,6; 4) 4,42; 5) -18; 6) -88; 7) -7,58; 8) 2,58; 9) -0,18; 10) -102,55; 11) 20,2; 12) -260.

В-29 1) -205; 2) 14,64; 3) -0,72; 4) 410; 5) -19,2; 6) 32,4; 7) -94,04; 8) -15; 9) -15,3; 10) -120,12; 11) 0,85; 12) 5,5.

В-30 .1) -149,49; 2) 37,48; 3) 96; 4) 13,43; 5) 0,32; 6) -0,24; 7) -14; 8) -480; 9) -7,5; 10) 56,4; 11) -6,4; 12) -77,08.

Карточки для самостоятельной работы по математике на тему «Сложение и вычитание положительных и отрицательных чисел» (6 класс)

В-1.1 1) -92; 2) 100; 3) 30; 4) 49; 5) -18; 6) 62; 7) -77; 8) 5; 9) 0; 10) -38; 11) -88; 12) 0.

В -1.2 1) 0; 2) 64; 3) 0; 4) -84; 5) 72; 6) -35; 7) 100; 8) -38; 9) 1; 10) 80; 11) -20; 12) -90.

В-1.3 1) 5; 2) 62; 3) 35; 4) -82; 5) 100; 6) 0; 7) 0; 8) -22; 9) -16; 10) -98; 11) 14; 12) -52.

В-1.4 1) 2; 2) 0; 3) 10; 4) -3; 5) -24; 6) 80; 7) -48; 8) 78; 9) -65; 10) -94; 11) 100; 12) 0.

В -1.5. 1) 64; 2) 100; 3) 5; 4) -98; 5) 0; 6) 58; 7) -63; 8) -36; 9) 0; 10) -32; 11) -24; 12) 96.

В-1.6 1) 5; 2) -56; 3) 10; 4) -92; 5) -42; 6) 72; 7) 0; 8) -11; 9) 68; 10) 100; 11) -38; 12) 0.

В-1.7 1) 0; 2) -19; 3) 86; 4) -66; 5) 6; 6) 52; 7) -74; 8) 100; 9) -30; 10) -84; 11) 42; 12) 0.

В- 1.8 1) 0; 2) 34; 3) -42; 4) 0; 5) 32; 6) 56; 7) -24; 8) -94; 9) 100; 10) 2; 11) -58; 12) -72.

В-1.9 1) 0; 2) 34; 3) -42; 4) 0; 5) 32; 6) 56; 7) -24; 8) -94; 9) 100; 10) 2; 11) -58; 12) -72.

В-1.10. 1) 4; 2) 98; 3) 100; 4) -96; 5) 0; 6) 0; 7) -64; 8) 38; 9) -33; 10) -66; 11) 78; 12) -24.

В-1.11 1) 0; 2) 8; 3) 83; 4) -71; 5) -37; 6) 42; 7) 100; 8) 0; 9) -48; 10) -39; 11) -88; 12) 92.

В-1.12 1) 0; 2) 8; 3) 83; 4) -71; 5) -37; 6) 42; 7) 100; 8) 0; 9) -48; 10) -39; 11) -88; 12) 92.

В-1.13 1) 54; 2) -97; 3) 0; 4) 3; 5) -98; 6) 25; 7) 0; 8) -46; 9) 100; 10) -41; 11) -84; 12) 26.

В-1.14. 1) -90; 2) 0; 3) -36; 4) 3; 5) -74; 6) 66; 7) -11; 8) 0; 9) 100; 10) -32; 11) 22; 12) 77.

В -1.15. 1) -29; 2) 0; 3) 86; 4) 49; 5) -32; 6) 0; 7) -92; 8) -27; 9) 100; 10) 50; 11) -68; 12) 3.

В-1.16. 1) -25; 2) -37; 3) 76; 4) 0; 5) 32; 6) -24; 7) 0; 8) -92; 9) 6; 10) -63; 11) 45; 12) 100.

В-1.10. 1) 54; 2) -86; 3) 100; 4) -64; 5) 1; 6) 27; 7) 34; 8) 0; 9) 0; 10) -37; 11) -26; 12) -39.

В-1.18. 1) 58; 2) 85; 3) 100; 4) 52; 5) 6; 6) 0; 7) -30; 8) 0; 9) -52; 10) -14; 11) -82; 12) -26.

В-1 .19. 1) 86; 2) 42; 3) -37; 4) 100; 5) -57; 6) -86; 7) 0; 8) -51; 9) 46; 10) 5; 11) 0; 12) -58

В-1.20. 1) 100; 2) 30; 3) 25; 4) -69; 5) 78; 6) -55; 7) 7; 8) -94; 9) -88; 10) 0; 11) -45; 12) 0.

В-1.21. 1) 52,92; 2) -12,6; 3) 60; 4) 9,8; 5) 3; 6) 0; 7) -3,6; 8) -101,41; 9) -8,8; 10) -49,74; 11) 79,23; 12) 69,55.

В-1.22. 1) -125,7; 2) -23,42; 3) 4; 4) 5,95; 5) 28,9; 6) -20,3; 7) 97,41; 8) 0; 9) 13,92; 10) -137,68; 11) 50; 12) -10,2.

В-1.23. 1) -7,3; 2) 32,4; 3) -18,8; 4) -142,35; 5) -103,2; 6) 0; 7) 10,95; 8) 5,73; 9) 50; 10) 97,14; 11) 7; 12) -25,7.

В-1.24. 1) -106,2; 2) -65,18; 3) 80; 4) -12,58; 5) 3,48; 6) -2,1; 7) -47,6; 8) 3,9; 9) 99; 10) 77,71; 11) 0; 12) 85,99.

В-1.25. 1) -19,3; 2) 47,17; 3) 107,95; 4) -75,68; 5) 5,9; 6) -8,02; 7) -22,4; 8) 9; 9) 20; 10) 0; 11) -4,4; 12) 1,55.

В-1.26. 1) 30; 2) -26,7; 3) -24,72; 4) 6,52; 5) -10,4; 6) 9; 7) -288,1; 8) -77,38; 9) 0; 10) 5,83; 11) 4,41; 12) 21,3.

В-1.27. 1) 30; 2) -26,7; 3) -24,72; 4) 6,52; 5) -10,4; 6) 9; 7) -288,1; 8) -77,38; 9) 0; 10) 5,83; 11) 4,41; 12) 21,3.

В-1.28. 1) 60; 2) -62,6; 3) 96; 4) 3,83; 5) -53,36; 6) 7,09; 7) 12,54; 8) -122,8; 9) 67,3; 10) 0; 11) -3,4; 12) -166,18.

В-1.29. 1) 3; 2) -6,4; 3) 5,26; 4) -155,6; 5) -23,34; 6) -27,9; 7) 4,87; 8) 80; 9) 0; 10) 96,79; 11) 28,6; 12) -66,12.

В-1.30. 1) 63,1; 2) 0; 3) 95,93; 4) -152,4; 5) -14,8; 6) -71,1; 7) 3,82; 8) 40; 9) -94,37; 10) 8,94; 11) 4; 12) -13,7.

Положительные и отрицательные числа

Определение положительных и отрицательных чисел

Для определения положительных и отрицательных чисел воспользуемся координатной прямой, которая располагается горизонтально и направлена слева направо.

Замечание 1

Началу отсчета на координатной прямой соответствует число нуль, которое не относится ни к положительным, ни к отрицательным числам.

Определение 1

Числа, соответствующие точкам координатной прямой, которые лежат правее от начала отсчета, называются положительными.

Определение 2

Числа, соответствующие точкам координатной прямой, которые лежат левее от начала отсчета, называются

отрицательными.

Из данных определений вытекает, что множество всех отрицательных чисел противоположно множеству всех положительных чисел.

Отрицательные числа всегда записывают со знаком «–» (минус).

Пример 1

Примеры положительных чисел:

• Натуральные числа $3$, $13$, $333$, $578$, $10456$ и т.д.
• Рациональные числа $\frac{9}{17}$, $4 \frac{11}{23}$, $5,25$, $4,(79)$.
• Иррациональные числа $π$, $е$, $\sqrt[3]{2}$, бесконечная непериодическая десятичная дробь $103,1012341981…$

Готовые работы на аналогичную тему

Пример 2

Примеры отрицательных чисел:

• Рациональные числа $-\frac{9}{17}$, $-4 \frac{11}{23}$, $–5,25$, $–4,(79)$.
• Иррациональные числа$ -\sqrt[3]{2}$, бесконечная непериодическая десятичная дробь $–103,1012341981…$

Для упрощения записи перед положительными числами часто не записывают знак «+» (плюс), а перед отрицательными знак «–» записывают всегда. В подобных случаях необходимо помнить, что запись «$17,4$» равносильна записи «$+17,4$», запись «$\sqrt{5}$» равносильна записи «$+\sqrt{5}$» и т.д.

Таким образом, можно использовать следующее определение положительных и отрицательных чисел:

Определение 3

Числа, записанные со знаком «+», называются положительными, а со знаком «–» – отрицательными.

Используется определение положительных и отрицательных чисел, которое основано на сравнении чисел:

Определение 4

Положительными числами являются числа больше нуля, а отрицательными числами – числа меньше нуля.

Замечание 3

Таким образом, число нуль разделяет положительные и отрицательные числа.

Правила чтения положительных и отрицательных чисел

Замечание 4

При чтении числа со знаком впереди него сначала читается его знак, а затем само число.

Пример 3

Например, «$+17$» читают «плюс семнадцать»,

«$-3 \frac{4}{11}$» читают «минус три целых четыре одиннадцатых».

Замечание 5

Стоит отметить, что названия знаков «плюс» и «минус» не склоняются, в то время как числа могут склоняться.

Пример 4

Например, «$x=-18$» можно читать как «икс равен минус восемнадцать», так и «икс равен минус восемнадцати».

Интерпретация положительных и отрицательных чисел

Положительные числа используются для обозначения увеличения какой-нибудь величины, прихода, прибавки, возрастание значения и т.д.

Отрицательные числа применяют для противоположных понятий – для обозначения уменьшения какой-нибудь величины, расхода, недостатка, долга, снижения значения и т.д.

Рассмотрим примеры.

Читатель взял в библиотеке $4$ книги. Положительное значение числа $4$ показывает число книг, которые есть у читателя. Если ему нужно сдать $2$ книги в библиотеку, можно использовать отрицательное значение $–2$, которое будет указывать на уменьшение числа книг у читателя.

Положительные и отрицательные числа часто используют для описания значений различных величин в измерительных приборах. Например, термометр для измерения температуры имеет шкалу, на которой отмечены положительные и отрицательные значения.

Похолодание на улице на $3$ градуса, т.е. снижение температуры, можно обозначить значением $–3$, а повышение температуры на $5$ градусов – значением $+5$.

Принято отрицательные числа изображать синим цветом, что символизирует холод, низкую температуру, а положительные числа – красным цветом, что символизирует тепло, высокую температуру. Обозначение положительных и отрицательных чисел с помощью красного и синего цвета используется в различных ситуациях для выделения знака чисел.

Отрицательные числа

Отрицательные числа — это числа со знаком минус (−), например −1, −2, −3. Читается как: минус один, минус два, минус три.

Примером применения отрицательных чисел является термометр, показывающий температуру тела, воздуха, почвы или воды. В зимнее время, когда на улице очень холодно, температура бывает отрицательной (или как говорят в народе «минусовой»).

Например, −10 градусов холода:

Обычные же числа, которые мы рассматривали ранее такие как 1, 2, 3 называют положительными. Положительные числа — это числа со знаком плюс (+).

При записи положительных чисел знак + не записывают, поэтому мы и видим привычные для нас числа 1, 2, 3. Но следует иметь ввиду, что эти положительные числа выглядят так: +1, +2, +3.

Координатная прямая

Координатная прямая это прямая линия, на которой располагаются все числа: и отрицательные и положительные. Выглядит следующим образом:

Здесь показаны только числа от −5 до 5. На самом деле координатная прямая бесконечна. На рисунке представлен лишь её небольшой фрагмент.

Числа на координатной прямой отмечают в виде точек. На рисунке жирная чёрная точка является началом отсчёта. Начало отсчёта начинается с нуля. Слева от начала отсчёта отмечают отрицательные числа, а справа — положительные.

Координатная прямая продолжается бесконечно по обе стороны. Бесконечность в математике обозначается символом ∞. Отрицательное направление будет обозначаться символом −∞, а положительное символом +∞. Тогда можно сказать, что на координатной прямой располагаются все числа от минус бесконечности до плюс бесконечности:

(−∞; +∞)

Каждая точка на координатной прямой имеет своё имя и координату. Имя — это любая латинская буква. Координата — это число, которое показывает положение точки на этой прямой. Проще говоря, координата это то самое число, которое мы хотим отметить на координатной прямой.

Например, точка А(2) читается как «точка А с координатой 2« и будет обозначаться на координатной прямой следующим образом:

Здесь A — это имя точки, 2 — координата точки A.

---

Пример 2. Точка B(4) читается как «точка B с координатой 4« и будет обозначаться на координатной прямой так:

Здесь B — это имя точки, 4 — координата точки B.

---

Пример 3. Точка M(−3) читается как «точка M с координатой минус три» и будет обозначаться на координатной прямой так:

Здесь M — это имя точки, −3 — координата точки M.

Точки можно обозначать любыми буквами. Но общепринято обозначать их большими латинскими буквами. Более того, начало отчёта, которое по другому называют началом координат принято обозначать большой латинской буквой O

 

Легко заметить, что отрицательные числа лежат левее относительно начала отсчёта, а положительные числа правее.

Существуют такие словосочетания как «чем левее, тем меньше» и «чем правее, тем больше». Наверное, вы уже догадались о чём идёт речь. При каждом шаге влево число будет уменьшаться в меньшую сторону. И при каждом шаге вправо число будет увеличиваться. Стрелка, направленная вправо, указывает на положительное направление отсчёта.

---

Сравнение отрицательных и положительных чисел

Правило 1. Любое отрицательное число меньше любого положительного числа.

Например, сравним два числа: −5 и 3. Минус пять меньше, чем три, несмотря на то, что пятёрка бросается в глаза в первую очередь, как цифра большая, чем три.

Связано это с тем, что −5 является отрицательным числом, а 3 — положительным. На координатной прямой можно увидеть, где располагаются числа −5 и 3

Видно, что −5 лежит левее, а 3 правее. А мы говорили, что «чем левее, тем меньше». И правило говорит, что любое отрицательное число меньше любого положительного числа. Отсюда следует, что

−5 < 3

«Минус пять меньше, чем три»

---

Правило 2. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой.

Например, сравним числа −4 и −1. Минус четыре меньше, чем минус единица.

Связано это опять же с тем, что на координатной прямой −4 располагается левее, чем −1

Видно, что −4 лежит левее, а −1 правее. А мы говорили, что «чем левее, тем меньше». И правило говорит, что из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Отсюда следует, что

−4 < −1

Минус четыре меньше, чем минус единица

---

Правило 3. Ноль больше любого отрицательного числа.

Например, сравним 0 и −3. Ноль больше, чем минус три. Связано это с тем, что на координатной прямой 0 располагается правее, чем −3

Видно, что 0 лежит правее, а −3 левее. А мы говорили, что «чем правее, тем больше». И правило говорит, что ноль больше любого отрицательного числа. Отсюда следует, что

0 > −3

Ноль больше, чем минус три

---

Правило 4. Ноль меньше любого положительного числа.

Например, сравним 0 и 4. Ноль меньше, чем 4. Это в принципе ясно и так. Но мы попробуем увидеть это воочию, опять же на координатной прямой:

Видно, что на координатной прямой 0 располагается левее, а 4 правее. А мы говорили, что «чем левее, тем меньше». И правило говорит, что ноль меньше любого положительного числа. Отсюда следует, что

0 < 4

Ноль меньше, чем четыре

Задания для самостоятельного решения

Задание 1. Сравните числа −2 и 1

Задание 2. Сравните числа −5 и −2

Задание 3. Сравните числа −5 и −16

Задание 4. Сравните числа 15 и 20

Задание 5. Сравните числа −7 и 0

Задание 6. Сравните числа 5 и 0

Задание 7. Сравните числа 5 и 7

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Урок 10: Действия с отрицательными числами

План урока:

Сложение отрицательных чисел

Сложение чисел с разными знаками

Вычитание отрицательных чисел и чисел с разными знаками

 

В субботу, ученики 6 класса договорились встретиться и погулять в парке. Утром Юля выглянула в окошко, ярко светит солнышко, но при этом морозно. Девочка взглянула на термометр. Он показывал -10˚C. Мама попросила Юлю пойти на улицу немного позже, когда на улице потеплеет. Юля расстроилась и стала ждать. Через два часа девочка снова взглянула на термометр. Он показал -3. Ого! Всего  два часа, а так потеплело – обрадовалась девочка и стала одеваться, чтобы идти гулять. В это время в комнату вошла мама и удивленно спросила «Уже потеплело? На сколько градусов?» Дочь не знала, что сказать и как правильно узнать, на сколько градусов стало теплее. Мама пришла на помощь и сообщила, что достаточно от -10 отнять -3, и мы узнаем, на сколько градусов изменилась температура воздуха за окном. Иначе, можно сказать, что шкала термометра поднялась вверх на 7 делений, значит, на улице стало теплее на 7 градусов. Запомнив все, что рассказала мама, Юля побежала в парк делиться новыми знаниями с друзьями.

Источник

 

Сложение  и вычитание отрицательных чисел

Давайте вспомним любимую многими сказку «Буратино» и разберем задачу с участием любимых персонажей.

В театре Карабаса-Барабаса актерам жилось очень сложно, все куклы мечтали  жить на свободе. Актеры тяжело работали,  но долги перед хозяином росли с каждым днем. Злой владелец пообещал отпустить Буратино и Мальвину из своего театра только тогда, когда кукольные герои вернут ему долг. Сколько монет нужно собрать героям, чтобы оказаться на свободе, если у Буратино было -15 монет, а у Мальвины -6?

Источник

Чтобы ответить на главный вопрос задачи, нам нужно понимать, о чем идет речь. Изучив условие, возникает вопрос «Как может быть -15 и -6 монет?». В данном случае выходит, что Буратино и Мальвина должны вернуть Карабасу-Барабасу 15 и 6 монет, поэтому перед данными числами и стоит знак «минус». Получается, кукольные персонажи смогут покинуть театр, когда полностью вернут долг. Для этого необходимо узнать общий размер долга Буратино и Мальвины. Чтобы узнать размер долга, суммируем монеты персонажей -15 и -6. Но как их сложить, когда перед слагаемыми стоит «минус»? В подобных ситуациях применяют правило сложения отрицательных чисел.

Возвращаемся к решению задачи.

Теперь, правильно запишем и суммируем известные данные.

Получается, что герои имеют -21 монету, следовательно, они должны собрать 21 монету и вернуть долг, только тогда появится возможность покинуть театр Карабаса-Барабаса.

Источник

 

Рассмотрим еще одно задание.

Найдите результат сложения -24 и -16.

Чтобы вычислить сумму двух значений со знаком «минус», достаточно суммировать их модули, и перед полученной цифрой записать «-».

-24+(-16)=-(24+16)=-40.

Запомни! Если складываем два отрицательных числа, то суммируем их модули, а перед результатом сложения записываем «-».

 

Сложение чисел с разными знаками

Рассмотрим ситуацию.

Мишин папа навещал бабушку в деревне, обещал привезти гостинец сыну – яблоки. Во дворе Миша рассказал мальчишкам про папино обещание, и решил угостить яблоком, каждого из трех друзей, то есть, у него уже стало -3 яблока. Папа привез сыну 10 яблок и мальчик с радостью поделился фруктами с друзьями. Сколько яблок осталось у мальчика?

Источник

Чтобы найти количество яблок у мальчика, нам нужно узнать, чему равна сумма яблок –тех которые были у мальчика(-3), и тех, которые дал папа(10). То есть, чтобы ответить на главный вопрос задачи, достаточно сложить -3 и 10. Но слагаемые имеют разные знаки «+» и «-». Как же выполнить сложение положительного и отрицательного чисел? Запомнив алгоритм сложения положительных и отрицательных чисел сделать это, будет очень просто.

Используем рассмотренный алгоритм при выполнении действий.

Суммируем-3 и 10. Для этого:

• определяем модули: -3=|3|, 10=|10|;
• сравниваем модули, определяя больший: |3|<|10|;
• от большего отнимаем меньший: 10 – 3=7;
• так как по условию 10 – число положительное, то и результат будет числом положительным.

Записывается в таком виде:

-3+10=10 – 3=7.

Выходит, у мальчика стало 7 яблок.

Источник

Рассмотрим еще один пример сложения чисел с разными знаками.

Вычислите сумму -28 и 11.

Известные слагаемые имеют разные знаки, то есть -28 является значением отрицательным, а 11–положительным. Чтобы суммировать слагаемые, необходимо воспользоваться ранее рассмотренным алгоритмом. Вначале, определяем модули и сравниваем их.

-28=|28|;

11=|11|;

28>11.

Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:

-28+11=-(28-11)=-17.

Учитывая рассмотренные примеры, можно сказать, что:

любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.

Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.

Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:

-150+50=-(150-50)=-100.

Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:

При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.

-150=|150|;

-100=|100|.

150>100;

-150<-100.

Действительно, при сложении с отрицательным числом уменьшаемое стало только меньше.

 

Вычитание отрицательных чисел и чисел с разными знаками

Мы уже знаем, как выполнять сложение и вычитание положительных и отрицательных чисел, но хочется сказать, что именно в этом разделе математики, большую роль играют противоположные числа. Для тех, кто забыл, напоминаем, какие числовые значения называются противоположными:

Если два числа отличаются только знаком, то они являются противоположными:-13 и 13, 141 и -141, 1000 и -1000.

Чтобы понять, какие правила необходимо соблюдать при выполнении вычитания чисел с разными знаками, давайте разберем задание.

Определите, чему будет равно значение выражения: от -510 отнять +210.

На первый взгляд задание очень простое и не вызывает никаких проблем. Но стоит записать разность в виде выражения:

-510-(+210)

сразу возникает вопрос «Как вычитать, если уменьшаемое со знаком «минус», а вычитаемое со знаком «плюс»?».Чтобы решение подобных выражений не вызывало у вас трудностей, возьмите на заметку правило:

Чтобы выполнить вычитание чисел с разными знаками, нужно уменьшаемое оставить без изменений и прибавить к нему число, противоположное вычитаемому.

Например: -5-(+2).

Минус пять оставляем без изменений. Вычитаемое +2, а противоположное ему -2. Складываем уменьшаемое(-5) и число противоположное вычитаемому(-2): -5+(-2).

По правилу сложения отрицательных чисел, складываем модули(5+2) и ставим знак «-»:

-5+(-2)=-(5+2)=-7

Учитывая данное правило, получается, что к уменьшаемому(-510) необходимо прибавить значение,противоположное вычитаемому(210), таким числом будет -210:

Запишем выражение:

-510-(+210)=-510+(-210). Чтобы вычислить полученное выражение нужно сложить отрицательные значения, согласно правилу сложения отрицательных чисел:

-510-(+210)=-510+(-210)=-(510+210)=-720.

Вычисления окончены.

Источник

Рассмотрим следующее задание.

Найдите значение выражения: -248+248.

Используем правило сложения значений с разными знаками.

-248=|248|;

248=|248|;

248 – 248=0.

Следовательно,

при сложении противоположных числовых значений в результате всегда будет 0.

Зная правило вычитания отрицательных чисел, можем сделать вывод, что знаки, стоящие перед скобками, могут менять знак числа, находящегося в скобках.

К примеру, в выражении 19-(-4), при вычислении используем правило, согласно которого, к уменьшаемому прибавляем, число противоположное вычитаемому, то есть знак вычитаемого «-» меняем на противоположный «+». Получим:

Запомни! Если перед скобкой в математическом выражении стоит знак «минус», то знак числа в скобках меняется на противоположный.

Ну а сейчас, разберем задание, в котором перед скобкой стоит знак «плюс».

Вычисли: -36+(-7).

В этом задании воспользуемся правилом сложения отрицательных чисел– сложим модули числовых значений, а перед суммой поставим знак «минус»:

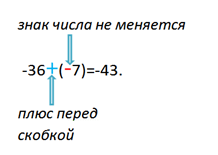
Мы видим, что «плюс» перед скобкой никак не повлиял на знак числа, стоящего в скобках. Запомни! Если перед скобками стоит «плюс», то знак числового значения, стоящего в скобках никак не меняется.

В выполнении рассматриваемых действий нет ничего сложного. Главное запомнить основные требования и придерживаться их в процессе любых вычислений! Если сразу запомнить все правила не получается, заходи на сайт 100уроков.ru и мы всегда с удовольствием напомним нужное правило или алгоритм.

 

Минутка истории

История математики утверждает, что человечество длительное время не принимало ряд отрицательных числовых значений. Данный вид чисел, казался непонятным и ненужным. Привычных нам знаков «плюс» и «минус» просто не существовало. Если возникала необходимость в записи отрицательно числа, то его записывали следующим образом «долг в 30 монет». И лишь математики Древней Индии и Китая, выполняли записи отрицательных чисел без употребления слова «долг», а просто использовали черные чернила, вместо синих.

Только в 3 веке греческий ученый Диофант, стал обозначать знак «минус» вот таким символом   .

Привычные нам знаки «+» и «-» появились в Германии в конце 15 века. Чешский ученый Ян Видман, отразил данные знаки в своей книге-пособии, помогающей подсчитывать прибыль и убытки чешским купцам. Стоит заметить, что данная книга была написана от руки и имела огромную популярность среди богатых людей того времени.

 

Сложение и вычитание положительных и отрицательных чисел

Числа могут быть положительными или отрицательными

Это числовая строка:

Отрицательные числа (-)	Положительные числа (+)

«-» — отрицательный знак.	«+» — положительный знак

Нет знака означает положительный

Если число имеет без знака , это обычно означает, что это положительное число .

Воздушные шары и гиря

Давайте подумаем о числах как о воздушных шарах (положительных) и весах (отрицательных):

К этой корзине привязаны воздушные шары и гирьки:

Добавление положительного числа

Сложение положительных чисел — это просто сложение.

Мы можем добавить шары (мы добавляем положительное значение ) корзина тянется вверх (положительно)

Пример: 2 + 3 = 5

действительно говорит

«Положительное 2 плюс Положительное 3 равно Положительное 5»

Мы могли бы записать это как (+2) + (+3) = (+5)

Вычитание положительного числа

Вычитание положительных чисел — это просто вычитание.

Воздушные шары можно забрать ( вычитаем положительное значение ) корзина тянется вниз (минус)

Пример: 6 — 3 = 3

действительно говорит

«Положительных 6 минус Положительных 3 равно Положительных 3»

Мы могли бы записать это как (+6) — (+3) = (+3)

Добавление отрицательного числа

Теперь посмотрим, как выглядит сложение и вычитание отрицательных чисел :

Мы можем добавлять веса (мы добавляем отрицательные значения ) корзина тянется вниз (минус)

Пример: 6 + (−3) = 3

действительно говорит

«Положительных 6 плюс отрицательных 3 равно положительных 3»

Мы могли бы записать это как (+6) + (−3) = (+3)

Последние два примера показали нам, что удаление воздушных шаров (вычитание положительного значения) или прибавление веса (добавление отрицательного числа) заставляют корзину опускаться.

Значит, результат тот же :

• (+6) — (+3) = (+3)
• (+6) + (−3) = (+3)

Другими словами, вычитание положительного — то же самое, что добавление отрицательного .

Вычитание отрицательного числа

Наконец, мы можем убрать веса (мы вычитаем отрицательных значений ) корзина тянется вверх (положительно)

Пример: Что такое 6 — (−3)?

6 — (- 3) = 6 + 3 = 9

Да, действительно! Вычесть отрицание — это то же самое, что добавить!

Два отрицания дают положительный результат

Что мы нашли?

Добавление положительного числа — это простое сложение…

Добавление положительного значения Добавление

Положительное и отрицательное вместе …

Вычитание положительного
или
Добавление отрицательного
равно
Вычитание

Пример: Что такое 6 — (+3)?

6 — (+ 3) = 6 — 3 = 3

Пример: Что такое 5 + (−7)?

5 + (- 7) = 5 — 7 = −2

Вычитание негатива…

Вычитание отрицательного числа аналогично Добавление

Пример: Что такое 14 — (−4)?

14 — (- 4) = 14 + 4 = 18

Правила:

Все это можно поместить в два правила :

	Правило				Пример
+ (+)	Два одинаковых знака превращаются в знак плюс				3 + (+ 2) = 3 + 2 = 5
— (-)					6 — (- 3) = 6 + 3 = 9
+ (-)	Два непохожих знака превращаются в знак минуса				7 + (- 2) = 7 — 2 = 5
— (+)					8 — (+ 2) = 8 — 2 = 6

Они «подобны знакам», когда они подобны друг другу (другими словами: одинаковы).

Итак, все, что вам нужно запомнить, это:

Два знака типа становятся положительным знаком

Два знака в отличие от становятся отрицательным знаком

Пример: Что такое 5 + (- 2)?

+ (-) — это в отличие от знаков (они не совпадают), поэтому они становятся отрицательным знаком .

5 + (- 2) = 5 — 2 = 3

Пример: Что такое 25 — (- 4)?

— (-) — это , как знак , поэтому они становятся положительным знаком .

25 — (- 4) = 25 + 4 = 29

Пример: Что такое −6 + (+ 3)?

+ (+) — это , как знак , поэтому они становятся положительным знаком и .

−6 + (+ 3) = −6 + 3 = −3

Начните с −6 на числовой прямой, двигайтесь вперед на 3, и вы получите −3

А теперь поиграйся!

Попробуйте сыграть в Casey Runner, вам нужно знать правила положительного и отрицательного, чтобы добиться успеха!

Объяснение здравого смысла

И есть объяснение «здравого смысла»:

Если я скажу «Ешь!» Я призываю вас поесть (положительный результат)

Если я скажу «Не ешьте!» Я говорю об обратном (отрицательном).

Теперь, если я скажу: « НЕ, не ешь!», Я говорю, что не хочу, чтобы вы умерли с голоду, поэтому я снова говорю: «Ешь!» (положительный).

Итак, два отрицания дают положительный результат, и если это вас устраивает, тогда вы сделали!

Другое объяснение здравого смысла

Друг +, враг —

.

+ + ⇒ +		друг друга мой друг
+ — ⇒ —		друг врага — мой враг
— + ⇒ —		враг друга — мой враг
— — ⇒ +		враг врага мой друг

Пример банка

Пример. В прошлом году банк по ошибке снял с вашего счета 10 долларов, и они хотят это исправить.

Значит, банк должен забрать отрицательные 10 долларов.

Допустим, ваш текущий баланс составляет 80 долларов, поэтому у вас будет:

80 долларов — (- 10 долларов) = 80 долларов + 10 долларов = 90 долларов

Итак, вы получаете на свой счет $, на 10 долларов больше .

Длинный пример, который вам может понравиться

Очки союзника

Элли может быть непослушным или милым. Так родители Элли сказали

«Если вы будете любезны, мы добавим 3 балла (+3).
Если непослушны, снимаем 3 балла (−3).
Когда вы набираете 30 очков, вы получаете игрушку. »

Ally начинает день с 9 очками:		9
Мама Элли обнаруживает пролитое молоко:		9 — 3 = 6
Тогда папа признается, что пролил молоко и пишет «отменить». Как «отменить» минус 3? Мы добавляем 3 снова!
Итак, мама считает:		6 — (−3) = 6 + 3 = 9

Таким образом, когда мы вычитаем отрицательное число, мы получаем
баллов (т.е.е. так же, как добавление очков).

Таким образом, вычитание отрицательного числа аналогично добавлению

Несколько дней спустя. У Элли 12 очков.
Мама добавляет 3 очка, потому что комната Элли чистая.		12 + 3 = 15
Папа говорит «Я убрал эту комнату» и пишет «отменить» на схеме.Мама считает:		15 — (+3) = 12
Папа видит, как Элли чистит собаку. Записывает на графике «+3». Мама считает:		12 + (+3) = 15
Элли бросает камень в окно.Папа пишет на диаграмме «−3». Мама считает:		15 + (−3) = 12

См .: как « 15 — (+3) », так и « 15 + (−3) » дают 12.

Итак:

Неважно, вычтите ли вы положительные
баллов или добавите отрицательные,
вы все равно потеряете баллы.

Таким образом, вычитание положительного
или
Добавление отрицательного
равно
Вычитание

Попробуйте эти упражнения…

Теперь попробуйте этот рабочий лист и посмотрите, как у вас дела.

А еще попробуйте эти вопросы:

.

положительных и отрицательных чисел | SkillsYouNeed

Стандартные числа, любые больше нуля, описываются как «положительные» числа. Мы не ставим перед ними знак плюса (+), потому что в этом нет необходимости, поскольку, по общему мнению, числа без знака положительны.

Числа меньше нуля известны как «отрицательные» числа. Перед ними стоит знак минус (-), указывающий, что они меньше нуля (например, -10 или « минус 10 »).

Визуализация отрицательных и положительных чисел

Вероятно, самый простой способ визуализировать отрицательные и положительные числа — использовать числовую линию, инструмент, с которым вы, возможно, хорошо знакомы, особенно если у вас есть дети в начальной школе.

Это выглядит примерно так:

Числовая линия может помочь вам визуализировать как положительные, так и отрицательные числа, а также операции (сложение и вычитание), которые вы можете с ними делать.

Когда вам нужно вычислить сложение или вычитание, вы начинаете с первого числа и перемещаете второе число разрядов вправо (для сложения) или влево (для вычитания).

Эта числовая линия является упрощенной версией, но вы можете нарисовать их с любым числом, если хотите. Большим преимуществом числовой линии является то, что ее очень легко нарисовать самостоятельно на обратной стороне конверта или клочка макулатуры, а также довольно сложно ошибиться в расчетах. Если вы внимательно подсчитываете количество мест, которые вы двигаетесь, вы получите правильный ответ.

Рабочие примеры

Что такое 10-25?

Начиная с 10, вы перемещаете 25 чисел влево и сразу видите, что ответ — -15.

---

Что такое −17 + 23?

На этот раз вы начинаете с -17 и перемещаетесь на 23 позиции вправо. Сразу видно, что ответ — 6.

---

Вычитание отрицательных чисел

Если вы вычесть отрицательное число, два отрицательных числа объединятся, чтобы получить положительное.

−10 — (- 10) не равно −20. Вместо этого вы можете думать об этом как о повороте одного из отрицательных знаков вертикально, чтобы пересечь другой и получить плюс.Тогда сумма будет -10 + 10 = 0.

Краткое примечание по скобкам

---

Для наглядности, вы никогда не написали бы два знака минус рядом без скобок.

Итак, если вас попросят вычесть отрицательное число, оно всегда будет заключено в скобки, чтобы вы могли увидеть, что использование двух отрицательных знаков было намеренным.

-10-10 неверно (и сбивает с толку)

-10 — (- 10) правильно (и яснее)

---

Умножение и деление на положительные и отрицательные числа

При умножении или делении с комбинациями положительных и отрицательных чисел вы можете упростить процесс, сначала игнорируя знаки (+/-) и просто умножая или деля числа, как если бы они оба были положительными.Получив числовой ответ, вы можете применить очень простое правило, чтобы определить знак ответа:

• Когда знаки двух чисел совпадают с , ответ будет положительным .
• Когда знаки двух чисел разные , ответ будет отрицательный .

Итак:

(положительное число) × (положительное число) = положительное число

(отрицательное число) × (отрицательное число) = положительное число

Но:

(положительное число) × (отрицательное число) = отрицательное число

В качестве побочного вопроса это каким-то образом объясняет, почему у вас не может быть квадратного корня из отрицательного числа (подробнее об этом читайте на нашей странице в Special Numbers and Concepts ).Квадратный корень — это число, которое умножается само на себя, чтобы получить число. Вы не можете умножить число на себя, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.

Правило работает точно так же, когда вам нужно умножить или разделить более двух чисел. Четное количество отрицательных чисел даст положительный ответ. Нечетное количество отрицательных чисел даст отрицательный ответ.

Рабочих примеров

Что такое −5 × 25?

5 x 25 равно 125.Но здесь у вас есть одно отрицательное и одно положительное число, поэтому знак ответа будет отрицательным. Следовательно, ответ — −125 .

Что такое −40 ÷ 8?

40 ÷ 8 равно 5. Опять же, у вас есть одно положительное и одно отрицательное число, поэтому знак ответа будет отрицательным. Ответ: −5 .

Что такое −50 ÷ −5?

50 ÷ 5 равно 10. На этот раз у вас есть два отрицательных числа, поэтому знак ответа будет положительным.Ответ: 10 .

Что такое −100 × −2?

100 x 2 равно 200. Опять же, у вас два отрицательных числа, поэтому ответ положительный. Это 200 .

Что такое 10 x −2 × 3?

Для начала рассмотрим первую часть расчета. 10 x 2 = 20. У вас есть одно положительное и одно отрицательное число, поэтому знак ответа будет отрицательным, то есть −20.

Теперь возьмем вторую часть вычисления: −20 × 3.Итак, 20 × 3 = 60, но опять же, у вас есть отрицательное и положительное число, поэтому ответ будет отрицательным: −60 .

---

Почему умножение двух отрицаний дает положительный ответ?

---

Тот факт, что отрицательное число, умноженное на другое отрицательное число, дает положительный результат, часто может сбивать с толку и казаться нелогичным.

Чтобы объяснить, почему это так, вспомните числовые линии, использованные ранее в этой статье, поскольку они помогают объяснить это визуально.

1. Во-первых, представьте, что вы стоите на числовой прямой в нулевой точке и смотрите в положительном направлении, то есть в сторону 1, 2 и так далее. Вы делаете два шага вперед, делаете паузу, затем делаете еще два шага. Вы переместились 2 × 2 шага = 4 шага.
   Следовательно, положительный × положительный = положительный
2. Теперь вернитесь к нулю и повернитесь в отрицательном направлении, то есть в сторону −1, −2 и т. Д. Сделайте два шага вперед, затем еще два. Теперь вы стоите на −4. Вы переместились на 2 × -2 шага = -4 шага.
   Следовательно, отрицательный × положительный = отрицательный

В обоих этих примерах вы двигались вперед (т. Е. В том направлении, куда вы смотрели), что является положительным шагом.

3. Вернитесь к нулю снова, но на этот раз вы собираетесь идти назад (отрицательное движение). Снова поверните голову в положительную сторону и сделайте два шага назад. Теперь вы стоите на -2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению.
   Следовательно, положительный × отрицательный = отрицательный
4. Наконец, снова вернемся к нулю, повернемся в отрицательном направлении. Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись в отрицательном направлении и идя назад ( два отрицательных ), вы достигли положительного результата.
   Следовательно, отрицательный × отрицательный = положительный

---

1. Два негатива компенсируют друг друга. Вы можете увидеть это в речи:
   • «Просто сделай это!» положительный стимул к чему-то.
   • «Не делай этого!» просит кого-то чего-то не делать. Это отрицательно.
   • «Не делай этого» означает «пожалуйста». Два отрицания компенсируют и дают положительный результат как в математике, так и в речи.
2. Знаки складываются физически. Когда у вас есть два отрицательных знака, один переворачивается, и они складываются, чтобы получить положительный. Если у вас есть положительный и отрицательный ответ, останется один штрих, и ответ будет отрицательным.Это простая и наглядная памятная записка, хотя она не обязательно удовлетворит тех, кто хочет понять правило.

---

Заключение

Отрицательные знаки могут выглядеть немного устрашающе, но правила, регулирующие их использование, просты и понятны. Помните об этом, и у вас не будет проблем.

.

Сложение положительных и отрицательных чисел

Как только вы поймете основы положительные и отрицательные числа, вы можете начать складывать их вместе. Иногда это кажется сложным, потому что есть множество правил, которые нужно запомнить и соблюдать. Хорошо пройдите их медленно, чтобы понять.

Правило 1: Добавление положительных чисел к положительным — это нормальное сложение.

Пример 1: Добавление положительных чисел к положительным — вот чем вы занимались занимаюсь давно; например 5 + 2 складывает два положительных числа.Вы можете вычислить эти проблемы обычным образом, как вы это делали все это время. Иногда вы можете увидеть что-то вроде этого: +5 + 2 = 7; это просто означает, что 5 тоже положительный. Не волнуйтесь — вы можете рассчитывать это, как обычно бы!

Правило 2: Добавление положительных чисел к отрицательным — подсчитайте сумму вперед. вы добавляете.

Добавление положительных чисел к отрицательным может оказаться непростым делом, потому что вам нужно Обратите особое внимание на то, где в проблеме находятся отрицательные знаки.

Пример 2: Допустим, у нас была проблема: -5 + 2. Это будет читаться как «отрицательный пять плюс два ». Это легче всего представить на числовой прямой. Вместо того, чтобы начинать при положительном числе вы начинаете с отрицательного числа, которое находится слева нуля на числовой прямой. Однако вы добавляете два, так что вы все равно будете считать переадресуйте два места, чтобы прийти к вашему ответу, например:

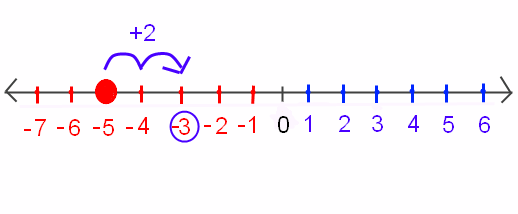
Большая красная точка над -5 показывает, что именно здесь мы начинаем нашу проблему.Синяя стрелка показывает, что мы посчитали (или добавили) 2. Синий кружок вокруг -3 показывает нам, что это наш ответ.

Таким образом, -5 + 2 = -3.

Правило 3: Добавление отрицательных чисел к положительным — считайте в обратном порядке, как если бы вы вычитание.

Пример 3: Допустим, у нас возникла проблема: 5 + (-2). Это будет читаться как «пять плюс отрицательные два.Это также можно представить в числовой строке. Теперь мы начинаем положительное число, но мы добавляем отрицательное число, что означает, что мы будем двигаться назад (влево), как если бы мы вычитали. Мы будем считать назад два места, чтобы прийти к ответу, например:

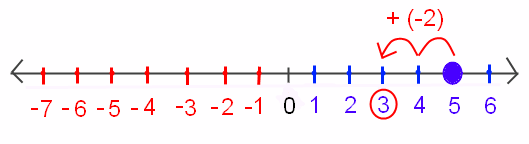
Большая синяя точка над цифрой 5 показывает, что именно здесь мы начинаем проблема.Красная стрелка показывает, что мы считали в обратном порядке (вычитали) 2. Красный кружок цифра 3 показывает, что это наш ответ.

Таким образом, 5 + (-2) = 3.

Правило 4: Добавление отрицательных чисел к отрицательным числам — игнорируйте знак сложения и относитесь к проблеме как к вычитанию (обратный отсчет).

Пример 4: Допустим, у нас была проблема -4 + -2.Это будет читаться как «отрицательный четыре плюс два минус «. Это также можно представить на числовой прямой. Ты первый нужно игнорировать знак плюса и понимать, что второе отрицательное число означает вы вычитаете это число. Таким образом, вы могли бы подумать об этой проблеме как о «отрицательном четыре минус два ». Начните с -4, затем сосчитайте в обратном порядке (вычтите) еще 2. Тогда ваш ответ будет -6. Вы бы увидели это в числовой строке, например:

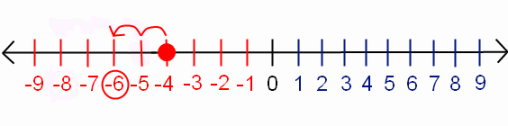
Красная точка над -4 показывает, что именно здесь мы начинаем нашу проблему.Затем, поскольку мы знаем, что нам нужно вычесть 2, мы считаем в обратном порядке (вычитаем) еще 2. Красный кружок вокруг -6 показывает, что это наш ответ.

Таким образом, -4 + -2 = -6.

Тест по сложению положительных и отрицательных чисел

Проблемы

1.4 + 5	2. -6 + 2	3 -9 + -4	4. 7 + -3	5. -10 + -3
6.8 + 4	7. 5 + -2	8. -3 + -9	9. 12 + -7	10. -13 + 9

Решения

1.9	2. -4	3. -13	4. 4	5. -13
6.12	7. 3	8. -12	9. 5	10 -4

.

Сложение положительных и отрицательных чисел

Сложить положительные числа, например 2 + 2, просто.

Когда мы добавляем отрицательное число к положительному или к двум отрицательным числам, это иногда может показаться сложным. Однако есть несколько простых правил, которым нужно следовать, и мы их здесь вводим.

Правило 1. Добавление положительных чисел к положительным — это обычное сложение.

Например: это то, что вы усвоили с самого начала. 3 + 2 — два положительных числа.Вы можете рассчитать эти задачи так, как всегда: 3 + 2 = 5.

Правило 2. Добавление положительных чисел к отрицательным — считайте добавляемую сумму вперед.

Здесь становится немного сложнее. Обратите особое внимание на то, где в проблеме помещены отрицательные знаки.

Например: -6 + 3. Это будет «минус шесть плюс три». Лучший способ подумать об этой проблеме — использовать числовую строку, которая продолжается до отрицательных чисел.

Вы начинаете с отрицательного числа -6.

И вы добавляете три к этому числу, что означает, что вы перемещаете три точки вправо.

Ответ -3. -6 + 3 = -3.

Правило 3: сложение отрицательных чисел с положительными — считайте в обратном порядке, как если бы вы вычитали.

Теперь посмотрим на обратное уравнение. Когда вы добавляете отрицательное число к положительному, вы фактически вычитаете второе число из первого.
Например, возьмите 4 + (-2). Как это выглядит в строке чисел?

Вы начинаете с 4.

А потом вы добавляете отрицательное число, что означает движение влево — в отрицательном направлении.Обычно вы вычитаете 2.

Ответ 2. 4 + (-2) = 2.

Правило 4: Сложение отрицательных чисел к отрицательным числам — относитесь к проблеме как к вычитанию (обратный счет).

Когда вы добавляете отрицательное число к отрицательному, это становится вычитанием, когда вы начинаете с отрицательной точки в строке чисел и двигаетесь влево.

Например, -3 + (-2). Это читается как «отрицательные три плюс отрицательные 2». Вам нужно игнорировать знак плюса и понимать, что второй минус означает, что вы вычитаете это число.

Мы начинаем с -3.

Затем вычитаем 2.

Ответ -5.-3 + (-2) = -5.

.