Работа единица измерения в физике – Механическая работа — Википедия

Механическая работа — Википедия

Мeханическая работа — это физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел)^[1].

Работа обычно обозначается буквой A (от нем. Arbeit — работа, труд) или буквой W (от англ. work — работа, труд).

Работа силы, приложенной к материальной точке[править | править код]

Суммарная работа по перемещению одной материальной точки, совершаемая несколькими силами, приложенными к этой точке, определяется как работа равнодействующей этих сил (их векторной суммой). Поэтому дальше будем говорить об одной силе, приложенной к материальной точке.

При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершённого точкой:

A=Fss=Fs cos(F,s)=F→⋅s→{\displaystyle A=F_{s}s=Fs\ \mathrm {cos} (F,s)={\vec {F}}\cdot {\vec {s}}}

Здесь точкой обозначено скалярное произведение, s→{\displaystyle {\vec {s}}} — вектор перемещения; подразумевается, что действующая сила F→{\displaystyle {\vec {F}}} постоянна в течение времени, за которое вычисляется работа.

В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки^[2]:

A=∫F→⋅ds→.{\displaystyle A=\int {\vec {F}}\cdot {\vec {ds}}.}

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений ds→,{\displaystyle {\vec {ds}},} если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат^[3], интеграл определяется^[4] следующим образом:

A=∫r→0r→1F→(r→)⋅dr→{\displaystyle A=\int \limits _{{\vec {r}}_{0}}^{{\vec {r}}_{1}}{\vec {F}}\left({\vec {r}}\right)\cdot {\vec {dr}}},

где r→0{\displaystyle {\vec {r}}_{0}} и r→1{\displaystyle {\vec {r}}_{1}} — радиус-векторы начального и конечного положения тела соответственно.

• Следствие. Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа (этой силы) равна нулю.

Работа сил, приложенных к системе материальных точек[править | править код]

Работа сил по перемещению системы материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершённые над каждой точкой системы, суммируются в работу этих сил над системой).

Даже если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.

• Эти определения могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаемся выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).

Если Atotal{\displaystyle A_{total}} — полная работа, совершённая над частицей, определяемая как сумма работ, совершенных приложенными к частице силами, то она выражается как:

Atotal=Δ(mv22)=ΔEk,{\displaystyle A_{total}=\Delta \left({\frac {mv^{2}}{2}}\right)=\Delta E_{k},}

где Ek{\displaystyle E_{k}} называется кинетической энергией. Для материальной точки кинетическая энергия определяется как половина произведения массы этой точки на квадрат её скорости и выражается как^[5]:

Ek=12mv2.{\displaystyle E_{k}={\frac {1}{2}}mv^{2}.}

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая Ep{\displaystyle E_{p}}, такая, что

F→=−∇Ep.{\displaystyle {\vec {F}}=-\nabla E_{p}.}

Если все силы, действующие на частицу, консервативны, и Ep{\displaystyle E_{p}} является полной потенциальной энергией, полученной суммированием потенциальных энергий, соответствующих каждой силе, тогда:

F→⋅Δs→=−∇→Ep⋅Δs→=−ΔEp⇒−ΔEp=ΔEk⇒Δ(Ek+Ep)=0{\displaystyle {\vec {F}}\cdot \Delta {\vec {s}}=-{\vec {\nabla }}E_{p}\cdot \Delta {\vec {s}}=-\Delta E_{p}\Rightarrow -\Delta E_{p}=\Delta E_{k}\Rightarrow \Delta (E_{k}+E_{p})=0}.

Этот результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы,

∑E=Ek+Ep{\displaystyle \sum E=E_{k}+E_{p}}

является постоянной во времени. Этот закон широко используется при решении задач классической механики.

В термодинамике работа, совершённая газом при расширении^[6], рассчитывается как интеграл давления по объёму:

A1→2=∫V1V2PdV.{\displaystyle A_{1\rightarrow 2}=\int \limits _{V_{1}}^{V_{2}}PdV.}

Работа, совершённая над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.

• Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
• В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет

dA=PdSh.{\displaystyle dA=PdSh.}

Видно, что это и есть произведение давления на приращение объёма вблизи данной элементарной площадкой. А просуммировав по всем dS, получим конечный результат, где будет уже полное приращение объёма, как и в главной формуле раздела.

Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.

Пусть материальная точка M{\displaystyle M} движется по непрерывно дифференцируемой кривой G={r=r(s)}{\displaystyle G=\{r=r(s)\}}, где s — переменная длина дуги, 0≤s≤S{\displaystyle 0\leq s\leq S}, и на неё действует сила F(s){\displaystyle F(s)}, направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под F(s){\displaystyle F(s)} проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина F(ξi)△si,△si=si−si−1,i=1,2,…,iτ{\displaystyle F(\xi _{i})\triangle s_{i},\triangle s_{i}=s_{i}-s_{i-1},i=1,2,…,i_{\tau }}, называется

элементарной работой силы F{\displaystyle F} на участке Gi{\displaystyle G_{i}} и принимается за приближённое значение работы, которую производит сила F{\displaystyle F}, воздействующая на материальную точку, когда последняя проходит кривую Gi{\displaystyle G_{i}}. Сумма всех элементарных работ ∑i=1iτF(ξi)△si{\displaystyle \sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} является интегральной суммой Римана функции F(s){\displaystyle F(s)}.

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма ∑i=1iτF(ξi)△si{\displaystyle \sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} всех элементарных работ, когда мелкость |τ|{\displaystyle |\tau |} разбиения τ{\displaystyle \tau } стремится к нулю, называется работой силы F{\displaystyle F} вдоль кривой G{\displaystyle G}.

Таким образом, если обозначить эту работу буквой W{\displaystyle W}, то, в силу данного определения,

W=lim|τ|→0∑i=1iτF(ξi)△si{\displaystyle W=\lim _{|\tau |\rightarrow 0}\sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}},

следовательно,

W=∫0sF(s)ds{\displaystyle W=\int \limits _{0}^{s}F(s)ds} (1).

Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра t{\displaystyle t} (например, времени) и если величина пройденного пути s=s(t){\displaystyle s=s(t)}, a≤t≤b{\displaystyle a\leq t\leq b} является непрерывно дифференцируемой функцией, то из формулы (1) получим

W=∫abF[s(t)]s′(t)dt.{\displaystyle W=\int \limits _{a}^{b}F[s(t)]s'(t)dt.}

Единицей измерения работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг

1 Дж = 1 кг·м²/с² = 1 Н·м

1 эрг = 1 г·см²/с² = 1 дин·см

1 эрг = 10⁻⁷Дж

1. ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193-194. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
2. ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения ds→{\displaystyle {\vec {ds}}}, на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях ds→{\displaystyle {\vec {ds}}} суммируется, что и дает в результате интеграл.
3. ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
4. ↑ По сути через предыдущий, поскольку здесь F→(t)=F→(r→(t)){\displaystyle {\vec {F}}(t)={\vec {F}}({\vec {r}}(t))}; вектор же малого перемещения ds→{\displaystyle {\vec {ds}}} совпадает с dr→{\displaystyle d{\vec {r}}}.
5. ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
6. ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле ∫PdV{\displaystyle \int PdV} давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить её к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

• История механики с древнейших времен до конца XVIII в. В 2 т. М.: Наука, 1972.
• Кирпичёв В. Л. Беседы о механике. М.-Л.: Гостехиздат, 1950.
• Льоцци М. История физики. М.: Мир, 1970.
• Мах Э. Принцип сохранения работы: История и корень его. СПб., 1909.
• Мах Э. Механика. Историко-критический очерк её развития. Ижевск: РХД, 2000.
• Тюлина И. А. История и методология механики. М.: Изд-во МГУ, 1979.

ru.wikipedia.org

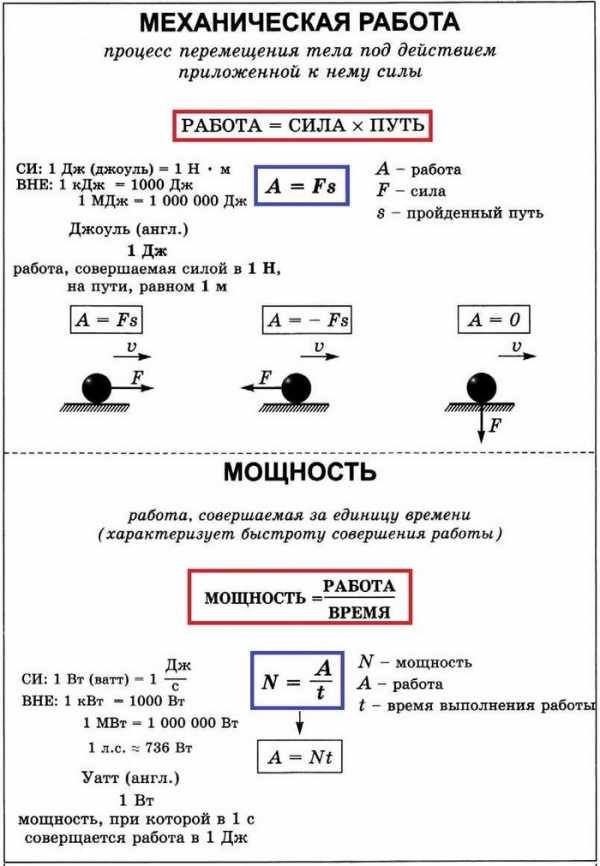
Конспект «Механическая работа. Механическая мощность»

«Механическая работа. Механическая мощность»

Код ОГЭ 1.16. Механическая работа. Формула для вычисления работы силы. Механическая мощность.

---

---

Работа силы – физическая величина, характеризующая результат действия силы.

Механическая работа А постоянной силы  равна произведению модуля вектора силы на модуль вектора перемещения  и на косинус угла а между вектором силы и вектором перемещения: А = Fs cos а.

Единица измерения работы в СИ – джоуль: [А] = Дж = Н • м.
Механическая работа равна 1 Дж, если под действием силы в 1 Н тело перемещается на 1 м в направлении действия этой силы.

Анализ формулы для расчёта работы показывает, что механическая работа не совершается если:

• сила действует, а тело не перемещается;
• тело перемещается, а сила равна нулю;
• угол между векторами силы и перемещения равен 90° (cos a = 0).

Внимание! При движении тела по окружности под действием постоянной силы, направленной к центру окружности, работа равна нулю, так как в любой момент времени вектор силы перпендикулярен вектору мгновенной скорости.

Работа – скалярная величина, она может быть как положительной, так и отрицательной.

1. Если угол между векторами силы и перемещения 0° ≤ а < 90°, то работа положительна.
2. Если угол между векторами силы и перемещения 90° < a ≤ 180°, то работа отрицательна.

Работа обладает свойством аддитивности: если на тело действует несколько сил, то полная работа (работа всех сил) равна алгебраической сумме работ, совершаемых отдельными силами, что соответствует работе равнодействующей силы.

Примеры расчёта работы отдельных сил:

Работа силы тяжести: не зависит от формы траектории и определяется только начальным и конечным положением тела:

A = mg(h₁ – h₂). По замкнутой траектории работа силы тяжести равна нулю.
Внимание! При движении вниз работа силы тяжести положительна, при движении вверх работа силы тяжести отрицательна.

Работа силы трения скольжения: всегда отрицательна и зависит от формы траектории. Если сила трения не изменяется по модулю, то её работа А = –F_тр l , где l – путь, пройденный телом (длина траектории). Очевидно, что чем больший путь проходит тело, тем большую по модулю работу совершает сила трения. Работа силы трения по замкнутой траектории не равна нулю!

Мощность N – физическая величина, характеризующая быстроту (скорость) совершения работы и равная отношению работы к промежутку времени, за который эта работа совершена: .

Мощность показывает, какая работа совершается за 1 с.
Единица измерения мощности в СИ – ватт: [ N ] = Дж/с = Вт.
Мощность равна одному ватту, если за 1 с совершается работа 1 Дж.

Может пригодиться! 1 л. с. (лошадиная сила) ~ 735 Вт.
Внимание! Для случая равномерного движения (равнодействующая сила равна нулю) при расчете мощности отдельных сил, действующих на тело, получим  .

Для равноускоренного движения (F = const)   где ʋ_ср– средняя скорость движения за расчётный промежуток времени.

---

Конспект урока «Механическая работа. Механическая мощность».

Следующая тема: «Кинетическая и потенциальная  энергия» (код ОГЭ 1.17)

 

uchitel.pro

Механическая работа. Мощность (Зотов А.Е.). Видеоурок. Физика 7 Класс

В ходе данного урока вы познакомитесь двумя новыми физическими величинами, описывающими действие силы на движущееся тело – работой и мощностью.

В нашем повседневном опыте слово «работа» встречается очень часто. Но следует различать работу физиологическую и работу с точки зрения науки физики. Когда вы приходите с уроков, вы говорите: «Ой, как я устал!». Это работа физиологическая. Или, к примеру, работа коллектива в народной сказке «Репка».

Рис 1. Работа в повседневном смысле слова

Мы же будем говорить здесь о работе с точки зрения физики.

Механическая работа совершается, если под действием силы происходит перемещение тела. Работа обозначается латинской буквой А. Более строго определение работы звучит так.

Работой силы называется физическая величина, равная произведению величины силы на расстояние, пройденное телом в направлении действия силы.

 

Рис 2. Работа – это физическая величина

Формула  справедлива, когда на тело действует постоянная сила.

В международной системе единиц СИ работа измеряется в джоулях.

Это означает, что если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа 1 джоуль.

Единица работы названа в честь английского ученого Джеймса Прескотта Джоуля.

 

Рис 3. Джеймс Прескотт Джоуль (1818 – 1889)

Из формулы для вычисления работы  следует, что возможны три случая, когда работа равна нулю.

Первый случай – когда на тело действует сила, но тело не перемещается. Например, на дом действует огромная сила тяжести. Но она не совершает работы, поскольку дом неподвижен.

Второй случай – когда тело перемещается по инерции, то есть на него не действуют никакие силы. Например, космический корабль движется в межгалактическом пространстве.

Третий случай – когда на тело действует сила, перпендикулярная направлению движения тела. В этом случае, хотя и тело перемещается, и сила на него действует, но нет перемещения тела

в направлении действия силы.

Рис 4. Три случая, когда работа равна нулю

Следует также сказать, что работа силы может быть отрицательной. Так будет, если перемещение тела происходит против направления действия силы. Например, когда подъемный кран с помощью троса поднимает груз над землей, работа силы тяжести отрицательна (а работа силы упругости троса, направленная вверх, наоборот, положительна).

Предположим, пр

interneturok.ru

Измерение единицы работы силы в физике

Прежде чем раскрывать тему «В чём измеряется работа», необходимо сделать небольшое отступление. Всё в этом мире подчиняется законам физики. Каждый процесс или явление можно объяснить на основе тех или иных законов физики. Для каждой измеряемой величины существует единица, в которой её принято измерять. Единицы измерения являются неизменными и имеют единое значение во всём мире.

Система международных единиц

Причиной этого является следующее. В тысяча девятьсот шестидесятом году на одиннадцатой генеральной конференции по мерам и весам была принята система измерений, которая признана во всём мире. Эта система получила наименование Le Système International d’Unités, SI (СИ система интернационал). Эта система стала базовой для определений принятых во всём мире единиц измерения и их соотношения.

Физические термины и терминология

В физике единица измерения работы силы называется Дж (Джоуль), в честь английского учёного физика Джеймса Джоуля, сделавшего большой вклад в развитие раздела термодинамики в физике. Один Джоуль равен работе, совершаемой силой в один Н (Ньютон), при перемещении её приложения на один М (метр) в направлении действия силы. Один Н (Ньютон) равен силе, массой в один кг (килограмм), при ускорении в один м/с2 (метр в секунду) в направлении силы.

Формула нахождения работы

К сведению. В физике всё взаимосвязано, выполнение любой работы связано с выполнением дополнительных действий. В качестве примера можно взять бытовой вентилятор. При включении вентилятора в сеть лопасти вентилятора начинают вращаться. Вращающиеся лопасти воздействуют на поток воздуха, придавая ему направленное движение. Это является результатом работы. Но для выполнения работы необходимо воздействие других сторонних сил, без которых выполнение действия невозможно. К ним относятся сила электрического тока, мощность, напряжение и многие другие взаимосвязанные значения.

Электрический ток, по своей сути, – это упорядоченное движение электронов в проводнике в единицу времени. В основе электрического тока лежит положительно или отрицательно заряжённые частицы. Они носят название электрических зарядов. Обозначается буквами C, q, Кл (Кулон), названо в честь французского учёного и изобретателя Шарля Кулона. В системе СИ является единицей измерения количества заряженных электронов. 1 Кл равен объёму заряженных частиц, протекающих через поперечное сечение проводника в единицу времени. Под единицей времени подразумевается одна секунда. Формула электрического заряда представлена ниже на рисунке.

Формула нахождения электрического заряда

Сила электрического тока обозначается буквой А (ампер). Ампер – это единица в физике, характеризующая измерение работы силы, которая затрачивается для перемещения зарядов по проводнику. По своей сути, электрический ток – это упорядоченное движение электронов в проводнике под воздействием электромагнитного поля. Под проводником подразумевается материал или расплав солей (электролит), имеющий небольшую сопротивляемость прохождению электронов. На силу электрического тока влияют две физические величины: напряжение и сопротивление. Они будут рассмотрены ниже. Сила тока всегда прямо пропорциональна по напряжению и обратно пропорциональна по сопротивлению.

Формула нахождения силы тока

Как было сказано выше, электрический ток – это упорядоченное движение электронов в проводнике. Но есть один нюанс: для их движения нужно определённое воздействие. Это воздействие создаётся путём создания разности потенциалов. Электрический заряд может быть положительным или отрицательным. Положительные заряды всегда стремятся к отрицательным зарядам. Это необходимо для равновесия системы. Разница между количеством положительно и отрицательно заряжённых частиц называется электрическим напряжением.

Формула нахождения напряжения

Мощность – это количество энергии, затрачиваемое на выполнение работы в один Дж (Джоуль) за промежуток времени в одну секунду. Единицей измерения в физике обозначается как Вт (Ватт), в системе СИ W (Watt). Так как рассматривается мощность электрическая, то здесь она является значением затраченной электрической энергии на выполнение определённого действия в промежуток времени.

Формула нахождения электрической мощности

В заключение следует отметить, что единица измерения работы является скалярной величиной, имеет взаимосвязь со всеми разделами физики и может рассматриваться со стороны не только электродинамики или теплотехники, но и других разделов. В статье кратко рассмотрено значение, характеризующее единицу измерения работы силы.

Видео

Оцените статью:

jelectro.ru

Единица измерения работы, теория и онлайн калькуляторы

Определение

Элементарной работой ($dA$) называют физическую величину, которая равна скалярному произведению силы ($\overline{F}$) на бесконечно малое перемещение ($d\overline{s}$), которое происходит под воздействием этой силы:

\[dA=\overline{F}\cdot d\overline{s}=F{\cos \alpha \ ds\ \left(1\right).\ }\]

Если тело перемещается по прямой линии на пути $s$ под воздействием постоянной силы $\overline{F}$, то работу можно вычислить как:

\[A=Fs{\cos \alpha \ \left(2\right),\ }\]

где $\alpha $ — угол между направлением силы и направлением перемещения тела.

Джоуль — единица измерения работы в системе СИ

Единица измерения работы носит название джоуль (Дж). Его можно определить исходя из выражения (2), так имеем:

\[\left[A\right]=\left[F\right]\left[s\right]=Н\cdot м=Дж.\]

Один джоуль равен работе, которая совершается при перемещении точки, к которой приложена сила величиной в один ньютон, на расстояние один метр в том направлении, в котором действует сила.

Джоуль — единица измерения работы, являющаяся производной в Международной системе единиц (СИ). Через основные единицы этой системы джоуль выражается как:

\[Дж=Н\cdot м=\frac{кг\cdot м}{с^2}\cdot м=\frac{кг\cdot м^2}{с^2}.\]

В электродинамике встречается определение работы, которую совершают силы электрического поля за промежуток времени равный одной секунде напряжении один вольт для того, чтобы поддерживать силу тока равному одному амперу. В таком случае джоуль можно выражать как:

\[Дж=Кл\cdot В.\]

Десятичные кратные и дольные единицы джоуля в системе СИ образуют при помощи стандартных приставок системы единиц. Например, кДж (килоджоуль): 1 кДж=1000 Дж; фДж (фемтоджоуль): 1фДж=${10}^{-15}Дж.$

Эрг — единица измерения работы в системе единиц СГС

В системе СГС (сантиметр, грамм, секунда) работа измеряется в эргах (эрг). При этом одни эрг равен:

\[1\ эрг=1\ дин\cdot 1\ см.\]

Зная, что:

\[1\ Н={10}^5{\rm дин};;1\ {\rm м}=100\ см,\]

получаем:

\[1\ Дж={10}^7эрг.\]

Единицы измерения работы в технической системе единиц (МКГСС)

В системе МКГСС (в данной системе единиц основными являются метр, килограмм-сила, секунда) един

www.webmath.ru

Вопрос 9

      Механическая работа и мощность. Единицы измерения работы и мощности.

Краткий ответ

   Механическая работа – это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и на косинус угла между вектором силы  и вектором перемещения (или скорости).

   A = Fs cos α

   Обозначения:

A — Механическая работа

F — Сила, действующая на тело

S — Перемещение, которое тело совершает под действием силы

a — Угол между направлением действия силы и вектором перемещения

   Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю.

   В системе СИ работа измеряется в джоулях (Дж).

   [1 Дж=1 Н·м]

   Работа силы, совершаемая в единицу времени, называется мощностью.

   Мощность N – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

N=A/t

   В Международной системе (СИ) единица мощности называется ватт (Вт). 

   Внесистемная единица мощности 1 л.с.=735 Вт

Развернутый ответ

   Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.

   Если на тело действует сила и тело под действием этой силы перемещается, то говорят, что сила совершает работу.

   Механическая работа – это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и на косинус угла между вектором силы  и вектором перемещения (или скорости).

A = Fs cos α

   Обозначения:

A — Механическая работа

F — Сила, действующая на тело

S — Перемещение, которое тело совершает под действием силы

a — Угол между направлением действия силы и вектором перемещения

   В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.

   [1 Дж=1 Н·м]

   Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю.

   1) Если направление силы совпадает с направлением движения тела, т.е.α = 0, cos α = 1  то

A=F·S

   2) Если сила направлена перпендикулярно к направлению движения тела, т.е. α = 90º, cos α = 0  то

A = 0

   Следовательно, если тело перемещается в направлении, перпендикулярном к направлению действия силы, то сила не производит работы.

   3) Если угол между направлением силы и направлением движения тупой, т.е. α > 90º, cos α < 0  то

A=-F·S·cosa

4) Если перемещение происходит в сторону, противоположную направлению вектора силы, т.е. α = 180 º, cos α = -1  то

A=-F·S

   Например, работа силы сопротивления отрицательна.

   Графически работа определяется по площади криволинейной фигуры под графиком F_s(x)

   Работа силы, совершаемая в единицу времени, называется мощностью.

   Мощность N – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

N=A/t

   В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.

   Внесистемная единица мощности 1 л.с.=735 Вт

Связь между мощностью и скоростью при равномерном движении:

   N=A/t  так как   A=FScosα      тогда   N=(FScosα)/t, но S/t = v   следовательно

   N=Fvcos α 

   В технике используются единицы работы и мощности:

   1 Вт·с = 1 Дж;     1Вт·ч = 3,6·10³ Дж;      1кВт·ч = 3,6·10⁶ Дж

infofiz.ru

Механическая работа — это… Что такое Механическая работа?

Механическая работа

Работа силы

Ключевые статьи

См. также: Портал:Физика

Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы^[1].

Определение

В механике можно ввести понятие работы, исходя из довольно простых представлений^[2]

Работа силы (сил) над одной точкой

• Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения^[3]:

Здесь точкой обозначено скалярное произведение^[4],  — вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа.

Если сила не постоянна, то в этом случае она вычисляется как интеграл^[5]:

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат^[6], интеграл определяется^[7] следующим образом:

,

где и  — радиус-векторы начального и конечного положения тела соответственно.

• Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.

Работа силы (сил) над системой или неточечным телом

Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой).

Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.

• Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Кинетическая энергия

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).

Если  — полная работа, совершённая над частицей, определяемая как сумма работ совершенных приложенными к частице силами, то она выражается как:

где называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до величины скорости и выражается как:

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Потенциальная энергия

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая , такая что

Если все силы, действующие на частицу консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:

.

Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы

является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.

Работа в термодинамике

В термодинамике работа, совершенная газом при расширении^[8], рассчитывается как интеграл давления по объёму:

Работа, совершенная над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.

• Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объема, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
• В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет

Видно, что это и есть произведение давления на приращение объема вблизи данной элементарной площадкой. А просуммировав по всем dS получим конечный результат, где будет уже полное приращение объема, как и в главной формуле параграфа.

Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.

Пусть материальная точка движется по непрерывно дифференцируемой кривой , где s — переменная длина дуги, и на неё действует сила , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина , называется элементарной работой силы на участке и принимается за приближенное значение работы, которую производит сила , воздействующая на материальную точку, когда последняя проходит кривую . Сумма всех элементарных работ является интегральной суммой Римана функции .

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма всех элементарных работ, когда мелкость разбиения стремится к нулю, называется работой силы вдоль кривой .

Таким образом, если обозначить эту работу буквой , то, в силу данного определения,

,

следовательно,

(1).

Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути , является непрерывно дифференцируемой функцией, то из формулы (1) получим

Единицей измерения работы в СИ является Джоуль, в СГС — эрг

1 Дж = 1 кг·м²/с² = 1 Н·м

1 эрг = 1 г·см²/с² = 1 дин·см

1 эрг = 10⁻⁷Дж

Ссылки

1. ↑ Концепции современного естествознания
2. ↑ Такие представления можно конкретизировать как систему постулатов, приводящую достаточно однозначно к определению, описанному в основной статье:
   1. работу совершает только компонента силы, совпадающая с направлением перемещения точки, к которой она приложена, или противоположная направлению перемещения точки (в последнем случае работа считается отрицательной),
   2. работа постоянной силы пропорциональна компоненте такой силы, описанной в пункте 1, и длине вектора перемещения,
   3. работа по перемещению точки за несколько последовательных промежутков времени суммируется (работа за всё это время равна сумме работ, совершенных за каждый промежуток),
   4. работа суммы (векторной суммы) сил, приложенных к точке равна сумме работ, совершенных каждой силой в отдельности,
   5. работа, совершенная над системой (телом) равна сумме работ, совершенных над каждой ее частью (в частности — равна сумме работ, совершенных над каждой точкой системы).
3. ↑ Механическая работа. Мощность
4. ↑ Можно считать, что механическая работа может служить в области физики одной из главных иллюстраций для скалярного произведения.
5. ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения , на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях суммируется, что и дает в результате интеграл.
6. ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
7. ↑ По сути через предыдущий, поскольку здесь ; вектор же малого перемещения совпадает с .
8. ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить ее к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

Литература

• Кудрявцев Л. Д. Курс математического анализа. — 5-е, переработанное и дополненное. — М.: Дрофа, 2003. — Т. 1. — С. 640—641. — 703 с.

См. также

dic.academic.ru