Расчёт LC — фильтров. Онлайн калькулятор ПФ, ФВЧ, ФНЧ.
LC — фильтры я оставил на десерт, подобно бутылке благородного вина, покрытой слоем вековой пыли. Это антиквариат, который на Сотбисе не купишь!
Как ни крути, а не получил бы Александр Степаныч наш Попов звание почётного инженера-электрика, не направь он искровой разряд
напрямик в колебательный контур для обретения благословения свыше и резонанса с передающей антенной.
И заскучала бы братва копателей свободной энергии эфира, не изобрети Никола Тесла свой резонансный трансформатор и
электрический автомобиль с неведомой коробочкой. А то и вовсе, заширялась бы в подъездах, лишённая идей вселенского масштаба.
И начнём мы с расчёта самого простого LC-фильтра — колебательного контура.
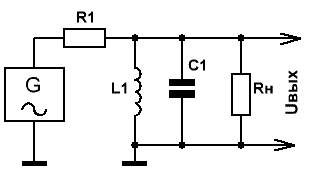
Включённый по приведённой на рис.1 схеме, он представляет собой узкополосный полосовой фильтр, настроенный на частоту
fо= 1/2π√LС.
Rо = pQ, где р — характеристическое сопротивление, равное реактивному сопротивлению катушки и конденсатора.
Оно в свою очередь рассчитывается по формуле р = √L/C.
Рис.1
На низких (звуковых) частотах конденсаторы практически не вносят потерь, поэтому добротность контура равна добротности катушки
индуктивности, величина которой напрямую зависит от активного сопротивления катушки. Чем ниже частота, тем больше витков и тоньше
провод, тем проще его измерить тестером. Если эта попытка удалась, то Q=2πfL/R, где R – активное сопротивление катушки индуктивности.
На радиочастотах значение активного сопротивления катушки может составлять доли ома, поэтому для расчёта добротности надо — либо
найти сопротивление в Омах по формуле R= 4ρ*L/(πd²), где ρ — удельное сопротивление меди, равное 0,017 Ом•мм²/м, L — длина в
метрах, d — диаметр провода в мм, либо вооружиться генератором сигналов, каким-либо измерителем уровня выходного сигнала с высоким
внутренним сопротивлением, и определить добротность экспериментально.
Нарисуем табличку с расчётом фильтра для низкочастотных приложений.
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ НЧ.
Если параметр активного сопротивления катушки R опущен, его значение принимается равным 200 омам.
Необходимо отметить, что все полученные в таблице данные верны и для последовательного колебательного контура.
При этом, если мы хотим использовать свойства контура полностью, т. е. получить острую резонансную кривую, соответствующую
конструктивной добротности, то параллельный контур надо нагружать слабо, выбирая R1 и Rн намного больше Rо (на практике
десятки кОм), для последовательного же контура, сопротивление генератора R1 наоборот должно быть на порядок меньше
характеристического сопротивления ρ.
Теперь, нарисуем таблицу для расчёта высокочастотных резонансных контуров.
Тут на добротность влияет не только активное сопротивление катушек, но и другие факторы, такие как — потери в ферритах, наличие экрана,
эффект близости витков и т. д.
Поэтому вводить этот параметр в качестве входного я не
стану — будем считать, что добротность катушки вы измерили, или подсмотрели в документации на готовые катушки. Естественным образом
значение добротности катушки должно измеряться на резонансной частоте контура, ввиду прямой зависимости этой величины от рабочей
частоты (Q=2πfL/R).
По умолчанию (для желающих оставить эти параметры без внимания), добротность катушки примем равной 100, конденсатора — 1000, а для испытывающих стремление измерить эти параметры в радиолюбительских условиях, рекомендую посетить страницу ссылка на страницу .
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ ВЧ.
Теперь плавно переходим к LC фильтрам верхних и нижних частот (ФВЧ и ФНЧ).
Рис.2
Крутизна спада АЧХ этих фильтров в полосе подавления — 12 дБ/октаву, коэффициент передачи в полосе пропускания К=1 при R1
Однако наилучшие параметры, с точки зрения равномерности АЧХ и передачи максимальной мощности в нагрузку, обеспечиваются
при R1=Rн=ρ. В этом случае фильтр является согласованным, правда коэффициент передачи в полосе пропускания становится равным К=0.5.
ТАБЛИЦА LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
А если надо рассчитать L и C при известных значениях Fср и ρ ? Не вопрос,
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
Данные ФВЧ и ФНЧ называются Г-образными.
Для получения более крутых скатов АЧХ используют два или более Г-образных звеньев, соединяя их последовательно,
чтобы образовать Т-образное звено (на Рис.3 сверху), или П-образное звено (на Рис.3 снизу).
При этом получаются ФНЧ третьего порядка. Обычно, ввиду меньшего количества катушек, предпочитают П-образные звенья.
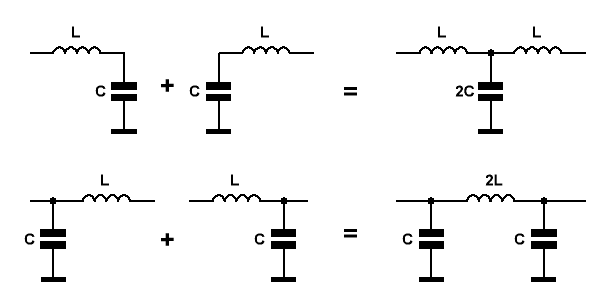
Рис.3
ФВЧ конструируют подобным же образом, лишь катушки заменяются конденсаторами, а конденсаторы — катушками.
Широкополосные полосовые LC — фильтры получают каскадным соединением ФНЧ и ФВЧ.
Что касается многозвенных LC-фильтров высоких порядков, то более грамотным решением (по сравнению с последовательным соединением фильтров низших порядков) будет построение подобных устройств с использованием полиномов товарищей Чебышева или Баттерворта.
Именно такие фильтры 3-го, 5-го и 7-го порядков мы и рассмотрим на следующей странице.
Онлайн расчёт многозвенных LC — фильтров. Калькулятор ПФ, ФВЧ, ФНЧ 3-го, 5-го и 7-го порядков.
Одиночный LC-фильтр, как ни бейся, не может обеспечить достаточного подавления сигналов вне заданного диапазона частот, поэтому для
формирования более крутой переходной области обычно используют многозвенные LC — фильтры.
В низкочастотной схемотехнике LC-фильтры фильтры решительно теряют позиции в пользу активных фильтров высоких порядков, за исключением, пожалуй, сглаживающих фильтров источников питания, LC-фильтров акустических систем, да изредка НЧ фильтров приёмников прямого преобразования.
Зато на непаханых полях радиочастотных диапазонов свободного пространства хоть отбавляй. То-то раздолье тут земледельцу!
По левую руку — входные фильтры приёмников и трансиверов, по правую — фильтры выходных каскадов передатчиков, посередине …
Да всё, что угодно, поля-то — непаханые.
Описания свободных и вынужденных колебаний в электрических цепях, и иже с ними дисперсионные и характеристические уравнения систем различных аппроксимаций оставим бедолагам студентам, а сами играючи воспользуемся таблицами элементов LC фильтров-прототипов, приведённых в справочнике по расчёту фильтров Г. Ханзела.
Как правило, с точки зрения минимизации количества катушек индуктивности, в многозвенных фильтрах используют П-образную схему для ФНЧ и Т-образную для ФВЧ.
На Рис.1 приведены схемы подобных фильтров нижних и верхних частот 3-го, 5-го и 7-го порядков.
Рис.1
Расчёт поведём доверившись многочленам Пафнутия Львовича нашего Чебышёва.
Почему на сей раз Чебышева, а не вездесущего Баттерворта?
Ответ не сложен — в погоне за максимальным наклоном переходного участка, в жертву некоторой неравномерности АЧХ фильтра в полосе пропускания.
При одном и том же числе элементов схемы у фильтров Чебышева крутизна характеристики ослабления в полосе задерживания
значительно больше, чем у фильтров Баттерворта и может составлять величину 8,5дб на октаву (против менее 6 дБ/окт) на каждый порядок
фильтра.
Значение же неравномерности в полосе пропускания можно ограничивать, выбирая коэффициенты из таблицы фильтра — прототипа. Я посчитал, что
неравномерность 0,28дБ окажется вполне приемлемой.
Ну и хватит, переходим к таблице.
ТАБЛИЦА РАСЧЁТА МНОГОЗВЕННЫХ ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
И как обычно не забываем — многозвенные полосовые LC-фильтры получаются каскадным соединением ФНЧ и ФВЧ, тем более что они отлично друг с другом согласуются.
Ну а если полученный спад амплитудной характеристики не кажется слишком крутым, то нам прямая дорога к эллиптическим фильтрам, которые мы и посчитаем на следующей странице.
Калькулятор расчёта полосно-заграждающих режекторных фильтров на LC цепях
Что такое режекторный фильтр (он же полосно-заграждающий, он же — фильтр-пробка) и с чем его едят, мы определились на предыдущей странице, рассматривая пассивные и активные режекторные RC-фильтры.
Так же, как и в случаях с НЧ, ВЧ и полосовыми собратьями, LC режекторные фильтры обладают рядом достоинств, таких как: высокая стабильность, низкий уровень собственных шумов, а также возможность работы с широким спектром сигналов, включая СВЧ диапазоны.
Простейший представитель режекторного LC-фильтра 2-го порядка представлен на Рис.1.
Рис.1 
Рис.2
Логика работы такого фильтра предельно проста.
На резонансной частоте fо= 1/2π√LС сопротивление параллельного
колебательного контура, образованного катушкой индуктивности L и конденсатором C, принимает максимальное значение, соответственно
максимальное значение принимает и коэффициент подавления сигнала на этой частоте.
Глубина режекции (подавления частоты fo) этого фильтра при работе на согласованную нагрузку, равную характеристическому сопротивлению
колебательного контура ρ = √L/C , достигает 45 дБ.
На Рис.2 представлена схема Г-образного режекторного фильтра 4-го порядка.
Принцип работы этого фильтра основан на использовании резонансов напряжений и токов в последовательных и параллельных
колебательных контурах.
На частоте резонанса сопротивление параллельного плеча оказывается максимальным, а последовательного – минимальным, что и
соответствует наибольшему затуханию цепи.
Глубина режекции в данной схеме уже может составлять величину 90 дБ.
Приведём таблицу для расчёта элементов этих фильтров.
Не забываем, что характеристическое сопротивление фильтра ρ
должно равняться Rг =Rн.
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ РЕЖЕКТОРНЫХ LC- ФИЛЬТРОВ 2-го и 4-го ПОРЯДКОВ
Для получения больших значений подавления центральной частоты (глубины режекции) используют два или более Г-образных звеньев,
соединяя их последовательно, чтобы образовать Т-образное звено, или П-образное звено.
На Рис.3 приведены схемы типовых полосно-заграждающих LC-фильтров 6-го порядка Т-образной (слева) и П-образной (справа) структур с
глубиной режекции — около 130 дБ.
Рис.3
Ничего не изменилось — последовательная ветвь обладает минимальным полным сопротивлением и оказывает шунтирующее воздействие на
центральной частоте диапазона.
Ее полное сопротивление начинает увеличиваться по обе стороны от частоты резонанса.
Параллельная же ветвь на центральной частоте имеет максимальное сопротивление, и оно уменьшается по обе стороны резонанса.
Центральная частота режекции равна fо= 1/2π√LС,
характеристическое сопротивление ρ = √L/C ,
а значения частотозадающих элементов рассчитываются исходя из следующих равенств:
L1 = L3 = L/2, L2 = L, C1 = C3 = C×2, C2 = C
для Т-образного фильтра,
L1 = L3 = L×2, L2 = L, C1 = C3 = C/2, C2 = C
для П-образного фильтра.
Приведём таблицу для расчёта элементов и этих фильтров.
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ РЕЖЕКТОРНЫХ Т- и П-образных LC- ФИЛЬТРОВ
Ширина полосы задержания представленных режекторных LC-фильтров составляет величину, примерно равную 50% от значения центральной частоты fo.
Что такое LC-фильтр, как он работает, формулы и схемы
Из чего состоит LC-фильтр и как он работает, формулы для расчетов, принципиальные схемы LC-фильтров, статья для начинающих радиолюбителей. Во многих электронных устройствах применяются LC-фильтры, как видно по названию, эти фильтры состоят из индуктивности (L) и емкости (С).
Самый простой LC-фильтр
Самый простой LC-фильтр — это колебательный контур, включенный так как показано на рис. 1. Входное переменное напряжение поступает на контур через резистор R1, а выходное снимается с самого контура.
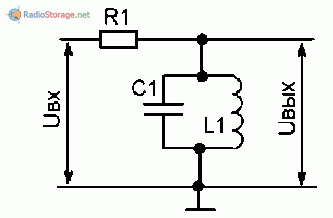
Рис. 1. Схема LC-фильтра.
Вообще это очень похоже на делитель напряжения на двух резисторах, но вместо одного из резисторов здесь контур. В сущности дела оно так и есть.
На резонансной частоте реактивное сопротивление контура сильно возрастает, а значит, коэффициент деления такого делителя уменьшается.
Эта схема (рис.1) действует как узкополосной полосовой фильтр, центральную частоту которого можно рассчитать по известной формуле:
, где частота в Гц, индуктивность в Гн, емкость в Ф.
Сопротивление контура на резонансной частоте:
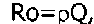
где р — характеристическое сопротивление, равное реактивному сопротивлению катушки и конденсатора. Величину р можно рассчитать по формуле:
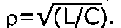
А вот рассчитать добротность Q значительно сложнее. Эта величина зависит от потерь в контуре. Так как конденсатор обычно вносит минимум потерь, то добротность контура чаще всего практически равна добротности индуктивности, входящей в состав этого контура.
Резонансную частоту и добротность можно определить измерениями. Нужно собрать схему по рисунку 2. Это практически такая же схема как на рис.1.
Переменное напряжение, соответствующее по частоте расчетному значению, подают от генератора «Г» на контур через сопротивление R1. Подстраивая генератор находят такую частоту, при которой возникает резонанс, то есть, при которой вольтметр переменного тока Р1 показывает наибольшую величину.
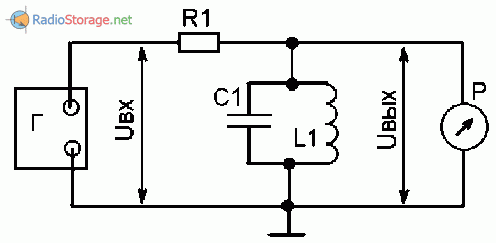
Рис. 2. Схема для измерения резонансной частоты и добротности.
Эта частота и будет реальной резонансной частотой. Она может отличаться от расчетной из-за погрешностей величин емкости и индуктивности. В идеале — равна расчетной.
На частоте резонанса R1 и резонансное сопротивление контура Ro образуют делитель напряжения, поэтому выходное напряжение Uвых = Uвх * Ro / (R1+Ro).
Измерив входное напряжение Uвх и выходное Uвых из этой формулы можно найти резонансное сопротивление контура Ro, ну а потом, зная величину характеристического сопротивления, из формулы
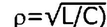
можно из формулы Ro=pQ найти добротность Q. Другой параметр LC-фильтра — это полоса пропускания 
где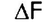 
— это отклонение частоты входного напряжения от резонанса в ту или другую сторону, при которой выходное напряжение, соответствующее резонансу (Uвых), уменьшается до 0,7Uвых. Зная величину полосы пропуская можно найти добротность по формуле Q = Fo/(2*дельтаF).
Таким образом становится ясно, что полоса пропускания LC-фильтра прежде всего зависит от добротности контура. При этом нужно учесть, что таким образом будет определена не собственная добротность контура, а величина меньше, из-за шунтирующего действия резистора R1.
Недостаток фильтра по рисунку 1 в том, что на него оказывает сильное влияние величина выходного сопротивления источника входного переменного напряжения.
Автотрансформаторное и трансформаторное включение
Желая получить более острую резонансную кривую, можно использовать трансформаторное (рис.3) или автотрансформаторное (рис.4) включение для подачи входного напряжения.
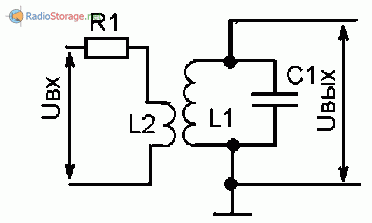
Рис. 3. Трансформаторное включение.
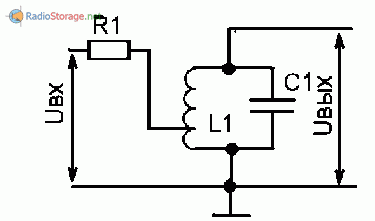
Рис. 4. Автотрансформаторное включение.
Число витков катушки связи (рис.З) или число витков отвода (считая от заземленного конца катушки) можно определить из формулы: R1 = Ro(N/No)^2 , где R1 — это фактически и есть выходное сопротивление источника входного переменного напряжения, Ro — сопротивление контура на резонансной частоте, N — число витков катушки связи (или число витков, от которых сделан отвод), No — число витков контурной катушки (или общее число витков катушки, если по рис.4).
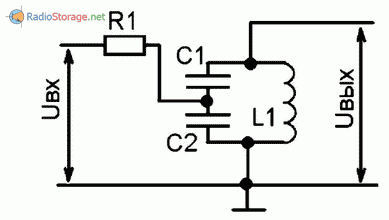
Рис. 5. Емкостный автотрансформатор.
Совсем не обязательно делать отвод именно от катушки, можно сделать отвод и от конденсатора, вернее от емкостной составляющей контура. Так получится — емкостный автотрансформатор (рис. 5).
А соотношение емкостей для определенной величины выходного сопротивления источника сигнала можно определить из формулы: R1 = Ro * C1^2 / (C1+C2)^2.
На контур может оказывать шунтирующее влияние не только выходное сопротивление источника Uвх, но и входное сопротивление каскада, на который с контура поступает выходное напряжение Uвых (R2 на рис. 6). Особенно если входное сопротивление каскада (R2) невелико (сопоставимо или даже меньше Ro).
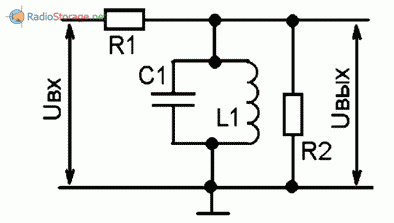
Рис. 6. Схема фильтра.
В этом случае необходимо сначала вычислить новое значение Ro, уменьшенное параллельным включением сопротивления R2. Расчет производить по известной формуле параллельных сопротивлений:
R = (RoR1) / (Ro+R2).
А потом уже рассчитывать согласование (взяв полученную величину R как Ro в формулах).
Контуры с индуктивной и емкостной связью
Параметры узкополосного фильтра можно существенно улучшить, используя в нем несколько контуров. Связь между этими контурами может быть индуктивной (рис. 7) или емкостной (рис. 8).
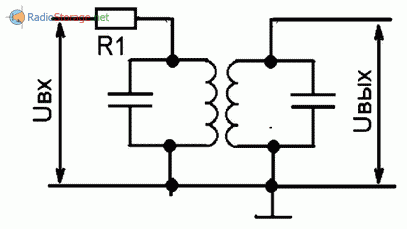
Рис. 7. Контуры с индуктивной связью.
При индуктивной связи коэффициент взаимной индукции выбирается в Q раз меньше индуктивности катушек, а емкость конденсатора связи — в Q раз меньше емкостей контурных конденсаторов.
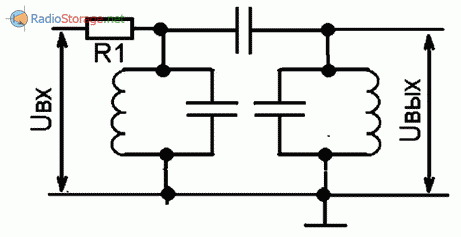
Рис. 8. Контуры с емкостной связью.
Подача сигнала последовательно
Сигнал на контур можно подавать не только параллельно, но и последовательно, как показано на рис. 9. При этом, в отличие от схемы на рис. 6, сопротивление R1 (сопротивление источника сигнала) для получения острой характеристики нужно выбирать как можно меньше, а вот входное сопротивление каскада (R2) должно быть как и на рис. 6, как можно больше.
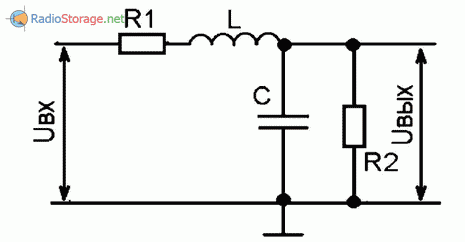
Рис. 9. Последовательная подача сигнала на контур.
Если в схеме на рис. 9
Онлайн расчёт полосовых LC — фильтров 3-го, 5-го и 7-го порядков.
Полосовой, он же полосно-пропускающий фильтр — это фильтр, пропускающий частоты в некоторой полосе частот,
находящейся между нижней и верхней частотами среза, и может быть легко представлен в виде последовательности,
состоящей из фильтра нижних частот и фильтра верхних частот.
Однако более рациональными с точки зрения оптимизации характеристик, являются фильтры, рассчитанные через ФНЧ-прототип.
Преобразование фильтра низких частот в полосовой фильтр осуществляется заменой емкостей ФНЧ прототипа параллельными контурами,
а индуктивностей — последовательными.
Примеры таких полосовых фильтров 3-го, 5-го и 7-го порядков приведены на Рис.1.
Рис.1
Расчёт поведём, используя прототипы фильтров нижних частот имени уважаемого Пафнутия Чебышева и таблицы не менее уважаемого господина Гранта Ханзела, приведённые в справочнике по расчёту фильтров.
ТАБЛИЦА РАСЧЁТА ПОЛОСОВЫХ LC ФИЛЬТРОВ.
На Рис.2 приведены амплитудно-частотные характеристики полосовых фильтров 3-го, 5-го и 7-го порядков с полосой пропускания 3-5 МГц.
Рис.2
Характеристики затухания фильтров вне полосы пропускания симметричны и составляют величины: 38 дБ на октаву для фильтров 3-го порядка, 75 дБ — для фильтров 5-го порядка и 112 дБ — для фильтров 7-го порядка. Неравномерность в полосе пропускания — менее 0,5 дБ.
Приведённая таблица может стать хорошим подспорьем при расчёте входных диапазонных фильтров радиоприёмников и трансиверов,
однако следует учитывать маленький, но ЖИРНЫЙ «НЮАНС»:
Фильтры Чебышева значительно лучше других справляются с подавлением внеполосных сигналов, но становятся
крайне неудобными (с точки зрения критически малых значений номиналов некоторых элементов) при выборе узкой полосы
прозрачности.
Поэтому наиболее выигрышно они будут смотреться в устройствах относительно широкополосных — с не менее, чем полуоктавной полосой
пропускания.
Расчет фильтров нижних и верхних частот
Практический расчет фильтров верхних и нижних частот (RC и LC фильтров)
Доброго дня уважаемые радиолюбители!
Сегодня, на сайте “Радиолюбитель”, на очередном занятии “Практикума начинающего радиолюбителя”, мы с вами рассмотрим порядок расчета фильтров верхних и нижних частот.
Из этой статьи вы узнаете, что фильтровать можно не только “базар”, но и многое другое. А изучив статью, научитесь самостоятельно проводить необходимые расчеты, которые вам помогут при конструировании или наладке различной аппаратуры (в статье много формул, но это не страшно, на самом деле все очень просто).
В первую очередь определимся, что понятия “верхние” и “нижние” частоты относятся к звукотехнике, а понятия “высокие” и “низкие” частоты – относятся к радиотехнике.
Фильтры верхних частот (далее ФВЧ) и фильтры нижних частот (далее ФНЧ) применяются во многих электрических схемах и служат для разных целей. Одним из ярких примеров их применения – цветомузыкальные устройства. К примеру, если вы наберете в поисковике “простая цветомузыка”, то заметите, насколько часто в результатах поиска показывается простейшая цветомузыка на одном транзисторе. Естественно, что такую конструкцию очень трудно назвать цветомузыкой. Зная что такое фильтры верхних и нижних частот и как они рассчитываются, вы сами, самостоятельно, можете переделать такую схему в более полноценное цветомузыкальное устройство. Простейший случай: вы берете две таких одинаковых схемы, но перед каждой ставите фильтр. Перед одним транзистором ФНЧ, а перед вторым – ФВЧ и у вас уже получается двухканальная цветомузыка. А если покумекать, то можно взять еще один транзистор и применив два фильтра (ФНЧ и ФВЧ или один средней частоты) получить третий канал – среднечастотный.
Прежде чем продолжить разговор о фильтрах коснемся очень важной их характеристики – амплитудно-частотная характеристика (АЧХ). Что это за показатель.
АЧХ фильтра показывает как изменяется уровень амплитуду сигнала проходящего через этот фильтр в зависимости от частоты сигнала.
Т.е., на одной частоте входящего на фильтр сигнала уровень амплитуды такой-же как и на выходе, а для другой частоты, фильтр, оказывая сопротивление сигналу, ослабляет амплитуду входящего сигнала.
Тут же появляется еще одно определение: частота среза.
Частота среза – это частота, на которой происходит спад амплитуды выходного сигнала до значения равного 0,7 от входного.
Например, если при частоте входного сигнала 1 кГц амплитудой 1 вольт на выходе фильтра амплитуда входного сигнала уменьшается до 0,7 вольта, то частота 1 кГц является частотой среза данного фильтра.
И последнее определение – крутизна частотной характеристики фильтра.
Крутизна частотной характеристики фильтра – это показатель того, на сколько резко изменяется амплитуда входного сигнала на выходе при изменении его частоты. Чем быстрее происходит спад АЧХ тем лучше.
Фильтры высоких и низких частот – это обыкновенные электрические цепи, состоящие из одного или нескольких элементов, обладающих нелинейной АЧХ, т.е. имеющих разное сопротивление на разных частотах.
Подытоживая вышесказанное можно сделать вывод, что по отношению к звуковому сигналу фильтры являются обыкновенными сопротивлениями, с тем лишь отличием, что их сопротивление меняется в зависимости от частоты звукового сигнала. Такое сопротивление называется реактивным и обозначается как Х.
Частотные фильтры изготавливают из элементов, обладающих реактивным сопротивлением – конденсаторов и катушек индуктивности. Рассчитать реактивное сопротивление конденсатора можно по нижеприведенной формуле:
Xc=1/2пFС где:
Хс – реактивное сопротивление конденсатора;
п – оно и в Африке “пи”;
F – частота;
С – емкость конденсатора.
То есть, зная емкость конденсатора и частоту сигнала, всегда можно определить какое сопротивление оказывает конденсатор для конкретной частоты.
А реактивное сопротивление катушки индуктивности вот этой формулой:
XL=2пFL где:
XL – реактивное сопротивление катушки индуктивности;
п – оно и в России “пи”;
F – частота сигнала;
L – индуктивность катушки
Частотные фильтры бывают нескольких типов:
– одноэлементные;
– Г- образные;
– Т – образные;
– П – образные;
– многозвенные.
В этой статье мы с вами не будем глубоко опускаться в теорию, а рассмотрим только поверхностные вопросы, и только фильтры состоящие из сопротивлений и конденсаторов (фильтры с катушками индуктивности трогать не будем).
Одноэлементный фильтр
— фильтр состоящий из одного элемента: или конденсатора (для выделения верхних частот), или катушки индуктивности (для выделения нижних частот).
Г – образный фильтр
Г-образный фильтр – это обыкновенный делитель напряжения с нелинейной АЧХ и его можно представить в виде двух сопротивлений:
С помощью делителя напряжения мы можем понизить входное напряжения до необходимого нам уровня.
Формулы для расчета параметров делителя напряжения:
Uвх=Uвых*(R1+R2)/R2
Uвых=Uвх*R2/(R1+R2)
Rобщ=R1+R2
R1=Uвх*R2/Uвых – R2
R2=Uвых*Rобщ/Uвх
К примеру, нам дано:
Rобщ=10 кОм, Uвх=10 В, на выходе делителя надо получить Uвых=7 В
Порядок расчета:
1. Определяем R2= 7*10000/10= 7000= 7 кОм
2. Определяем R1= 10*7000/7-7000= 3000= 3 кОм, или R1=Rобщ-R2=10-7= 3 кОм
3. Проверяем Uвых=10*7000/(3000+7000)= 7 В
Что нам и требовалось.
Знание этих формул необходимо не только для построения делителя напряжения с нужным выходным напряжением, но и для расчета фильтров нижних и верхних частот, в чем вы убедитесь ниже.
ВАЖНО!
Так как сопротивление нагрузки, подключаемой к выходу делителя, влияет на выходное напряжение, то значение R2 должно быть в 100 раз меньше входного сопротивления нагрузки. Если не нужна высокая точность, то это значение можно снизить до 10 раз.
Это правило также справедливо и при расчетах фильтров.
Чтобы из делителя напряжения на двух резисторах получить фильтр применяют конденсатор.
Как вы уже знаете, конденсатор обладает реактивным сопротивлением. При этом его реактивное сопротивление на высоких частотах минимально, а на низких частотах – максимально.
При замене сопротивления R1 на конденсатор (при этом на высоких частотах ток через него проходит беспрепятственно, а на низких ток через него не проходит) мы получим фильтр верхних частот.
А при замене конденсатором сопротивления R2 (при этом, обладая малым реактивным сопротивлением на высоких частотах, конденсатор шунтирует токи высокой частоты на землю, а на низких частотах его сопротивление велико и ток через него не проходит)- фильтр нижних частот.
Как я уже сказал, уважаемые радиолюбители, мы не будем глубоко нырять в дебри электротехники, иначе мы заблудимся и забудем о чем шла речь. Поэтому сейчас мы абстрагируемся от сложных взаимосвязей мира электротехники и будем рассматривать эту тему как частный случай, не привязанный ни к чему.
Но продолжим. Не так все плохо. Знание хотя бы элементарных вещей очень большое подспорье в радиолюбительской практике. Ну не рассчитаем мы точно фильтр, а рассчитаем с ошибкой. Ну и ничего страшного, в ходе настройки прибора мы подберем и уточним нужные номиналы радиодеталей.
Порядок расчета Г-образного фильтра верхней частоты
В приведенных примерах расчет параметров фильтра начинается с того, что нам известно общее сопротивление делителя напряжения, но наверное правильнее, при практическом расчете фильтров, определять сначала сопротивление резистора R2 делителя, значение которого должно быть в 100 раз меньше сопротивления нагрузки к которой фильтр будет подключен. А также следует не забывать что делитель напряжения тоже потребляет ток, так-что в конце, необходимо будет определить и рассеиваемую мощность на резисторах для их правильного выбора.
Пример: Нам надо рассчитать Г-образный фильтр верхней частоты с частотой среза 2 кГц.
Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7 (можно взять конкретные напряжения, но в нашем случае это никакой роли не играет).
Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R1, то реактивное сопротивление конденсатора Хс = R1.
2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.
5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R1 —> C=1/2пFR1:
C=1/2пFR1 = 1/2*3,14*2000*1500 =5,3*10-8 =0,053 мкФ.
Емкость конденсатора также можно определить по формуле: C=1,16/R2пF.
6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR1C= 1/2*3,14*1500*0,000000053 = 2003 Гц.
Таким образом мы определили, что для построения фильтра высокой частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R2= 3,5 кОм и конденсатор емкостью С= 0,053 мкФ.
? Для справки:
? 1 мкФ = 10-6 Ф = 0,000 001 Ф
? 0,1 мкФ = 10-7 Ф = 0,000 000 1 Ф
? 0,01 мкФ = 10-8 Ф = 0,000 000 01 Ф
и так далее…
Порядок расчета Г-образного фильтра нижней частоты
Пример: Нам надо рассчитать Г-образный фильтр нижней частоты с частотой среза 2 кГц.
Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7 (как и в предыдущем случае).
Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R2, то реактивное сопротивление конденсатора Хс = R2.
2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.
5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R2 —> C=1/2пFR2:
C=1/2пFR2 = 1/2*3,14*2000*3500 =2,3*10-8 =0,023 мкФ.
Емкость конденсатора также можно определить по формуле: C=1/4,66*R2пF.
6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR2C= 1/2*3,14*3500*0,000000023 = 1978 Гц.
Таким образом мы определили, что для построения фильтра нижней частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R1= 1,5 кОм и конденсатор емкостью С= 0,023 мкФ.
Т – образный фильтр
Т- образные фильтры высоких и низких частот, это те же Г- образные фильтры, к которым добавляется ещё один элемент. Таким образом, они рассчитываются так же как делитель напряжения, состоящий из двух элементов с нелинейной АЧХ. А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента. Другой, менее точный способ расчёта Т-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «первого» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента Т-образного фильтра. Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза:
П – образный фильтр
П-образные фильтры, это те же Г- образные фильтры, к которым добавляется ещё один элемент впереди фильтра. Всё, что было написано для Т-образных фильтров справедливо для П-образных.
Как и в случае с Т-образными фильтрами, для расчёта П-образных используют формулы делителя напряжения, с добавлением дополнительного шунтирующего сопротивления первого элемента фильтра. Другой, менее точный способ расчёта П-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «последнего» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента П-образного фильтра. В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза.
Как правило, одноэлементные фильтры применяют в акустических системах. Фильтры верхних частот обычно делают Т-образными, а фильтры нижних частот П-образными. Фильтры средних частот, как правило, делают Г-образными, их двух конденсаторов.
Для написания статьи, кроме всего прочего использовались материалы с сайта www.meanders.ru, автором и владельцем которого является Александр Мельник, за что ему большое и бесконечное (меандровское) спасибо.
Расчет LC-фильтров
Комбинируя катушки индуктивности и конденсаторы, удается построить фильтры, во-первых, более высоких порядков (порядок фильтра, как правило, равен числу его реактивных элементов), т. е. имеющие более крутые скаты АЧХ в полосе задерживания, во-вторых, вносящие значительно меньшее затухание в полосе пропускания. В идеальном случае, когда катушки и конденсаторы не имеют потерь (их добротность бесконечна), LC-фильтры вообще не вносят потерь.
Самый простой LC-фильтр — колебательный контур. Включенный по приведенной на рис. 38 схеме, он будет действовать как узкополосный полосовой фильтр, настроенный на частоту
f0= 1/2π√LС.
На резонансной частоте сопротивление контура активно:
R0 = pQ.
где р — характеристическое сопротивление, равное реактивному сопротивлению катушки и конденсатора. Его удобнее подсчитать по формуле
р = √L/C.
Поскольку конденсатор, как правило, почти не вносит потерь, добротность контура равна добротности катушки. Проще определить резонансную частоту и добротность экспериментально, собрав каскад по приведенной выше схеме. Понадобятся генератор сигналов, создающий входное напряжение Uвх, и какой-либо измеритель выхода с высоким внутренним сопротивлением, лучше всего осциллограф. Он послужит для регистрации напряжения Uвых.
Изменяя частоту генератора, удастся зарегистрировать максимум Uвых на резонансной частоте контура f0. Резистор R1 и резонансное сопротивление контура r0 образуют делитель, и
Uвых = Uвх/(R1+r0).
Измерив напряжения на входе и выходе, теперь легко рассчитать резонансное сопротивление, а затем и добротность контура.
Другой способ измерения добротности состоит в измерении полосы пропускания контура 2Δf, где Δf есть отклонение частоты генератора, при котором Uвых падает до 0,7 от резонансного значения. Добротность связана с полосой пропускания простой формулой
Q = f0/2Δf.
При этом надо иметь в виду, что будет измерена не собственная (конструктивная) добротность контура Q0, а несколько меньшая величина — добротность контура, зашунтированного резистором R1. Поэтому сопротивление резистора в этом эксперименте следует выбирать как можно больше. Часто резистор заменяют конденсатором малой емкости, практически бывает достаточно поднести щуп генератора к верхнему (по схеме) выводу контура.
Входное сопротивление осциллографа, или другого прибора, подключенного к контуру, также не бесконечно большое, и, конечно, оно уменьшает его добротность. Методика расчета «нагруженной» добротности проста: надо найти новое резонансное сопротивление, образованное параллельным соединением R1 и R0, после чего разделить его на р. Затем аналогично учитывается и сопротивление R2, подключенное к выходу.
Одноконтурный полосовой фильтр — весьма несовершенное устройство. Если мы хотим использовать свойства контура полностью, т. е. получить острую резонансную кривую, соответствующую конструктивной добротности, то контур надо нагружать слабо выбирая R1 и R2 намного больше R0. Тогда коэффициент передачи мощности получается малым, что означает большие потери в полосе пропускания. Если же нагрузить контур сильно, выбрав R1 = R2 << R0, то коэффициент передачи стремится к максимально возможному (-6 дБ), но зато контур практически полностью теряет свои резонансные свойства. Тем не менее одиночный контур часто используют на входе радиоприемников или в резонансных усилителях из-за его простоты.
Коэффициент передачи напряжения увеличивается, если хотя бы R2 можно сделать большим (например, подключив контур к затвору полевого транзистора, служащего для дальнейшего усиления сигнала). Остается согласовать контур со стороны входа (например, с 75-омным фидером антенны). Используют автотрансформаторную связь (рис. 39) или емкостный делитель (рис. 40).
В первом случае
R1 = R0(n1/n0)2,
где n1 — число витков от «земли» до отвода: n0 — общее число витков катушки (связь частей катушки полагается сильной) Во втором случае
R1 = R0C12/(C1 +С2)2.
Если R2 не бесконечно, то сначала надо учесть его, вычислив новое R0 (уменьшенное параллельным подключением R2), а потом уже рассчитывать согласование по входу. Параметры узкополосного полосового фильтра удается значительно улучшить, включая два, три и более контуров. Связь между ними может быть индуктивной или внешней емкостной. Коэффициент взаимоиндукции выбирается в Q раз меньше индуктивности катушек, а емкость конденсаторов связи — в Q раз меньше контурных емкостей, причем Q определяется из требуемой полосы пропускания фильтра. Если О намного меньше конструктивной добротности катушек, потери в фильтре получаются малыми. Вход и выход фильтра нагружаются резисторами R = рQ.
Сигнал в контур можно подать не только параллельным способом, как описано выше, но и последовательно, как на рис. 41. При этом, если необходимо получить острую резонансную кривую, сопротивление R2, как и прежде, надо выбирать возможно больше, a R1, напротив, возможно меньше. При малом внутреннем сопротивлении генератора такой контур имеет большой коэффициент передачи напряжения на резонансной частоте, в пределе равный Q. На самых низких частотах коэффициент передачи стремится не к нулю, как в уже рассмотренных фильтрах, а к единице.
Весьма интересен случай, если в фильтре по схеме рис. 41 сопротивления на входе и выходе выбрать равными характеристическому, т. е. R1 = R2 = р.
Получается согласованный ФНЧ, коэффициент передачи которого постоянен и равен 1/2 (-6 дБ) на всех частотах от нуля до резонансной частоты контура L1C1, а при дальнейшем повышении частоты уменьшается. Крутизна ската АЧХ составляет 12 дБ на октаву как и должно быть у фильтра второго порядка.
В полосе пропускания фильтра 0…f0 коэффициент передачи часто полагают равным единице, считая входным напряжением не ЭДС генератора, а напряжение между верхним по схеме выводом резистора R1 и общим проводом. Более того, резистором R1 может быть внутреннее сопротивление генератора. Генератор как бы «видит» сопротивление нагрузки R2 сквозь прозрачный в полосе пропускания фильтр и отдает максимальную мощность при R1 = R2.
Кстати сказать, большинство измерительных генераторов имеют стандартное внутреннее сопротивление 50 Ом, и шкала выходного напряжения проградуирована для случая их нагрузки также на 50 Ом. Если выход такого генератора ничем не нагружать, выходное напряжение будет вдвое больше, чем показывает шкала выходного аттеннюатора!
Для получения более крутых скатов АЧХ используют пару описанных Г-образных звеньев, соединяя их в соответствии с рис. 42, чтобы образовать Т-образное звено, или в соответствии с рис. 43 чтобы образовать П-образное звено. При этом получаются ФНЧ третьего порядка. Обычно предпочитают П-образные звенья, поскольку в них меньше трудоемких в изготовлении катушек индуктивности.
Возможно и дальнейшее «наращивание» порядка фильтров, Для примера на рис. 44 показано, как из двух П-образных звеньев составлен двухзвенный ФНЧ пятого порядка.
Он имеет весьма крутую АЧХ в полосе задерживания — 30 дБ на октаву. Ее удается сделать еще круче если параллельно катушкам подключить дополнительные конденсаторы небольшой емкости. На частотах образовавшихся резонансных контуров получаются две точки «бесконечного затухания», лежащие в полосе задерживания. В ряде случаев роль дополнительных конденсаторов может выполнять междувитковая емкость катушек.
ФВЧ конструируют подобным же образом, лишь катушки заменяются конденсаторами, а конденсаторы — катушками. Широкополосные полосовые фильтры получают каскадным соединением ФНЧ и ФВЧ, желательно с разделительным усилительным каскадом между ними.
Вопрос для самопроверки. Пользуясь формулами этой главы, выведите расчетные формулы для индуктивности и емкости Г-образного звена ФНЧ. Рассчитайте ФНЧ по рис. 44 для радиолюбительского гетеродинного приемника. Заданы частота среза фильтра 2,7 кГц и характеристическое сопротивление 1,6 кОм.
Нарисуйте схему фильтра с обозначением номиналов элементов и постройте его АЧХ в логарифмическом масштабе.
Ответ. Параметры согласованного Г-образного звена ФНЧ (рис. 41, 42) находятся из соотношения R = р, где R — сопротивление нагрузки фильтра; р — его характеристическое сопротивление, равное реактивному сопротивлению его элементов на частоте среза:
L=R/2πf c,C=1/2πf cR.Получив эти формулы, уже не составляет большого труда рассчитать элементы двузвенного ФНЧ (рис. 44) гетеродинного приемника с учетом того, что индуктивности обеих катушек должны составить 2L, емкости крайних конденсаторов — С, емкость среднего конденсатора — 2С:
L= 1,6-103/6,28.2,7-103 — 0,095Гн = 95 мГн, 2L= 190 мГн;С = 1/6,28·2,7·103·1,6·103 = 0,037х10-6Ф = 0,037 мкФ, 2С = 0,074 мкФ.
При практическом изготовлении фильтра число витков катушки рассчитывают, пользуясь сведениями, изложенными в главе 5. В данном случае целесообразно использовать ферритовые кольца, обеспечивающие неплохую добротность катушки и мало подверженные наводкам от посторонних полей. Несколько хуже и в том, и в другом отношении магнитопроводы из Ш-образных стальных пластин, например, от трансформаторов, использовавшихся ранее в портативных транзисторных приемниках.
Для примера рассчитаем число витков катушки на ферритовом кольце К16x8x4 из феррита марки 2000НМ. Воспользуемся формулой L=μμ0N2/l. Подставив в нее значения μ = 2000, μ0 = 4π-10-7rH/M,S=16·10-6M2, l=38·10-3M, получаем L -10-6N2 или N — 103L Подставляя значение L = 0,19 Гн, получаем N = 430 витков. Надо заметить, что, вопреки распространенному мнению, подобные простые фильтры довольно-таки некритичны к разбросу параметров их элементов, во всяком случае отклонения на ± 5 % практически мало сказываются на форме АЧХ. С соответствующей точностью допустимо проводить и расчеты. Сопротивления источника и нагрузки фильтра еще менее критичны, и здесь допустимы отклонения до ± 25 %.
Автор: В.Поляков, г.Москва
Расчеты ЖК-фильтра| Форум по электронике
Хорошо, поехали. Это очень сложная задача для обеспечения полного и точного моделирования различных индексов модуляции, частот переключения и импедансов нагрузки. Однако для первого прохода я нашел пример, в котором кто-то рассчитал спектры для синусоиды 100% модуляции.(http://www.wpi.edu/Pubs/E-project/A…-190851/unrestricted/PWM_Techniques_final.pdf)
Назначение фильтра — уменьшить амплитуду гармоник до заданного максимального уровня.Обычно люди смотрят только на первые три-три больших гармоники низкого порядка, поскольку обычно гармоники высокого порядка имеют меньшую амплитуду и их легче фильтровать. В гипертекстовой статье Crowley & Lueng на рисунке 9 показана третья гармоника, равная примерно 15% от основной гармоники (160 В для основной гармоники, 25 В для третьей гармоники). Чтобы уменьшить третью гармонику до 3% от основной гармоники (для THD около 5%, что является такой же уродливой формой волны, какую могут выдержать большинство чувствительных схем), вам понадобится фильтр, который уменьшает третью гармонику в 5 раз ( 3% / 15%).Двухполюсный фильтр, такой как LC, уменьшает амплитуду в 4 раза на каждую октаву, поэтому ваш фильтр должен иметь угловую частоту чуть меньше 1,5 * основной частоты.
А вот и действительно неприятная часть вашего LC-фильтра: он настолько близок к основной частоте (меньше октавы), что будет усиливать основную частоту (пик) вместо того, чтобы иметь плоские характеристики.
Это явный пример того, что один из моих друзей называет «принципом сохранения страданий».Вы можете сделать сигнал чище с помощью фильтра более низкой частоты, но это сделает ваш выходной сигнал нестабильным. Вы можете сделать выходной сигнал стабильным, но ваша форма волны не будет тем, что вы хотите показать своим детям.
— — — Обновлено — — —
Возможно, я неправильно ответил на ваш вопрос. Я ответил на вопрос — «Какую частоту выбрать для резонансной частоты фильтра?» Если вопрос звучал так: «Мне нужно создать LC-фильтр, например, с резонансной частотой 80 Гц. Как выбрать L и C?»
Ответ на второй вопрос: (2 * пи * 80 Гц) в квадрате = 1 / LC или 252,000 = 1 / LC в этом примере.
Давайте сначала попробуем конденсатор 1 мкФ: L = 1 / (252 000 * C) = 1 / (252 000 * 1 мкФ) = 3,96 ч.
Хорошо, индуктор довольно большой. Давайте вместо этого выберем L как 396uH (1/10000 размера 3.96H, который мы сначала рассчитали), теперь C составляет 10000uF. Это довольно большой конденсатор. Как насчет чего-нибудь посередине? Как насчет 39 мГн и 100 мкФ? или 50 мГн и 80 мкФ? или 25 мГн и 160 мкФ?
Откуда берется индуктор 25 мГн (или другое значение)? Разберите старый силовой трансформатор от старого телевизора (не ЖК-телевизора) и начните наматывать на него повороты, пока не получите желаемую букву L.
Надеюсь, это поможет.
Проектирование и расчеты схемы простого LC фильтра верхних частот »Электроника
Соображения по конструкции, схема и формулы для базового 3-полюсного LC-фильтра верхних частот для ВЧ приложений.
Фильтр постоянного K Включает:
Фильтр постоянного k
Простая конструкция LC LPF
Конструкция LC HPF
Конструкция полосового фильтра LC
Основы фильтра включают: : RF фильтры — основы Характеристики фильтра Основы проектирования ВЧ-фильтров Конструкция фильтра высоких и низких частот Постоянный k-фильтр Фильтр Баттерворта Фильтр Чебычева Фильтр Бесселя Эллиптический фильтр
Фильтры верхних частот и, в частности, LC фильтры верхних частот используются во многих радиочастотных приложениях, где они блокируют более низкие частоты и пропускают более высокочастотные сигналы.
Хотя LC фильтры верхних частот не так широко используются, как фильтры нижних частот, они используются во многих областях проектирования ВЧ для удаления нежелательных сигналов и пропуска полезных.
Обычно LC-фильтры используются для более высоких радиочастот, где активные фильтры не так удобны, а катушки индуктивности более подходят. В низкочастотных конструкциях, как правило, не используются индукторы, поскольку более распространены активные конструкции, а индукторы могут стать большими и дорогими.
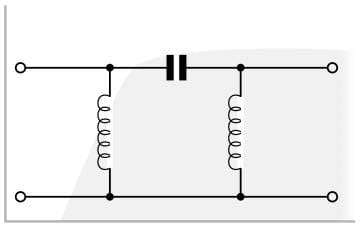
Топологии фильтра верхних частот
Фильтры высоких частот с использованием ЖК-компонентов, т.е.е. катушки индуктивности и конденсаторы или даже резисторы и конденсаторы могут быть скомпонованы в простой пи- или Т-схеме. Как следует из названия, основной элемент π-сети имеет один последовательный конденсатор, а с обеих сторон от него есть индуктор, подключенный к земле. Дополнительные элементы сети могут быть включены в каскад, если требуется более высокая скорость спада.
Топология 3-полюсного π LC-фильтра высоких частот ВЧТочно так же сетевой фильтр верхних частот T имеет одну катушку индуктивности, соединенную с землей, и с каждой стороны имеется последовательно включенный конденсатор.Как и в случае сети с π-секциями, дополнительные элементы могут быть соединены каскадом для улучшения характеристик спада.
Топология для 3-полюсного ВЧ-фильтра верхних частот T LCТаким образом, эти фильтры пропускают высокочастотные сигналы и отклоняют низкочастотные сигналы. Эти фильтры могут использоваться в приложениях, где есть нежелательные сигналы в полосе частот ниже частоты среза и необходимо пропускать полезные сигналы в полосе выше частоты среза фильтра.
Конструкция ЖК-фильтра высоких частот
Существует множество различных вариантов фильтра, которые могут использоваться в зависимости от требований с точки зрения пульсации в полосе, скорости, с которой достигается окончательный спад, и т. Д. Используемый здесь тип — константа-k, что дает некоторые управляемые уравнения :
Сечение π может быть вычислено по приведенным ниже уравнениям и с использованием множителей, показанных на диаграмме, то есть 2L и C.
3-полюсный, LC фильтр высоких частот RFТ-образный фильтр верхних частот может быть спроектирован с использованием приведенных ниже уравнений для расчета L и C, но обратите внимание, что диаграмма показывает, что это должно быть масштабировано, поскольку 2C и L.
3-полюсный высокочастотный фильтр T LCЗначения C и L, используемые в двух конструктивных конфигурациях LC-фильтра верхних частот, можно рассчитать с помощью приведенных ниже уравнений.
L знак равно Z 0 4 π ж c ГенриC знак равно 1 4 Z 0 π ж c Фарады
F c знак равно 1 4 π L C Герц
Где
Z 0 = характеристический импеданс в омах
C = емкость в фарадах
L = индуктивность в Генри
f c = частота среза в герцах
Конструкция фильтра и меры предосторожности при изготовлении
Есть несколько рекомендаций, советов и советов, которые можно включить в конструкцию и конструкцию фильтра верхних частот, чтобы гарантировать, что он соответствует требованиям конструкции и максимально приближен к теоретическим характеристикам.
- Каскадные секции фильтра для лучшего затухания: Чтобы обеспечить больший наклон или спад в фильтре высоких частот, можно каскадировать несколько секций фильтра. При этом фильтрующие элементы из соседних секций можно комбинировать. Например, если два Т-образных фильтра подключены каскадом, и каждая Т-образная секция имеет индуктор 1 мкГн в каждом плече Т, их можно объединить в смежных секциях и использовать индуктор 2 мкГн.
- Используйте компоненты с жесткими допусками: Выбор компонентов для любого фильтра, и в данном случае для фильтра верхних частот, важен.Следует использовать компоненты с жесткими допусками, чтобы гарантировать получение требуемых характеристик. Также необходимо проверить температурную стабильность, чтобы гарантировать, что компоненты фильтра не изменяются значительно с температурой, тем самым изменяя производительность.
- Расположение фильтра: Следует соблюдать осторожность при расположении фильтра, особенно когда фильтр используется для высоких частот. Емкостная и индуктивная связь являются основными элементами, которые ухудшают характеристики фильтра.Соответственно, вход и выход фильтра должны быть разделены. Следует использовать короткие провода и дорожки. Компоненты из соседних секций фильтра должны быть разнесены. При необходимости используются экраны, а на входе и выходе используются качественные разъемы и коаксиальный кабель.
| ||||||||||||||
Chebyshev Pi LC Калькулятор фильтра низких частот
| Калькулятор низкочастотного фильтра Chebyshev Pi LC |
| Введите значение, выберите единицу измерения и нажмите «Рассчитать». Результат будет отображаться. |
Фильтр типа Чебышева назван в честь Пафнутия Чебышева, потому что их математические характеристики полученные из полиномов Чебышева. |
ПИ-фильтр — это фильтр, который состоит из последовательного элемента и двух параллельных элементов, соединенных в форма греческой буквы Пи.
Фильтры Чебышева — аналоговые или цифровые фильтры с более крутым спадом и большей полосой пропускания. пульсации или пульсации полосы задерживания, чем фильтры Баттерворта. Фильтры Чебышева обладают тем свойством, что они минимизируют ошибку между идеализированной характеристикой фильтра и фактический во всем диапазоне фильтра, но с рябью в полосе пропускания.
Фильтры Чебышева обеспечивают более резкое затухание за пределами точки -3 дБ. Фильтры Чебышева более чувствительны к допуски компонентов, чем фильтры Баттерворта.
Для фильтров четного порядка все пульсации выше нормированной по постоянному току полосы пропускания чувствительность усиления, поэтому отсечка находится на уровне 0 дБ. Для фильтров нечетного порядка вся пульсация ниже Нормированная по постоянному току характеристика усиления полосы пропускания, поэтому отсечка составляет — (пульсация) дБ.
Фильтр нижних частот — это фильтр, который пропускает низкочастотные сигналы, но ослабляет сигналы с частотами выше, чем частота среза.
.