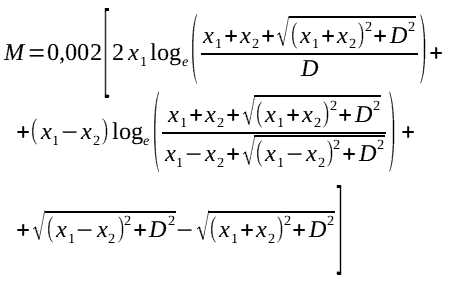Рассчитать катушку индуктивности – Расчет катушки индуктивности | Онлайн калькулятор

Как рассчитать сердечник и витки самодельных катушек индуктивности

Катушки индуктивности предназначены для фильтрации токов высокой частоты. Они устанавливаются в колебательных контурах и используются для других целей в электрических и электронных схемах. Готовое устройство заводского изготовления надёжнее в работе, но дороже, чем изготовленное своими руками. Кроме того, не всегда удаётся приобрести элемент с необходимыми характеристиками. В этом случае расчёт катушки  индуктивности и само устройство можно сделать самостоятельно.

Устройство катушки индуктивности

Конструкция катушки

Каркас устройства изготавливается из диэлектрика. Это может быть тонкий (нефольгированный) гетинакс, текстолит, а на тороидальных сердечниках –просто обмотка из лакоткани или аналогичного материала.

Обмотка выполняется из одножильного или многожильного изолированного провода.

Внутрь обмотки вставляется сердечник. Он изготавливается из железа, трансформаторной стали, феррита и других материалов. Он может быть замкнутым, тороидальным (бублик), квадратным или незамкнутым (стержень). Выбор материала зависит от условий работы: частоты, магнитного потока и других параметров.

Кроме того, есть приборы, в которых сердечник отсутствует. Они характеризуются большой линейностью импеданса, но при намотке тороидальной формы обладают паразитной ёмкостью.

Расчет параметров катушки индуктивности

Протекающий по проводу электрический ток создаёт вокруг него электромагнитное поле. Соотношение величины поля к силе тока называется индуктивностью. Если провод свернуть кольцом или намотать на каркас, то получится катушка индуктивности. Её параметры рассчитывают по определённым формулам.

Расчёт индуктивности прямого провода

Индуктивность прямого стержня – 1-2мкГн на метр. Она зависит от его диаметра. Точнее можно рассчитать по формуле:

L=0.2l(logl/d-1), где:

• d – диаметр провода,
• l – длина провода.

Эти величины нужно измерять в метрах (м). При этом результат будет иметь размерность микрогенри (мкГн). Вместо натурального логарифма ln допустимо использовать десятичный lg, который в 2,3 раза меньше.

Предположим, что какая-то деталь подключена проводами длиной 4 см и диаметром 0,4 мм. Произведя при помощи калькулятора расчет по выше приведённой формуле, получаем, что индуктивность каждого из этих проводов составит (округлённо) 0,03 мкГн, а двух – 0,06 мкГн.

Ёмкость монтажа составляет порядка 4,5пФ. При этом резонансная частота получившегося контура составит 300 МГц. Это диапазон УКВ.

Важно! Поэтому при монтаже устройств, работающих в частотах УКВ, длину выводов деталей нужно делать минимальной.

Расчёт однослойной намотки

Для увеличения индуктивности провод сворачивается кольцом. Величина магнитного потока внутри кольца выше примерно в три раза. Рассчитать её можно при помощи следующего выражения:

L = 0,27D(ln8D/d-2), где D – диаметр кольца, измеренный в метрах.

При увеличении количества витков индуктивность продолжает расти. При этом индукция отдельных витков влияет на соседние, поэтому получившиеся параметры пропорциональны не количеству витков N, а их квадрату.

Однослойная намотка

Дроссель с сердечником

Параметры обмотки, намотанной на каркас, диаметром намного меньше длины рассчитывается по формуле:

L=*0*N2*S.

Она справедлива для устройства большой длины или большого тора.

Размерность в ней дана в метрах (м) и генри (Гн). Здесь:

• 0 = 4•10-7 Гн/м – магнитная константа,
• S = D2/4 – площадь поперечного сечения обмотки, магнитная проницаемость магнитопровода, которая меньше проницаемости самого материала и учитывает длину сердечника; в разомкнутой конструкции она намного меньше, чем у материала.

Например, если стержень антенны изготовить из феррита с проницаемостью 600 (марки 600НН), то у получившегося изделия она будет равна 150. При отсутствии магнитного сердечника = 1.

Для того чтобы использовать это выражение для расчёта обмоток, намотанных на тороидальном сердечнике, его необходимо измерять по средней линии “бублика”. При расчёте обмоток, намотанных на железе Ш-образной формы без воздушного зазора, длину пути магнитного потока измеряют по средней линии сердечника.

Катушка с Ш-образным сердечником

В расчёте диаметр провода не учитывается, поэтому в низкочастотных конструкциях сечение провода выбирается по таблицам, исходя из допустимого нагрева проводника.

В высокочастотных устройствах, так же как и в остальных, стремятся свести омическое сопротивление к минимуму для достижения максимальной добротности прибора. Простое повышение сечения провода не помогает. Это приводит к необходимости наматывать обмотку в несколько слоёв. Но ток ВЧ идёт преимущественно по поверхности, что приводит к увеличению сопротивления. Добротность в высокочастотных элементах растёт вместе с увеличением всех размеров: длины и диаметров обмотки и провода.

Максимальная добротность получается в короткой обмотке большого диаметра, с соотношением диаметр/длина, равным 2,5. Параметры такого устройства вычисляются по формуле:

L=0.08D2N2/(3D+9b+10c).

В этой формуле все параметры измеряются в сантиметрах (см), а результат получается в микрогенри (мкГн).

По этой формуле рассчитывается также плоская катушка. Диаметр “D” измеряется по среднему витку, а длина “l” по ширине:

l=Dmax-Dmin.

Плоская катушка

Многослойная намотка

Многослойная намотка без сердечника вычисляется по формуле:

L=0.08D2N2/(3D+9b+10c).

Размеры здесь измеряются в сантиметрах (см), а результат получается в микрогенри (мкГн).

Добротность такого устройства зависит от способа намотки:

• обычная плотная намотка – самая плохая, не более 30-50;
• внавал и универсал;
• “сотовая”.

Многослойная катушка

Для увеличения добротности при частоте до 10 мГц вместо обычного, одножильного провода, можно взять литцендрат или посеребренный проводник.

Справка. Литцендрат – это провод, скрученный из большого количества тонких изолированных друг от друга жил.

Литцендрат имеет большую поверхность, по сравнению с одножильным проводником того же сечения, поэтому на высоких частотах его сопротивление ниже.

Использование сердечника в высокочастотных устройствах повышает индуктивность и добротность катушки. Особенно большой эффект даёт использование замкнутых сердечников. При этом добротность дросселя зависит не от активного сопротивления провода, а от проницаемости магнитопровода. Рассчитывается такой прибор по обычным формулам для низкочастотных устройств.

Сделать катушку или дроссель можно самостоятельно. Перед тем, как её изготавливать, необходимо рассчитать индуктивность катушки по формулам или при помощи онлайн-калькулятора.

Видео

Оцените статью:

jelectro.ru

Coil32 — Одиночный круглый виток

Подробности

Опубликовано: 28 августа 2013

Просмотров: 9042

Расчет индуктивности одиночного круглого витка

 

Индуктивность, реализованная в виде простой петли провода, другими словами в виде одного витка, чаще всего применяется в диапазоне метровых волн. Ввиду отсутствия эффекта близости, имеет довольно высокую добротность, зависящую от диаметра провода и небольшую собственную емкость.

---

Одновитковую петлю можно рассчитывать численными методами по уравнению Д.К.Максвелла:

где:

• E(k) — полный эллиптический интеграл первого рода
• K(k) — полный эллиптический интеграл второго рода
• r = D/2 — радиус петли (м)
• a = d/2 — радиус поперечного сечения провода, половина диаметра (м)

, а параметр k рассчитывается следующим образом:

---

Однако в программе Coil32 расчет катушки ведется по простой эмпирической формуле, которую впервые вывел в 1946 году F.W.Grover. Применять более сложные алгоритмы расчета в этом случае не имеет смысла, т.к. точность расчета вполне достаточна для практических целей, при D/d > 5 около 1%. Численный алгоритм расчета в программе основан на методе последовательных приближений, до достижения заданной индуктивности. При расчете по заданной индуктивности максимально возможный диаметр петли принят за 10 м. Если при расчете получается бóльшая величина, программа выдает сообщение: «Катушка не может быть реализована». В таком случае необходимо выбрать другую форму катушки, например — однослойную.

---

Формула расчета:

• L— индуктивность (мкГн)
• D— диаметр витка (мм)
• d— диаметр провода (мм)

Диаметр петли считается от центра до центра провода.

---

Вперед…

Добавить комментарий

coil32.ru

Coil32 — Однослойная катушка

Расчет индуктивности однослойной катушки

Однослойная катушка индуктивности представляет собой провод, свернутый в спираль. Для придания жесткости, провод обычно наматывают на цилиндрический каркас. Поэтому в Coil32 в качестве исходных параметров приняты размеры каркаса и диаметр провода, т.к. их легче измерить практически. В расчетных формулах, однако, используются геометрические параметры самой спирали. Во избежании путаницы на этой страничке справки можно подробнее ознакомиться с этими тонкостями.

Однослойные катушки получили широкое распространение, особенно для конструкций коротковолнового и средневолнового любительских и радиовещательных диапазонов. Основные свойства однослойных катушек — высокая добротность, относительно небольшая собственная емкость, удобство изготовления. Рассмотрим методы расчета такой катушки без промежутка между витками — «виток к витку«…

---

Начнем с того, что в конце XIX века Х.А.Лоренц вывел формулу с применением эллиптических интегралов для расчета соленоида. Отличием модели Лоренца от модели Максвелла являлся тот момент, что витки соленоида представлялись не бесконечно тонким круговым проводом, а бесконечно тонкой спиральной проводящей лентой с шириной равной реальной толщине провода, без промежутка между витками. Формула имеет высокую точность при расчете реальной катушки в случае если последняя имеет большое количества витков и имеет намотку виток к витку. В 1909 г. японский физик Х.Нагаока преобразовал формулу Лоренца и привел ее к виду из которого следовал важный вывод — индуктивность соленоида зависит исключительно от формы и размеров катушки. Формула Нагаока имеет следующий вид:

[2]

, где

• L_s — индуктивность катушки
• N — число витков катушки
• r — радиус намотки
• l — длина намотки
• k_L — коэффициент Нагаока

Важнейшим выводом из анализа этой формулы был тот, что коэффициент Нагаока зависел только от отношения l/D, который был назван форм-фактором катушки. Коэффициент Нагаока вычислялся с применением эллиптических интегралов. Подробнее на этой формуле останавливаться не будем, т.к. Coil32 ее не использует в расчетах. Стоит только отметить, что в случае длинного соленоида формула упрощается до следующего вида:

[3]

где S — площадь поперечного сечения катушки. Эта формула имеет только академический интерес и не пригодна для расчетов реальных катушек, т.к. справедлива только для бесконечно длинных соленоидов, которых в природе не существует.

---

Однослойную катушку можно рассчитать численным методом, используя формулу Максвелла или формулу Нагаока для соленоида. Однако современные эмпирические формулы дают очень высокую точность расчетов и вполне достаточны для практических целей.

---

Обзор и выбор эмпирических формул начнем с самой известной формулы Г.Вилера. Обычно именно эта формула чаще всего используется в различных программах, онлайн калькуляторах, справочниках и статьях, посвященных расчетам индуктивностей.

В оригинале эта формула выглядит так:

L = a² N² / ( 9 a + 10 b )

где N — число витков, а

a и b — соответственно радиус и длина намотки катушки. Размерности в дюймах. Адаптировав эту формулу для метрической системы (вернее сказать для СГС) и поменяв радиус на диаметр, получаем следующее:

[4]

, где

• L — индуктивность катушки [мкГн];
• N — число витков катушки;
• D — диаметр намотки [см];
• l — длина намотки [см];

Это самый известный у нас вариант этой формулы. Раньше на сайте С.-Петербуржского университета телекоммуникаций — sut.ru был довольно информативный ресурс — dvo.sut.ru, на котором можно было найти много информации о катушках индуктивности, включая и эту формулу. Теперь это ресурс к сожалению удален. Но удалось обнаружить клон этого ресурса на qrz.ru, на который перекочевала даже старая ошибка (0,5ё1.0) в формуле 2.37. Там можно найти и формулу Нагаока (формула 2.28) и выражение коэффициента Нагаока через формулу Вилера (формула 2.29).

Формула была предложена Вилером в далеком 1928 году, когда еще о компьютерах только мечтали и была очень полезна в то время, т.к. позволяла «в столбик» на бумажке рассчитать практическую катушку. Формула «укоренилась» в массовом сознании радиолюбителей. Однако мало кто знает, что она, как любая эмпирическая формула, имеет ограничения. Эта формула дает погрешность до 1% при l/D > 0,4, т.е если катушка не слишком короткая. Для коротких катушек эта формула не пригодна.

---

Последовало несколько попыток устранить этот недостаток. В 1985 г. Р.Лундин опубликовал две свои эмпирические формулы, одна — для «длинных», другая — для «коротких» катушек, позволяющие рассчитать коэффициент Нагаока с точностью не менее чем 3ppM (±0.0003%), что несомненно выше точности изготовления или измерения индуктивности катушки. Вот калькулятор, основанный на этих формулах.
В 1982 г., спустя 54 года, с наступлением эры компьютеров, Вилер опубликовал свою «длинную» формулу, которая рассчитывала однослойную катушку с погрешностью не более ±0.1%, как длинную, так и короткую. В дальнейшем эта формула была усовершенствована Р.Розенбаумом, а в последствии Р.Вивером (Robert Weaver — анализ и вывод формулы у него на сайте).

[5]

где:

• D_k — диаметр намотки
• N — число витков
• k = l/D_k — форм-фактор катушки, отношение длины намотки к ее диаметру

---

В результате мы имеем формулу, позволяющую рассчитать однослойную катушку с точностью не менее 18.5 ppM (в сравнении с формулой Нагаока), что хуже чем по формулам Лундина, но во-первых вполне достаточно для практических расчетов, во-вторых мы имеем одну более простую формулу вместо двух, рассчитывающую однослойную катушку независимо от ее форм-фактора.

Формула [5] и используется в онлайн-калькуляторе однослойной катушки, старых версиях Coil32, а также во всех версиях программы для Linux и в J2ME приложении для мобильных телефонов.

В основной версии Coil32 для Windows, а также начиная с версии 3.0 для Android, применена более сложная методика расчета однослойной катушки, учитывающая спиральную форму витков и произвольный шаг намотки.

---

В 1907 году Э.Роза, сравнивая расчеты по методу Максвелла и по методу Лоренца, вывел таблицу поправок, существенно увеличивающих точность расчета по методу Лоренца, особенно если катушка имеет небольшое число витков. Эти поправки стали именоваться «поправки на круглость провода» — Round Wire Corrections. В дальнейшем эти поправки использовались для увеличения точности расчета коэффициента Нагаока и эмпирических формул Лундина и Вивера. В 2008 г. Р.Вивер создал эмпирический алгоритм, позволяющий численным методом рассчитать «поправки на круглость провода» не прибегая к помощи таблиц. Этот алгоритм применяется в Coil32 начиная с версии 8.0, в онлайн-калькуляторе, а также в версиях Coil32 для Андроид и J2ME, для увеличения точности расчета индуктивности однослойных катушек.

---

Кроме индуктивности, как основного параметра однослойной катушки, программа Coil32 вычисляет и другие параметры:

Этих данных вполне достаточно для создания реалистичной модели катушки в программах схемотехнического моделирования. Например, в популярных RFSim99 или LTSpice IV. В RFSim99 необходимо поставить галочку в чекбоксе «Вкл. физ. модель» и ввести частоту собственного резонанса и добротность. Тип добротности необходимо выбрать третий — Q(f)=Q(F). В LTSpice необходимо задать R_ser — это наше сопротивление потерь (r) и C_par — это собственная емкость катушки Cs.

Кроме того можно рассчитать дополнительные результаты для параллельного колебательного контура на рабочей частоте. Характеристическое сопротивление такого контура равно реактивному сопротивлению катушки

на рабочей частоте.

Назад…      Вперед…

coil32.ru

Coil32 — Методы расчета индуктивности катушки.

Методы расчета индуктивностей

Наиболее полно теоретические основы методов расчета индуктивностей изложены в справочной книге: «Расчет индуктивностей. П.Л.Калантаров Л.А.Цейтлин». Здесь же хотелось бы немного систематизировать подходы к расчету индуктивностей.

---

Прежде всего отметим, что расчет индуктивности можно вести двумя способами:

∙ Численный метод с различной степенью упрощения задачи

∙ Расчет по упрощенным эмпирическим формулам

---

Эмпирический подход предполагает подбор (подгонку) относительно несложных аппроксимирующих формул по результатам измерений индуктивности реальных катушек. Расчет по упрощенным эмпирическим формулам имеет ограничения в точности и применим только к катушкам с определенной геометрией намотки. Большинство таких формул можно найти здесь. Несмотря на невысокую точность, такой расчет чаще всего вполне достаточен в радиолюбительской практике.

---

Численные методы основываются на реальных физических моделях катушек индуктивности и их, в свою очередь, можно разбить на две категории:

1. Расчет в программах основанных на фундаментальных законах классической электродинамики, так называемых электромагнитных симуляторах. К ним можно отнести COMSOL Multiphysics, FEMM, ANSYS, GAL-ANA и т.п. Эти программы используют специальные численные методы, такие как метод моментов и метод конечных элементов. Расчет в таких программах довольно точен, позволяет учесть множество нюансов, рассчитать катушку произвольной формы, однако требует огромных ресурсов компьютера. Применяется при научном анализе или если катушка работает в режиме, когда ее нельзя представлять как сосредоточенный элемент [пример]
2. Численные методы расчета, основанные на фундаментальных формулах физики, применимых к круговым проводникам, выведенных в XIX веке Д.К.Максвеллом. Позволяют провести расчет более точно, чем по эмпирическим формулам, но не требуют запредельных аппаратных ресурсов компьютера. На них следует остановится подробнее, т.к их и использует Coil32…

---

Расчет индуктивности в программе Coil32 основан на модели Максвелла, в которой катушка представляется как множество соосных бесконечно тонких круговых проводников.
Из Теоремы Гаусса следует, что силовые линии магнитного поля всегда замкнуты. Из этого следует, что магнитный поток порожденный круговым контуром с током весь проходит через поверхность, ограниченную этим контуром. Это обстоятельство отражено в следующей формуле:

Из этой формулы можно вывести определение для собственной индуктивности кругового проводника через двойной контурный интеграл Ф.Е.Неймана для взаимоиндукции [вывод здесь]:

Как показал Д.К.Максвелл, для двух бесконечно тонких круговых соосных проводников этот интеграл имеет однозначное решение, которое выглядит следующим образом:

[1]

, где: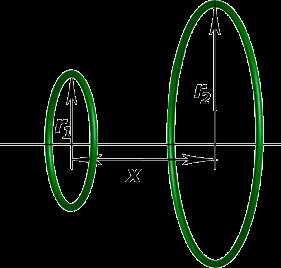

• M — взаимоиндукция;
• r₁, r₂ — радиусы двух бесконечно тонких круговых проводников;
• x — расстояние между центрами кругов, ограниченных этими проводниками;
• K,E — эллиптические интегралы, соответственно первого и второго рода;

Численный метод расчета по формуле Максвелла сводится к численным методам решения эллиптических интегралов.

По формуле Максвелла можно рассчитывать как индуктивность многослойных и однослойных катушек, так и взаимную индуктивность двух отдельных катушек. Погрешности модели, связанные с допущением, что провод бесконечно тонкий и представляет собой набор круговых проводников (хотя на самом деле — это спираль), можно уменьшить с помощью соответствующих поправок.

Рассчитывая взаимоиндукцию проводника «самого на себя», т.е. его самоиндукцию (собственную индуктивность), Максвелл использует понятие — «среднее геометрическое расстояние» — GDM (g), для круглого провода:

g = e^0.25*r_w, где r_w — радиус провода.

---

Очень важен следующий момент. Вся вышеприведенная логика рассуждений и вывода формул, начиная от формулы Неймана, справедлива в случае равномерного распределения плотности тока вдоль катушки. В подавляющем большинстве практических случаев так и есть. Однако если катушка работает вблизи частот собственного резонанса, начинает проявляться неравномерность распределения плотности тока по проводнику! Другими словами, начинает проявляться зависимость индуктивности от частоты, которая в наших расчетах не учитывается. Поэтому индуктивность катушки можно рассчитать корректно только на частотах не превышающих 60-70% от частоты ее собственного резонанса. Таким образом Coil32 не годится для точных расчетов, например, катушек Тесла или спиральных резонаторов. В этом случае и в случае если катушка работает в режиме выше частоты собственного резонанса — ее нужно представлять только в виде модели длинной линии и рассчитывать в программах-электромагнитных симуляторах, либо пользоваться специальными эмпирическими формулами.

---

Ссылки:

1. An introduction to the art of Solenoid Inductance Calculation D W Knight 2013
2. Numerical Methods for Inductance Calculation Robert Weaver 2012
3. Inductance Calculation Techniques — Part II: Approximations and Handbook Methods Marc T. Thompson 1999
4. A new method for inductance calculation M.A.Bueno A K T Assis 1995

coil32.ru

справка, Расчет многослойной катушки на прямоугольном каркасе

Подробности

Опубликовано: 20 февраля 2016

Просмотров: 3911

 

Столкнувшись с трудностями при расчете многослойной катушки на круглом каркасе, мы отказались от простой эмпирической формулы Вилера и пошли по пути усложнения модели катушки и алгоритма расчета. В случае с многослойной катушкой на прямоугольном каркасе, которая довольно часто используется, совершенно очевидно, что следует пойти аналогичным путем. При этом катушку можно представить как набор соосных прямоугольных рамок и рассчитывать общую индуктивность катушки как сумму их собственных и взаимных индуктивностей.

Но мы можем пойти дальше и представить катушку как набор линейных проводов. Каждый виток представляет из себя набор из четырех таких отрезков. Причем взаимно-перпендикулярные отрезки  не взаимодействуют между собой и их взаимная индуктивность равна нулю. Пользуясь тем, что прямоугольник — симметричная фигура, мы можем провести вычисления только для двух его сторон. Удвоив результат вычислений, мы получим общую индуктивность катушки. На следующем рисунке изображены два параллельных отрезка провода неодинаковой длины для наглядности и понимания формул расчета.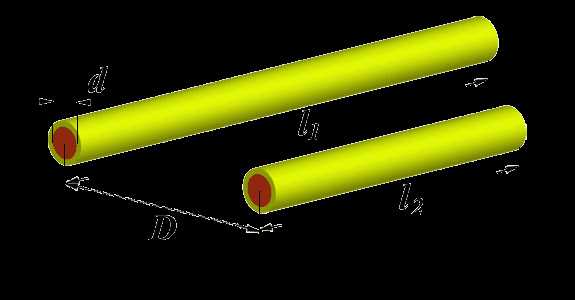
Для таких расчетов нам необходимо знать следующее…

1. Формулу собственной индуктивности отрезка провода:

   [1]

   где:
   • L — индуктивность [мкГн]
   • l = l₁ или l = l₂ — длина проводника [мм];
   • r = d/2 — радиус проводника [мм];
   
   Более известна формула, которая является упрощением вышеприведенной, но мы ее не используем, как менее точную:

   [2]

2. Формулу взаимной индуктивности двух отрезков провода неодинаковой длины:

   [3]

   где:
   • M — величина взаимоиндукции [мкГн];
   • x₁ = l₁/2 — половина длины первого проводника [мм];
   • x₂ = l₂/2 — половина длины второго проводника [мм];
   • D — расстояние между центрами проводников [мм];
   
   Формула верна для проводников центры которых лежат на одной оси, что у нашей катушки, в принципе, имеет место.

---

Катушка рассчитывается численным методом «виртуальной намотки». При добавлении нового витка, рассчитывается собственная индуктивность всех его отрезков, а также возможная взаимоиндукция со всеми другими отрезками с учетом взаимного направления тока в них. В общей сумме мы получаем собственную индуктивность многослойной катушки. Попутно рассчитывается длина провода, необходимая для намотки и его сопротивление постоянному току. Кроме плагина multi_rectangular к программе Coil32 для Windows, который доступен для загрузки из меню программы и рассчитывает такую катушку индуктивности, вы можете воспользоваться онлайн калькулятором многослойной катушки на прямоугольном каркасе.

Реальный виток имеет скругленные углы, а не представляет из себя идеальный прямоугольник. Это обстоятельство, а также ограниченная точность исходных формул, не позволяют достичь высокой точности расчетов. Погрешность расчета составляет около ±5% от величины индуктивности. Имеется ввиду, что намотка плотная, без зазоров и межслойных прокладок. Несмотря на невысокую точность, этот численный алгоритм позволяет рассчитать произвольную многослойную катушку на прямоугольном каркасе не прибегая к поиску сложных эмпирических формул, всегда имеющих ограничения по геометрии намотки. С помощью данного алгоритма, например, мы можем без труда рассчитать индуктивность многовитковой прямоугольной рамки большого диаметра.

Ссылки по теме:

1. The self and mutual inductances of linear conductors. (E. B. Rosa 1908) — формулы индуктивности и взаимоиндукции линейных проводников, формула [1] в статье соответствует фомуле 9 на стр.305. Формула собственной индуктивности линейного отрезка провода.
2. American National Bureau of Standarts circular C74 — формула [3] в статье соотвествует формуле 182 на стр.273 с исправлениями. Формула взаимоиндукции двух симметрично расположенных линейных проводников неодинаковой длины.

Добавить комментарий

coil32.ru