Равнопеременное прямолинейное движение – Равнопеременное прямолинейное движение | Физика для всех

Равнопеременное прямолинейное движение | Физика для всех

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.

vcp = s / t

Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

Проекция вектора скорости на ось ОХ:

vx = x’

это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

 

Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

vx = v0x ± axt

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

Рис. 1.15. Зависимость ускорения тела от времени.

Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).

Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

0a = v0
bc = v

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а_x < 0 и х₀ = 0 ветви параболы направлены вниз (рис. 1.18).

av-mag.ru

Равнопеременное движение. Ускорение. | Объединение учителей Санкт-Петербурга

Равнопеременное движение. Ускорение.
Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением.
Обозначим: — вектор начальной скорости,  — изменение скорости, а Δt — промежуток времени. Пусть  Δt1= Δt2=Δt3=…, тогда по определению
Следовательно,   Т.о., это характеристика движения.
Если t0=0, то
УСКОРЕНИЕ — физическая величина, характеризующая быстроту изменения скорости и (при равнопеременном движении) численно равная отношению вектора изменения скорости к промежутку времени, в течение которого это изменение произошло.
Ускорение при равнопеременном движении показывает, насколько меняется мгновенная скорость движения тела за единицу времени. Единица ускорения в СИ —    м/с2.	Например, ускорение равно 5 м/с2  — это значит, что, двигаясь равноускоренно, тело изменяет скорость на 5 м/с за каждую секунду своего движения.
В случае не равнопеременного движения: тогда мгновенное ускорение
Равнопеременное движение называется равноускоренным, если модуль скорости возрастает.	Условие р.у.д. —.
Равнопеременное движение называется равнозамедленным, если модуль скорости уменьшается.	Условие р.з.д. — .
Графики равнопеременного движения.
или  — в проекциях; или – через модули.
Линейная функция. График — прямая.
Движения, совпадающие с направлением координатной оси: равноускоренноес начальной скоростью равноускоренное без начальной скорости равнозамедленное Движения против координатной оси. равнозамедленное равноускоренное без начальной скорости равноускоренное с начальной скоростью
Перемещение при равнопеременном движении.
Площадь под графиком скорости численно равна перемещению. Следовательно, площадь трапеции численно равна перемещению.
	Решение основной задачи механики для р.у.д. :
Графики перемещения и координаты.
Функции   и   — квадратичные. График – парабола!

www.eduspb.com

Репетитор-онлайн — подготовка к ЦТ

Пример 2. Материальная точка движется вдоль оси Ox. Проекция ее скорости с течением времени меняется по закону v = 9,0 − 1,5t, где скорость задана в метрах в секунду, время — в секундах. Определить путь, пройденный материальной точкой за интервал времени от 4,0 с до 7,0 с.

Решение. При равнопеременном движении зависимость проекции скорости от времени имеет вид:

v_x = v_0x + a_xt,

где v_0x = 9,0 м/с — проекция начальной скорости; a_x = −1,5 м/с² — проекция ускорения на указанную координатную ось.

Запишем уравнение движения материальной точки:

x(t)=x0+v0xt+axt22=x0+9,0t−0,75t2,

где x0 — начальная координата точки.

Точка остановки, вычисленная по формуле

τост=v0a=9,01,5=6,0 c,

попадает в интервал времени, указанный в условии задачи.

В интервале времени от t1 = 4,0 c до τост = 6,0 с точка движется равнозамедленно. Следовательно, пройденный путь вычисляем по формуле

S1=|x(τост)−x(t1)|,

где

x(τост)=x0+9,0τост−0,75τост2=

=x0+9,0⋅6,0−0,75⋅(6,0)2=(x0+27) м;

x(t1)=x0+9,0t1−0,75t12=x0+9,0⋅4,0−0,75⋅(4,0)2=(x0+24) м.

Таким образом, путь S1, пройденный материальной точкой в указанном интервале времени, равен:

S1=|x(τост)−x(t1)|=|(x0+27)−(x0+24)|=3,0 м.

В интервале времени от τост = 6,0 с до t2 = 7,0 c точка движется равноускоренно. Следовательно, пройденный путь вычисляем по формуле

S1=|x(t2)−x(τост)|,

где

x(τост)=x0+9,0τост−0,75τост2=

=x0+9,0⋅6,0−0,75⋅(6,0)2=(x0+27) м;

x(t2)=x0+9,0t2−0,75t22=

=x0+9,0⋅7,0−0,75⋅(7,0)2=(x0+26,25) м.

Таким образом, путь S₂, пройденный материальной точкой в указанном интервале времени, равен:

S2=|x(t2)−x(τост)|=|(x0+26,25)−(x0+27)|=0,75 м≈0,8 м.

Суммарный путь S, пройденный материальной точкой в интервале времени от 4,0 с до 7,0 с, составляет

S=S1+S2≈3,0+0,8=3,8 м.

vedy.by

Равнопеременное движение. Законы и уравнения. Видеоурок. Физика 11 Класс

На этом уроке мы рассмотрим уравнения равнопеременного движения вдоль его траектории, то есть движения с постоянным ускорением. Также на этом уроке будут подробно показаны решения четырёх типовых задач на равнопеременное движение различной сложности, которые взяты из сборника задач для подготовки к единому государственному экзамену

Равнопеременное движение – это движение с постоянным ускорением.

 

1. Уравнение скорости в любой момент времени:

,

где  – начальная скорость;  – время.

2. Формулы пути:

—  

— ,

где  – конечная скорость.

—  

—  

3. Пути, пройденные за последовательные равные промежутки времени, составляют ряд нечётных чисел:

,

где  – путь, пройденный за n-ый промежуток времени;  – путь, пройденный за первый промежуток времени.

 

4. Равнопеременное движение, происходящее по прямой линии, описывается с помощью уравнения в проекциях на координатную ось, которую совмещают с траекторией движения.

 

 ,

где  – проекция начальной скорости на ось;  – проекция ускорения на ось.

Координата тела вдоль выбранной координатной оси изменяется по такому закону:

,

где   – начальная координата.

Поезд при скорости  начал тормозить с ускорением . Найти время торможения. Варианты ответа: 1. 25 с; 2. 30 с; 3. 50 с; 4. 90 с. Чему равен тормозной путь поезда?

Дано: ; ;

Найти:

Решение

Из формулы

 

Выразим время:

 

Пройденный путь равен:

 

Ответ: 1. 25 с;

Пуля, летящая со скоростью , попадает в доску и проникает на глубину 6 см. Если пуля в доске двигается равнозамедленно, то на глубине 3 см её скорость была равна: 1. ; 2. ; 3. ; 4. .

Дано: ; ; ; ;

Найти:

Решение

Для нахождения скорости воспользуемся формулой пути, в которой фигурирует конечная, начальная скорость и ускорение.

 

 

Разделим первое уравнение на второе и учтём, что  больше  в два раза:

 

 

Так как , то:

 

 

 

 

Ответ: 2.

Тело начало двигаться из состояния покоя с ускорением . Какой путь оно пройдёт за четвёртую секунду движения?

Дано: ; ; ;

Найти:

Решение

Для решения данной задачи воспользуемся следующей формулой:

 

В эту формулу подставим известные данные:

 

Ответ:  

Свободно падающее без начальной скорости тело за последнюю секунду прошло путь на  больший, чем в предыдущую. С какой скоростью оно упало на землю? С какой высоты падало тело? Чему равно время падения тела?

Дано:  – путь, пройденный за последний (n-ый) промежуток времени; ; ;

Найти: ; ;

Решение

С учетом того, что начальная скорость равна нулю:

— скорость падения равна:

 

— высота, с которой тело упало (пройденный путь):

 

Время падения можно записать как:

 

Путь, пройденный за последний (n-ый) промежуток времени, равен:

 

Путь, пройденный за предыдущую секунду (-ый промежуток времени), равен:

 

По условию задачи:

 

Следовательно:

 

 

Сократим обе части выражения на :

 

 

 

Следовательно, тело падало:

 

Подставляем это время в формулу высоты падения:

 

Подставляем время падения в формулу скорости падения:

 

Ответ: ; ;  

 

Домашнее задание

1. Упражнение 3 (1, 2) стр. 36 – Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотс

interneturok.ru

3. Равномерное прямолинейное движение.

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

v_cp = v

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:

V(вектор) = s(вектор) / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

s(вектор) = V(вектор)  • t

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

v_x = v, то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x – x₀

где x₀ – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x₀ + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x₀ — vt

4. Равнопеременное движение.

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.

v_cp = s / t

Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

V=lim(^t-0) ^s/^t

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

V(вектор) = s’(вектор)

Проекция вектора скорости на ось ОХ:

v_x = x’

это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

а(вектор) = lim (t-0) ^v(вектор)/^t

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

a(вектор) = v(вектор)’ = s(вектор)»

Учитывая, что ₀ – скорость тела в начальный момент времени (начальная скорость), – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости,формула ускорения будет следующей:

a(вектор) = v(вектор)-v0(вектор)/t

Отсюда формула скорости равнопеременного движения в любой момент времени:

v(вектор) = v₀(вектор) + a(вектор)t

Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

v_x = v_0x ± a_xt

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

  Рис. 1.15. Зависимость ускорения тела от времени.

Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).

  Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

0a = v₀

bc = v

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

  Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

  Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а_x < 0 и х₀ = 0 ветви параболы направлены вниз (рис. 1.18).

studfiles.net

2) Прямолинейное равнопеременное движение. При таком виде движения

Если начальный момент времени, а начальная скоростьто, обозначив

иполучимоткуда

Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, найдем, что длина пути, пройденного точкой, в случае равнопеременного движения

Рис. 5

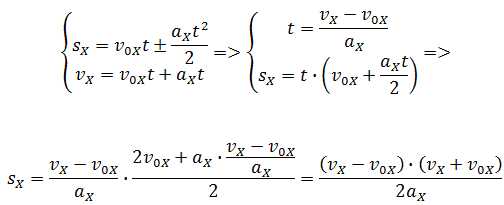
3)— прямолинейное движение с переменным ускорением;

4)Прискорость по модулю не изменяется, а изменяется по направлению. Из формулыследует, что радиус кривизны должен быть посто­янным. Следовательно, движение по окружности является равномерным;

5)— равномерное криволинейное движение;

6)— криволинейное равнопеременное движение;

7)— криволинейное движение с переменным ускорением.

§ 4. Угловая скорость и угловое ускорение

Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдель­ные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис. 6). Ее положение через промежуток временизададим угломЭлементар­ные (бесконечно малые) повороты можно рассматривать как векторы (они обозначают­сяилиМодуль вектораравен углу поворота, а его направление совпадаетс направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т. е. подчиняется правилу правого винта (рис. 6). Векторы, направления которых связываются с направлением вращения, назы­ваются псевдовекторами или аксиальными векторами. Эти векторы не имеют опреде­ленных точек приложения: они могут откладываться из любой точки оси вращения.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

Векторнаправлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор(рис. 7). Размерность угловой скорости, а ее единица — ради-

ан в секунду (рад/с).

Линейная скорость точки (см. рис. 6)

т. е.

В векторном виде формулу для линейной скорости можно написать как векторное произведение:

При этом модуль векторного произведения, по определению, равен

а направление совпадает с направлением поступательного движения правого винта при

его вращения от

Еслито вращение равномерное и его можно характеризовать периодом

вращения Т — временем, за которое точка совершает один полный оборот, т. с. поворачивается на уголТак как промежутку временисоответствует

тооткуда

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

откуда

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении векторсонаправлен вектору(рис. 8), при замедлен­ном — противонаправлен ему (рис. 9).

Тангенциальная составляющая ускорения

Нормальная составляющая ускорения

Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скоростьтангенциальное ускорениенормальноеускорениеи угловыми величинами (угол поворотаугловая скоростьугловоеускорениевыражается следующими формулами:

В случае равнопеременного движения точки по окружности

где— начальная угловая скорость.

studfiles.net

1.3. Прямолинейное равнопеременное движение

При рассмотрении равномерного прямолинейного движения допускалось, что его скорость во всех точках на участке движения остаётся постоянной по направлению и величине; .Однако на участке начала движения скорость изменяется от нуля до необходимого значения, тогда как на участке окончания движения уменьшается до нуля. Не вдаваясь пока в причины неравномерности движения на начальном и конечном участках движения, можно ожидать, что должна быть физическая величина, характеризующая быстроту изменения скорости. Количественная математика подсказывает, если мы знаем величину изменения скорости и промежуток времени, в течение которого это изменение скорости произошло t  t₂ – t₁, то быстрота изменения скорости может быть найдена математической операцией деления. Отношение изменения скорости к промежутку времени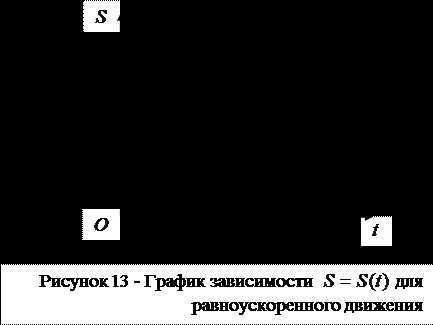,за которое это изменение произошло, называется ускорением. В символическом представлении ускорение запишется так: 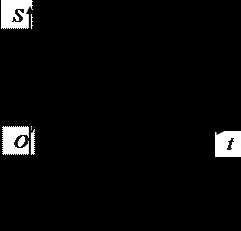.Поскольку скорость величина векторная, ускорение также является векторной величиной; кроме численного значения новая физическая величина имеет направление. В частности, в приведённом примере на участке начала движения направление вектора ускорения совпадает с направлением вектора скорости, тогда как на участке прекращения движения – противоположно по направлению вектору скорости (отобразите на рисунке). Из символической записи ускорения следует, оно измеряется в метрах на секунду в квадрате (м/с²).

Основная задача кинематики – определить положение движущегося тела в пространстве в любой момент времени. Для этого необходимо знать закон изменения положения движущегося тела, ;закон движения. Найдём для равнопеременного движения уравнение, отражающее изменение координаты (положения) тела в пространстве с течением времени.

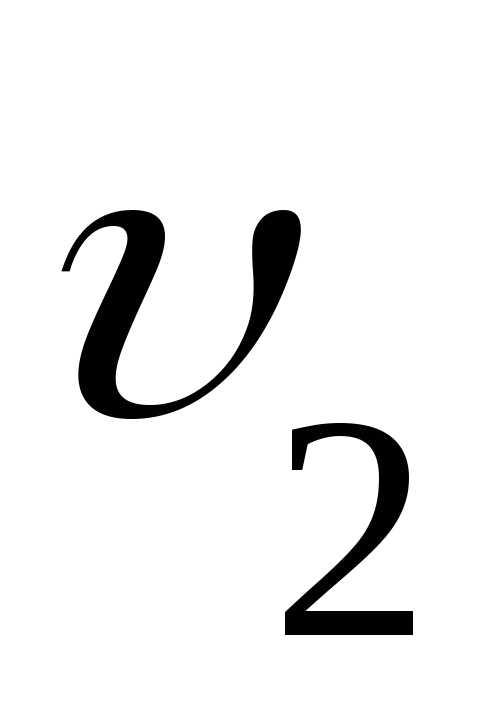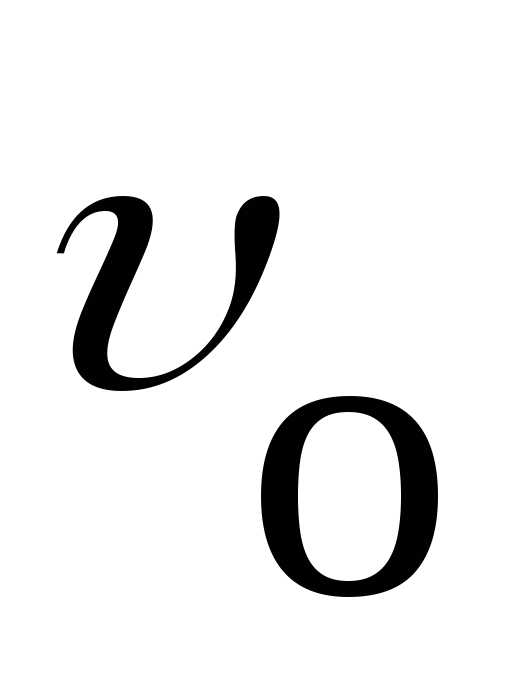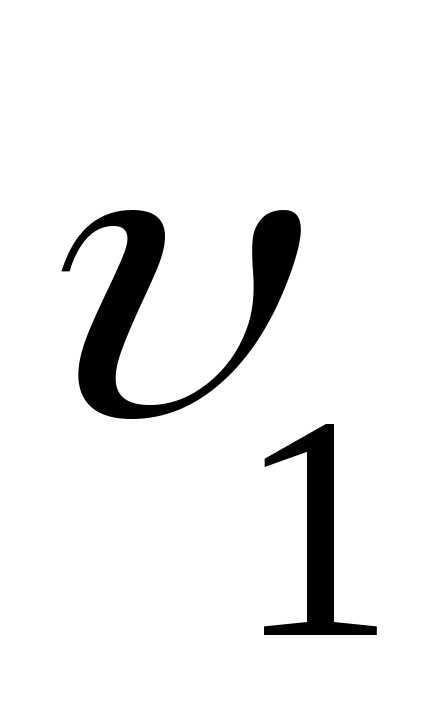Символическое представление ускорения позволяет записать уравнение скорости как функцию времени: .Здесь – отображает скорость ,с которой будет двигаться тело через время t после начала отсчёта; – представляет скорость ,с которой двигалось тело в тот момент, когда запустили время отсчёта. Эти пояснения важны, когда кратко записывается «дано» из условия задачи.

Из уравнения скорости следует, для равнопеременного движения скорость является линейной функцией времени. Из алгебры известно, среднее значение линейной функции равно половине суммы её начального и конечного значений на любом временном интервале. В этом случае средняя скорость равнопеременного движения запишется: .Это позволяет записать закон изменения положения движущегося тела при равнопеременном движении в виде: 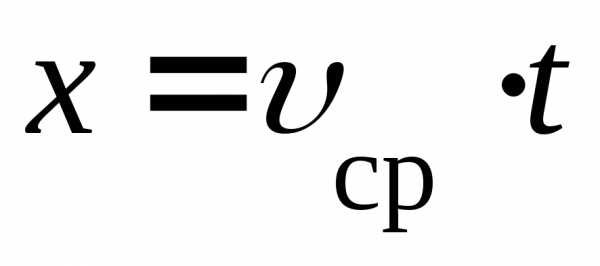.Если учесть символическую запись средней скорости, уравнение равнопеременного движения примет вид: 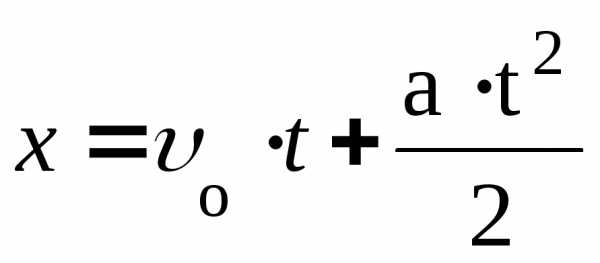(самостоятельно преобразования проделали?). 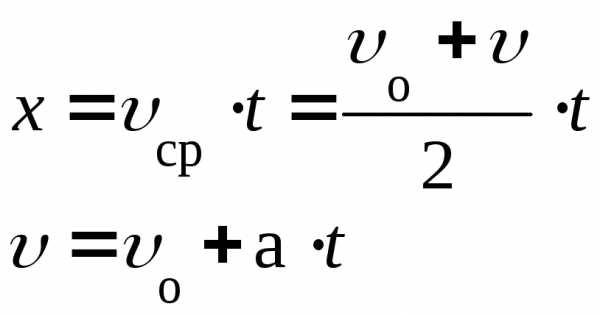Для этого необходимо записать систему из двух уравнений и преобразовать её. Удачи!

Решение задач равнопеременного движения сложнее. Почему? Во-первых, возникает необходимость в двух уравнениях – координаты и скорости. Во-вторых, чтобы записать уравнения, необходимо сделать чертёж для правильного понимания условия задачи. И, в-третьих, чертёж помогает записать промежуточные математические операции, без которых подчас нельзя определить «скрытый» параметр. Например: С крыши дома высотой 16 метров через равные промежутки времени падают капли воды, причём первая ударяется о землю в тот момент, когда пятая отделяется от крыши. Найти расстояние четвёртой капли от крыши в момент удара первой капли о землю.Если нарисовать чертёж, из него следует, первая капля падала четыре равных промежутка времени. Об этих равных промежутках времени упоминается в условии задачи. Следовательно, четвёртая капля падала в течение одного промежутка времени. Найти время падения первой капли просто: вблизи земли все тела падают с известным ускорением свободного падения; высота падения известна; начальная скорость оговорена словом «отделяется», то есть без … Догадались? Удачи. Кстати, вопрос задачи можно переформулировать:Найти расстояние между четвёртой и первой каплей в момент удара первой капли о землю.

Итак, решение задач равнопеременного движения позволяет приобрести навыки понимания текста, осуществлять поиск заданных физических величин, формировать аналитическую запись происходящего в задаче.

Завершая экскурс в раздел кинематики «равнопеременное движение», перечислим его ключевые слова: скорость, изменение скорости, ускорение, уравнение скорости, уравнение движения.

studfiles.net