Резонанс в электрической цепи
Начнём с основных определений.
Определение 1
Резонанс — это явление, при котором частота колебаний какой-либо системы увеличивается колебаниями внешней силы.
Вынужденные колебания, источником которых является внешняя сила, увеличивают даже те колебания, амплитуда которых имеет довольно небольшие значения. Максимальный резонанс с наибольшей амплитудой возможен именно при совпадении частот внешнего воздействия и рассматриваемой системы.
Примером резонанса является раскачивание моста ротой солдат. Частота шага солдат, являющаяся по отношению к мосту примером вынужденных колебаний, при этом синхронизирована и может совпасть с собственной частотой колебаний моста. В результате мост может разрушиться.
Электрический резонанс в физике считается одним из распространенных в мире физических явлений, без которого было бы невозможным, например, телевидение и диагностика с помощью медицинских аппаратов.
Одними из наиболее полезных видов резонанса в электрической цепи являются:
- резонанс токов;
- резонанс напряжений.
Возникновение резонанса в электрической цепи
Замечание 1
Возникновению резонанса в электрической цепи способствует резкое увеличение амплитуды стационарных собственных колебаний системы при условии совпадения частоты внешней стороны воздействия и соответствующей колебательной резонансной частоты системы.
Схема $RLC$ представляет электрическую цепь с соединенными последовательным или параллельным образом элементами (резистора, индуктора, конденсатора). Название $RLC$ состоит из простых символов электрических элементов: сопротивления, емкости, индуктивности.
Векторная диаграмма последовательной $RLC$-цепи представлена в одной из трех вариаций:
- емкостной;
- активной;
- индуктивной.
В последней вариации резонанс напряжений возникает при условии нулевого сдвига фаз, и совпадении значений индуктивного и емкостного сопротивлений.
Резонанс напряжений
При последовательном соединении активного элемента $r$, емкостного $С$ и индуктивного $L$ в цепях переменного тока может возникать такое физическое явление, как резонанс напряжений. Колебания источника напряжения в этом случае будут равны по частоте колебаниям контура. При этом известна как полезность (например, в радиотехнике) этого явления, так и негативные последствия (для электрических установок большой мощности), например, при резком скачке напряжения в системах возможно возникновение неисправности или даже пожара.
Резонанс напряжений обычно достигается тремя способами:
- подбором индуктивности катушки;
- подбором емкости конденсатора;
- подбором угловой частоты $w_0$.
При этом все значения емкости, частоты и индуктивности определяются с использованием формул:
$L_0 = \frac{1}{w^2C}$
$C_0 = \frac{1}{w^2L}$
Частота $w_0$ считается резонансной. При условии неизменности в цепи и напряжения, и активного сопротивления $r$, сила тока при резонансе напряжения в ней окажется максимальной и равной:
$\frac{U}{r}$
Это предполагает полную независимость силы тока от реактивного сопротивления цепи. В ситуации, когда реактивные сопротивления $XC = XL$ по своему значению будут превосходить активное сопротивление $r$, на зажимах катушки и конденсатора появится напряжение, существенно превосходящее напряжение на зажимах цепи.
Кратность превышения на зажимах емкостного и индуктивного элемента напряжения по отношению к сети определяется выражением:
$Q = \frac{U_c0}{U}$
Величина $Q$ характеризует резонансные свойства контура, называясь при этом добротностью контура. Также резонансные свойства характеризуются величиной $\frac{1}{Q}$, то есть — затуханием контура.
Резонанс токов через реактивные элементы
Резонанс токов появляется в электроцепях цепях переменного тока при условии параллельного соединения ветвей с разнохарактерными реактивными сопротивлениями. В резонансном режиме токов реактивная индуктивная проводимость цепи будет равнозначной ее собственной реактивной емкостной проводимости, т.е. $BL = BC$.
Колебания контура, частота которых имеет определённое значение, в данном случае совпадают по частоте с источником напряжения.
Простейшей электроцепью, в которой мы наблюдаем резонанс токов, считается цепь с параллельным соединением конденсатора с катушкой индуктивности.
Поскольку сопротивления реактивности равнозначны по модулю, амплитуды токов $I_c$ и $I_u$ будут одинаковыми и смогут достигать максимальной амплитуды. На основании первого закона Кирхгофа $IR$ равен току источника. Ток источника, иными словами, протекает только через резистор. При рассмотрении отдельного параллельного контура $LC$, на резонансной частоте его сопротивление оказывается бесконечно большим: $ZL = ZC$. При установлении гармонического режима с резонансной частотой, в контуре наблюдается обеспечение источником установившейся определенной амплитуды колебаний, а мощность источника тока при этом расходуется исключительно на пополнение потерь в активном сопротивлении.
Таким образом, у последовательной $RLC$ цепи импеданс оказывается минимальным на резонансной частоте и равным активному сопротивлению контура. В то же время, у параллельной $RLC$ цепи импеданс максимальный на резонансной частоте и считается равным сопротивлению утечки, фактически также активному сопротивлению контура. С целью обеспечения условий для резонанса силы тока или напряжения, требуется проверка электрической цепи для предопределения ее комплексного сопротивления или проводимости. Помимо этого, её мнимая часть должна приравниваться к нулю.
Применение явления резонанса
Хороший пример использования резонансного явления представляет электрический резонансный трансформатор, разработанный Николой Тесла ещё в 1891 году. Ученый проводил эксперименты на разных конфигурациях, состоящих в сочетании из двух, а зачастую и трех резонансных электроцепей.
Замечание 2
Термин «катушки Теслы» применяют к высоковольтным резонансным трансформаторам. Устройства используют при получении высокого напряжения, частоты переменного тока. Обычный трансформатор необходим для эффективной передачи энергии с первичной на вторичную обмотку, резонансный используется для временного хранения электроэнергии.
Устройство отвечает за управление воздушным сердечником настроенного резонансно трансформатора с целью получения высоких напряжений при малых значениях силы токов. Каждая обмотка обладает емкостью и функционирует в качестве резонансного контура. Для произведения наибольшего выходного напряжения первичный и вторичный контуры настраивают в резонанс друг с другом.
spravochnick.ru
Резонанс напряжений в электрической цепи и его последствия
В цепях переменного тока при последовательном соединении активного элемента r, емкостного С и индуктивного L может возникнуть такое явление как резонанс напряжений. Это явление можно использовать с пользой (например, в радиотехнике), но также оно может и нанести серьезный вред (в электрических установках большой мощности резонанс напряжений может вызвать серьезные последствия).
Принципиальная схема и векторная диаграмма при резонансе напряжений показаны ниже:

При последовательном включении всех трех элементов данной электрической цепи будет справедливо следующее:

Также нужно помнить, что резонанс возможен только при φ = 0, что при последовательном соединении равносильно вот такому соотношению х = ωL – 1/(ωC) = 0, то есть должно выполняться условие ωL = 1/(ωC) или ω2LC = 1. Резонанса напряжений можно достичь тремя способами:
- Подобрать индуктивность катушки;
- Подобрать емкость конденсатора;
- Подобрать угловую частоту ω0;
Причем все эти значения частоты, емкости и индуктивности можно определить используя формулы:

Частота ω0 носит название резонансной частоты. Если в цепи не изменяется ни напряжение, ни активное сопротивление r, то при резонансе напряжения ток в этой цепи будет максимален, и равен U/r. Это значит, что ток будет полностью не зависим от реактивного сопротивления цепи. В случае же, когда реактивные сопротивления X C = XL будут превосходить по своему значению активное сопротивление r, то на зажимах катушки и конденсатора начнет появляться напряжение, значительно превосходящее напряжение на зажимах цепи. Условие, при котором напряжение на зажимах цепи будет меньше напряжения реактивных элементов будет иметь вид:

Величина  , имеющая размерность сопротивления и для удобства расчетов обозначена нами как ρ, называется волновым сопротивлением контура.
, имеющая размерность сопротивления и для удобства расчетов обозначена нами как ρ, называется волновым сопротивлением контура.
Кратность превышения напряжения на зажимах емкостного и индуктивного элемента по отношению к сети можно определить из выражения:

Величина Q определяет резонансные свойства контура и носит названия добротность контура. Также еще резонансные свойства могут характеризовать величиной 1/Q – затухание контура.
Мгновенная мощность для индуктивности и емкости будет равна pL = ULIsin2ωt и pС = -UСIsin2ωt. При резонансе напряжения, когда UL = UС, эти мощности будут равны в любой момент времени и противоположны по знаку. А это означает, что в данной цепи будет происходит обмен энергией между магнитным полем катушки и электрическим полем конденсатора, при этом обмена энергией между энергией полей и энергией источника электрической энергии (источника питания) и не происходит. Это вызвано тем, что p L + pС = dWм/dt + dWэ/dt и Wм + Wэ = const, то есть суммарная энергия полей в цепи постоянна. При работе такой системы энергия от конденсатора будет переходить в катушку в течении четверти периода, когда ток на катушке возрастает, а напряжение на конденсатора снижается. В течении следующей четверти периода картина противоположна – ток катушки будет снижаться, а напряжения конденсатора расти, то есть энергия от индуктивности будет переходить емкости. При этом источник электрической энергии, питающий данную цепь, будет покрывать только расход энергии, связанный с наличием в цепи активного сопротивления r.
elenergi.ru
Резонансные режимы работы электрических цепей
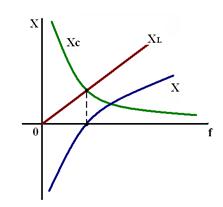
Пусть пассивный двухполюсник содержит одну или несколько индуктивностей и один или несколько конденсаторов. Под резонансным режимом работы такого двухполюсника понимают режим (режимы) двухполюсника при котором входное сопротивление является чисто активным. По отношению к внешней цепи двухполюсник ведет себя как активное сопротивление, вследствие чего входные напряжение и ток совпадают по фазе. Различают две разновидности резонансных режимов: резонанс напряжения и резонанс тока.
Резонанс напряжений
В простейшем случае резонанс напряжений может быть получен в электрической цепи переменного тока при последовательном включении катушки индуктивности и конденсаторов. При этом, изменяя емкость конденсаторов при постоянных параметрах катушки, получают резонанс напряжений при неизменных значениях напряжения и индуктивности, частоты и активного сопротивления цепи. При изменении емкости конденсаторов Спроисходит изменение реактивного емкостного сопротивления. При этом полное сопротивление цепи также изменяется, следовательно, изменяются ток, коэффициент мощности, напряжения на катушке индуктивности, конденсаторах, а также активная, реактивная и полная мощности электрической цепи. Зависимости токаI, коэффициента мощности cosи полного сопротивления
Как видно из этой диаграммы, реактивная составляющая напряжения ULна катушке при резонансе равна напряжениюUСна конденсаторе. При этом напряжение на катушке индуктивностиUкпри резонансе вследствие того, что катушка кроме реактивного сопротивленияXLобладает еще и активным сопротивлениемR, несколько больше, чем напряжение на конденсаторе.
Анализ представленных выражений (2), а также рис. 9,аибпоказывают, что резонанс напряжений имеет ряд отличительных особенностей.
1. При резонансе напряжений полное сопротивление электрической цепи переменного тока принимает минимальное значение и оказывается равным ее активному сопротивлению, т.е.

2. Из этого следует, что при неизменном напряжении питающей сети (U= const) при резонансе напряжений ток в цепи достигает наибольшего значенияI =U/Z =U/R. Теоретически ток может достигать больших значений, определяемых напряжением сети и активным сопротивлением катушки.
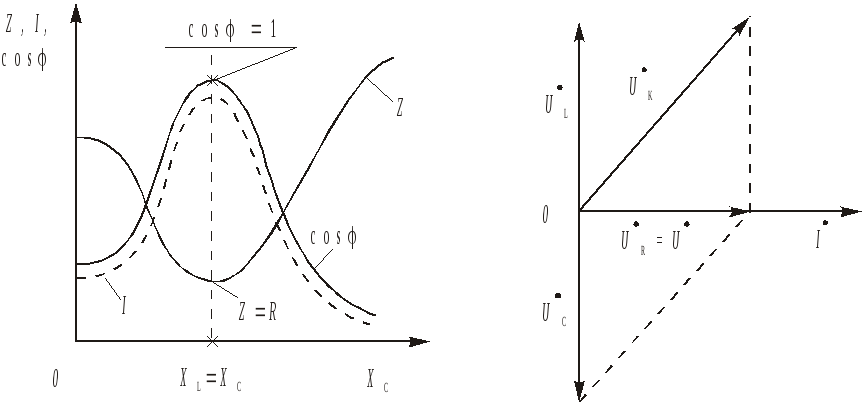
а)б)
Рис. 9
3. Коэффициент мощности при резонансе
cos=R/Z =R/R = 1,
т.е. принимает наибольшее значение,
которому соответствует угол= 0.
Это означает, что вектор тока и вектор напряжения сети
и вектор напряжения сети
4. Активная мощность при резонансе P=RI 2имеет наибольшее значение, равное полной мощностиS, в то же время реактивная мощность цепиQ=XI 2= (XLXC)I 2оказывается равной нулю:Q =QLQC= 0.
5. При резонансе напряжений напряжения на емкости и индуктивности оказываются равными UС=UL=XCI =XLIи в зависимости от тока и реактивных сопротивлений могут принимать большие значения, во много раз превышающие напряжение питающей сети. При этом напряжение на активном сопротивлении оказывается равным напряжению питающей сети, т.е.UR=U.
Резонанс напряжений в промышленных электротехнических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденсаторов при возможном перенапряжении на отдельных участках цепи. В то же время резонанс напряжений широко используется в различного рода приборах и устройствах электроники.
studfile.net
6 Резонансные режимы в электрических цепях синусоидального тока » СтудИзба
ЛЕКЦИЯ 6
Резонансные режимы в электрических цепях синусоидального тока.
Резонанс напряжений
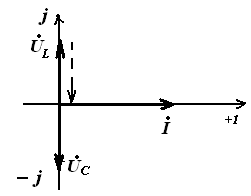
Режим работы RLC цепи или LC—цепи, при условии равенства реактивных сопротивлений XC= XL, когда общее напряжение цепи совпадает по фазе с её током  , называется резонансом напряжения.
, называется резонансом напряжения.
XC= XL – условие резонанса


RLC цепь LC цепь.
Признаки резонанса напряжения:
1. Напряжение на входе совпадает по фазе с током, т.е. сдвиг фаз между I и U φ = 0, cos φ = 1
2. Ток в цепи будет наибольшим и как следствие Pmax= I2maxR тоже максимальна, а реактивная мощность равна нулю.
3. Резонансная частота 
4. 
Резонанс можно достигнуть, изменяя L, C или ω.
Векторные диаграммы при резонансе напряжений
LC цепь RLC цепь

Случаи других режимов работы RLC цепи
- Если XL>XC т.е.


 U опережает I, значит цепь имеет активно-индуктивный характер
U опережает I, значит цепь имеет активно-индуктивный характер
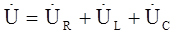 напряжение на катушке больше напряжения на конденсаторе.
напряжение на катушке больше напряжения на конденсаторе.
Векторная диаграмма

- Если XL<XC , т.е.


 U отстает от I, значит цепь имеет активно-емкостной характер
U отстает от I, значит цепь имеет активно-емкостной характер
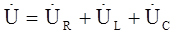 напряжение на конденсаторе больше напряжения на катушке.
напряжение на конденсаторе больше напряжения на катушке.
Векторная диаграмма

Параллельное соединение элементов в цепи синусоидального тока
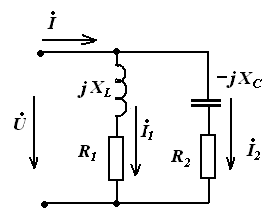
На входе параллельной цепи напряжение 
Закон Ома

Эквивалентные сопротивления ветвей:
Запишем эквивалентные проводимости:
 ;
; 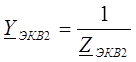
по первому закону Кирхгофа: 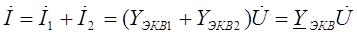
где 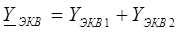
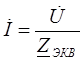 , где
, где 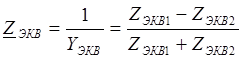
Треугольники проводимостей и токов
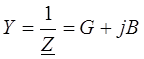 алгебраическая форма
алгебраическая форма
G – действительная часть, активная составляющая
B – мнимая часть, реактивная составляющая.
 ;
; 
или  ;
; 
Треугольник тока
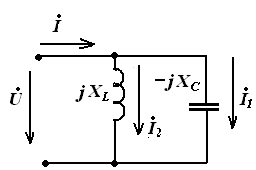
Резонанс токов
Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.
 Условие резонанса токов:
Условие резонанса токов: 
В1 – реактивная проводимость первой ветви,
В2 – реактивная проводимость второй ветви
Признаки резонанса токов:
- Реактивные составляющие токов ветвей равны IPC = IPL и находятся в противофазе в случае, когда напряжение на входе чисто активное;
- Токи ветвей превышают общий ток цепи, который имеет минимальное значение;
 и
и  совпадают по фазе
совпадают по фазе
RLC – цепь Векторная диаграмма
LC – цепь Векторная диаграмма

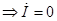
Резонансная частота
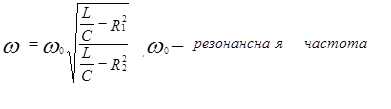 |
Случаи резонансных цепей
цепей
 |
Если R2=0 резонанс наступит, при
 Случаи резонанса токов
Случаи резонанса токов
Случай 1. Один резонанс в цепи, при условии:
Случай 2. Два резонанса в цепи, при определенном соотношении сопротивлений элементов
 Случай 3. Нет резонанса в цепи – частота является величиной неопределенной, при
Случай 3. Нет резонанса в цепи – частота является величиной неопределенной, при
Частотные характеристики колебательного контура
Баланс мощностей в цепях переменного тока
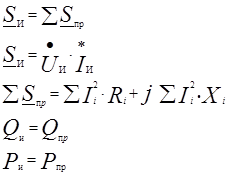 |
Коэффициент мощности
• Генератор или электрооборудование энергетически выгодно эксплуатировать, если оно совершает максимальную работу. Работа в электрической цепи определяется активной мощностью Р.
• Коэффициент мощности показывает, насколько эффективно используется генератор или электрооборудование
λ=P/S=cosφ≤1
С уменьшением коэффициента мощности стоимость потребляемой электроэнергии возрастает .
Способы увеличения коэффициента мощности
• Мощность максимальна в случае, когда Р = S, т.е. в случае резистивной цепи.
• Генератор осуществляет только необратимые преобразования энергии и не участвует в колебательных процессах обмена энергией с электромагнитным полем приемников, в режиме максимальной мощности.
• Потребители электрической энергии в основном имеют схему замещения RL элемента, поэтому увеличение коэффициента мощности возможен с помощью компенсации реактивной мощности подключением емкостного элемента (QL—QС), подключение емкостного элемента снижает ток в линии электропередачи, что позволяет уменьшить сечение электропроводов, а это приводит к экономии электропроводящих материалов.
• Значение коэффициента мощности в энергосистемах зависит насколько грамотно эксплуатируется электротехнические установки и приборы.
• сosφ может снижаться, если установки работают в режиме холостого хода, или недогружены.
studizba.com
условия возникновения и применение, как сделать самому, Ремонт и Строительство
Явление резонанса токов и напряжений наблюдается в цепях индуктивно-емкостного характера. Это явление нашло применение в радиоэлектронике, став основным способов настройки приемника на определенную волну. К сожалению, резонанс может нанести вред электрооборудованию и кабельным линиям. В физике резонансом является совпадение частот нескольких систем. Давайте рассмотрим, что такое резонанс напряжений и токов, какое значение он имеет и где используется в электротехнике.
Реактивные сопротивления индуктивности и емкости
Индуктивностью называется способность тела накапливать энергию в магнитном поле. Для нее характерно отставание тока от напряжения по фазе. Характерные индуктивные элементы — дросселя, катушки, трансформаторы, электродвигатели.

Емкостью называются элементы, которые накапливают энергию с помощью электрического поля. Для емкостных элементов характерно отставание по фазе напряжения от тока. Емкостные элементы: конденсаторы, варикапы.

Приведены их основные свойства, нюансы в пределах этой статьи во внимание не берутся.
Кроме перечисленных элементов другие также имеют определенную индуктивность и емкость, например в электрических кабелях распределенные по его длине.
Емкость и индуктивность в цепи переменного тока
Если в цепях постоянного тока емкость в общем смысле представляет собой разорванный участок цепи, а индуктивность — проводник, то в переменном конденсаторы и катушки представляют собой реактивный аналог резистора.
Реактивное сопротивление катушки индуктивности определяется по формуле:

Векторная диаграмма:

Реактивное сопротивление конденсатора:

Здесь w — угловая частота, f — частота в цепи синусоидального тока, L — индуктивность, C — емкость.
Векторная диаграмма:

Стоит отметить, что при расчете соединенных последовательно реактивных элементов используют формулу:

Обратите внимание, что емкостная составляющая принимается со знаком минус. Если в цепи присутствует еще и активная составляющая (резистор), то складывают по формуле теоремы Пифагора (исходя из векторной диаграммы):

От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока.
Если посмотреть на формулу реактивной составляющей, то можно заметить, что при определенных значениях емкостной или индуктивной составляющей их разность будет равна нулю, тогда в цепи останется только активное сопротивление. Но это не все особенности такой ситуации.
Резонанс напряжений
Если последовательно с генератором соединить конденсатор и катушку индуктивности, то, при условии равенства их реактивных сопротивлений, возникнет резонанс напряжений. При этом активная часть Z должно быть как можно меньшей.

Стоит отметить, что индуктивность и емкость обладает только реактивными качествами лишь в идеализированных примерах. В реальных же цепях и элементах всегда присутствует активное сопротивление проводников, хоть оно и крайне мало.
При резонансе происходит обмен энергией между дросселем и конденсатором. В идеальных примерах при первоначальном подключении источника энергии (генератора) энергия накапливается в конденсаторе (или дросселе) и после его отключения происходят незатухающие колебания за счет этого обмена.
Напряжения на индуктивности и емкости примерно одинаковы, согласно закону Ома:
U=I/X
Где X — это Xc емкостное или XL индуктивное сопротивление соответственно.
Цепь, состоящую из индуктивности и емкости, называют колебательным контуром. Его частота вычисляется по формуле:

Период колебаний определяется по формуле Томпсона:

Так как реактивное сопротивление зависит от частоты, то сопротивление индуктивности с ростом частоты увеличивается, а у ёмкости падает. Когда сопротивления равны, то общее сопротивление сильно снижается, что отражено на графике:

Основными характеристиками контура являются добротность (Q) и частота. Если рассмотреть контур в качестве четырехполюсника, то его коэффициент передачи после несложных вычислений сводится к добротности:
K=Q

А напряжение на выводах цепи увеличивается пропорционально коэффициенту передачи (добротности) контура.
Uк=Uвх*Q
При резонансе напряжений, чем выше добротность, тем больше напряжение на элементах контура будет превышать напряжение подключенного генератора. Напряжение может повышаться в десятки и сотни раз. Это отображено на графике:

Потери мощности в контуре обусловлены только наличием активного сопротивления. Энергия из источника питания берется только для поддержания колебаний.
Коэффициент мощности будет равен:
cosФ=1
Эта формула показывает, что потери происходят за счет активной мощности:
S=P/Cosф
Резонанс токов
Резонанс токов наблюдается в цепях, где индуктивность и емкость соединены параллельно.

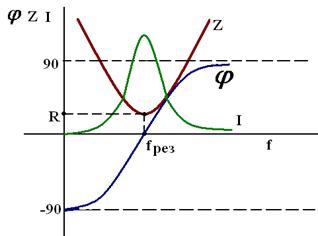
Явление заключается в протекании токов большой величины между конденсатором и катушкой, при нулевом токе в неразветвленной части цепи. Это объясняется тем, что при достижении резонансной частоты общее сопротивление Z возрастает. Или простым языком звучит так – в точке резонанса достигается максимальное общее значение сопротивления Z, после чего одно из сопротивлений увеличивается, а другое снижается в зависимости от того растет или снижается частота. Это наглядно отображено на графике:

В общем, всё аналогично предыдущему явлению, условия возникновения резонанса токов следующие:
- Частота питания аналогична резонансной у контура.
- Проводимости у индуктивности и ёмкости по переменному току равны BL=Bc, B=1/X.
Применение на практике
Рассмотрим, какая польза и вред резонанса токов и напряжений. Наибольшую пользу явления резонанса принесли в радиопередающей аппаратуре. Простыми словами, а схеме приемника установлены катушка и конденсатор, подключенные к антенне. С помощью изменения индуктивности (например, перемещая сердечник) или величины емкости (например, воздушным переменным конденсатором) вы настраиваете резонансную частоту. В результате чего напряжение на катушке повышается и приемник ловит определенную радиоволну.

Вред эти явления могут на нести в электротехнике, например, на кабельных линиях. Кабель представляет собой распределенную по длине индуктивность и емкость, если на длинную линию подать напряжение в режиме холостого хода (когда на противоположном от источника питания конце кабеля нагрузка не подключена). Поэтому есть опасность того, что произойдет пробой изоляции, во избежание этого подключается нагрузочный балласт. Также аналогичная ситуация может привести к выходу из строя электронных компонентов, измерительных приборов и другого электрооборудования – это опасные последствия возникновения этого явления.
Заключение
Резонанс напряжений и токов — интересное явление, о котором нужно знать. Он наблюдается только в индуктивно-емкостных цепях. В цепях с большим активным сопротивлениям он не может возникнуть. Подведем итоги, кратко ответив на основные вопросы по этой теме:
- Где и в каких цепях наблюдается явление резонанса?
В индуктивно-емкостных цепях.
- Какие условия возникновения резонанса токов и напряжений?
Возникает при условии равенства реактивных сопротивлений. В цепи должно быть минимальное активное сопротивление, а частота источника питания совпадать с резонансной частотой контура.
- Как найти резонансную частоту?
В обоих случаях по формуле: w=(1/LC)^(1/2)
- Как устранить явление?
Увеличив активное сопротивление в цепи или изменив частоту.
Теперь вы знаете, что такое резонанс токов и напряжений, каковы условия его возникновения и варианты применения на практике. Для закрепления материала рекомендуем просмотреть полезное видео по теме:
Материалы по теме:
www.remontostroitel.ru
Резонанс в электрических цепях
Резонанс в электрических цепях
Реактивное
сопротивление или проводимость
двухполюсника, в состав которого входят
конденсаторы и катушки индуктивности,
в зависимости от частоты приложенного
напряжения могут принимать как
положительные, так и отрицательные
значения. При определенных условиях
реактивное сопротивление (проводимость)
может оказаться равным нулю, а эквивалентное
сопротивление (проводимость) всей цепи
становится активным. В этом случае ток
и напряжение на входе цепи совпадают
по фазе. Такое явление называют резонансом,
а соотношение 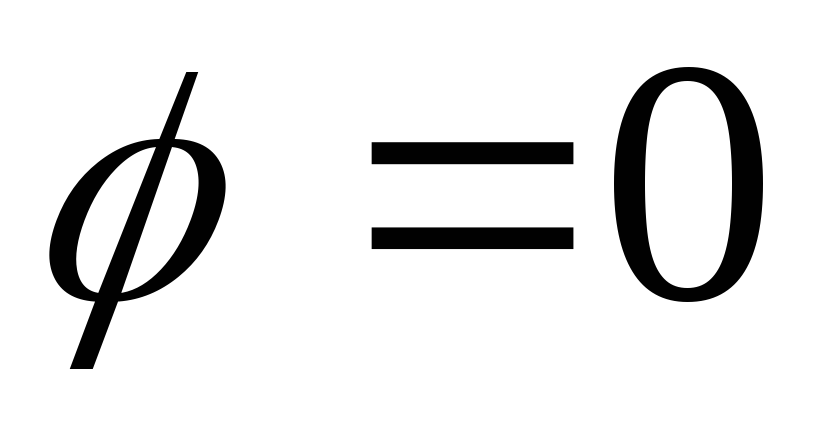 −условием
резонанса.
−условием
резонанса.
Эквивалентные параметры двухполюсника связаны соотношениями
 и
и  ,
,
поэтому
условие  эквивалентно выполнению равенств
эквивалентно выполнению равенств или
или .
.
Из
условий  ,
, могут быть определены значения параметров
элементов электрической цепи, при
которых наблюдается явление резонанса,
а также значения частотырезонанса.
могут быть определены значения параметров
элементов электрической цепи, при
которых наблюдается явление резонанса,
а также значения частотырезонанса.
Если
для двухполюсника  и
и ,
то для определения значений резонансных
частот может быть использовано любое
из условий
,
то для определения значений резонансных
частот может быть использовано любое
из условий или
или .
.
В
случае, когда активное эквивалентное
сопротивление или активная эквивалентная
проводимость двухполюсника равны нулю,
для определения значений резонансных
частот следует использовать оба условия  и
и ,
так как при этом
,
так как при этом .
Равенства
.
Равенства и
и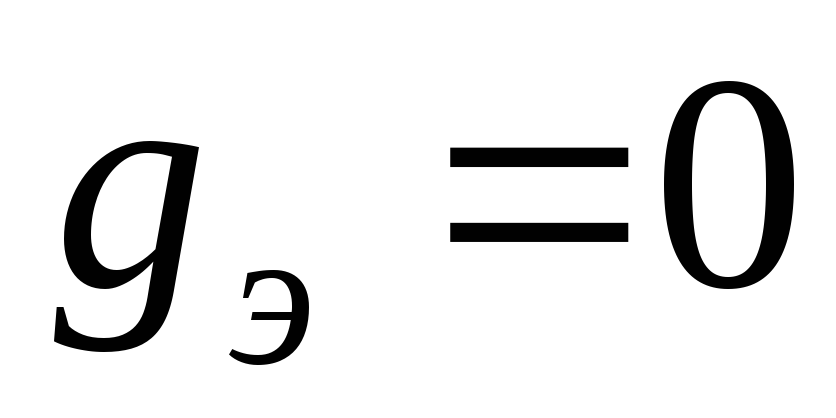 выполняются, в частности, для цепей,
содержащих только катушки индуктивности
и конденсаторы.
выполняются, в частности, для цепей,
содержащих только катушки индуктивности
и конденсаторы.
Для
описания частотных свойств электрических
цепей широко используются частотные
характеристики. Под частотными
характеристиками понимают зависимости
от частоты входных параметров цепи: r , x , z , g , b , y , а также
величин, определяемых этими параметрами  ,
,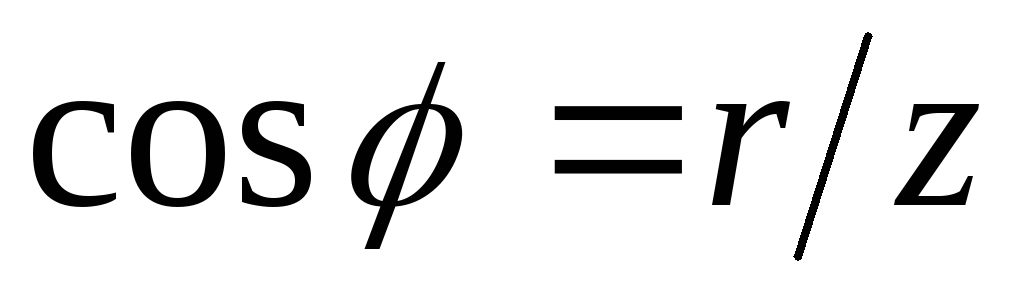 и т.д. Рассмотрим далее частотные
свойства простейших цепей, в которых
возможен резонанс.
и т.д. Рассмотрим далее частотные
свойства простейших цепей, в которых
возможен резонанс.
Резонанс в цепи при последовательном соединении элементов
Рассмотрим цепь, изображенную на рис. 10.1а
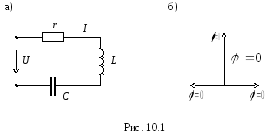
Комплексное сопротивление цепи равно

Угол
сдвига между входным током и напряжением  обращается в нуль при равенстве нулю
реактивного сопротивления цепи, то есть
при выполнении условия
обращается в нуль при равенстве нулю
реактивного сопротивления цепи, то есть
при выполнении условия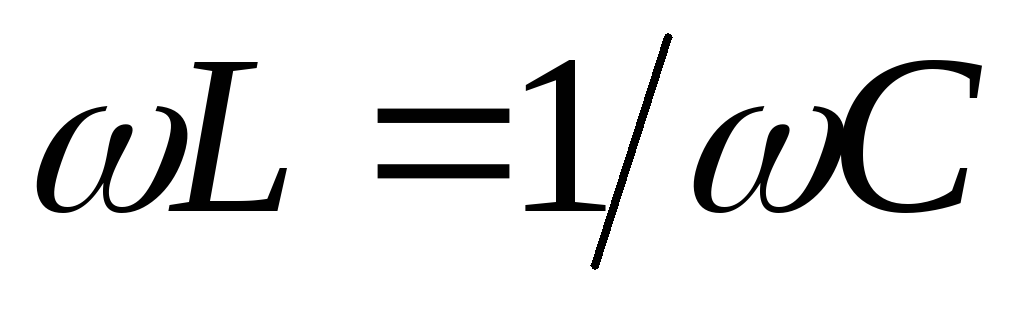 .
Таким образом, состояние резонанса в
цепи наступает при частоте
.
Таким образом, состояние резонанса в
цепи наступает при частоте .
Эта угловая частота называетсярезонансной.
Векторная диаграмма для токов и напряжений
в последовательном rLC контуре,
построенная при
.
Эта угловая частота называетсярезонансной.
Векторная диаграмма для токов и напряжений
в последовательном rLC контуре,
построенная при  ,
изображена на рис. 10.1б. Как видно из
векторной диаграммы, вектора
,
изображена на рис. 10.1б. Как видно из
векторной диаграммы, вектора и
и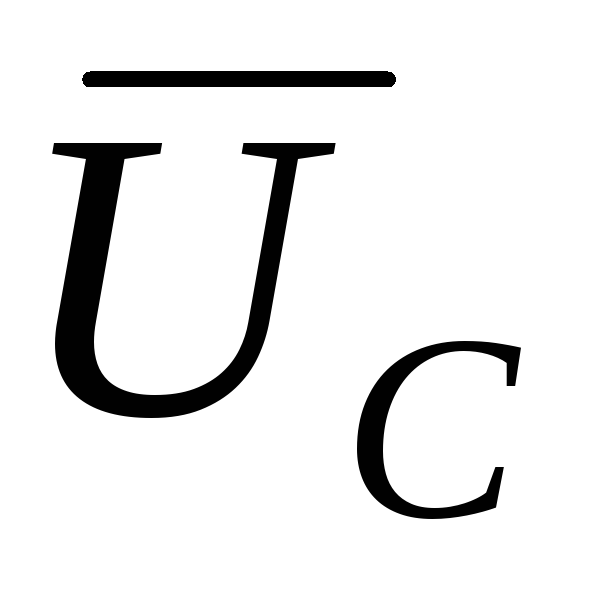 равны по величине и противоположны по
направлению, таким образом, напряжение
равны по величине и противоположны по
направлению, таким образом, напряжение при резонансной частоте равно нулю.
Индуктивное и равное ему емкостное
сопротивление цепи при резонансной
частоте
при резонансной частоте равно нулю.
Индуктивное и равное ему емкостное
сопротивление цепи при резонансной
частоте
 ,
,
обозначаемое
символом  ,
носит названиеволнового
сопротивления колебательного контура и измеряется в
омах.
,
носит названиеволнового
сопротивления колебательного контура и измеряется в
омах.
Отношение волнового сопротивления к активному сопротивлению в последовательном колебательном контуре называется добротностью, а величина, обратная добротности − затуханием:
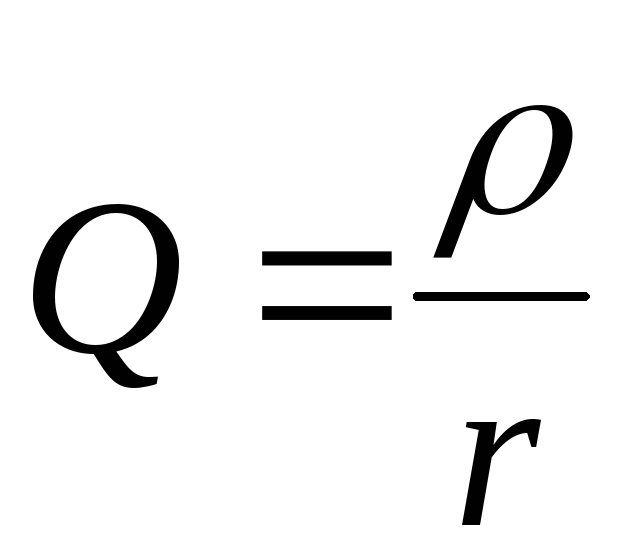 ,
, 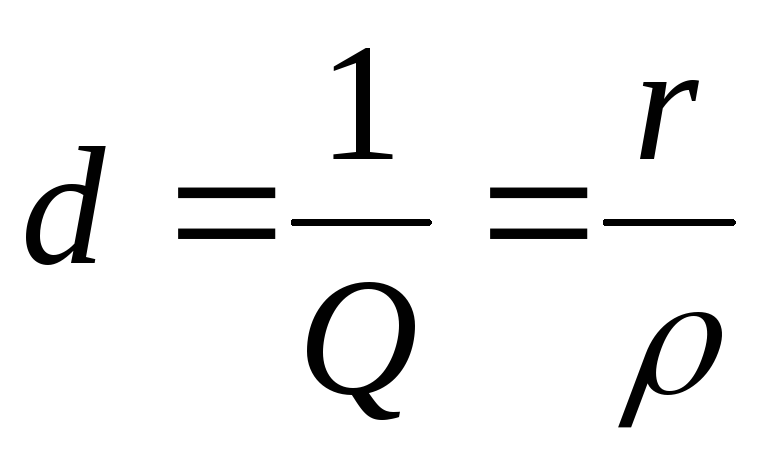 .
.
Как следует из приведенных соотношений, добротность и затухание являются безразмерными величинами. Поскольку во всех элементах цепи, изображенной на рис. 10.1а протекает один и тот же ток, добротность показывает, во сколько раз напряжение на реактивных элементах при резонансе превышает входное напряжение. В реальных колебательных контурах эта величина может достигать значительного уровня. Поэтому резонанс в цепи с последовательным соединением элементов r ,L ,C иногда называютрезонансом напряжений.
При резонансной частоте полное сопротивление z
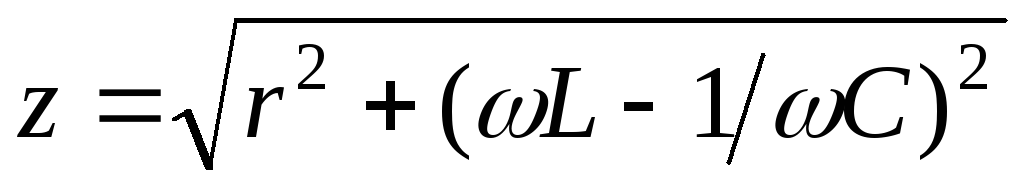
равно сопротивлению резистора r , ток и входное напряжение совпадают по фазе.
Таким образом, вся мощность, поставляемая в цепь источником, равна активной мощности, потребляемой единственным резистивным элементом, а реактивная мощность цепи равна нулю. Это означает, что в резонансе взаимный обмен энергии происходит только между конденсатором и катушкой индуктивности. Уменьшение энергии электрического поля при разряде конденсатора сопровождается увеличением энергии магнитного поля катушки и наоборот. Обмен энергией между источником и реактивными элементами отсутствует.
Рассмотрим
частотные свойства цепи с последовательно
соединенными элементами r ,L ,C . Будем
считать, что на входе цепи действует
синусоидальное напряжение с постоянной
амплитудой и угловой частотой  ,
меняющейся в пределах от 0 до ∞ .
Изменение частоты приводит к изменению
параметров цепиx , z ,
,
меняющейся в пределах от 0 до ∞ .
Изменение частоты приводит к изменению
параметров цепиx , z ,  . На рисунке 10.2 приведены соответствующие
частотные характеристики
. На рисунке 10.2 приведены соответствующие
частотные характеристики

 ,
, 
Рис. 10.2
Активное
сопротивление рассматриваемой цепи не
зависит от частоты, а реактивное при
определенных значениях частоты (  )
становится равным либо нулю либо
бесконечности. Эти характерные значения
называют соответственно нулями и
полюсами частотной характеристики.
Важным свойством функции
)
становится равным либо нулю либо
бесконечности. Эти характерные значения
называют соответственно нулями и
полюсами частотной характеристики.
Важным свойством функции является то, что она монотонно возрастает
при увеличении частоты
является то, что она монотонно возрастает
при увеличении частоты .
В интервале частот
.
В интервале частот реактивное сопротивление возрастает
от − ∞ до 0 и имеетемкостнойхарактер, при
реактивное сопротивление возрастает
от − ∞ до 0 и имеетемкостнойхарактер, при реактивное сопротивление возрастает
от 0 до ∞ и имеетиндуктивныйхарактер.
реактивное сопротивление возрастает
от 0 до ∞ и имеетиндуктивныйхарактер.
Рассмотрим зависимость тока в rLC контуре от частоты приложенного напряжения:
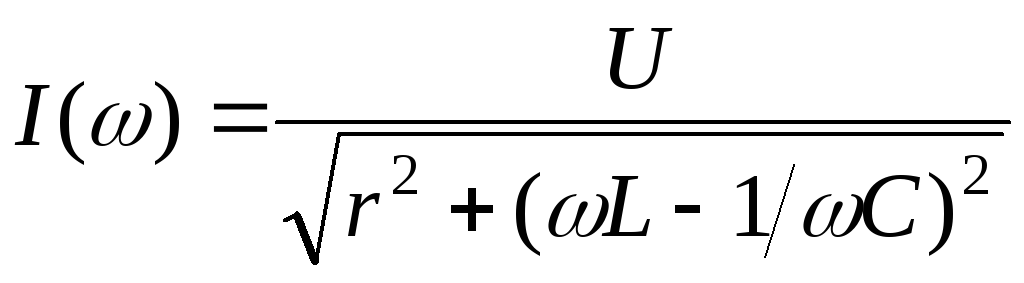 .
.
Анализ этого
выражения показывает, что при  максимального значения
максимального значения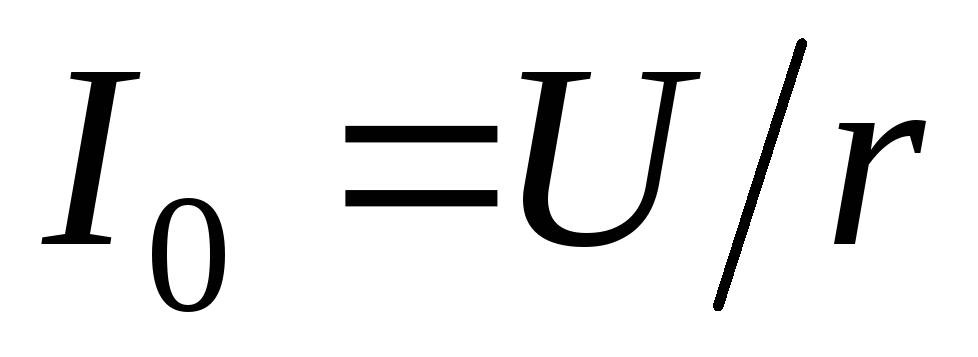 ток достигает в точке, соответствующей
резонансной частоте.
ток достигает в точке, соответствующей
резонансной частоте.
Важной характеристикой rLC контура является
ширина резонансной кривой или полоса
пропускания, которую определяют как
разность верхней и нижней
и нижней частот, для которых отношение
частот, для которых отношение составляет
составляет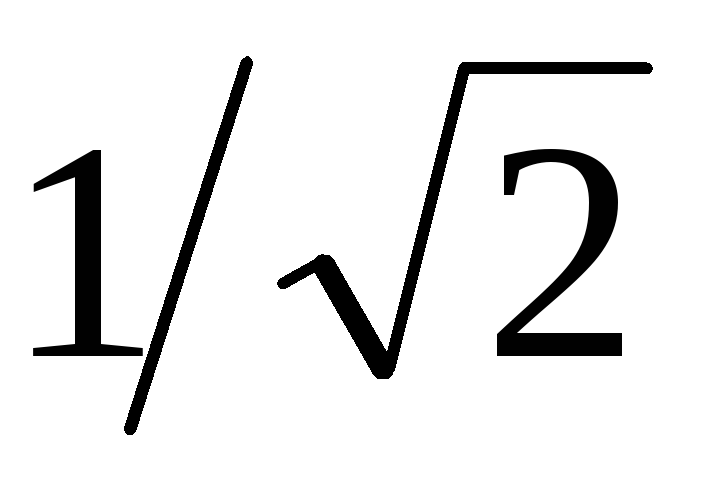 :
:
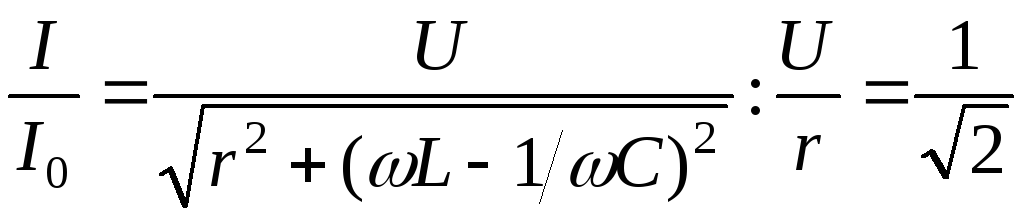 .
.
Частоты  и
и , ограничивающие полосу пропускания,
могут быть определены из соотношения
, ограничивающие полосу пропускания,
могут быть определены из соотношения
 ,
,
откуда следует, что на границах полосы пропускания реактивные сопротивления по абсолютной величине равны активному
 .
.
Последнее соотношение эквивалентно равнству
 ,
,
Откуда 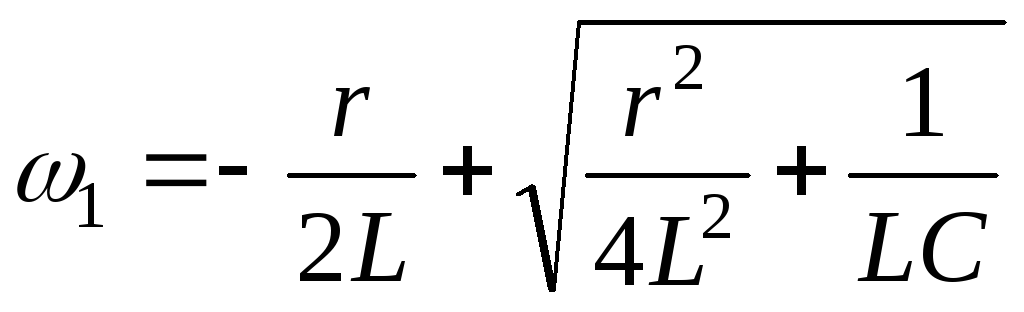 ,
, .
.
Разность
частот  и
и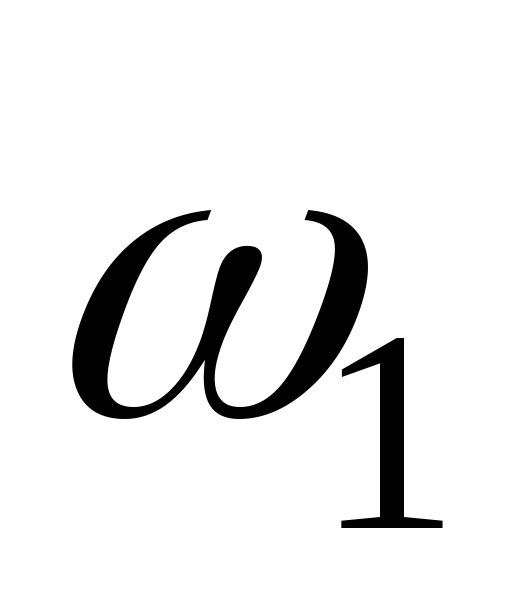 ( полоса пропускания ) определяется
выражением
( полоса пропускания ) определяется
выражением

Если построить
зависимость  в системе относительных координат,
в системе относительных координат, (рис.10.3), то ширина полосы пропускания
оказывается равной затуханию контура.
(рис.10.3), то ширина полосы пропускания
оказывается равной затуханию контура.

В
выражении напряжения на катушке
индуктивности 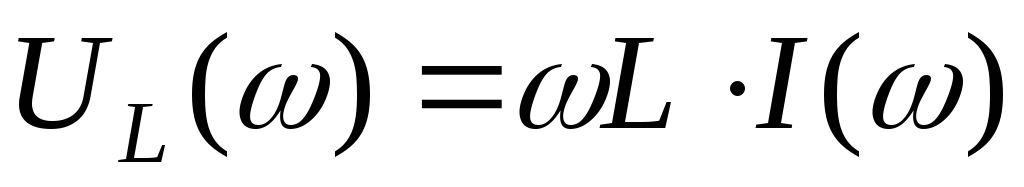 оба сомножителя зависят от частоты.
При
оба сомножителя зависят от частоты.
При напряжение
напряжение .
С увеличением частоты напряжение
.
С увеличением частоты напряжение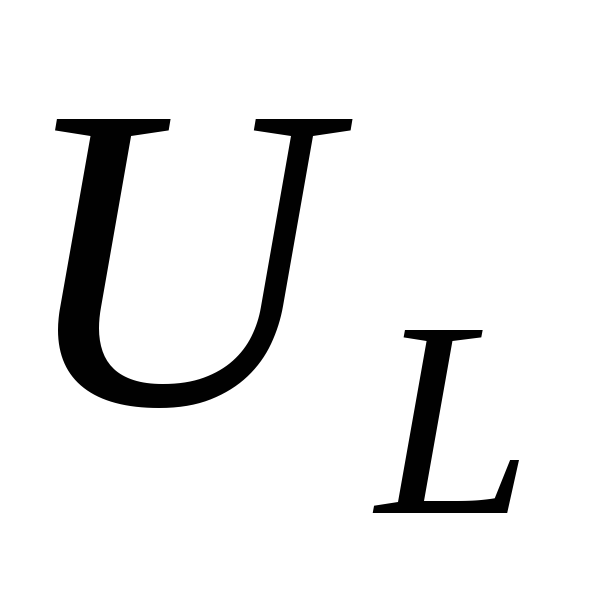 возрастает и стремится к входному при
возрастает и стремится к входному при .
Можно показать, что при
.
Можно показать, что при эта зависимость монотонна, а при
эта зависимость монотонна, а при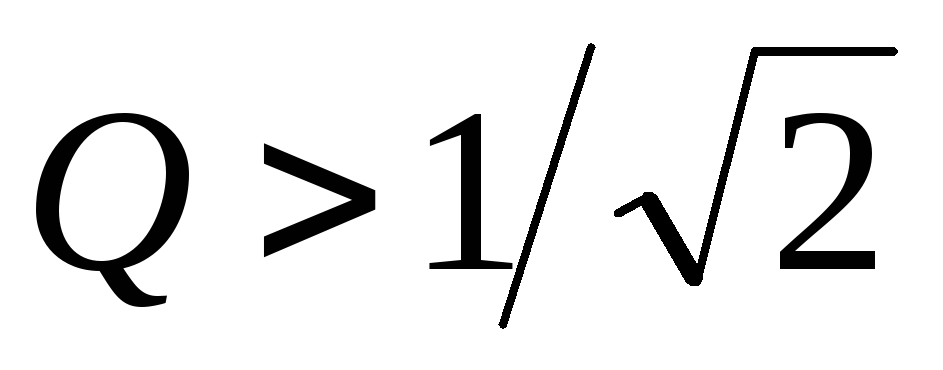 имеет максимум ( рис. 10.4 ).
имеет максимум ( рис. 10.4 ).

Напряжение
на конденсаторе  .
При
.
При ток в контуре отсутствует и все входное
напряжение оказывается приложенным к
конденсатору. При
ток в контуре отсутствует и все входное
напряжение оказывается приложенным к
конденсатору. При напряжение на конденсаторе стремится
к нулю. Для цепи, добротность которой
превышает
напряжение на конденсаторе стремится
к нулю. Для цепи, добротность которой
превышает ,
зависимость
,
зависимость имеет максимум; если
имеет максимум; если ,
напряжение на конденсаторе монотонно
уменьшается с ростом частоты.
,
напряжение на конденсаторе монотонно
уменьшается с ростом частоты.
studfile.net
§56. Резонанс напряжений и резонанс токов
Явление резонанса. Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими. При подсоединении колебательного контура к источнику переменного тока угловая частота источника ? может оказаться равной угловой частоте ?0, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ?0, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ?, сообщаемых этой системе внешними силами.
Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ? источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ?0, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.

Резонанс напряжений. При резонансе напряжений (рис. 196, а) индуктивное сопротивление XL равно емкостному Хси полное сопротивление Z становится равным активному сопротивлению R:
Z = ?( R2 + [?0L — 1/(?0C)]2 ) = R
В этом случае напряжения на индуктивности UL и емкости Uc равны и находятся в противофазе (рис. 196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = XL—Xс становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений UL и Uc, причем их значения могут во много раз превышать напряжение U источника, питающего цепь.
Угловая частота ?0, при которой имеют место условия резонанса, определяется из равенства ?oL = 1/(?0С).
Рис. 196. Схема (а) и векторная диаграмма (б) электрической цепи, содержащей R, L и С, при резонансе напряжений
Отсюда имеем
?o = 1/?(LC) (74)
Если плавно изменять угловую частоту ? источника, то полное сопротивление Z сначала начинает уменьшаться, достигает наименьшего значения при резонансе напряжений (при ?o), а затем увеличивается (рис. 197, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.
Резонанс токов. Резонанс токов может возникнуть при параллельном соединении индуктивности и емкости (рис. 198, а). В идеальном случае, когда в параллельных ветвях отсутствует активное сопротивление (R1=R2 = 0), условием резонанса токов является равенство реактивных сопротивлений ветвей, содержащих индуктивность и емкость, т. е. ?oL = 1/(?oC). Так как в рассматриваемом случае активная проводимость G = 0, ток в неразветвленной части
цепи при резонансе I=U?(G2+(BL-BC)2)= 0. Значения токов в ветвях I1 и I2 будут равны (рис. 198,б), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости I с опережает напряжение U на 90°). Следовательно, такой резонансный контур представляет собой для тока I бесконечно большое сопротивление и электрическая энергия в контур от источника не поступает. В то же время внутри контура протекают токи IL и Iс, т. е. имеет место процесс непрерывного обмена энергией внутри контура. Эта энергия переходит из индуктивности в емкость и обратно.
Как следует из формулы (74), изменяя значения емкости С или индуктивности L, можно изменять частоту колебаний ?0 электрической энергии и тока в контуре, т. е. осуществлять настройку контура на требуемую частоту. Если бы в ветвях, в которых включены индуктивность и емкость, не было активного сопротивления, этот процесс колебания энергии продолжался бы бесконечно долго, т. е. в контуре возникли бы незатухающие колебания энергии и токов IL и Iс. Однако реальные катушки индуктивности и конденсаторы всегда поглощают электрическую энергию (из-за наличия в катушках активного сопротивления проводов и возникновения
Рис. 197. Зависимость тока I и полного сопротивления Z от ? для последовательной (а) и параллельной (б) цепей переменного тока
Рис. 198. Электрическая схема (а) и векторные диаграммы (б и в) при резонансе токов
в конденсаторах токов смещения, нагревающих диэлектрик), поэтому в реальный контур при резонансе токов поступает от источника некоторая электрическая энергия и по неразветвленной части цепи протекает некоторый ток I.
Условием резонанса в реальном резонансном контуре, содержащем активные сопротивления R1 и R2, будет равенство реактивных проводимостей BL = BC ветвей, в которые включены индуктивность и емкость.
Из рис. 198, в следует, что ток I в неразветвленной части цепи совпадает по фазе с напряжением U, так как реактивные токи 1L и Iс равны, но противоположны по фазе, вследствие чего их векторная сумма равна нулю.
Если в рассматриваемой параллельной цепи изменять частоту ?о источника переменного тока, то полное сопротивление цепи начинает увеличиваться, достигает наибольшего значения при резонансе, а затем уменьшается (см. рис. 197,б). В соответствии с этим ток I начинает уменьшаться, достигает наименьшего значения Imin = Ia при резонансе, а затем увеличивается.
В реальных колебательных контурах, содержащих активное сопротивление, каждое колебание тока сопровождается потерями энергии. В результате сообщенная контуру энергия довольно быстро расходуется и колебания тока постепенно затухают. Для получения незатухающих колебаний необходимо все время пополнять потери энергии в активном сопротивлении, т. е. такой контур должен быть подключен к источнику переменного тока соответствующей частоты ?0.
Явления резонанса напряжения и тока и колебательный контур получили весьма широкое применение в радиотехнике и высокочастотных установках. При помощи колебательных контуров мы получаем токи высокой частоты в различных радиоустройствах и высокочастотных генераторах. Колебательный контур — важнейший элемент любого радиоприемника. Он обеспечивает его избирательность, т. е. способность выделять из радиосигналов с различной длиной волны (т. е. с различной частотой), посланных различными радиостанциями, сигналы определенной радиостанции.

electrono.ru

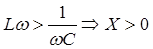
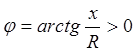

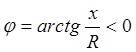
 и
и  совпадают по фазе
совпадают по фазе