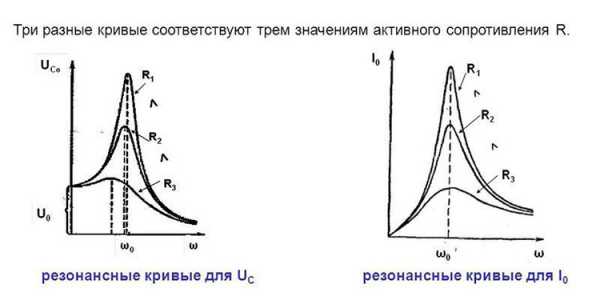
Схема и резонансные кривые для резонанса токов.
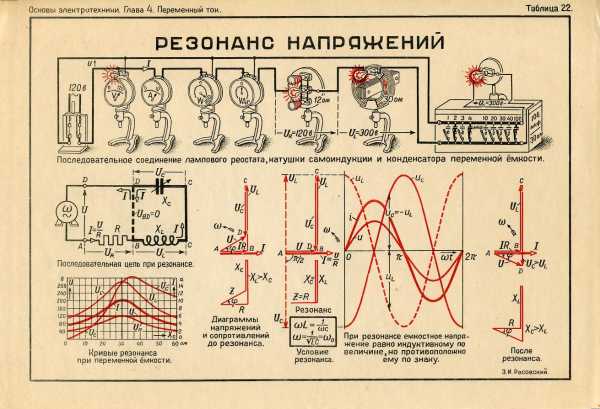
Резонанс напряжений в цепи переменного тока.
Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем если бы они были включены в цепь по отдельности.
Резонанс напряжений возникает в последовательной RLC-цепи.
От одновременного действия двух различных по своему характеру реактивных сопротивлений в цепи происходит компенсация (взаимное уничтожение) сдвига фаз.
Полная компенсация, т. е. полное уничтожение сдвига фаз между током и напряжением в такой цепи, наступит тогда, когда индуктивное сопротивление окажется равным емкостному сопротивлению цепи, т. е. когда X
ωL = 1 / ωС.
Цепь в этом случае будет вести себя как чисто активное сопротивление, т. е. как будто в ней нет ни катушки, ни конденсатора. Величина этого сопротивления определится суммой активных сопротивлений катушки и соединительных проводов. При этом действующее значение тока в цепи будет наибольшим и определится формулой закона Ома
I = U / R,
Где вместо Z теперь поставлено R.
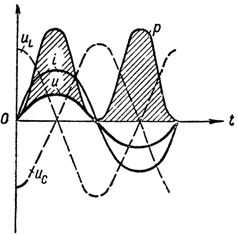
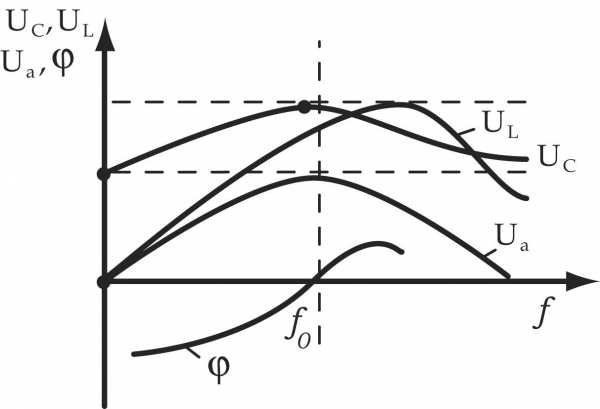
Одновременно с этим действующие напряжения как на катушке UL = IXL так и на конденсаторе Uc = IХС окажутся равными и будут максимально большой величины. При малом активном сопротивлении цепи эти напряжения могут во много раз превысить общее напряжение U на зажимах цепи. Это интересное явление называется в электротехнике резонансом напряжений.
Кривые напряжений, тока и мощности при резонансе напряжений в цепи.
Сопротивления XL и ХС являются переменными, зависящими от частоты тока, и стоит хотя бы немного изменить частоту его, например, увеличить, как XL = ωLвозрастет, а ХС = 1 / ωС уменьшится, и тем самым в цепи сразу нарушится резонанс напряжений, при этом наряду с активным сопротивлением в цепи появится и реактивное. То же самое произойдет, если изменить величину индуктивности или емкости цепи.
При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.
Цепь переменного тока, состоящая из генератора и последовательно соединенных катушки индуктивности и конденсатора, при определенных условиях X
Из равенства XL = ХС можно определить значения частоты генератора, при которой наступает явление резонанса напряжений:
Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений:
Таким образом, изменяя любую из этих трех величин (fрез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур.
Резонанс токов.
Резонанс токов, параллельный резонанс — получается в случае, когда генератор нагружен на индуктивность и емкость, соединенные параллельно, т.е. когда генератор вне контура..
Весь контур в целом является нагрузочным сопротивлением для генератора и поэтому генератор
Схема и резонансные кривые для резонанса токов.
включен последовательно, как это и бывает всегда в замкнутой цепи.
Условия получения резонанса токов такие же, как и для резонанса напряжений: f = f0 или xL = хC. Однако по своим свойствам резонанс токов во многом противоположен резонансу напряжений. В этом случае на катушке и на конденсаторе напряжение такое же, как у генератора. При резонансе сопротивление контура между точками разветвления становится максимальным, а ток генератора будет минимальным. Полное (эквивалентное) сопротивление контура для генератора при резонансе токов Rэ можно подсчитать по любой из следующих формул
,
где L и С — в генри и фарадах, а Rэ, р и r — в омах.
Сопротивление Rэ, называемое резонансным сопротивлением, является чисто активным и поэтому при резонансе токов нет сдвига фаз между напряжением генератора и его током.
На (рис.1 б) для резонанса токов показано изменение полного сопротивления контура z и тока генератора I при изменении частоты генератора f.
В самом контуре при резонансе происходят сильные колебания и поэтому ток внутри контура во много раз больше, чем ток генератора. Токи в индуктивности и емкости IL и IС можно рассматривать как токи в ветвях или как ток незатухающих колебаний внутри контура, поддерживаемых генератором. По отношению к напряжению U ток в катушке отстает на 90°, а ток в емкости опережает это напряжение на 90°, т. е. друг относительно друга токи сдвинуты по фазе на 180°. Вследствие наличия активного сопротивления, сосредоточенного главным образом в катушке, токи IL, и IC в действительности имеют сдвиг фаз несколько меньше 180° и ток IL немного( меньше IC
. Поэтому по первому закону Кирхгофа для точки разветвления можно написать
Чем меньше активное сопротивление в контуре, тем меньше разница между IC и IL, тем меньше ток генератора и тем больше сопротивление контура. Ток, идущий от генератора, пополняет энергию в контуре, компенсируя потери ее в активном сопротивлении. При уменьшении активного сопротивления уменьшается потеря энергии в нем и генератор расходует меньше энергии на поддержание незатухающих колебаний.
Если бы контур был идеальным, то начавшиеся колебания продолжались бы непрерывно без затухания и не требовалось бы энергии от генератора на их поддержание. Ток генератора был бы равен нулю, а сопротивление контура — бесконечности.

Активная мощность, расходуемая генератором, может быть подсчитана как
или как мощность потерь в активном сопротивлении контура
где Iк — ток в контуре, равный IL или IC.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
2.4. Резонансная кривая последовательного контура
Когда частота питающего генератора не равна собственной частоте контура, контур называют расстроенным.
Разность
между частотой генератора и собственной
частотой контура принято называть абсолютной расстройкой и обозначать  :
:
.
Абсолютная расстройка выражается в единицах частоты. При резонансе частота генератора и собственная частота контура равны и абсолютная расстройка равна нулю.
Есличастота генератора больше собственной частоты
больше собственной частоты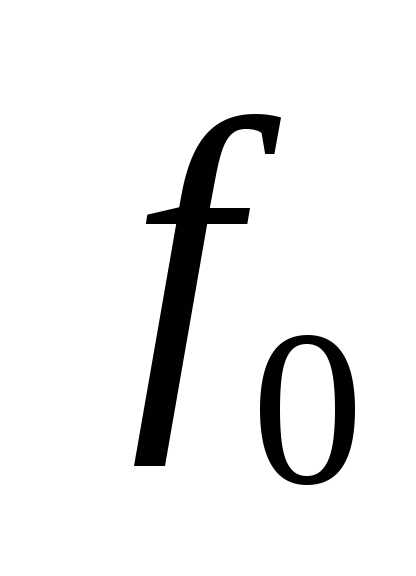 контура, расстройка
считается положительной (
контура, расстройка
считается положительной (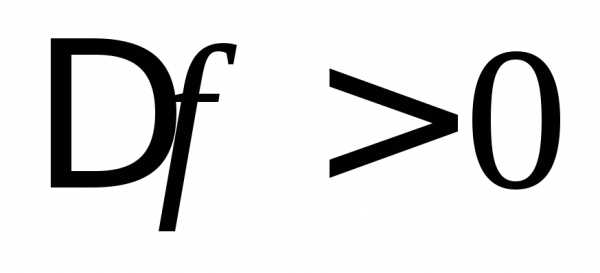 ).
При частоте генератора меньше собственной
частоты контура расстройка отрицательна
(
).
При частоте генератора меньше собственной
частоты контура расстройка отрицательна
(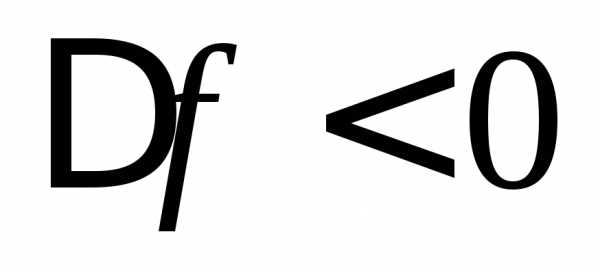 ).
).
Отношение
абсолютной расстройки к собственной
частоте контура 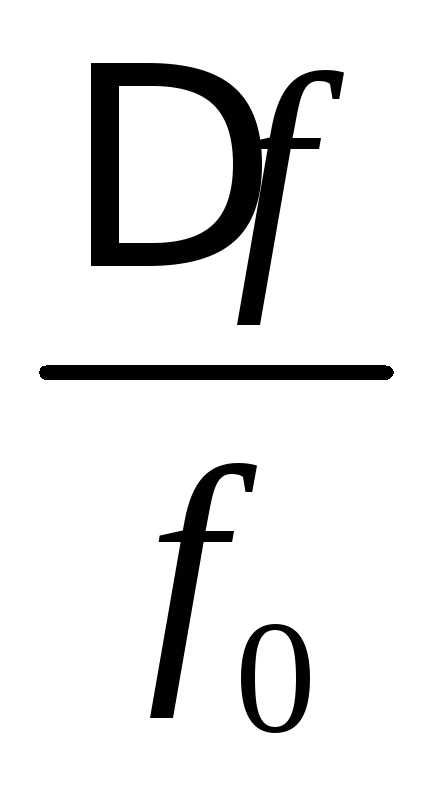 называютотносительной расстройкой.
называютотносительной расстройкой.
При резонансе относительная расстройка равна нулю:
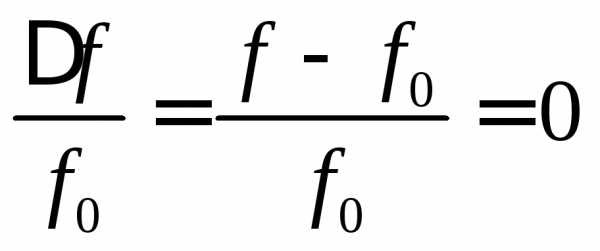 .
.
Ток в контуре тем меньше, чем больше расстройка контура.
Иногда
оказывается более удобной резонансная
кривая, построенная в относительном
масштабе. Для получения такой кривой
вдоль вертикальной оси откладывается
отношение тока в контурепри
данной расстройке к току при резонансе 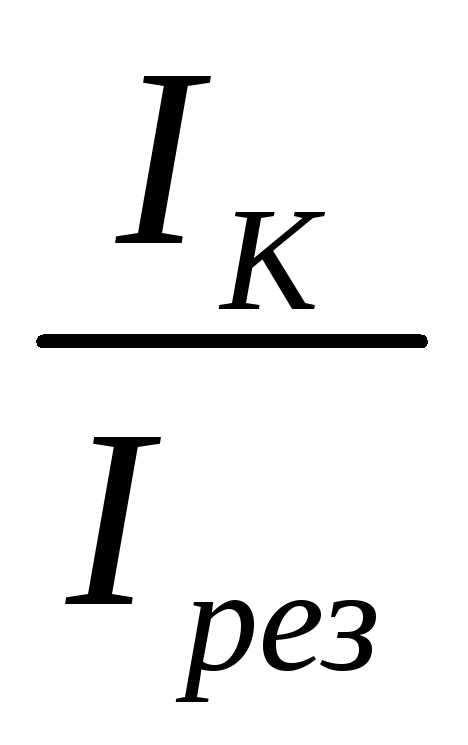 ,
а вдоль горизонтальной оси –
абсолютная или относительная расстройка
(на рис.9 – абсолютная
расстройка).Выведем
уравнение резонансной кривой.
,
а вдоль горизонтальной оси –
абсолютная или относительная расстройка
(на рис.9 – абсолютная
расстройка).Выведем
уравнение резонансной кривой.
Ток в
контуре при любой частоте  равен
равен
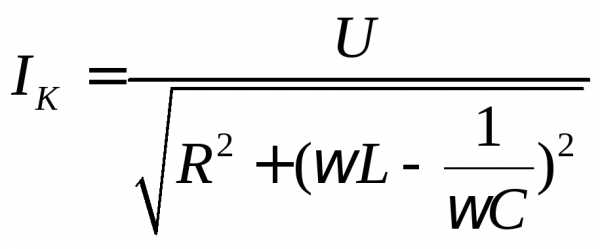 .
.
Ток при резонансе
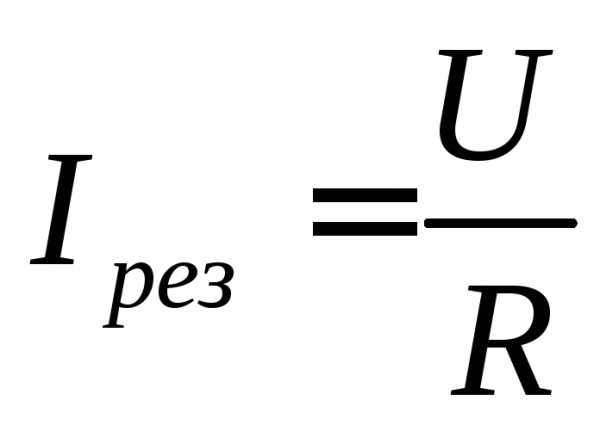 .
.
Отсюда получаем:
.
Числитель
и знаменатель полученной дроби сначала
разделим на 
 – собственная частота
контура, умножим на
– собственная частота
контура, умножим на  ,
и преобразуем выражение
,
и преобразуем выражение.
Получаем следующее выражение:
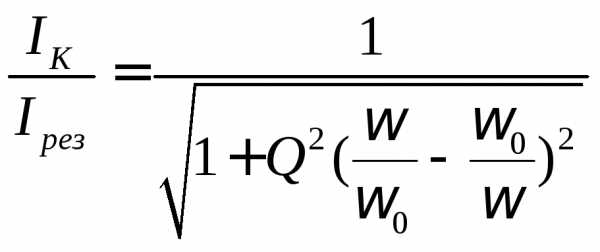 .
.
Учитывая,
что 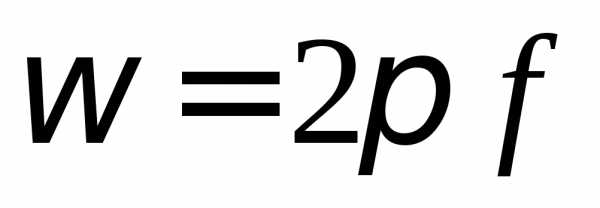 ,
получим
,
получим
.
Преобразуем
выражение 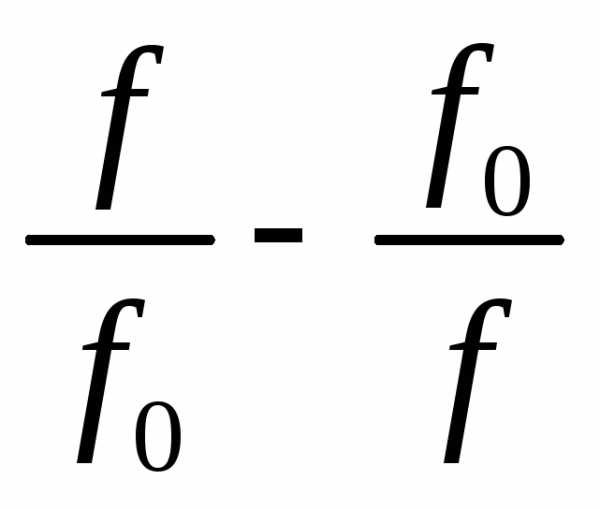 :
:
.
Считая приближенно, что и обозначив(абсолютная расстройка), получим
.
Тогда
.
Относительная расстройка
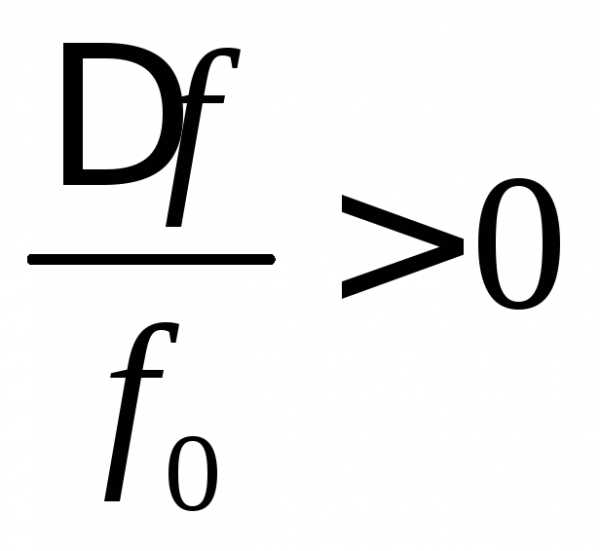
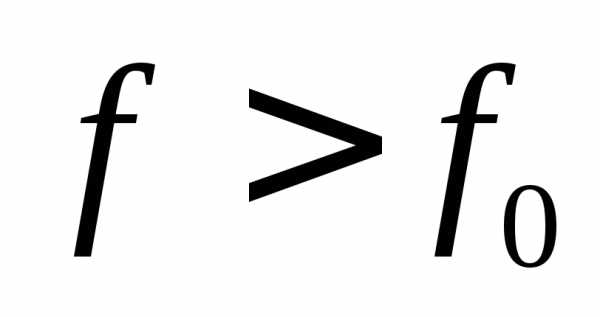 ,
, 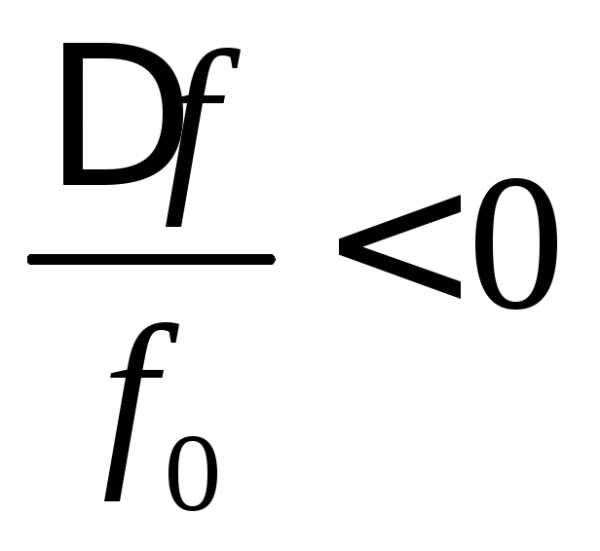 ,если
,если 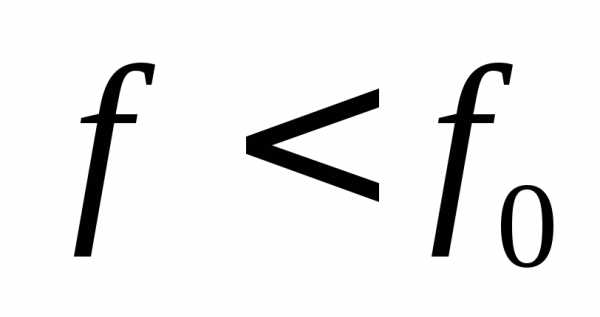 .
.
Введем обозначения:
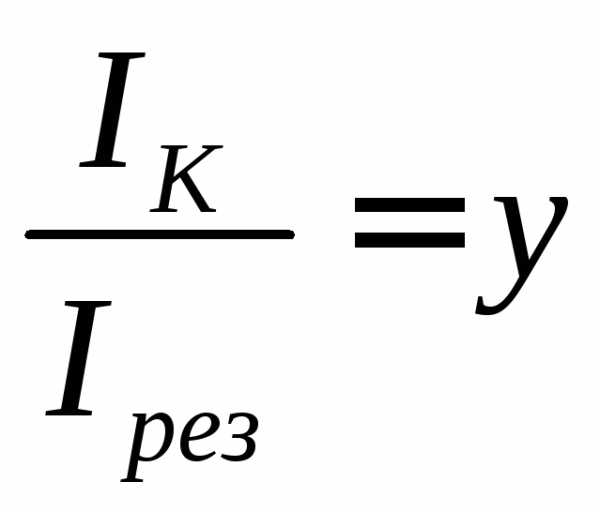 и
и 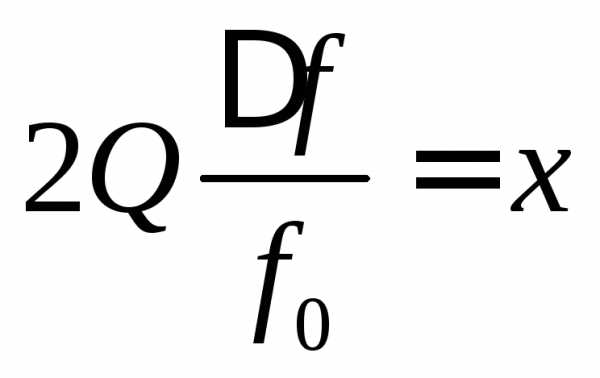 .
.
Тогда для уравнения резонансной кривой в относительном масштабе получим выражение
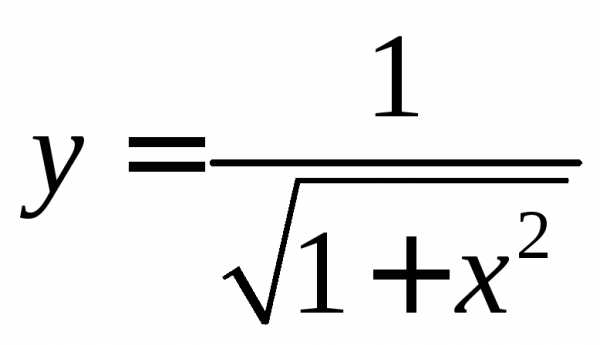
Уравнению такого вида соответствует кривая, изображенная на рис.9.
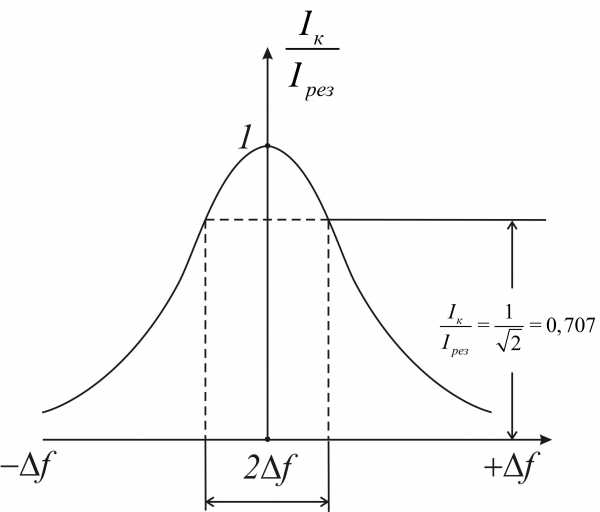
Рис.9. Резонансная кривая последовательного контура
Построение резонансных кривых в относительном масштабе дает возможность легко и удобно сравнивать между собою различные по качеству контуры, а также производить расчеты элементов радиотехнических схем
2.5. Полоса пропускания последовательного контура
Сопротивление последовательного контура вблизи резонанса резко изменяется в зависимости от частоты генератора; в соответствии с этим резко изменяется и ток в контуре. Контур по-разному ведет себя при различных значениях частоты питающего тока. Эти свойства могут быть оценены формой резонансной кривой или добротностью контура. Однако во многих случаях для такой оценки оказывается более удобным пользоваться понятием полосы пропускания контура, так как сигнал каждого передатчика представляет собой спектр частот и занимает некоторую полосу частот. Для неискаженной передачи и приема сигналов необходимо, чтобы все частоты, входящие в состав сигнала, в одинаковой степени излучались передающим устройством, а будучи приняты приемной антенной, в одинаковой степени усиливались приемником. Необходимо, чтобы колебательные контуры пропускали полосу частот, соответствующую спектру сигнала. Поэтому вопрос о полосе частот, пропускаемых контуром, имеет важное значение в радиотехнических устройствах.
Полосой
пропускания контура называют полосу частот, в пределах
которой ток в контуре уменьшается не
более чем в 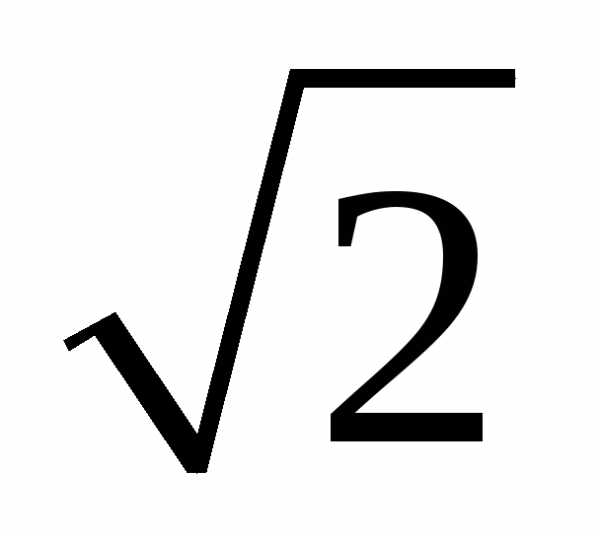 раз по сравнению с током при резонансе.
Иначе, полосой пропускания контура
называют полосу частот, в пределах
которой контурный ток составляет 0,7 или
больше от тока при резонансе. На
рис.10 изображена резонансная
кривая последовательного контура.
Полоса пропускания этого контура равна
раз по сравнению с током при резонансе.
Иначе, полосой пропускания контура
называют полосу частот, в пределах
которой контурный ток составляет 0,7 или
больше от тока при резонансе. На
рис.10 изображена резонансная
кривая последовательного контура.
Полоса пропускания этого контура равна 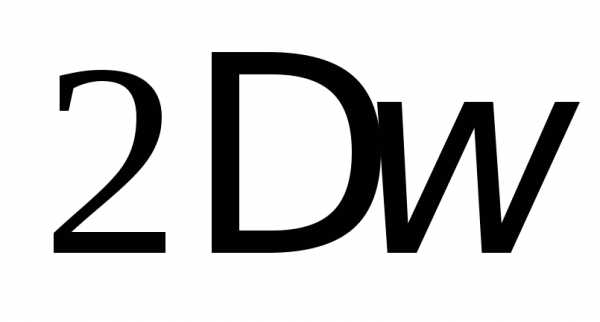 .
Условно считается, что частоты в пределах
от
.
Условно считается, что частоты в пределах
от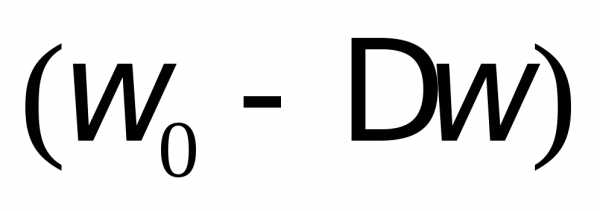 до
до 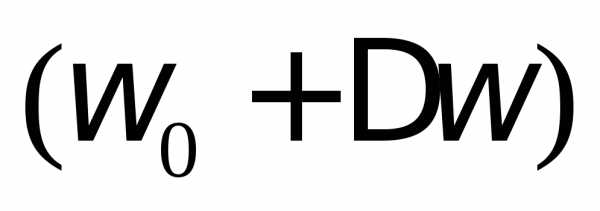 контур пропускает, а частоты ниже
контур пропускает, а частоты ниже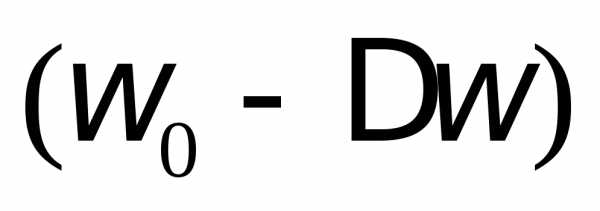 и выше
и выше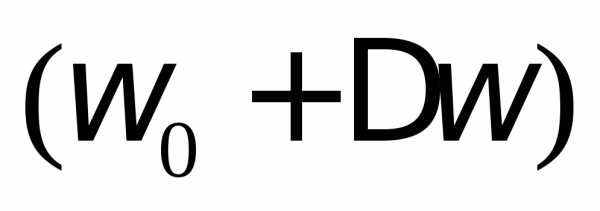 не пропускает.
не пропускает.
Ширина полосы пропускания прямо пропорциональна резонансной частоте и обратно пропорциональна добротности контура, или прямо пропорциональна затуханию при неизменной резонансной частоте.
Полоса пропускания контура зависит от его добротности: чем ниже добротность, тем «тупее» резонансная кривая и тем шире полоса пропускания контура.
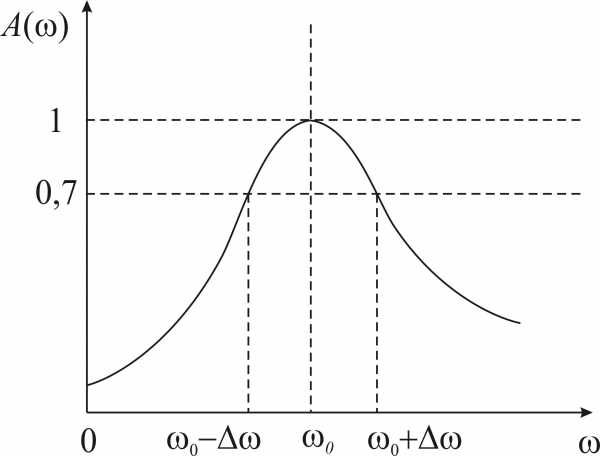
Рис.10. Полоса пропускания последовательного контура
Зависимость модуля
тока от частоты, выражаемая обычно в
виде отношения 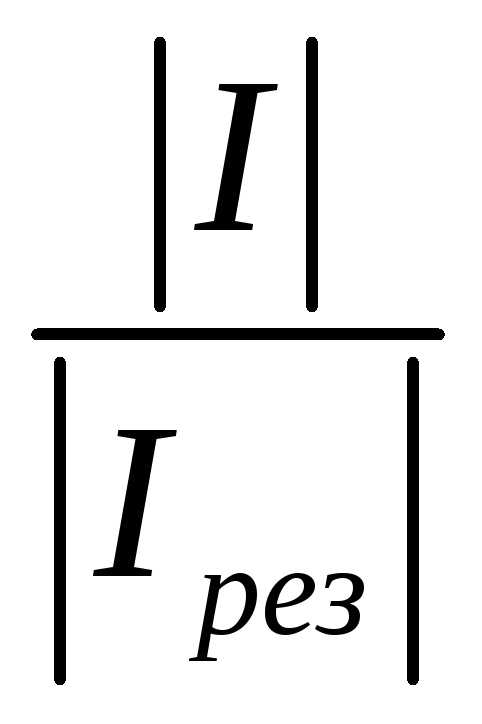 ,
носит названиерезонансной
характеристики последовательного
контура:
,
носит названиерезонансной
характеристики последовательного
контура:
.
На границах полосы
пропускания контура 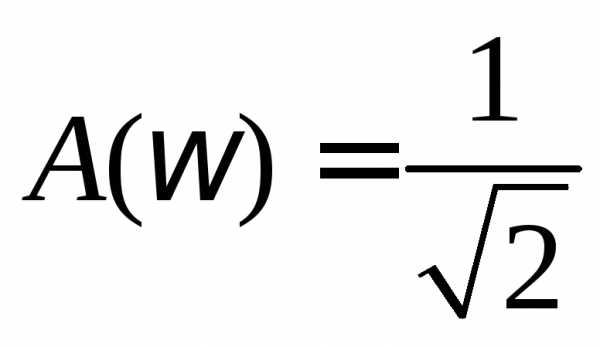 ,
откуда следует простая формула для
практического определения добротности:
,
откуда следует простая формула для
практического определения добротности: 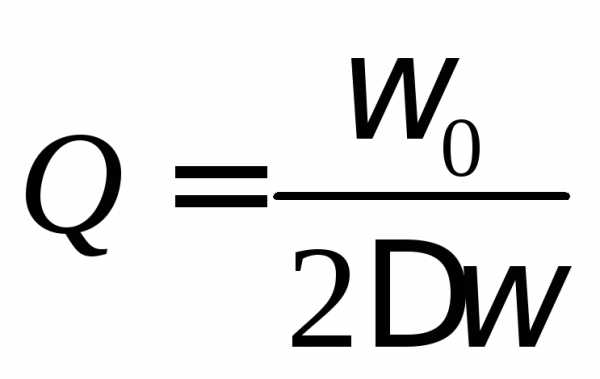 .
.
studfile.net
Резонансные кривые для амплитуды силы тока в контуре, для амплитуды скорости материальной точки в механической системе
Запишем
формулу (5.68) для амплитуды силы тока 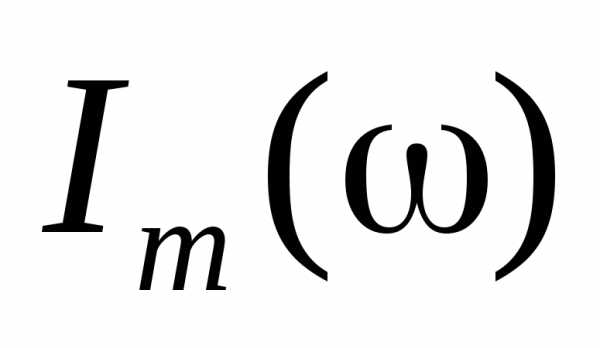 в наиболее удобном виде
в наиболее удобном виде
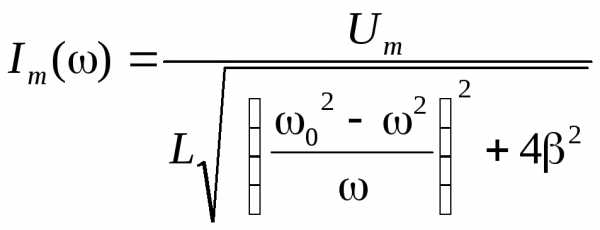 ,
,
и
исследуем эту зависимость для различных
значений  .
.
1. ω=0
: 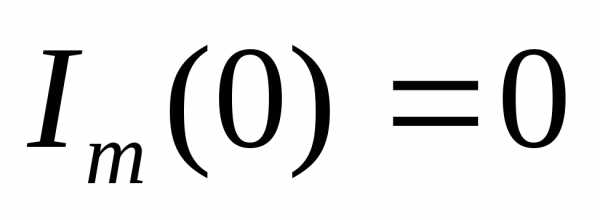 ,
т.е. постоянный электрический ток через
цепь, содержащую конденсатор, не
протекает.
,
т.е. постоянный электрический ток через
цепь, содержащую конденсатор, не
протекает.
2.  :
.
:
.
3.
Максимум функции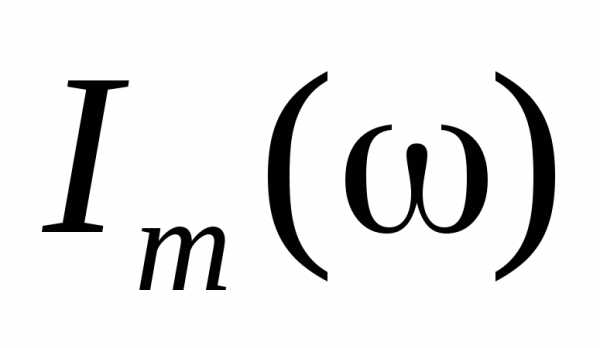 наблюдается тогда, когда подкоренное
выражение в знаменателе будет минимальным,
т.е. первое слагаемое в подкоренном
выражении должно быть равным нулю.
Поэтому максимум
наблюдается тогда, когда подкоренное
выражение в знаменателе будет минимальным,
т.е. первое слагаемое в подкоренном
выражении должно быть равным нулю.
Поэтому максимум 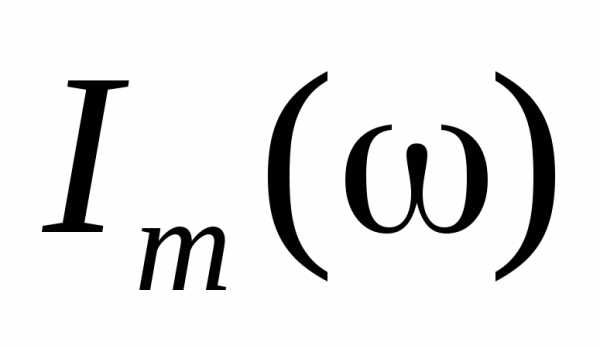 соответствует
частоте
соответствует
частоте  ,
а само максимальное значение будет
равно
,
а само максимальное значение будет
равно
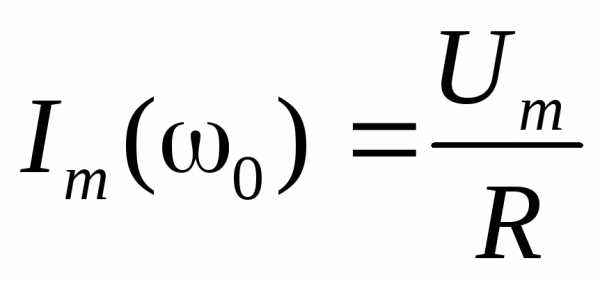 .
(5.74)
.
(5.74)
На
рис. 5.18 приведены резонансные кривые 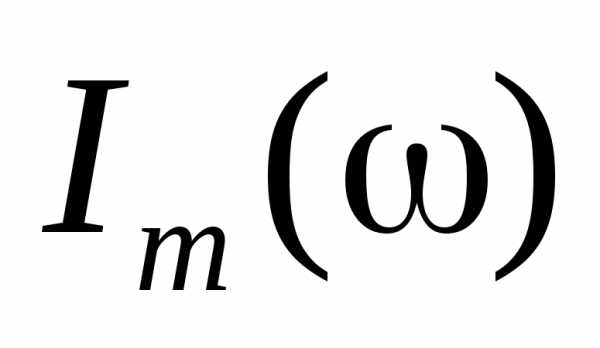 в случае идеального колебательного
контура ()
и для двух разных значений сопротивления
в случае идеального колебательного
контура ()
и для двух разных значений сопротивления 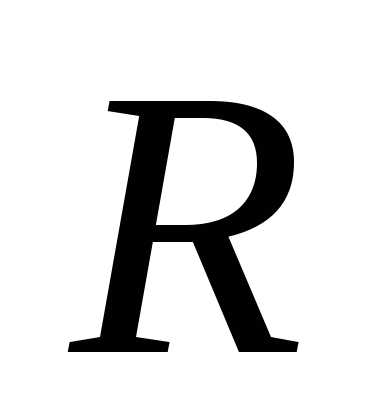 в нем (
в нем ( ,
т.е.
,
т.е.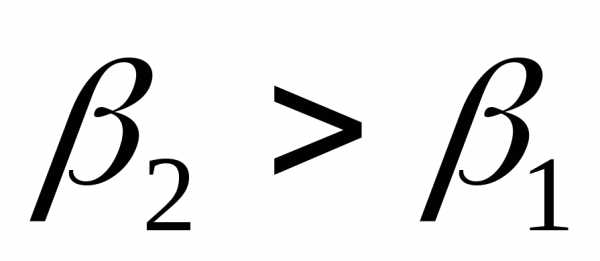 )
при постоянном значении
)
при постоянном значении 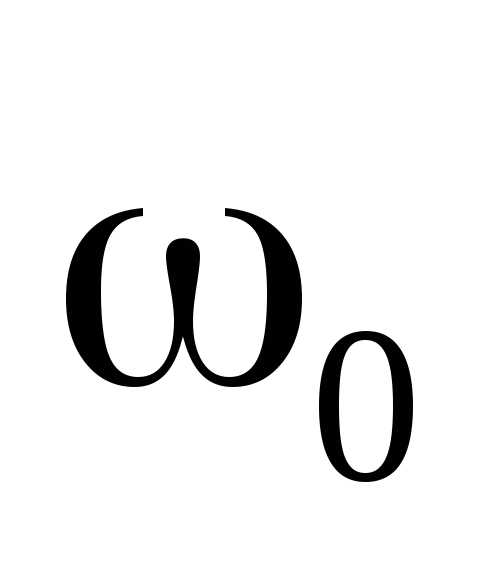 .
Как видно, максимум функции с увеличением
.
Как видно, максимум функции с увеличением  уменьшается, а его смещение по оси частот
уменьшается, а его смещение по оси частот не происходит.
не происходит.
Используя
табл. аналогий 5.1, можно записать формулы,
описывающие резонансные кривые для
амплитуды колебаний скорости 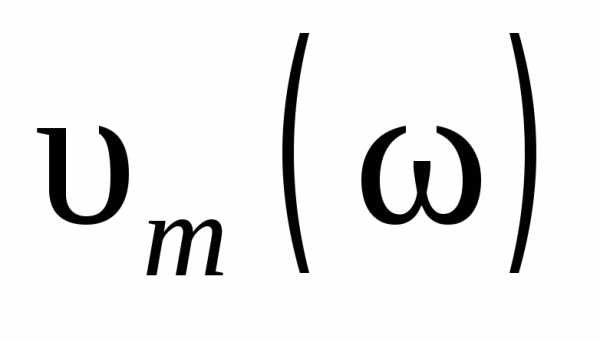 тела (м.т.) в механической системе:
тела (м.т.) в механической системе:
, (5.75)
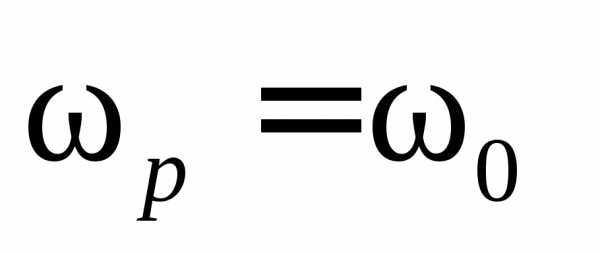 :
: 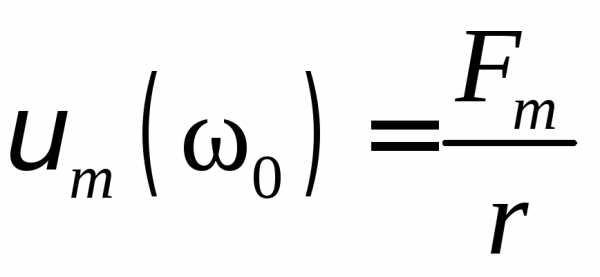 .
(5.76)
.
(5.76)
График 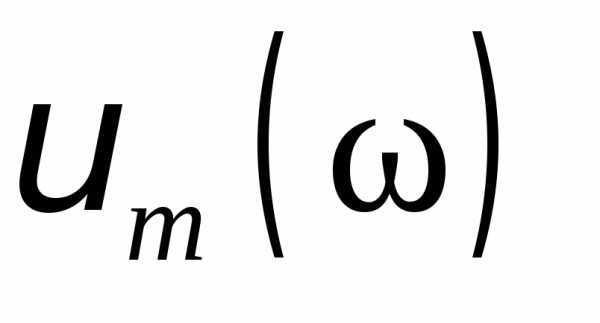 для трех значений коэффициента
сопротивления ()
среды приведены на рис. 5. 18,б. Эти графики
аналогичны графикам резонансных кривых
для трех значений коэффициента
сопротивления ()
среды приведены на рис. 5. 18,б. Эти графики
аналогичны графикам резонансных кривых 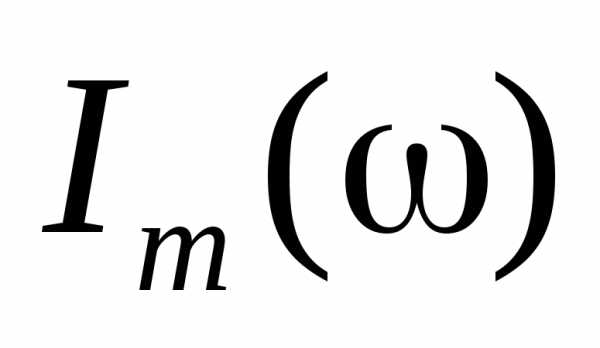 .
.
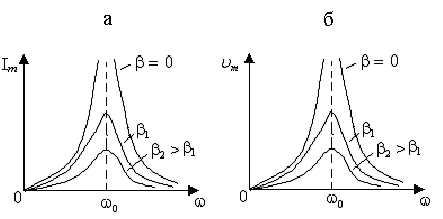
Рис. 5.18
Разность фаз колебаний между силой тока и напряжениями на конденсаторе, индуктивности и активном сопротивлении колебательного контура. Фазовые резонансные кривые
Перепишем
формулы (5.64) для I и 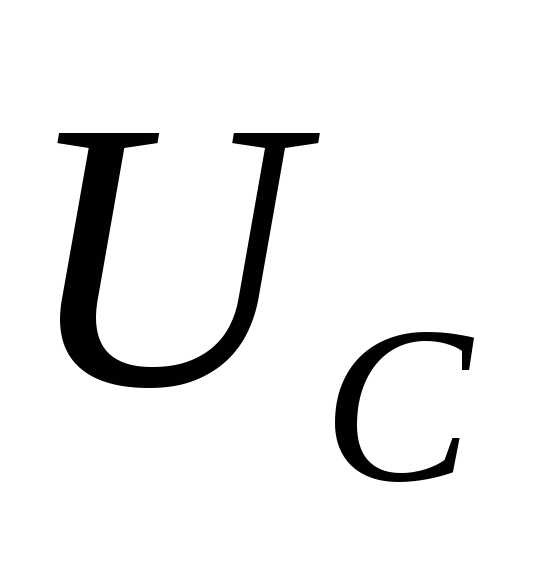 в
удобном виде
в
удобном виде
, ,
и добавим к ним формулы для UL и UR:
,.(5.77)
Найдем
в соответствии с полученными формулами
разность фаз колебаний между силой тока 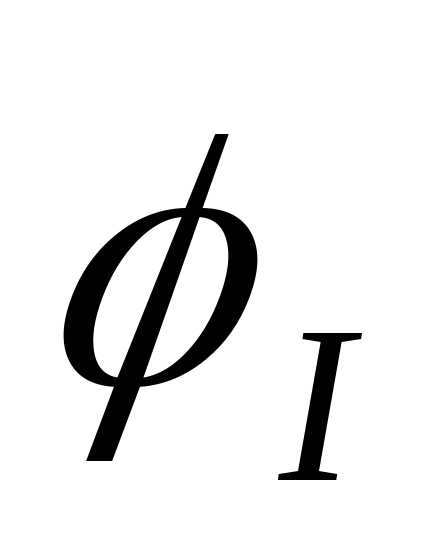 и напряжениями на конденсаторе
и напряжениями на конденсаторе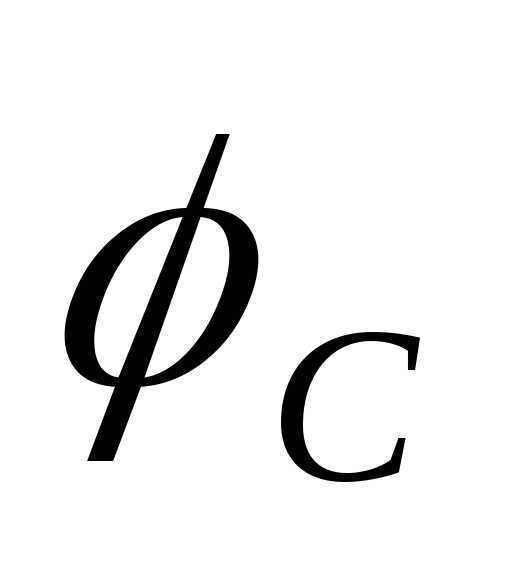 ,
индуктивности
,
индуктивности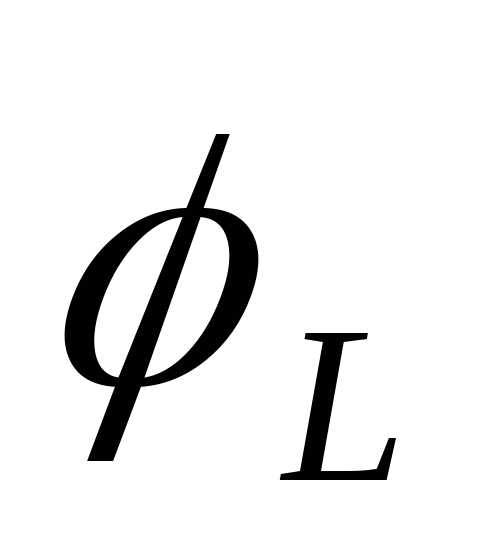 и активного сопротивления
и активного сопротивления :
:
, (5.78)
, (5.79)
. (5.80)
Рис. 5.19
Как следует из формул (5.78) – (5.80) фаза колебаний напряжения на конденсаторе отстает по фазе от колебаний тока в цепи на π/2, а фаза колебаний напряжения на катушке опережает фазу колебаний силы тока на π/2. Фазы колебаний напряжения на активном сопротивлении R и силы тока в цепи совпадают. Это наглядно видно на векторной диаграмме, приведенной на рис. 5.19.На
ней указаны амплитуды векторов напряжений
на отдельных участках электрической
цепи. При этом фаза колебания силы тока
в контуре принимается равной нулю, т.е.
амплитуда вектора силы тока располагается
вдоль оси 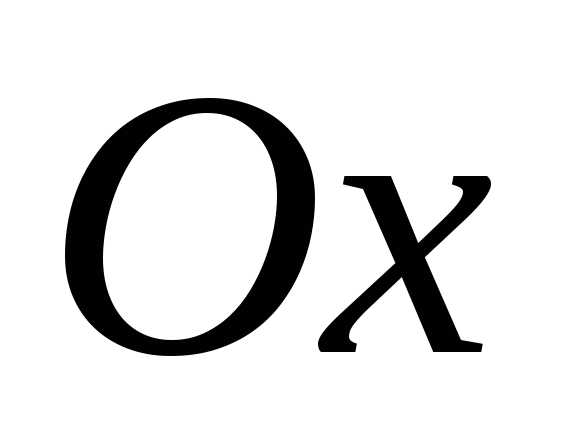 .
.
На
такой диаграмме вектор амплитуды
внешнего напряжения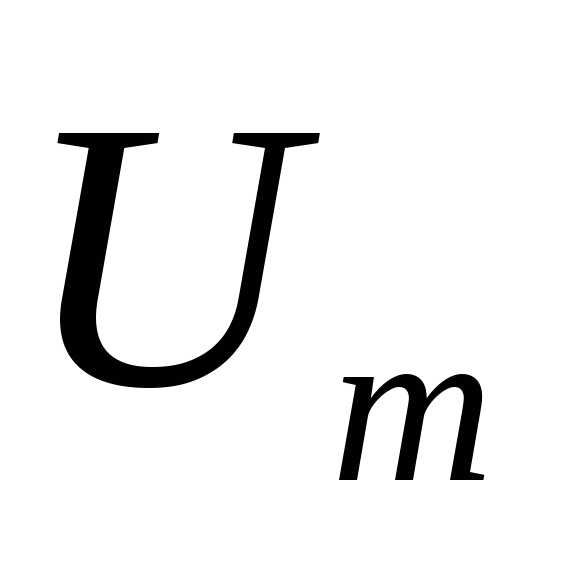 ,
подаваемого в колебательный контур,
можно представить как сумму векторов
амплитуд напряжений (
,
подаваемого в колебательный контур,
можно представить как сумму векторов
амплитуд напряжений (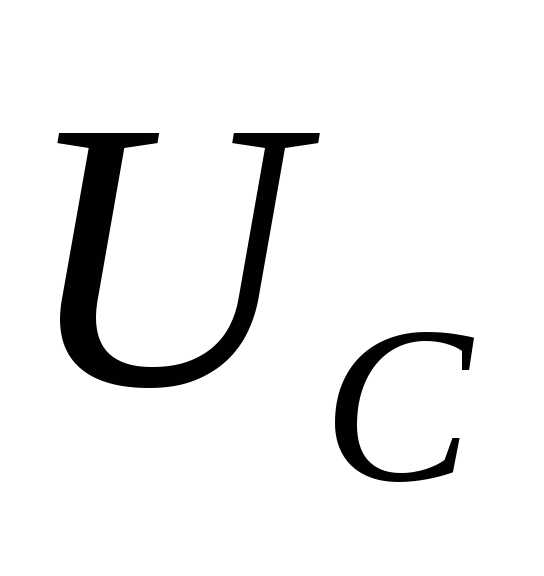 ,
,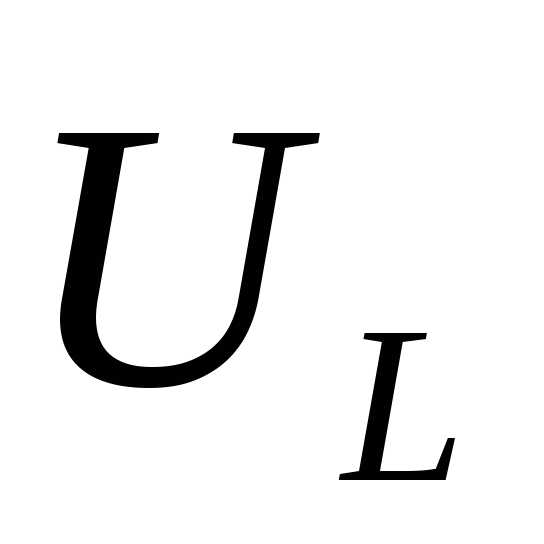 ,
,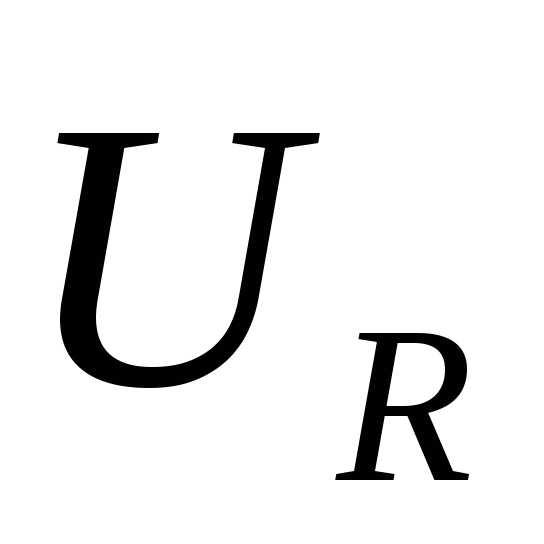 )
на разных его участках. Это позволяет
записать следующую формулу для модуля
вектора амплитуды внешнего напряжения
(например, для частот
)
на разных его участках. Это позволяет
записать следующую формулу для модуля
вектора амплитуды внешнего напряжения
(например, для частот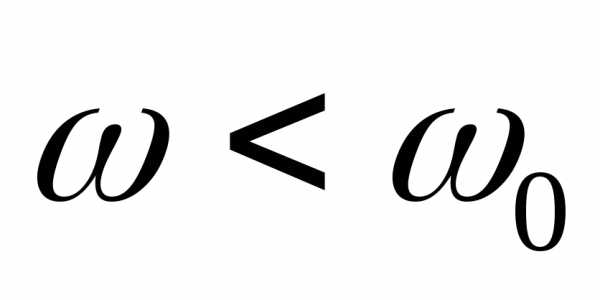 ,
рис. 5.20,а):
,
рис. 5.20,а):
, (5.81)
из которой с учетом формул (5.19) и (5.20) () можно получить выражение (5.65) для зависимости амплитуды колебания заряда от частоты внешнего напряжения
 .
.
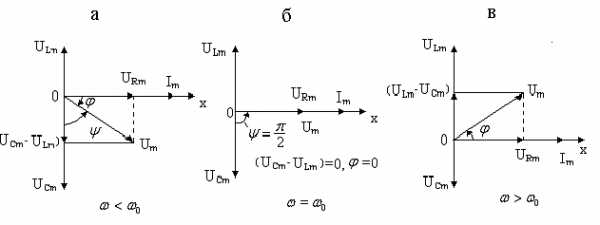
Рис. 5.20
Под фазовыми
резонансными кривыми понимают, например, зависимости разности
фаз
между внешним напряжением  и напряжением
и напряжением 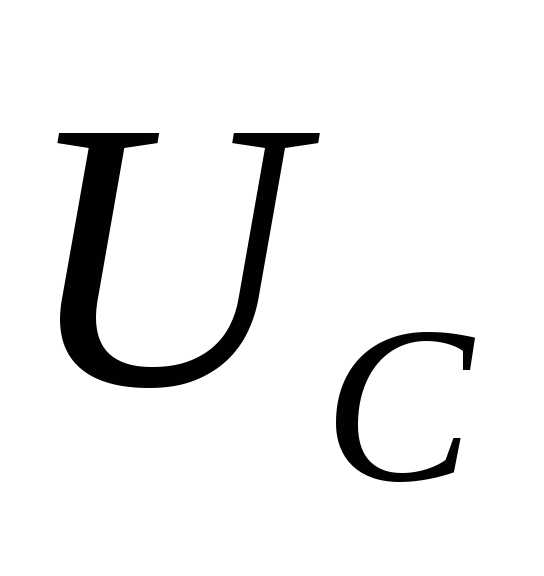 на конденсаторе, разности фаз
на конденсаторе, разности фаз  между внешним напряжением
между внешним напряжением  и силой токаI в контуре от частоты
и силой токаI в контуре от частоты  внешнего напряжения. Наиболее интересными
из них являются зависимости ,
так как они позволяют выяснить
эффективность поступления энергии в
контур (колебательную систему). В
соответствии с формулами (5.64) и (5.66) для
разности фаз
внешнего напряжения. Наиболее интересными
из них являются зависимости ,
так как они позволяют выяснить
эффективность поступления энергии в
контур (колебательную систему). В
соответствии с формулами (5.64) и (5.66) для
разности фаз  и
и  можно
записать
можно
записать
,. (5.82)
Отметим,
что разность фаз  для цепей переменного тока обозначают
буквой
для цепей переменного тока обозначают
буквой  :
.
:
.
На
рис. 5.21 приведены фазовые резонансные
кривые
и,
построенные по формулам (5.66) и (5.82) при
значениях параметра  :
.
:
.
Рис. 5.21
Из
них следует, что внешнее напряжение
опережает по фазе напряжение на
конденсаторе на угол  .
На векторной диаграмме это означает,
что вектор амплитуды
.
На векторной диаграмме это означает,
что вектор амплитуды 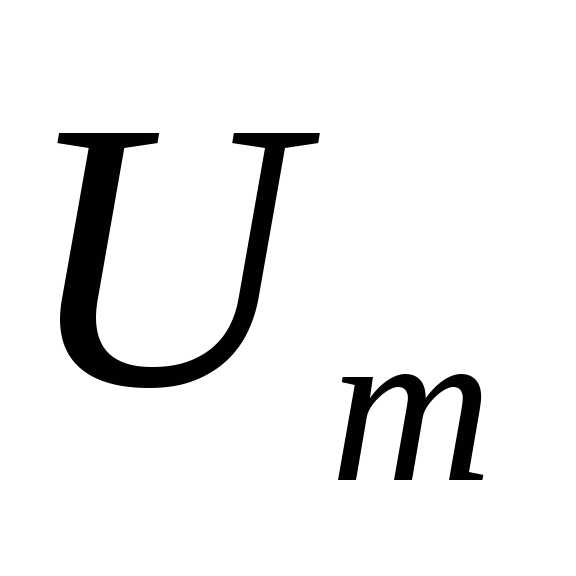 располагается выше вектора амплитуды
располагается выше вектора амплитуды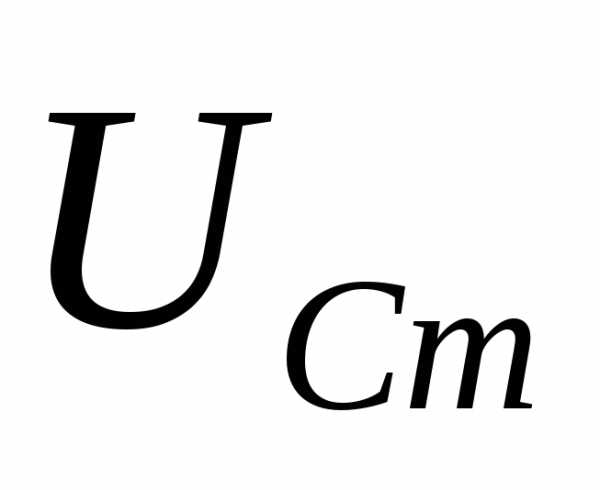 (рис. 5.20 а,б,в). Причем угол
(рис. 5.20 а,б,в). Причем угол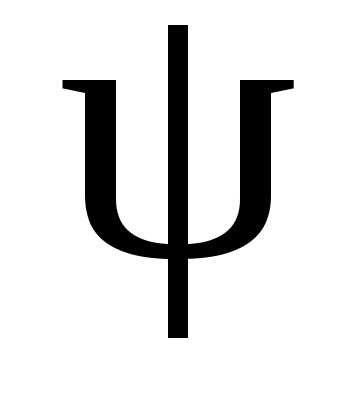 изменяется от нулевого значения для
частоты
изменяется от нулевого значения для
частоты  , равной нулю
(
, равной нулю
(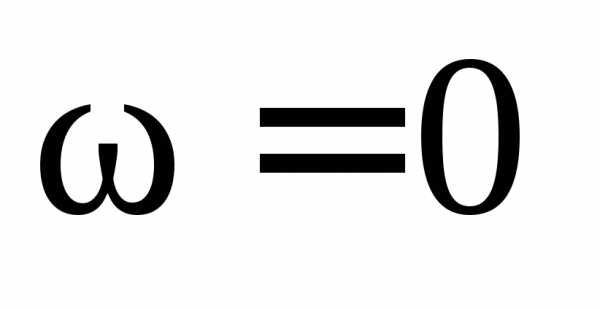 ),
до значения равного
),
до значения равного  при частоте внешнего напряжения
стремящегося к бесконечности (,
рис. 5.21,а). При резонансе амплитуды
векторов внешнего напряжения
при частоте внешнего напряжения
стремящегося к бесконечности (,
рис. 5.21,а). При резонансе амплитуды
векторов внешнего напряжения 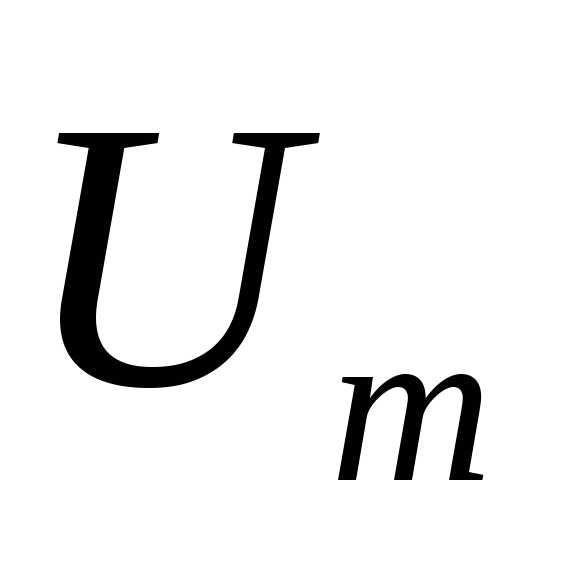 и напряжения на конденсаторе
и напряжения на конденсаторе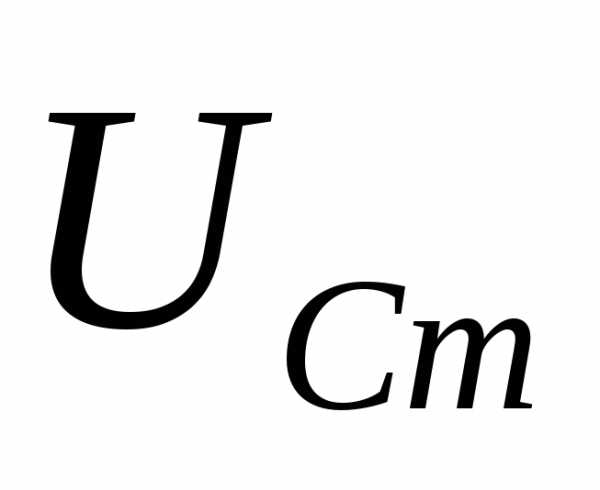 взаимно перпендикулярны (см. рис. 5.20,б),
что приводит к разности фаз между ними,
равной
взаимно перпендикулярны (см. рис. 5.20,б),
что приводит к разности фаз между ними,
равной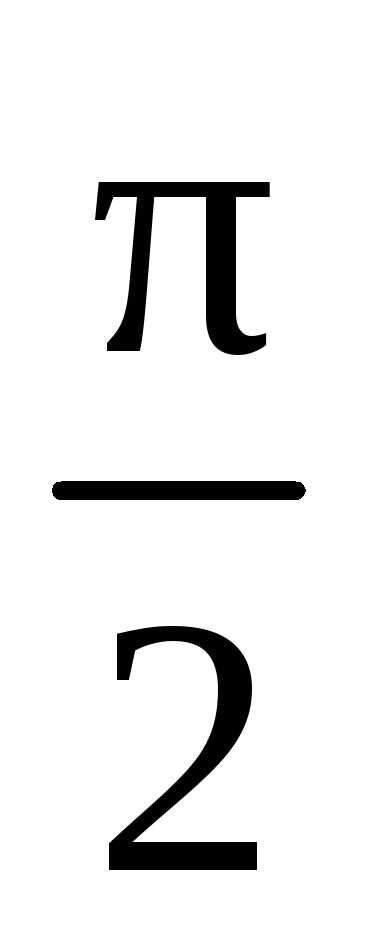 (,
Рис. 5.21,а).
(,
Рис. 5.21,а).
Из
другой фазовой резонансной кривой
следует, что фаза внешнего напряжения
для частот 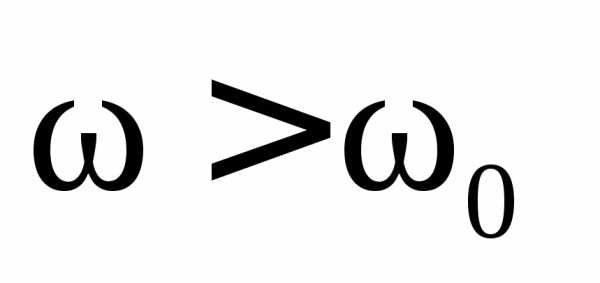 отстает от
фазы тока в контуре на угол
отстает от
фазы тока в контуре на угол  (рис.5.21,б). Для частот
(рис.5.21,б). Для частот 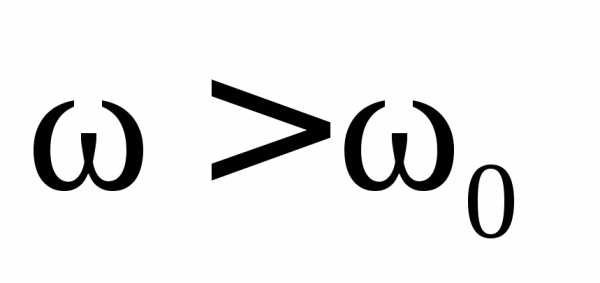 фаза внешнего
напряжения опережает на угол
фаза внешнего
напряжения опережает на угол  фазу колебаний силы тока в контуре и
при увеличении частоты
фазу колебаний силы тока в контуре и
при увеличении частоты  стремится к значению, равному
стремится к значению, равному 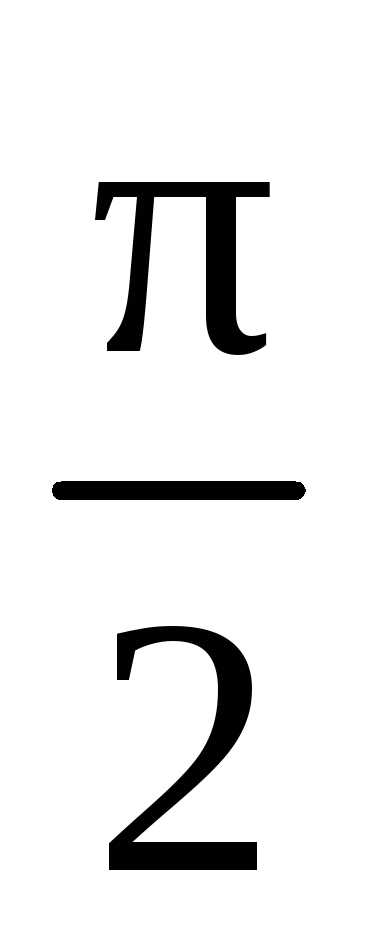 . При резонансе
(
. При резонансе
(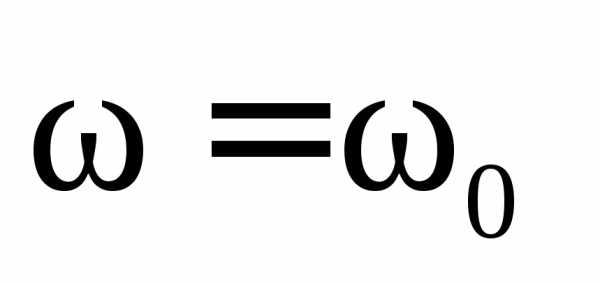 ,.)
фаза колебаний силы тока и внешнего
напряжения совпадают, т.е.
,.)
фаза колебаний силы тока и внешнего
напряжения совпадают, т.е.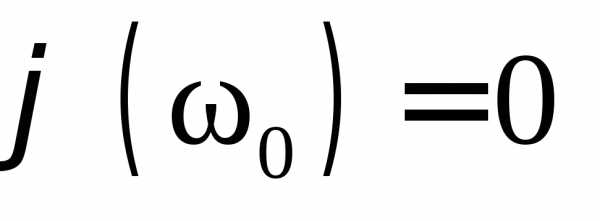 и вектора амплитуд
и вектора амплитуд 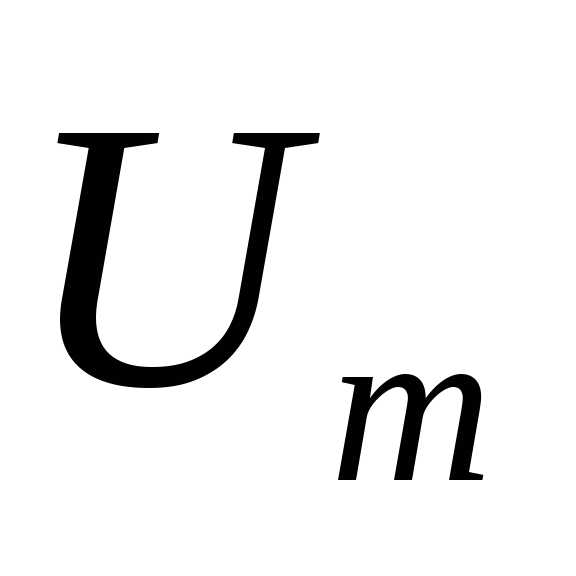 и
и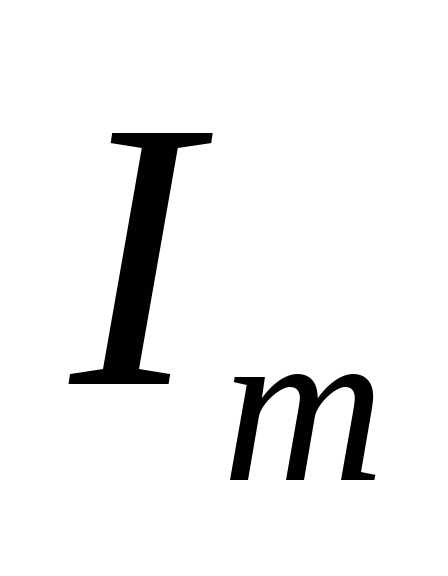 направлены одинаково, вдоль оси
направлены одинаково, вдоль оси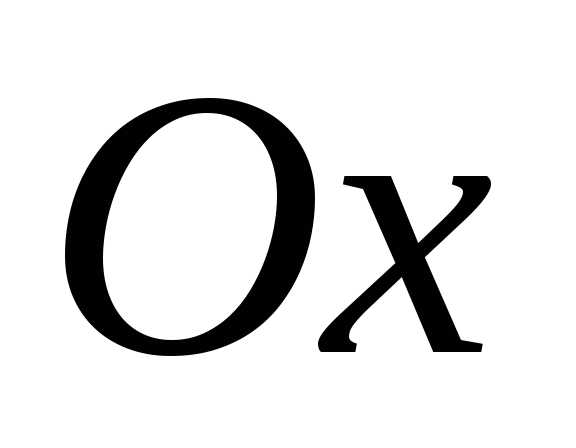 (рис.
5.21,б).
(рис.
5.21,б).
При этом энергия поступает в контур согласованно с колебаниями в ней. Действительно, учитывая выполнение условий малого затухания (Q >>1) и формулы (5.64) и (5.66) запишем
: ;
, .
Такое поступление энергии в контур при резонансе приводит к большим амплитудам колебаний, их числовые значения определяются диссипацией (рассеянием) энергии системы, т. е. коэффициентом затухания (формула (5.70)).
При
частотах  ,
больших или меньших
,
больших или меньших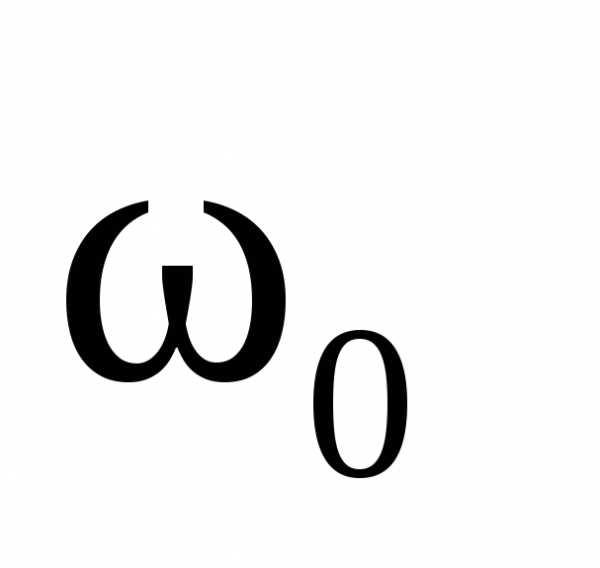 ()
амплитуда вынужденных колебаний даже
в отсутствии диссипации энергии (
()
амплитуда вынужденных колебаний даже
в отсутствии диссипации энергии ( )
будет уменьшаться, она определяется
расстройкой резонанса (
)
будет уменьшаться, она определяется
расстройкой резонанса (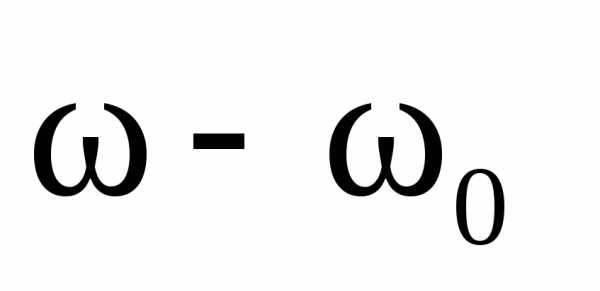 ),
т.е. разностью частот
),
т.е. разностью частот  и
и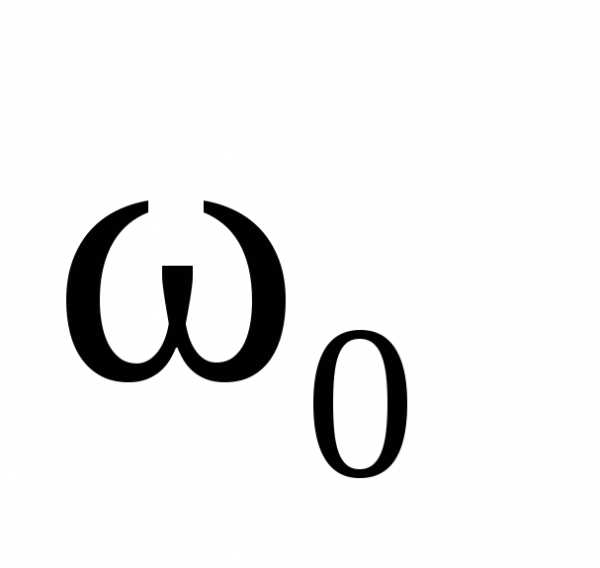 .
.
Можно отметить, что с использованием таблицы аналогий можно построить фазовые резонансные кривые для разности фаз между скоростью колебаний тела и действующей на него внешней силой в случае механической системы и т.д.
studfile.net
в цепи переменного тока и напряжения
Многие люди, изучая электронику и все, что с ней связано, сталкиваются с таким понятием как резонанс токов. Что оно собой представляет, при каких условиях возникает резонанс токов, как используется и как его правильно подсчитать? Об этом далее.
Что это такое
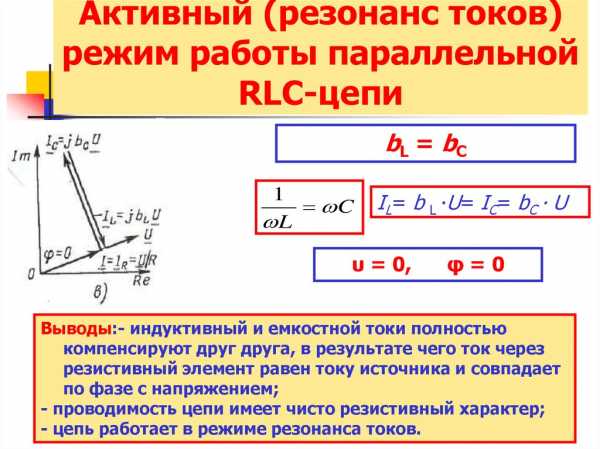
Резонанс токов — разновидность состояния электрической цепи, когда общий вид токовых показателей совпадает по фазам уровню напряжения, а мощность реактивного вида равна нулю или же она представлена в активном виде.

. Резонанс токов
Этот вариант развития событий характерен для переменного тока и имеет не только положительные свойства, но и некоторые нежелательные последствия. Так, благодаря резонансу работает радиотехника, автоматика и проволочная телефония, но в то же время возникают перенапряжения и сбои в работе электрической системы.

Определение из учебного пособия
При каких условиях возникает
Условием того, чтобы возникло это явление, является равные показатели проводниковой частоты, где BL=BC. То есть емкостная с индуктивной проводимостью должна быть равна. Только тогда подобное явление резонанса токов наблюдается в электрической цепи. Он при этом может быть как положительным, так и отрицательным. В любом радиоприемнике есть колебательный контур, который из-за индуктивного или емкостного изменения, настраивается на нужный сигнал радиоволны. В другом случае, это ведет к тому, что появляются скачки напряжения или ток в цепи и появляется аварийная ситуация.
В условиях лаборатории, он возникает во время, когда изменяется емкость и не изменяется индуктивность катушки L. В таком случае формула выглядит как Bc=C

При каких условиях возникает
Как используется
Резонансные токи используются сегодня в некоторых фильтрующих системах, радиотехнике, электричестве, радиостанциях, асинхронных двигателях, высокоточных электрических сварных установках, колебательных генераторных электрических контурах и высокочастотных приборах. Нередко, когда они применяются, чтобы снизить генераторную нагрузку.
Обратите внимание! Простейшая цепь, где наблюдаются они, это параллельного вида колебательный контур. Такие контуры используются в современном промышленном индукционном котловом оборудовании и улучшают показатели КПД.
Сфера применения
Принцип действия
Токовый резонанс можно заметить во внутренней поверхности электрической цепи, которая имеет параллельное катушечное, резисторное и конденсаторное подсоединение. Главный принцип того, как работает стандартный аппарат, не сложен в понимании.
Когда включается электрическое питание, внутри конденсаторной установки накапливается заряд до номинального напряжения. В этом время отключается питающий источник и замыкается цепь в контур. Этот момент сопровождается переносом разряда на часть катушки. Далее показатели тока, которые проходят по катушке, генерируют магнитное поле. Создается электродвижущая самостоятельная индукционная сила по направлению встречному току. При полном конденсаторном разряде максимально увеличиваются токовые показатели. Объем энергии становится магнитным индукционным полем. В результате данный цикл повторяется, и катушечное поле преобразовывается в конденсаторный заряд.
Принцип работы
Как правильно рассчитать
Токовый резонанс очень важно правильно рассчитать, если есть параллельное соединение, предотвращающая появление помех около системы. Для правильного расчета необходимо понять, какие показатели мощности в электросети. Средняя стандартная мощность, рассеивающаяся при резонансном контуре, выражается при помощи среднеквадратичных токовых показателей и напряжения. При резонансе мощностный коэффициент равен единице и формула имеет вид, как на картинке.
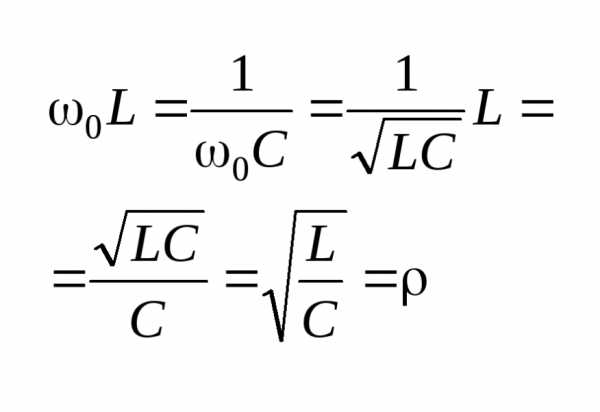
Формула расчета
Чтобы правильно определить нулевой импеданс, понадобиться воспользоваться стандартной формулой, которая дана ниже.
Формула резонансных кривых
Что касается аппроксимирования резонанса колебательных частот, это можно выяснить по следующей формуле.
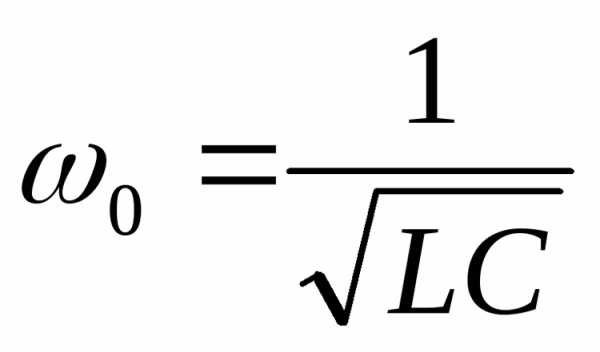
Расчет колебательного контура
Обратите внимание! Для получения максимально точных данных по приведенным формулам, округлять данные не нужно. Благодаря этому получится грамотный расчет, который приведет к достойной экономии переменного тока, если речь идет о подсчете в целях снижения счетов.
В целом, резонанс токов — это то, что происходит в части параллельного колебательного контура, в случае его подключения к источнику напряжения, частота какого может совпадать с контурной. Возникает при условиях, когда цепь, имеющая параллельное соединение резисторной катушки и конденсатора, равна проводимости BL=BC. Правильно сделать весь необходимый подсчет можно по специальной формуле или, прибегая к использованию специальных измерительных инструментов в виде мультиметра.
rusenergetics.ru
Резонансные кривые
Зависимость параметров цепи от частоты характеризуется резонансными кривыми.
|
|
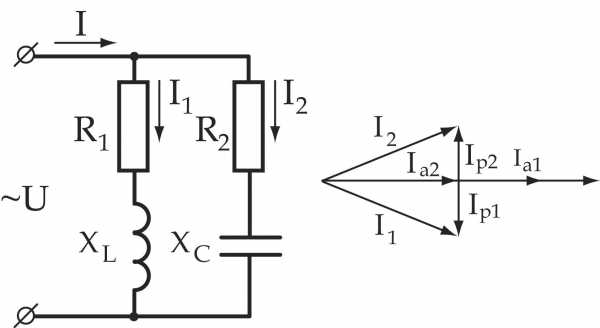
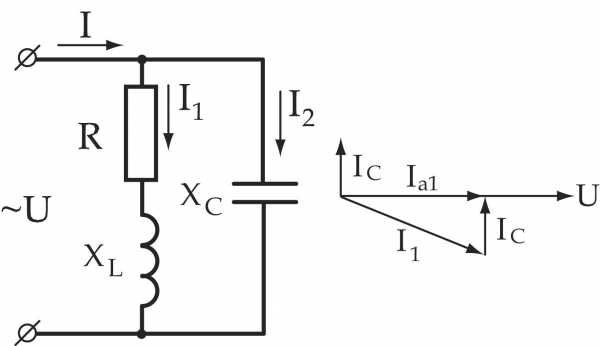
Разветвленные цепи переменного тока
Рассмотрим цепь с двумя параллельно соединенными катушками.
Для определения
тока неразветвленной части цепи
необходимо разложить токи 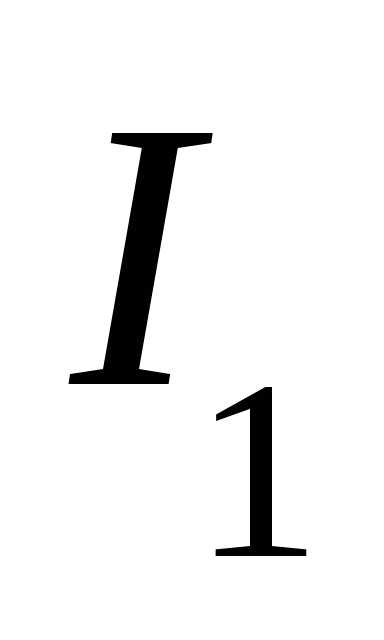 и
и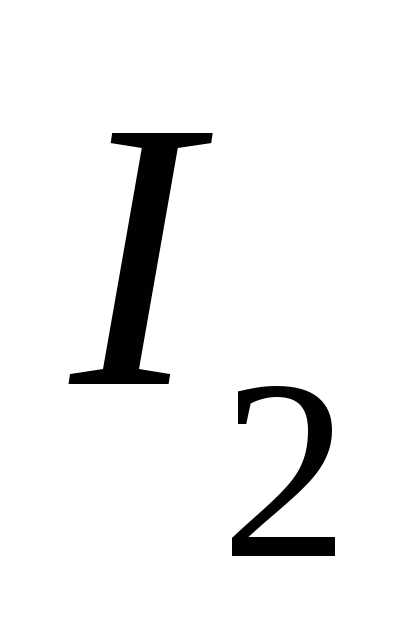 на активные и реактивные составляющие.
на активные и реактивные составляющие.
Метод проводимостей
При
этом ток каждой ветви рассматривают
как бы состоящим из двух составляющих:
активной 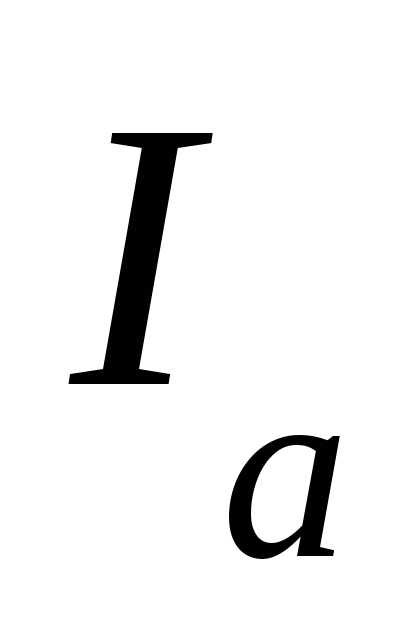 и реактивной
и реактивной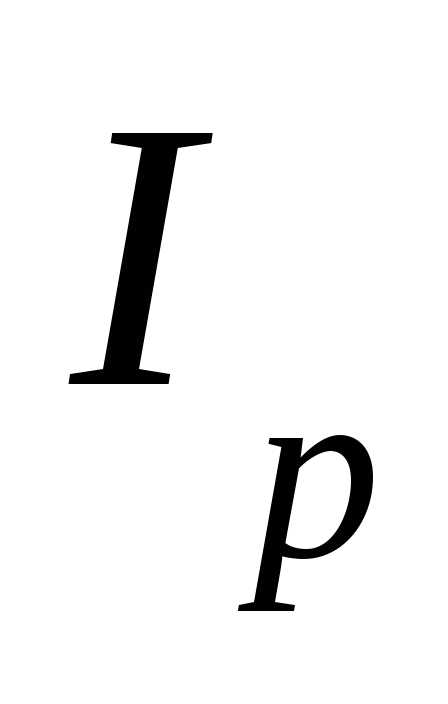 .
.
,
где 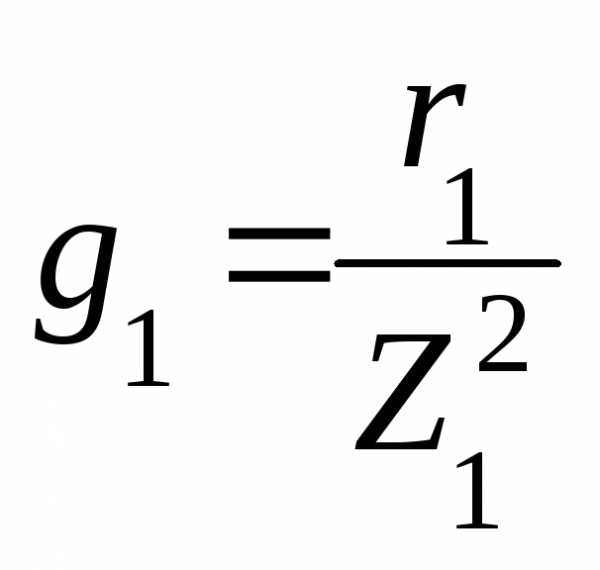 —активная
проводимость ветви
—активная
проводимость ветви
,
где 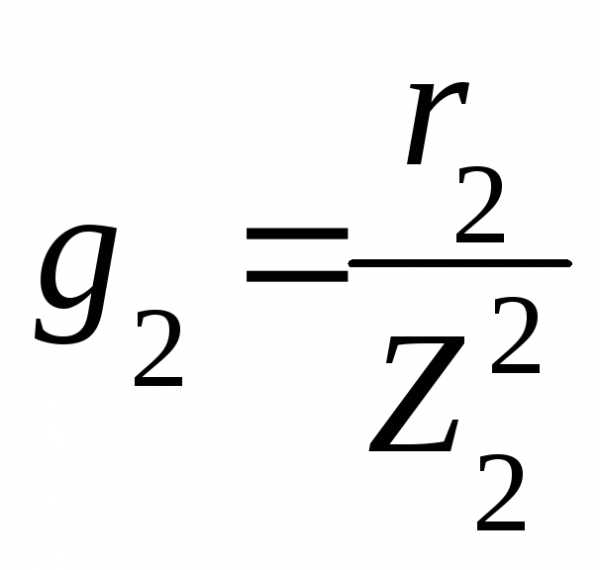
,
где 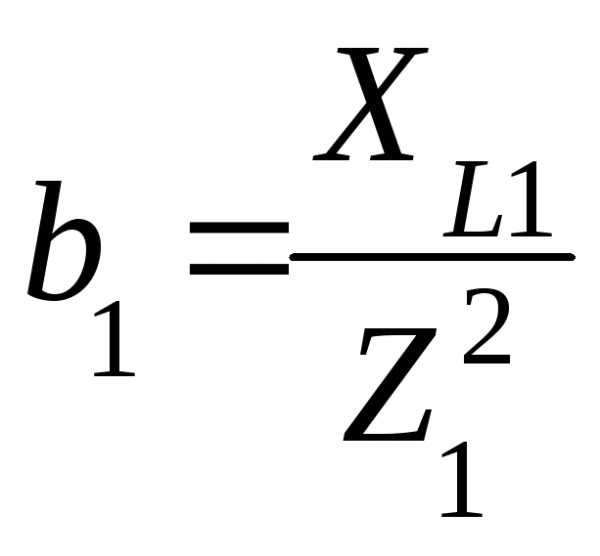 —реактивная
проводимость ветви
—реактивная
проводимость ветви
, где 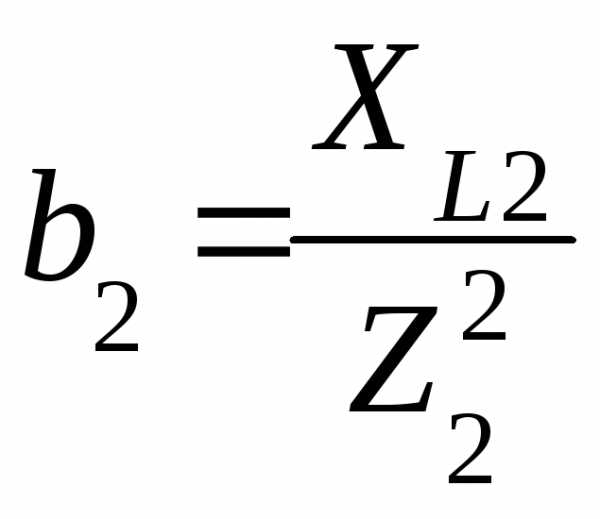
где
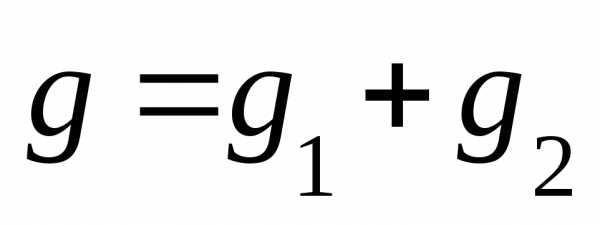 —
полная активная проводимость цепи;
—
полная активная проводимость цепи;
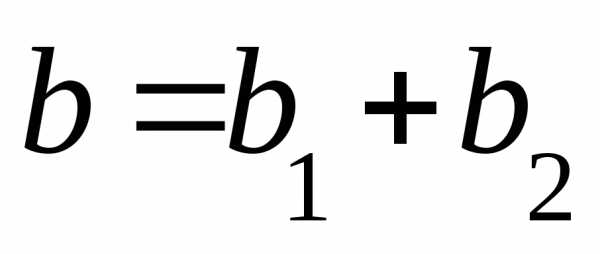 —
полная реактивная проводимость цепи.
—
полная реактивная проводимость цепи.
, где
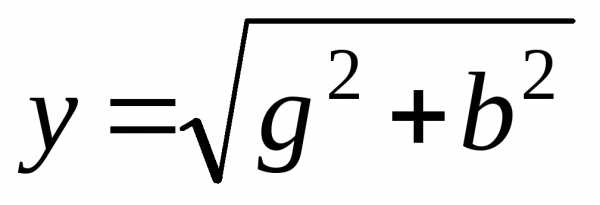 —
полная проводимость цепи.
—
полная проводимость цепи.
.
Порядок расчета
1. Определяем активные, реактивные и полные проводимости ветвей по формулам:
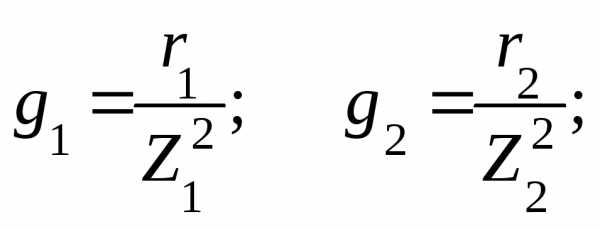
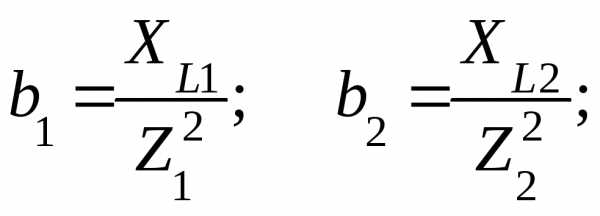
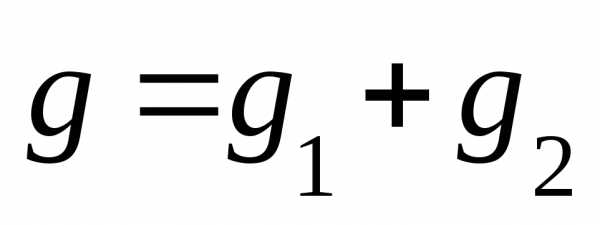
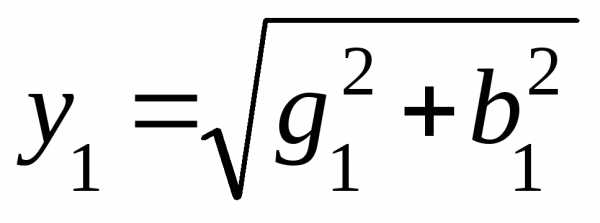
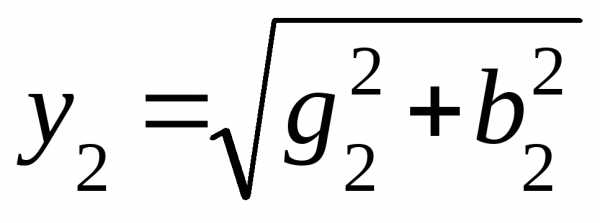
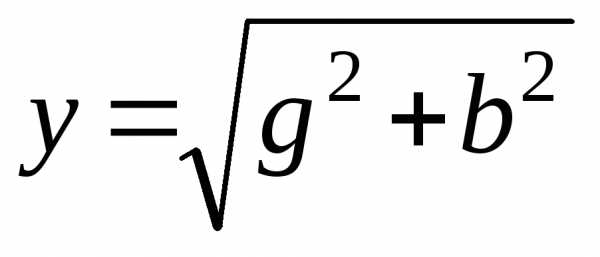
2. Определяем
токи в ветвях: 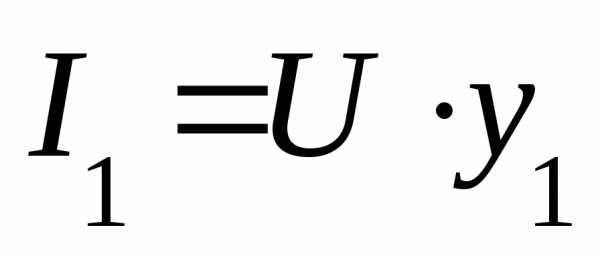
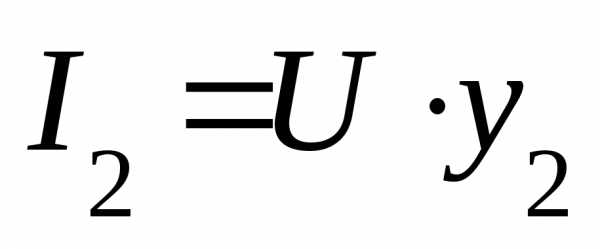
3. Определяем мощности ветвей и всей цепи:
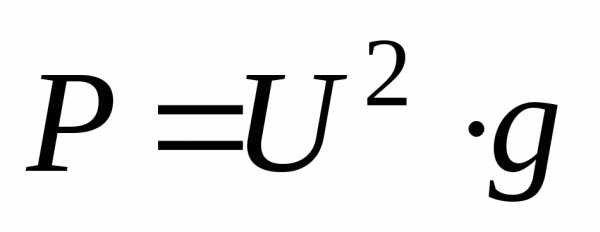
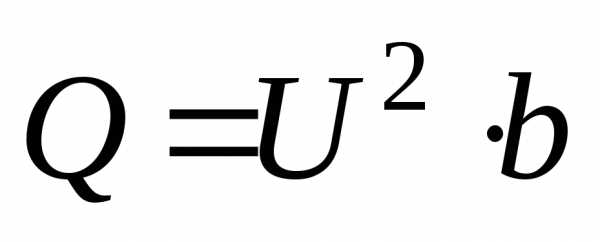
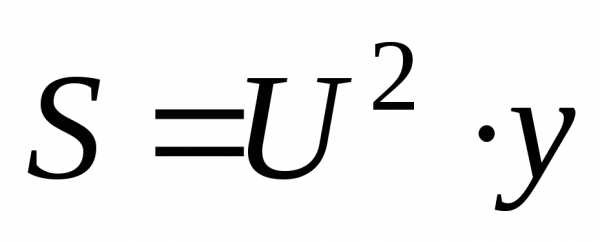 .
.
Параллельное соединение активно-индуктивного и активно-емкостного сопротивления
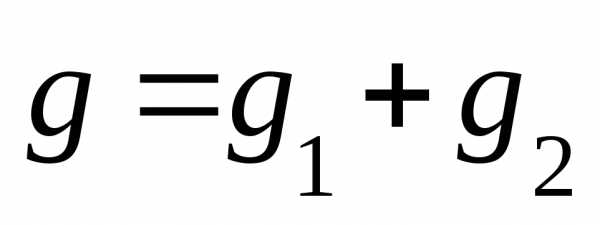
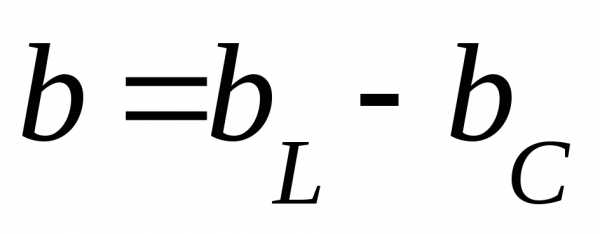
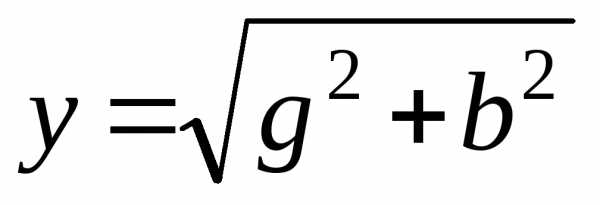
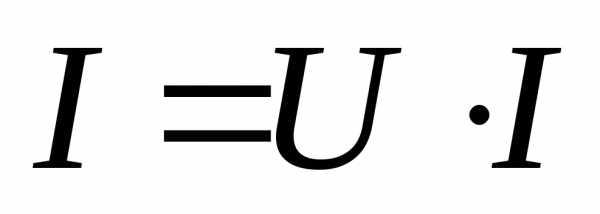
Общий случай неразветвленной цепи
Резонанс токов
В цепи резонанс токов наступает, если .
|
|
Реактивная проводимость всей цепи
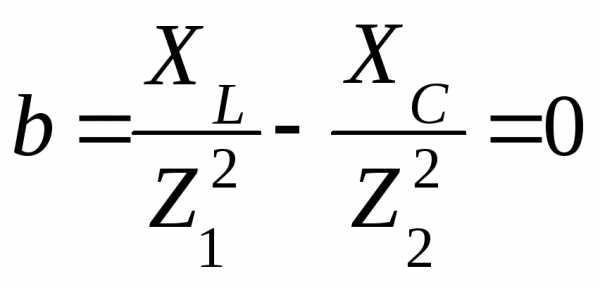
Решая это уравнение относительно частоты, получим выражение для резонансной частоты:
При резонансе полная проводимость цепи будет минимальной, а полное сопротивление – максимальным. Следовательно, ток будет минимальным.
| Реактивные мощности ветвей равны, поэтому реактивная мощность всей цепи равна нулю. Это означает, что обмена энергией между цепью и источником нет. Источник обеспечивает цепь только активной энергией. |
Активная и реактивная энергии
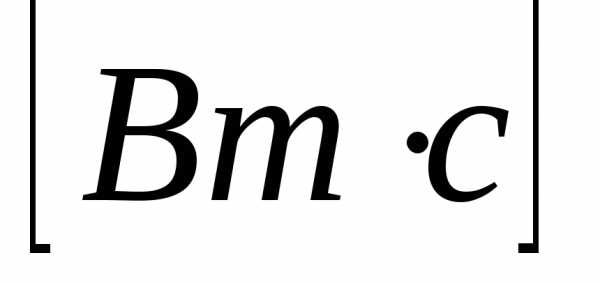 — измеряется счетчиком активной энергии.
Характеризует энергию, израсходованную
в цепи переменного тока.
— измеряется счетчиком активной энергии.
Характеризует энергию, израсходованную
в цепи переменного тока.
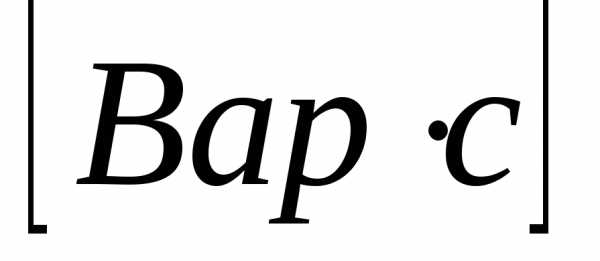 — является расчетной величиной. Измеряется
счетчиком реактивной энергии.
— является расчетной величиной. Измеряется
счетчиком реактивной энергии.
Коэффициент мощности и его значения
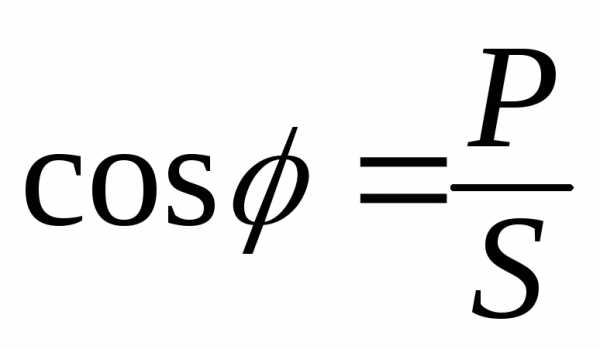
Электрические и другие устройства характеризуются:
номинальным током;
номинальным напряжением;
номинальной мощностью.
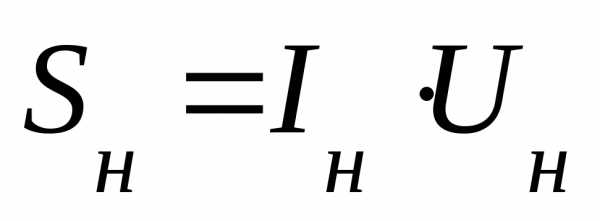 .
.
Полное использование
мощности генератора происходи при 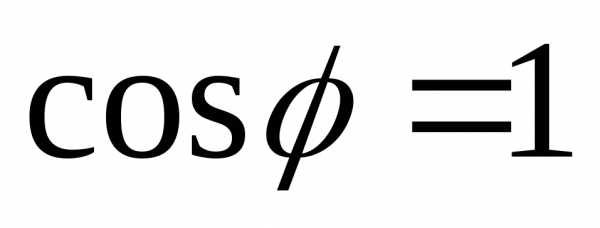 ,
т.к..
,
т.к..
При уменьшении 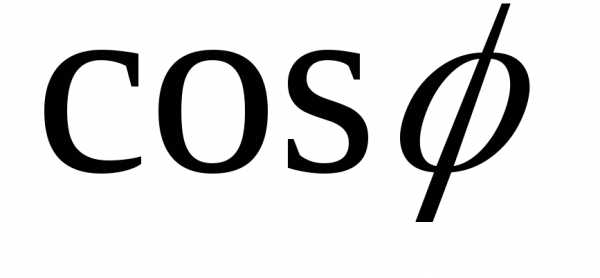 ,
величина которого определяется приемником
электроэнергии, мощность генератора
используется не полностью.
,
величина которого определяется приемником
электроэнергии, мощность генератора
используется не полностью.
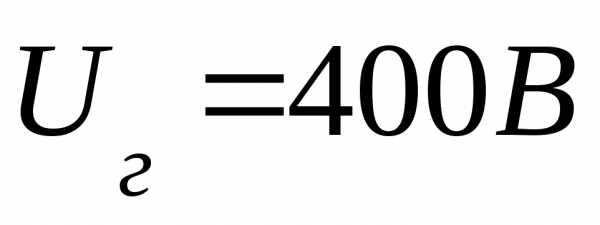
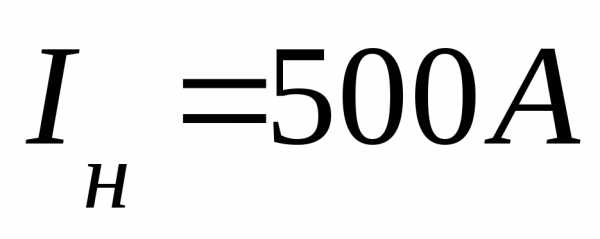
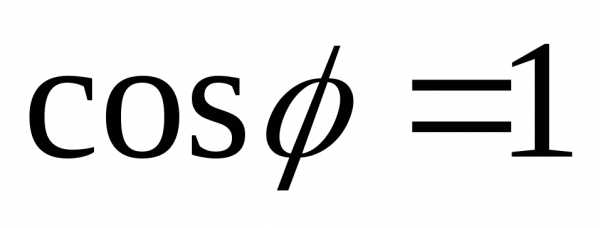
Т.о., увеличивая
значение 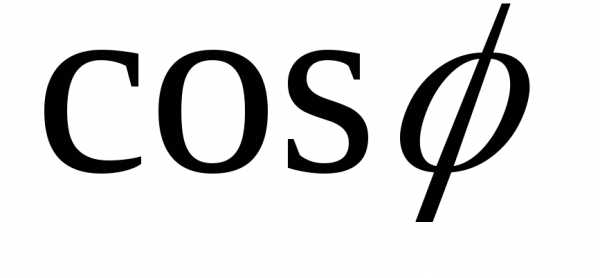 мы добивается того, что мощность
генератора используется полностью.
мы добивается того, что мощность
генератора используется полностью.
Способы повышения 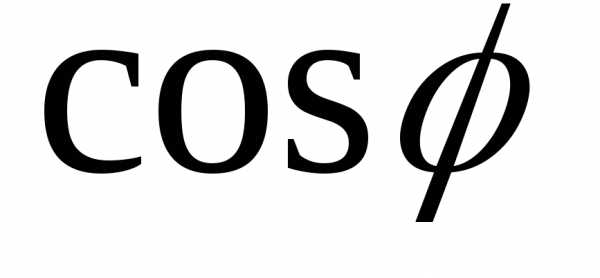
1. Соответствие мощности механизма и мощности электродвигателя, приводимого им (естественный способ).
2. Включение батареи конденсаторов параллельно потребителям.
3. Использование синхронных компенсаторов.
| На
практике пользуются средним
значением |
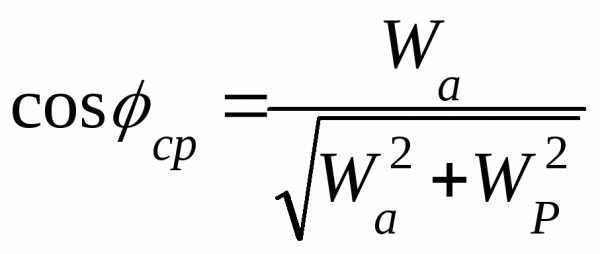
Комплексный метод расчета цепей переменного тока
Комплексным
числомназывается сумма вещественного
числа и мнимого
и мнимого .
.
где 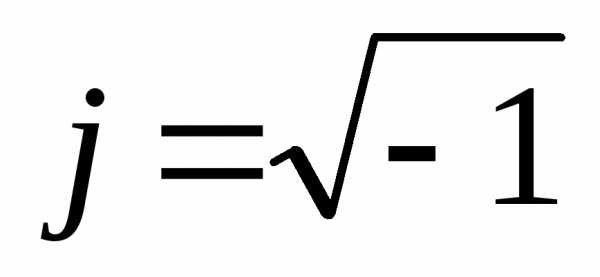 .
.
|
|
Различают алгебраическую, тригонометрическую и комплексную форму записи комплексного числа.
алгебраическая тригонометрическая показательная
studfile.net
Резонанс напряжений и резонанс токов
В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.
Резонанс напряжений
Резонанс напряжений возникает в последовательной RLC-цепи.
Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=wр, а следовательно и индуктивного и емкостного сопротивлений xL=xC. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке UL и на конденсаторе UC будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.
При резонансе напряжения UC и UL могут быть намного больше, чем напряжение источника, что опасно для цепи.
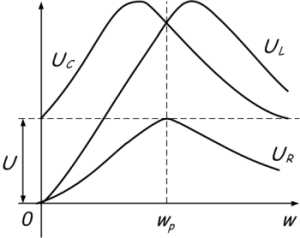
С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.
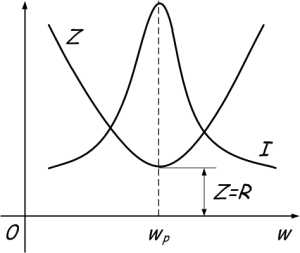
Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту
Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.
Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.
Резонанс токов
Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.
Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.
Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.
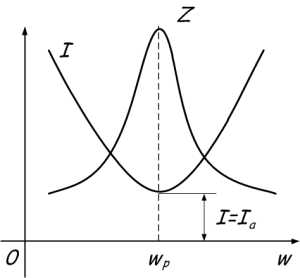
Выразим резонансную частоту
Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.
Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.
electroandi.ru
РЕЗОНАНСНЫЕ КРИВЫЕ ТОКА И НАПРЯЖЕНИЯ
Рисунок 11.5
Рисунок 11.4
Рисунок 11.3
Рисунок 11.2
Рисунок 11.1
Кривая, которая соединяет концы векторов , носит название годографа передаточной функции (годографом амплитудно-фазовой характеристики). Годограф строят при изменении частоты от нуля к бесконечности.
Пример.Определить комплексный коэффициент передачи по напряжению , АЧХ и ФЧХ для схемы (рис.11.2а).
Согласно с определением: . Задача решается в такой последовательности: 1) задаемся ; 2) определяем комплексное значение выходного напряжения по закону Ома:
;
3) находим ;
4) подаем в показательной форме, находим АЧХ и ФЧХ (рис.11.2б,в):
.
а) б) в)
11.2 Последовательный резонансный контур.
Размещено на реф.рф
Определение и условия резонанса
Колебательный контур — электрический круг, в котором возможны колебание свободной составной тока. Резонансный контур — электрическая цепь, в которой имеет место явление резонанса (напряжений или токов).
Последовательный резонансный контур — резонансный контур, который состоит из индуктивного и емкостного элементов, соединенных последовательно (рис.11.3а,б). На схеме (рис.11.3в) R, L, C — первичные параметры контура, причем , где — активное сопротивление катушки индуктивности, — сопротивление растекания конденсатора, перерасчитанное в последовательное соединение, — сопротивление проводов (потерь). Чтобы дать определение резонанса, найдем ток в цепи (рис.11.3в):
,
где — реактивное сопротивление контура.
Запишем комплексное действующее значение тока в показательной форме
,
где — полное сопротивление контура.
Итак, резонанс — это явление в электрической цепи, которая имеет участки с индуктивными и емкостными элементами, по которому разница фаз напряжения и тока на входе цепи равняется нулю.
Из этого определения вытекает, что полное сопротивление контура должно быть активным. Тогда реактивное сопротивление или проводимость цепи, в которой наблюдается резонанс, равняются нулю.
а) б) в)
Итак, в случае если в общем случае действительны соотношения
; , то при резонансе:
1) — это условие амплитудного резонанса;
2) ; ; — условие возникновения фазового резонанса.
11.3 Вторичные параметры последовательного резонансного контура
1. Резонансная частота — частота тока (напряжения) во время резонанса в цепи. Обозначается и определяется, исходя из условия резонанса X = 0; :
; .
Значению циклической частоты соответствует резонансная длина волны:
,
где c — скорость распространение электромагнитных волн.
2. Характеристическое (волновое) сопротивление контура — сопротивление каждого из реактивных элементов при резонансе: .
3. Добротность — отношение характеристического сопротивления к активному сопротивлению контура: , где d — затухание — величина, обратная к добротности, которая характеризует интенсивность затухания колебаний в контуре.
Добротность характеризует длительность собственных колебаний в контуре, ее можно определить также как коэффициент качества, который равняется отношению абсолютного значения реактивной мощности к активной мощности.
4. Полное сопротивление — модуль входного комплексного сопротивления контура Z .
,
где — модуль Z;
— аргумент Z.
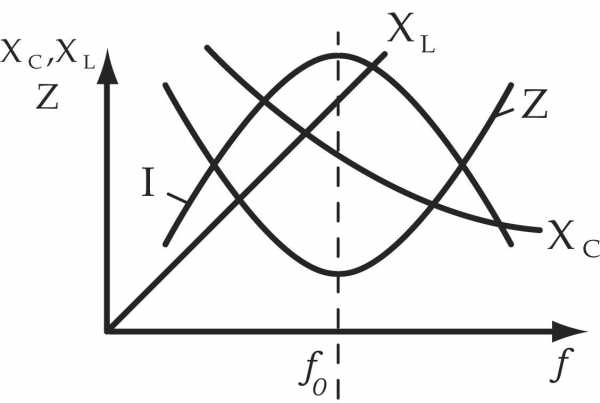
Частотные зависимости полного и реактивного сопротивления , изображены на рис.11.4. Из графика видно, что на резонансной частоте реактивное сопротивление контура равняется нулю, а равняется сопротивлению потерь R.
а) б)
5. Фазовая характеристика — зависимость аргумента входного сопротивления последовательного контура от частоты (рис.11.5а): .
6. Резонансная кривая тока — зависимость модуля комплексного действующего (амплитудного) значения тока от частоты (рис.11.5б):
.
Очевидно, что на частоте резонанса , выполняются такие соотношение: , .
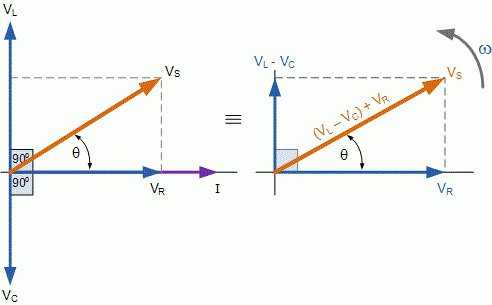
11.4 Векторная диаграмма напряжений при резонансе
Запишем для последовательного резонансного контура уравнения по второму закону Кирхгофа:
.
В случае если частота равняется резонансной частоте , то
,
где — напряжение на сопротивлении R при резонансе;
— напряжение на индуктивности при резонансе;
— напряжение на емкости при резонансе.
В соответствии с полученными выражениями на рис.11.5в изображена векторная диаграмма тока и напряжений при резонансе. Как видно из рисунка, при выполняются такие соотношения:
1) напряжение на сопротивлении R совпадает по фазе с током I, а модуль равняется значению E; напряжения на реактивных элементах равны между собой по модулю и противоположны по направлению;
2) по абсолютной величине напряжения на реактивных элементах последовательного резонансного контура в Q раз превышают значение ЭДС, которая действует на входе: . Итак, в последовательном контуре наблюдается резонанс напряжений.
Резонанс напряжений — явление резонанса на участке электрической цепи, в которую входят последовательно соединенные индуктивный и емкостной элементы.
а) б) в)
referatwork.ru

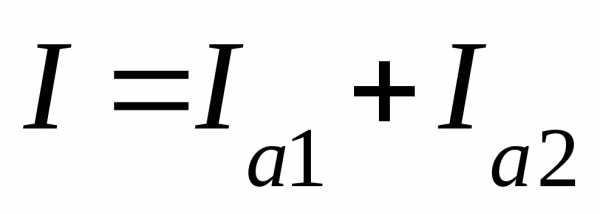 —
чисто активный характер, т.к. реактивные
точки
—
чисто активный характер, т.к. реактивные
точки 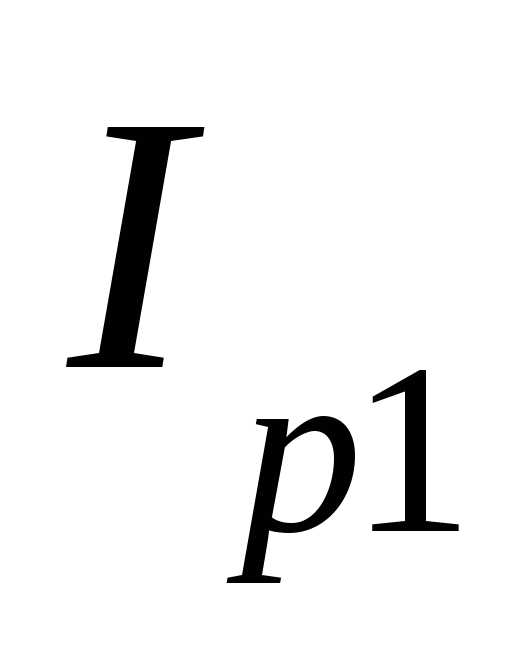 икомпенсируют друг друга
икомпенсируют друг друга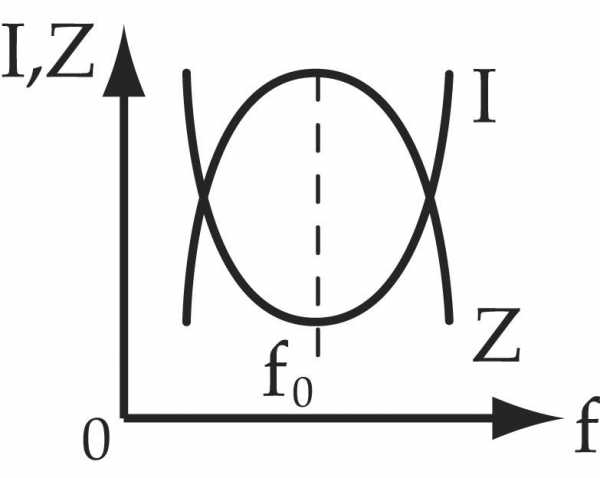
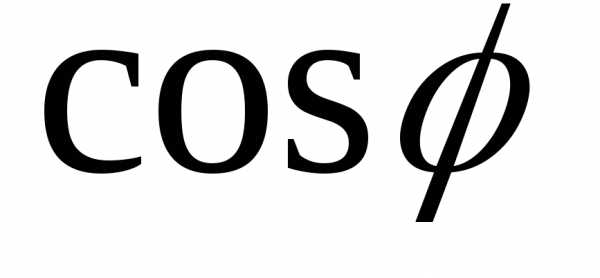 .
Для этого с помощью счетчиков измеряют
активную (
.
Для этого с помощью счетчиков измеряют
активную (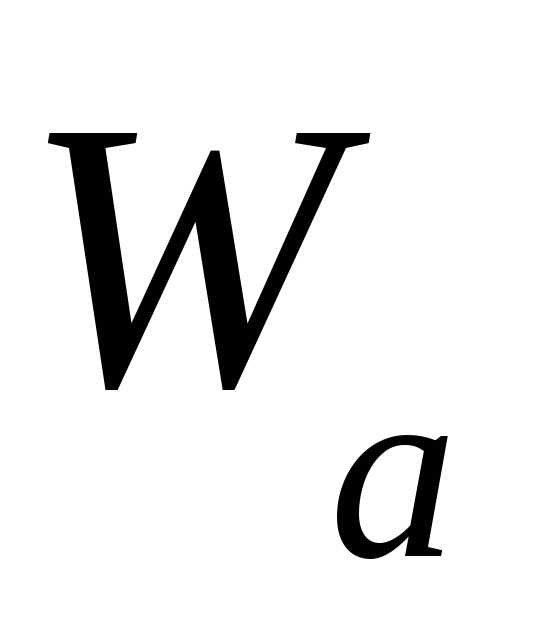 )
и реактивную (
)
и реактивную (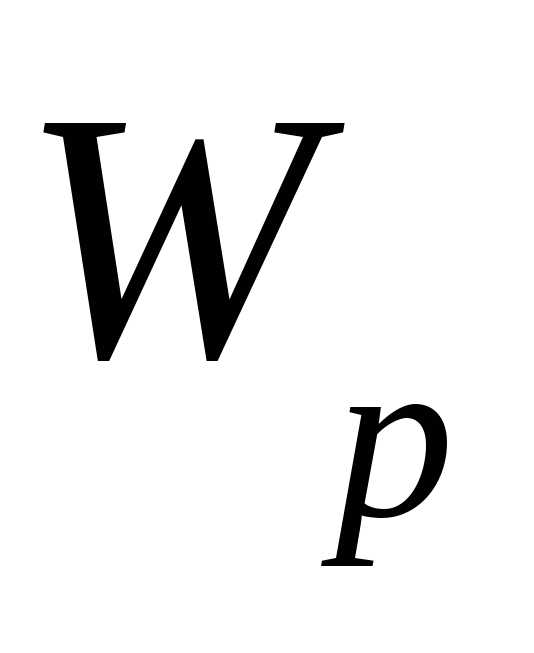 )энергии.
)энергии.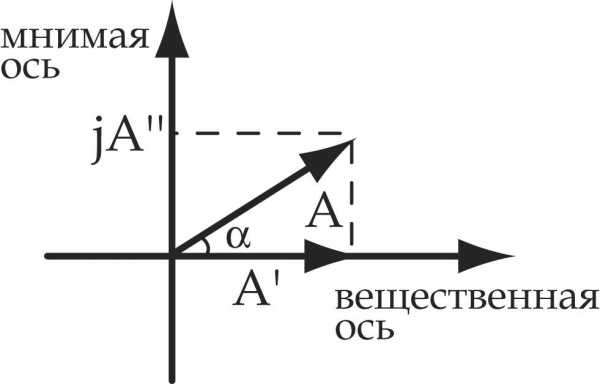
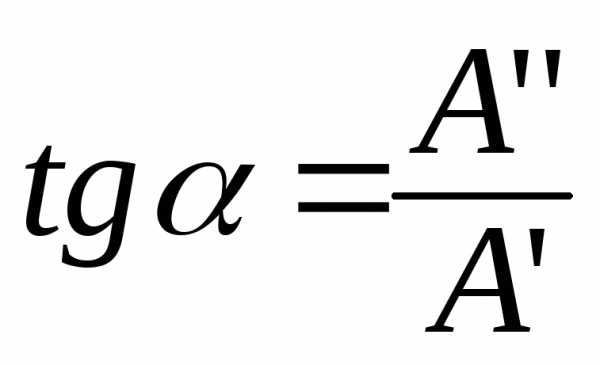
 —
аргумент комплексного числа
—
аргумент комплексного числа