Схема и резонансные кривые для резонанса токов.
Поиск ЛекцийРезонанс напряжений в цепи переменного тока.
Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем если бы они были включены в цепь по отдельности.
Резонанс напряжений возникает в последовательной RLC-цепи.
От одновременного действия двух различных по своему характеру реактивных сопротивлений в цепи происходит компенсация (взаимное уничтожение) сдвига фаз.
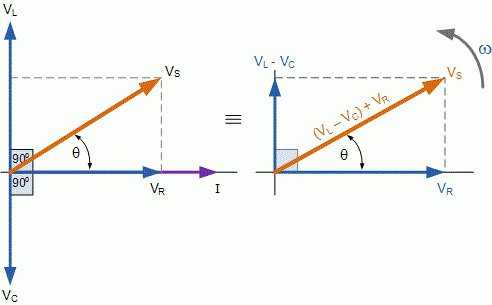
Полная компенсация, т. е. полное уничтожение сдвига фаз между током и напряжением в такой цепи, наступит тогда, когда индуктивное сопротивление окажется равным емкостному сопротивлению цепи, т. е. когда X
ωL = 1 / ωС.
Цепь в этом случае будет вести себя как чисто активное сопротивление, т. е. как будто в ней нет ни катушки, ни конденсатора. Величина этого сопротивления определится суммой активных сопротивлений катушки и соединительных проводов. При этом действующее значение тока в цепи будет наибольшим и определится формулой закона Ома
I = U / R,
Где вместо Z теперь поставлено R.
Одновременно с этим действующие напряжения как на катушке UL = IXL так и на конденсаторе Uc = IХС окажутся равными и будут максимально большой величины. При малом активном сопротивлении цепи эти напряжения могут во много раз превысить общее напряжение U на зажимах цепи. Это интересное явление называется в электротехнике резонансом напряжений.
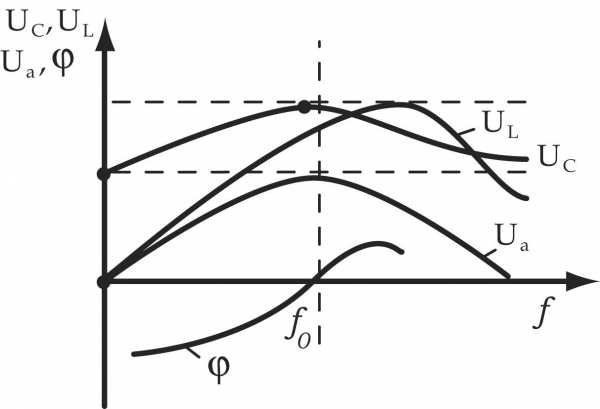
Кривые напряжений, тока и мощности при резонансе напряжений в цепи.
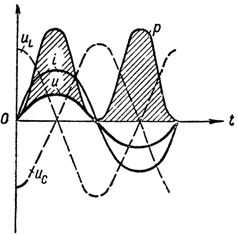
Сопротивления XL и ХС являются переменными, зависящими от частоты тока, и стоит хотя бы немного изменить частоту его, например, увеличить, как XL = ωLвозрастет, а ХС = 1 / ωС уменьшится, и тем самым в цепи сразу нарушится резонанс напряжений, при этом наряду с активным сопротивлением в цепи появится и реактивное. То же самое произойдет, если изменить величину индуктивности или емкости цепи.
При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.
Цепь переменного тока, состоящая из генератора и последовательно соединенных катушки индуктивности и конденсатора, при определенных условиях X
Из равенства XL = ХС можно определить значения частоты генератора, при которой наступает явление резонанса напряжений:
Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений:
Таким образом, изменяя любую из этих трех величин (fрез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур.
Резонанс токов.
Резонанс токов, параллельный резонанс — получается в случае, когда генератор нагружен на индуктивность и емкость, соединенные параллельно, т.е. когда генератор вне контура..
Весь контур в целом является нагрузочным сопротивлением для генератора и поэтому генератор
Схема и резонансные кривые для резонанса токов.
включен последовательно, как это и бывает всегда в замкнутой цепи.
Условия получения резонанса токов такие же, как и для резонанса напряжений: f = f0 или xL = хC. Однако по своим свойствам резонанс токов во многом противоположен резонансу напряжений. В этом случае на катушке и на конденсаторе напряжение такое же, как у генератора. При резонансе сопротивление контура между точками разветвления становится максимальным, а ток генератора будет минимальным. Полное (эквивалентное) сопротивление контура для генератора при резонансе токов Rэ можно подсчитать по любой из следующих формул
,
где L и С — в генри и фарадах, а Rэ, р и r — в омах.
Сопротивление Rэ
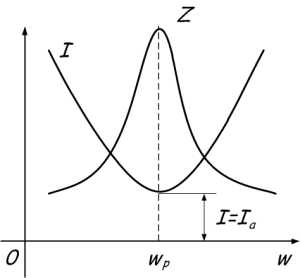
На (рис.1 б) для резонанса токов показано изменение полного сопротивления контура z и тока генератора I при изменении частоты генератора f.
В самом контуре при резонансе происходят сильные колебания и поэтому ток внутри контура во много раз больше, чем ток генератора. Токи в индуктивности и емкости IL и IС можно рассматривать как токи в ветвях или как ток незатухающих колебаний внутри контура, поддерживаемых генератором. По отношению к напряжению U ток в катушке отстает на 90°, а ток в емкости опережает это напряжение на 90°, т. е. друг относительно друга токи сдвинуты по фазе на 180°. Вследствие наличия активного сопротивления, сосредоточенного главным образом в катушке, токи IL, и IC в действительности имеют сдвиг фаз несколько меньше 180° и ток IL немного( меньше I C. Поэтому по первому закону Кирхгофа для точки разветвления можно написать
Чем меньше активное сопротивление в контуре, тем меньше разница между IC и IL, тем меньше ток генератора и тем больше сопротивление контура. Ток, идущий от генератора, пополняет энергию в контуре, компенсируя потери ее в активном сопротивлении. При уменьшении активного сопротивления уменьшается потеря энергии в нем и генератор расходует меньше энергии на поддержание незатухающих колебаний.
Если бы контур был идеальным, то начавшиеся колебания продолжались бы непрерывно без затухания и не требовалось бы энергии от генератора на их поддержание. Ток генератора был бы равен нулю, а сопротивление контура — бесконечности.

Активная мощность, расходуемая генератором, может быть подсчитана как
или как мощность потерь в активном сопротивлении контура
где Iк — ток в контуре, равный IL или IC.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
2.4. Резонансная кривая последовательного контура
Когда частота питающего генератора не равна собственной частоте контура, контур называют расстроенным.
Разность
между частотой генератора и собственной
частотой контура принято называть абсолютной расстройкой и обозначать  :
:
.
Абсолютная расстройка выражается в единицах частоты. При резонансе частота генератора и собственная частота контура равны и абсолютная расстройка равна нулю.
Есличастота генератора больше собственной частоты
больше собственной частоты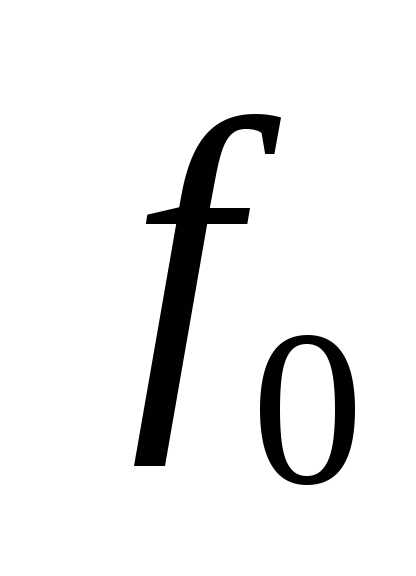 контура, расстройка
считается положительной (
контура, расстройка
считается положительной (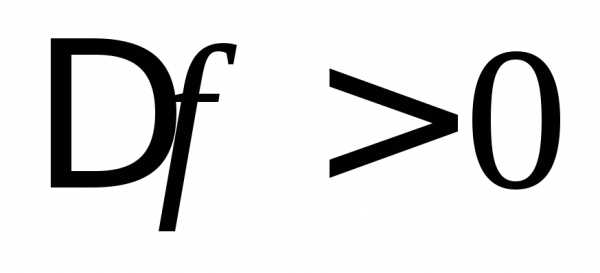 ).
При частоте генератора меньше собственной
частоты контура расстройка отрицательна
(
).
При частоте генератора меньше собственной
частоты контура расстройка отрицательна
(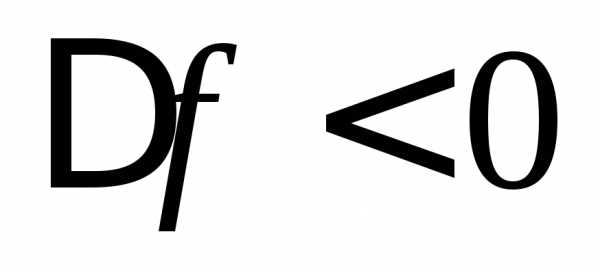 ).
).
Отношение
абсолютной расстройки к собственной
частоте контура 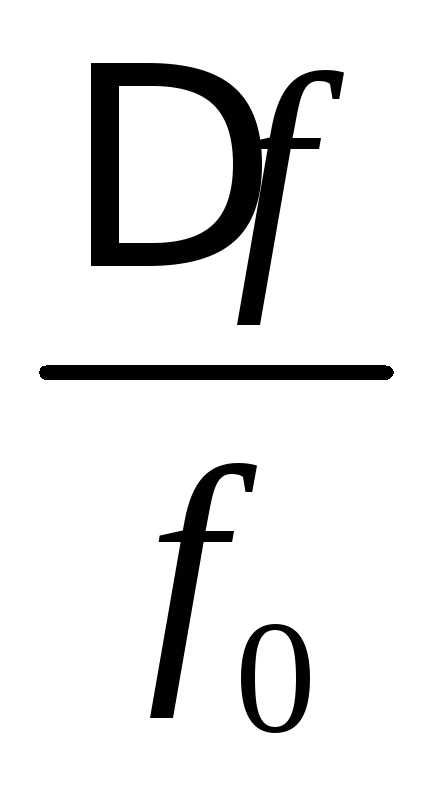 называютотносительной расстройкой.
называютотносительной расстройкой.
При резонансе относительная расстройка равна нулю:
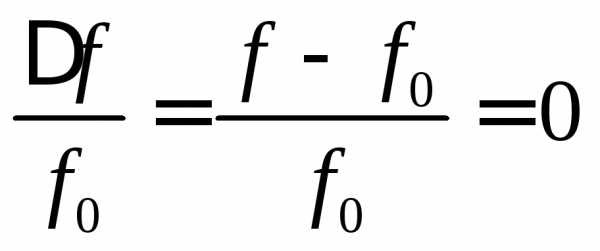 .
.
Ток в контуре тем меньше, чем больше расстройка контура.
Иногда
оказывается более удобной резонансная
кривая, построенная в относительном
масштабе. Для получения такой кривой
вдоль вертикальной оси откладывается
отношение тока в контурепри
данной расстройке к току при резонансе 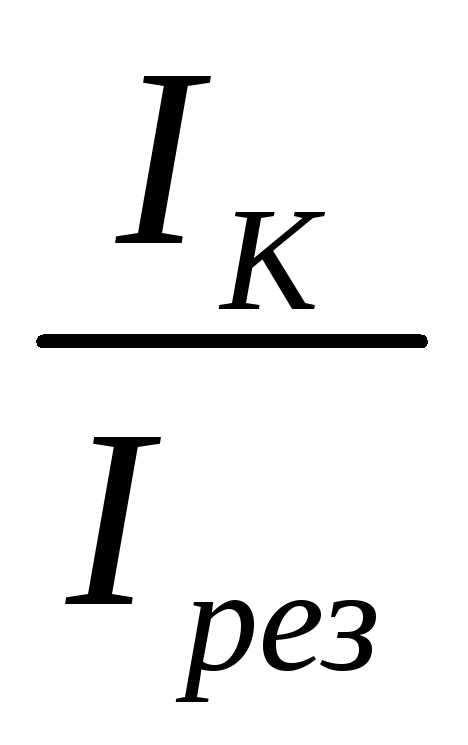 ,
а вдоль горизонтальной оси –
абсолютная или относительная расстройка
(на рис.9 – абсолютная
расстройка).Выведем
уравнение резонансной кривой.
,
а вдоль горизонтальной оси –
абсолютная или относительная расстройка
(на рис.9 – абсолютная
расстройка).Выведем
уравнение резонансной кривой.
Ток в
контуре при любой частоте  равен
равен
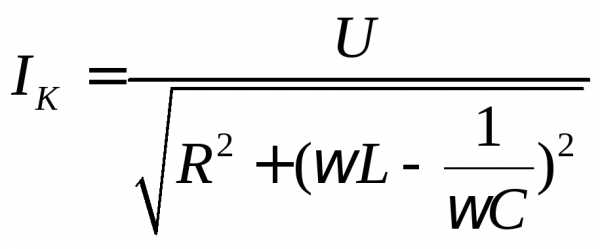 .
.
Ток при резонансе
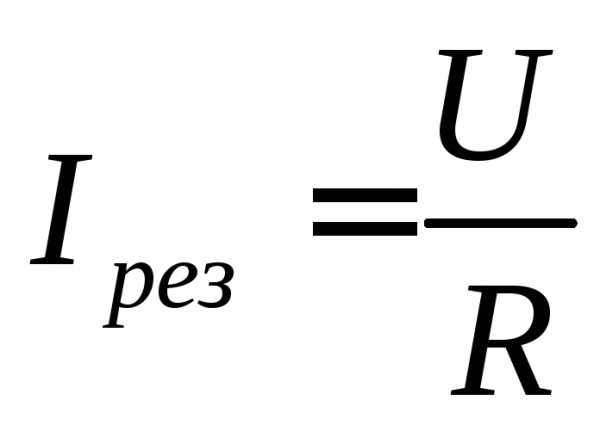 .
.
Отсюда получаем:
.
Числитель
и знаменатель полученной дроби сначала
разделим на 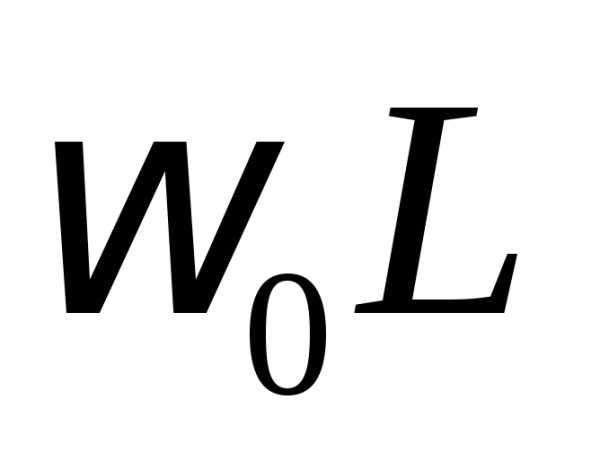
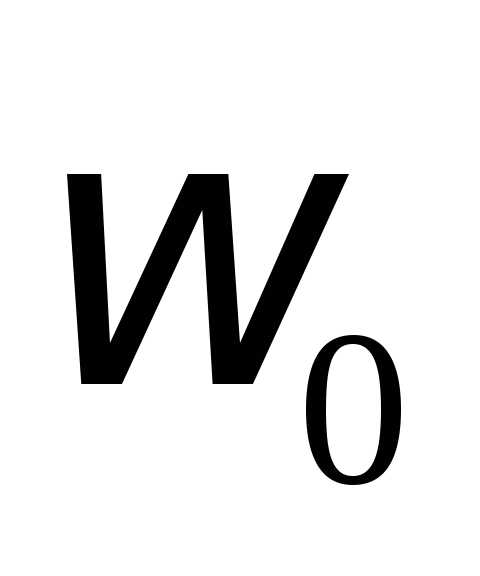 – собственная частота
контура, умножим на
– собственная частота
контура, умножим на  ,
и преобразуем выражение
,
и преобразуем выражение.
Получаем следующее выражение:
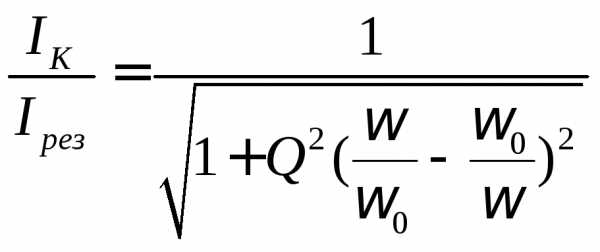 .
.
Учитывая,
что 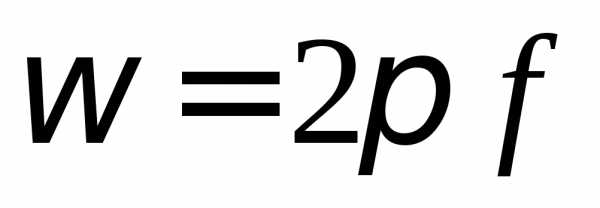 ,
получим
,
получим
.
Преобразуем
выражение 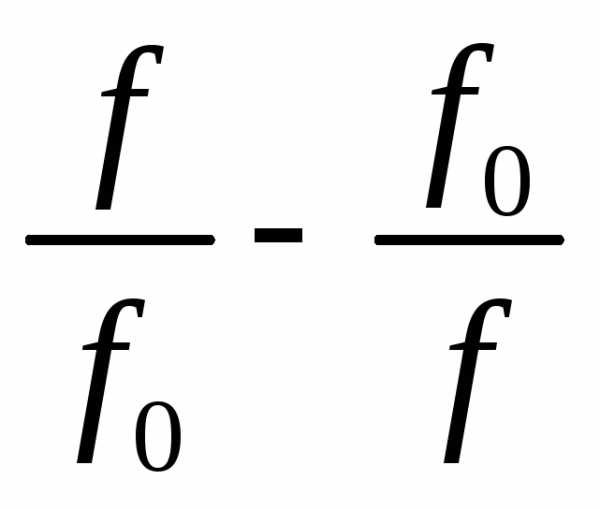 :
:
.
Считая приближенно, что и обозначив(абсолютная расстройка), получим
.
Тогда
.
Относительная расстройка
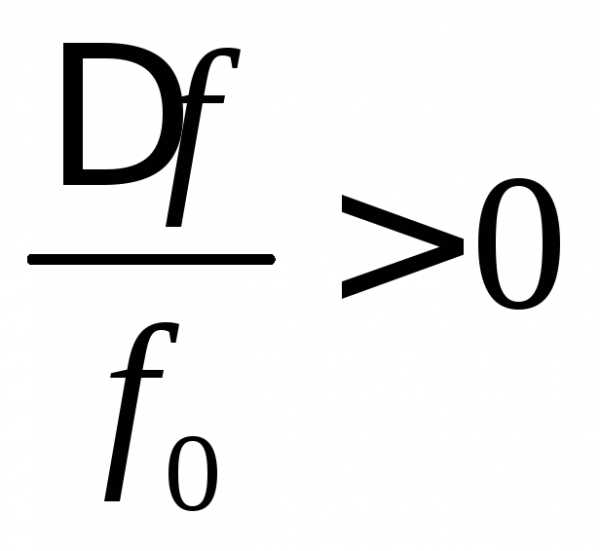
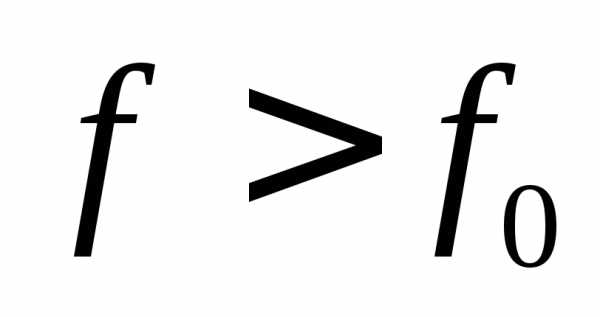 ,
, 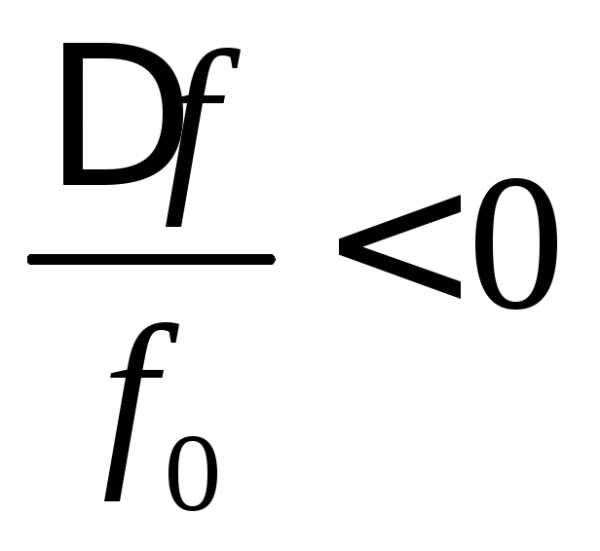 ,если
,если 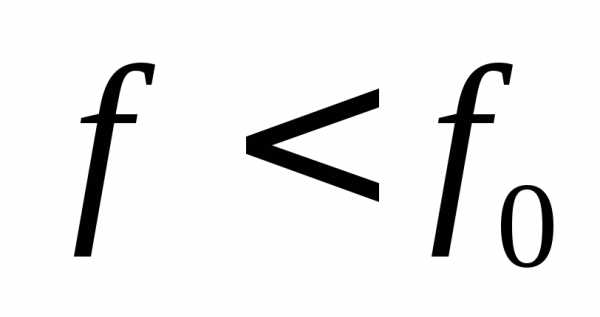 .
.
Введем обозначения:
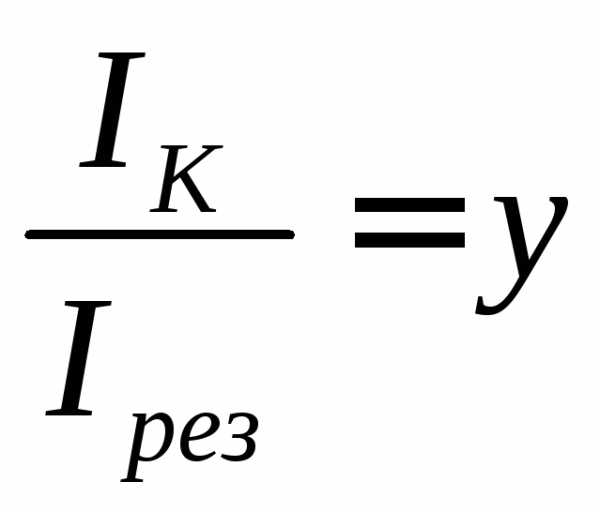 и
и 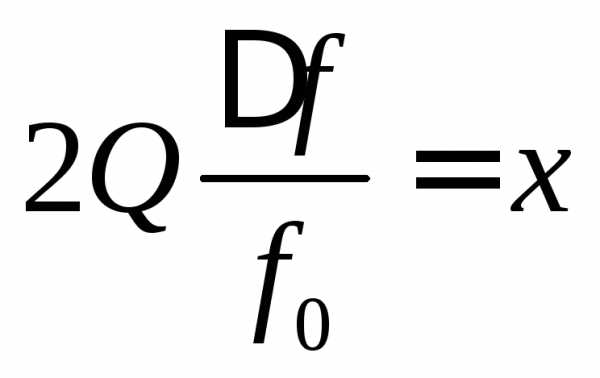 .
.
Тогда для уравнения резонансной кривой в относительном масштабе получим выражение
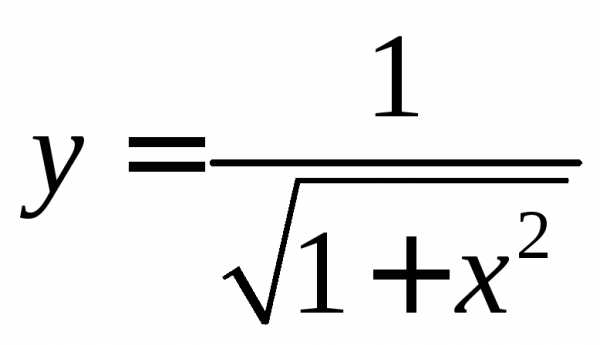
Уравнению такого вида соответствует кривая, изображенная на рис.9.
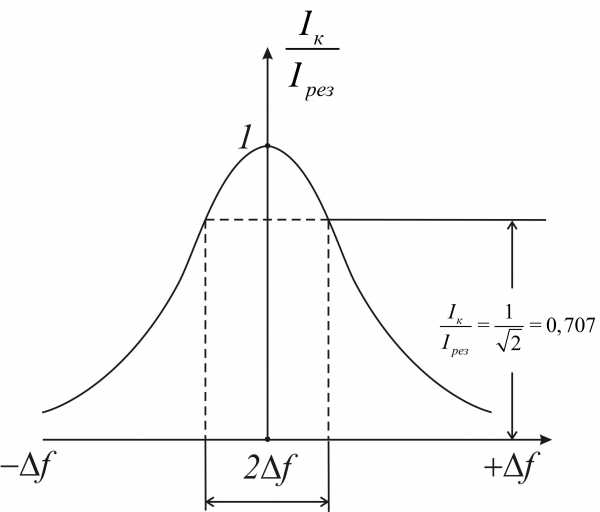
Рис.9. Резонансная кривая последовательного контура
Построение резонансных кривых в относительном масштабе дает возможность легко и удобно сравнивать между собою различные по качеству контуры, а также производить расчеты элементов радиотехнических схем
2.5. Полоса пропускания последовательного контура
Сопротивление последовательного контура вблизи резонанса резко изменяется в зависимости от частоты генератора; в соответствии с этим резко изменяется и ток в контуре. Контур по-разному ведет себя при различных значениях частоты питающего тока. Эти свойства могут быть оценены формой резонансной кривой или добротностью контура. Однако во многих случаях для такой оценки оказывается более удобным пользоваться понятием полосы пропускания контура, так как сигнал каждого передатчика представляет собой спектр частот и занимает некоторую полосу частот. Для неискаженной передачи и приема сигналов необходимо, чтобы все частоты, входящие в состав сигнала, в одинаковой степени излучались передающим устройством, а будучи приняты приемной антенной, в одинаковой степени усиливались приемником. Необходимо, чтобы колебательные контуры пропускали полосу частот, соответствующую спектру сигнала. Поэтому вопрос о полосе частот, пропускаемых контуром, имеет важное значение в радиотехнических устройствах.
Полосой
пропускания контура называют полосу частот, в пределах
которой ток в контуре уменьшается не
более чем в 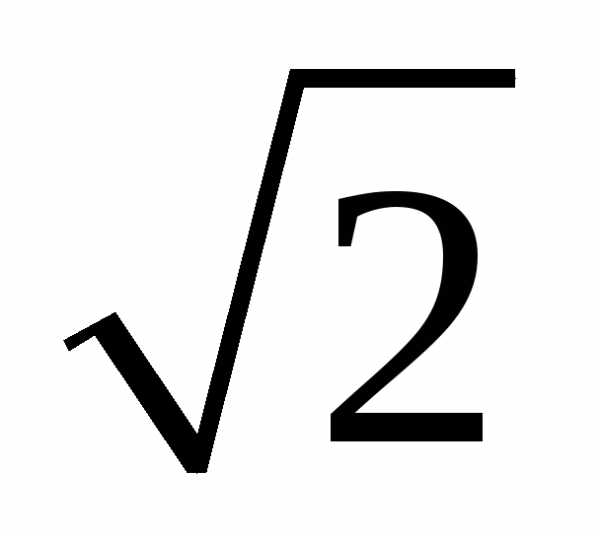 раз по сравнению с током при резонансе.
Иначе, полосой пропускания контура
называют полосу частот, в пределах
которой контурный ток составляет 0,7 или
больше от тока при резонансе. На
рис.10 изображена резонансная
кривая последовательного контура.
Полоса пропускания этого контура равна
раз по сравнению с током при резонансе.
Иначе, полосой пропускания контура
называют полосу частот, в пределах
которой контурный ток составляет 0,7 или
больше от тока при резонансе. На
рис.10 изображена резонансная
кривая последовательного контура.
Полоса пропускания этого контура равна 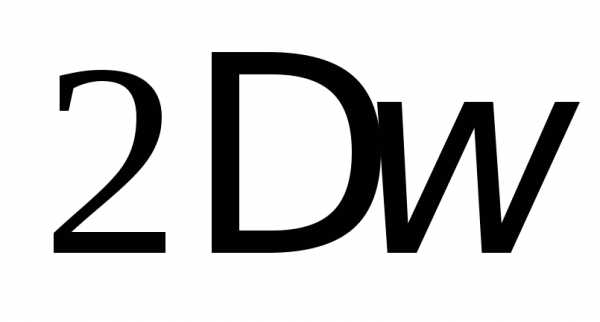 .
Условно считается, что частоты в пределах
от
.
Условно считается, что частоты в пределах
от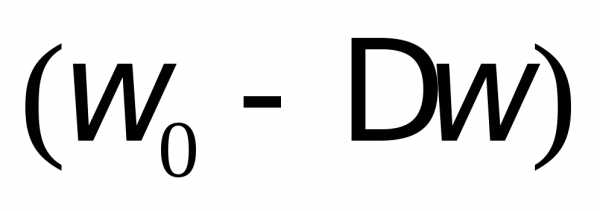 до
до 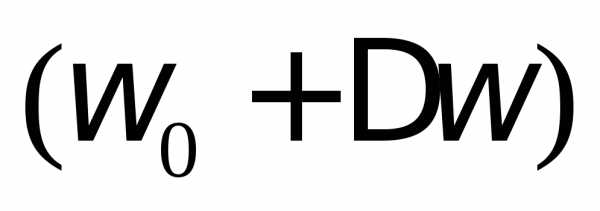 контур пропускает, а частоты ниже
контур пропускает, а частоты ниже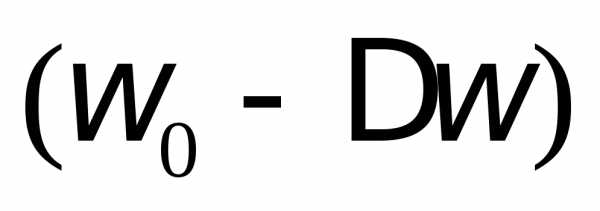 и выше
и выше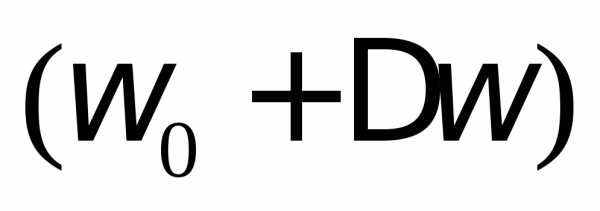 не пропускает.
не пропускает.
Ширина полосы пропускания прямо пропорциональна резонансной частоте и обратно пропорциональна добротности контура, или прямо пропорциональна затуханию при неизменной резонансной частоте.
Полоса пропускания контура зависит от его добротности: чем ниже добротность, тем «тупее» резонансная кривая и тем шире полоса пропускания контура.
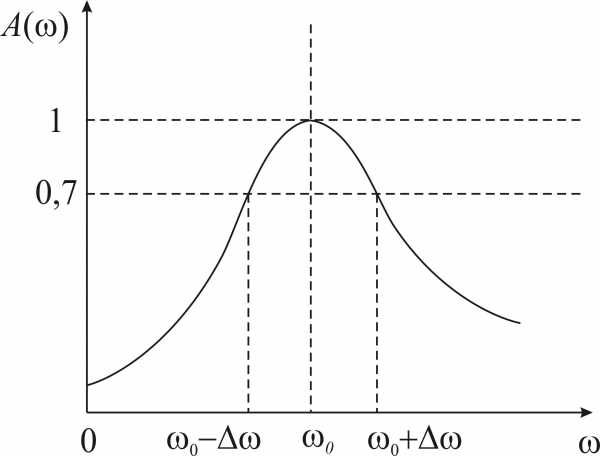
Рис.10. Полоса пропускания последовательного контура
Зависимость модуля
тока от частоты, выражаемая обычно в
виде отношения 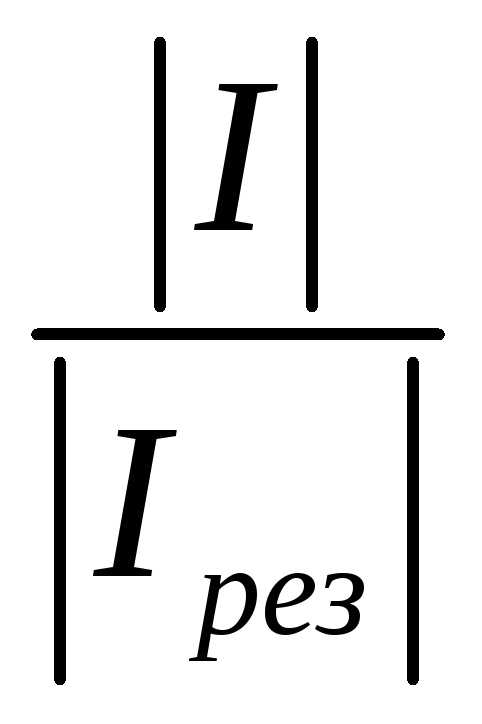 ,
носит названиерезонансной
характеристики последовательного
контура:
,
носит названиерезонансной
характеристики последовательного
контура:
.
На границах полосы
пропускания контура 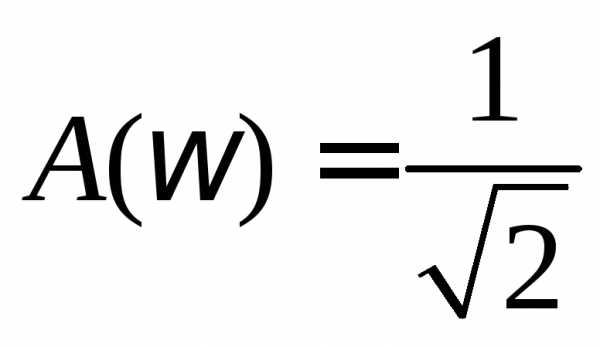 ,
откуда следует простая формула для
практического определения добротности:
,
откуда следует простая формула для
практического определения добротности: 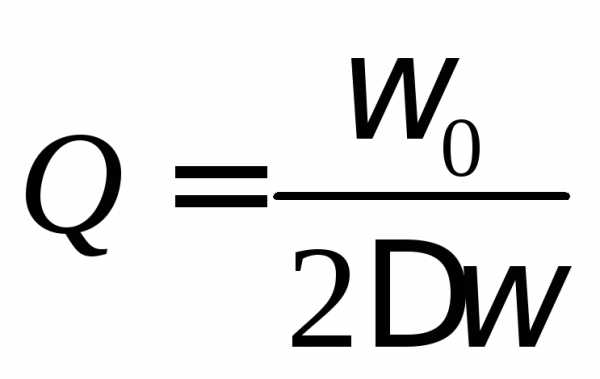 .
.
studfiles.net
§5. Резонансные кривые.
Чтобы определить
резонансную частоту 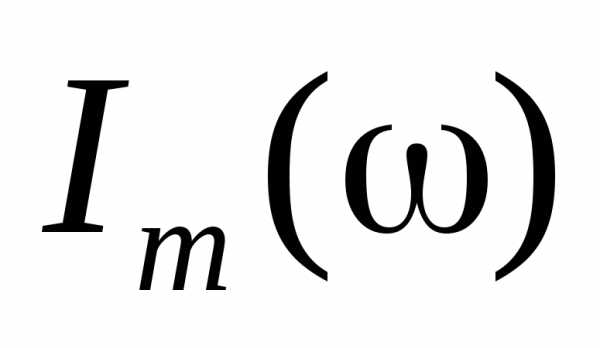 для
амплитуды падения напряжения на емкости,
нужно найти максимум функции:
для
амплитуды падения напряжения на емкости,
нужно найти максимум функции:
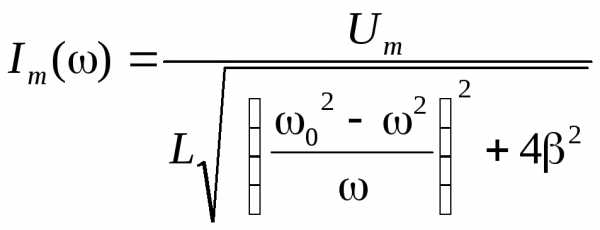 (21)
(21)
Продифференцировав
выражение (21) по  и приравняв 0, получим уравнение:
и приравняв 0, получим уравнение:
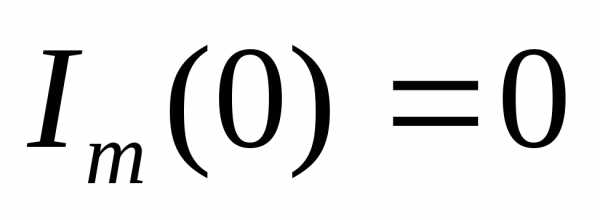 (22)
(22)
Решая уравнение (22), можно получить, что максимум амплитуды падения напряжения на емкости достигается при
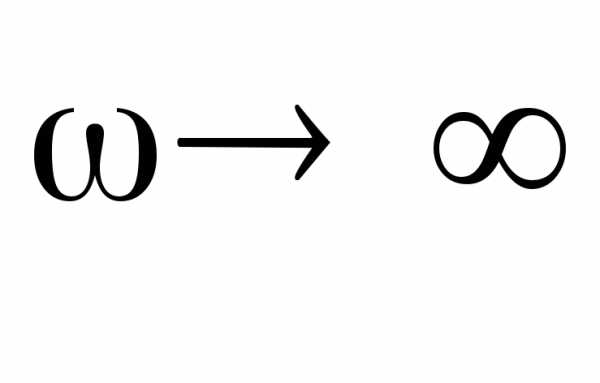 (23)
(23)
Таким образом,
резонансная частота для 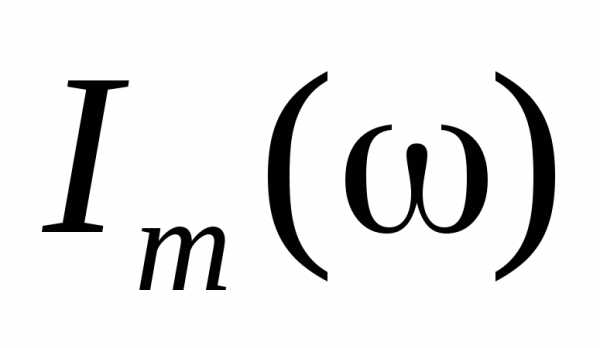 несколько меньше чем собственная частота
колебаний в контуре. Если ввести
обозначения
несколько меньше чем собственная частота
колебаний в контуре. Если ввести
обозначения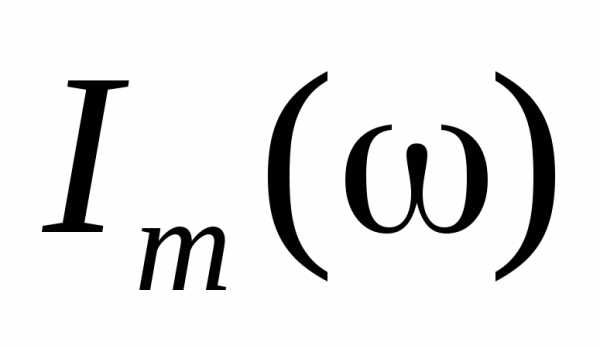 и
и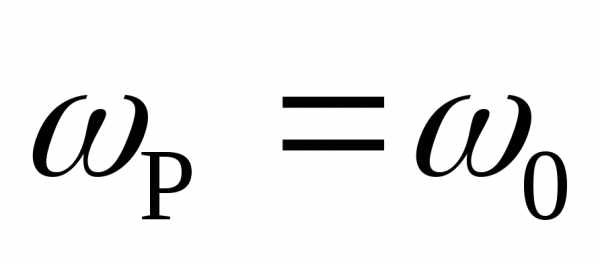 ,
то выражение (23) перепишется так:
,
то выражение (23) перепишется так:
Резонансные кривые
для 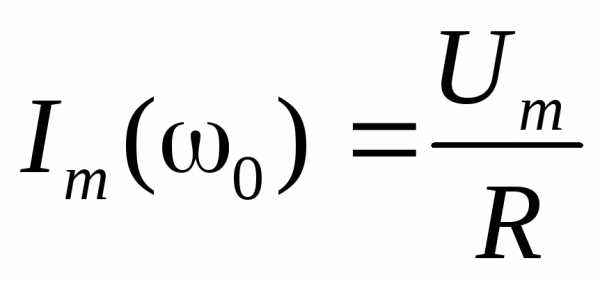 изображены на (рис.7) при различных
изображены на (рис.7) при различных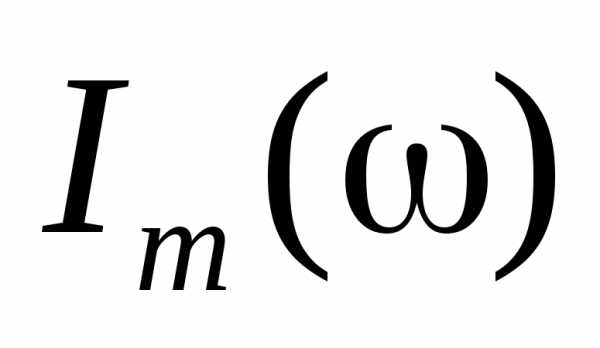 .
В соответствии с (20), (21), чем меньше
коэффициент затухания
.
В соответствии с (20), (21), чем меньше
коэффициент затухания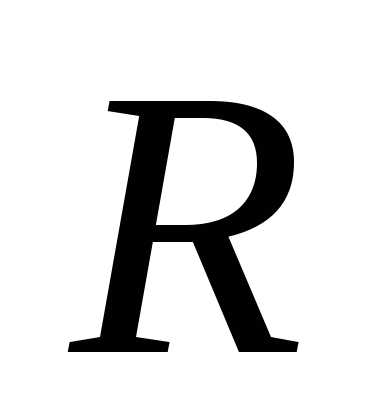 ,
тем выше и правее лежит максимум данной
кривой. По поводу этих резонансных
кривых (рис.7) можно сделать следующие
замечания. При стремлении частоты
,
тем выше и правее лежит максимум данной
кривой. По поводу этих резонансных
кривых (рис.7) можно сделать следующие
замечания. При стремлении частоты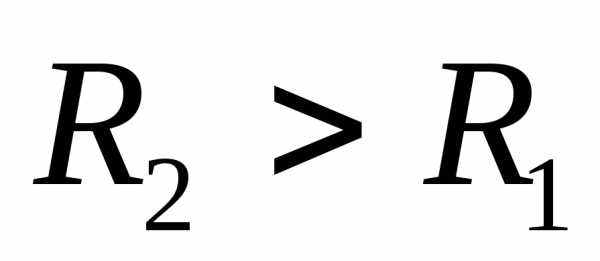 к нулю кривые стремятся к одному значению
к нулю кривые стремятся к одному значению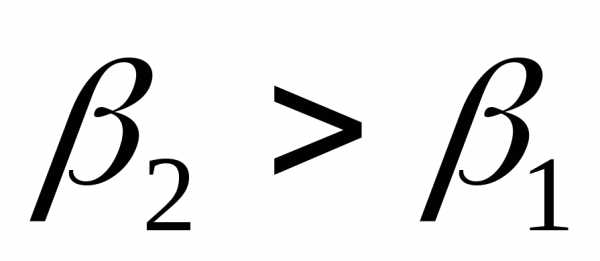 ,
то есть к напряжению, возникающему на
конденсаторе при подключении его к
источнику постоянного напряжения
величиной
,
то есть к напряжению, возникающему на
конденсаторе при подключении его к
источнику постоянного напряжения
величиной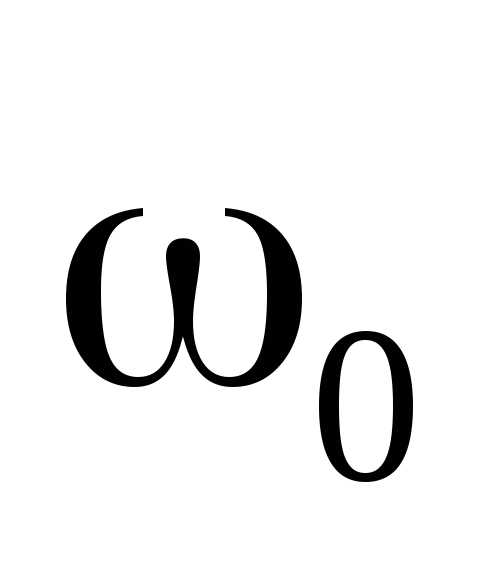 .
При стремлении
.
При стремлении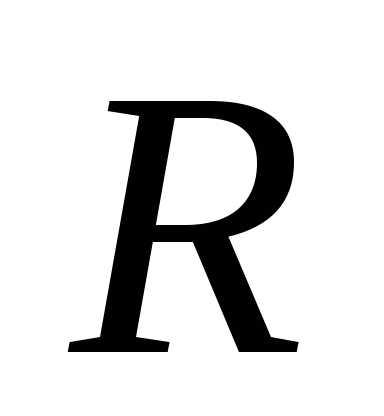 к бесконечности все кривые асимптотически
стремятся к нулю. Чем меньше
к бесконечности все кривые асимптотически
стремятся к нулю. Чем меньше ,
тем сильнее изменяется с частотой
амплитуда
,
тем сильнее изменяется с частотой
амплитуда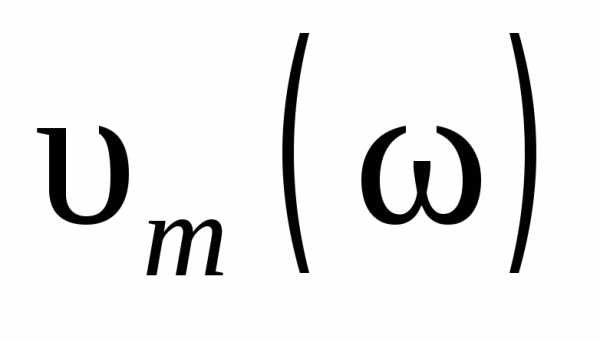 вблизи резонанса, тем “острее” максимум
резонансной кривой. Остроту резонансных
кривых характеризует также добротность
вблизи резонанса, тем “острее” максимум
резонансной кривой. Остроту резонансных
кривых характеризует также добротность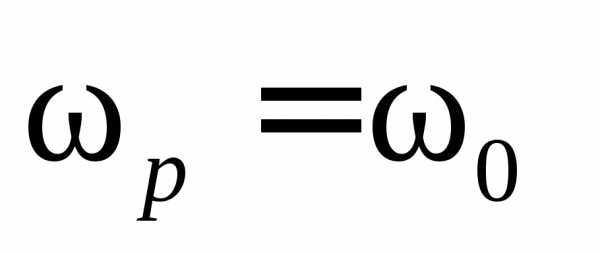 ,
чем больше добротность контура, тем уже
и выше максимум на кривой зависимости
амплитуды вынужденного колебания от
частоты
,
чем больше добротность контура, тем уже
и выше максимум на кривой зависимости
амплитуды вынужденного колебания от
частоты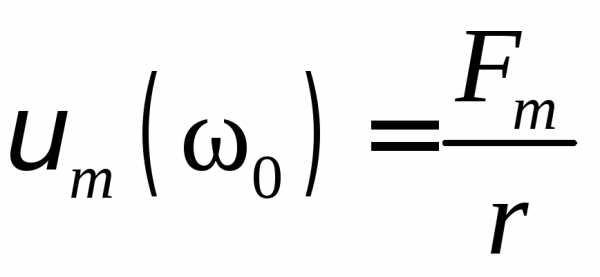 внешнего воздействия. Резонанс напряжений
широко используется в радиотехнике,
когда нужно усилить колебание напряжения
какой-либо определенной частоты, что
позволяет выделить из многих сигналов
различных радиостанций только одно
колебание определенной частоты
(настроиться на определенную станцию).
внешнего воздействия. Резонанс напряжений
широко используется в радиотехнике,
когда нужно усилить колебание напряжения
какой-либо определенной частоты, что
позволяет выделить из многих сигналов
различных радиостанций только одно
колебание определенной частоты
(настроиться на определенную станцию).
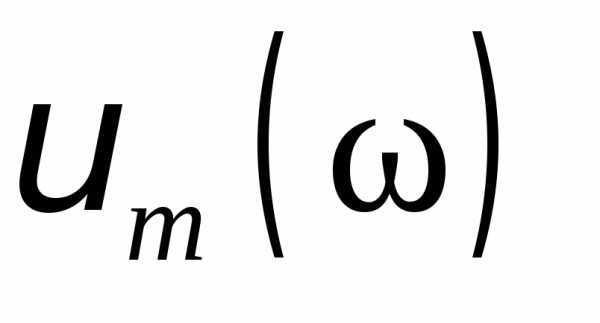
рис.7
Изучение резонанса напряжений.
Приборы и принадлежности:
1. Генератор сигналов звуковой частоты представляет собой источник переменного напряжения звуковой частоты в пределах от 17,7 до 200000 Гц (рис.8).
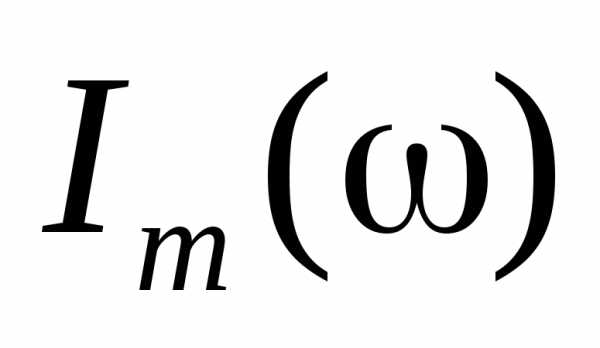
рис.8
На передней панели звукового генератора находится:
1.1. Тумблер подключения прибора к сети “вкл.” – “откл.”.
1.2. Вольтметр на выходе генератора является индикатором напряжения (Регулятор амплитуды напряжения грубой и тонкой настройки).
1.3. Ручка переключения предела частот (множитель частоты) на четыре положения: 17,7–200 Гц; 177–2000 Гц; 1770–200000 Гц.
1.4. Лимб со шкалой (главный регулятор частоты), поворачивая который избирается нужная частота.
1.5. Клеммы – выход звукового генератора, к которым подключается нагрузка (в данном случае колебательный контур).
2. Ламповый милливольтметр (предназначен для замеров напряжения в колебательном контуре) (рис.9).
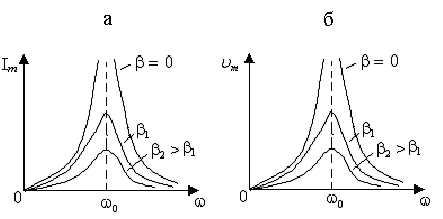
рис.9
На передней панели лампового милливольтметра находится:
2.1. Ручка переключения пределов амплитуды сигнала (замеряемой величины напряжения).
2.2. Клеммы — вход вольтметра.
2.3 Тумблер подключения прибора к сети “вкл.” – “откл.”.
В случае больших или наоборот малых значении напряжения, измеряемого ламповым вольтметром, необходимо изменить предел измерения напряжений ручкой переключения амплитуды сигнала (пределов).
После подключения приборов к сети нужно дать им прогреться 2–3 мин., после чего приступить к работе.
studfiles.net
Резонансные кривые
Зависимость параметров цепи от частоты характеризуется резонансными кривыми.
|
|
Разветвленные цепи переменного тока
Рассмотрим цепь с двумя параллельно соединенными катушками.
Для определения
тока неразветвленной части цепи
необходимо разложить токи 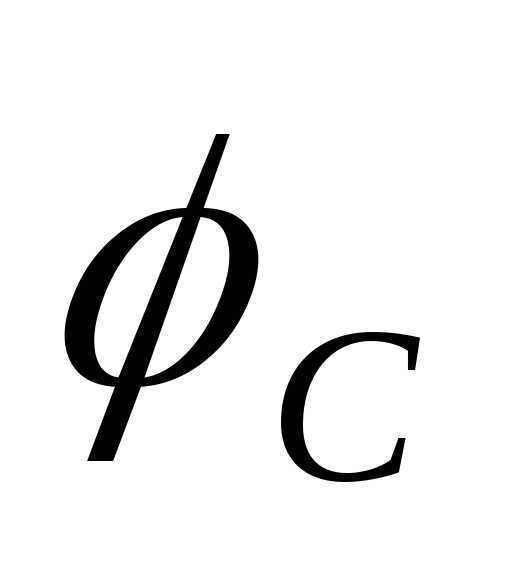 и
и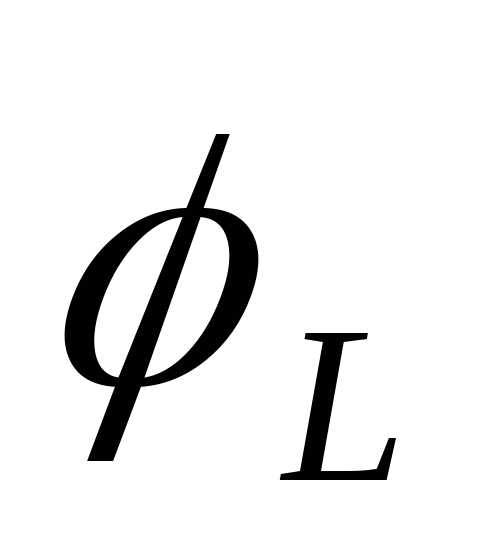 на активные и реактивные составляющие.
на активные и реактивные составляющие.
Метод проводимостей
При
этом ток каждой ветви рассматривают
как бы состоящим из двух составляющих:
активной  и реактивной
и реактивной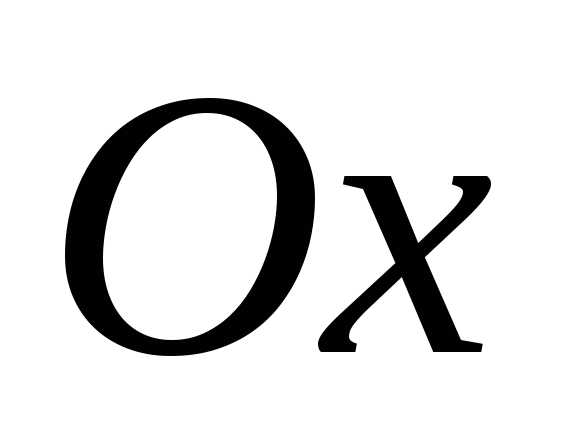 .
.
,
где 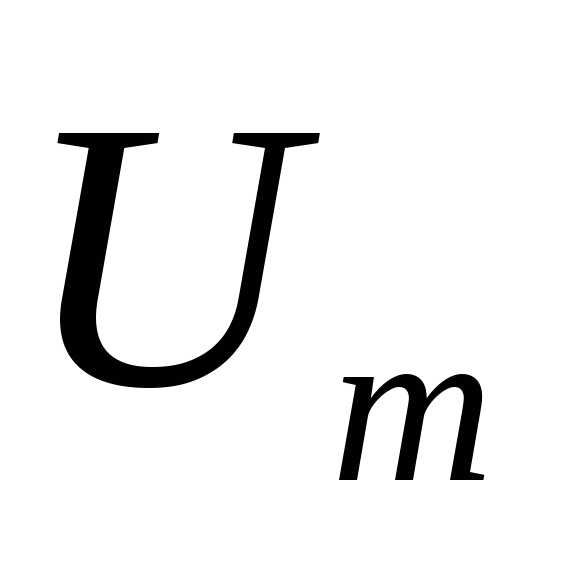 —активная
проводимость ветви
—активная
проводимость ветви
,
где 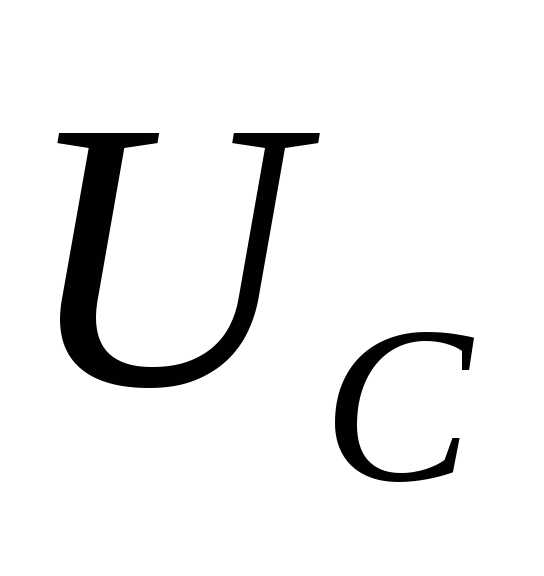
,
где 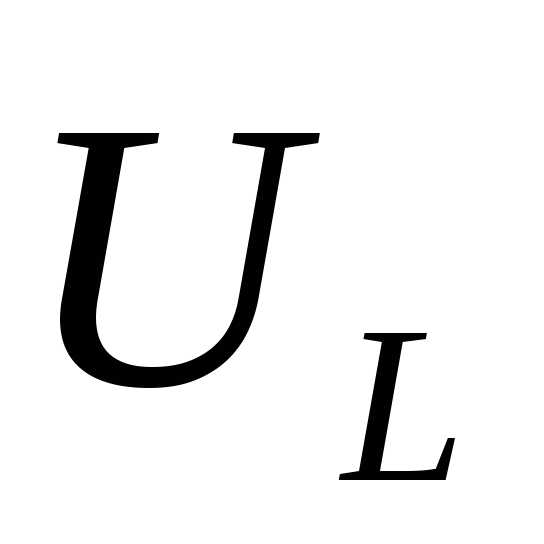 —реактивная
проводимость ветви
—реактивная
проводимость ветви
, где 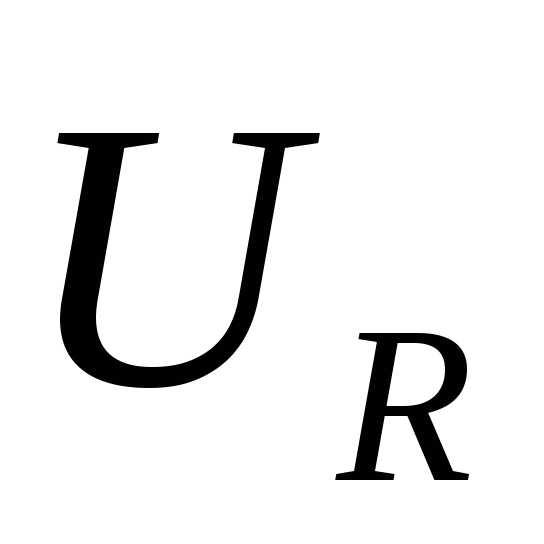
где
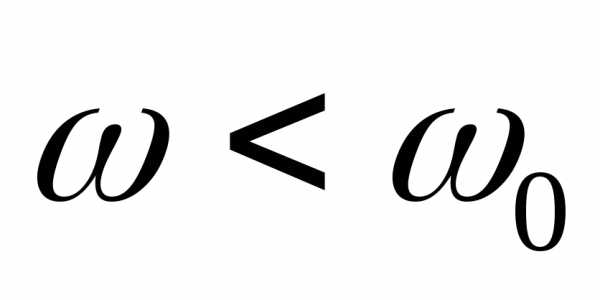 —
полная активная проводимость цепи;
—
полная активная проводимость цепи;
 —
полная реактивная проводимость цепи.
—
полная реактивная проводимость цепи.
, где
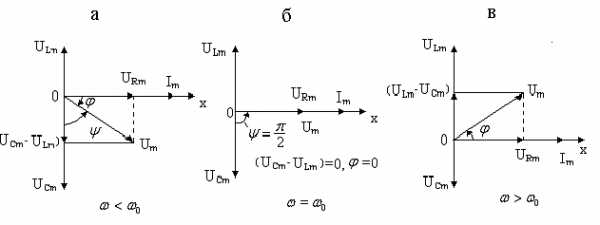 —
полная проводимость цепи.
—
полная проводимость цепи.
.
Порядок расчета
1. Определяем активные, реактивные и полные проводимости ветвей по формулам:

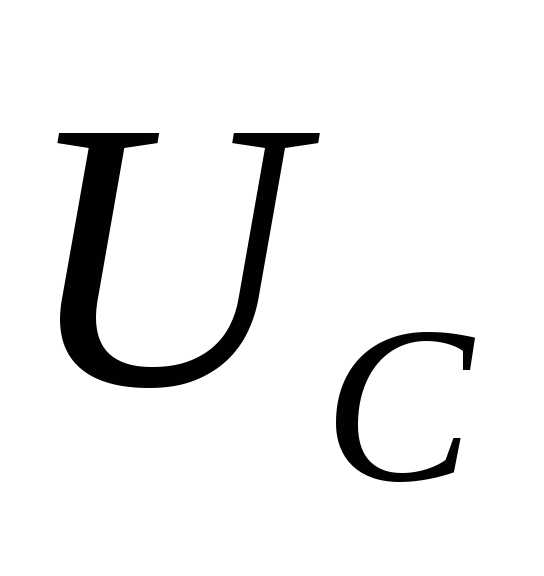

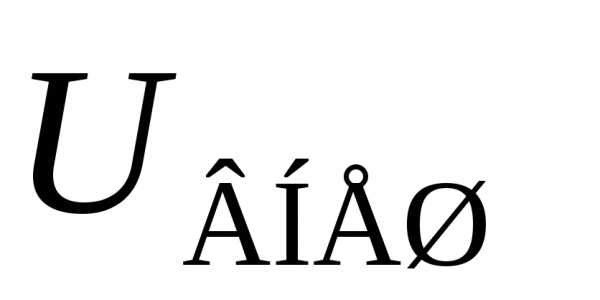


2. Определяем
токи в ветвях: 


3. Определяем мощности ветвей и всей цепи:

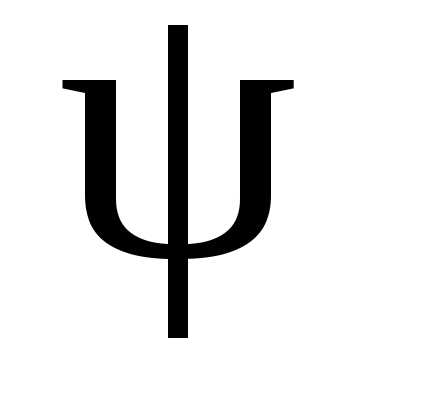
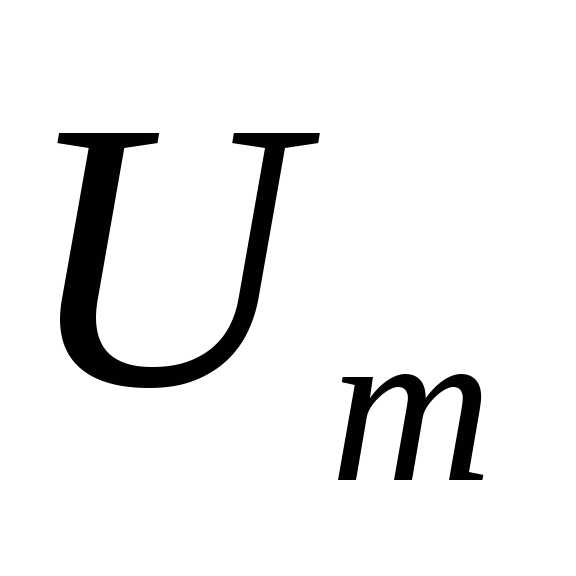 .
.
Параллельное соединение активно-индуктивного и активно-емкостного сопротивления
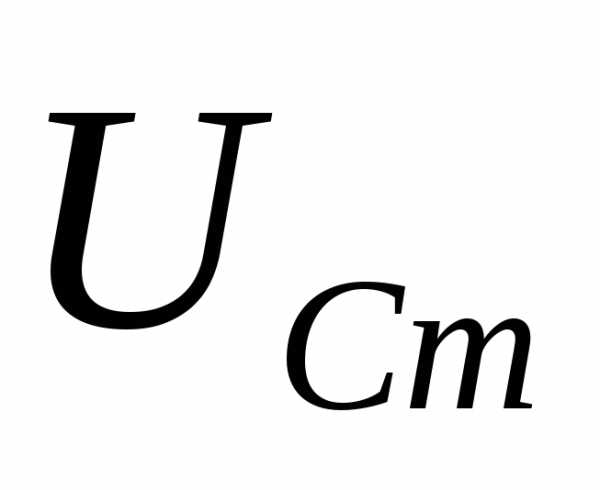
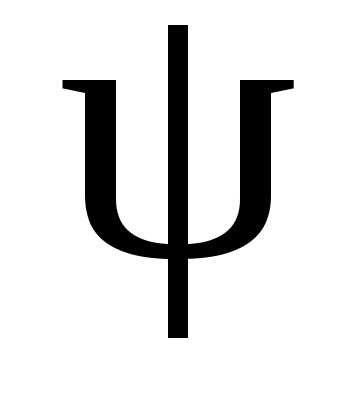

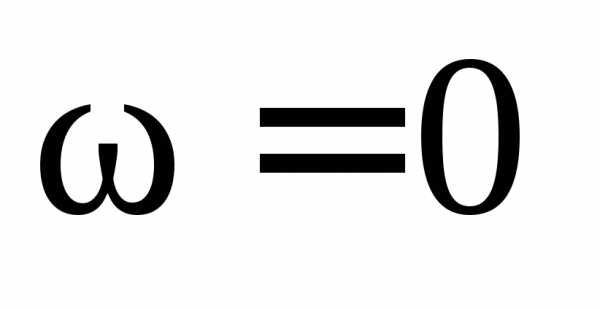
Общий случай неразветвленной цепи
Резонанс токов
В цепи резонанс токов наступает, если .
|
|
Реактивная проводимость всей цепи
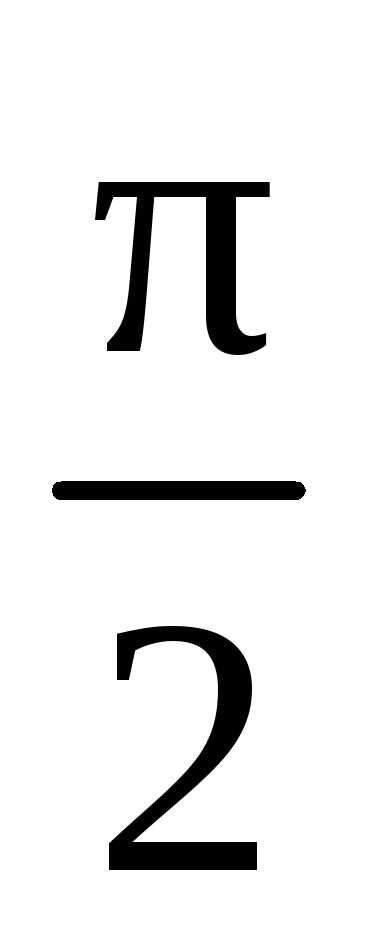
Решая это уравнение относительно частоты, получим выражение для резонансной частоты:
При резонансе полная проводимость цепи будет минимальной, а полное сопротивление – максимальным. Следовательно, ток будет минимальным.
| Реактивные мощности ветвей равны, поэтому реактивная мощность всей цепи равна нулю. Это означает, что обмена энергией между цепью и источником нет. Источник обеспечивает цепь только активной энергией. |
Активная и реактивная энергии
 — измеряется счетчиком активной энергии.
Характеризует энергию, израсходованную
в цепи переменного тока.
— измеряется счетчиком активной энергии.
Характеризует энергию, израсходованную
в цепи переменного тока.
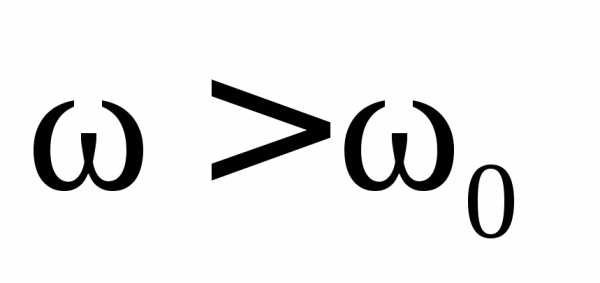 — является расчетной величиной. Измеряется
счетчиком реактивной энергии.
— является расчетной величиной. Измеряется
счетчиком реактивной энергии.
Коэффициент мощности и его значения

Электрические и другие устройства характеризуются:
номинальным током;
номинальным напряжением;
номинальной мощностью.
 .
.
Полное использование
мощности генератора происходи при 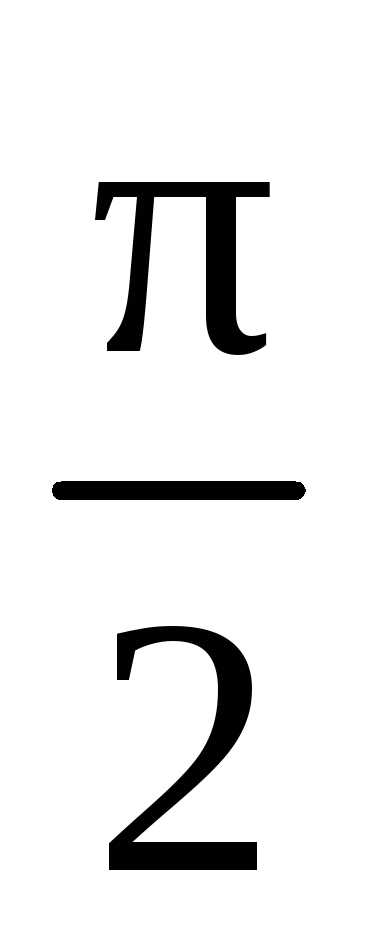 ,
т.к..
,
т.к..
При уменьшении 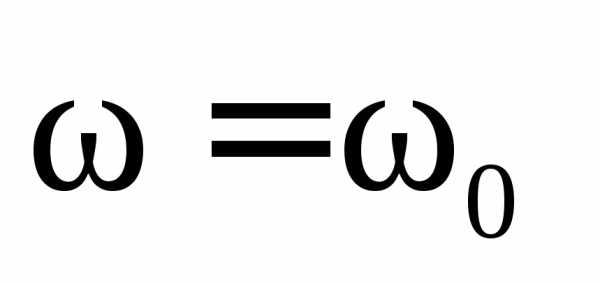 ,
величина которого определяется приемником
электроэнергии, мощность генератора
используется не полностью.
,
величина которого определяется приемником
электроэнергии, мощность генератора
используется не полностью.
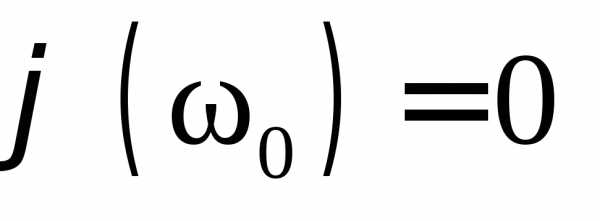
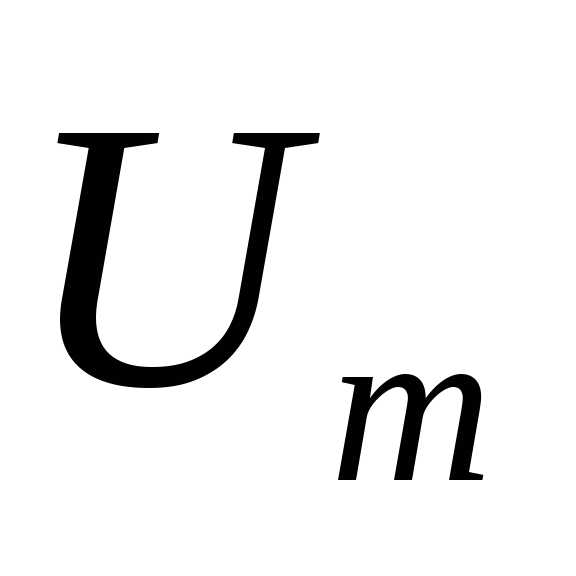
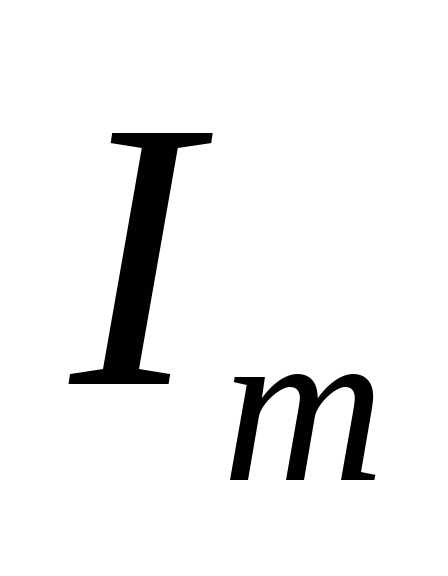
Т.о., увеличивая
значение 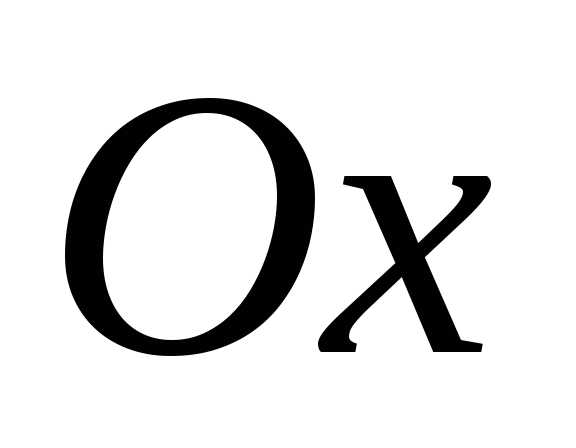 мы добивается того, что мощность
генератора используется полностью.
мы добивается того, что мощность
генератора используется полностью.
Способы повышения 
1. Соответствие мощности механизма и мощности электродвигателя, приводимого им (естественный способ).
2. Включение батареи конденсаторов параллельно потребителям.
3. Использование синхронных компенсаторов.
| На
практике пользуются средним
значением |
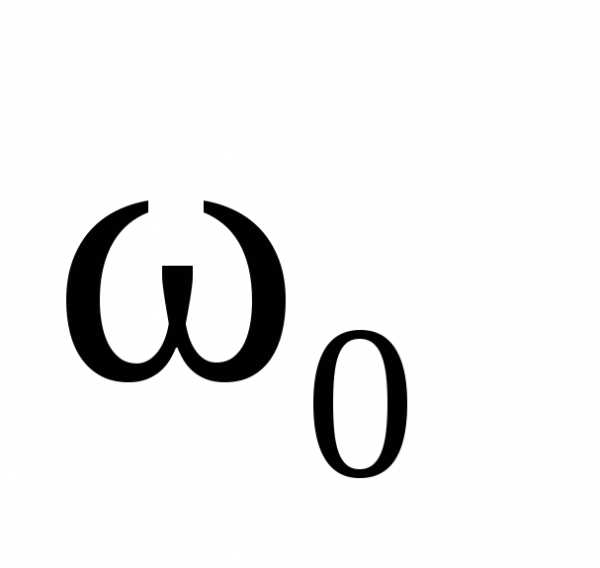
Комплексный метод расчета цепей переменного тока
Комплексным
числомназывается сумма вещественного
числа и мнимого
и мнимого .
.
где  .
.
|
|
Различают алгебраическую, тригонометрическую и комплексную форму записи комплексного числа.
алгебраическая тригонометрическая показательная
studfiles.net
Резонансные кривые для амплитуды силы тока в контуре, для амплитуды скорости материальной точки в механической системе
Запишем
формулу (5.68) для амплитуды силы тока 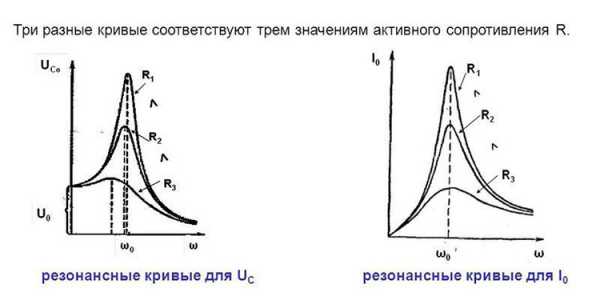 в наиболее удобном виде
в наиболее удобном виде
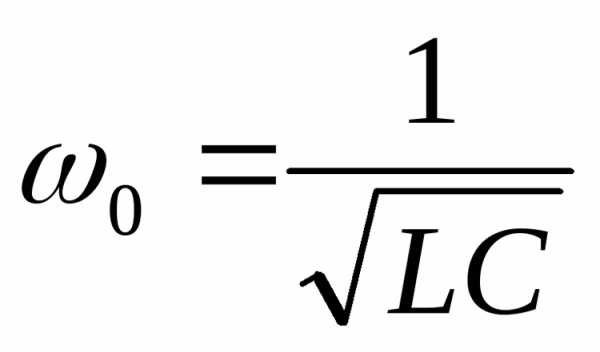 ,
,
и
исследуем эту зависимость для различных
значений 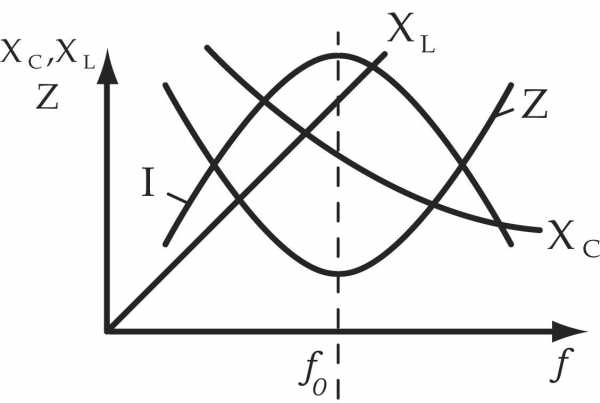 .
.
1. ω=0
:  ,
т.е. постоянный электрический ток через
цепь, содержащую конденсатор, не
протекает.
,
т.е. постоянный электрический ток через
цепь, содержащую конденсатор, не
протекает.
2. 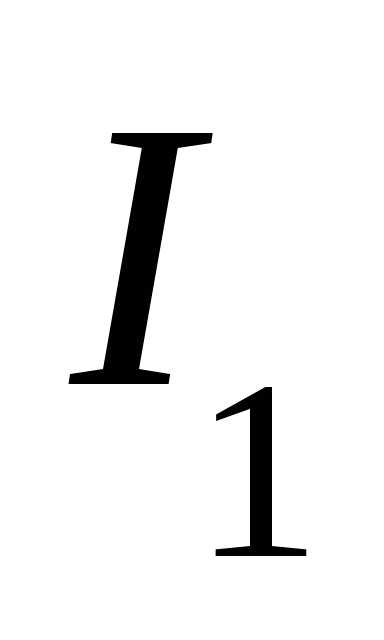 :
.
:
.
3.
Максимум функции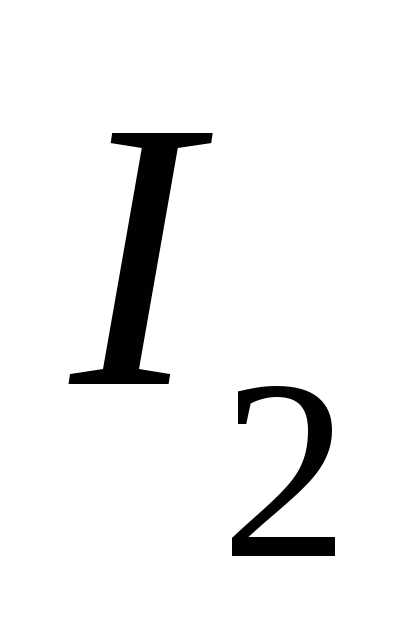 наблюдается тогда, когда подкоренное
выражение в знаменателе будет минимальным,
т.е. первое слагаемое в подкоренном
выражении должно быть равным нулю.
Поэтому максимум
наблюдается тогда, когда подкоренное
выражение в знаменателе будет минимальным,
т.е. первое слагаемое в подкоренном
выражении должно быть равным нулю.
Поэтому максимум 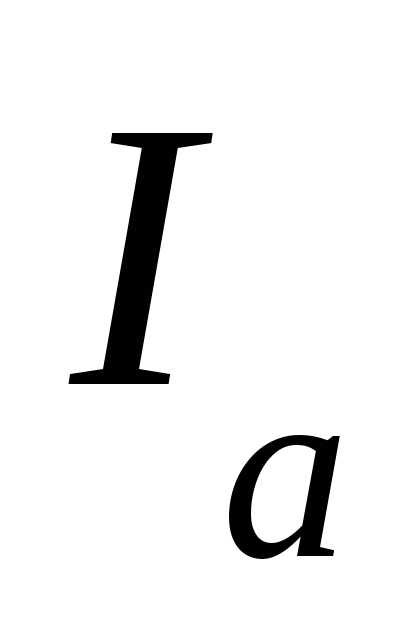 соответствует
частоте
соответствует
частоте 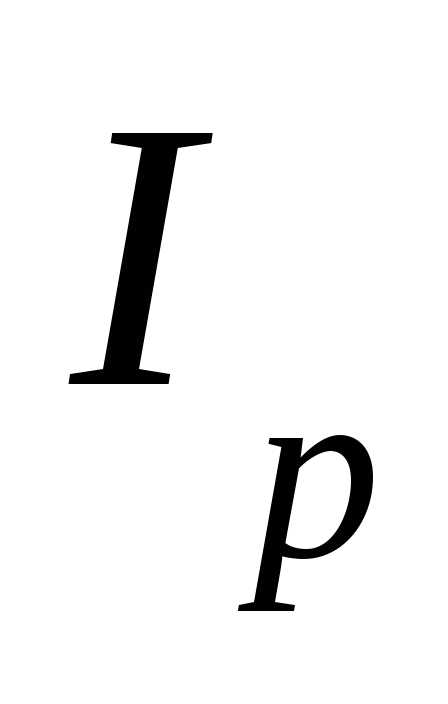 ,
а само максимальное значение будет
равно
,
а само максимальное значение будет
равно
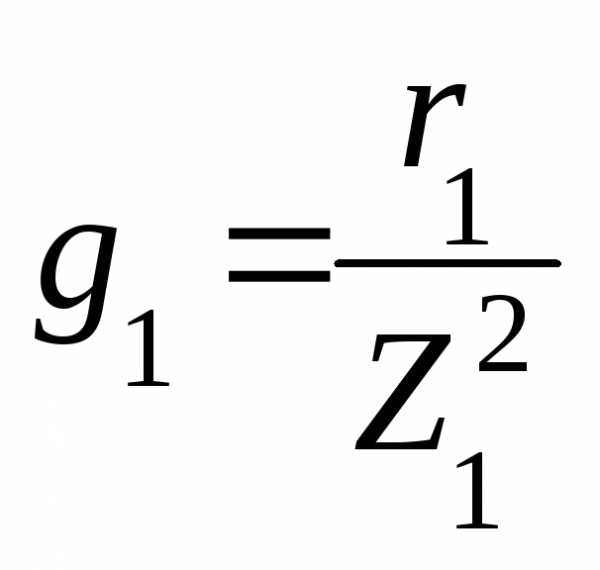 .
(5.74)
.
(5.74)
На
рис. 5.18 приведены резонансные кривые 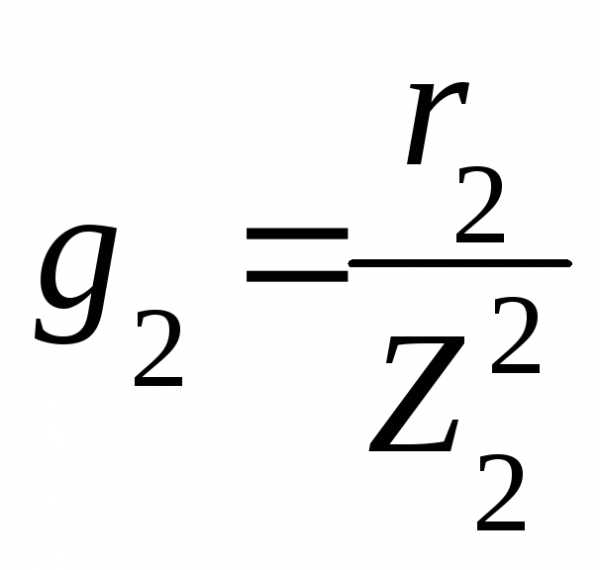 в случае идеального колебательного
контура ()
и для двух разных значений сопротивления
в случае идеального колебательного
контура ()
и для двух разных значений сопротивления 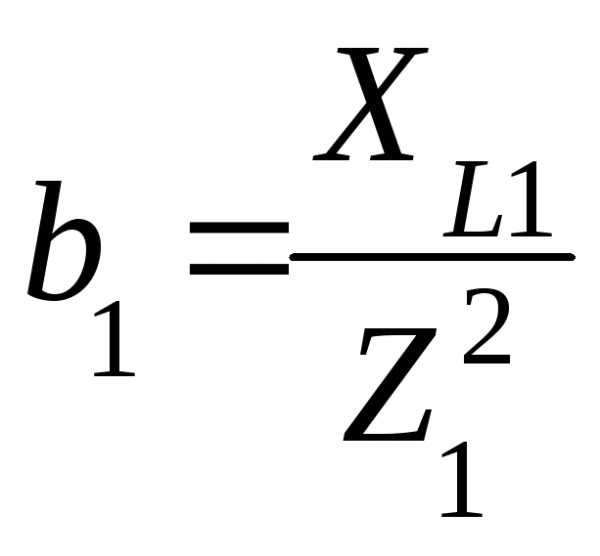 в нем (
в нем (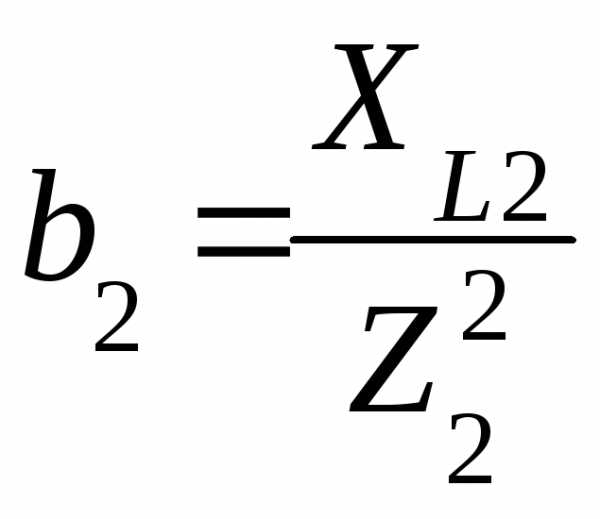 ,
т.е.
,
т.е.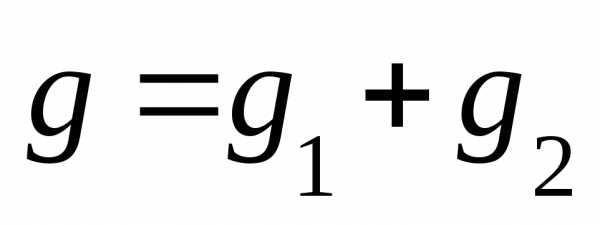 )
при постоянном значении
)
при постоянном значении 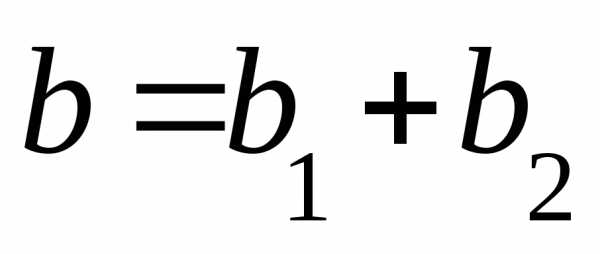 .
Как видно, максимум функции с увеличением
.
Как видно, максимум функции с увеличением 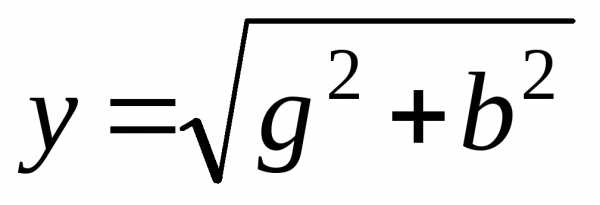 уменьшается, а его смещение по оси частот
уменьшается, а его смещение по оси частот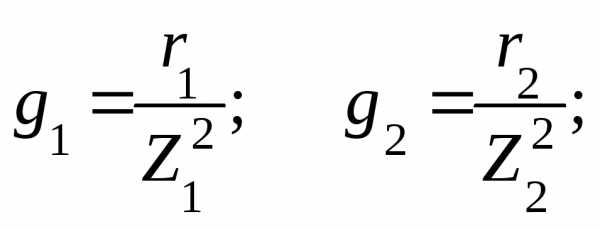 не происходит.
не происходит.
Используя
табл. аналогий 5.1, можно записать формулы,
описывающие резонансные кривые для
амплитуды колебаний скорости 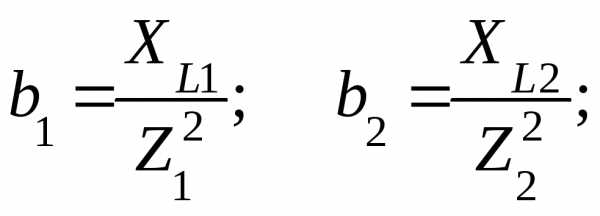 тела (м.т.) в механической системе:
тела (м.т.) в механической системе:
, (5.75)
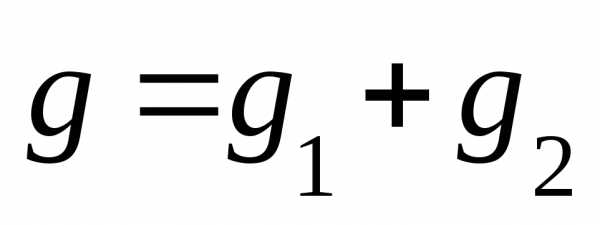 :
: 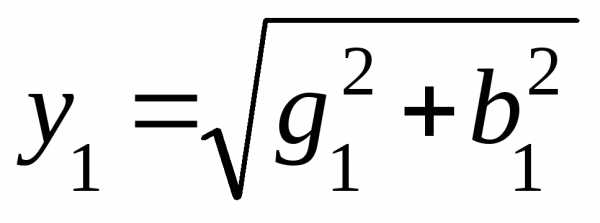 .
(5.76)
.
(5.76)
График 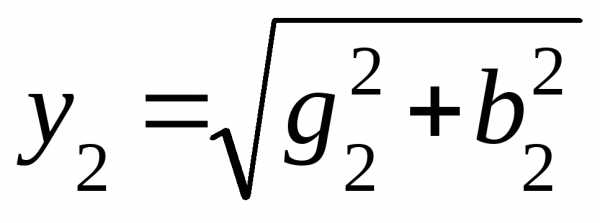 для трех значений коэффициента
сопротивления ()
среды приведены на рис. 5. 18,б. Эти графики
аналогичны графикам резонансных кривых
для трех значений коэффициента
сопротивления ()
среды приведены на рис. 5. 18,б. Эти графики
аналогичны графикам резонансных кривых 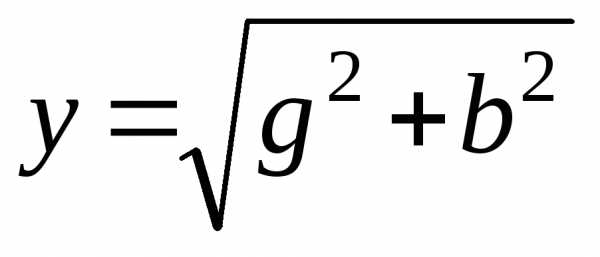 .
.
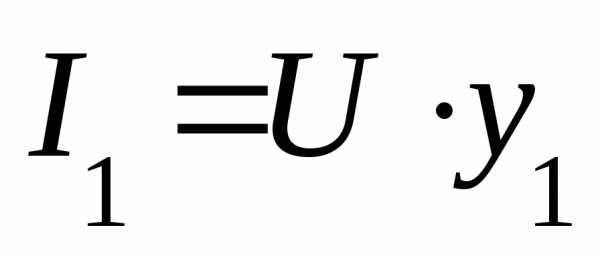
Рис. 5.18
Разность фаз колебаний между силой тока и напряжениями на конденсаторе, индуктивности и активном сопротивлении колебательного контура. Фазовые резонансные кривые
Перепишем
формулы (5.64) для I и 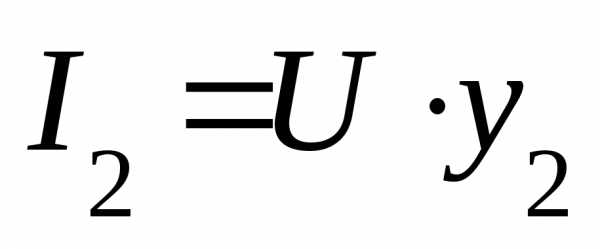 в
удобном виде
в
удобном виде
, ,
и добавим к ним формулы для UL и UR:
,.(5.77)
Найдем
в соответствии с полученными формулами
разность фаз колебаний между силой тока 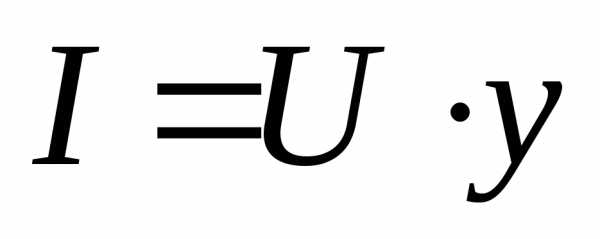 и напряжениями на конденсаторе
и напряжениями на конденсаторе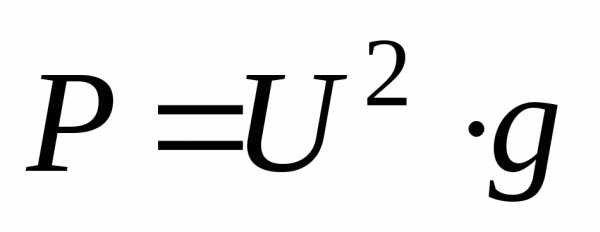 ,
индуктивности
,
индуктивности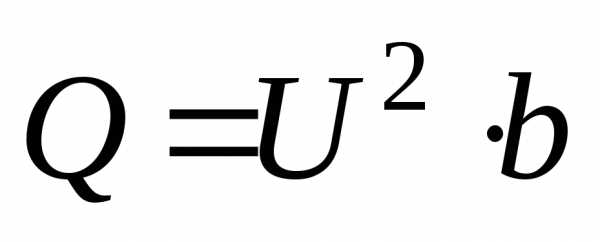 и активного сопротивления
и активного сопротивления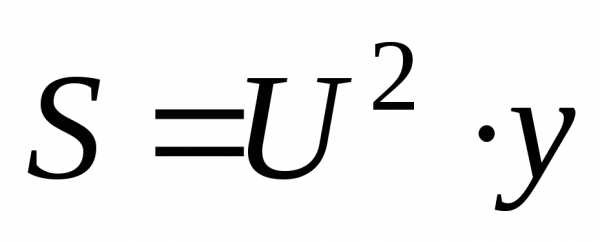 :
:
, (5.78)
, (5.79)
. (5.80)
Рис. 5.19
Как следует из формул (5.78) – (5.80) фаза колебаний напряжения на конденсаторе отстает по фазе от колебаний тока в цепи на π/2, а фаза колебаний напряжения на катушке опережает фазу колебаний силы тока на π/2. Фазы колебаний напряжения на активном сопротивлении R и силы тока в цепи совпадают. Это наглядно видно на векторной диаграмме, приведенной на рис. 5.19.На
ней указаны амплитуды векторов напряжений
на отдельных участках электрической
цепи. При этом фаза колебания силы тока
в контуре принимается равной нулю, т.е.
амплитуда вектора силы тока располагается
вдоль оси 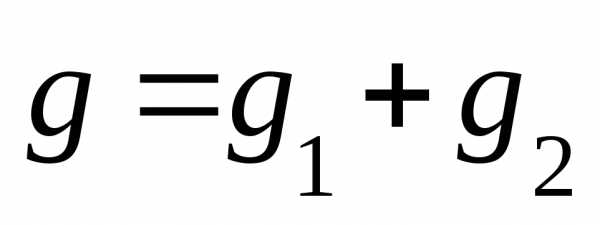 .
.
На
такой диаграмме вектор амплитуды
внешнего напряжения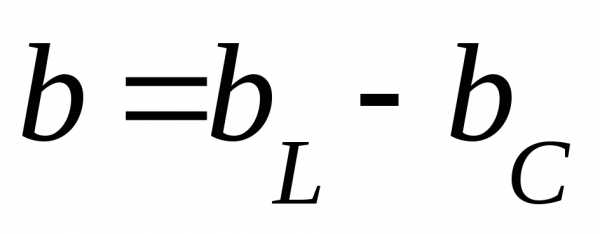 ,
подаваемого в колебательный контур,
можно представить как сумму векторов
амплитуд напряжений (
,
подаваемого в колебательный контур,
можно представить как сумму векторов
амплитуд напряжений (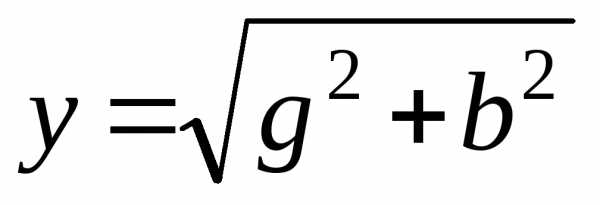 ,
,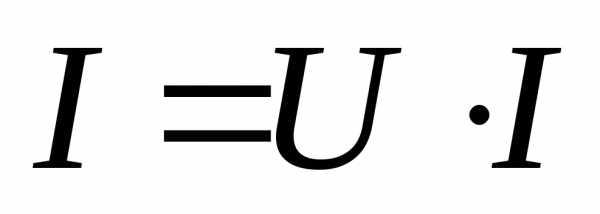 ,
,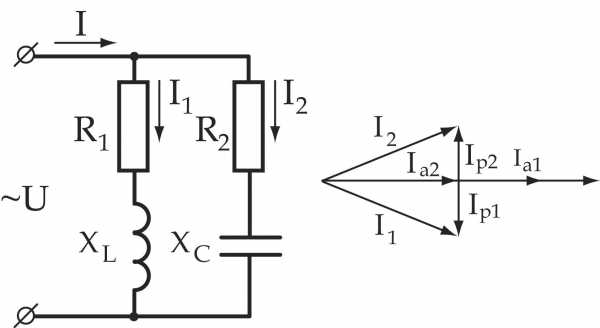 )
на разных его участках. Это позволяет
записать следующую формулу для модуля
вектора амплитуды внешнего напряжения
(например, для частот
)
на разных его участках. Это позволяет
записать следующую формулу для модуля
вектора амплитуды внешнего напряжения
(например, для частот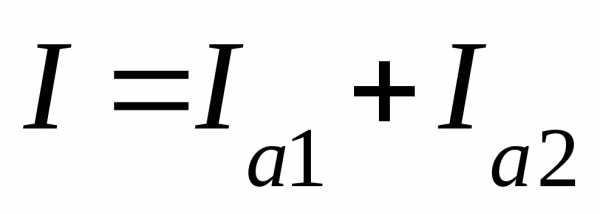 ,
рис. 5.20,а):
,
рис. 5.20,а):
, (5.81)
из которой с учетом формул (5.19) и (5.20) () можно получить выражение (5.65) для зависимости амплитуды колебания заряда от частоты внешнего напряжения
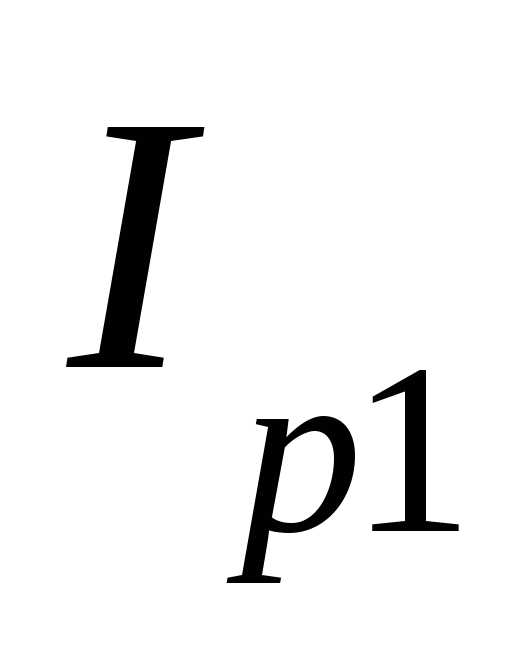 .
.
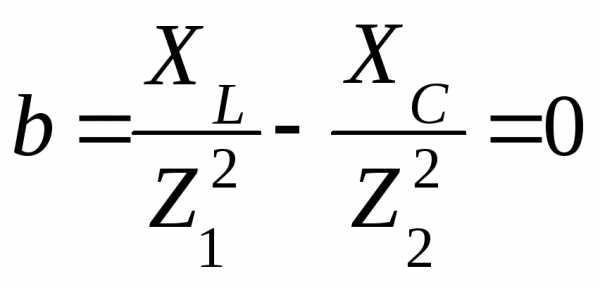
Рис. 5.20
Под фазовыми
резонансными кривыми понимают, например, зависимости разности
фаз
между внешним напряжением 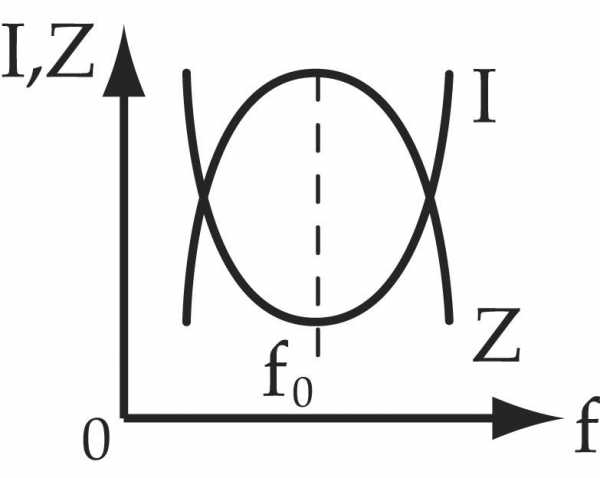 и напряжением
и напряжением 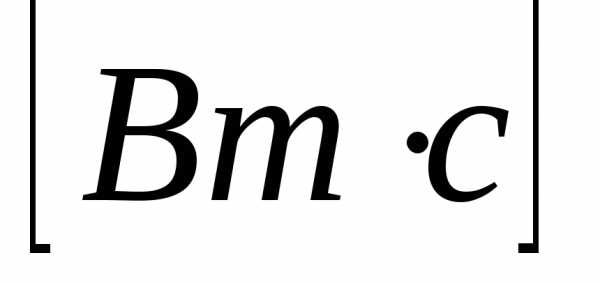 на конденсаторе, разности фаз
на конденсаторе, разности фаз 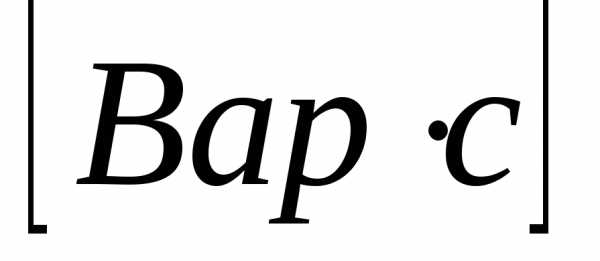 между внешним напряжением
между внешним напряжением 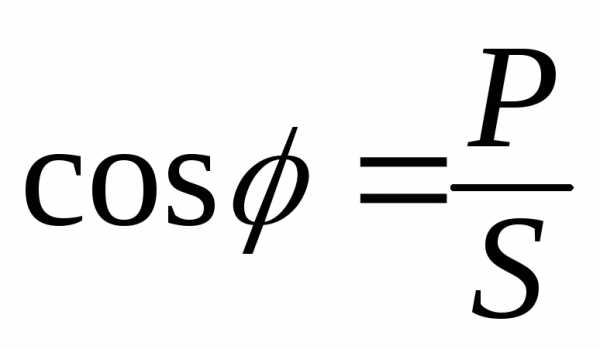 и силой токаI в контуре от частоты
и силой токаI в контуре от частоты 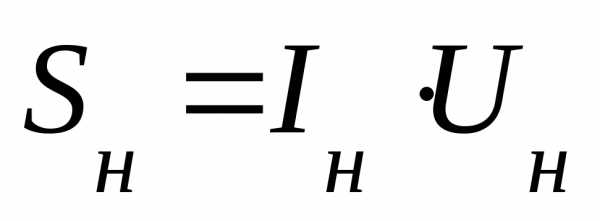 внешнего напряжения. Наиболее интересными
из них являются зависимости ,
так как они позволяют выяснить
эффективность поступления энергии в
контур (колебательную систему). В
соответствии с формулами (5.64) и (5.66) для
разности фаз
внешнего напряжения. Наиболее интересными
из них являются зависимости ,
так как они позволяют выяснить
эффективность поступления энергии в
контур (колебательную систему). В
соответствии с формулами (5.64) и (5.66) для
разности фаз 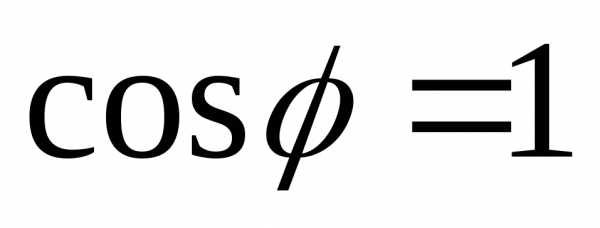 и
и 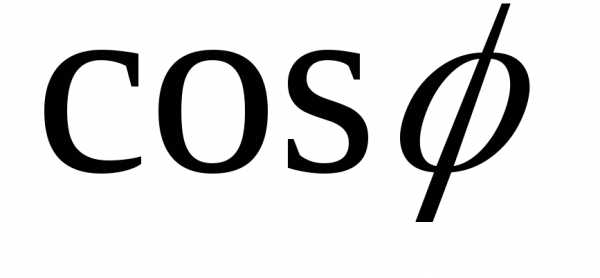 можно
записать
можно
записать
,. (5.82)
Отметим,
что разность фаз 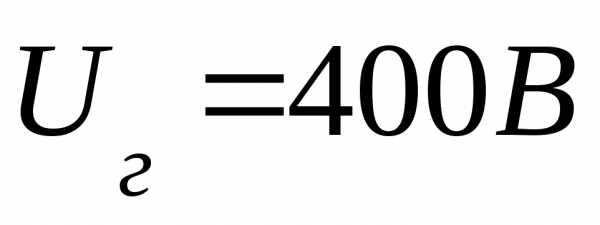 для цепей переменного тока обозначают
буквой
для цепей переменного тока обозначают
буквой 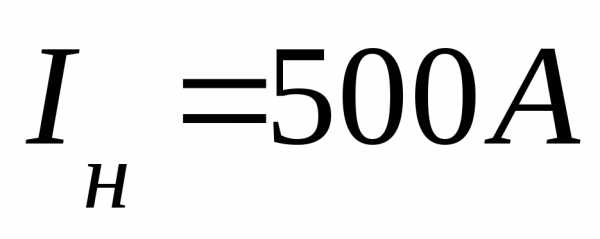 :
.
:
.
На
рис. 5.21 приведены фазовые резонансные
кривые
и,
построенные по формулам (5.66) и (5.82) при
значениях параметра 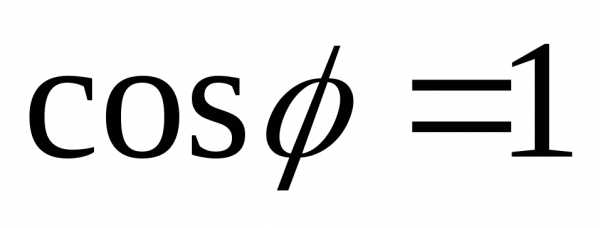 :
.
:
.
Рис. 5.21
Из
них следует, что внешнее напряжение
опережает по фазе напряжение на
конденсаторе на угол 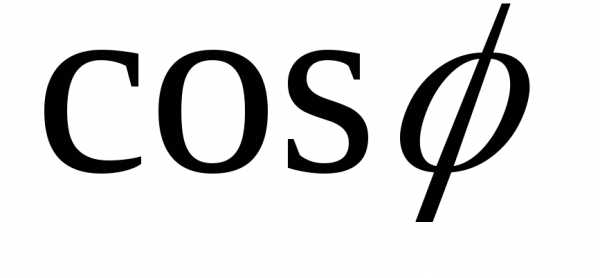 .
На векторной диаграмме это означает,
что вектор амплитуды
.
На векторной диаграмме это означает,
что вектор амплитуды 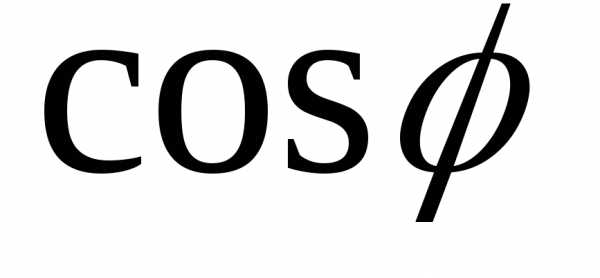 располагается выше вектора амплитуды
располагается выше вектора амплитуды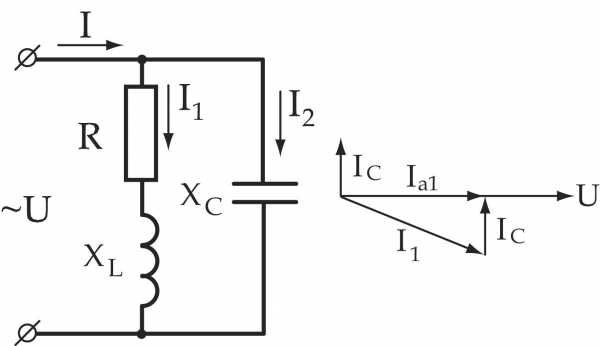 (рис. 5.20 а,б,в). Причем угол
(рис. 5.20 а,б,в). Причем угол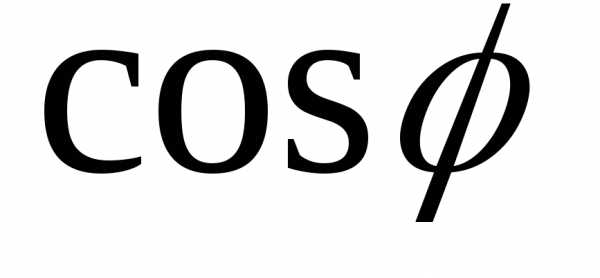 изменяется от нулевого значения для
частоты
изменяется от нулевого значения для
частоты 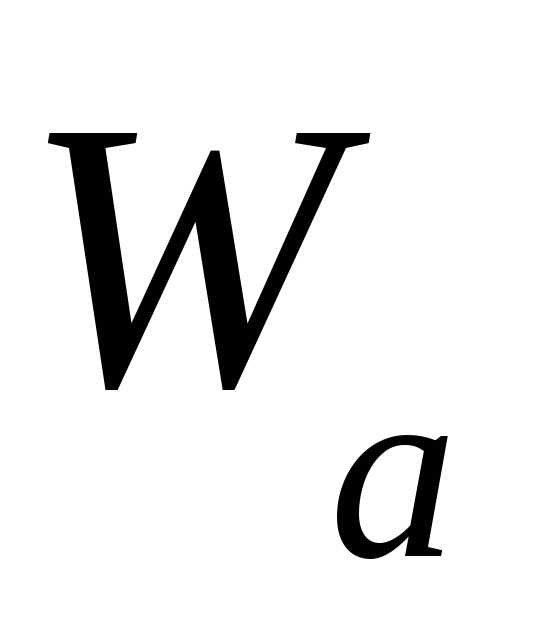 , равной нулю
(
, равной нулю
(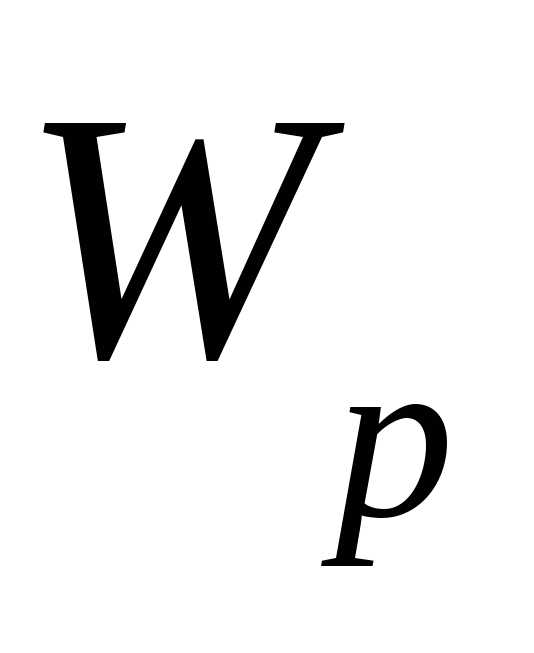 ),
до значения равного
),
до значения равного 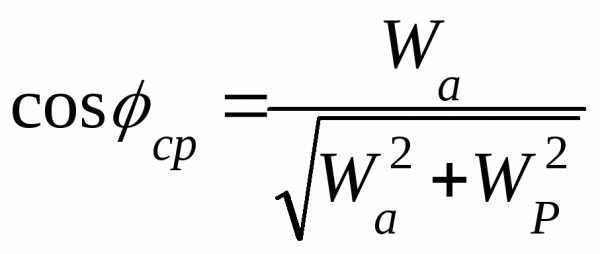 при частоте внешнего напряжения
стремящегося к бесконечности (,
рис. 5.21,а). При резонансе амплитуды
векторов внешнего напряжения
при частоте внешнего напряжения
стремящегося к бесконечности (,
рис. 5.21,а). При резонансе амплитуды
векторов внешнего напряжения  и напряжения на конденсаторе
и напряжения на конденсаторе взаимно перпендикулярны (см. рис. 5.20,б),
что приводит к разности фаз между ними,
равной
взаимно перпендикулярны (см. рис. 5.20,б),
что приводит к разности фаз между ними,
равной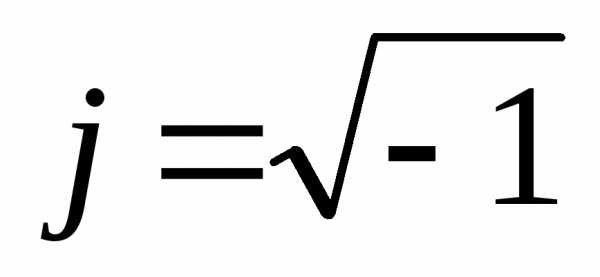 (,
Рис. 5.21,а).
(,
Рис. 5.21,а).
Из
другой фазовой резонансной кривой
следует, что фаза внешнего напряжения
для частот 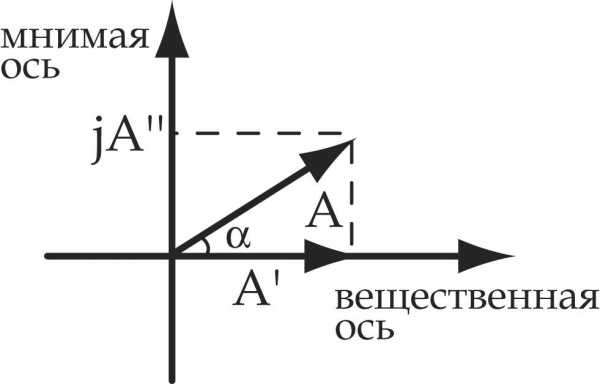 отстает от
фазы тока в контуре на угол
отстает от
фазы тока в контуре на угол 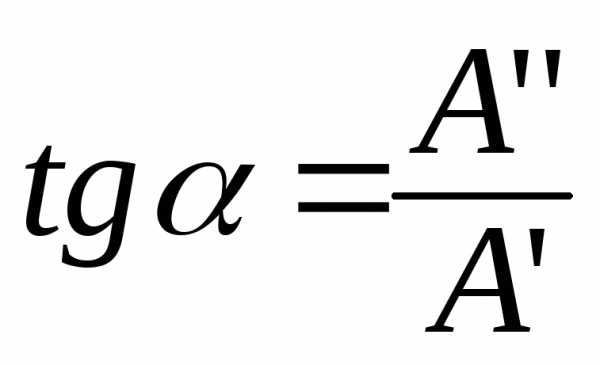 (рис.5.21,б). Для частот
(рис.5.21,б). Для частот  фаза внешнего
напряжения опережает на угол
фаза внешнего
напряжения опережает на угол 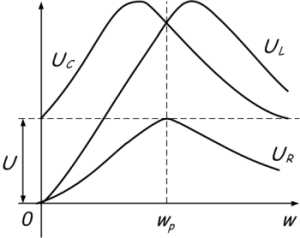 фазу колебаний силы тока в контуре и
при увеличении частоты
фазу колебаний силы тока в контуре и
при увеличении частоты 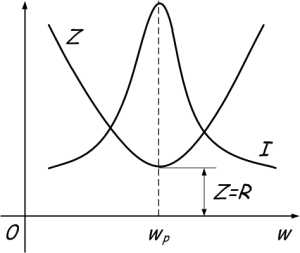 стремится к значению, равному
стремится к значению, равному 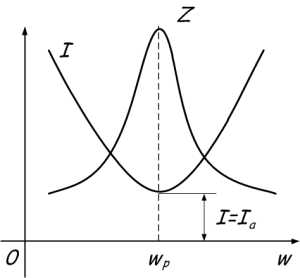 . При резонансе
(
. При резонансе
(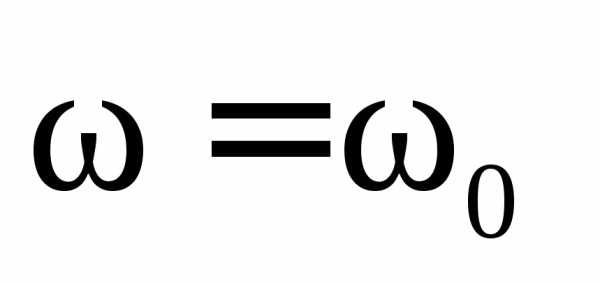 ,.)
фаза колебаний силы тока и внешнего
напряжения совпадают, т.е.
,.)
фаза колебаний силы тока и внешнего
напряжения совпадают, т.е.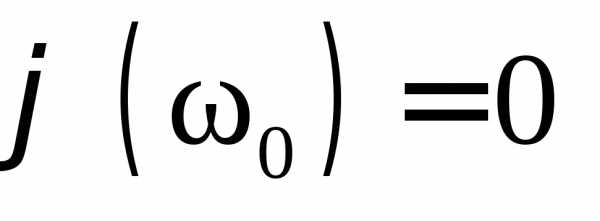 и вектора амплитуд
и вектора амплитуд 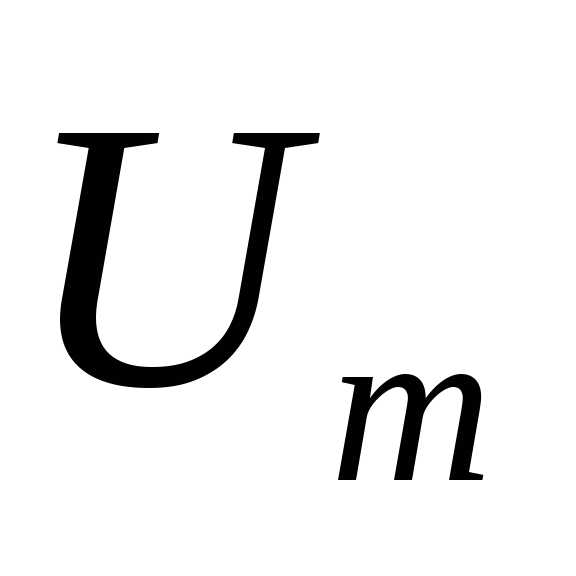 и
и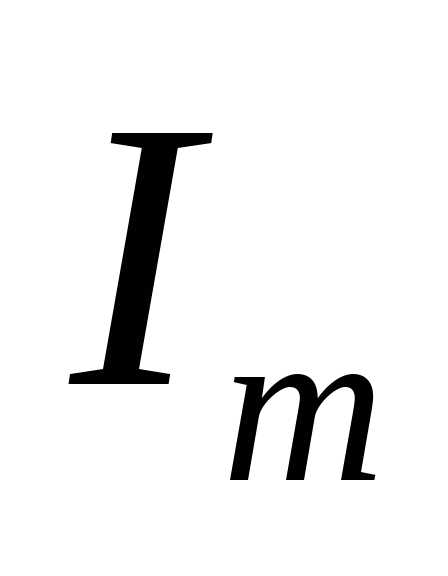 направлены одинаково, вдоль оси
направлены одинаково, вдоль оси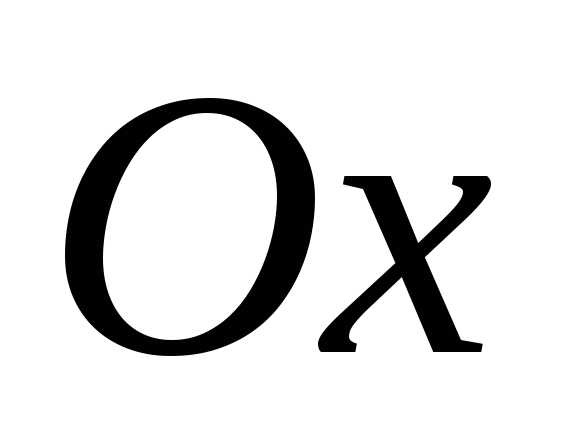 (рис.
5.21,б).
(рис.
5.21,б).
При этом энергия поступает в контур согласованно с колебаниями в ней. Действительно, учитывая выполнение условий малого затухания (Q >>1) и формулы (5.64) и (5.66) запишем
: ;
, .
Такое поступление энергии в контур при резонансе приводит к большим амплитудам колебаний, их числовые значения определяются диссипацией (рассеянием) энергии системы, т. е. коэффициентом затухания (формула (5.70)).
При
частотах  ,
больших или меньших
,
больших или меньших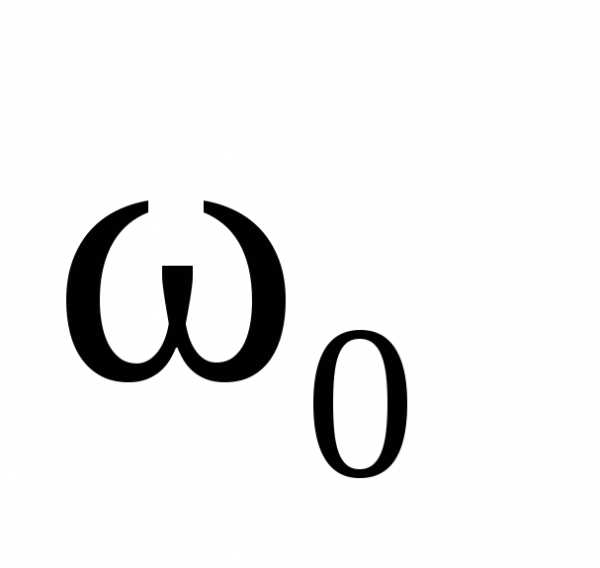 ()
амплитуда вынужденных колебаний даже
в отсутствии диссипации энергии (
()
амплитуда вынужденных колебаний даже
в отсутствии диссипации энергии (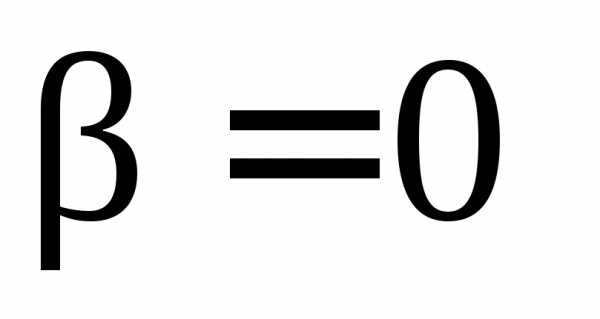 )
будет уменьшаться, она определяется
расстройкой резонанса (
)
будет уменьшаться, она определяется
расстройкой резонанса (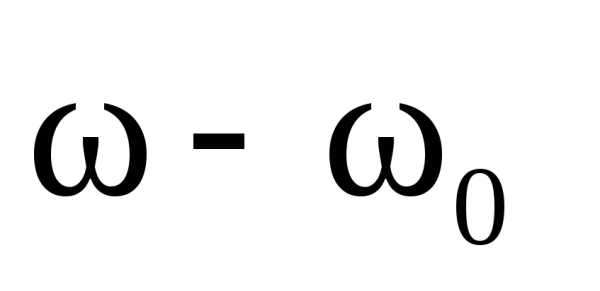 ),
т.е. разностью частот
),
т.е. разностью частот  и
и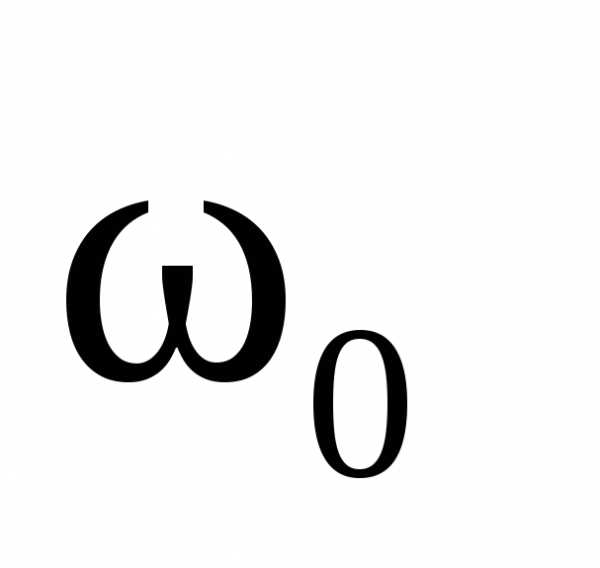 .
.
Можно отметить, что с использованием таблицы аналогий можно построить фазовые резонансные кривые для разности фаз между скоростью колебаний тела и действующей на него внешней силой в случае механической системы и т.д.
studfiles.net
Резонанс токов — описание явления и области применения

Резонанс токов, хорошо известный как естественный токовый «параллельный резонанс» — процесс или явление, которое протекает в условиях параллельного типа колебательного контура и наличия напряжения.
В данном случае частота источника напряжения должна иметь совпадение с аналогичными резонансными показателями контура.
Что такое резонанс?
Токовым резонансом называется особый вид состояния цепи, когда общие токовые показатели совпадают по фазным параметрам с уровнем напряжения, а реактивная мощность равняется нулю и цепью потребляется исключительно активная мощность.Данный вариант является характерным преимущественно для схем с переменными показателями токовых величин и обладает не только положительными свойствами, но и некоторыми совершенно нежелательными качествами, которые в обязательном порядке учитываются еще в процессе проектирования.
Положительное резонансное действие — явление из области радиотехники, автоматики и проволочной телефонии. Резонанс напряжений относится к категории нежелательных явлений, обусловленных перенапряжениями. При этом добротным электрическим контуром принято считать величину:
Достижение токового резонанса осуществляется подбором необходимого индуктивного или емкостного значения, а также показателей частотности питающих сетей.
Токовый резонанс получается подбором параметров электроцепи в условиях заданной частоты источника питания, а также посредством выбора обратных показателей.
Применение токового резонанса
Основная область активного применения широко востребованных резонансных токов сегодня представлена:
- некоторыми видами фильтрующих систем, в которых току с определенными частотными параметрами оказываются значительные показатели сопротивления;
- радиотехникой в виде приемников, выделяющих сигналы, предназначенные для конкретных точек радиостанций. Оказание значительного сопротивления току сопровождается снижением показателей контурного напряжения при максимальной частоте;
- асинхронного типа двигателями, в особенности функционирующими в условиях неполной нагрузки;
- установками высокоточной электрической сварки;
- колебательными контурами внутри узлов генераторов электронного типа;
- приборами, отличающимися высокочастотной закалкой;
- снижением показателей генераторной нагрузки. При таких условиях в приемном трансформаторе с первичной обмоткой делается колебательный контур.
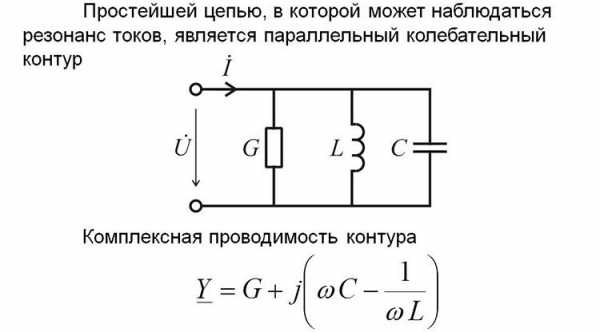
Схема цепи
Особенно часто колебательные контуры или токовые резонансы применяются в производстве современного промышленного индукционного котлового оборудования, что позволяет в значительной степени улучшить стартовые показатели коэффициента полезного действия.
Стандартные колебательные контуры, функционирующие в условиях режима токового резонанса, массово применяются в качестве одного из наиболее важных узлов в современных электронных генераторах.
Принцип резонанса токов
Токовый резонанс наблюдается внутри электроцепи, обладающей параллельным катушечным, резисторным и конденсаторным подсоединением. Основной принцип работы стандартного резонанса токов не слишком сложен для понимания простого обывателя:
- включение электропитания сопровождается накоплением заряда внутри конденсатора до номинальных показателей напряжения источника;
- отключение питающего источника с последующим замыканием цепи в контур сопровождается процессом переноса разряда на катушечную часть прибора;
- токовые показатели, проходящие по катушке, вызывают генерирование магнитного поля и создание электродвижущей силы самоиндукции, в направлении, встречном току;
- максимальное значение токовых показателей достигается на стадии полного конденсаторного разряда;
- весь объем накопленной энергетической емкости легко преобразуется в магнитное индукционное поле;
- катушечная самоиндукция не провоцирует остановку заряженных частиц, а повторный этап зарядки с другим типом полярности обусловлен отсутствием конденсаторного противотока.
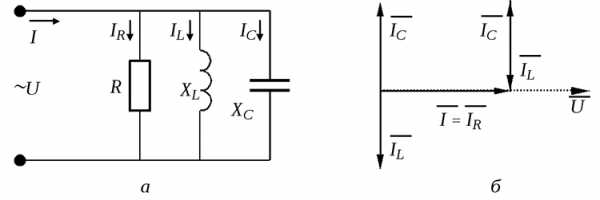
Резонанс в параллельной цепи (резонанс токов)
Итогом данного цикла является повторяющееся преобразование всего катушечного поля в конденсаторный заряд. Определение стандартной резонансной частоты осуществляется аналогично расчетам резонанса напряжения.
Присутствующая внутренняя активная составляющая R вызывает постепенное угасание колебательного процесса, чем и обуславливается токовый резонанс.
Резонанс токов в цепи с переменным током
Протекание тока внутри электрической цепи с последовательным, параллельным или смешанным типом соединения элементов, вызывает получение различных режимов функционирования.Таким образом, резонанс электрической цепи является режимом участка, который содержит элементы индуктивного и емкостного типа, а угол фазового сдвига между токовыми величинами и показателями напряжения нулевые.
В соединяемых параллельным способом конденсаторе и катушечной части наблюдается равное реактивное сопротивление, чем обусловлен резонанс.
Также должен учитываться тот факт, что для катушечной части и конденсатора характерно полное отсутствие активного сопротивления, а равенство реактивного сопротивления делает нулевыми общие токовые показатели внутри неразветвленной части электрической цепи и большие величины тока в ветвях.
В условиях параллельного соединения индуктивной катушки и конденсатора получается колебательный контур, который отличается наличием создающего колебания генератора, не подключенного в контур, что делает систему замкнутой.
Явление, сопровождающееся резким уменьшением амплитуды силы токовых величин внешней цепи, которая используется для питания параллельно включенного конденсатора и обычной индуктивной катушки в условиях приближения частоты приложенного напряжения к частоте резонанса, носит название токового или параллельного резонанса.
Расчет резонансного контура
Необходимо помнить, что явление, представленное токовым резонансом, нуждается в очень грамотном и тщательном расчете резонансного контура. Особенно важно выполнить правильный и точный расчет при наличии параллельного соединения, что позволит предотвратить развитие помех внутри системы. Чтобы расчет был правильным, требуется определиться с показателями мощности электрической сети. Среднюю стандартную мощность, которая рассеивается в условиях резонансного контура, можно выразить среднеквадратичными показателями тока и напряжения.
В условиях резонанса стандартный коэффициент мощности составляет единицу, а формула расчета имеет вид:
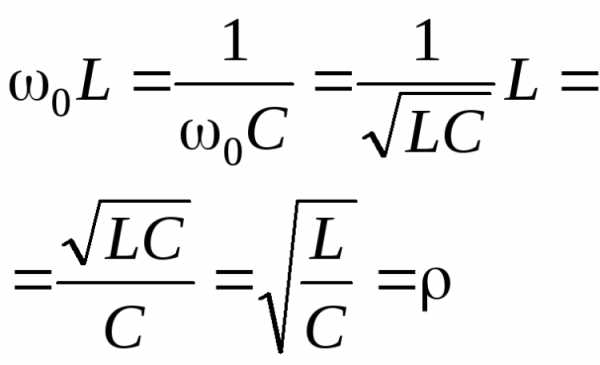
Формула расчета
С целью правильного определения нулевого импеданса в условиях резонанса потребуется использовать стандартную формулу:
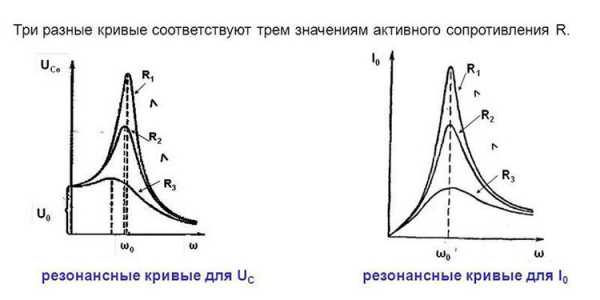
Резонансные кривые
Резонанс колебательной частоты аппроксимируется по следующей формуле:
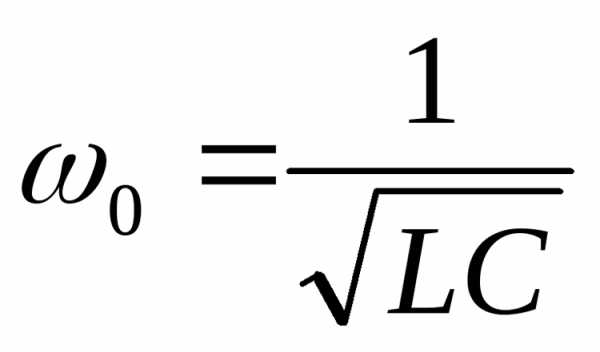
Резонанс колебательного контура
Чтобы получить максимально точные данныепо формулам, все получаемые в процессе расчетов значения рекомендуется не подвергать округлению. Некоторыми физиками расчеты значений резонансного контура осуществляются в соответствии с методом векторной диаграммы активных токовых величин. В таком случае грамотный расчет и правильная настройка приборов гарантирует достойную экономию при условии переменного тока.
Резонансные цепи применяются преимущественно для выделения сигнала на нужных частотах в результате фильтрования других сигналов, поэтому самостоятельные расчеты контура должны быть предельно точными.
Заключение
Резонанс токовых величин в физике — это естественное явление, сопровождающееся резким возрастанием амплитуды колебания внутри системы, что обусловлено совпадением показателей собственных и внешних возмущающих частот.
Подобный вариант явлений характеризует электрические схемы с наличием элементов, представленных нагрузками активного, индуктивного и емкостного типа. Таким образом, токовый резонанс — один из наиважнейших параметров, широко используемых в настоящее время в целом ряде современных отраслей, включая промышленное электрическое снабжение и радиосвязь.
proprovoda.ru
Резонанс напряжений и резонанс токов
В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.
Резонанс напряжений
Резонанс напряжений возникает в последовательной RLC-цепи.
Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=wр, а следовательно и индуктивного и емкостного сопротивлений xL=xC. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке UL и на конденсаторе UC будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.
При резонансе напряжения UC и UL могут быть намного больше, чем напряжение источника, что опасно для цепи.
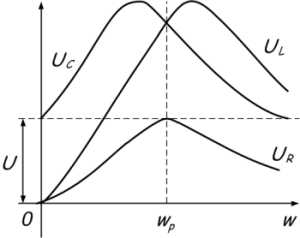
С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.
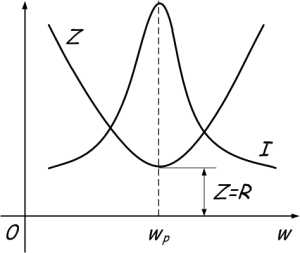
Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту
Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.
Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.
Резонанс токов
Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.
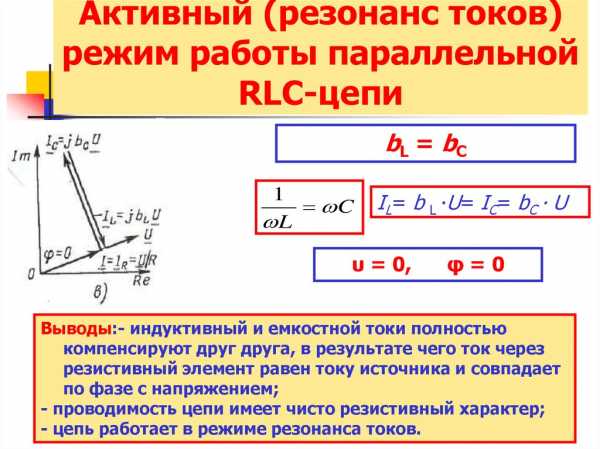
Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.
Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.
Выразим резонансную частоту
Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.
Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.
electroandi.ru

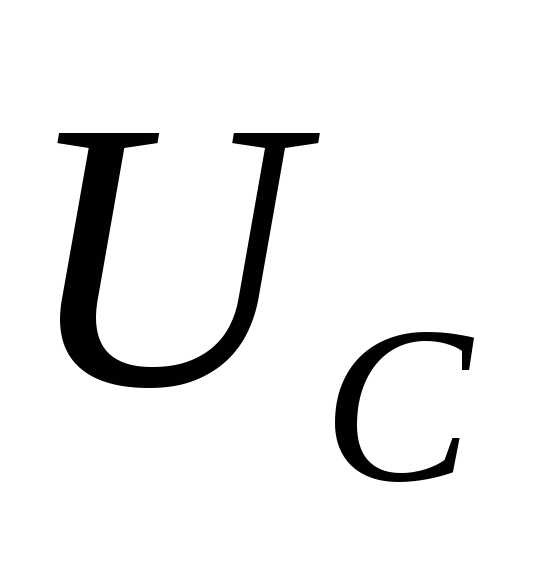
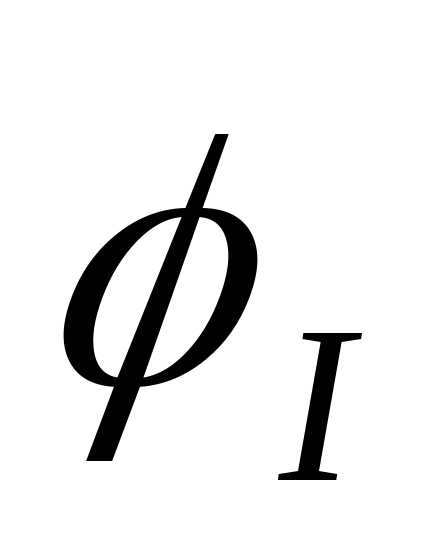

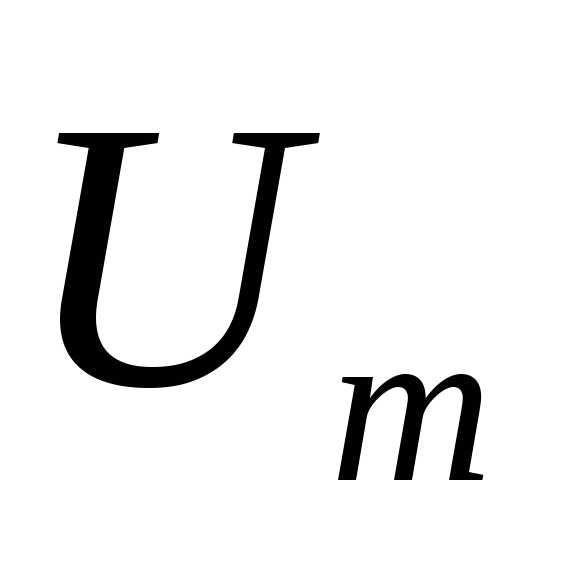 —
чисто активный характер, т.к. реактивные
точки
—
чисто активный характер, т.к. реактивные
точки 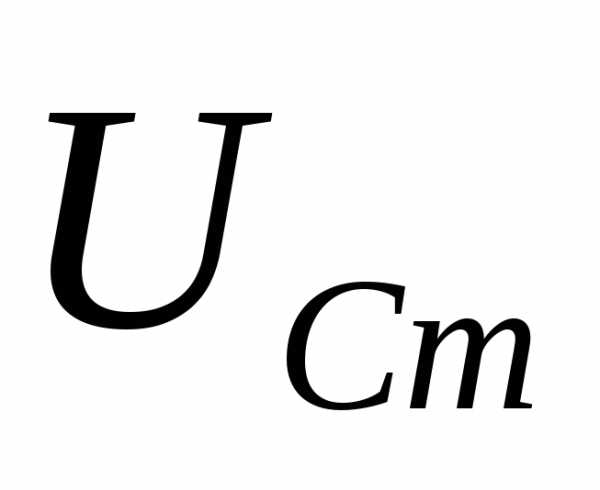 икомпенсируют друг друга
икомпенсируют друг друга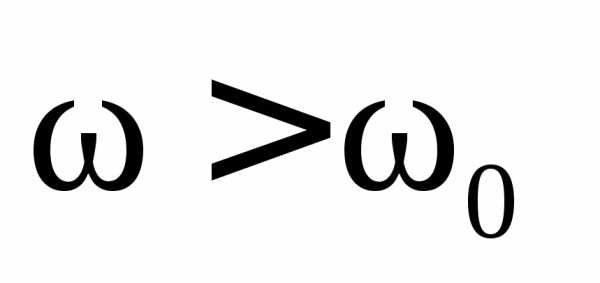
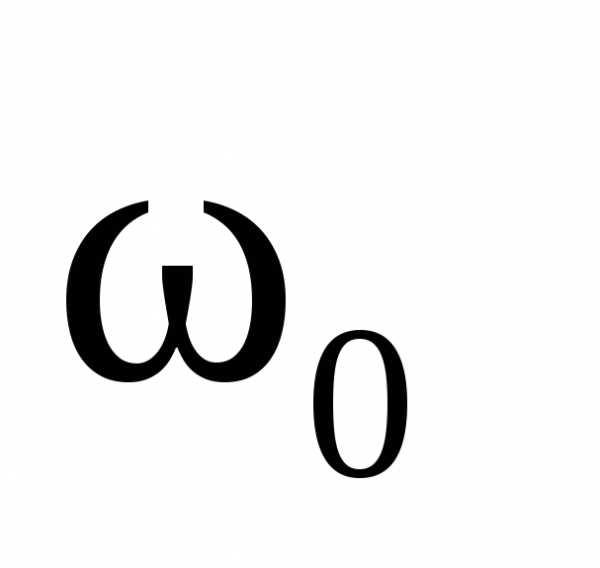
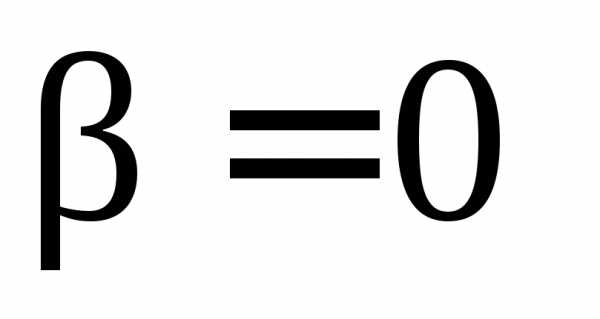 .
Для этого с помощью счетчиков измеряют
активную (
.
Для этого с помощью счетчиков измеряют
активную (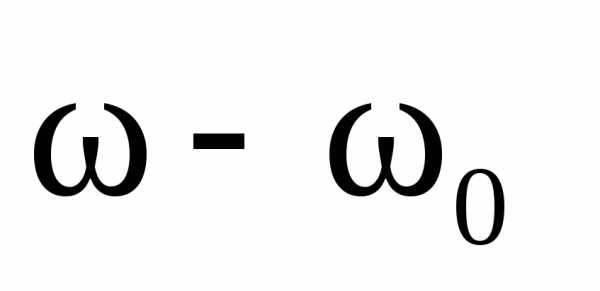 )
и реактивную (
)
и реактивную ( )энергии.
)энергии.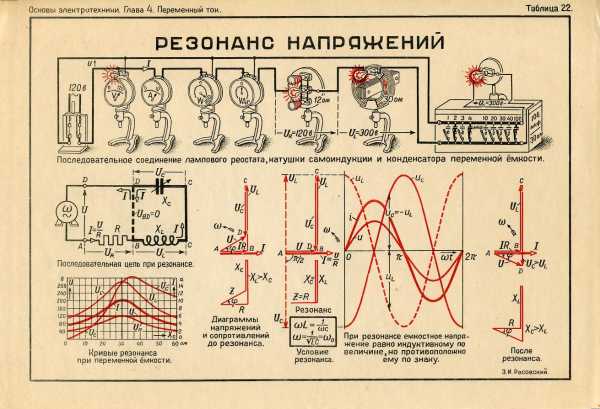
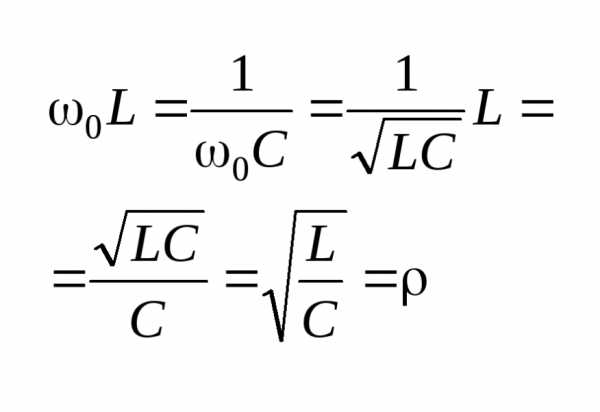 —
аргумент комплексного числа
—
аргумент комплексного числа