РИМСКАЯ СИСТЕМА СЧИСЛЕНИЯ — PDF Free Download
Понятие системы счисления
Понятие системы счисления Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления (с/с). Алфавит
ПодробнееКодирование числовой информации
Кодирование числовой информации Для представления чисел используются системы счисления. Система счисления это знаковая система, в котор ой числа записываются по определенным правилам с помощью символов
ПодробнееТема 1 Системы счисления Теория
Тема 1 Системы счисления Теория Для начала надо вспомнить, что же такое системы счисления. Система счисления (СС) это совокупность правил записи чисел посредством конечного набора символов (цифр). Системы
Система счисления (СС) это совокупность правил записи чисел посредством конечного набора символов (цифр). Системы
ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ
ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ Информация в ЭВМ кодируется, как правило, в двоичной или в двоично-десятичной системе счисления. Система счисления это способ наименования и изображения чисел с помощью
Подробнее1 (базовый уровень, время 1 мин)
1 (базовый уровень, время 1 мин) Тема: Системы счисления и двоичное представление информации в памяти компьютера. Теория: алгоритм перевода чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной
ПодробнееСистемы счисления (СС)
Системы счисления (СС) I. Двоичная система счисления. Как устроено число в десятичной СС: 579 0 =5 0 7 0 9 0 0 ( a 0, a 0).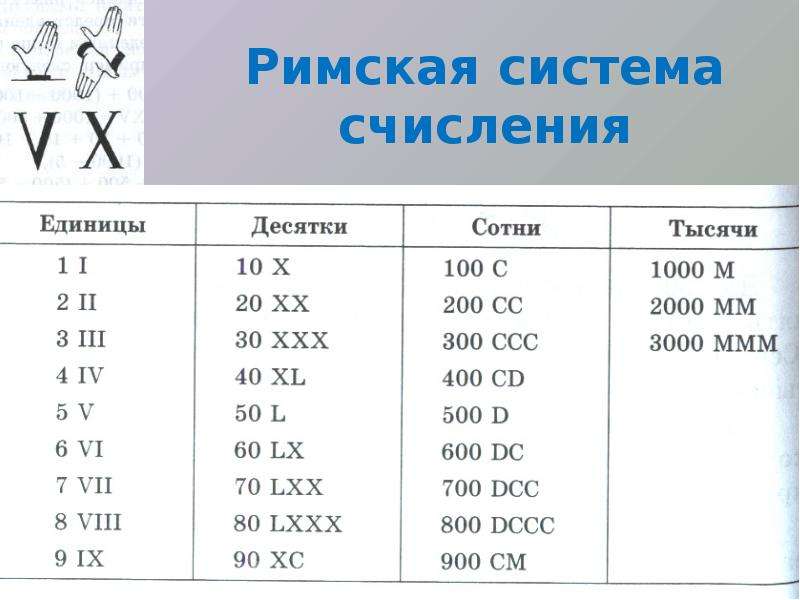 В любой другой позиционной системе счисления числа устроены точно таким же образом.
В любой другой позиционной системе счисления числа устроены точно таким же образом.
Введение в системы счисления
Введение в системы счисления А.А. Вылиток Система счисления это способ записи чисел с помощью заданного набора специальных знаков (цифр). Существуют позиционные и непозиционные системы счисления. В непозиционных
ПодробнееТема 7. Представление информации в ЭВМ.
Тема 7. Представление информации в ЭВМ.. Единицы информации. Бит — (bit-biry digit — двоичный разряд) наименьшая единица информации — количество её, необходимое для различения двух равновероятных событий.
Тема: Системы счисления
Коротко о главном Тема: Системы счисления Системы счисления — это способ представления чисел и соответствующие ему правила действия над числами. Разнообразные системы счисления, который существовали раньше
Разнообразные системы счисления, который существовали раньше
А4 (базовый уровень, время 2 мин)
А4 (базовый уровень, время 2 мин) Тема: Выполнение арифметических операций в двоичной, восьмеричной и шестнадцатеричной системах Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной
ПодробнееЛабораторная работа 1 Системы счисления
Лабораторная работа 1 Системы счисления Цель работы: овладеть приемами перевода чисел из одной системы счисления в другую Теоретические сведения Под системой счисления понимается способ представления чисел
ПодробнееА4 (базовый уровень, время 2 мин)
А4 (базовый уровень, время 2 мин) Тема: Выполнение арифметических операций в двоичной, восьмеричной и шестнадцатеричной системах счисления.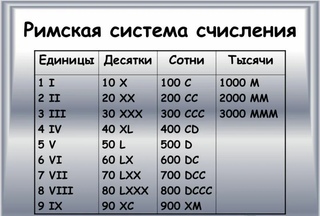 Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной
Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной
Укажите, сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12,, 17 в системе счисления с основанием 5.
Уравнения и различные системы счисления 1. Укажите, сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12,, 17 в системе счисления с основанием 5. 2. 121 x + 1 10 = 101 7 Ответ запишите в троичной
Системы счисления План лекции П. 1.
Системы счисления План лекции П. 1. Понятие системы счисления. Виды систем счисления…. 1 П. 2. Основные определения позиционной системы счисления…. 1 П. 3. Перевод чисел из одной системы счисления
ПодробнееКодирование информации
Кодирование представление символов одного алфавита символами другого по определённым правилам.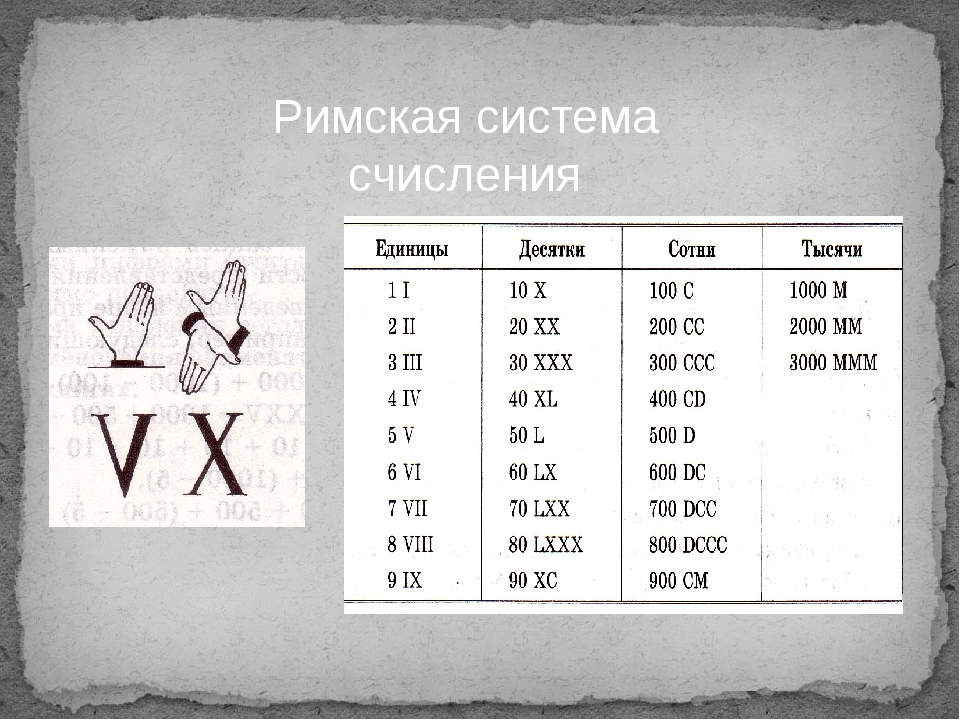 Система счисления способ представления любого числа с помощью алфавита символов, называемых цифрами. Непозиционная
Система счисления способ представления любого числа с помощью алфавита символов, называемых цифрами. Непозиционная
Введение. Уважаемые восьмиклассники!
Введение Уважаемые восьмиклассники! Мы живём во время стремительных перемен, когда для человека важна способность к постоянному развитию, готовность к освоению новых, в том числе информационных, технологий.
ПодробнееА1 (базовый уровень, время 1 мин)
А1 (базовый уровень, время 1 мин) Тема: Системы счисления и двоичное представление информации в памяти компьютера. Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной
ПодробнееСистема счисления. Система счисления способ записи чисел с помощью набора специальных знаков, называемых цифрами.
Привет! 1001011 Система счисления Система счисления способ записи чисел с помощью набора специальных знаков, называемых цифрами. Числа: 123, 45678, 1010011, CXL Цифры: 0, 1, 2, I, V, X, L, Алфавит это
Числа: 123, 45678, 1010011, CXL Цифры: 0, 1, 2, I, V, X, L, Алфавит это
16 (повышенный уровень, время 2 мин)
16 (повышенный уровень, время мин) Тема: Кодирование чисел. Системы счисления. Что нужно знать: принципы кодирования чисел в позиционных системах счисления чтобы перевести число, скажем, 15, из системы
ПодробнееА1 (базовый уровень, время 1 мин)
А1 (базовый уровень, время 1 мин) Тема: Системы счисления и двоичное представление информации в памяти компьютера. Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной
ПодробнееА1 (базовый уровень, время 1 мин)
А1 (базовый уровень, время 1 мин) Тема: Системы счисления и двоичное представление информации в памяти компьютера. Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной
ПодробнееB8 (повышенный уровень, время 2 мин)
К. Поляков, 009-011 B8 (повышенный уровень, время мин) Тема: Кодирование чисел. Системы счисления. Что нужно знать: принципы кодирования чисел в позиционных системах счисления чтобы перевести число, скажем,
Поляков, 009-011 B8 (повышенный уровень, время мин) Тема: Кодирование чисел. Системы счисления. Что нужно знать: принципы кодирования чисел в позиционных системах счисления чтобы перевести число, скажем,
ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Известно множество способов представления чисел. В любом случае число изображается символом или группой символов (словом) некоторого алфавита. Будем называть такие символы
ПодробнееB7 (повышенный уровень, время 2 мин)
К Поляков, 009-01 B7 (повышенный уровень, время мин) Тема: Кодирование чисел Системы счисления Что нужно знать: принципы кодирования чисел в позиционных системах счисления чтобы перевести число, скажем,
1 (базовый уровень, время 1 мин)
1 (базовый уровень, время 1 мин) Тема: Системы счисления и двоичное представление информации в памяти компьютера. Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной
Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной
Системы счисления Пример 1.
Системы счисления В наше время человек всё время сталкивается с числами. Все мы с детства знакомы с общепринятой записью чисел при помощи арабских цифр. Однако этот способ записи использовался далеко не
ПодробнееА1 (базовый уровень, время 1 мин)
А1 (базовый уровень, время 1 мин) Тема: Системы счисления и двоичное представление информации в памяти компьютера. Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной
ПодробнееА1 (базовый уровень, время 1 мин)
А1 (базовый уровень, время 1 мин) Тема: Системы счисления и двоичное представление информации в памяти компьютера. Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной
Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной
А1 (базовый уровень, время 2 мин)
А1 (базовый уровень, время 2 мин) Тема: Системы счисления и двоичное представление информации в памяти компьютера. Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной
Подготовка к ЕГЭ. Занятие октября 2016 г.
Подготовка к ЕГЭ. Занятие 1 16 октября 2016 г. 27 заданий на 35 баллов: Часть I: 23 задания на короткий ответ (число или слово) 23 балла Часть II: 4 задания на развернутый ответ (код или описание результата)
ПодробнееСИСТЕМЫ СЧИСЛЕНИЯ. Методическое пособие
СИСТЕМЫ СЧИСЛЕНИЯ Методическое пособие Понятие системы счисления Система счисления это способ записи чисел с помощью заданного набора специальных знаков. Римская система счисления Большинство историков
Римская система счисления Большинство историков
16 (повышенный уровень, время 2 мин)
К. Поляков, 009-016 16 (повышенный уровень, время мин) Тема: Кодирование чисел. Системы счисления. Что нужно знать: принципы кодирования чисел в позиционных системах счисления чтобы перевести число, скажем,
ПодробнееАрифметические основы работы компьютера
Министерство образования и науки Российской Федерации Государственное образовательное учреждение высшего профессионального образования «Тихоокеанский государственный университет» Арифметические основы
ПодробнееTecт 1. Системы счисления. Вариант 1
Tecт 1. Системы счисления Вариант 1 1. Что такое система счисления? A) Цифры 1, 2, 3, 4, 5, 6, 7, 8, 9; B) правила арифметических действий; C) компьютерная программа для арифметических вычислений; D) Это
Подробнее«Римская система счисления» | Тест по алгебре (5, 6 класс) на тему:
Кружок «Занимательная математика»
Медведева Татьяна Петровна, учитель математики МКОУ Новомеловатская СОШ
«Римская система счисления»
Тест для учащихся 5 – 6 классов с ответами.
Данный тест может использоваться учителями математики как на уроках, так и во внеурочной деятельности.
1. Среди множества иероглифических систем счисления, которые существовали в разные времена у разных народов, только одна используются до сих пор. Какая?
1) критская 2) сирийская 3) римская 4) пальмирская
2. Где придумана римская нумерация?
1) Древний Египет 2) Древний Вавилон 3) Древняя Греция 4) Древней Рим
3. Сколько цифр в римской нумерации?
1) 3 2) 5 3) 7 4) 9
4. Какими буквами обозначаются римские цифры?
1) заглавными латинскими;
2) прописными немецкими;
3) прописными латинскими;
4) русскими
5. Какая римская цифра обозначает число 1000?
1) X 2) M 3) V 4) C
6. Какое число записано римскими цифрами – XLVII?
Какое число записано римскими цифрами – XLVII?
1) 47 2) 53 3) 69 4) 74
7. Одно из правил записи римских чисел гласит: «Если большая цифра стоит перед меньшей, то они …»
1) вычитаются 2) складываются 3) умножаются 4) делятся
8. Какая из записей числа 99 считается верной?
1) IC 2) LXXXXIX 3) XCIX 4) XLLIX
9. Какие римские цифры не претерпели изменений с течением времени?
1) I, V, X 2) все 3) C, D 4) L, D, M
10. В наши дни любую из римских цифр запрещается записывать в одном числе более трёх раз подряд. Какая из записей считается некорректной?
1) XIV 2) LXIII 3) XXXXV 4) DCCC
Список используемой литературы:
1. Депман И. Я., Виленкин Н. Я. «За страницами учебника математики». Пособие для учащихся 5 -6 классов ср. школы. – М.: Просвещение, 1989.
Пособие для учащихся 5 -6 классов ср. школы. – М.: Просвещение, 1989.
2. Математика: Учеб.- собеседник для 5 кл. сред. шк. / Л. Н. Шеврин, А. Г. Гейн, И. О. Коряков, М. В. Волков.-2-е изд. – М.: просвещение, 1994.
3. Я познаю мир: Детская энциклопедия: Математика / Сост. А.П. Савин, В. В. Станцо, А. Ю. Котова: — М: ООО «Фирма «Издательство АСТ», 1999.
Римская система счисления (самостоятельная работа)
Задание 1. Переведите число из римской системы счисления в десятичную:
a) MCMXCIX = ___________________________________________________
Задание 2. Запишите десятичное число в римской системе счисления:
145 = ____________________________________________________________
Задание 3. А. С. Пушкин родился в MDCCXCIX году. Запишите год в десятичной форме__________
Задание 4. Приведите примеры унарной системы счисления: ___________________________
Задание 5. Запишите пример в десятичной системе, вычислите ответ и запишите его в римской системе:
Запишите пример в десятичной системе, вычислите ответ и запишите его в римской системе:
a) MCM — XC = _______________________________________________________
Задание 1. Переведите число из римской системы счисления в десятичную:
б) CMLXXXVIII = ___________________________________________________
Задание 2. Запишите десятичное число в римской системе счисления:
473 = ____________________________________________________________
Задание 3. Приведите пример непозиционной системы счисления: ________________________
Задание 4. Куликовская битва произошла в MCCCLXXX году. Запишите год в десятичной форме____
Задание 5. Запишите пример в десятичной системе, вычислите ответ и запишите его в римской системе:
б) LX + XXVIII = ____________________________________________________
Задание 1. Переведите числа из римской системы счисления в десятичную:
в) MCXLVII = ___________________________________________________
Задание 2. Запишите десятичные числа в римской системе счисления:
Запишите десятичные числа в римской системе счисления:
1948 = ____________________________________________________________
Задание 3. Приведите пример позиционной системы счисления: _______________________
Задание 4. Год основания Петербурга MDCCIII. Запишите год в десятичной форме._____________
Задание 5. Запишите пример в десятичной системе, вычислите ответ и запишите его в римской системе:
г) IX +MC =_________________________________________________________
Задание 1. Переведите число из римской системы счисления в десятичную:
a) MCMXCIX = ___________________________________________________
Задание 2. Запишите десятичное число в римской системе счисления:
145 = ____________________________________________________________
Задание 3. А. С. Пушкин родился в MDCCXCIX году. Запишите год в десятичной форме_____________
Задание 4. Приведите примеры унарной системы счисления: ___________________________
Задание 5. Запишите пример в десятичной системе, вычислите ответ и запишите его в римской системе:
Запишите пример в десятичной системе, вычислите ответ и запишите его в римской системе:
a) MCM — XC = _______________________________________________________
Задание 1. Переведите число из римской системы счисления в десятичную:
б) CMLXXXVIII = ___________________________________________________
Задание 2. Запишите десятичное число в римской системе счисления:
473 = ____________________________________________________________
Задание 3. Приведите пример непозиционной системы счисления: ________________________
Задание 4. Куликовская битва произошла в MCCCLXXX году. Запишите год в десятичной форме______
Задание 5. Запишите пример в десятичной системе, вычислите ответ и запишите его в римской системе:
б) LX + XXVIII = ____________________________________________________
Задание 1. Переведите числа из римской системы счисления в десятичную:
в) MCXLVII = ___________________________________________________
Задание 2. Запишите десятичные числа в римской системе счисления:
Запишите десятичные числа в римской системе счисления:
1948 = ____________________________________________________________
Задание 3. Приведите пример позиционной системы счисления: _______________________
Задание 4. Год основания Петербурга MDCCIII. Запишите год в десятичной форме.______________
Задание 5. Запишите пример в десятичной системе, вычислите ответ и запишите его в римской системе:
г) IX +MC =_________________________________________________________
Ответы:
Задание 1. Переведите число из римской системы счисления в десятичную:
a) MCMXCIX = 1999
Задание 2. Запишите десятичное число в римской системе счисления:
145 = CXLV
Задание 3. А. С. Пушкин родился в MDCCXCIX году. Запишите год в десятичной форме. 1799
Задание 4. Приведите примеры унарной системы счисления: зарубки, узелковое письмо (пример)
Задание 5. Запишите пример в десятичной системе, вычислите ответ и запишите его в римской системе:
a) MCM — XC = 1900-90=1810 MDCCCX
Задание 1.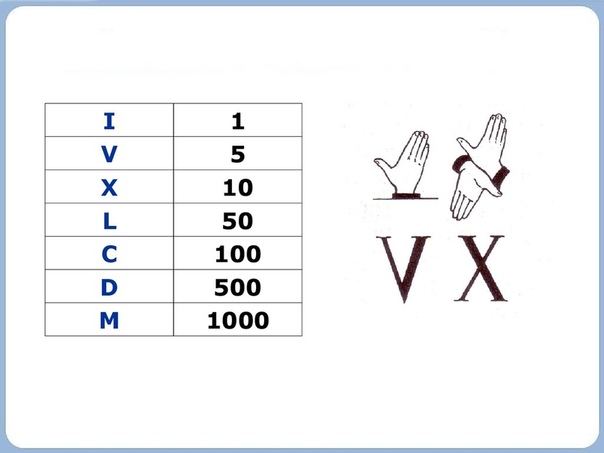 Переведите число из римской системы счисления в десятичную:
Переведите число из римской системы счисления в десятичную:
б) CMLXXXVIII = 988
Задание 2. Запишите десятичное число в римской системе счисления:
473 = CDLXXIII
Задание 3. Приведите пример непозиционной системы счисления: римская
Задание 4. Куликовская битва произошла в MCCCLXXX году. Запишите год в десятичной форме 1380
Задание 5. Запишите пример в десятичной системе, вычислите ответ и запишите его в римской системе:
б) LX + XXVIII = 60+28=88 LXXXVIII
Задание 1. Переведите числа из римской системы счисления в десятичную:
в) MCXLVII = 1147
Задание 2. Запишите десятичные числа в римской системе счисления:
1948 = MCMXLVIII
Задание 3. Приведите пример позиционной системы счисления: двоичная (один из вариантов)
Задание 4. Год основания Петербурга MDCCIII. Запишите год в десятичной форме. 1703
Задание 5. Запишите пример в десятичной системе, вычислите ответ и запишите его в римской системе:
г) IX +MC =9+1100=1109 MCIX
Системы счисления.
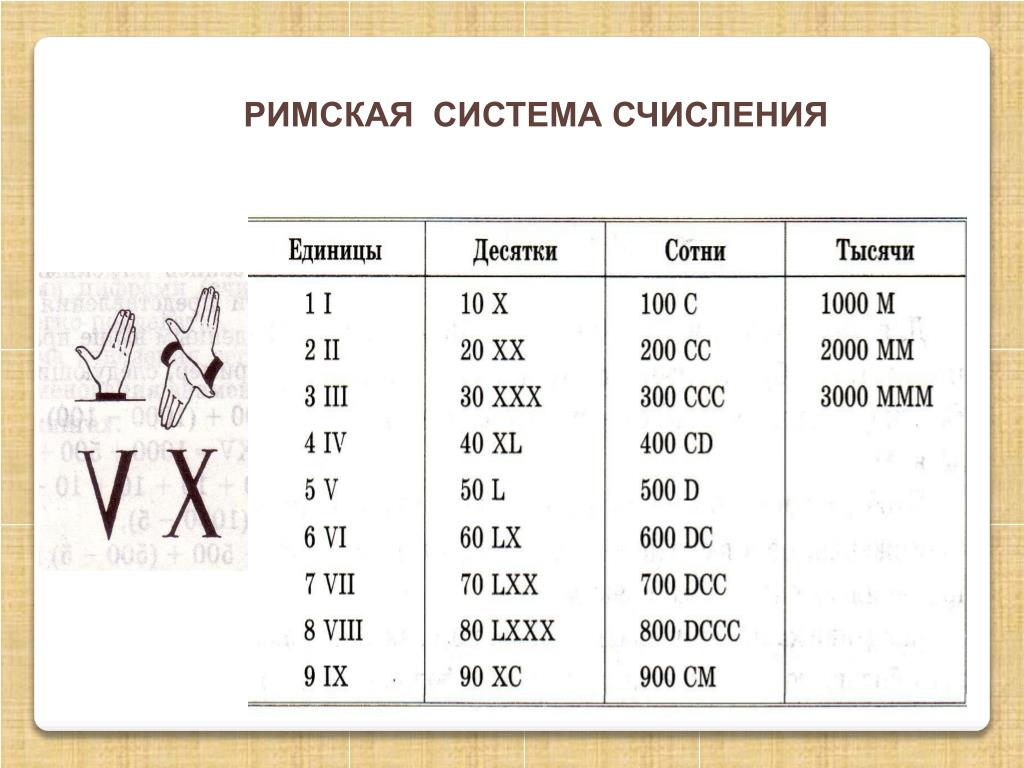 Позиционная и непозиционная системы счисления
Позиционная и непозиционная системы счисления☰
Систему счисления можно определить как способ записи чисел как количественной характеристики (отвечает на вопрос «сколько») чего-либо. Синонимом понятию «система счисления» является слово «нумерация».
В любой системе счисления числа записываются с помощью специальных, используемых в данной системе знаков-символов, которые все вместе формируют алфавит этой системы счисления. Пользуясь десятичной системой счисления мы привыкли называть символы ее алфавита цифрами.
Одно и тоже число (значение, количество) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.
Широко известны две системы счисления – арабская и римская.
Алфавит арабской системы счисления:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Арабская система счисления – это позиционная система счисления.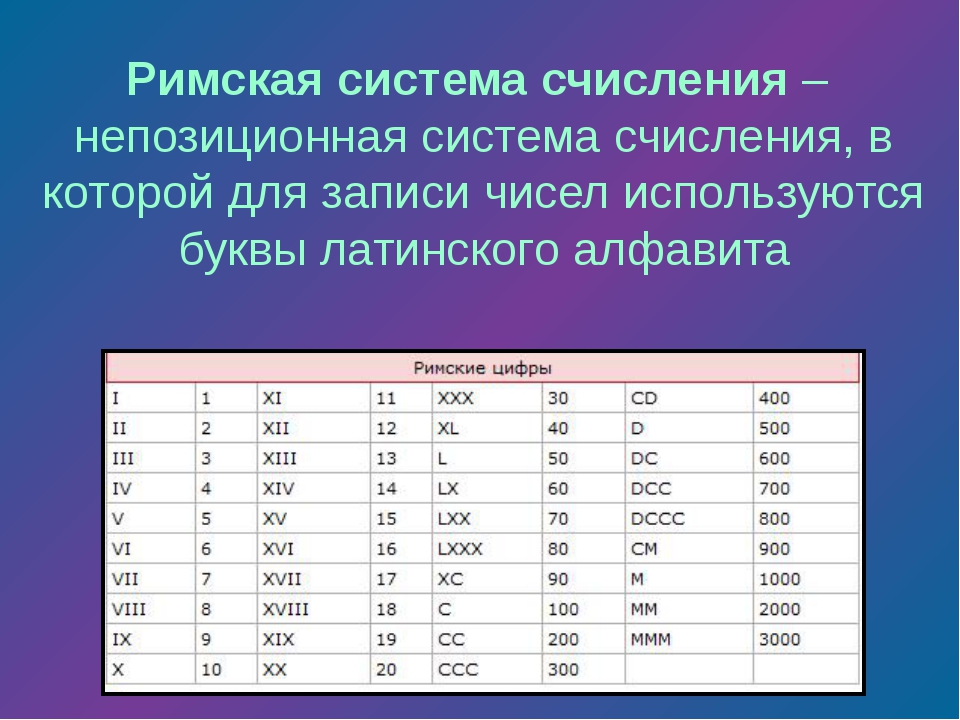
Алфавит римской системы счисления:
I, V, X, L, C, D, M
Римская система счисления относится к непозиционным.
В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, в непозиционных такой однозначной зависимости нет. Например:
11– здесь первая единица обозначает десять количественных единиц, вторая – только одну единицу.II– здесь обе единицы обозначают одну единицу.345,259,521– здесь цифра 5 в первом случае обозначает 5 единиц, во втором – 50, в третьем – 500.XXV,XVI,VII– здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.
Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, так как они легко описываются с помощью универсальных алгоритмов. Например, умножение в столбик или поразрядное сравнение двух чисел.
Например, умножение в столбик или поразрядное сравнение двух чисел.
В связи с этим позиционные системы счисления нашли более широкое распространение. Помимо всем известной десятичной, в которой используются десять цифр от 0 до 9, в вычислительных технике и технологиях нашли применение такие системы как двоичная (алфавит состоит из цифр 0 и 1), восьмеричная (алфавит: 0, 1, 2, 3, 4, 5, 6, 7) и шестнадцатеричная (алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Следует отметить, важную роль нуля. Открытие этой цифры в истории человечества сыграло большое значение в формировании позиционных систем счисления.
Ключевые понятия позиционных систем счисления
Основание системы счисления – это количество знаков, которое используется для записи цифр. Так основанием десятичной системы счисления является число десять, так как ее алфавит состоит из десяти знаков. Основание двоичной системы счисления является число два.
Основание системы счисления равно размерности алфавита системы счисления. Размерность алфавита – это количество цифр, составляющих алфавит.
Размерность алфавита – это количество цифр, составляющих алфавит.
Разряд – это позиция цифры в числе. От того, в каком месте числа находится цифра, зависит обозначаемое ею количество, то есть то, что она значит.
Разрядность числа – количество цифр, из которых состоит число. Например, 264 – трехразрядное число в десятичной системе счисления, 00010101 – восьмиразрядное число в двоичной системе счисления. Разряды нумеруются справа налево. Например, в числе 598 восьмерка занимает первый разряд, а пятерка – третий.
В позиционных системах счисления числа записываются таким образом, что каждый следующий при движении справа налево разряд больше другого на одну степень основания системы счисления.
Другими словами, у каждого разряда есть свой вес, представляющий собой основание системы счисления, возведенное в степень, соответствующую данному разряду. Показатель степени соотносится с разрядом как разряд-1. Например, в примере десятичного числа ниже цифра 8 находится в четвертом разряде числа. Значит, обозначаемое ею количество вычисляется вычисляется как произведение числа 8 на основание системы счисления (здесь 10) в степени 3.
Например, в примере десятичного числа ниже цифра 8 находится в четвертом разряде числа. Значит, обозначаемое ею количество вычисляется вычисляется как произведение числа 8 на основание системы счисления (здесь 10) в степени 3.
8325 = 8 * 1000 + 3 * 100 + 2 * 10 + 5
8325 = 8 * 103 + 3 * 102 + 2 * 101 + 5 * 100
урок 32 — Информатика 8 класс
Обучающие: Познакомиться с системами счисления.
Развивающие: Иметь представление о способах представления числовых данных.
Воспитательные: Развитие познавательного интереса, логического мышления.
Сегодня мы с вами познакомимся с основными принципами записи числовой информации, узнаем о новом понятии – системе счисления и рассмотрим, какие системы счисления бывают. Тема сегодняшнего урока: “Кодирование числовой информации”.
Давайте вспомним:
— Что такое информация?
— Каким образом человек воспринимает информацию?
— Какие виды информации нам известны?
— А чем отличается текстовая информация от числовой?
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит систем счисления состоит из символов, которые называются цифрами.
Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит систем счисления состоит из символов, которые называются цифрами.
Определение системы счисления.
Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Позиционные, непозиционные системы счисления.
Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления.
В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Непозиционные системы счисления.
Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, черточек, точек.
Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.
Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.
Сами того не осознавая, единичной системой счисления пользуются малыши, показывая на пальцах свой возраст, или используя для этого счетные палочки.
Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 50, 100, 500 и 1000 используются латинские буквы L, С, D и М.
В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе ХХХ (30) цифра Х встречается трижды и в каждом случае обозначает одну и туже величину – число 10, три раза по 10 в сумме дают 30.
Пример римской системы счисления.
Величина числа в римской системе счисления определяется как сумма или разность цифр в числе.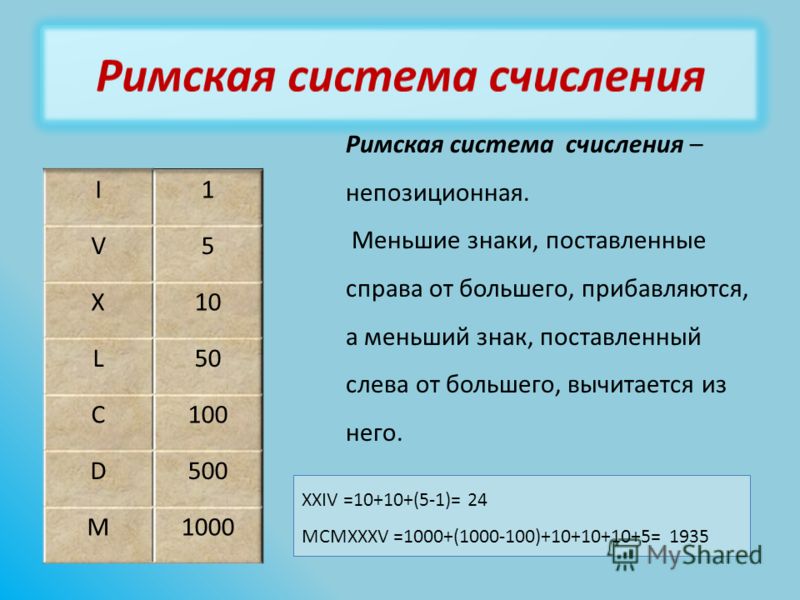 Если меньшая цифра стоит слева от большей, то она вычитается, если справа — прибавляется. Например, запись десятичного числа 28 в римской системе счисления будет выглядеть следующим образом:
Если меньшая цифра стоит слева от большей, то она вычитается, если справа — прибавляется. Например, запись десятичного числа 28 в римской системе счисления будет выглядеть следующим образом:
XХVIII = 10 + 10 + 5 + 1 + 1 + 1.
ХСIХ = -10 + 100 – 1 + 10
Позиционная система счисления.
Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значение одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.
В десятичной системе счисления цифра в крайней справа позиции обозначает единицы, цифра, смещенная на одну позицию влево, обозначает десятки, еще левее — сотни, затем тысячи и т. д.
Рассмотрим в качестве примера десятичное число 555. Цифра 5 встречается в числе трижды, причем самая правая обозначает пять единиц, вторая справа — пять десятков и, наконец, третья — пять сотен.
Таблица – позиционная система счисления.
В настоящее время наиболее распространенными позиционными системами счисления являются десятичная и двоичная. Десятичная система счисления имеет алфавит цифр, который состоит из десяти всем известных, так называемых арабских цифр. Алфавит двоичной системы – две цифры.
| Система счисления | Основание | Алфавит цифр |
| Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Двоичная | 2 | 0, 1 |
Любое число, записанное в позиционной системе счисления с произвольным основанием, можно записать в развернутой форме.
Пример записи чисел в развернутой форме.
Выше десятичное число 555 было записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10, которое является основанием десятичной системы счисления.
В развернутой форме записи числа умножение цифр числа на основание производится в явной форме. Так, в развернутой форме запись числа 555 в десятичной системе будет выглядеть следующим образом:
55510 = 5*102 + 5*101 + 5*10°.
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 555,55 в развернутой форме будет записываться следующим образом:
555,5510 = 5*102 + 5*101 + 5*10°+ 5*10-1 + 5*10-2.
Число в позиционной системе счисления записывается в виде суммы числового ряда степеней основания, в качестве коэффициентов которых выступают цифры данного числа.
Числа в двоичной системе в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.
Например, развернутая запись двоичного числа выглядит следующим образом:
101,012 = 1*22 + 0*21 + 1*2° + 0*2-1 + 1*2-2.
Человек использует десятичную систему счисления, а компьютер – двоичную. Поэтому часто возникает необходимость перевода чисел из десятичной системы счисления в двоичную и наоборот.
Перевод чисел из двоичной системы счисления в десятичную.
Преобразование чисел из двоичной системы счисления в десятичную выполнит довольно легко. Для этого необходимо записать двоичное число в развернутой форме и вычислить его значение.
Возьмем двоичное число 10,112. запишем его в развернутой форме и произведем вычисления:
10,112 = 1*21+0*20+1*2-1+1*2-2 = 1*2+0*1+1*1/2+1*1/4=2,7510
Перевод чисел из десятичной системы счисления в двоичную.
Алгоритм перевода десятичного числа в двоичное следующий:
1) последовательно выполнять деление исходного десятичного числа и получаемых частных на основание системы счисления (2) до тех пор, пока частное от деления не окажется равным единице;
2) получить искомое двоичное число, для чего записать полученные остатки в обратной последовательности.
Закрепление нового материала.
1-й вариант.
1. Верно ли, что число 1001101 может быть записано в двоичной системе счисления?
2. Верно ли, что римская система счисления непозиционная?
3. Верно ли, что в компьютерах используется римская система счисления?
4. Верно ли, что для сложных арифметических вычислений удобно пользоваться римской системой счисления?
5. Верно ли, что в двоичной системе счисления существует цифра 2?
2-й вариант.
1. Верно ли, что число 23222112 может быть записано в четырехричной системе счисления?
2. Верно ли, что арабские цифры удобны для сложных арифметических вычислений?
3. Верно ли, что в памяти компьютера используется десятичная система счисления?
4. Верно ли, что все системы счисления делятся на две большие группы?
5. Верно ли, что десятичная система счисления позиционная?
| Вариант | Номера ответов | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 1 | да | да | нет | нет | нет |
| 2 | да | да | нет | да | да |
Отработка практических навыков.
1. Решите следующие примеры:
а) VII – V =
б) X – II =
в) V + IV =
г) II + VI =
2. Какие числа записаны римскими цифрами:
а) XXII;
б) LXXIX;
в) DXLIV;
г) MCMXСIX.
3. Запишите год, месяц и число своего рождения с помощью римских цифр.
4. Запишите в развернутом виде числа:
а) А2 = 100111;
б) А10 = 123,456;
5. Запишите в свернутой форме следующие числа:
а) А10 = 9*101 + 8*100 + 7*10-1 + 6*10-2;
б) А2 = 1*21 + 1*20 + 0*2-1 + 1*2-2.
6. Правильно ли записаны числа в соответствующих системах счисления:
а) А10 = 1,01;
б) А2 = -5678;
в) А10 = 234,56;
г) А2 = 10,1.
7. Переведите из десятичной системы счисления в двоичную число 5610.
8. Чему равен десятичный эквивалент числа 101012?
Системы счисления | Практическая информатика
Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами.
Знаки, используемые при записи чисел, называются цифрами.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы:
I V X L C D M 1 5 10 50 100 500 1000
Например, VI = 5 + 1 = 6, а IX = 10 — 1 = 9.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией. Первая известная нам система, основанная на позиционном принципе — шестидесятeричная вавилонская. Цифры в ней были двух видов, одним из которых обозначались единицы, другим — десятки. Следы вавилонской системы сохранились до наших дней в способах измерения и записи величин углов и промежутков времени.
Однако наибольшую ценность для нас имеет индо-арабская десятичная система. Индийцы первыми использовали ноль для указания позиционной значимости величины в строке цифр. Эта система получила название десятичной, так как в ней десять цифр.
Для того чтобы лучше понять различие позиционной и непозиционной систем счисления, рассмотрим пример сравнения двух чисел. В позиционной системе счисления сравнение двух чисел происходит следующим образом: в рассматриваемых числах слева направо сравниваются цифры, стоящие в одинаковых позициях. Большая цифра соответствует большему значению числа. Например, для чисел 123 и 234, 1 меньше 2, поэтому число 234 больше, чем число 123. В непозиционной системе счисления это правило не действует. Примером этого может служить сравнение двух чисел IX и VI. Несмотря на то, что I меньше, чем V, число IX больше, чем число VI.
Далее мы будем рассматривать только позиционные системы счисления.
Основание системы счисления, в которой записано число, обычно обозначается нижним индексом. Например, 5557 — число, записанное в семеричной системе счисления. Если число записано в десятичной системе, то основание, как правило, не указывается. Основание системы — это тоже число, и его мы будем указывать в обычной десятичной системе. Вообще, число x может быть представлено в системе с основанием p, как x=an*pn+an-1*pn-1+ a1*p1+a0*p0, где an…a0 — цифры в представлении данного числа. Так, например,
Например, 5557 — число, записанное в семеричной системе счисления. Если число записано в десятичной системе, то основание, как правило, не указывается. Основание системы — это тоже число, и его мы будем указывать в обычной десятичной системе. Вообще, число x может быть представлено в системе с основанием p, как x=an*pn+an-1*pn-1+ a1*p1+a0*p0, где an…a0 — цифры в представлении данного числа. Так, например,
103510=1*103+0*102+3*101+5*100; 10102 = 1*23+0*22+1*21+0*20 = 10.
Наибольший интерес при работе на ЭВМ представляют системы счисления с основаниями 2, 8 и 16. Вообще говоря, этих систем счисления обычно хватает для полноценной работы как человека, так и вычислительной машины. Однако иногда в силу различных обстоятельств все-таки приходится обращаться к другим системам счисления, например к троичной, семеричной или системе счисления по основанию 32.
Для того чтобы нормально оперировать с числами, записанными в таких нетрадиционных системах, важно понимать, что принципиально они ничем не отличаются от привычной нам десятичной. Сложение, вычитание, умножение в них осуществляется по одной и той же схеме.
Почему же мы не пользуемся другими системами счисления? В основном потому, что в повседневной жизни мы привыкли пользоваться десятичной системой счисления, и нам не требуется никакая другая. В вычислительных же машинах используется двоичная система счисления, так как оперировать над числами, записанными в двоичном виде, довольно просто.
Часто в информатике используют шестнадцатеричную систему, так как запись чисел в ней значительно короче записи чисел в двоичной системе. Может возникнуть вопрос: почему бы не использовать для записи очень больших чисел систему счисления, например по основанию 50? Для такой системы счисления необходимы 10 обычных цифр плюс 40 знаков, которые соответствовали бы числам от 10 до 49 и вряд ли кому-нибудь понравится работать с этими сорока знаками. Поэтому в реальной жизни системы счисления по основанию, большему 16, практически не используются.
Поэтому в реальной жизни системы счисления по основанию, большему 16, практически не используются.
СИСТЕМЫ СЧИСЛЕНИЯ | Энциклопедия Кругосвет
Содержание статьиСИСТЕМЫ СЧИСЛЕНИЯ (нумерация) – совокупность способов обозначения натуральных чисел.
На ранних ступенях развития общества люди почти не умели считать. Они различали совокупности двух и трех предметов; всякая совокупность, содержавшая бóльшее число предметов, объединялась в понятии «много». Предметы при счете сопоставлялись обычно с пальцами рук и ног. По мере развития цивилизации потребность человека в счете стала необходимой. Первоначально натуральные числа изображались с помощью некоторого количества черточек или палочек, затем для их изображения стали использовать буквы или специальные знаки. В древнем Новгороде использовалась славянская система, где применялись буквы славянского алфавита; при изображении чисел над ними ставился знак ~ (титло).
Древние римляне пользовались нумерацией, сохраняющейся до настоящего времени под именем «римской нумерации», в которой числа изображаются буквами латинского алфавита. Сейчас ею пользуются для обозначения юбилейных дат, нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т.д. В позднейшем своем виде римские цифры выглядят так:
Сейчас ею пользуются для обозначения юбилейных дат, нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т.д. В позднейшем своем виде римские цифры выглядят так:
I = 1; V = 5; X = 10; L = 50; С = 100; D = 500; M = 1000.
О происхождении римских цифр достоверных сведений нет. Цифра V могла первоначально служить изображением кисти руки, а цифра Х могла составиться из двух пятерок. В римской нумерации явственно сказываются следы пятеричной системы счисления. Все целые числа (до 5000) записываются с помощью повторения вышеприведенных цифр. При этом, если бóльшая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед бóльшей (в этом случае она не может повторяться), то меньшая вычитается из бóльшей). Например, VI = 6, т.е. 5 + 1, IV = 4, т.е. 5 – 1, XL = 40, т е. 50 – 10, LX = 60, т.е. 50 + 10. Подряд одна и та же цифра ставится не более трех раз: LXX = 70; LXXX = 80; число 90 записывается ХС (а не LXXXX).
Первые 12 чисел записываются в римских цифрах так:
I, II, III, IV, V, VI, VII, VIII. IX, X, XI, XII.
Другие же числа записываются, например, как:
XXVIII = 28; ХХХIХ = 39; CCCXCVII = 397; MDCCCXVIII = 1818.
Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Тем не менее, римская нумерация преобладала в Италии до 13 в., а в других странах Западной Европы – до 16 в.
В славянской системе нумерации для записи чисел использовались все буквы алфавита, правда, с некоторым нарушением алфавитного порядка. Различные буквы означали различное количество единиц, десятков и сотен. Например, число 231 записывалось в виде ~ СЛА (C – 200, Л – 30, А – 1).
Этим системам свойственны два недостатка, которые привели к их вытеснению другими: необходимость большого числа различных знаков, особенно для изображения больших чисел, и, что еще важнее неудобство выполнения арифметических операций.
Более удобной и общепринятой и наиболее распространенной является десятичная система счисления, которая была изобретена в Индии, заимствована там арабами и затем через некоторое время пришла в Европу. В десятичной системе счисления основанием является число 10.
В десятичной системе счисления основанием является число 10.
Существовали системы исчисления и с другими основаниями. В Древнем Вавилоне, например, применялась шестидесятеричная система счисления. Остатки ее мы находим в сохранившемся до сих пор делении часа или градуса на 60 минут, а минуты – на 60 секунд.
Широкое распространение имела в древности и двенадцатеричная система, происхождение которой, вероятно, связано, как и десятичной системы, со счетом на пальцах: за единицу счета принимались фаланги (отдельные суставы) четырех пальцев одной руки, которые при счете перебирались большим пальцем той же руки. Остатки этой системы счисления сохранились и до наших дней и в устной речи, и в обычаях. Хорошо известно, например, название единицы второго разряда – числа 12 – «дюжина». Сохранился обычай считать многие предметы не десятками, а дюжинами, например, столовые приборы в сервизе или стулья в мебельном гарнитуре. Название единицы третьего разряда в двенадцатеричной системе – гросс – встречается теперь редко, но в торговой практике начала столетия оно еще бытовало. Например, в написанном в 1928 стихотворении Плюшкин В.В.Маяковский, высмеивая людей, скупающих все подряд, писал: «…укупил двенадцать гроссов дирижерских палочек». У ряда африканских племен и в Древнем Китае была употребительна пятеричная система счисления. В Центральной Америке (у древних ацтеков и майя) и среди населявших Западную Европу древних кельтов была распространена двадцатеричная система. Все они также связаны со счетом на пальцах.
Например, в написанном в 1928 стихотворении Плюшкин В.В.Маяковский, высмеивая людей, скупающих все подряд, писал: «…укупил двенадцать гроссов дирижерских палочек». У ряда африканских племен и в Древнем Китае была употребительна пятеричная система счисления. В Центральной Америке (у древних ацтеков и майя) и среди населявших Западную Европу древних кельтов была распространена двадцатеричная система. Все они также связаны со счетом на пальцах.
Самой молодой системой счисления по праву можно считать двоичную. Эта система обладает рядом качеств, делающей ее очень выгодной для использования в вычислительных машинах и в современных компьютерах.
Позиционные и непозиционные системы счисления.
Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы.
Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией. Первая известная нам система, основанная на позиционном принципе – шестидесятeричная вавилонская. Цифры в ней были двух видов, одним из которых обозначались единицы, другим – десятки.
Однако наиболее употребительной оказалась индо-арабская десятичная система. Индийцы первыми использовали ноль для указания позиционной значимости величины в строке цифр. Эта система получила название десятичной, так как в ней десять цифр.
Различие между позиционой и непозиционной систем счисления легче всего понять на примере сравнения двух чисел. В позиционной системе счисления сравнение двух чисел происходит следующим образом: в рассматриваемых числах слева направо сравниваются цифры, стоящие в одинаковых позициях. Бóльшая цифра соответствует бóльшему значению числа. Например, для чисел 123 и 234, 1 меньше 2, поэтому число 234 больше, чем число 123. В непозиционной системе счисления это правило не действует. Примером этого может служить сравнение двух чисел IX и VI. Несмотря на то, что I меньше, чем V, число IX больше, чем число VI.
Бóльшая цифра соответствует бóльшему значению числа. Например, для чисел 123 и 234, 1 меньше 2, поэтому число 234 больше, чем число 123. В непозиционной системе счисления это правило не действует. Примером этого может служить сравнение двух чисел IX и VI. Несмотря на то, что I меньше, чем V, число IX больше, чем число VI.
Позиционные системы счисления.
Основание системы счисления, в которой записано число, обычно обозначается нижним индексом. Например, 5557 – число, записанное в семеричной системе счисления. Если число записано в десятичной системе, то основание, как правило, не указывается. Основание системы – это тоже число, и его мы будем указывать в обычной десятичной системе. Вообще, число x может быть представлено в системе с основанием p, как x = an·pn +an – 1·pn–1 + a1·p1 + a0·p0, где an…a0 – цифры в представлении данного числа. Так, например,
Так, например,
103510=1·103 + 0·102 + 3·101 + 5·100;
10102 = 1·23 + 0·22 + 1·21 + 0·20 = 10.
Наибольший интерес при работе на ЭВМ представляют системы счисления с основаниями 2, 8 и 16. Вообще говоря, этих систем счисления обычно хватает для полноценной работы как человека, так и вычислительной машины, однако иногда в силу различных обстоятельств все-таки приходится обращаться к другим системам счисления, например к троичной, семеричной или системе счисления по основанию 32.
Чтобы оперировать с числами, записанными в таких нетрадиционных системах, нужно иметь в виду, что принципиально они ничем не отличаются от привычной десятичной. Сложение, вычитание, умножение в них осуществляется по одной и той же схеме.
Почему же не используются другие системы счисления? В основном, потому, что в повседневной жизни люди привыкли пользоваться десятичной системой счисления, и не требуется никакая другая. В вычислительных же машинах используется двоичная система счисления, так как оперировать числами, записанными в двоичном виде, довольно просто.
В вычислительных же машинах используется двоичная система счисления, так как оперировать числами, записанными в двоичном виде, довольно просто.
Часто в информатике используют шестнадцатеричную систему, так как запись чисел в ней значительно короче записи чисел в двоичной системе. Может возникнуть вопрос: почему бы не использовать для записи очень больших чисел систему счисления, например по основанию 50? Для такой системы счисления необходимы 10 обычных цифр плюс 40 знаков, которые соответствовали бы числам от 10 до 49 и вряд ли кому-нибудь понравится работать с этими сорока знаками. Поэтому в реальной жизни системы счисления по основанию, большему 16, практически не используются.
Перевод чисел из одной системы счисления в другую.
Наиболее часто встречающиеся системы счисления – это двоичная, шестнадцатеричная и десятичная. Как же связаны между собой представления числа в различных системах счисления? Есть различные способы перевода чисел из одной системы счисления в другую на конкретных примерах.
Пусть нужно перевести число 567 из десятичной в двоичную систему. Сначала определяется максимальная степень двойки, такая, чтобы два в этой степени было меньше или равно исходному числу. В данном случае это 9, т.к. 29 =512, а 210 = 1024, что больше начального числа. Таким образом получается число разрядов результата, оно равно 9 + 1 = 10, поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные цифры. Вторая цифра результата находится так – двойка возводится в степень 9 и вычитается из исходного числа: 567 – 29 = 55. Остаток сравнивается с числом 28 = 256. Так как 55 меньше 256, то девятый разряд – нуль, т.е. результат имеет вид 10хххххххх. Рассмотрим восьмой разряд. Так как 27 = 128 > 55, то и он будет нулевым.
Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 25 = 32 ххххх). Для остатка 55 – 32 = 23 справедливо неравенство 24 = 16
567 = 1·29 + 0·28 + 0·27 + 0·26 + 1·25 + 1·24 + 0·23 + 1·22 + 1·21 + 1·20
При другом способе перевода чисел используется операция деления в столбик. Если взять то же число 567 и разделить его на 2, получается частное 283 и остаток 1. Та же операция производится и с числом 283. Частное – 141, остаток – 1. Опять полученное частное делится на 2 и так до тех пор, пока частное не станет меньше делителя. Теперь, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, т.е. 1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.
Если взять то же число 567 и разделить его на 2, получается частное 283 и остаток 1. Та же операция производится и с числом 283. Частное – 141, остаток – 1. Опять полученное частное делится на 2 и так до тех пор, пока частное не станет меньше делителя. Теперь, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, т.е. 1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.
Результат, естественно, не изменился: 567 в двоичной системе счисления записывается как 1 000 110 111.
Эти два способа применимы при переводе числа из десятичной системы в систему с любым основанием. Например, при переводе числа 567 в систему счисления с основанием 16 число сначала разлагается по степеням основания. Искомое число состоит из трех цифр, т.к. 162 = 256 3 = 4096. Определяется цифра старшего разряда. 2·162 = 512 2 = 768, следовательно, искомое число имеет вид 2хх, где вместо х могут стоять любые шестнадцатеричные цифры. Остается распределить по следующим разрядам число 55 (567 – 512). 3·16 = 48
Остается распределить по следующим разрядам число 55 (567 – 512). 3·16 = 48
Второй способ состоит в последовательном делении в столбик, с единственным отличием в том, что делить надо не на 2, а на 16, и процесс деления заканчивается, когда частное становится строго меньше 16.
Конечно, для записи числа в шестнадцатеричной системе счисления, необходимо заменить 10 на A, 11 на B и так далее.
Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a0·pn + a1·pn–1 +… + an–1·p1 + an·p0, где a0 … an – это цифры данного числа в системе счисления с основанием p.
Например,так можно перевести число 4A3F в десятичную систему. По определению, 4A3F= 4·163 + A·162 + 3·16 + F. При замене A на 10, а F на 15, получается 4·163 + 10·162 + 3·16 + 15= 19007.
Проще всего переводить числа из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое двоичное число записать в системе счисления с основанием 2n, нужно данное двоичное число разбить справа налево на группы по n-цифр в каждой; если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов; рассмотреть каждую группу, как n-разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2n.
| Таблица 1. ДВОИЧНО-ШЕСТНАДЦАТЕРИЧНАЯ ТАБЛИЦА | ||||||||
| 2-ная | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| 16-ная | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2-ная | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 16-ная | 8 | 9 | A | B | C | D | E | F |
| Таблица 2. ДВОИЧНО-ВОСЬМЕРИЧНАЯ ТАБЛИЦА | ||||||||
| 2-ная | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 8-ная | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Известный французский астроном, математик и физик Пьер Симон Лаплас (1749–1827) писал об историческом развитии систем счисления, что «Мысль выражать все числа девятью знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этому методу, мы видим на примере величайших гениев греческой учености Архимеда и Аполлония, от которых эта мысль осталась скрытой.»
Сравнение десятичной системы исчисления с иными позиционными системами позволило математикам и инженерам-конструкторам раскрыть удивительные возможности современных недесятичных систем счисления, обеспечившие развитие компьютерной техники.
Анна Чугайнова
Компьютерные науки для развлечения — cs4fn: Почему римляне не справились с математикой
Пол Керзон, Лондонский университет королевы Марии
Римляне были великолепны в подсчете и сложении, но они были абсолютно умны. штаны при умножении. Не потому, что они были глупы. Это было потому что они не изобрели хороший способ представления чисел, и что означало, что им нужны действительно запутанные алгоритмы.
Римская система основана на более раннем действительно простом способе письма числа.Вы просто ставите черту за каждую вещь, которую вы посчитали. Это, вероятно как пастухи вели счет овец, проводя линию для каждой овцы. Эти строки превратились в римскую букву I. Чтобы добавить 1 к числу, вы просто добавьте еще один I. Вы считаете: I, II, III и так далее, и это дает считать легко. Эта система называется унарной, в то время как двоичная включает считая с двумя символами, 1 и 0, в унарном у вас есть только один символ для считать с. Сложение в унарном тоже несложно, по крайней мере, для небольших чисел. Возьмите первое число и добавьте в конце все Is для второго и у вас есть номер ответа.Это именно то, как мы все начинаем делать сложение на наших пальцах.Чтобы сложить 2 + 3, поднимите 2 пальца (II), затем поднимите еще три пальца (III), и у вас есть ответ (IIIII).
Это нормально для небольших чисел, но становится немного утомительно, так как числа увеличиваются (и у вас кончатся пальцы!) Сравнивать числа легко в принцип — у вас такое же количество Is, но тяжело на практике для большое количество. Мы не можем держать все это в голове, так что большое количество трудно думать об этом.Чтобы обойти это, римляне изобрели новые буквы для обозначения групп Ис. Это то, что мы делаем, когда подсчитываем числа, образующие перекладину, для каждого пятого числа мы считаем. Это помогает нам отслеживать большие числа. Римляне изобрели целую кучу символы в помощь: так, например, в римской системе счисления V означает для 5 (IIIII), X означает 10, L для 50, C для 100, D для 500 и M на 1000. Они изобрели новый способ представления чисел.
Это значительно упрощает запись и сравнение больших чисел.Теперь, когда подсчитывая, и вы получаете 5, вы просто заменяете все эти Is на V и затем продолжайте добавлять Is: VI, VII, VIII, VIIII. Затем вы попадете на VIIIII (10) так что замените все на X, снова начав добавлять новую партию Is: XI, XII, XIII, XIIII, XV и так далее. Считать большие числа теперь немного более сложный — алгоритм включает в себя больше, чем просто добавление I на конец, но это намного удобнее. Алгоритм сложения теперь становиться более сложным, хотя это все еще довольно просто.Возьми любой два числа, которые нужно сложить, например, VII и VIII, и связать их вместе: VIIVIII. Теперь сгруппируйте одинаковые буквы: VVIIIII. Везде вам достаточно чтобы заменить символы на следующий символ, сделайте это. ВВ можно заменить на X и IIIII можно заменить на V, чтобы получить XV в приведенном выше. Продолжайте делать замены, пока вы больше не сможете их производить. Расставьте символы по порядку от символ от наибольшего к наименьшему, и у вас есть свой ответ.
Теперь римляне явно поленились, так как им надоело писать даже четыре Спустя некоторое время они иногда вводили новый набор сокращений, поэтому что IIII стало IV, а VIIII стало IX.Помещая меньший символ (например, I) перед большим (например, X), а не после означает вычесть его до получить номер. поэтому IX означает «на единицу меньше 10» или 9. При подсчете немного сложнее, чтобы получить преимущество написания меньшего количества символов. Однако добавление теперь требует более запутанного алгоритма. Есть несколько способы сделать это. Самый простой — просто изменить числа, чтобы добавить к более простой форме (так что IV восходит к IIII). Вы их делаете добавление таким образом и преобразовать обратно в конце.Добавление только что немного сложнее, а все из-за смены представительства.
Хуже того, выполнять более сложные математические вычисления еще труднее, используя Представление римских чисел. Посмотрите, сможете ли вы научиться умножать Римские числа. Римская система счисления совершенно не помогает. Единственный действительно простой способ — просто многократно добавлять (так что III x VI равно VI + VI + VI). Это просто непрактично для больших чисел. Примерь на XXIII x LXV1. Есть и другие возможные способы, в том числе тот, который фактически основан на об алгоритмах двоичного умножения, используемых компьютерами — умножении и многократное деление на 2.Посмотрим, сможешь ли ты решить, как это сделать. Что бы ни как вы это делаете, ясно, что система счисления, которую выбрали римляне, сделала им сложно заниматься математикой!
Хорошее представление упрощает математику. Плохой делает это намного сложнее.
К счастью, индийские и арабские ученые поняли, что представление они имели значение. Они изобрели и распространили индуистско-арабские числа. и десятичная система, которую мы используем сегодня. Что в нем особенного, так это то, что чем вводить новые символы для все больших чисел, позиция символа.Переходя с девяти до десяти, мы возвращаемся к начало наших символов, от 9 до 0, но вставьте 1 через новые 10 столбец, чтобы подсчитать, сколько у нас десятков. Считать все еще довольно просто, но вдруг не только алгоритм сложения прост, но и может придумать довольно простые алгоритмы умножения и деление тоже. Это алгоритмы, которые вы изучаете в школе, хотя с любым алгоритмом, убедившись, что вы точно следуете шагам и не человеку сложно пропустить шаги (в отличие от компьютер).Вот почему поначалу нам сложно изучать математику. и чем больше мы практикуемся, тем легче становится.
На самом деле римляне, которым нужно было серьезно заниматься математикой, вероятно, использовали вариант счеты, представляющие числа с камнями. Они сделали бы расчет на счетах, а затем преобразовать ответ обратно в римское число система. И угадай что. Римские счеты используют столбцы для представления большие числа очень похожи на индуистско-арабскую систему. В Римляне понимали, что репрезентация тоже имеет значение.
Иногда что-то сложно сделать только потому, что мы усложняем это! В секрет создания хороших алгоритмов часто заключается в том, чтобы придумать хорошие представление в первую очередь. В программировании тоже, если вы придумаете хороший способ для представления данных, хорошей структуры данных, вы часто можете сделать это намного проще написать эффективную программу.
Системы счисления — Системы счисления — двоичные, десятичные, числовые и —
Система позиционных значений присваивает определенное значение пространственному положению числа в ряду.Например, в десятичной системе положение числа относительно других чисел в ряду определяет его категорию как десятки, сотни, тысячи, десятки тысяч и т. Д. В номере 1,234 «4» занимает слот, представляющий от нуля до 9, «3» занимает слот, представляющий от 10 до 99, «2» занимает слот, представляющий от 100 до 999, а «1» занимает слот, представляющий С 1000 по 9999.
Системы значенийважны, потому что они делают обычные арифметические функции и намного более эффективными.Если люди хотят легко манипулировать пространственными символами, им нужен простой, последовательный и симметричный метод, позволяющий визуально выстраивать числа и быстро группировать их по их значению. Без разрядов десятичной системы простые арифметические функции сложения, вычитания, умножения и деления чрезвычайно сложны, потому что они устрашающи, отнимают много времени, слишком сложны и подвержены ошибке .
Римская система счисления (I, II, III, IV ,…) не имеет эффективного способа представления места и делает простые арифметические функции очень сложными для большинства людей. Сравните ниже простой процесс сложения 17, 38 и 3 римскими цифрами и индо-арабскими цифрами.
| XVII | 17 |
| XXXVIII | 38 |
| III | 3 |
| LVIII | 58 |
Большинство людей, знакомых с индуистско-арабскими числами, считают, что добавление римских цифр слева вызывает недоумение.
Хотя системы значений чисел упрощают арифметические операции, они также помогают компьютерам выполнять электронные вычисления с невероятной скоростью. Распространенной системой счисления, используемой в компьютерах, является двоичная система счисления, которая является системой с основанием 2. В двоичной системе есть два значения: «0» и «1». Эти значения соответствуют сигналам «высокий» и «низкий» в электронных схемах компьютеров. Поскольку эти числа настолько просты, компьютеры могут обрабатывать их электронным способом до триллиона раз в секунду, в зависимости от скорости компьютера.
В двоичной системе счисления каждое место справа налево оценивается в 2 раза больше, чем место справа. Таким образом, первое место может быть равно нулю или единице, второе место слева оценивается в два, третье место слева оценивается в четыре, четвертое место слева оценивается в восемь и так далее. В следующем списке указаны двоичные значения первых десяти чисел десятичной системы счисления:
| десятичный | двоичный | |
| 0 | = | 0 |
| 1 | = | 1 |
| 2 | = | 10 |
| 3 | = | 11 |
| 4 | = | 100 |
| 5 | = | 101 |
| 6 | = | 110 |
| 7 | = | 111 |
| 8 | = | 1000 |
| 9 | = | 1001 |
| 10 | = | 1010 |
Например, десятичное число 3 выше имеет две единицы в двоичном формате.1 справа в двоичном формате равна 1, потому что его разрядное значение может быть только 1 или 0. Но 1 слева в двоичном формате (для десятичного числа 3) занимает место, которое оценивается как 2 в двоичной системе. Рассмотрим другой пример: посмотрите на десятичное число 10, отформатированное в двоичной системе: 1010. Четвертое число (1) справа занимает место с оценкой 8; 0 на третьем месте означает, что он оценивается в ноль; 1 во втором месте справа означает, что он оценивается в 2; а 0 в крайнем правом месте означает ноль.Таким образом, в двоичной системе счисления 8 + 0 + 2 + 0 = 10.
Хотя эта система кажется громоздкой для людей, которые привыкли к десятичной системе счисления, она идеально подходит для способов, которыми компьютеры управляют электрическими токами, чтобы обрабатывать большие объемы данных с очень высокой скоростью.
Книги
Болл, W.W. Роуз. Краткое изложение истории математики. Лондон: Sterling Publications, 2002.
Барроу, Джон Д. Пи в небе: счет, мышление и бытие. Оксфорд: Oxford University Press, 1992.
Клоусон, Кальвин К. Путешественник по математике: Изучение Великой истории чисел. Кембридж, Массачусетс: Perseus Publishing, 2003.
Свец, Фрэнк Дж. Капитализм и арифметика: новая математика 15 века. LaSalle, IL: Open Court Press, 1987.
Виноградов Иван Матвеевич. Элементы теории чисел. Dover Publications, 2003.
Вайсштейн, Эрик В. Краткая энциклопедия математики CRC. Нью-Йорк: CRC Press, 1998.
Система счисления | математика | Britannica
Система счисления , любой из различных наборов символов и правила их использования для представления чисел, которые используются для обозначения количества объектов в данном наборе. Таким образом, идея «единства» может быть представлена римской цифрой I, греческой буквой альфа α (первая буква), используемой в качестве числительного, еврейской буквой алеф (первая буква), используемой в качестве числа, или современная цифра 1, которая имеет индуистско-арабское происхождение.
Подробнее по этой теме
математика: Система счисления и арифметические операции
Египтяне, как и римляне после них, выражали числа по десятичной схеме, используя отдельные символы для 1, 10, 100, 1000, …
Далее следует краткое описание систем счисления. Для дальнейшего обсуждения, см. числительные и системы счисления: Системы счисления.
Очень вероятно, что самой ранней системой письменных символов в древней Месопотамии была система символов для чисел. Современные системы счисления — это системы счисления. То есть значение символа зависит от положения или места символа в представлении; например, 2 из 20 и 200 представляют две десятки и две сотни соответственно. Большинство древних систем, таких как египетская, римская, еврейская и греческая системы счисления, не имели позиционной характеристики, что усложняло арифметические вычисления.Однако в других системах, включая вавилонскую, по одной версии китайской и индийской, а также в системе майя, действительно использовался принцип числовой стоимости. Наиболее часто используемой системой счисления является десятичная позиционная система счисления, десятичная относится к использованию 10 символов — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 — для построения всех чисел. Это было изобретение индейцев, усовершенствованное средневековым исламом. В компьютерах и информатике используются две другие общие системы позиционирования, а именно двоичная система с двумя символами 0, 1 и шестнадцатеричная система с ее 16 символами 0, 1, 2,…, 9, A, B,… , Ф.
2.3 Непозиционная система счисления — S10659003
2.3 Непозиционная система счисления
Непозиционная система счисления использует ограниченное количество символов, в которых каждый символ имеет значение. число обычно не имеет отношения к своему значению — значение каждого символа фиксировано.
Римская система счисления является хорошим примером непозиционной системы счисления. Эта система счисления имеет набор символов S = {I, V, X, L, C, D, M}.
Значения символов в римской системе счисления
| Символ | I | V | X | L | C | D | M |
| Значение | 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
Чтобы найти значение числа, нам нужно сложить значение символов согласно определенным правилам:
1. Когда символ с меньшим значением помещается после символа, имеющего такое же или большее значение, значения добавляются.
2. Когда символ с меньшим значением помещается перед символом, имеющим большее значение, меньшее значение вычитается из большего.
3. Символ S 1 не может стоять перед другим символом S 2 , если S 1 ≤10xS 2 . Например, I или V не могут предшествовать C.
4. Для больших числа над любым из шести символов (всеми символами, кроме I) помещается полоса, чтобы выразить умножение на 1000.
5. Хотя римляне использовали слово nulla (ничего), чтобы передать понятие нуля, римские цифры не имеют нулевой цифры в их системе.
Ниже показаны некоторые римские числа и их значения.
| III → 1 + 1 + 1 | = 3 |
| IV → 5-1 | = 4 |
| VIII → 5 + 1 + 1 + 1 | = 8 |
| XVIII → 10 + 5 + 1 + 1 + 1 | = 18 |
| XIX → 10 + (10-1) | = 19 |
| LXXII → 50 + 10 + 10 + 1 + 1 | = 72 |
| CI → 100 + 1 | = 101 |
| MMVII → 1000 + 1000 + 5 + 1 + 1 | = 2007 |
| MDC → 1000 + 500 + 100 | = 1600 |
Преобразование двоичного кода в основание 11 • Конвертер чисел • Стандартные преобразователи единиц • Компактный калькулятор • Онлайн-конвертеры единиц
Конвертер длины и расстояния Конвертер массы Конвертер сухого объема и общих измерений при приготовлении пищи Конвертер площади Конвертер объема и общих измерений при приготовлении пищи Конвертер температуры Конвертер давления, напряжения, модуля Юнга КонвертерМощный преобразовательСиловой преобразовательКонвертер времениЛинейный Конвертер скорости и скоростиКонвертер углового КПД, расхода топлива и экономии топливаКонвертер чиселПреобразователь единиц информации и хранения данныхКурсы валютЖенская одежда и размеры обувиМужская одежда и размеры обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияПреобразователь удельной силыКонвертер удельной силы Конвертер энергии, теплоты сгорания (на массу) Конвертер удельной энергии, теплоты сгорания (на единицу объема) Конвертер интервалов температурКонвертер теплового расширенияКонвертер теплового сопротивленияКонвертер теплопроводностиКонвертер удельной теплоемкости Конвертер расхода Конвертер массового потока Конвертер молярной концентрации Концентрация массы в растворе Con verterПреобразователь динамической (абсолютной) вязкостиКинематический преобразователь вязкостиКонвертер поверхностного натяженияПроницаемость, проницаемость, проницаемость водяного параКонвертер скорости передачи водяного параКонвертер уровня звукаКонвертер чувствительности микрофона Конвертер оптической мощности (диоптрий) в увеличение (X) Конвертер электрического зарядаЛинейный преобразователь плотности зарядаПреобразователь плотности поверхностного зарядаПреобразователь объемной плотности зарядаПреобразователь электрического токаЛинейный преобразователь плотности токаПреобразователь плотности поверхностного токаПреобразователь электрического сопротивленияПреобразователь электрического сопротивленияПреобразователь электрического сопротивления rПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь американского калибра проводовПреобразование уровней в дБм, дБВ, ваттах и других единицахПреобразователь магнитодвижущей силыПреобразователь напряженности магнитного поляПреобразователь магнитного потокаПреобразователь плотности магнитного потокаКонвертер мощности поглощенной дозы излучения, полной мощности ионизирующего излученияКонвертер радиоактивного распада Конвертер радиоактивного облученияРадиация. Конвертер поглощенной дозы Конвертер метрических префиксовКонвертер передачи данныхПреобразователь единиц типографии и цифрового изображенияКонвертер единиц измерения объема древесиныКалькулятор молярной массыПериодическая таблица
Обзор
Приложение для калькулятора iPhone
Число — это абстрактное математическое понятие, обозначающее количество. Используется при подсчете. Числа использовались с древних времен, сначала в виде счетных отметок — царапин на дереве или кости, а затем в качестве более абстрактных систем.Есть несколько способов выражения чисел в числовых системах. Некоторые из них сегодня не используются.
Различные способы представления чисел
Некоторые исследователи считают, что понятие числа возникло независимо в разных регионах. Первоначально письменные представления чисел с помощью символов развивались независимо, но когда торговля между странами и континентами стала широко распространенной, люди учились и заимствовали друг у друга, а системы счисления, используемые в настоящее время, были созданы на основе коллективного знания.
Индо-арабские цифры
Индо-арабская система счисления — одна из наиболее широко используемых в современном мире. Первоначально он был разработан в Индии и усовершенствован персидскими и арабскими математиками. В средние века он распространился на западный мир через торговлю, заменив римскую систему счисления. Он был дополнительно модифицирован и широко принят во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на десятичных числах и использует десять символов для представления всех чисел.
Десять — это обычное число, которое используют для счета, потому что у людей десять пальцев, а исторически часто для счета использовались части тела. Даже сегодня люди, которые учатся считать или хотят проиллюстрировать в разговоре какую-либо мысль о счете, часто используют пальцы. В некоторых культурах для счета также использовались пальцы ног, промежутки между пальцами и суставы. Любопытно, что числа представлены «цифрами» — тем же словом, которое используется для обозначения пальцев рук и ног в английском и многих других языках.
Надпись на латыни и римскими цифрами на Адмиралтейской арке в Лондоне.Он гласит: ANNO: DECIMO: EDWARDI: SEPTIMI: REGIS: VICTORIÆ: REGINÆ: CIVES: GRATISSIMI: MDCCCCX: (На десятом году правления короля Эдуарда VII королеве Виктории от самых благодарных граждан, 1910).
Римские
Римские цифры использовались в Римской империи и Европе до 14 века. Они все еще используются сегодня в некоторых контекстах, например, в часах, для обозначения часов. Римские цифры основаны на семи числах, написанных буквами латинского алфавита:
Порядок важен в римской системе, потому что большее число, за которым следует меньшее, означает, что нужно сложить два, но меньшее число перед больший означает, что меньшее число вычитается из большего.Например, XI равно 11, а IX равно 9. Правило вычитания не универсальное, оно работает только для этих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, а вместо них последовательно пишутся цифры.
Системы в других культурах
Люди во многих географических регионах имели системы представления чисел, похожие на римские или индуистско-арабские. Например, некоторые славяне использовали кириллицу для обозначения чисел, таких как от 1 до 9, кратных 10 и кратных 100, со специальными символами для больших чисел, а также символами, чтобы отличать цифры от букв.В еврейской системе счисления используется еврейский алфавит для обозначения чисел от одного до десяти, кратных десяти, 100, 200, 300 и 400. Остальные числа представлены в виде кратных или сумм. Греческая система счисления также похожа.
В некоторых культурах используются более простые представления, такие как вавилонская система, в которой есть только два клинописных символа: один (несколько напоминающий букву «Т») и десять (немного похожий на букву «С»). Так, например, 32 будет записано (с использованием соответствующих символов) как CCCTT.Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы нуля, единицы и пяти, со специальными обозначениями для чисел больше девятнадцати.
Унарная система счисления. Счетные метки в различных культурах
Унарный
Унарная система представляет каждое число с тем же количеством символов, что и его значение.Эти символы обычно одинаковы, поэтому, если 1 представлен как A, то 5 будет представлен как AAAAA. Когда дети учатся считать, их учителя часто используют эту систему, чтобы помочь установить связь между конкретной, простой для понимания системой и более абстрактным представлением чисел. Эта система также иногда используется в играх и других простых вычислениях. В разных странах для этого могут использоваться разные типы представительств. Например, при подсчете очков команд-победителей или подсчете пунктов или дней люди в западном мире и некоторых других регионах часто пишут четыре вертикальные линии, затем пересекают их пятой горизонтальной линией и повторяют процесс.Например, в части A) на картинке человек, считающий до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал ставить счетные отметки, пока не сумел до двенадцати. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части B) на картинке человек считает до пяти, завершая образ, а затем начинает новый персонаж, продолжая счет до семи.Порядок штриха задан заранее, как показано на рисунке. Унарная система также используется в информатике.
Арифмометр, использующий десятичную систему, и микросхему микропроцессора, использующую двоичную систему
Позиционная система
Позиционная система работает с основанием. Например, по основанию 10 мы имеем следующее:
- Первая позиция предназначена для чисел от нуля до девяти, то есть число в первой позиции должно быть умножено на десять в степени нуля.
- Число во второй позиции умножается на десять в степени единицы.
- Число в третьей позиции умножается на десять в степени двойки и так далее, пока числа во всех позициях не будут исчерпаны.
Чтобы получить окончательное значение представленного числа, необходимо сложить все значения в каждой позиции. Это удобный способ представления чисел, поскольку он позволяет работать с числами, имеющими относительно большие значения, без использования большого пространства для их записи.
Пример: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰
Двоичная
Двоичная система счисления широко используется в математике и информатике. Он основан на двух символах «0» и «1» для представления всех возможных чисел. Другими словами, это система base-2. Числа представлены следующим образом: 0 = 0, 1 = 1, а от 2 используется принцип сложения. Добавление в основании-2 аналогично добавлению в основании-10. Чтобы увеличить число на единицу:
Художественное представление двоичных чисел
- Если число заканчивается нулем, последний ноль заменяется единицей: e.грамм. 100 (4) + 1 (1) = 101 (5). Здесь для сравнения в скобках используются десятичные числа.
- Если число заканчивается единицей, но не все единицы, первый ноль справа заменяется единицей, а все следующие за ним справа становятся нулями: 1011 (11) + 1 (1) = 1100.
- Если исходное число — это все единицы, то все они заменяются нулями, а впереди добавляется единица: 111 (7) + 1 (1) = 1000 (8).
Чтобы сложить два числа, они выравниваются друг относительно друга, и для каждого места 0 + 0 дает 0, 1 + 0 дает 1, а 1 + 1 дает 10, где 0 помещается в эту позицию, а 1 переносится на следующую позицию.Например:
11111 (31)
+1011 (11)
———————————
101010 (42)
В этом случае, работая справа налево:
- 1 + 1 дает 0, один переносится
- 1 + 1 + 1 дает 1, один переносится
- 1 + 1 дает 0, один переносится
- 1 + 1 + 1 дает 1, один переносится
- 1 +1 дает 10
Итак, сложив это вместе, мы получаем 101010.
Вычитание работает по тому же принципу, за исключением того, что вместо переноса мы «заимствуем».Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например:
101 (5)
× 10 (2)
————————————
000
101
———————————
1010 (10)
Деление и вычисление квадратных корней также очень похоже на основание 10.
Классификация номеров
Все номера можно разделить на подмножества. Некоторые из приведенных ниже подмножеств частично перекрываются.
Долг — отрицательное число
Отрицательные числа
Отрицательные числа — это числа, представляющие отрицательное значение.Перед ними ставится знак минус. Например, если у человека A нет денег, и он должен 5 долларов человеку B, то у человека A -5 долларов. Здесь –5 — отрицательное число.
Рациональные числа
Рациональные числа — это числа, которые могут быть выражены в виде дробей, где знаменатель — натуральное число, не равное нулю, а числитель — целое число. Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.
Натуральные числа
Натуральные числа — это положительные числа (включая 0), а не дроби, например 7 или 86 766 575 675 456.
Целые числа
Целые числа включают ноль, отрицательные и положительные числа, не являющиеся дробями. Примеры включают -65 и 11 223.
Комплексные числа
Комплексные числа — это все числа, которые представляют собой сумму одного действительного числа и произведения другого действительного числа и квадратного корня из отрицательного числа.
Простые числа
Простые числа — это натуральные числа больше единицы, которые дают целое число только при делении на единицу или само по себе. Некоторые примеры: 3, 5 и 11.2 57 885 161 −1 — наибольшее известное простое число на зиму 2013 года. Оно состоит из 17 425 170 цифр. Простые числа используются в криптографии с открытым ключом, системе кодирования данных, часто используемой при безопасном онлайн-обмене данными, например, в онлайн-банкинге.
Интересные факты о числах
Китайские номера по борьбе с мошенничеством
Цифры по борьбе с мошенничеством
Чтобы предотвратить мошенничество при написании чисел в бизнесе и торговле, в китайском языке используются специальные сложные символы, которые трудно подделать, добавив лишние штрихи.Это сделано потому, что часто используемые китайские символы для чисел слишком просты, и их значение легко изменить, добавив штрихи.
Современный счет в торговле
Некоторые языки в странах, где в настоящее время используется система счисления 10, все еще отражают то, что другие системы счисления были распространены в прошлом. Например, в английском языке есть специальное слово для двенадцати, «дюжина» — в настоящее время оно используется в основном для подсчета яиц, выпечки, вина и цветов. В кхмерском есть особые слова, основанные на древней системе 20, для подсчета фруктов.
Группировка цифр
И в Китае, и в Японии принята индийско-арабская система счисления, но большие числа сгруппированы по 10 000, и это отражено в языке. Например, в английском языке есть слово «1000», а одно указывает, сколько их тысяч, вплоть до 999 999. Затем следует слово «миллион», обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000.
Несчастливые числа
Леонардо да Винчи. Последний ужин. Церковь Пресвятой Богородицы (Санта-Мария-делле-Грацие), Милан, Италия.
В западной традиции число 13 считается несчастливым. Многие считают, что это заимствовано из иудео-христианской традиции, где тринадцать было числом учеников Иисуса Христа во время последней вечери, после которой тринадцатый ученик, Иуда, предал Иисуса. Среди викингов также существовало суеверие, что один из тринадцати собравшихся умрет в следующем году.
В России и многих странах бывшего СССР все четные числа считаются несчастливыми. Возможно, эта традиция возникла из убеждения, что четные числа полны, стабильны и статичны, неподвижны и, следовательно, не являются живыми. С другой стороны, нечетные числа представляют собой изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, дарить живым людям четное количество цветов считается невезением — эти числа обычно предназначаются для похорон.
В странах, говорящих на китайском, японском и корейском языках, номер номер 4 считается несчастливым, потому что он произносится так же, как «смерть». В некоторых случаях все числа, в которых есть четверка, считаются несчастливыми. Например, в здании может не быть этажей 4, 14 и 24. В Китае номер 7 тоже несчастлив, потому что он представляет духовный мир и призраков. Седьмой месяц в китайском календаре называется «месяцем призрака», когда открыта связь между мирами живых и духов.В Японии еще одно неудачное число — 9 , которое произносится так же, как «страдание».
В Италии 17 — неудачное число, потому что, когда его римское представление «XVII» переставляется, оно читается как VIXI или «vixi», что переводится с латыни как «Я жил». Это означает, что жизнь окончена, и относится к смерти.
666 — еще одно неудачное число, которое в Библии называется «Число зверя». Иногда считается, что это 616, но чаще встречается 666.Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, который ассоциируется с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают, что Нерон был поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками.
В Афганистане, особенно в Кабуле и его окрестностях 39 считается проклятым или постыдным числом, связанным с проституцией.Это связано с историей о сутенере, у которого на номерном знаке и в номере квартиры был номер 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия с целью получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Суеверие настолько сильны, что люди насмехаются и иным образом оскорбляют тех, у кого номер 39 в номере, квартире или номере телефона. По слухам, один из таких случаев насмешек привел к трагедии, когда против кандидата в депутаты, внесенного в бюллетень для голосования, издевались проезжающие мимо водители, что привело к дорожно-транспортному происшествию.Телохранители, опасаясь за его жизнь, застрелили двух человек. Эти утверждения опровергаются телохранителями и депутатом, и никаких обвинений предъявлено не было, поэтому неясно, является ли это городской легендой или реальным происшествием, но об этом говорят в Кабуле.
Список литературы
Эту статью написала Екатерина Юрий
Есть ли у вас трудности с переводом единицы измерения на другой язык? Помощь доступна! Задайте свой вопрос в TCTerms , и вы получите ответ от опытных технических переводчиков в считанные минуты.
Решено: Задача 2: В этом вопросе мы будем использовать упрощение …
- инженерия
- информатика
- вопросы и ответы по информатике
- Задача 2: в этом вопросе мы будем использовать упрощенную версию римского Система цифр Кому …
ИСПОЛЬЗОВАНИЕ C ++
Пожалуйста, не используйте жесткий код.
Показать транскрибированный текст изображения
Ответ эксперта
100% (1 оценка) решение 2: #include using namespace std; int main () {двойное число; int nn, m, d, c, l, x, v, i, n; cout> число; nn = (int) число; просмотреть полный ответПредыдущий вопрос Следующий вопросВопрос 2: В этом вопросе мы будем использовать упрощенную версию системы римских цифр для представления положительных целых чисел.Цифрами в этой системе являются I, V, X, L, C, D и M. Каждая цифра соответствует десятичному значению, как показано в следующей таблице. Римская цифра Десятичное значение 1 10 50 100 500 1000 Число в упрощенном римском алфавите. Система счисления представляет собой последовательность римских цифр, которая подчиняется этим двум правилам: 1. Цифры образуют монотонно невозрастающую последовательность. То есть значение каждой цифры меньше или равно значению цифры, которая была перед ней. Например, DLXXVI — это монотонно невозрастающая последовательность римских цифр, а XIV — нет.2. Не существует ограничений на количество раз, которое буква «M» может встречаться в числе. D ‘,’ L ‘и’ V могут появляться не более одного раза в числе C ‘,’ X ‘и 1, каждое может встречаться в числе не более четырех раз. Например: IIII, XVIl и MMMMMDCCLXXXXVII — допустимые числа в нашей упрощенной римской системе счисления, но IIIII, XIV, VVI и CCXLIII не являются. Напишите программу, которая считывает от пользователя (десятичное) число и печатает его представление в упрощенной римской системе счисления. numerals systenm Ваша программа должна взаимодействовать с пользователем точно так, как показано в следующем примере. Введите десятичное число: 147 147 — CXXXXVII. Вопрос 3: Напишите программу, которая считывает от пользователя положительное целое число (в десятичном представлении) и печатает его двоичное число. (основание 2) представление. Ваша программа должна взаимодействовать с пользователем точно так, как показано в следующем примере. Введите десятичное число: 76 Двоичное представление 76 — это 1001100
Системы счисления и основы — лучше объяснено
Базовые системы, такие как двоичная и шестнадцатеричная, сначала кажутся немного странными.Ключ в понимании того, как разные системы «работают», как одометр, когда они заполнены. База 10, наша десятичная система, «переключает», когда она получает 10 элементов, создавая новую цифру. Мы ждем 60 секунд, прежде чем «перейти» к новой минуте. Шестнадцатеричный и двоичный значения похожи, но отметьте галочкой каждые 16 и 2 элемента соответственно.
Попробуйте преобразовать числа в шестнадцатеричное и двоичное здесь:
Путь назад, когда: унарные числа
Раньше у нас не было базовых систем! Он шел в обе стороны, сквозь снег и палящую жару.Если вы хотите сосчитать один, вы должны написать:
л
Если вам нужно 5, вы должны написать
lllll
И ясно, 1 + 5 = 6
l + lllll = llllll
Это самый простой способ подсчета.
Введите римлян
В римских цифрах два означает один, дважды. Три было один, трижды:
один = я два = II три = III
Однако они решили, что могут добиться большего успеха, чем старая традиция линий на песке. Для пяти мы могли бы использовать V для представления lllll и получить что-то вроде
л + V = Vl
Неплохо, а? И, конечно же, есть еще много символов (L, C, M и т. Д.) ты можешь использовать.
Ключевым моментом является то, что V и lllll — это два способа кодирования числа 5.
Дайте каждому номеру имя
Еще одним прорывом стало осознание того, что каждое число может быть отдельной концепцией. Вместо того, чтобы представлять три как ряд единиц, дайте ему собственный символ: «3 ″. Проделайте это от одного до девяти, и вы получите символы:
1 2 3 4 5 6 7 8 9
Римляне были близки, так близки, но давали уникальные символы только 5, 10, 50, 100, 1000 и т. Д.
Используйте свою позицию
Теперь ясно, что вы не можете давать каждому номеру свой собственный символ. Их просто слишком много.
Но обратите внимание на одну особенность римских цифр: они используют позицию символов для обозначения значения.
IV означает «вычесть 1 из 5»
и VI означает «прибавить 1 к 5».
В нашей системе счисления мы используем позицию аналогичным образом. Мы всегда прибавляем и никогда не вычитаем. И каждая позиция на 10 больше, чем предыдущая.
Итак, 35 означает «прибавить 3 * 10 к 5 * 1 », а 456 означает 4 * 100 + 5 * 10 + 6 * 1 . Эта «позиционная десятичная» система исчисления является индуистско-арабской системой счисления, которую мы используем сегодня.
Наш выбор базы 10
Почему мы решили каждый раз умножать на 10? Скорее всего потому, что у нас 10 пальцев.
Следует понимать, что вам нужно достаточно цифр, чтобы «заполнить», пока вы не наберете следующее число. Позвольте мне продемонстрировать.
Если мы хотим, так сказать, проверять одометр каждые 10, нам нужны символы для чисел от одного до девяти; мы еще не добрались до десяти.Представьте, что числа медленно тикают вверх — в какой момент вы переворачиваете следующую единицу и начинаете с нуля?
Введите ноль
А что будет, когда мы дойдем до десяти? Как показать, что мы хотим ровно одну «десять» и ничего в столбце «единицы»?
Мы используем ноль, число, которого не существует. Ноль — это довольно концептуальная концепция, это заполнитель, пробел, пробел и многое другое. Достаточно сказать, что Зеро — одно из величайших изобретений всех времен.
Zero позволяет нам иметь пустой заполнитель, чего не было у римлян.Посмотрите, как без него их число велико.
Знаменитый роман Джорджа Оруэлла «1984» будет «MCMLXXXIV»! Сходит с языка, не так ли?
С учетом других баз
Помните, что мы, , выбрали , чтобы пересчитывать одометр каждые десять. Наш подсчет выглядит так:
1 2 3 4 5 6 7 8 9 (ох, я наелась!) 10 (отмечено галочкой - начало новой цифры)
Что, если бы мы отметили 60, когда считаем, как мы делаем секунды и минуты?
1 секунда 2 3 4 5 … 58 59 1:00 (60 секунд или 1 минута.Мы начали новую цифру.)
Пока все в порядке, верно? Обратите внимание, что мы используем двоеточие (:), указывающее, что мы находимся на новой «цифре». В базе 10 каждая цифра может стоять сама по себе.
Пробная база 16
Если нам нужна основа 16, мы могли бы сделать что-то подобное:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 (мы набираемся) 1:00 (16 - мы начали новую цифру)
Однако мы не хотим записывать шестнадцатеричные числа с двоеточием (хотя мы могли бы).Мы лучше приготовим отдельные символы для 10–15, чтобы можно было просто писать числа, как мы привыкли. У нас закончились числа (1–9 уже используются, 0 используется в качестве заполнителя), поэтому нам нужны другие символы. Мы могли бы использовать какие-то волнистые линии или другие формы, но обычно используются буквы в римском стиле. Так же, как 5 превратилось в V, программисты используют буквы A-F, чтобы получить достаточно цифр до 16. То есть
1 2 3 4 5 6 7 8 9 A (10 - мы используем символ «A») В (11) С (12) D (13) E (14) F (15 - ох, мы набираемся) 10 (16 - начинаем новую цифру)
Ага! Теперь мы можем использовать одну цифру для каждого «места», и мы знаем, что 10 на самом деле означает, что мы «перешли на 16 ″ один раз.
20 означает, что мы дважды отметили 16 (32).
25 означает, что мы дважды повысили до 16 (что дает нам 32) и получили еще 5. Итого 32 + 5 = 37.
Быстрый просмотр
Со мной так далеко? Это круто, правда? Мы можем считать в любой системе, какой захотим. Также обратите внимание, что основание 16 более экономно по пространству в том смысле, что мы можем записать число вроде 11 одной цифрой: B.
База 16 на самом деле не сильно отличается от базы 10, просто нам нужно больше времени для заполнения.
Удивительный мир двоичного кода
Мы видели множество базовых систем, от очень простых унарных до несвязных римских цифр, устойчивой базы 10 и компактной базы 16.
Что хорошего в двоичном формате? Чтобы упростить задачу, это самая простая система счисления, в которой используется концепция «тиканья». Унарный, где мы просто пишем 1, 11, 111 … просто продолжается вечно. Бинарный, с двумя вариантами (1 и 0) выглядит так:
1: 1 2:10 (мы полны - отметьте галочкой) 3: 11 4: 100 (мы снова наелись - отметьте галочкой) 5: 101 6: 110 7: 111 8: 1000 (отметьте еще раз) …
и так далее.
Поскольку двоичный файл настолько прост, его очень легко встроить в оборудование. Вам просто нужны вещи, которые могут включаться или выключаться (представляющие 1 и 0), а не вещи, которые имеют 10 возможных состояний (для представления десятичных чисел).
Благодаря своей простоте двоичный файл устойчив к ошибкам. Если ваш сигнал «частично включен» (допустим, 0,4), вы можете считать, что это ноль. А если он в основном на (скажем, 0,8), то вы можете предположить, что это 1. Если вы используете систему с 10 возможными состояниями, трудно определить, когда произошла ошибка.Это одна из причин, по которой цифровые сигналы настолько устойчивы к шумам.
Другие примеры баз
Мы постоянно используем другие базы, даже динамически меняющиеся. Обычно мы так не думаем:
Часы, минуты, секунды: 1:32:04
- Мы знаем, что это 1 час 32 минуты 4 секунды. В секундах это 1 60 60 + 32 * 60 + 4.
Футы и дюймы: 3 фута 5 дюймов
- Это 3 фута, 5 дюймов или 3 * 12 + 5 дюймов.
Фунты и унции: 8 фунтов, 5 унций
- Поскольку фунт равен 16 унциям, это 8 * 16 + 5 унций.Мы все время использовали систему счисления с основанием 16!
Расставания
«10» в любой системе счисления обозначает основание и означает, что мы один раз отметили галочкой. 10 в двоичной системе счисления означает два, 10 в десятичной системе счисления означает десять, а 10 в шестнадцатеричной системе счисления означает шестнадцать.
Как вы разделяете эти числа? Программисты часто пишут «0b» перед двоичными числами. Итак, 2 в двоичном формате — это
0b10
Точно так же они пишут 0x перед шестнадцатеричными числами. Итак, 16 в шестнадцатеричном формате:
0 × 10
Если впереди нет никаких символов (0b или 0x), мы предполагаем, что это обычное число с основанием 10.
А теперь вперед и наслаждайтесь новыми знаниями!
Другие сообщения в этой серии
- Системы счисления и базы
- Краткое руководство по GUID
- Понимание быстрого обратного квадратного корня землетрясения
- Простое введение в компьютерные сети
- Поменять местами две переменные с помощью XOR
- Общие сведения о порядке байтов с прямым и обратным порядком байтов
- Юникод и вы
- Немного о форматах двоичных файлов
- Алгоритмы сортировки

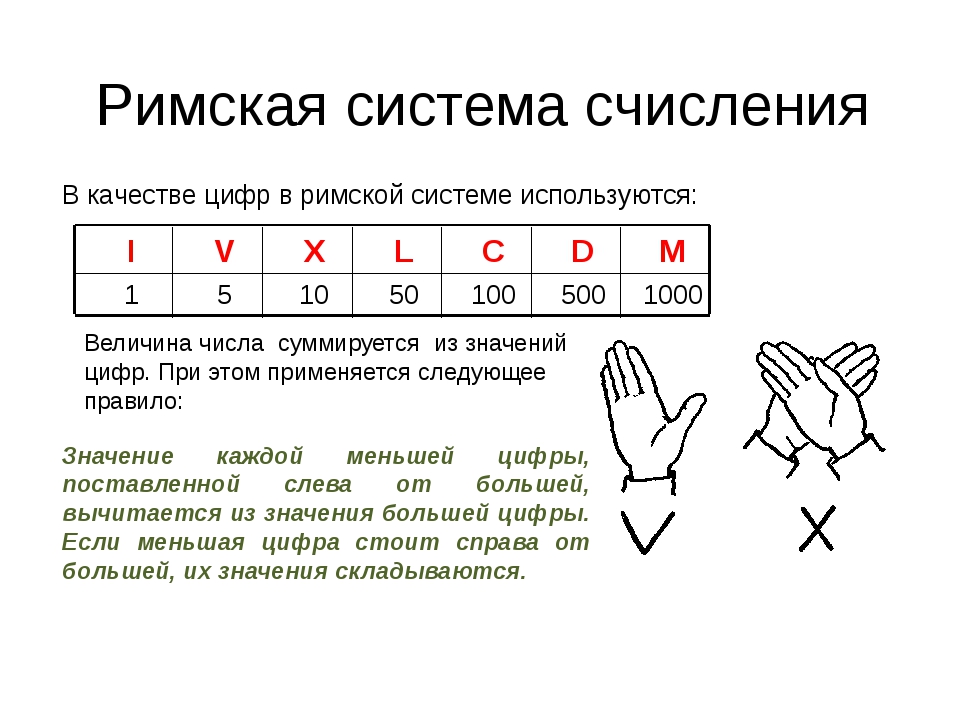 Двоично-восьмеричная таблица
Двоично-восьмеричная таблица