Сложение и умножение векторов: 1. Сложение и вычитание векторов. Умножение вектора на число

определение, сложение, умножение, скалярное и векторное произведение

В статье узнаете что такое вектор, векторные компоненты, единичный вектор, как складывать вектора, умножать вектора на скаляр, скалярное, векторное и смешанное произведение двух векторов.

Сохранение физической величины с вектором обычно означает совершенно иную ситуацию, чем просто сохранение ее скалярной длины. Постоянное значение импульса p (скаляр) может означать совершенно иную ситуацию, чем постоянный вектор p.

Вектор должен иметь три необходимые характеристики: значение (длина), направление, начало и конец.

Любое изменение любого из этих признаков — длины, направления или начало с концом — означает, что создан другой вектор. Два вектора равны тогда и только тогда, когда они имеют равную длину, направление и начало с концом.

Векторные компоненты

Компонентами вектора являются его проекции на оси системы координат.

Также в трехмерном пространстве векторы A называются векторами, которые являются проекциями этого вектора A на оси системы координат.

Имея вектор A, мы погружаем его в систему координат x, y, z. Векторы, являющиеся проекциями вектора A на оси системы, называются векторными компонентами вектора A. Вектор A является векторной суммой составляющих векторов A_x, A_y и A_z .

Единичный вектор

Единичный вектор, имеющий то же направление, что и вектор, на который он ссылается, важен, но его длина всегда равна 1.

Единичные векторы осей координат. Мы также присваиваем единичные векторы оси системы отсчета. а) относится к правовращающей системе и б) к левосторонней системе.

Сложение векторов

Сумма вектора обычно не совпадает с суммой скалярных величин:

Добавление двух или более векторов друг к другу сводится к добавлению их компонентов, то есть проекций на опорные оси. Результирующий вектор называется случайным вектором. Для двух векторов результирующий вектор является диагональю параллелограмма, построенного на этих векторах. Метод параллелограмма.

 В случае большего числа векторов результирующий вектор получается путем рисования одного из этих векторов, затем в конце первого вектора мы начинаем второй, в конце второго мы даем начало третьего и так далее. Полученный вектор является вектором, начало которого находится в начале первого из добавленных векторов. и его конец в конце последнего. При изменении порядка сложения результирующий вектор (красный) не меняет длину, направление:

Это правило добавления векторов также действует в трехмерном пространстве:

Умножение вектора на скаляр

Самым простым умножением, выполняемым на векторах, является умножение вектора на скаляр (число). Такое умножение не меняет направление вектора, но, как правило, меняет его длину и может изменить его конец (когда скаляр является отрицательным числом). Когда вектор A умножается на α-скаляр, мы получаем новый вектор B:

Скалярное произведение и векторное произведение двух векторов являются очень важными направления в физике и геометрии. Существует также смешанное произведение трех векторов.

Скалярное произведение двух векторов

Формально скалярное произведение векторов представляет собой точку, и ее значение определяется зависимостью

Скалярное произведение описывает способ, которым оба вектора видят друг друга, то есть как долго тень (проекция) отбрасывает каждый из векторов в своего партнера, когда угол между ними равен φ

B cos φ — длина тени, которую вектор B выбрасывает в вектор A. Аналогично, A cos φ — длина тени, которую вектор A выбрасывает в вектор B.

Когда длина проекции (тени) одного из векторов равна нулю, тогда длина проекции второго вектора равна нулю, то есть A • B = 0. Это означает, что эти векторы не работают в одном и том же направлении вообще. Работа, которую мы выполняем при движении автомобиля, зависит не только от приложенной силы F, но и от угла, который создает направление силы и направление пути.

Так как единичные векторы оси системы отсчета х, у и z, которые обозначают векторы е_х, е_Y и е_z, перпендикулярны друг к другу, то в виду того, что А • В = АВcosφ и что cos 0 = 1 и cos 90^o = 0, мы получаем произведение значений этих единичных векторов:

Выполнение аналогичного умножения на векторы A и B

мы получили новое выражение для скалярного произведения двух векторов A и B

Значение скалярного произведения двух векторов A и B можно записать в виде двух эквивалентных выражений:

Сравнивая оба выражения, мы находим выражение для угла между векторами A и B:

Векторное произведение двух векторов

Многие важные величины в науке и технике определяются вектором, который является произведением двух других векторов. В таких случаях произведение этих векторов, называемое векторным произведением , приводит к третьему вектору.

В этом случае задача состоит в том, чтобы определить все три особенности вектора C, являющегося произведением векторного произведения векторов A и B:

• длина
• направление
• начало и конец

Произведение векторов A и B , приводящее к третьему вектору C, отмечено диагональным крестом

Направление

Вектор С такой, что вектор перпендикулярен к плоскости, образованной векторами A и B, которая перпендикулярна как к вектору A и B.

Длина

вектор С равен значению параллелограмма, построенного на векторах А и В. Числовой C = ABsin φ.

Начало и конец

Вектор С определяет правое направление движения шнека во время нанесения первого вектора, а именно А или B.

Изменение порядка применения векторов означает изменение знака векторного произведения.

Таким образом, действительное свойство векторного произведения выглядит следующим образом A*B= -B*A

В отличие от скалярного произведения, векторное произведение некоммутативно.

Мы встретимся с векторным произведением на протяжении всего курса физики. Это также часто встречается в механике, а также в науке об электричестве и магнетизме.

В повседневной жизни векторное произведение находится в виде момента силы во вращательном движении. Мы воздействуем на вращательное движение тем эффективнее, чем больше применяем момент силы.

При откручивании гайки гаечным ключом речь идет не только о силе F, но и о способе ее применения (длина рычага R и угол, который создает рычаг с направлением силы).

Все эти зависимости элегантно включены в одно выражение в виде векторного произведения:

Хотя составляющие вектора C, который является произведением векторного произведения векторов A и B, уже включены в его длину и направление, но имея данные составляющих векторов A и B, мы можем использовать их для определения компонентов вектора C в форме матрицы:

Удобнее всего рассчитать этот определитель, расширив относительно первой строки.

Смешанное произведение трех векторов

Смешанное произведение трех векторов является скалярным значением, равным значению детерминанта

Геометрическая интерпретация: смешанное произведение численно равно объему V параллелепипеда, растянутому по векторам A, B и C:

Циклическая корректировка векторов в смешанном произведении не меняет значение этого произведения, то есть:

Сложение и вычитание векторов. Умножение вектора на число

1.	Выражение, содержащее векторы	1 вид — рецептивный	лёгкое	2 Б.	Упрощение выражения, содержащего векторы.
2.	Сумма векторов	1 вид — рецептивный	среднее	3 Б.	Вычисление суммы векторов, которые отложены на сторонах параллелепипеда.
3.	Сумма и разность векторов	1 вид — рецептивный	лёгкое	2 Б.	Сложение и вычитание векторов.
4.	Сложение и вычитание векторов	1 вид — рецептивный	лёгкое	2 Б.	Отработка простых операций с векторами.
5.	Арифметические операции с векторами	1 вид — рецептивный	лёгкое	2 Б.	Простейшие операции с векторами.
6.	Выражение вектора суммы	1 вид — рецептивный	среднее	3 Б.	Выражение вектора суммы через данный вектор.
7.	Выражение вектора разности	1 вид — рецептивный	среднее	3 Б.	Выражение вектора разности через данный вектор.
8.	Выражение с векторами	2 вид — интерпретация	среднее	5 Б.	Выполнение арифметических действий с векторами.
9.	Сложение и вычитание векторов	2 вид — интерпретация	среднее	4 Б.	Сложение и вычитание нескольких векторов.
10.	Сумма нескольких векторов	1 вид — рецептивный	среднее	3 Б.	Вычисление суммы нескольких векторов.
11.	Умножение вектора на число	2 вид — интерпретация	среднее	4 Б.	Нахождение числового коэффициента, выражающего отношение векторов.
12.	Сложение и умножение на число	3 вид — анализ	сложное	10 Б.	Вычисление результата нескольких операций с векторами.
13.	Арифметические действия с векторами, длина вектора	3 вид — анализ	сложное	8 Б.	Вычисление результата нескольких операций с векторами.
14.	Уравнение с векторами	3 вид — анализ	сложное	8 Б.	Нахождение неизвестного слагаемого.

Операции с векторами, сложение векторов, умножение вектора на действительное число.

Рассмотрим вектор v с начальной точкой в начале координат в любой координатной системе x-y и с конечной точкой в (a,b). Мы говорим, что вектор находится в стандартном положении и ссылаемся на него как на радиус-вектор. Обратите внимание, что пара точек определяет этот вектор. Таким образом, мы можем использовать это для обозначения вектора. Чтобы подчеркнуть, что мы имеем в виду вектор, и, чтобы избежать путаницы, как правило, пишут:

v = .

Координата a есть скаляром горизонтальной компоненты вектора, и координата b есть скаляром вертикальной компоненты вектора. Под скаляром мы подразумеваем численное количество, а не векторную величину. Таким образом, это рассматривается как компонентная форма v. Обратите внимание, что a и b НЕ вектора и их не надо путать с определением компонента вектора.

Теперь рассмотрим с A = (x₁, y₁) и C = (x₂, y₂). Давайте рассмотрим, как найти радиус вектор, эквивалентный . Как Вы видите на рисунке внизу, начальная точка A перемещена в начало координат (0, 0). Координаты P находятся вычитанием координат A из координат C. Таким образом, P = (x₂ — x₁, y₂ — y₁) и радиус вектор есть .

Можно показать, что и имеют одну и ту же величину и направление, и поэтому эквивалентны. Таким образом, = = 2 — x₁, y₂ — y₁ >.

Компонентная форма с A = (x₁, y₁) и C = (x₂, y₂) есть
= 2 — x₁, y₂ — y₁ >.

Пример 1 Найдите компонентную форму если C = (- 4, — 3) и F = (1, 5).

Решение Мы имеем
= = .

Обратите внимание, что вектор есть равным радиус-вектору , как показано на рисунке вверху.

Теперь, когда мы знаем, как записать вектор в компонентной форме, давайте изложим некоторые определения.
Длину вектора v легко определить, когда известны компоненты вектора. Для v = 1, v₂ >, мы имеем
|v|² = v²₁ + v²₂          Используя теорему Пифагора
|v| = √v²₁ + v²₂.

Длина, или величина ветктора v = 1, v₂ > находится как |v| = √v²₁ + v²₂.

Два вектора равны или эквивалентны, если они имеют одну и ту же величину и одно и то же направление.

Пусть u = 1, u₂ > и v = 1, v₂ >. Tогда
1, u₂ > = 1, v₂ >          только если u₁ = v₁ and u₂ = v₂.

Операции с векторами

Чтобы умножить вектор V на положительное число, мы умножаем его длину на это число. Его направление остается прежним. Когда вектор V умножается на 2, например, его длина увеличивается в два раза, но его направление не изменяется. Когда вектор умножается на 1,6, его длина увеличивается на 60%, а направление остается прежним. Чтобы умножить вектор V на отрицательное действительное число, умножаем его длину на это число и изменяем направление на противоположное. Например, Когда вектор умножается на (-2), его длина увеличивается в два раза и его направление изменяется на противоположное. Так как действительные числа работают как скалярные множители в умножении векторов, мы называем их скаляры и произведение kv называется скалярные кратные v.

Для действительного числа k и вектора v = 1, v₂ >, скалярное произведение k и v есть
kv = k.1, v₂ > = 1, kv₂ >.
Вектор kv есть скалярным кратным вектора v.

Пример 2 Пусть u = и w = . Найдите — 7w, 3u и — 1w.

Решение
— 7w = — 7. = ,
3u = 3. = ,
— 1w = — 1. = .

Теперь мы м

Понятие вектора. Действия с векторами, их свойства — сложение и вычитание векторов, умножение на число, коллинеарность. Скалярное умножение (произведение) векторов. Проекции, разложение векторов, координаты, действия в координатах, взаимное расположение

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа.  / / Понятие вектора. Действия с векторами, их свойства — сложение и вычитание векторов, умножение на число, коллинеарность. Скалярное умножение (произведение) векторов. Проекции, разложение векторов, координаты, действия в координатах, взаимное расположение Поделиться:    Понятие вектора. Коллинеарные векторы. Действия с векторами и их свойства — сложение и вычитание векторов, умножение вектора на число, критерий коллинеарности. Скалярное умножение (произведение) векторов. Проекция вектора на вектор. Разложение векторов по неколлинеарным векторам. Координаты вектора на плоскости. Действия с векторами в координатах на плоскости. Взаимное расположение векторов. Разложение вектора по координатным векторам.

Сложение и вычитание векторов. Умножение вектора на число. Геометрия, 10 класс: уроки, тесты, задания.

1.	Выражение, содержащее векторы Сложность: лёгкое	2
2.	Сумма векторов Сложность: среднее	3
3.	Сумма и разность векторов Сложность: лёгкое	2
4.	Сложение и вычитание векторов Сложность: лёгкое	2
5.	Арифметические операции с векторами Сложность: лёгкое	2
6.	Выражение вектора суммы Сложность: среднее	3
7.	Выражение вектора разности Сложность: среднее	3
8.	Выражение с векторами Сложность: среднее	5
9.	Сложение и вычитание векторов Сложность: среднее	4
10.	Сумма нескольких векторов Сложность: среднее	3
11.	Умножение вектора на число Сложность: среднее	4
12.	Сложение и умножение на число Сложность: сложное	10
13.	Арифметические действия с векторами, длина вектора Сложность: сложное	8
14.	Уравнение с векторами Сложность: сложное	8

10 класс. Геометрия. Сложение и вычитание векторов. Умножение вектора на число. — Сложение и вычитание векторов. Умножение вектора на число.

Комментарии преподавателя

От­ме­тим, что сло­же­ние век­то­ров про­из­во­дит­ся ана­ло­гич­но пла­ни­мет­рии, толь­ко все дей­ствия вы­пол­ня­ют­ся в про­стран­стве.

Итак, пусть за­да­ны два про­из­воль­ных век­то­ра в про­стран­стве (рис. 1):

Рис. 1. Про­из­воль­ные век­то­ры в про­стран­стве

Опре­де­лим, что же на­зы­ва­ет­ся сум­мой двух этих век­то­ров.

Точно так же, как в пла­ни­мет­рии, из любой удоб­ной точки, на­зо­вем ее точ­кой А, можно един­ствен­ным об­ра­зом от­ло­жить век­тор, рав­ный век­то­ру . На­пом­ним, что за­дан­ные век­то­ры, как и любые дру­гие, сво­бод­ны, важно лишь на­прав­ле­ние и длина, сам век­тор можно па­рал­лель­но пе­ре­но­сить в любое место как на плос­ко­сти, так и в про­стран­стве. Так, мы по­лу­чи­ли век­тор  – в ре­зуль­та­те дей­ствия век­то­ра  точка А пе­ре­ме­сти­лась в точку В. Те­перь из точки В от­кла­ды­ва­ем един­ствен­но воз­мож­ным об­ра­зом век­тор , по­лу­ча­ем век­тор  – так, в ре­зуль­та­те дей­ствия век­то­ра  точка В пе­ре­ме­сти­лась в точку С. В ре­зуль­та­те точка А пе­ре­ме­сти­лась в точку С, по­лу­чен век­тор , ко­то­рый и на­зы­ва­ет­ся сум­мой век­то­ров  и  (рис. 2).

Рис. 2. Сумма двух век­то­ров в про­стран­стве

Так, по­лу­че­но пра­ви­ло тре­уголь­ни­ка для сло­же­ния век­то­ров в про­стран­стве.

Пра­ви­ло тре­уголь­ни­ка

Из любой точки про­стран­ства (точка А) от­кла­ды­ва­ем пер­вый век­тор, из конца пер­во­го век­то­ра (точка В) от­кла­ды­ва­ем вто­рой век­тор и по­лу­ча­ем точку С. Век­тор, со­еди­ня­ю­щий на­ча­ло пер­во­го век­то­ра (точка А) и конец вто­ро­го (точка С), и будет ре­зуль­ти­ру­ю­щим.

От­ме­тим, что ре­зуль­тат сло­же­ния век­то­ров не за­ви­сит от вы­бо­ра на­чаль­ной точки, су­ще­ству­ет со­от­вет­ству­ю­щая тео­ре­ма, ко­то­рая это до­ка­зы­ва­ет на ос­но­ва­нии того, что из точки можно от­ло­жить век­тор, рав­ный за­дан­но­му, един­ствен­ным об­ра­зом.

Опре­де­ле­ние

Раз­но­стью двух век­то­ров на­зы­ва­ет­ся такой тре­тий век­тор, ко­то­рый, бу­дучи сло­жен­ным со вто­рым век­то­ром, даст пер­вый век­тор.

Вве­дем раз­ность век­то­ров  и , для этого сло­жим век­тор  с про­ти­во­по­лож­ным век­то­ром :

Итак, из про­из­воль­ной точки А от­кла­ды­ва­ем век­тор , по­лу­ча­ем точку В. Чтобы по­лу­чить век­тор  мы стро­им век­тор, рав­ный век­то­ру  по длине, но про­ти­во­на­прав­лен­ный. По­лу­чен­ный век­тор от­кла­ды­ва­ем из точки В – по­лу­ча­ем точку D. Век­тор  и будет ис­ко­мым век­то­ром раз­но­сти.

Про­ил­лю­стри­ру­ем (рис. 3):

Рис. 3. Вы­чи­та­ние двух век­то­ров в про­стран­стве

По­стро­им на за­дан­ных век­то­рах  и  па­рал­ле­ло­грамм (рис. 4):

Рис. 4. Па­рал­ле­ло­грамм на двух за­дан­ных век­то­рах

Т. к. век­тор ; ана­ло­гич­но .

По пра­ви­лу тре­уголь­ни­ка:

Так, одна из диа­го­на­лей па­рал­ле­ло­грам­ма, по­стро­ен­но­го на двух век­то­рах, со­от­вет­ству­ет сумме этих век­то­ров.

Рас­смот­рим раз­ность век­то­ров. По пра­ви­лу тре­уголь­ни­ка:

.

Так, вто­рая диа­го­наль па­рал­ле­ло­грам­ма, по­стро­ен­но­го на двух век­то­рах, со­от­вет­ству­ет раз­но­сти этих век­то­ров.

Для сло­же­ния и вы­чи­та­ния несколь­ких век­то­ров при­ме­ня­ет­ся пра­ви­ло мно­го­уголь­ни­ка. Пусть за­да­ны век­то­ры  и :

Рис. 5. Три век­то­ра в про­стран­стве

Необ­хо­ди­мо по­стро­ить век­тор .

Видим, что перед неко­то­ры­ми век­то­ра­ми стоят чис­лен­ные мно­жи­те­ли. На­пом­ним, что при умно­же­нии век­то­ра на число по­лу­ча­ем со­на­прав­лен­ный век­тор, длина ко­то­ро­го – это длина ис­ход­но­го век­то­ра, умно­жен­ная на за­дан­ное число. По­лу­чим век­то­ры  и . Век­тор  со­на­прав­лен с век­то­ром , длина его в три раза боль­ше. Век­тор  про­ти­во­на­прав­лен век­то­ру , длина его в два раза боль­ше. Про­ил­лю­стри­ру­ем (рис. 6):

Рис. 6. Умно­же­ние век­то­ра на число

При­сту­па­ем к сло­же­нию. Из про­из­воль­ной точки А от­кла­ды­ва­ем по­лу­чен­ный век­тор  – по­лу­ча­ем точку В. Из точки В от­кла­ды­ва­ем век­тор  – по­лу­ча­ем точку С. Из точки С от­кла­ды­ва­ем век­тор  – по­лу­ча­ем точку D. Со­глас­но пра­ви­лу мно­го­уголь­ни­ка, век­тор  со­от­вет­ству­ет ис­ко­мо­му век­то­ру :

Рис. 7. Сло­же­ние век­то­ров по пра­ви­лу мно­го­уголь­ни­ка

За­да­ча 1:

Задан тет­ра­эдр ABCD (ри­су­нок 8). До­ка­зать:

  

Рис. 8. Тет­ра­эдр, за­да­ча 1

Ре­ше­ние:

По пра­ви­лу тре­уголь­ни­ка: 

Ана­ло­гич­но: 

, ч. т. д.

По пра­ви­лу тре­уголь­ни­ка: 

Ана­ло­гич­но: , ч. т. д.

За­да­ча 2

Упро­стить вы­ра­же­ние: 

Рас­смот­рим от­дель­но сумму двух век­то­ров: , ее зна­че­ние оче­вид­но:

Про­ил­лю­стри­ру­ем (рис. 9):

Рис. 9. Сумма двух век­то­ров

Те­перь со­кра­тим про­ти­во­по­лож­ные век­то­ры:

Можно было сразу за­ме­тить:

.

В ре­зуль­та­те упро­ще­ния по­лу­че­но:

.

Итак, мы ввели опе­ра­ции сло­же­ния и вы­чи­та­ния век­то­ров, умно­же­ния век­то­ра на число в сте­рео­мет­рии, от­ме­ти­ли, что опе­ра­ции ана­ло­гич­ны таким же для пла­ни­мет­рии. Кроме того, ре­ши­ли несколь­ко задач, ба­зи­ру­ю­щих­ся на опи­сан­ных опе­ра­ци­ях.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/10-klass/vektory-v-prostranstve/slozhenie-i-vychitanie-vektorov-umnozhenie-vektora-na-chislo

http://www.youtube.com/watch?v=a0ohdyq56vQ

http://www.youtube.com/watch?v=JQzv4c5ak-0

http://www.youtube.com/watch?v=sKCfeWlmsLk

http://azdekor.ru/Spektr/SREDN_SKOOL/MATEM/026/images/Vkt3.jpg

https://www.kursoteka.ru/teacher//index.cfm/getfile/2364/7703/4155

 http://azdekor.ru/Spektr/SREDN_SKOOL/MATEM/026/images/Vkt4.jpg

http://portfoliosmolgu.ucoz.ru/_ph/8/2/143950352.jpg?1445058118

http://www.mathprofi.ru/vektory_dlya_chainikov.html

 

5.6.3 Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число

Видеоурок 1: Понятие вектора

Видеоурок 2: Равенство векторов

Видеоурок 3: Сложение и вычитание векторов

Видеоурок 4: Умножение вектора на число

Лекция: Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число

Вектор

Вектор – это тело, которое изучается в математике, но используется в большом количестве наук. Например, в физике существуют скалярные величины (те, что характеризуются значением – масса, температура и т.д.), а также векторные величины (сила, работа и другие).

Вектор – это величина, которая характеризуется не только значением, но и направлением. Иными словами, это направленный отрезок. 

Но кроме его длины, нам также важно, где находится его начало, а где конец.

Если вектор имеет свое начало в некоторой точке А, а заканчивается в точке В, то его обозначают следующим образом:

Кроме двух букв, вектор можно обозначить одной буквой со значком вектора сверху.

Длиной вектора (его модулем) называют расстояние между концом вектора и его началом. 

Для определения модуля вектора следует воспользоваться следующей формулой:

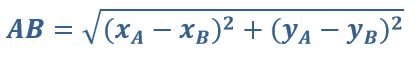
Кроме этого, модуль вектора может обозначаться следующим образом:

Если некоторый вектор имеет начало и конец в одной и той же точке, то такой вектор называют нулевым. Нулевой вектор обозначают, как

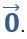
Если длина некоторого вектора равна единичному отрезку, то его называют единичным.

Если некоторые векторы расположены на одной прямой или же параллельны друг другу, то такие векторы называются коллинеарными.

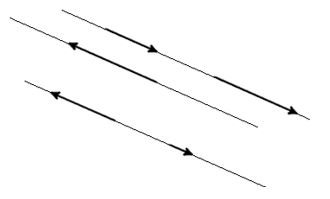
Если некоторые векторы можно назвать коллинеарными, но кроме этого они направлены в одну сторону, то их можно назвать сонаправленными.

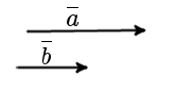
Если же наоборот два коллинеарных вектора смотрят в разные стороны, то их называют противоположно направленными.

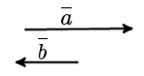
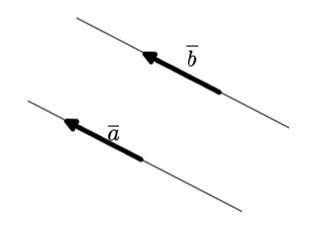
Если же некоторые векторы являются коллинеарными, сонаправленными, а также имеют одинаковую длину (модуль), то их можно назвать равными.

Координаты вектора

Для нахождения координаты вектора следует вычесть соответствующие координаты его конца и начала.

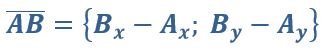
Например, если начало вектора А (3; 6), а конец В (5;9), то этот вектор будет иметь следующие координаты: {2;3}.

Сложение и вычитание векторов

Чтобы сложить два вектора для получения нового, необходимо сложить соответствующие координаты.

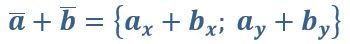
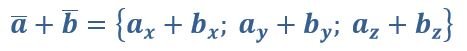
Например, сложим вектор {2;3} с вектором {5;7}. В результате получим новый вектор с координатами {7;10}. С вычитанием все аналогично.

Умножение вектора на некоторое число

Чтобы умножить вектор на некоторое число, следует умножить каждую его координату на данное число.

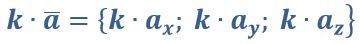
Свойства:

• Первоначальный вектор и вектор умноженный на некоторое число, который равный ему, являются параллельными.
• Если число, на которое умножался вектор, больше нуля, то новый вектор будет сонаправлен первоначальному. Если же число меньше нуля, то векторы будут противоположно направленны.

 

Скалярное умножение и сложение векторов

Двумя основными векторными операциями являются скалярное умножение и сложение векторов . В общем, при работе с векторами числа или константы называются скалярами .

Скалярное умножение — это когда вектор умножается на скаляр (число или константу). Если вектор v умножить на скаляр k, то получится k v . Если k положительно, то k v будет иметь те же направления, что и v .Если k отрицательно, k v будет иметь направление, противоположное v .

СКАЛЯРНОЕ УМНОЖЕНИЕ:

Пусть v = < v 1 , v 2 > и k — скаляр.

k v = k < v 1 , v 2 > знак равно <к v 1 , к v 2 >

Чтобы сложить два вектора u и v , поместите начальную точку второго вектора (без изменения длины или направления) в конечную точку первого вектора.Затем соедините начальную точку первого вектора с концом второго вектора. Эта линия соединения представляет собой сумму двух векторов.

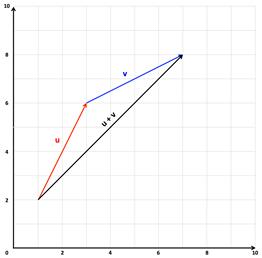
Сумма векторов u и v в компонентной форме равна:

ДОБАВЛЕНИЕ ВЕКТОРОВ:

Пусть u = < U 1 , U 2 > и v = < v 1 , v 2 >

U + V = < U 1 + v 1 , U 2 + v 2 >

U-V = U + ( -v знак равно U 1 — v 1 , U 2 — v 2 >

Скалярное умножение и сложение векторов имеют следующие общие свойства:

СВОЙСТВА СКАЛЯРНОГО УМНОЖЕНИЯ И ДОБАВЛЕНИЯ ВЕКТОРОВ:

Пусть u , v и w — векторы, а c и d — скаляры.

1. u + v = v + u 2. ( u + v ) + w = u + ( v + w )

3. u + 0 = u 4. u + (- u ) = 0

5. c (d u ) = (cd) u 6. (c + d) u = c u + d u

7. c ( u + v ) = c u + c v 8.1 · u = u , 0 · u = 0

9. || c v || = | c ||| v ||

Давайте рассмотрим пару примеров.

Пример 1: Если и = <- 2,1> и v = <7, -3> найти (а) u + v и (б) u — v.

Шаг 1. Вычислить u + v с помощью сложения векторов. Добавьте x-компонент обоих векторов. Сделайте то же самое для y-компонентов.	и + v = <- 2 + 7, 1+ ( -3 )> и + v = <5, -2>
Шаг 2: Вычислить u — v с помощью сложения векторов. Помните u — v = u + (-v), поэтому вычтите x-компонент v из u . Сделайте то же самое для y-компонентов.	U-V = U + ( -v ) = <- 2-7, 1- ( -3 )> U-V = <- 9, 4>

Пример 2: Если и = <6,15> и v = <- 5,20> найти (а) 2u + v и (б) 5u — 2v.

Шаг 1. Вычислить 2u + v, используя скалярное умножение и сложение векторов. а) Сначала вычислите 2 и , используя скалярное умножение. б) Затем вычислите 2 u + v , используя сложение векторов.	2u = 2 <6,15> = <2 · 6, 2 · 15> 2u = <12, 30> 2u + у = <12+ ( -5 ), 30 + 20> 2u + у = <7,50>
Шаг 2: Вычислите 5u — 2v, используя скалярное умножение и сложение векторов. a) Сначала вычислите 5 u и 2 v , используя скалярное умножение. б) Затем вычислите 5 u +2 v , используя сложение векторов.	5u = 5 <6,15> = <5 · 6, 5 · 15> 5u = <30, 75> 2v = 2 <-5,20> = <2 · (

.

Векторов

Это вектор:

Вектор имеет величину , (размер) и направление :

Длина линии показывает ее величину, а стрелка указывает направление.

Мы можем сложить два вектора, соединив их голова к хвосту:

И неважно, в каком порядке мы их добавляем, результат будет тот же:

Пример: самолет летит на север, но дует ветер с северо-запада.

Два вектора (скорость, создаваемая воздушным винтом, и скорость ветра) приводят к немного более низкой путевой скорости при движении немного к востоку от севера.

Если бы вы смотрели на самолет с земли, казалось бы, он немного поскользнулся.

Вы когда-нибудь видели это? Возможно, вы видели птиц, борющихся с сильным ветром, которые, кажется, летят боком. Векторы помогают это объяснить.

Скорость, ускорение, сила и многое другое — векторы.

Вычитание

Мы также можем вычесть один вектор из другого:

• сначала мы меняем направление вектора, который хотим вычесть,
• , затем добавьте их как обычно:

а — б

Обозначение

Вектор часто пишется полужирным шрифтом , например a или b .

Вектор также может быть записан в виде букв его головы и хвоста со стрелкой над ним, например:

Расчеты

Сейчас… как мы делаем расчеты?

Самый распространенный способ — сначала разбить векторы на части x и y, например:

Вектор a разбивается на
, два вектора a _x и a _y

(Позже мы увидим, как это сделать.)

Добавление векторов

Затем мы можем сложить векторы на , сложив части x и , добавив части y :

Сумма вектора (8, 13) и вектора (26, 7) дает вектор (34, 20)

Пример: складываем векторы a = (8, 13) и b = (26, 7)

c = a + b

c = (8, 13) + (26, 7) = (8 + 26, 13 + 7) = (34, 20)

Когда мы разбиваем такой вектор, каждая часть называется компонентом :

Вычитание векторов

Для вычитания сначала переверните вектор, который мы хотим вычесть, а затем сложите.

Пример: вычесть k = (4, 5) из v = (12, 2)

a = v + — k

a = (12, 2) + — (4, 5) = (12, 2) + (−4, −5) = (12−4, 2−5) = (8, −3)

Величина вектора

Величина вектора показана двумя вертикальными полосами по обе стороны от вектора:

| a |

ИЛИ можно написать с двойной вертикальной чертой (чтобы не путать с абсолютным значением):

|| a ||

Для его вычисления мы используем теорему Пифагора:

| a | = √ (х ² + у ² )

Пример: какова величина вектора b = (6, 8)?

| b | = √ (6 ² + 8 ² ) = √ (36 + 64) = √100 = 10

Вектор с величиной 1 называется единичным вектором.

Вектор против скалярного

Скаляр имеет величину (размер) только .

Скаляр: просто число (например, 7 или -0,32) … определенно не вектор.

Вектор имеет величину и направление и часто выделяется полужирным шрифтом , поэтому мы знаем, что это не скаляр:

• , поэтому c — вектор, его величина и направление
• , но c — это просто значение, например 3 или 12.4

Пример: k b на самом деле является скаляром k, умноженным на вектор b .

Умножение вектора на скаляр

Когда мы умножаем вектор на скаляр, это называется «масштабированием» вектора, потому что мы изменяем размер вектора.

Пример: умножить вектор m = (7, 3) на скаляр 3

a = 3 м = (3 × 7, 3 × 3) = (21, 9)

Он по-прежнему указывает в том же направлении, но в 3 раза длиннее

(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз.)

Умножение вектора на вектор (скалярное произведение и перекрестное произведение)

Как умножить два вектора вместе? Есть несколько способов! (Более подробную информацию см. На этих страницах.)

Более двух размеров

Векторы также отлично работают в трех и более измерениях:

Вектор (1, 4, 5)

Пример: складываем векторы a = (3, 7, 4) и b = (2, 9, 11)

c = a + b

c = (3, 7, 4) + (2, 9, 11) = (3 + 2, 7 + 9, 4 + 11) = (5, 16, 15)

Пример: какова величина вектора w = (1, −2, 3)?

| w | = √ (1 ² + (−2) ² + 3 ² ) = √ (1 + 4 + 9) = √14

Вот пример с 4-мя измерениями (но его сложно нарисовать!):

Пример: вычесть (1, 2, 3, 4) из (3, 3, 3, 3)

(3, 3, 3, 3) + — (1, 2, 3, 4)
= (3, 3, 3, 3) + (−1, −2, −3, −4)
= (3 −1, 3−2, 3−3, 3−4)
= (2, 1, 0, −1)

Звездная величина и направление

Мы можем знать величину и направление вектора, но нам нужны его длины по осям x и y (или наоборот):

	<=>
Вектор a в полярных координатах		Вектор a в декартовых координатах

Вы можете прочитать, как преобразовать их в полярные и декартовы координаты, но вот краткое описание:

От полярных координат (r, θ ) до декартовых координат (x, y)		От декартовых координат (x, y) до полярных координат (r, θ)
x = r × cos ( θ ) y = r × sin ( θ )		r = √ (x 2 + y 2 ) θ = tan -1 (y / x)

Пример

Сэм и Алекс тянут ящик.

• Сэм тянет с силой 200 Ньютонов при 60 °
• Алекс тянет с усилием 120 Ньютонов под углом 45 °, как показано на рисунке

Что такое общая сила и ее направление?

Давайте сложим два вектора голова к хвосту:

Первое преобразование из полярного числа в декартово (до 2 десятичных знаков):

Вектор Сэма:

• x = r × cos ( θ ) = 200 × cos (60 °) = 200 × 0,5 = 100
• y = r × sin ( θ ) = 200 × sin (60 °) = 200 × 0.8660 = 173,21

Вектор Алекса:

• x = r × cos ( θ ) = 120 × cos (-45 °) = 120 × 0,7071 = 84,85
• y = r × sin ( θ ) = 120 × sin (-45 °) = 120 × -0,7071 = -84,85

Теперь у нас:

Добавьте их:

(100, 173,21) + (84,85, -84,85) = (184,85, 88,36)

Этот ответ верен, но давайте вернемся к полярному, поскольку вопрос был в полярном:

• r = √ (x ² + y ² ) = √ (184.85 ² + 88,36 ² ) = 204,88
• θ = tan ^-1 (y / x) = tan ^-1 (88,36 / 184,85) = 25,5 °

И мы получили результат (округленный):

А для Сэма и Алекса это выглядит так:

Они могли бы получить лучший результат, если бы стояли плечом к плечу!

,

операций над векторами, сложение векторов, умножение вектора на действительное число.

Рассмотрим вектор v, начальная точка которого — , в системе координат xy, а конечной точкой является. Мы говорим, что вектор находится в стандартной позиции , и называем его вектором позиции. Обратите внимание, что упорядоченная пара однозначно определяет вектор. Таким образом, мы можем использовать для обозначения вектора. Чтобы подчеркнуть, что мы думаем о векторе, и чтобы избежать путаницы с обозначениями упорядоченных пар и интервалов, мы обычно пишем
v =.

Координата a — это скаляр , горизонтальный компонент вектора, а координата b — это скаляр , вертикальный компонент вектора. Под скаляром мы подразумеваем числовую величину , а не вектор . Таким образом, компонент считается формой v. Обратите внимание, что a и b НЕ являются векторами, и их не следует путать с определением компонента вектора.

Теперь рассмотрим с A = (x ₁ , y ₁ ) и C = (x ₂ , y ₂ ).Давайте посмотрим, как найти вектор положения, эквивалентный. Как вы можете видеть на рисунке ниже, начальная точка A перемещается в начало координат (0, 0). Координаты P находятся путем вычитания координат A из координат C. Таким образом, P = (x ₂ — x ₁ , y ₂ — y ₁ ) и вектор положения равен.

Можно показать, что и имеют одинаковую величину и направление и, следовательно, эквивалентны. Таким образом, = = 2 — x ₁ , y ₂ — y ₁ >.

Компонент формирует of с A = (x ₁ , y ₁ ) и C = (x ₂ , y ₂ ) равен
= 2 — x ₁ , y ₂ — y ₁ >.

Пример 1 Найдите форму компонента, если C = (- 4, — 3) и F = (1, 5).

Решение У нас
= =.

Обратите внимание, что вектор эквивалентен вектору положения, как показано на рисунке выше.

Теперь, когда мы знаем, как записывать векторы в компонентной форме, давайте еще раз сформулируем некоторые определения.
Длину вектора v легко определить, когда известны компоненты вектора. Для v = 1, v ₂ > имеем
| v | ² = v ² ₁ + v ² ₂ Использование теоремы Пифагора
| v | = √v ² ₁ + v ² ₂ .

Длина , или величина вектора v = 1, v ₂ > задается как | v | = √v ² ₁ + v ² ₂ .

Два вектора эквивалентны , если они имеют одинаковую величину и одинаковое направление.

Пусть u = 1, u ₂ > и v = 1, v ₂ >. Тогда
1, u ₂ > = 1, v ₂ > тогда и только тогда, когда u ₁ = v ₁ и u ₂ = v ₂ .

Операции над векторами

Чтобы умножить вектор v на положительное действительное число, мы умножаем его длину на число. Его направление остается прежним.Когда вектор v умножается, например, на 2, его длина удваивается и его направление не изменяется. Когда вектор умножается на 1,6, его длина увеличивается на 60%, а его направление остается прежним. Чтобы умножить вектор v на отрицательное действительное число, мы умножаем его длину на число и меняем его направление на обратное. Когда вектор умножается на 2, его длина удваивается, а его направление меняется на противоположное. Поскольку действительные числа работают как коэффициенты масштабирования при векторном умножении, мы называем их скалярами , а произведения kv называются скалярными кратными v.

Для действительного числа k и вектора v = 1, v ₂ >, скалярное произведение k и v составляет
kv = k.1, v ₂ > = 1, kv ₂ >.
Вектор kv является скалярным , кратным вектора v.

Пример 2 Пусть u = и w =. Найти — 7w, 3u и — 1w.

Решение
— 7w = — 7. =,
3u = 3. =,
— 1w = — 1. =.

Теперь мы можем сложить два вектора с помощью компонентов.Чтобы сложить два вектора, представленных в форме компонентов, мы добавляем соответствующие компоненты. Пусть u = 1, u ₂ > и v = 1, v ₂ >. Тогда
u + v = 1 + v ₁ , u ₂ + v ₂ >

Например, если v = и w =, то
v + w = ​​=

Если u = 1, u ₂ > и v = 1, v ₂ >, то
u + v = 1 + v ₁ , u ₂ + v ₂ >.

Прежде чем мы определим вычитание векторов, нам нужно определить — v.Противоположность v = 1, v ₂ >, показанная ниже, это
— v = (- 1) .v = (- 1) 1, v ₂ > = 1, — v ₂ >

Вычитание вектора, такое как u — v, включает вычитание соответствующих компонентов. Покажем это, переписав u — v как u + (- v). Если u = 1, u ₂ > и v = 1, v ₂ >, то
u — v = u + (- v) = 1, u ₂ > + 1, — v ₂ > = 1 + (- v ₁ ), u ₂ + (- v ₂ )> = 1 — v ₁ , u ₂ — v ₂ >

Мы можем проиллюстрировать векторное вычитание с помощью параллелограммов, точно так же, как мы делали векторное сложение.

Вычитание вектора

Если u = 1, u ₂ > и v = 1, v ₂ >, то
u — v = 1 — v ₁ , u ₂ — v ₂ >.

Интересно сравнить сумму двух векторов с разностью тех же двух векторов в одном параллелограмме. Векторы u + v и u — v — диагонали параллелограмма.

Пример 3 Выполните следующие вычисления, где u = и v =.
a) u + v
b) u — 6v
c) 3u + 4v
d) | 5v — 2u |

Решение
а) u + v = + = =;
б) и — 6в = — 6. = — =;
в) 3u + 4v = 3. + 4. = + =;
d) | 5v — 2u | = | 5. — 2. | = | — | = || = √ (- 29) ² + 21 ² = √1282 ≈ 35,8

Прежде чем мы сформулируем свойства сложения векторов и скалярного умножения, нам нужно определить другой специальный вектор — нулевой вектор. Вектор, у которого обе точки являются начальной и конечной, — это нулевой вектор , обозначенный буквой O или.Его величина равна 0. Помимо векторов, нулевой вектор является аддитивным вектором идентичности:
v + O = v. 1, v ₂ > + = 1, v ₂ >
Операции над векторами имеют много общего. свойства как операции с действительными числами.

Свойства сложения векторов и скалярного умножения

Для всех векторов u, v и w и для всех скаляров

.