Сравнение логарифмов – Как сравнивать логарифмы | Логарифмы

Приемы и методы сравнения логарифмов

Сравнение значений логарифмов или значения логарифма с некоторым числом встречается в школьной практике решения задач не только как самостоятельная задача. Сравнивать логарифмы приходится, например, при решении уравнений и неравенств. Материалы статьи (задачи и их решения) располагаются по принципу “от простого к сложному” и могут быть использованы для подготовки и проведения урока (уроков) по данной теме, а также на факультативных занятиях. Количество рассматриваемых задач на уроке зависит от уровня класса, его профильного направления. В классах с углубленным изучением математики этот материал может быть использован для двухчасового урока-лекции.

1. (Устно.) Какие из функций являются возрастающими, а какие убывающими:

Замечание. Это упражнение является подготовительным.

2. (Устно.) Сравните с нулем:

Замечание. При решении упражнения № 2 можно использовать как свойства логарифмической функции с привлечением графика логарифмической функции, так и следующее полезное свойство:

если положительные числа a и b лежат на числовой прямой правее 1 или левее 1 (то есть a>1 и b>1 или 0<a<1 и 0<b<1), то log_ab > 0 ;
если положительные числа a и b лежат на числовой прямой по разные стороны от 1(то есть 0<a<1<b или 0<b<1<a), то log_ab < 0 [4].

Покажем использование этого свойства при решении № 2(а).

Так как

Так как функция y = log₇t возрастает на R₊, 10 > 7, то log₇10 > log₇7, то есть log₇10 > 1. Таким образом, положительные числа sin3 и log₇10 лежат по разные стороны от 1. Следовательно, log

sin3log₇10 < 0.

3. (Устно.) Найдите ошибку в рассуждениях:

. Функция y = lgt возрастает на R₊, тогда ,

Разделим обе части последнего неравенства на . Получим, что 2 > 3.

Решение.

Положительные числа и 10 (основание логарифма) лежат по разные стороны от 1. Значит, < 0. При делении обеих частей неравенства на число знак неравенства следует изменить на противоположный.

4. (Устно.) Сравните числа:

Замечание. При решении упражнений № 4(a–c) используем свойство монотонности логарифмической функции. При решении № 4(d) используем свойство:

если c > a >1, то при b>1 справедливо неравенство log_ab > log_cb.

Решение 4(d).

Так как 1 < 5 < 7 и 13 > 1, то log

513 > log₇13.

5. Сравните числа log₂6 и 2.

Решение.

Первый способ (использование монотонности логарифмической функции).

2 = log₂4;

Функция y = log₂t возрастает на R₊, 6 > 4. Значит, log₂6 > log₂4  и log₂5 > 2.

Второй способ (составление разности).

Составим разность .

6. Сравните числа и -1.

Решение.

-1 = ;

Функция y =   убывает на R_+, 3 < 5. Значит, >  и > -1.

7. Сравните числа и 3log₈26.

Решение.

Функция y = log₂t возрастает на R

+, 25 < 26. Значит, log₂25 < log₂26  и .

Решение.

Первый способ.

Умножим обе части неравенства на 3: 

Функция y = log ₅t возрастает на R₊ , 27 > 25. Значит,

Второй способ.

Составим разность
. Отсюда .

9. Сравните числа log₄26 и log₆17.

Решение.

Оценим логарифмы, учитывая, что функции y = log₄t и y = log₆t возрастающие на R₊:

Решение.

Учитывая, что функции   убывающие на R₊, имеем:

. Значит,

Замечание. Предложенный метод сравнения называют методом “вставки” или методом “разделения” (мы нашли число 4, разделяющее данные два числа).

11. Сравните числа log₂3 и  log₃5.

Решение.

Заметим, что оба логарифма больше 1, но меньше 2.

Первый способ. Попробуем применить метод “разделения”. Сравним логарифмы с числом .

Второй способ (умножение на натуральное число).

Замечание 1. Суть метода “умножения на натуральное число” в том, что мы ищем натуральное число k, при умножении на которое сравниваемых чисел a и b получают такие числа ka и kb, что между ними находится хотя бы одно целое число.

Замечание 2. Реализация вышеописанного метода бывает весьма трудоемка, если сравниваемые числа очень близки друг к другу.
В этом случае можно попробовать сравнение методом “вычитания единицы”. Покажем его на следующем примере.

12. Сравните числа log₇8 и log₆7.

Решение.

Первый способ (вычитание единицы).

Вычтем из сравниваемых чисел по 1.

В первом неравенстве мы воспользовались тем, что

если c > a > 1, то при b > 1 справедливо неравенство log_ab > log_cb.

Во втором неравенстве – монотонностью функции y = log_ax.

Замечание. Вычитать из сравниваемых чисел можно любое натуральное число n. При этом часто бывает достаточно взять n = 1.

Второй способ (применение неравенства Коши).

13. Сравните числа log₂₄72 и log₁₂18.

Решение.

14. Сравните числа log₂₀

80 и log₈₀640.

Решение.

Решение.

Пусть log₂5 = x . Заметим, что x > 0.

Получаем неравенство .

Найдем множество решений неравенства , удовлетворяющих условию x > 0.

Возведем обе части неравенства в квадрат (при x > 0 обе части неравенства положительны). Имеем 9x² < 9x + 28.

Множеством решений последнего неравенства является промежуток .

Учитывая, что x > 0, получаем: .

Ответ: неравенство верно.

Практикум по решению задач.

1. Сравните числа:

2. Расположите в порядке возрастания числа:

3. Решите неравенство

4⁴ – 2·2⁴⁺¹ – 3 < 0. Является ли число √2 решением данного неравенства? (Ответ: (–∞; log₂3); число √2 является решением данного неравенства.)

Заключение.

Методов сравнения логарифмов много. Цель уроков по данной теме – научить ориентироваться в многообразии методов, выбирать и применять наиболее рациональный способ решения в каждой конкретной ситуации.

В классах с углубленным изучением математики материал по данной теме может быть изложен в форме лекции. Такая форма учебной деятельности предполагает, что материал лекции должен быть тщательно отобран, проработан, выстроен в определенной логической последовательности. Записи, которые делает учитель на доске, должны быть продуманными, математически точными.

Закрепление лекционного материала, отработку навыков по решению задач целесообразно проводить на уроках-практикумах. Цель практикума – не только закрепить и проверить полученные знания, но и пополнить их. Поэтому задания должны содержать задачи разного уровня, от самых простых задач до задач повышенной сложности. Учитель на таких практикумах выступает в роли консультанта.

Литература.

1. Галицкий М.Л. и др.Углубленное изучение курса алгебры и математического анализа: Метод. рекомендации и дидактические материалы: Пособие для учителя.– М.: Просвещение, 1986.
2. Зив Б.Г., Гольдич В.А. Дидактические материалы по алгебре и началам анализа для 10 класса. – СПб.: “ЧеРо-на-Неве”, 2003.
3. Литвиненко В.Н., Мордкович А. Г. Практикум по элементарной математике. Алгебра. Тригонометрия.: Учебное издание. – М.: Просвещение, 1990.
4. Рязановский А.Р. Алгебра и начала анализа:500 способов и методов решения задач по математике для школьников и поступающих в вузы. – М.: Дрофа, 2001.
5. Садовничий Ю.В. Математика. Конкурсные задачи по алгебре с решениями. Часть 4. Логарифмические уравнения, неравенства, системы. Учебное пособие.-3-е изд., стер.-М.:Издательский отдел УНЦДО, 2003.
6. Шарыгин И.Ф., Голубев В.И.Факультативный курс по математике: Решение задач: Учеб. пособие для 11 кл. сред.шк.– М.: Просвещение, 1991.

urok.1sept.ru

Как сравнивать логарифмы с разным основанием

Как сравнивать логарифмы с разным основанием.

При решении показательных и логарифмических неравенств нередко возникает необходимость сравнить логарифмы с разным основанием.

Рассмотрим, как это сделать.

Пример 1. Сравнить и .

Чтобы сравнить эти логарифмы, нужно найти число, которое стоит на числовой прямой между  и .

Нетрудно увидеть, что ,

То есть , следовательно, 

 

Чаще ситуация выглядит сложнее.

 

Пример 2. Сравнить  и .

Так как , следовательно, . Аналогично,  , следовательно, .

То есть значение обоих логарифмов — дробное число, лежащее в пределах от 1 до 2. Подобрать промежуточное число, которое стоит на числовой прямой между и  уже сложнее.

Поступим так. Предположим, в знаменателе промежуточного числа стоит 2. Умножим оба логарифма на 2, то есть сравним числа

и 

Перенесем 2 в показатель степени:

и 

и 

Теперь нетрудно увидеть, что ,  следовательно, .

Если умножение на 2 не приводит к желаемому результату, нужно попытаться умножить на 3, потом на 4  и т.д.

 

Пример 3. В некоторых случаях прежде чем сравнивать логарифмы, нужно выполнить определенные преобразования.

Сравнить  и 

Так как , мы можем преобразовать логарифм с основанием 2:

Итак, мы сравниваем числа  и .

Прибавим к обоим числам 2:

и 

Преобразуем: 

Теперь нам нужно сравнить числа

и 

Значение обоих логарифмов — дробное число, принадлежащее промежутку .

Предположим, в знаменателе промежуточного числа стоит 2. Умножим оба логарифма на 2, то есть сравним числа

и 

Перенесем 2 в показатель степени:

и 

и 

, следовательно, .

, следовательно, .

Получили, что , следовательно, .

 

Репетитор по математике Инна Владимировна Фельдман.

ege-ok.ru

Сравнение логарифмов

Ни для кого не секрет, что с помощью применения логарифмов мы упрощаем довольно много сложных алгебраических операций и не только. Логарифмы дают возможность заменять более сложные операции умножения на операции сложения, деление на вычитание. Согласитесь, ведь это намного проще. Если уже быть совсем точными, то логарифм заданного числа – это показатель степени, в которую нужно возвести другое, также заданное число, чтобы получить данное. На первый взгляд все запутано и непонятно, но это только на первый, на самом деле, все до нельзя просто. Для того, чтобы закреплять знания о логарифмах (да и не только о них), конечно же, рекомендовано после прочтения теории выполнять самостоятельные практические упражнения, это не только поможет усвоить материал, но и выявить все недочеты.

Но вернемся к логарифмам, а точнее к их сравнению. Разумеется, вам в голову может прийти вопрос: «что такое сравнение логарифмов? и как это делается?».

Зачем мы сравниваем логарифмы? Ответ достаточно прост. При решении неравенств и уравнений, довольно часто возникает вопрос, когда нужно определить принадлежность корня области допустимых значений или же сделать соотношение решений двух или более неравенств на числовой прямой, а решение, при этом, выражается иррациональным числом, которое, в свою очередь, записано с помощью логарифма. Вот тут-то нам и необходимо сравнение этих логарифмов.

Существуют несколько способов сравнения логарифмов. Какой из них использовать зависит, в первую очередь, от того, одинаковые основания у логарифмов или нет. Если первый вариант, то тут выход один – использовать монотонность логарифмических функций.

Если числа равные, но основания разные, то тут можно пойти несколькими путями:

1. Графический способ
2. Сравнение логарифмов через переход к одному основанию
3. Метод оценки
4. введение промежуточного числа
5. Алгебраические методы, которые, в свою очередь делятся еще на несколько.

Например: log[2,x]>log[4,x]

Сравнение логарифмов

Если 0   1   2 , то

log   a x   1 > log   a x   2 — знак неравенства меняется

Если a > 1 и 0   1   2 , то

log   a x   1   a x   2 — знак неравенства не меняется

Если 1 1, то log   a x > log   b x

Если 0 1, то log   a x > log   b x

mateshka.ru

Как сравнивать степени | Логарифмы

Как сравнивать степени с одинаковыми основаниями? С одинаковыми показателями? Можно ли сравнить степени, если и основания, и показатели различны?

Как и сравнение логарифмов, сравнение степеней основано на свойстве показательной функции.

Сравнение степеней с одинаковыми основаниями

• Если основание степени больше единицы (a>1), показательная функция возрастает, большему значению аргумента соответствует большее значение функции, соответственно, знак неравенства между показателями степеней и между степенями одинаковый.

• Если основание степени меньше единицы (0<a<1), функция убывает, большему значению аргумента соответствует меньшее значение функции, знак неравенства между показателями степеней противоположен знаку между степенями.

С помощью схемы сравнение степеней с равными основаниями можно изобразить так:

Примеры.

№1. Сравнить значения выражений:

   

Решение:

Сравниваем показатели степеней: 1,5<1,9.

Основание a=2/7 меньше единицы, функция убывает, знак неравенства между степенями меняется на противоположный:

   

   

Решение:

Сравниваем показатели степеней:

   

Основание a=5,2 больше единицы, функция возрастает, знак неравенства между степенями не меняется:

   

№2. Сравнить показатели m и n, если известно, что для степеней выполняется неравенство:

   

Решение:

Основание a=0,21<1, функция убывает, поэтому знак неравенства между показателя степеней нужно изменить на противоположный: m>n.

   

Решение:

Основание

   

функция возрастает, поэтому знак неравенства между показателями степеней не изменяется: m<n.

Сравнение степеней с одинаковыми показателями.

1) Для возрастающих функций ( x>0):

   

   

Пример.

Для положительных значений аргумента

   

например,

   

Для отрицательных значений аргумента

   

например,

   

 

2) Для убывающих функций:

   

   

Пример.

Для положительных значений аргумента

   

например,

   

Для отрицательных значений аргумента:

   

например,

   

 

Как сравнивать степени, если и основания, и показатели различны?

Можно попробовать, например, сравнить каждую из степеней с единицей. Любая степень с основанием, большим единицы, при положительных значениях аргумента принимает значения, большие единицы:

   

при отрицательных — меньшие 1:

   

Если основание меньше единицы — соответственно,

   

   

Пример.

Сравнить

   

Решение:

   

В алгебре сравнивать степени чаще всего приходится при решении показательных неравенств.

Как решать показательные неравенства, мы рассмотрим позже.

www.logarifmy.ru

Приемы и методы сравнения логарифмов

Неравенства С3, С5. Подготовка к ЕГЭ 2011.

Неравенства С С Подготовка к ЕГЭ 0 (материал для лекции для учителей 8040) Прокофьев АА aaprokof@yanderu Основные способы решения: Задачи С Решение неравенства на промежутках Упрощение неравенства и сведение

Подробнее

Логарифмические уравнения

И В Яковлев Материалы по математике MathUsru Логарифмические уравнения и неравенства Логарифмические уравнения и неравенства это уравнения и неравенства, в которых переменная величина находится под знаком

Подробнее

РАЗДЕЛ 14. ЗАДАЧИ С ПАРАМЕТРАМИ

РАЗДЕЛ ЗАДАЧИ С ПАРАМЕТРАМИ Комментарий Задачи с параметрами традиционно являются сложными заданиями в структуре ЕГЭ, требующими от абитуриента не только владения всеми методами и приемам решения различных

Подробнее

РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ

РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ Оглавление РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ I Рациональные алгебраические уравнения Равносильность уравнений Равносильность уравнений на множестве Равносильность

Подробнее

x 4 ; x log 6 — логарифмические неравенства

Вопрос. Неравенства, система линейных неравенств Рассмотрим выражения, которые содержат знак неравенства и переменную:. >, — +х -это линейные неравенств с одной переменной х.. 0 — квадратное неравенство.

Подробнее

РАЦИОНАЛИЗАЦИЯ НЕРАВЕНСТВ

ВА Шилинец доцент кафедры математики БГПУ РАЦИОНАЛИЗАЦИЯ НЕРАВЕНСТВ Данная статья посвящена методу решения неравенств основанном на замене некоторых функций более простыми Материал статьи может быть использован

Подробнее

Теоретический материал.

0.5 Логарифмические уравнения и неравенства. Используемая литература:. Алгебра и начала анализа 0- под редакцией А.Н.Колмогорова. Самостоятельные и контрольные работы по алгебре 0- под редакцией Е.П.Ершова

Подробнее

Показательные неравенства

Показательные неравенства Решение показательных неравенств основано на строгой монотонности показательной функции Известно, что при основании, большем единицы, показательная функция возрастает, при положительном

Подробнее

Логарифмические неравенства

Логарифмические неравенства 1. 1. Решите неравенство: Решим неравенство:. 2. 2. Решите неравенство: Найдём значения, при которых определены обе части неравенства: Для таких получаем: Тогда исходное неравенство

Подробнее

МАТЕМАТИКА. Квадратные корни

МАТЕМАТИКА Квадратные корни Задание для 8-х классов (006-00 учебный год) 4 Введение Дорогие ребята! Вы получили очередное задание по математике. В этом задании мы знакомим вас с важным математическим понятием

Подробнее

Глава 1 ВВЕДЕНИЕ В АЛГЕБРУ

Глава ВВЕДЕНИЕ В АЛГЕБРУ.. КВАДРАТНЫЙ ТРЕХЧЛЕН… Вавилонская задача о нахождении двух чисел по их сумме и произведению. Одна из древнейших задач алгебры была предложена в Вавилоне, где была распространена

Подробнее

Занятие 1 (2 часа) Ход занятия.

Тема Целая и дробная части числа Занятие 1 ( часа) Цель занятия Дидактическая Познакомить учащихся с целой и дробной частью числа Установить их свойства и соотношения между ними Научить строить простейшие

Подробнее

ОГЛАВЛЕНИЕ. Предисловие… 5

ОГЛАВЛЕНИЕ Предисловие……………………………………… 5 Глава первая Арифметика и алгебра………………………………. 6 1.1. Числа и действия с ними………………………..

Подробнее

Логарифмические уравнения

Тишин В И Логарифмические уравнения год Предисловие к книге «Логарифмические уравнения» Методика изложения решений логарифмических уравнений выдержана в таком же стиле как и решение показательных уравнений

Подробнее

Глава 6 Числовые ряды

Глава 6 Числовые ряды Определение числового ряда и основные теоремы Определение : Последовательностью действительных чисел называется функция f, определённая на множестве всех натуральных чисел Число f

Подробнее

10 класс, Математика (профиль) уч.год Тема модуля 1 «Корни, степени, логарифмы»

0 класс, Математика (профиль) 0-08 учгод Тема модуля «Корни, степени, логарифмы» Знать Понятия действительного числа, множества чисел, свойства действительных чисел, делимость целых чисел****, свойства

Подробнее

Делимость целых чисел в задачах

Югорский физико-математический лицей В.П. Чуваков Делимость целых чисел в задачах Сборник задач Ханты-Мансийск 05 Делимость целых чисел в задачах: Сборник задач, — Ханты-Мансийск, Югорский физико-математический

Подробнее

ЕГЭ Математика Простейшие уравнения

ГОТОВИМСЯ К ЕГЭ С. А. Шестаков ЕГЭ 208. Математика Простейшие уравнения Задача 5 (профильный уровень) Задачи 4 и 7 (базовый уровень) Рабочая тетрадь Под редакцией И. В. Ященко Издание соответствует Федеральному

Подробнее

ПРЕДЕЛЫ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ

Министерство образования Московской области Государственное бюджетное образовательное учреждение высшего профессионального образования Московской области «Международный университет природы, общества и

Подробнее

ФДП МАТЕМАТИКА ЕГЭ 2012

Корянов АГ, Прокофьев АА Системы неравенств с одной переменной ФДП МАТЕМАТИКА ЕГЭ 0 Системы неравенств с одной переменной типовые задания С) Прокофьев АА, Корянов АГ Прокофьев АА доктор педагогических

Подробнее

ÌÀÒÅÌÀÒÈÊÀ: ÇÀÄÀ È Ñ ÌÎÄÓËÅÌ

 À Äàëèíãåð ÌÀÒÅÌÀÒÈÊÀ: ÇÀÄÀ È Ñ ÌÎÄÓËÅÌ УЧЕБНОЕ ПОСОБИЕ ДЛЯ СПО -е издание, исправленное и дополненное Ðåêîìåíäîâàíî Ó åáíî-ìåòîäè åñêèì îòäåëîì ñðåäíåãî ïðîôåññèîíàëüíîãî îáðàçîâàíèÿ â êà åñòâå ó åáíîãî

Подробнее

Лекция 1 (13 января 2017)

КОНСПЕКТ ЛЕКТОРА математический анализ, курс, 2 семестр, 207, А.М. Красносельский Числовые ряды Лекция (3 января 207) Рассмотрим последовательность R и напишем «бесконечную сумму»: a k a + a 2 +… + a

Подробнее

МЕТОДИЧЕСКОЕ ПОСОБИЕ

ВОЕННО-ТЕХНИЧЕСКИЙ КАДЕТСКИЙ КОРПУС Дисциплина: «Математика, основы информатики и вычислительной техники» МЕТОДИЧЕСКОЕ ПОСОБИЕ для кадет Тема: Уравнения и неравенства с параметрами. Преподаватель: Молоткова

Подробнее

МОНОТОННОСТЬ ПРИ РЕШЕНИИ ЗАДАЧ

Министерство образования и науки Российской Федерации ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САРАТОВСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТИМЕНИ

Подробнее

Алгебраические уравнения

Алгебраические уравнения где Определение. Алгебраическим называется уравнение вида 0, P () 0,,, некоторые действительные числа. 0 0 При этом переменная величина называется неизвестным, а числа 0,,, коэффициентами

Подробнее

1 Степень с целым показателем

Глава 9 Степени Степень с целым показателем. 0 = 0; 0 = ; 0 = 0. > 0 > 0 ; > >.. >. Если четно, то ( ) < ( ). Например, ( ) 0 = 0 < 0 = = ( ) 0. Если нечетно, то ( ) > ( ). Например, ( ) = > = = ( ), так

Подробнее

Учебный центр «Резольвента»

ООО «Резольвента», www.resolventa.ru, [email protected], (9) 09-8-0 Учебный центр «Резольвента» Кандидат физико-математических наук, доцент С. С. САМАРОВА РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ Учебно-методическое

Подробнее

Домашняя работа по алгебре за 10 класс

Домашняя работа по алгебре за 0 класс к учебнику «Алгебра и начала анализа 0- класс» Алимов ША и др, М: «Просвещение», 00 г учебно-практическое пособие Содержание Глава I Действительные числа Глава II

Подробнее

6 Предисловие автора. М. И. Шабунин

Книга предназначена для учащихся старших классов средних школ, гимназий, лицеев и особенно для тех, кто, обладая знаниями основ школьного курса математики, стремится систематизировать эти знания и успешно

Подробнее

1. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ

КЛАССИФИКАЦИЯ УРАВНЕНИЙ 1 Алгебраические уравнения: рациональные (содержат только целые степени неизвестной) и иррациональные (содержат дробные степени неизвестной) ) Показательные и логарифмические (неизвестная

Подробнее

Иррациональные неравенства

Иррациональные неравенства Неравенства, в которых переменная содержится под знаком корня, называются иррациональными Основным методом решения иррациональных неравенств является метод сведения исходного

Подробнее

Решение задач заочного тура 2011

Решение задач заочного тура 0 I Математический блок Задача Найдите число натуральных корней уравнения Ответ: 00 0 решений Решение задачи Представим число в виде Тогда правая часть данного уравнения равна

Подробнее

Пояснительная записка

Пояснительная записка Рабочая программа по алгебре и началам анализа для 11-Б класса составлена в соответствии с правовыми и нормативными документами: Федеральный Закон от 29.12. 2012 г. 273-ФЗ «Об образовании

Подробнее

1. Числовые последовательности

ТЕОРИЯ ПРЕДЕЛОВ И НЕПРЕРЫВНОСТЬ 1. Числовые последовательности Определение 1. Отображение a: N R множества натуральных, принимающее свои значения в множестве действительных чисел, называется числовой последовательностью.

Подробнее

МЕТОДИЧЕСКОЕ ПОСОБИЕ по математике

Орлова О.А. МЕТОДИЧЕСКОЕ ПОСОБИЕ по математике «Решение показательных и логарифмических уравнений» 0 г. Оглавление Введение… Логарифмические уравнения… Способы решения:…9 Показательные уравнения…

Подробнее

Уважаемые коллеги! Желаем успеха!

06 год Уважаемые коллеги! Вам предлагаются два блока заданий: 5. «Математический» (задачи для решения). 6 8. «Методический» (задания, моделирующие работу учителя). Оцениваются только те работы, в которых

Подробнее

Тема 39. «Производные функций»

Тема 39. «Производные функций» Функция Производной функции в точке х 0 называется предел отношения приращения функции к приращению переменной, то есть = lim = lim + ( ) Таблица производных: Производная

Подробнее

docplayer.ru

Логарифмы | Все о логарифмах

Показательные уравнения: вынесение вынесение общего множителя за скобки — следующий шаг в рассмотрении видов показательных уравнений и способов их решения.

Признаки показательного уравнения, решаемого вынесением общего множителя за скобки:

1) все степени имеют одинаковые основания;

2) все показатели степеней имеют одинаковые коэффициенты при переменных.

Количество степеней может быть любым.

Выносить за скобки можно степень с любым показателем, но удобнее всего в качестве общего множителя вынести степень с наименьшим показателем если основание a>1, с наибольшим — при a<1.

(далее…)

Продолжаем рассматривать показательные уравнения. Примеры решения показательных уравнений, в которых задействованы степени с одинаковыми показателями — наш следующий шаг на этом пути.

В этих примерах акцент сделан на следующих свойствах степеней:

   

   

(далее…)

Рассмотрим решение простейших показательных уравнений, приводимых к уравнениям вида

   

с помощью свойств степеней:

   

   

   

   

   

   

   

   

ОДЗ (Область допустимых значений уравнения) — x∈R.

(далее…)

Показательные уравнения — это уравнения, в которых переменная входит в показатель степени, а основание степени переменной не содержит.

Простейшие показательные уравнения — это уравнения вида

   

где a>0, a≠1.

Так как показательная функция

   

строго монотонна (возрастает при a>1, убывает при 0<a<1), то каждое свое значение она принимает только при одном значении аргумента, следовательно, простейшее показательное уравнение имеет единственный корень (или не имеет корней).

(далее…)

Как сравнивать степени с одинаковыми основаниями? С одинаковыми показателями? Можно ли сравнить степени, если и основания, и показатели различны?

Как и сравнение логарифмов, сравнение степеней основано на свойстве показательной функции.

Сравнение степеней с одинаковыми основаниями

• Если основание степени больше единицы (a>1), показательная функция возрастает, большему значению аргумента соответствует большее значение функции, соответственно, знак неравенства между показателями степеней и между степенями одинаковый.

• Если основание степени меньше единицы (0<a<1), функция убывает, большему значению аргумента соответствует меньшее значение функции, знак неравенства между показателями степеней противоположен знаку между степенями.

(далее…)

Показательная функция и логарифмическая функция тесно связаны между собой: они являются взаимно-обратными.

Определение

Показательная функция — это функция вида

   

гле a>0, a≠1.

График показательной функции:

(далее…)

Однородные логарифмические уравнения первого порядка —

   

— не нуждаются в особом подходе для их решения.

С помощью свойств логарифмов такое уравнение можно привести к простейшему логарифмическому.

В общем виде решение таких уравнений можно представить, например, так: (далее…)

www.logarifmy.ru

Практическая работа по математике на тему «ВЫЧИСЛЕНИЕ И СРАВНЕНИЕ ЛОГАРИФМОВ»

Математика 1 курс 234 часа

Шаповалова Н.В.

ПРАКТИЧЕСКАЯ РАБОТА

Тема работы: ВЫЧИСЛЕНИЕ И СРАВНЕНИЕ ЛОГАРИФМОВ.

Тип занятия: практическое занятие.

Цели работы:

• Образовательная – закрепить понятие логарифма, научить применять свойства логарифмов при решении логарифмических выражений;

• Развивающая — содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать; формировать и развивать общеучебные умения и навыки: обобщение, поиск способов решения;

• Воспитательная — вырабатывать самостоятельность при работе на уроке; способствовать формированию максимальной работоспособности.

Организационный момент: дежурные, отсутствующие.

Ход работы:

Основная часть урока

Повторение лекционного материала

Задачи этапа: повторить пройденный материал, необходимый для выполнения практической работы.

Рассмотрим действие обратное действию возведения в степень – нахождение логарифма

Вопрос: в какую степень надо возвести число 3, чтобы получить 243?

Ответ на этот вопрос дает действие нахождения логарифма

Говорится так: «логарифм по основанию 3 от числа 243». Тройка (маленькая и пишется чуть ниже) называется «основанием логарифма», а число 243 так и называют «числом». 

Найти логарифм – это значит найти показатель степени, в которую надо возвести основание логарифма, чтобы получить стоящее под логарифмом число.

Определения

Логарифмом числа b по основанию a называется такое число, обозначаемое , что . Т.е. .

a – основание логорифма,

Десятичный логарифм: .

Натуральный логарифм: , где e=2,71828…

Функция, заданная формулой , где , называется логарифмической

Основные логарифмические тождества.

Примеры

Закрепление нового материала:

Задачи этапа: научить применять практические приемы решения показательных уравнений

Практические задания:

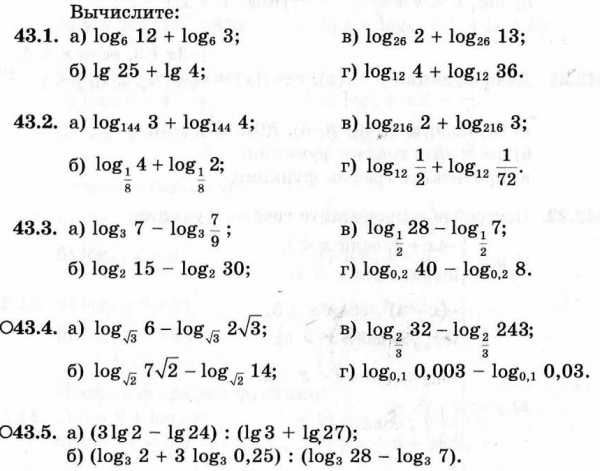
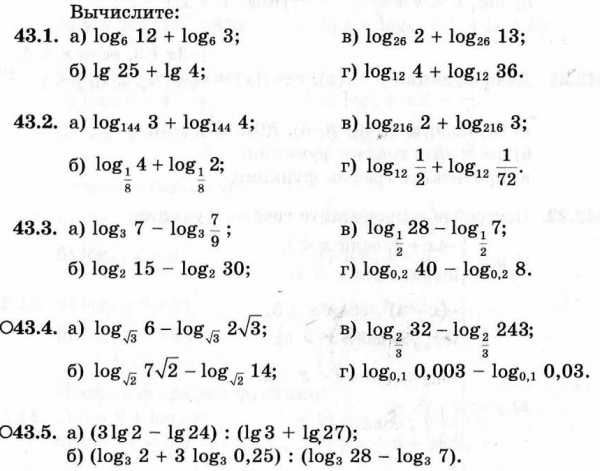
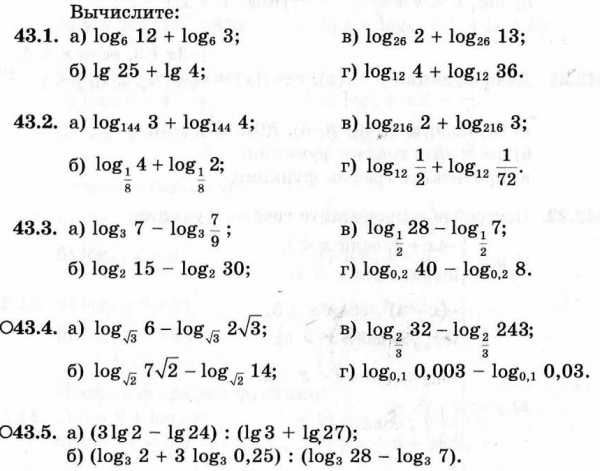
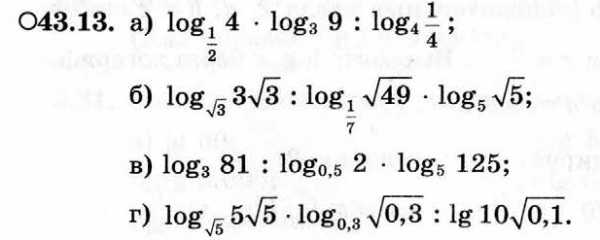
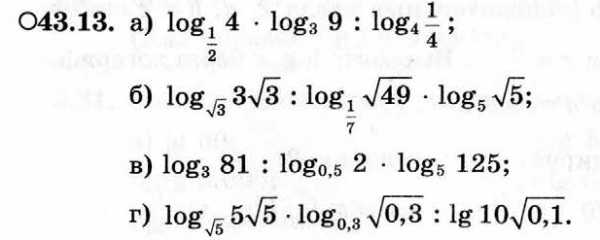
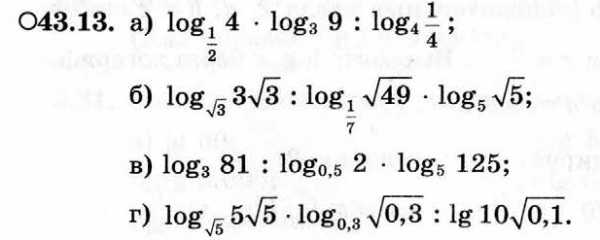
Задание на дом: невыполненные задания завершить и сдать на следующее занятие.

Вопросы:

1. Определение логарифма.

2. Виды логарифмов.

3. Что такое основание логарифма, что оно показывает?

4. Как задается логарифмическая функция?

5. Перечислите основные логарифмические свойства.

infourok.ru

No related posts.