Степень с натуральным показателем это: Степень с натуральным показателем

Что такое степень с натуральным показателем. Алгебра, 7 класс: уроки, тесты, задания.

1.	Произведение в виде степени (положительные числа) Сложность: лёгкое	3,5
2.	Основание и показатель степени (числа) Сложность: лёгкое	3
3.	Степень бинома Сложность: лёгкое	1,5
4.	Основание и показатель степени (бином) Сложность: лёгкое	2
5.	Произведение одинаковых множителей (одночлен) Сложность: лёгкое	1
6.	Произведение одинаковых множителей (бином) Сложность: лёгкое	1
7.	Степень числа (показатель степени — n) Сложность: лёгкое	2
8.	Степень числа (основание) Сложность: лёгкое	2
9.	Значение степени (обыкновенная дробь) Сложность: лёгкое	2
10.	Площадь квадрата Сложность: лёгкое	2
11.	Квадрат числа (минус перед числом) Сложность: лёгкое	2
12.	Числовые неравенства, сравнение Сложность: лёгкое	1
13.	Возведение в степень десятичных дробей Сложность: лёгкое	1
14.	Возведение в степень целых чисел Сложность: лёгкое	1
15.	Возведение в степень дробей (смешанных чисел) Сложность: среднее	2
16.	Произведение степеней и простых чисел Сложность: среднее	3
17.	Произведение (целые числа) Сложность: среднее	3
18.	Частное (чётная степень) Сложность: среднее	3
19.	Дробь Сложность: среднее	3
20.	Разность произведений Сложность: среднее	4
21.	Сумма произведений Сложность: среднее	5
22.	Уравнение Сложность: среднее	5
23.	Убывание (возрастание) степеней Сложность: среднее	4

Степень числа. Степень с натуральным показателем

Правило чтения и записи степеней с натуральным показателем

Краткую запись произведения одинаковых сомножителей очень удобно использовать, — длинная строка описания математических действий сокращается до записи нескольких шагов:

17^5=17 \cdot 17 \cdot 17 \cdot 17 \cdot 17=1\,419\,857

17 — основание степени,

5 — показатель степени,

1419857 — значение степени.

Степень с нулевым показателем равна 1, при условии, что a \neq 0:

a^0=1.

Например: 2^0=1

Когда нужно записать большое число обычно используют степень числа 10.

Например, один из самых древних динозавров на Земле жил около 280 млн. лет назад. Его возраст записывается следующим образом: 2,8 \cdot 10^8.

Каждое число большее 10 можно записать в виде a \cdot 10^n, при условии, что 1 < a < 10 и n является положительным целым числом. Такую запись называют стандартным видом числа.

Примеры таких чисел: 6978=6,978 \cdot 10^3, 569000=5,69 \cdot 10^5.

Можно говорить как и «a в n-ой степени», так и «n-ая степень числа a» и «a в степени n».

4^5 — «четыре в степени 5 » или «4 в пятой степени» или также можно сказать «пятая степень числа 4»

В данном примере 4 — основание степени, 5 — показатель степени.

Приведем теперь пример с дробями и отрицательными числами. Для избежания путаницы принято записывать основания, отличные от натуральных чисел, в скобках:

(7,38)^2, \left(\frac 12 \right)^7, (-1)^4 и др.

Заметьте также разницу:

(-5)^6 — означает степень отрицательного числа −5 с натуральным показателем 6.

-5^6 — соответствует числу противоположному 5^6.

Свойства степеней с натуральным показателем

Основное свойство степени

a^n \cdot a^k = a^{n+k}

Основание остается прежним, а складываются показатели степеней.

Например: 2^3 \cdot 2^2 = 2^{3+2}=2^5

Свойство частного степеней с одинаковыми основаниями

a^n : a^k=a^{n-k}, если n > k.

Показатели степени вычитаются, а основание остается прежним.

Данное ограничение n > k вводится для того, чтобы не выходить за рамки натуральных показателей степени. Действительно, при n > k показатель степени a^{n-k} будет являться натуральным числом, иначе он будет либо отрицательным числом (k < n), либо нулем (k-n).

Например: 2^3 : 2^2 = 2^{3-2}=2^1

Свойство возведения степени в степень

(a^n)^k=a^{nk}

Основание остается прежним, перемножаются лишь показатели степеней.

Например: (2^3)^6 = 2^{3 \cdot 6}=2^{18}

Свойство возведения в степень произведения

В степень n возводится каждый множитель.

a^n \cdot b^n = (ab)^n

Например: 2^3 \cdot 3^3 = (2 \cdot 3)^3=6^3

Свойство возведения в степень дроби

\frac{a^n}{b^n}=\left(\frac{a}{b} \right) ^n, b \neq 0

В степень возводится и числитель и знаменатель дроби. \left(\frac{2}{5} \right)^3=\frac{2^3}{5^3}=\frac{8}{125}

Конспект «Степени. Свойства степеней» — УчительPRO

Степени. Свойства степеней.

Ключевые слова конспекта: степень с натуральным показателем, основание степени, показатель степени, возведение в степень, дисперсия, умножение и деление степеней, свойства степеней.

Произведение 7 • 7 • 7 • 7 • 7 записывают короче: 7⁵. Выражение вида 7⁵ называют пятой степенью числа 7 (читают: «семь в пятой степени»). В записи 7⁵ число 7, которое означает повторяющийся множитель, называют основанием степени, а число 5, показывающее, сколько раз этот множитель повторяется, называют показателем степени.

Умножим 7⁵ на 7³:
7⁵ • 7³ = (7 • 7 • 7 • 7 • 7) • (7 • 7 • 7) = 7 • 7 • 7 • 7 • 7 • 7 • 7 • 7 = 7⁸.
Показатель степени увеличился на 3. Естественно считать, что 7 = 7¹. Вообще считают, что первой степенью числа является само число. Например, 18¹ = 18, 104¹ = 104.

Степень с натуральным показателем

✅ Определение. Степенью числа а с натуральным показателем n, большим 1, называют выражение аⁿ, равное произведению n множителей, каждый из которых равен а.
Степенью числа а с показателем 1 называют выражение а¹, равное а.

По определению

Запись аⁿ читается так: «а в степени n» или «n-я (энная) степень числа а». Для второй и третьей степеней числа используют специальные названия: вторую степень числа называют квадратом, а третью степень — кубом.

Возведение в степень

Нахождение n-й степени числа а называют возведением в n-ю степень.

Пример 1. Возведём число -3 в четвёртую и пятую степени:
(-3)⁴ = (-3) • (-3) • (-3) • (-3) = 81;
(-3)⁵ = (-3) • (-3) • (-3) • (-3) • (-3) = -243.

Из свойств умножения следует, что:

при возведении нуля в любую степень получается нуль;
при возведении положительного числа в любую степень получается положительное число;
при возведении отрицательного числа в степень с чётным показателем получается положительное число, а при возведении отрицательного числа в степень с нечётным показателем — отрицательное число.

Пример 2. Возведём число 6,1 в седьмую степень, воспользовавшись калькулятором. Для этого надо выполнить умножение:
6,1 • 6,1 • 6,1 • 6,1 • 6,1 • 6,1 • 6,1.
Калькулятор позволяет выполнять возведение в степень проще, не повторяя основание степени и знак умножения. Для того чтобы возвести число 6,1 в седьмую степень, достаточно ввести число 6,1, нажать клавишу УМНОЖИТЬ и шесть раз нажать клавишу РАВНО . Получим, что 6,1⁷ = 314274,28.

При вычислении значений числовых выражений, не содержащих скобки, принят следующий порядок действий: сначала выполняют возведение в степень, затем умножение и деление, далее сложение и вычитание.

Пример 3. Найдём значение выражения -6² + 64 : (-2)⁵. Последовательно находим:
1) 6² = 36;
2) (–2)⁵ = –32;
3) 64 : (–32) = –2;
4) –36 + (–2) = –38.

Пример 4. Найдём множество значений выражения 5 • (–1)^{n + 1} + 2, где n ∈ N.
Если n — нечётное число, то (-1)^{n + 1} = 1; тогда 5 • (-1)^{n + 1} + 2 = 5 • 1 + 2 = 7.
Если n — чётное число, то (-1)^{n + 1} = -1; тогда 5 • (-1)^{n + 1} + 2 = 5 • (-1) + 2 = -5 + 2 = -3.
Множество значений данного выражения: {-3; 7}.

В рассмотренном примере было указано, что n ∈ N. Условимся в дальнейшем такое указание опускать и считать, что если показатель степени содержит переменную, то значениями этой переменной являются натуральные числа.

Дисперсия

Степень с натуральным показателем широко используется в естествознании для вычисления различных характеристик. Например, в статистике, для того чтобы узнать, как числа некоторой выборки расположены по отношению к среднему арифметическому этой выборки, используют отклонения, их квадраты и среднее арифметическое квадратов отклонений — дисперсию.

Пример 5. Дана выборка: 4, 6, 7, 8, 10. Среднее арифметическое этой выборки равно 7. Тогда отклонения вариант данной выборки от среднего арифметического равны: 4 – 7 = –3, 6 – 7 = –1, 7 – 7 = 0,8 – 7 = 1, 10 – 7 = 3, т. е. мы получили ещё один набор чисел — отклонения каждой варианты выборки от среднего арифметического. По новой выборке (–3; –1; 0; 1; 3) можно судить о том, насколько близки к среднему арифметическому числа исходного набора. Но поскольку сумма отклонений равна нулю, то и среднее арифметическое этой новой выборки также равно нулю. Поэтому для дальнейших исследований исходного набора находят квадраты отклонений и их среднее арифметическое

Полученное число и есть дисперсия исходной выборки.

Умножение степеней

Представим произведение степеней а⁵ и а² в виде степени:
а⁵ • а² = (а • а • а • а • а) • (а • а) = а • а • а • а • а • а • а = а⁷.
Мы получили степень с тем, же основанием и показателем, равным сумме показателей множителей. Подмеченное свойство выполняется для произведения любых двух степеней с одинаковыми основаниями.

Если а — произвольное число, m и n — любые натуральные числа, то а^m • аⁿ = а^{m+ n}

Докажем это. Из определения степени и свойств умножения следует, что

Доказанное свойство называется основным свойством степени. Оно распространяется на произведение трёх и более степеней. Это нетрудно показать с помощью таких же рассуждений.

Из основного свойства степени следует правило:

чтобы перемножить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели степеней сложить.

Деление степеней

Представим теперь в виде степени частное степеней а⁸ и а³, где а ≠ 0. Так как а³ • а⁵ = а⁸, то по определению частного а⁸ : а³ = а⁵.

Мы получили степень с тем же основанием и показателем, равным разности показателей делимого и делителя. Такое свойство выполняется для частного любых степеней с одинаковыми основаниями, не равными нулю, у которых показатель делимого больше показателя делителя.

Если а — произвольное число, не равное нулю, m и n — любые натуральные числа, причём m > n, то а^m : аⁿ = а^{m — n}, где а ≠ 0, m ≥ n

Докажем это. Умножим а^{m —}ⁿ на аⁿ, используя основное свойство степени:
a^{m – n} • aⁿ = a^{(m – n) + n} = a^{m – n + n} = a^m

Из доказанного свойства следует правило:

чтобы выполнить деление степеней с одинаковыми основаниями, надо основание оставить тем же, а из показателя делимого вычесть показатель делителя.

Степень с нулевым показателем

Мы рассматривали степени с натуральными показателями. Введём теперь понятие степени с нулевым показателем.

✅ Определение. Степенью числа а, где а ≠ 0, с нулевым показателем называется выражение а⁰, равное 1.

Например, 5⁰ = 1; (–6,3)⁰ = 1. Выражение 0⁰ не имеет смысла.

Это конспект по математике на тему «Степени. Свойства степеней». Выберите дальнейшие действия:

Степень с натуральным показателем и её свойства. Алгебра, 7 класс: уроки, тесты, задания.

Вход Вход Регистрация Начало Поиск по сайту ТОПы Учебные заведения Предметы Проверочные работы Обновления Новости Переменка Отправить отзыв

Предметы

Алгебра

7 класс

Что такое степень с натуральным показателем

Таблица основных степеней

Свойства степени с натуральным показателем

Умножение и деление степеней с одинаковым показателем

Степень с нулевым показателем

Отправить отзыв Нашёл ошибку? Сообщи нам! Copyright © 2020 ООО ЯКласс Контакты Пользовательское соглашение
Урок 2. степень числа — Алгебра — 7 класс
Алгебра
7 класс
Урок № 2
Степень числа
Перечень вопросов, рассматриваемых в теме:
Понятие степени числа.
Свойства степеней.
Тезаурус
Степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.
Свойства степеней:
Произведение степеней с одним и тем же показателем равно степени с тем же показателем и основанием, равным произведению оснований.
Произведение степеней с одним и тем же основанием – это степень с тем же основанием и показателем, равным сумме показателей этих степеней.
Степень степени числа равна степени того же числа с показателем, равным произведению показателей этих степеней.
Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
1. Макарычев Ю. Н. Алгебра: 7 класс. // Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. – М.: Просвещение, 2019. – 256 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.
Произведение шести множителей, каждый из которых равен 8, называют шестой степенью числа 8 и обозначают 8⁶, т.е.
8 ∙ 8 ∙ 8 ∙ 8 ∙ 8 ∙ 8 = 8⁶.
При этом число 8 называют основанием степени, а число 6 – показателем степени.
А теперь давайте сформулируем общее определение степени числа, опираясь на предыдущий пример:
степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.
Запись aⁿ читается как: а в степени n, или n-ая степень числа a.
А вот следующие записи можно произносить по-разному:
a²– её можно произносить «а в квадрате» или «а во второй степени»;
a³ – её можно произносить «а в кубе» или «а в третьей степени».
Стоит отметить, что особые случаи возникают, если показатель степени равен нулю или единице:
степенью числа а с показателем n = 1 является само это число:
a¹= a;
любое число в нулевой степени равно единице:
a⁰= 1;
ноль в любой натуральной степени равен нулю:
0ⁿ= 0;
единица в любой степени равна 1:
1ⁿ= 1.
Выражение 0⁰(ноль в нулевой степени) считают неопределенным.
Примеры. Возведём в степени:
(−91)⁰= 1
0¹⁴⁴= 0
1²³⁶= 1.
При решении задач, нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.
Рассмотрим несколько примеров.
Возведём в степень
2⁵= 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 32
2,5³= 2,5 ∙ 2,5 ∙ 2,5 = 15,625
Основание степени может быть любым числом – положительным, отрицательным или нулём.
При возведении в степень положительного числа получается положительное число.
При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа, в результате может получиться как положительное число, так и отрицательное число. Это зависит от того, чётным или нечётным числом был показатель степени.
Например, (-2)⁵. Ответ будет отрицательным, так как показатель степени, 5- нечётное число. (-2)⁵= (-2) ∙ (-2) ∙ (-2) ∙ (-2) ∙ (-2) = -32.
(-5)⁴. А вот в этом примере ответ будет положительным, так как показатель степени, 4 – чётное число.
(-5)⁴= (-5) ∙ (-5) ∙ (-5) ∙ (-5) = 625.
Рассмотрим такой пример: 4² ∙ 5²= 4 ∙ 4 ∙ 5 ∙ 5 = (4 ∙ 5) ∙ (4 ∙ 5) = (4 ∙ 5)²= 20²= 400.
Данный пример подтверждает справедливость следующего свойства степеней:
Произведение степеней с одним и тем же показателем равно степени с тем же показателем и основанием, равным произведению оснований:
aⁿ∙ bⁿ = (a ∙ b)ⁿ
Приведём еще такой пример: 5² ∙ 5⁵= (5 ∙ 5) ∙ (5 ∙ 5 ∙ 5 ∙ 5 ∙ 5) = 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 = 5⁷.
Этот пример подтверждает справедливость следующего свойства степеней:
Произведение степеней с одним и тем же основанием это степень с тем же основанием и показателем, равным сумме показателей этих степеней, т.е.
aⁿ ∙ a^m = a^n+m
Наконец, рассмотрим равенство:
(7²)³= (7 ∙ 7)³= (7 ∙ 7) ∙ (7 ∙ 7) ∙ (7 ∙ 7) = 7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 = 7⁶.
Это равенство подтверждает справедливость следующего свойства степеней:
Степень степени числа равна степени того же числа с показателем, равным произведению показателей этих степеней, т.е.
(aⁿ)^m= a^n∙m
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
Число
Основание
Показатель степени
1.
25⁵
2.
11¹³
3.
135⁶
Для заполнения пропусков вспомним, что такое основание и показатель степени.
Число
Основание
Показатель степени
1.
25⁵
25
5
2.
11¹³
11
13
3.
135⁶
135
6
№2. Тип задания: Чему равно произведение 5⁴∙ 5¹¹∙ 4²∙ 4¹³?
Варианты ответов:
(4 ∙ 5)¹⁵
4¹³∙ 5¹⁴
(4 ∙ 5)³⁰
4¹⁵∙ 5³⁰
Для решения задания, воспользуемся свойствами степеней: aⁿ∙a^m= a^n+m и aⁿ∙bⁿ= (a ∙ b)ⁿ
5⁴∙ 5¹¹∙ 4²∙ 4¹³= 5¹⁵∙ 4¹⁵= (4 ∙ 5)¹⁵.
Верный ответ: (4 ∙ 5)¹⁵.
Свойства степени с натуральным показателем. Алгебра, 7 класс: уроки, тесты, задания.

1. Умножение степеней
Сложность: лёгкое
1

2. Степень в степени
Сложность: лёгкое
1

3. Возведение степени в степень (буквы)
Сложность: лёгкое
2

4. Степень в степени (основание)
Сложность: лёгкое
2

5. Степень в степени (показатель степени)
Сложность: лёгкое
2

6. Произведение трёх степеней
Сложность: лёгкое
2

7. Произведение степеней (основание — бином)
Сложность: лёгкое
1

8. Частное трёх степеней
Сложность: лёгкое
2

9. Произведение степеней с одинаковыми основаниями (буквы)
Сложность: лёгкое
3

10. Произведение двух степеней (числа)
Сложность: лёгкое
2

11. Частное двух степеней (отрицательное основание)
Сложность: лёгкое
2

12. Возведение степени в степень (числа)
Сложность: лёгкое
2

13. Частное двух степеней (дробь)
Сложность: лёгкое
3

14. Частное двух степеней (отрицательные смешанные числа)
Сложность: лёгкое
1

15. Произведение степеней с одним основанием (числа)
Сложность: среднее
3

16. Произведение отрицательных и противоположных степеней
Сложность: среднее
5

17. Уравнение (частное степеней, целые числа)
Сложность: среднее
3

18. Дробь (буквы)
Сложность: среднее
2

19. Произведение степени и степени в степени
Сложность: среднее
2

20. Деление и умножение степеней
Сложность: среднее
3

21. Произведение двух дробей
Сложность: среднее
2

22. Произведение степеней в степени
Сложность: среднее
3

23. Частное степени в степени и степени
Сложность: среднее
2

24. Умножение и деление степеней
Сложность: среднее
1

25. Вычисление выражения со степенями
Сложность: среднее
1

Презентация «Степень с натуральным показателем»

Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Степень с натуральным показателем Разработала: учитель математики Хантулина Татьяна Павловна МОУ «Большовская оош имени М.Д. Чубарых» Красненского района Белгородской области
2 слайд Описание слайда:
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
3 слайд Описание слайда:
«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь» М.В.Ломоносов
4 слайд Описание слайда:
Цели урока: Систематизировать и обобщить знания о степени с натуральным показателем и её свойствах. Закрепить и усовершенствовать навыки преобразования выражений, содержащих степени с натуральным показателем. Углубить полученные знания и умения. Развивать логическое мышление, математическую речь.
5 слайд Описание слайда:
Я слышу – я забываю, я вижу – я запоминаю, я делаю – я понимаю. Китайская мудрость
6 слайд Описание слайда:
Повторим!
7 слайд Описание слайда:
Определение степени с натуральным показателем Степенью числа a с натуральным показателем n называется произведение n множителей, каждый из которых равен a.
8 слайд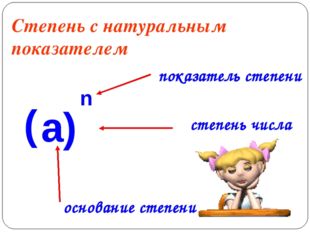 Описание слайда:
Степень с натуральным показателем основание степени показатель степени ( а ) n степень числа
9 слайд Описание слайда:
Определение степени с нулевым показателем Степень числа a, не равного нулю, с нулевым показателем равна единице
10 слайд Описание слайда:
Вычислите = — 12,5 = 10 = 21 = 5 = 41 = 6
11 слайд Описание слайда:
ТЕСТ Степень положительного числа есть число … Степень отрицательного числа с нечётным показателем есть число … Степень отрицательного числа с чётным показателем есть число … — + +
12 слайд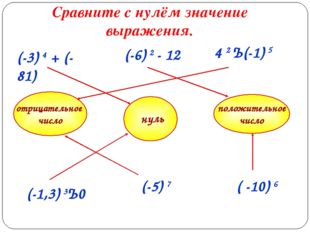 Описание слайда:
Сравните с нулём значение выражения. отрицательное число положительное число нуль (-6) 2 — 12 (-3) 4 + (-81) 4 2 · (-1) 5 (-1,3) 3· 0 (-5) 7 ( -10) 6
13 слайд Описание слайда:
Свойства степени с натуральным показателем
14 слайд Описание слайда:
Свойства степени с натуральным показателем n > k
15 слайд Описание слайда:
Свойства степени с натуральным показателем
16 слайд Описание слайда:
Свойства степени с натуральным показателем
17 слайд Описание слайда:
Умножение степеней с одинаковыми основаниями При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают
18 слайд Описание слайда:
Деление степеней с одинаковыми основаниями При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя делимого вычитают показатель делителя
19 слайд Описание слайда:
Возведение в степень произведения При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают
20 слайд Описание слайда:
Возведение в степень степени При возведении степени в степень основание оставляют прежним, а показатели перемножают
21 слайд Описание слайда:
Представьте в виде степени выражения
22 слайд Описание слайда:
Ответы
23 слайд Описание слайда:
Найдите ошибки 54 7 1 210 210 8х3 а6 220
24 слайд Описание слайда:
Подумайте, чем можно заменить ?
25 слайд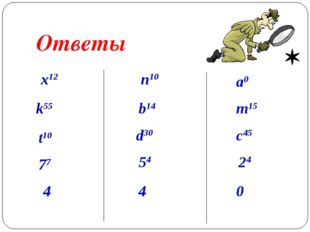 Описание слайда:
Ответы x12 k55 t10 77 4 n10 b14 d30 54 4 a0 m15 c45 24 0

Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-269595
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
экспонентов
Показатель числа означает , сколько раз использовать при умножении.
В 8 ² «2» означает использование 8 дважды при умножении,
, поэтому 8 ² = 8 × 8 = 64
Словами: 8 ² можно было бы назвать «8 в степени 2» или «8 во второй степени», или просто «8 в квадрате»
Экспоненты также называются степенями или индексами.
Еще несколько примеров:
Пример: 5 ³ = 5 × 5 × 5 = 125
Прописью: 5 ³ можно было бы назвать «5 в третьей степени», «5 в степени 3» или просто «5 кубов»
Пример: 2 ⁴ = 2 × 2 × 2 × 2 = 16
Прописью: 2 ⁴ можно было бы назвать «2 в четвертой степени» или «2 в степени 4» или просто «2–4»
Показатели упрощают запись и использование множества умножений
Пример: 9 ⁶ легче писать и читать, чем 9 × 9 × 9 × 9 × 9 × 9
Вы можете умножить любое число само на себя столько раз , сколько хотите, используя экспоненты.4 = 2 × 2 × 2 × 2 = 16
Отрицательные экспоненты
Отрицательно? Что может быть противоположностью умножения?
Деление!
Отрицательная экспонента означает, сколько раз разделите на число.
Пример: 8 ^-1 = 1 ÷ 8 = 0,125
У вас может быть много делений:
Пример: 5 ^-3 = 1 ÷ 5 ÷ 5 ÷ 5 = 0,008
Но это можно сделать и проще:
5 ^-3 также можно рассчитать как:
1 ÷ (5 × 5 × 5) = 1/5 ³ = 1/125 = 0.008
Отрицательно? Переверните позитив!
Последний пример показал более простой способ работы с отрицательными показателями:
Вычислить положительный показатель степени (a ⁿ)
Затем возьмите Взаимное (т.е. 1 / a ⁿ)
Другие примеры:
Отрицательная экспонента Взаимное значение положительной экспоненты Ответ
4 ^-2 = 1/4 ² = 1/16 = 0.0625
10 ^-3 = 1/10 ³ = 1/1000 = 0,001
(-2) ^-3 = 1 / (-2) ³ = 1 / (- 8) = -0,125
Что делать, если экспонента равна 1 или 0?
1 Если показатель степени равен 1, то у вас есть только само число (например, 9 ¹ = 9 )
0 Если показатель степени равен 0, то вы получите 1 (например, 9 ⁰ = 1 )
А как насчет 0 ⁰ ? Это может быть либо 1, либо 0, поэтому люди говорят, что это «неопределенный» .
Все имеет смысл
Мой любимый метод — начать с «1», а затем умножить или разделить столько раз, сколько говорит показатель степени, тогда вы получите правильный ответ, например:
Пример: Полномочия 5
.. и т.д ..
5 ² 1 × 5 × 5 25
5 ¹ 1 × 5 5
5 ⁰ 1 1
5 ^-1 1 ÷ 5 0.2
5 ^-2 1 ÷ 5 ÷ 5 0,04
.. и т.д ..
Если вы посмотрите на эту таблицу, вы увидите, что положительный, нулевой или отрицательный показатель степени на самом деле являются частью одного (довольно простого) паттерна.
Будьте осторожны при группировке
Чтобы избежать путаницы, используйте круглые скобки () в таких случаях:
С (): (-2) ² = (-2) × (-2) = 4
Без (): -2 ² = — (2 ²) = — (2 × 2) = -4

С (): (ab) ² = ab × ab
Без (): ab ² = a × (b) ² = a × b × b
,
Правила экспоненты | Законы экспонентов
Правила экспоненты, законы экспоненты и примеры.
Что такое показатель степени
Основание a в степени n равно умножению числа a, n раз:
a ⁿ = а × а × … × а
п раз
a — основание, n — показатель степени.
Примеры
3 ¹ = 3
3 ² = 3 × 3 = 9
3 ³ = 3 × 3 × 3 = 27
3 ⁴ = 3 × 3 × 3 × 3 = 81
3 ⁵ = 3 × 3 × 3 × 3 × 3 = 243
Экспоненты правила и свойства
Название правила Правило Пример
Правила продукта a ⁿ ⋅ a ^m = a ^{n + m} 2 ³ ⋅ 2 ⁴ = 2 ^{3 + 4} = 128
a ⁿ ⋅ b ⁿ = ( a ⋅ b ) ⁿ 3 ² ⋅ 4 ² = (3⋅4) ² = 144
Частные правила a ⁿ / a ^m = a ⁿ ^{— m} 2 ⁵/2 ³ = 2 ^5-3 = 4
a ⁿ / b ⁿ = ( a / b ) ⁿ 4 ³/2 ³ = (4/2) ³ = 8
Правила мощности ( b ⁿ ) ^m = b ^нм (2 ³) ² = 2 ^3⋅2 = 64
_b n ^m _{= b} ( n ^м) ₂ 3 ² _{= 2} (3 ²) _{= 512}
^м √ ( b ⁿ ) = б ^{n / м} ² √ (2 ⁶) = 2 ^6/2 = 8
b ^{1/ n} = ⁿ √ b 8 ^1/3 = ³ √8 = 2
Отрицательные показатели b ^-n = 1/ b ⁿ 2 ^-3 = 1/2 ³ = 0.125
Нулевые правила b ⁰ = 1 5 ⁰ = 1
0 ⁿ = 0, для n > 0 0 ⁵ = 0
Единые правила b ¹ = b 5 ¹ = 5
1 ⁿ = 1 1 ⁵ = 1
Минус одно правило (-1) ⁵ = -1
Производное правило ( x ⁿ ) ‘ = n ⋅ x ⁿ ^-1 ( x ³) ‘ = 3⋅ x ^3-1
Интегральное правило ∫ x ⁿ dx = x ⁿ ⁺¹ / ( n +1) + C ∫ x ² dx = x ^{2 + 1} / (2 + 1) + C
Правила произведения экспонентов
Правило продукта с той же базой
a ⁿ ⋅ a ^m = a ^{n + m}
Пример:
2 ³ ⋅ 2 ⁴ = 2 ^{3 + 4} = 2 ⁷ = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128
Правило произведения с той же степенью
a ⁿ ⋅ b ⁿ = ( a ⋅ b ) ⁿ
Пример:
3 ² ⋅ 4 ² = (3⋅4) ² = 12 ² = 12⋅12 = 144
См .: Показатели умножения
Правила частного экспонента
Правило частных с той же базой
a ⁿ / a ^м = a ⁿ ^{— м}
Пример:
2 ⁵/2 ³ = 2 ^5-3 = 2 ² = 2⋅2 = 4
Правило частных с тем же показателем
a ⁿ / b ⁿ = ( a / b ) ⁿ
Пример:
4 ³/2 ³ = (4/2) ³ = 2 ³ = 2⋅2⋅2 = 8
См .: Показатели деления
Правила степени экспоненты
Правило мощности I
( a ⁿ ) ^m = a ^n⋅m
Пример:
(2 ³) ² = 2 ^3⋅2 = 2 ⁶ = 2⋅2⋅2⋅2⋅2⋅2 = 64
Правило власти II
_a n ^m ₌ _a ( n ^m)
Пример:
₂ 3 ² _{= 2} (3 ²) _{= 2} (3⋅3) _{= 2} 9 _{= 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512}
Силовое правило с радикалами
^м √ ( a ⁿ ) = a ⁿ ^{/ м}
Пример:
² √ (2 ⁶) = 2 ^6/2 = 2 ³ = 2⋅2⋅2 = 8
Правило отрицательных показателей
b ^-n = 1/ b ⁿ
Пример:
2 ^-3 = 1/2 ³ = 1 / (2⋅2⋅2) = 1/8 = 0.125
См .: Отрицательные показатели
Калькулятор экспонент ►
См. Также
,
Полиномы
Полином выглядит так:
пример полинома
, у этого есть 3 члена
Многочлен происходит от поли- (что означает «много») и -номина (в данном случае означает «термин») … поэтому он говорит «много терминов»
Полином может иметь:
, которые можно объединить, используя сложение, вычитание, умножение и деление …
… кроме …
… не деление на переменную (так что что-то вроде 2 / x прямо)
Итак:
Многочлен может иметь константы, переменные и показатели,
, но никогда не деление на переменную.
Также они могут иметь один или несколько терминов, но не бесконечное количество терминов.
Полином или нет?
Эти являются полиномами :
(Да, «5» — многочлен, допускается один член , и это может быть просто константа!)
Это , а не многочленов
3xy ^-2 нет, потому что показатель степени равен «-2» (показатель степени может быть только 0,1,2 ,…)
2 / (x + 2) нет, потому что деление на переменную недопустимо
1 / x не равно
√x нет, потому что показатель степени равен «½» (см. Дробные показатели)
Но эти разрешены :
x / 2 разрешено , потому что можно делить на константу
также 3x / 8 по той же причине
√2 допускается, потому что это константа (= 1.4142 … и т. Д.)
Мономиальное, Биномиальное, Трехчленное
Существуют специальные названия многочленов с 1, 2 или 3 членами:
Как вы запоминаете имена? Думайте циклы!
Есть также четырехчлен (4 члена) и квинтиномиальный (5 членов),
, но эти названия используются нечасто.
Переменные
Полиномы вообще не могут иметь переменных
Пример: 21 — многочлен.В нем всего один член, который является постоянным.
Или одна переменная
Пример: x ⁴ — 2x ² + x имеет три члена, но только одну переменную (x)
Или две или более переменных
Пример: xy ⁴ — 5x ² z имеет два члена и три переменные (x, y и z)
Что особенного в многочленах?
Из-за строгого определения полиномы легко работают с .
Например, мы знаем, что:
Таким образом, вы можете выполнять множество операций сложения и умножения, и в результате получить многочлен.
Кроме того, многочлены одной переменной легко графически отображать, поскольку они имеют плавные и непрерывные линии.
Пример: x ⁴ −2x ² + x
Видите, насколько хороша и сглажена
кривая?
Вы также можете делить многочлены (но результат может не быть многочленом).
градусов
градусов полинома только с одной переменной — это наибольший показатель этой переменной.
Пример:
Степень: 3 (наибольший показатель x )
Для более сложных случаев прочтите Степень (выражения).
Стандартная форма
Стандартная форма записи многочлена — ставить сначала члены с наивысшей степенью.
Пример: поместите это в стандартную форму: 3 x ² — 7 + 4 x ³ + x ⁶
Наивысшая степень — 6, поэтому сначала идет 3, затем 2 и затем последняя константа:
x ⁶ + 4 x ³ + 3 x ² — 7
не обязательно использовать стандартную форму , но это помогает.
,
Что такое экспонента? | Math Review [видео]
Используйте приведенный ниже информационный бюллетень по показателям, чтобы лучше понять, как работают показатели. Вам предлагается распечатать или загрузить информационный бюллетень об экспонентах со ссылкой в формате PDF после изображения.
Показатели
Возможно, вы слышали, как один или два учителя математики говорили: «Математика — это язык». Если это так, то алгебраические правила и обозначения следует рассматривать как грамматику и пунктуацию языка математики. Некоторые учащиеся, испытывающие трудности с математикой, не понимают, как применять правила и интерпретировать обозначения.В этом видео мы сосредоточимся на обозначении и интерпретации экспонент.
В этом видео основное внимание уделяется значению показателей степени, которые являются натуральными числами, также называемыми «подсчетом чисел» (например, 1, 2, 3,…). Другие типы показателей интерпретируются по-другому и будут рассмотрены в других видеороликах.
Давайте начнем с быстрого изучения терминологии. Показатель степени записывается как надстрочный индекс числа или алгебраического выражения, которое обозначается как основание .3 = (- 5) (- 5) (- 5) = -125 \)
Степень десяти часто используется в математических и научных приложениях. Научная нотация использует степень десяти для эффективного и организованного выражения очень больших или малых значений, но мы рассмотрим эту тему в другом видео.
Показатели также используются для возведения алгебраических выражений в степени, но смысл тот же: умножьте основание на себя, сколько бы раз оно не обозначалось показателем!
Вот несколько примеров:
\ (x ^ 3 = x \ times x \ times x \)
Как видите, запись \ (x ^ 3 \) является более эффективным способом написания расширенной версии \ (х \ раз х \ раз х \).2 + 4x + 4 \)
Итак, до тех пор, пока вы можете идентифицировать базу, умножение этой базы само по себе становится довольно простым. Как уже упоминалось, интерпретация обозначений в математике — это половина дела! Практика основ — ключ к достижению уверенности в более сложном математическом содержании.
Спасибо за просмотр и удачной учебы!
.
No related posts.

	Число	Основание	Показатель степени
1.	25⁵
2.	11¹³
3.	135⁶

1.	Умножение степеней Сложность: лёгкое	1
2.	Степень в степени Сложность: лёгкое	1
3.	Возведение степени в степень (буквы) Сложность: лёгкое	2
4.	Степень в степени (основание) Сложность: лёгкое	2
5.	Степень в степени (показатель степени) Сложность: лёгкое	2
6.	Произведение трёх степеней Сложность: лёгкое	2
7.	Произведение степеней (основание — бином) Сложность: лёгкое	1
8.	Частное трёх степеней Сложность: лёгкое	2
9.	Произведение степеней с одинаковыми основаниями (буквы) Сложность: лёгкое	3
10.	Произведение двух степеней (числа) Сложность: лёгкое	2
11.	Частное двух степеней (отрицательное основание) Сложность: лёгкое	2
12.	Возведение степени в степень (числа) Сложность: лёгкое	2
13.	Частное двух степеней (дробь) Сложность: лёгкое	3
14.	Частное двух степеней (отрицательные смешанные числа) Сложность: лёгкое	1
15.	Произведение степеней с одним основанием (числа) Сложность: среднее	3
16.	Произведение отрицательных и противоположных степеней Сложность: среднее	5
17.	Уравнение (частное степеней, целые числа) Сложность: среднее	3
18.	Дробь (буквы) Сложность: среднее	2
19.	Произведение степени и степени в степени Сложность: среднее	2
20.	Деление и умножение степеней Сложность: среднее	3
21.	Произведение двух дробей Сложность: среднее	2
22.	Произведение степеней в степени Сложность: среднее	3
23.	Частное степени в степени и степени Сложность: среднее	2
24.	Умножение и деление степеней Сложность: среднее	1
25.	Вычисление выражения со степенями Сложность: среднее	1

Отрицательная экспонента		Взаимное значение положительной экспоненты		Ответ
4 ^-2	=	1/4 ²	=	1/16 = 0.0625
10 ^-3	=	1/10 ³	=	1/1000 = 0,001
(-2) ^-3	=	1 / (-2) ³	=	1 / (- 8) = -0,125

1		Если показатель степени равен 1, то у вас есть только само число (например, 9 ¹ = 9 )

0		Если показатель степени равен 0, то вы получите 1 (например, 9 ⁰ = 1 )

		А как насчет 0 ⁰ ? Это может быть либо 1, либо 0, поэтому люди говорят, что это «неопределенный» .

Пример: Полномочия 5
	.. и т.д ..
5 ²	1 × 5 × 5	25
5 ¹	1 × 5	5
5 ⁰	1	1
5 ^-1	1 ÷ 5	0.2
5 ^-2	1 ÷ 5 ÷ 5	0,04
	.. и т.д ..

С ():	(-2) ² = (-2) × (-2) = 4
Без ():	-2 ² = — (2 ²) = — (2 × 2) = -4

С ():	(ab) ² = ab × ab
Без ():	ab ² = a × (b) ² = a × b × b

Название правила	Правило	Пример
Правила продукта	a ⁿ ⋅ a ^m = a ^{n + m}	2 ³ ⋅ 2 ⁴ = 2 ^{3 + 4} = 128
Правила продукта	a ⁿ ⋅ b ⁿ = ( a ⋅ b ) ⁿ	3 ² ⋅ 4 ² = (3⋅4) ² = 144
Частные правила	a ⁿ / a ^m = a ⁿ ^{— m}	2 ⁵/2 ³ = 2 ^5-3 = 4
Частные правила	a ⁿ / b ⁿ = ( a / b ) ⁿ	4 ³/2 ³ = (4/2) ³ = 8
Правила мощности	( b ⁿ ) ^m = b ^нм	(2 ³) ² = 2 ^3⋅2 = 64
	_b n ^m _{= b} ( n ^м)	₂ 3 ² _{= 2} (3 ²) _{= 512}
	^м √ ( b ⁿ ) = б ^{n / м}	² √ (2 ⁶) = 2 ^6/2 = 8
	b ^{1/ n} = ⁿ √ b	8 ^1/3 = ³ √8 = 2
Отрицательные показатели	b ^-n = 1/ b ⁿ	2 ^-3 = 1/2 ³ = 0.125
Нулевые правила	b ⁰ = 1	5 ⁰ = 1
Нулевые правила	0 ⁿ = 0, для n > 0	0 ⁵ = 0
Единые правила	b ¹ = b	5 ¹ = 5
Единые правила	1 ⁿ = 1	1 ⁵ = 1
Минус одно правило		(-1) ⁵ = -1
Производное правило	( x ⁿ ) ‘ = n ⋅ x ⁿ ^-1	( x ³) ‘ = 3⋅ x ^3-1
Интегральное правило	∫ x ⁿ dx = x ⁿ ⁺¹ / ( n +1) + C	∫ x ² dx = x ^{2 + 1} / (2 + 1) + C

Что такое степень с натуральным показателем. Алгебра, 7 класс: уроки, тесты, задания.

Степень числа. Степень с натуральным показателем

Правило чтения и записи степеней с натуральным показателем

Свойства степеней с натуральным показателем

Основное свойство степени

Свойство частного степеней с одинаковыми основаниями

Свойство возведения степени в степень

Свойство возведения в степень произведения

Свойство возведения в степень дроби

Конспект «Степени. Свойства степеней» — УчительPRO

Степени. Свойства степеней.

Степень с натуральным показателем

Возведение в степень

Дисперсия

Умножение степеней

Деление степеней

Степень с нулевым показателем

Степень с натуральным показателем и её свойства. Алгебра, 7 класс: уроки, тесты, задания.

Что такое степень с натуральным показателем

Таблица основных степеней

Свойства степени с натуральным показателем

Умножение и деление степеней с одинаковым показателем

Степень с нулевым показателем

Урок 2. степень числа — Алгебра — 7 класс

Свойства степени с натуральным показателем. Алгебра, 7 класс: уроки, тесты, задания.

Презентация «Степень с натуральным показателем»

Оставьте свой комментарий

экспонентов

Пример: 5 3 = 5 × 5 × 5 = 125

Пример: 2 4 = 2 × 2 × 2 × 2 = 16

Отрицательные экспоненты

Отрицательно? Переверните позитив!

Что делать, если экспонента равна 1 или 0?

Все имеет смысл

Будьте осторожны при группировке

Правила экспоненты | Законы экспонентов

Что такое показатель степени

Примеры

Экспоненты правила и свойства

Правила произведения экспонентов

Правило продукта с той же базой

Правило произведения с той же степенью

Правила частного экспонента

Правило частных с той же базой

Правило частных с тем же показателем

Правила степени экспоненты

Правило мощности I

Правило власти II

Силовое правило с радикалами

Правило отрицательных показателей

См. Также

Полиномы

Полином или нет?

Мономиальное, Биномиальное, Трехчленное

Переменные

Что особенного в многочленах?

Пример: x 4 −2x 2 + x

градусов

Пример:

Стандартная форма

Пример: поместите это в стандартную форму: 3 x 2 — 7 + 4 x 3 + x 6

Что такое экспонента? | Math Review [видео]

Показатели

0 comments on “Степень с натуральным показателем это: Степень с натуральным показателем”

Добавить комментарий Отменить ответ

Рубрики

Пример: 5 ³ = 5 × 5 × 5 = 125

Пример: 2 ⁴ = 2 × 2 × 2 × 2 = 16

Пример: x ⁴ −2x ² + x

Пример: поместите это в стандартную форму: 3 x ² — 7 + 4 x ³ + x ⁶