Свойства окружности и касательной – Свойства касательных к окружности, с примерами

Касательная к окружности

8 июля 2018

Определение. Касательная к окружности — это прямая на плоскости, имеющая ровно одну общую точку с окружностью.

Вот парочка примеров:

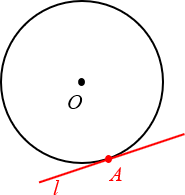Окружность с центром O касается прямой l в точке A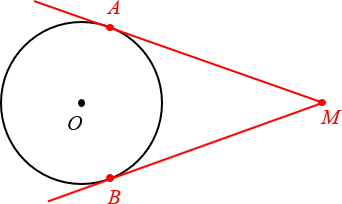Из любой точки M за пределами окружности можно провести ровно две касательных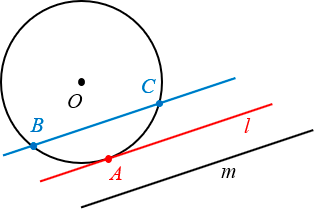Различие между касательной l, секущей BC и прямой m, не имеющей общих точек с окружностью

На этом можно было бы закончить, однако практика показывает, что недостаточно просто зазубрить определение — нужно научиться видеть касательные на чертежах, знать их свойства и вдобавок как следует попрактиковаться в применении этих свойств, решая реальные задачи. Всем этим всем мы сегодня и займёмся.

Основные свойства касательных

Для того, чтобы решать любые задачи, нужно знать четыре ключевых свойства. Два из них описаны в любом справочнике / учебнике, а вот последние два — про них как-то забывают, а зря.

1. Отрезки касательных, проведённых из одной точки, равны

Чуть выше мы уже говорили про две касательных, проведённых из одной точки M. Так вот:

Отрезки касательных к окружности, проведённых из одной точки, равны.

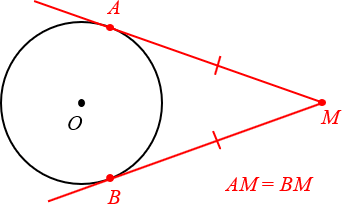Отрезки AM и BM равны

2. Касательная перпендикулярна радиусу, проведённому в точку касания

Ещё раз посмотрим на картинку, представленную выше. Проведём радиусы OAи OB, после чего обнаружим, что углы

OAMи OBM — прямые.

Радиус, проведённый в точку касания, перпендикулярен касательной.

Этот факт можно использовать без доказательства в любой задаче:

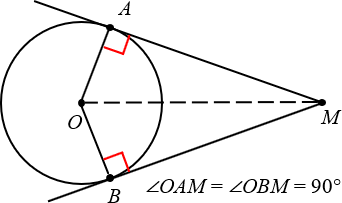Радиусы, проведённые в точку касания, перпендикулярны касательным

Кстати, заметьте: если провести отрезок OM, то мы получим два равных треугольника: OAM и OBM.

3. Соотношение между касательной и секущей

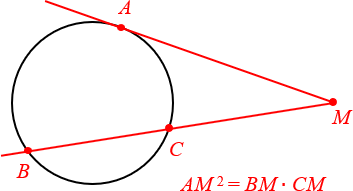
А вот это уже факт посерьёзнее, и большинство школьников его не знают. Рассмотрим касательную и секущую, которые проходят через одну и ту же общую точку M. Естественно, секущая даст нам два отрезка: внутри окружности (отрезок BC — его ещё называют хордой) и снаружи (его так и называют — внешняя часть MC).

Произведение всей секущей на её внешнюю часть равно квадрату отрезка касательной

Соотношение между секущей и касательной

4. Угол между касательной и хордой

Ещё более продвинутый факт, который часто используется для решения сложных задач. Очень рекомендую взять на вооружение.

Угол между касательной и хордой равен вписанному углу, опирающемуся на эту хорду.

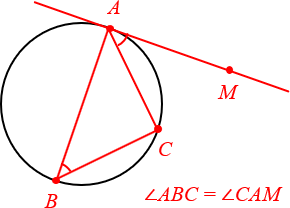
Откуда берётся точка B? В реальных задачах она обычно «всплывает» где-то в условии. Поэтому важно научиться распознавать данную конфигурацию на чертежах.

Иногда всё-таки касается 🙂

Смотрите также:

1. Пробный ЕГЭ 2012. Вариант 5 (без производных)
2. Формула полной вероятности
3. Сводный тест по задачам B12 (2 вариант)
4. Иррациональные неравенства. Часть 2
5. Нестандартные задачи B2: кредит в банке
6. Выделение полного квадрата

www.berdov.com

Свойства касательной

Относительное положение прямой и окружности

Прямая относительно окружности может находиться в следующих трех положениях:

1. Расстояние от центра окружности до прямой больше радиуса. В этом случае все точки прямой лежат вне круга.


2. Расстояние от центра окружности до прямой меньше радиуса. В этом случае прямая имеет точки, лежащие внутри круга и так как прямая бесконечна в обе стороны, то она пересекается сокружностью в 2 точках.


3. Расстояние от центра окружности до прямой равно радиусу. Прямая — касательная.

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности.

Общая точка называется в этом случае точкой касания.

Возможность существования касательной, и притом проведенной через любую точку окружности, как точку касания, доказывается следующей теоремой.

Теорема. Если прямая перпендикулярна к радиусу в его конце, лежащем на окружности, то эта прямая — касательная.

Пусть O (рис) — центр некоторого круга и OA какой-нибудь его радиус. Через его конец A проведем MN ^ OA.

Требуется доказать, что прямая MN — касательная, т.е. что эта прямая имеет с окружностью только одну общую точку A.

Допустим противное: пусть MN имеет с окружностью еще другую общую точку, например B.

Тогда прямая OB была бы радиусом и, следовательно, равнялась бы OA.

Но этого быть не может, так как, если OA -перпендикуляр, то OB должна быть наклонной к MN, а наклонная больше перпендикуляра.

Обратная теорема. Если прямая касательна к окружности, то радиус, проведенный в точку касания, перпендикулярен к ней.

Пусть MN — касательная к окружности, A — точка касания и O — центр этой окружности.

Требуется доказать, что OA^MN.

Допустим противное, т.е. предположим, что перпендикуляром, опущенным из O на MN, будет не OA , а какая-нибудь другая прямая, например, OB.

Возьмем BС = AB и проведем OС.

Тогда OA и OС будут наклонные, одинаково удаленные от перпендикуляра OB, и следовательно, OС = OA.

Из этого следует, что окружность, учитывая наше предположение, будет иметь с прямой MN две общие точки: A  и  С , т.е. MN будет не касательная, а секущая, что противоречит условию.

Следствие. Через всякую данную на окружности точку можно провести касательную к этой окружности и притом только одну, так как через эту точку можно провести перпендикуляр, и притом только один, к радиусу, проведенному в нее.

Теорема. Касательная, параллельная хорде, делит в точке касания дугу, стягиваемую хордой, пополам.

Пусть прямая AB (рис.) касается окружности в точке M и параллельна хорде СD.

Требуется доказать, что ÈCM = ÈMD.

Проведя через точку касания диаметр ME, получаем: EM ^ AB, и следовательно, EM ^ СВ.

Поэтому СM=MD.

Задача. Через данную точку провести касательную к данной окружности.

Если данная точка находится на окружности, то проводят через нее радиус и через конец радиуса перпендикулярную прямую. Эта прямая будет искомой касательной.

Рассмотрим тот случай, когда точка дана вне круга.

Пусть требуется (рис.) провести к окружности с центром O касательную через точку A.

Для этого из точки A, как из центра, описываем дугу радиусом AO, а из точки O, как центра, пересекаем эту дугу в точках B и С раствором циркуля, равным диаметру данного круга.

Проведя затем хорды OB и OС, соединим точку A с точками D и E, в которых эти хорды пересекаются с данной окружностью.

Прямые AD и AE — касательные к окружности O.

Действительно, из построения видно, что тр-ки AOB и AOС равнобедренные (AO = AB =AС ) с основаниями OB и OС, равными диаметру круга O.

Так как OD и OE — радиусы, то D — середина OB, а E — середина OС, значит AD и AE — медианы, проведенные к основаниям равнобедренных тр-ков, и потому перпендикулярны к этим основаниям. Если же прямые DA и EA перпендикулярны к радиусам OD и OE, то они — касательные.

Следствие. Две касательные, проведенные из одной точки к окружности, равны и образуют равные углы с прямой, соединяющей эту точку с центром.

Так AD=AE и ÐOAD = ÐOAE (рис.), потому что прямоугольные тр-ки AOD и AOE, имеющие общую гипотенузу AO и равные катеты OD и OE (как радиусы), равны.

Заметим, что здесь под словом “касательная” подразумевается собственно “отрезок касательной” от данной точки до точки касания.

Задача. Провести касательную к данной окружности O параллельно данной прямой AB (рис.).

Опускаем на AB из центра O перпендикуляр OС и через точку D, в которой этот перпендикуляр пересекается с окружностью, проводим EF || AB.

Искомая касательная будет EF.

Действительно, так как OС ^ AB и EF || AB, то EF ^ OD, а прямая, перпендикулярная к радиусу в его конце, лежащем на окружности — касательная.

Задача. К двум окружностям O и O₁ провести общую касательную (рис.).

Анализ. Предположим, что задача решена.

Пусть AB будет общая касательная, A и B — точки касания.

Очевидно, что если мы найдем одну из этих точек, например, A, то затем легко найдем и другую.

Проведем радиусы OA и O₁B. Эти радиусы, будучи перпендикулярны к общей касательной, параллельны между собой.

Поэтому, если из O₁ проведем O₁С || BA, то тр-к OСO₁ будет прямоугольный при вершине С.

Вследствие этого, если опишем из O, как центра, радиусом OС окружность, то она будет касаться прямой O₁С в точке С.

Радиус этой вспомогательной окружности известен: он равен OA – СA= OA — O₁B, т.е. он равен разности радиусов данных окружностей.

Построение. Из центра O описываем окружность радиусом, равным разности данных радиусов.

Из O₁ проводим к этой окружности касательную O₁С (способом, указанным в предыдущей задаче).

Через точку касания С проводим радиус OС и продолжаем его до встречи с данной окружностью в точке A. Наконец из A проводим AB параллельно СO_1.

Совершенно таким же способом мы можем построить другую общую касательную A₁B₁ (рис.). Прямые AB и A₁B₁ называют внешними общими касательными.

Можно еще провести две внутренние касательные следующим образом:

Анализ. Предположим, что задача решена (рис.). Пусть AB — искомая касательная.

Проведем радиусы OA и O₁B в точки касания A и B. Так как эти радиусы оба перпендикулярны к общей касательной, то они параллельны между собой.

Поэтому, если из O₁ проведем O₁С || BA и продолжим OA до точки С, то OС будет перпендикуляр к O₁С.

Вследствие этого окружность, описанная радиусом OС из точки O, как центра, будет касаться прямой O₁С в точке С.

Радиус этой вспомогательной окружности известен: он равен OA+AС = OA+O₁B, т.е. он равен сумме радиусов данных окружностей.

Построение. Из O как центра, описываем окружность радиусом, равным сумме данных радиусов.

Из O₁ проводим к этой окружности касательную O₁С.

Точку касания С соединяем с O.

Наконец через точку A, в которой OС пересекается с данной окружностью, проводим AB = O₁С.

Подобным же способом можем построить другую внутреннюю касательную A₁B₁.

Общее определение касательной

Пусть к окружности с центром (рис.) проведены через точку A касательная AT и какая-нибудь секущая AM.

Станем вращать эту секущую вокруг точки A так, чтобы другая точка пересечения B все ближе и ближе придвигалась к A.

Тогда перпендикуляр OD, опущенный из центра на секущую, будет все больше и больше приближаться к радиусу OA, и угол AOD может стать меньше всякого малого угла.

Угол MAT, образованный секущей и касательной, равен углу AOD (вследствие перпендикулярности их сторон).

Поэтому при неограниченном приближении точки B к A угол MAT также может стать как угодно мал.

Это выражают иными словами так:

касательная есть предельное положение, к которому стремится секущая, проведенная через точку касания, когда вторая точка пересечения неограниченно приближается к точке касания.

Это свойство принимают за определение касательной, когда речь идет о какой угодно кривой.

Так, касательной к кривой AB (рис.) называется предельное положение MT, к которому стремится секущая MN, когда точка пересечения P неограниченно приближается к M.

Заметим,что определяемая таким образом касательная может иметь с кривой более одной общей точки (как это видно на рис).

razdupli.ru

Окружность. Основные теоремы

\[{\Large{\text{Центральные и вписанные углы}}}\]

Определения

Центральный угол – это угол, вершина которого лежит в центре окружности.

 

Вписанный угол – это угол, вершина которого лежит на окружности.

 

Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.

 

Теорема

Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

 

Доказательство

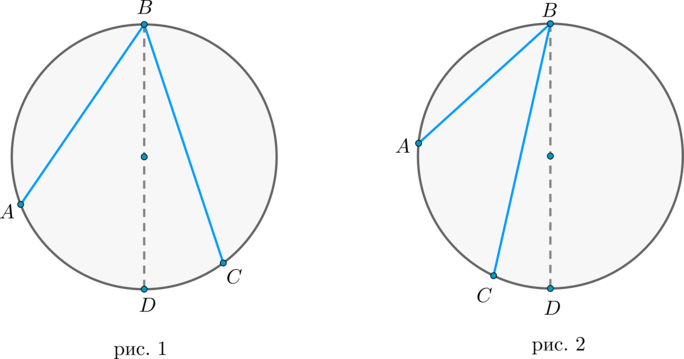
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка \(B\) – вершина вписанного угла \(ABC\) и \(BC\) – диаметр окружности:

 

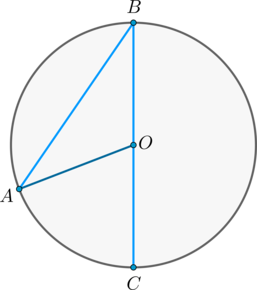
Треугольник \(AOB\) – равнобедренный, \(AO = OB\), \(\angle AOC\) – внешний, тогда \(\angle AOC = \angle OAB + \angle ABO = 2\angle ABC\), откуда \(\angle ABC = 0,5\cdot\angle AOC = 0,5\cdot\buildrel\smile\over{AC}\).

 

Теперь рассмотрим произвольный вписанный угол \(ABC\). Проведём диаметр окружности \(BD\) из вершины вписанного угла. Возможны два случая:

 

1) диаметр разрезал угол на два угла \(\angle ABD, \angle CBD\)(для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.

 

2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла \(\angle ABD, \angle CBD\), у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2.

 

Следствия

1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

 

2. Вписанный угол, опирающийся на полуокружность, прямой.

 

3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.  

\[{\Large{\text{Касательная к окружности}}}\]

Определения

Существует три типа взаимного расположения прямой и окружности:

 

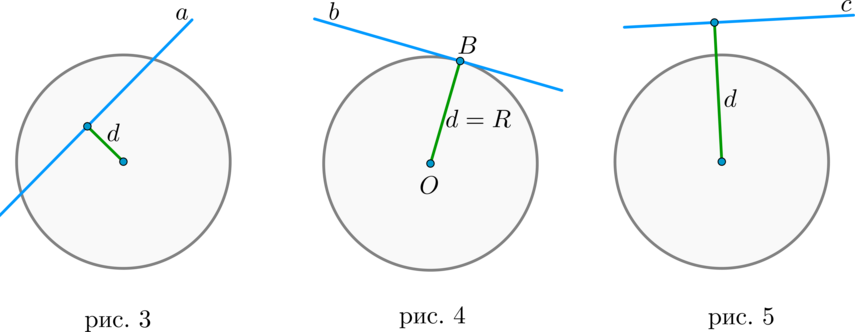
1) прямая \(a\) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние \(d\) от центра окружности до прямой меньше радиуса \(R\) окружности (рис. 3).

 

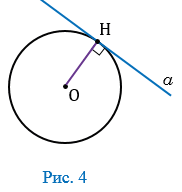
2) прямая \(b\) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка \(B\) – точкой касания. В этом случае \(d=R\) (рис. 4).

 

3) прямая \(c\) не имеет общих точек с окружностью (рис. 5).

 

Теорема

1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

 

2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.

 

Следствие

Отрезки касательных, проведенных из одной точки к окружности, равны.

 

Доказательство

Проведем к окружности из точки \(K\) две касательные \(KA\) и \(KB\):

 

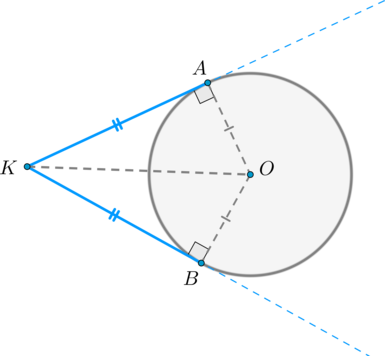
Значит, \(OA\perp KA, OB\perp KB\) как радиусы. Прямоугольные треугольники \(\triangle KAO\) и \(\triangle KBO\) равны по катету и гипотенузе, следовательно, \(KA=KB\).

 

Следствие

Центр окружности \(O\) лежит на биссектрисе угла \(AKB\), образованного двумя касательными, проведенными из одной точки \(K\).  

\[{\Large{\text{Теоремы, связанные с углами}}}\]

Теорема об угле между секущими

Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.

 

Доказательство

Пусть \(M\) – точка, из которой проведены две секущие как показано на рисунке:

 

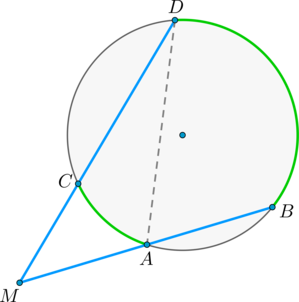
Покажем, что \(\angle DMB = \dfrac{1}{2}(\buildrel\smile\over{BD} — \buildrel\smile\over{CA})\).

 

\(\angle DAB\) – внешний угол треугольника \(MAD\), тогда \(\angle DAB = \angle DMB + \angle MDA\), откуда \(\angle DMB = \angle DAB — \angle MDA\), но углы \(\angle DAB\) и \(\angle MDA\) – вписанные, тогда \(\angle DMB = \angle DAB — \angle MDA = \frac{1}{2}\buildrel\smile\over{BD} — \frac{1}{2}\buildrel\smile\over{CA} = \frac{1}{2}(\buildrel\smile\over{BD} — \buildrel\smile\over{CA})\), что и требовалось доказать.

 

Теорема об угле между пересекающимися хордами

Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: \[\angle CMD=\dfrac12\left(\buildrel\smile\over{AB}+\buildrel\smile\over{CD}\right)\]

Доказательство

\(\angle BMA = \angle CMD\) как вертикальные.

 

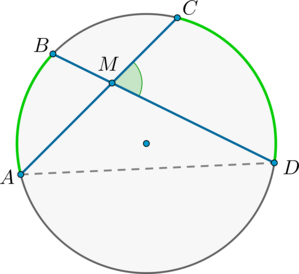
Из треугольника \(AMD\): \(\angle AMD = 180^\circ — \angle BDA — \angle CAD = 180^\circ — \frac12\buildrel\smile\over{AB} — \frac12\buildrel\smile\over{CD}\).

 

Но \(\angle AMD = 180^\circ — \angle CMD\), откуда заключаем, что \[\angle CMD = \frac12\cdot\buildrel\smile\over{AB} + \frac12\cdot\buildrel\smile\over{CD} = \frac12(\buildrel\smile\over{AB} + \buildrel\smile\over{CD}).\]

Теорема об угле между хордой и касательной

Угол между касательной и хордой, проходящей через точку касания, равен половине градусной меры дуги, стягиваемой хордой.

 

Доказательство

Пусть прямая \(a\) касается окружности в точке \(A\), \(AB\) – хорда этой окружности, \(O\) – её центр. Пусть прямая, содержащая \(OB\), пересекает \(a\) в точке \(M\). Докажем, что \(\angle BAM = \frac12\cdot \buildrel\smile\over{AB}\).

 

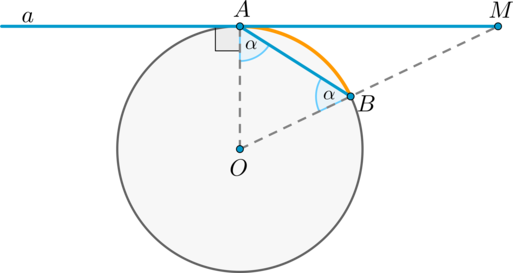
Обозначим \(\angle OAB = \alpha\). Так как \(OA\) и \(OB\) – радиусы, то \(OA = OB\) и \(\angle OBA = \angle OAB = \alpha\). Таким образом, \(\buildrel\smile\over{AB} = \angle AOB = 180^\circ — 2\alpha = 2(90^\circ — \alpha)\).

Так как \(OA\) – радиус, проведённый в точку касания, то \(OA\perp a\), то есть \(\angle OAM = 90^\circ\), следовательно, \(\angle BAM = 90^\circ — \angle OAB = 90^\circ — \alpha = \frac12\cdot\buildrel\smile\over{AB}\).

 

Теорема о дугах, стягиваемых равными хордами

Равные хорды стягивают равные дуги, меньшие полуокружности.

 

И наоборот: равные дуги стягиваются равными хордами.

 

Доказательство

1) Пусть \(AB=CD\). Докажем, что меньшие полуокружности дуги \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\).

 

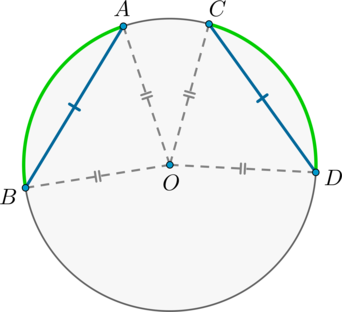
\(\triangle AOB=\triangle COD\) по трем сторонам, следовательно, \(\angle AOB=\angle COD\). Но т.к. \(\angle AOB, \angle COD\) — центральные углы, опирающиеся на дуги \(\buildrel\smile\over{AB}, \buildrel\smile\over{CD}\) соответственно, то \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\).

 

2) Если \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\), то \(\triangle AOB=\triangle COD\) по двум сторонам \(AO=BO=CO=DO\) и углу между ними \(\angle AOB=\angle COD\). Следовательно, и \(AB=CD\).

 

Теорема

Если радиус делит хорду пополам, то он ей перпендикулярен.

Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.

 

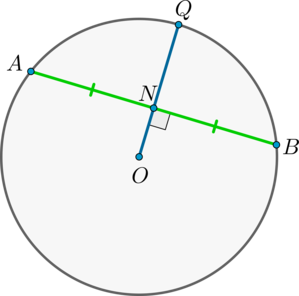
Доказательство

1) Пусть \(AN=NB\). Докажем, что \(OQ\perp AB\).

 

Рассмотрим \(\triangle AOB\): он равнобедренный, т.к. \(OA=OB\) – радиусы окружности. Т.к. \(ON\) – медиана, проведенная к основанию, то она также является и высотой, следовательно, \(ON\perp AB\).

 

2) Пусть \(OQ\perp AB\). Докажем, что \(AN=NB\).

 

Аналогично \(\triangle AOB\) – равнобедренный, \(ON\) – высота, следовательно, \(ON\) – медиана. Следовательно, \(AN=NB\).  

\[{\Large{\text{Теоремы, связанные с длинами отрезков}}}\]

Теорема о произведении отрезков хорд

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

 

Доказательство

Пусть хорды \(AB\) и \(CD\) пересекаются в точке \(E\).

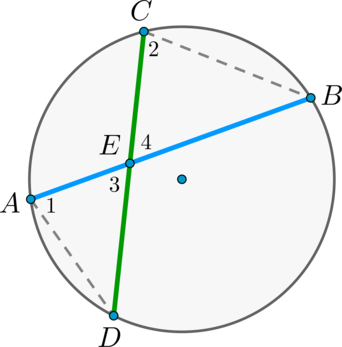
Рассмотрим треугольники \(ADE\) и \(CBE\). В этих треугольниках углы \(1\) и \(2\) равны, так как они вписанные и опираются на одну и ту же дугу \(BD\), а углы \(3\) и \(4\) равны как вертикальные. Треугольники \(ADE\) и \(CBE\) подобны (по первому признаку подобия треугольников).

 

Тогда \(\dfrac{AE}{EC} = \dfrac{DE}{BE}\), откуда \(AE\cdot BE = CE\cdot DE\).

 

Теорема о касательной и секущей

Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.

 

Доказательство

Пусть касательная проходит через точку \(M\) и касается окружности в точке \(A\). Пусть секущая проходит через точку \(M\) и пересекает окружность в точках \(B\) и \(C\) так что \(MB < MC\). Покажем, что \(MB\cdot MC = MA^2\).

 

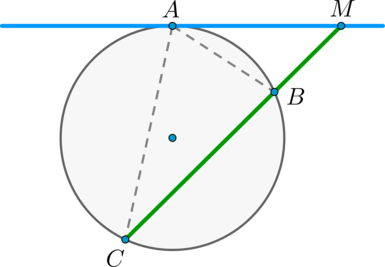
Рассмотрим треугольники \(MBA\) и \(MCA\): \(\angle M\) – общий, \(\angle BCA = 0,5\cdot\buildrel\smile\over{AB}\). По теореме об угле между касательной и секущей, \(\angle BAM = 0,5\cdot\buildrel\smile\over{AB} = \angle BCA\). Таким образом, треугольники \(MBA\) и \(MCA\) подобны по двум углам.

Из подобия треугольников \(MBA\) и \(MCA\) имеем: \(\dfrac{MB}{MA} = \dfrac{MA}{MC}\), что равносильно \(MB\cdot MC = MA^2\).

 

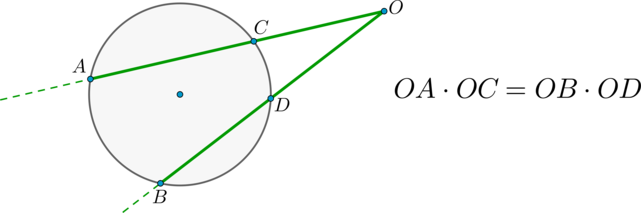
Следствие

Произведение секущей, проведённой из точки \(O\), на её внешнюю часть не зависит от выбора секущей, проведённой из точки \(O\):

 

shkolkovo.net

Окружность и касательная — урок. Геометрия, 8 класс.

В плоскости прямая и окружность могут пересекаться или не пересекаться. При пересечении могут иметь одну или две общие точки.

 

1. Если расстояние от центра окружности до прямой больше радиуса, то у прямой и окружности общих точек нет.

 

 

2. Если расстояние от центра окружности до прямой меньше радиуса, то у прямой и окружности две общие точки.

 

 

В этом случае прямую называют секущей окружности.

Если прямая имеет две общие точки с окружностью, то она называется секущей.

3. Если расстояние от центра окружности до прямой равно радиусу, то у прямой и окружности одна общая точка.

 

 

В этом случая прямую называют касательной к окружности.

Касательной к окружности называется прямая, имеющая с окружностью одну общую точку.

Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

 

Предположим, что радиус \(OA\) не перпендикулярен к прямой, но является наклонной. Тогда из точки \(O\) можно провести перпендикуляр к прямой, который будет короче радиуса. А это означает, что расстояние от центра окружности до прямой меньше радиуса, и у прямой и окружности должны быть две общие точки. Но это противоречит данной информации, наше предположение неверно.

Если из точки к окружности проведены две касательные, то
а) длины отрезков касательных от этой точки до точки касания равны,

б) прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам.

 

Пусть \(AB\) и \(AC\) — касательные к окружности с центром \(O\).

Требуется доказать, что \(AB = AC\) и \(OA\) является биссектрисой угла \(A\).

 

Треугольники \(OBA\) и \(OCA\) — прямоугольные, так как касательные перпендикулярны к радиусам в точках \(B\) и \(C\). Сторона \(OA\) — общая. Катеты \(OB\) и \(OC\) равны как радиусы одной и той же окружности. Треугольники равны по гипотенузе и катету, отсюда равны и катеты \(AB\) и \(AC\), и углы \(BAO\) и \(CAO\), то есть \(OA\) делит угол пополам.

www.yaklass.ru

Касательная к окружности / Окружность / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Окружность
5. Касательная к окружности

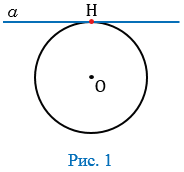
Касательная к окружности — прямая, имеющая с окружностью одну общую точку, которая называется точкой касания прямой и окружности. На рисунке 1 прямая — касательная к окружности, точка Н — точка касания прямой и окружности с центром в точке О.

Свойство касательной к окружности

Теорема

Доказательство

Дано: — касательная к окружности с центром в точке О, Н — точка касания (Рис. 2).

Доказать: ОН.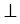

Доказательство:

Предположим, что ОН. Тогда радиус ОН является наклонной к прямой . При этом перпендикуляр, проведенный из точки О к прямой , меньше наклонной ОН, тогда расстояние от центра О окружности до прямой меньше радиуса. Следовательно прямая и окружность будут иметь две общие точки, что противоречит условию: прямая — касательная. Поэтому наше предположение неверно, значит, ОН 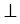. Теорема доказана.

Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Доказательство

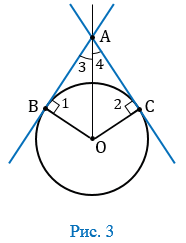
Дано: АВ и АС — касательные к окружности с центром в точке О, В и С — точки касания (Рис. 3).

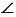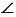Доказать: АВ = АС и 3 =4.

Доказательство:

1 =2 = 90⁰, т.к. ОВАВ, ОС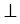АС по теореме о свойстве касательной (смотри выше), поэтому 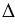АВО и 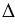АСО прямоугольные. При этом ОВ = ОС (радиусы), АО — общая, следовательн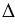о, АВО =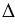АСО (по гипотенузе и катету). Из равенства треугольников следует, что АВ = АС и 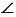3 =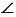4. Что и требовалось доказать.

Теорема, обратная теореме о свойстве касательной (признак касательной)

Теорема

Доказательство

Дано: ОН — радиус окружности с центром в точке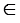 О, Н, ОН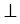 (Рис. 4).

Доказать: — касательная.

Доказательство:

По условию радиус ОН 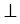, поэтому расстояние от центра окружности до прямой равно радиусу, и, следовательно, прямая и окружность имеют только одну общую точку, значит, данная прямая является касательной к окружности (по определению касательной). Теорема доказана.

Задача

Через данную точку А окружности с центром О провести касательную к этой окружности.

Дано: точка А лежит на окружности с центром в точке О.

Провести касательную к окружности так, что А.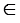

Решение:

Строим с помощью циркуля окружность с центром в точке О, отмечаем на данной окружности точку А.

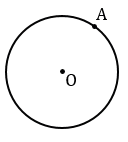
Далее проводим прямую ОА и строим прямую , проходящую через точку А перпендикулярно к прямой ОА. Для этого с помощью циркуля строим окружность произвольного радиуса с центром в точке А (всю окружность строить необязательно, смотри выделенное красным). Точки пересечения данной окружности с прямой ОА обозначаем буквами В и С.

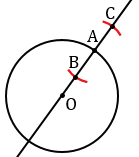
Затем строим две окружности радиуса ВС с центрами в точках В и С (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Данные окружности пересекаются в двух точках, обозначим их Р и Q. Через точки Р и Q с помощью линейки проводим прямую , которая будет перпендикулярна к прямой ОА.

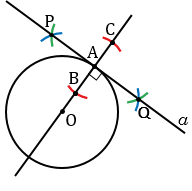
Итак, ОА, ОА — радиус, следовательно, — искомая касательная к окружности с центром в точке О радиуса ОА (по признаку касательной).

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Взаимное расположение прямой и окружности

Градусная мера дуги окружности

Теорема о вписанном угле

Свойство биссектрисы угла

Свойства серединного перпендикуляра к отрезку

Теорема о пересечении высот треугольника

Вписанная окружность

Описанная окружность

Окружность

Правило встречается в следующих упражнениях:

7 класс

Задание 634, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 635, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 645, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 647, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 648, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 689, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 693, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 21, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 723, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 724, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© budu5.com, 2019

Пользовательское соглашение

Copyright

budu5.com

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Отрезки и прямые, связанные с окружностью

Фигура	Рисунок	Определение и свойства
Окружность		Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Круг		Конечная часть плоскости, ограниченная окружностью
Радиус		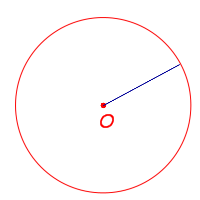Отрезок, соединяющий центр окружности с любой точкой окружности
Хорда		Отрезок, соединяющий две любые точки окружности
Диаметр		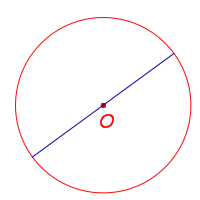Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности
Касательная		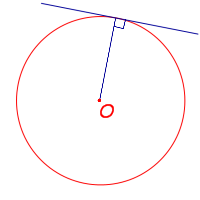Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания
Секущая		Прямая, пересекающая окружность в двух точках

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		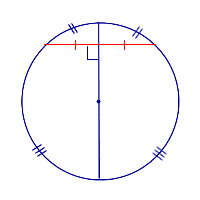Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		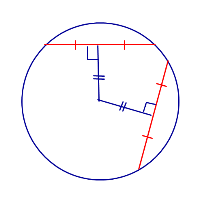Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		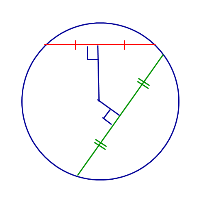Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		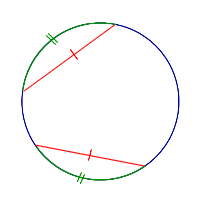У равных дуг равны и хорды.
Параллельные хорды		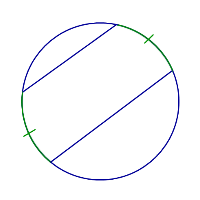Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Фигура	Рисунок	Теорема
Пересекающиеся хорды		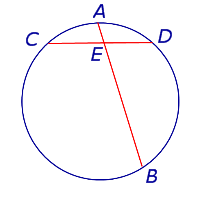Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство
Касательные, проведённые к окружности из одной точки		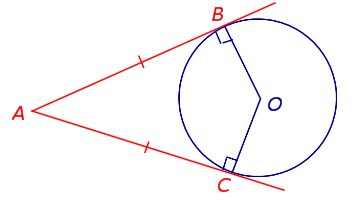Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство
Касательная и секущая, проведённые к окружности из одной точки		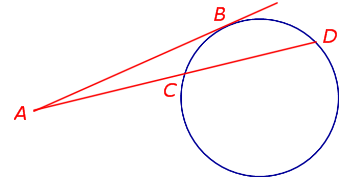Справедливо равенство Посмотреть доказательство
Секущие, проведённые из одной точки вне круга		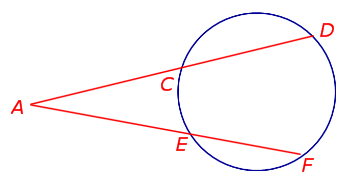Справедливо равенство: Посмотреть доказательство

Пересекающиеся хорды
	Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство
Касательные, проведённые к окружности из одной точки
	Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство
Касательная и секущая, проведённые к окружности из одной точки
	Справедливо равенство Посмотреть доказательство
Секущие, проведённые из одной точки вне круга
	Справедливо равенство: Посмотреть доказательство

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство

Касательные, проведённые к окружности из одной точки

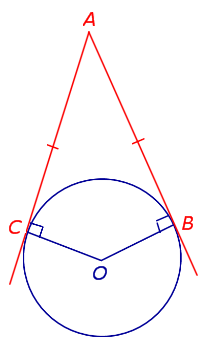Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство

Касательная и секущая, проведённые к окружности из одной точки

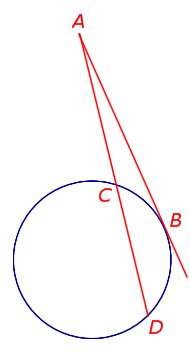Справедливо равенство Посмотреть доказательство

Секущие, проведённые из одной точки вне круга

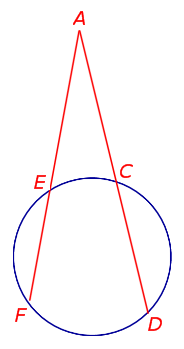Справедливо равенство: Посмотреть доказательство

Доказательства теорем о длинах хорд, касательных и секущих

      Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

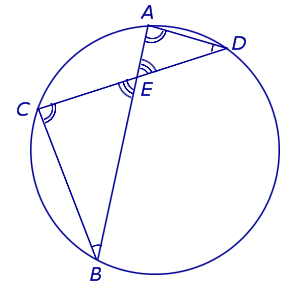
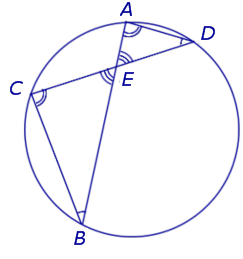
Рис. 1

      Тогда справедливо равенство

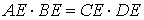
      Доказательство. Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

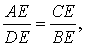
откуда и вытекает требуемое утверждение.

      Теорема 2 . Предположим, что из точки A, лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

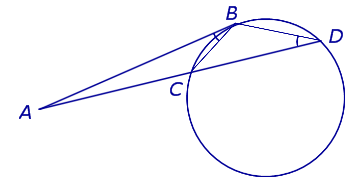
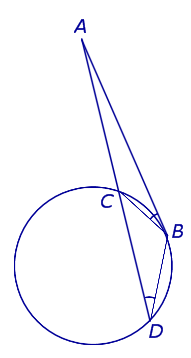
Рис. 2

      Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

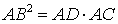
      Доказательство. Заметим, что угол ABC образован касательной AB и хордой BC, проходящей через точку касания B. Поэтому величина угла ABC равна половине угловой величины дуги BC. Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC. Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

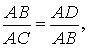
откуда и вытекает требуемое утверждение.

      Теорема 3 . Предположим, что из точки A, лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Рис. 3

      Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

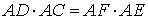
      Доказательство. Проведём из точки A касательную AB к окружности (рис. 4).

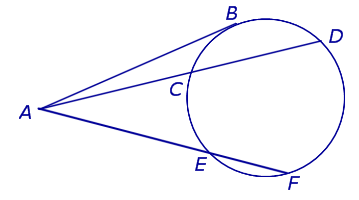
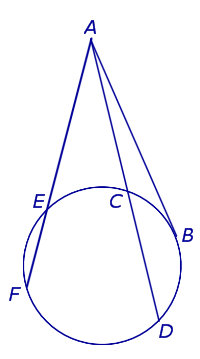
Рис. 4

      Точка B – точка касания. В силу теоремы 2 справедливы равенства

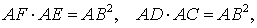
откуда и вытекает требуемое утверждение.

Теорема о бабочке

      Теорема о бабочке. Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

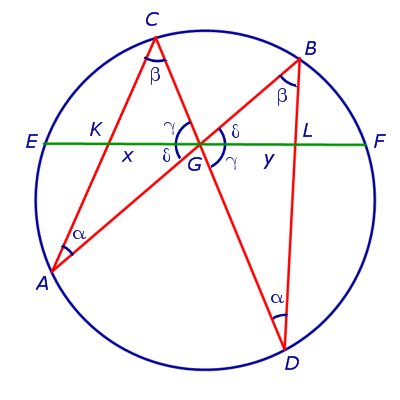
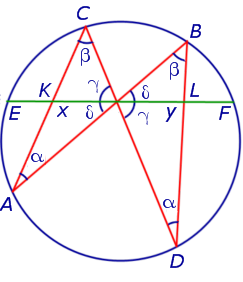
Рис. 5

      Доказательство. Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B. Теперь введём следующие обозначения:

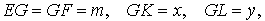
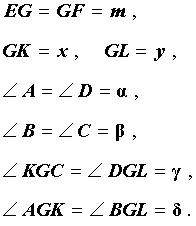
      Воспользовавшись теоремой синусов, применённой к треугольнику CKG, получим

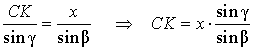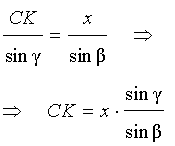(1)

Воспользовавшись теоремой синусов, применённой к треугольнику AKG, получим

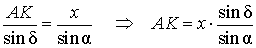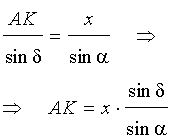(2)

Воспользовавшись теоремой 1, получим

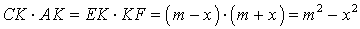
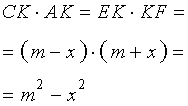
Воспользовавшись равенствами (1) и (2), получим

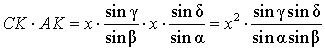
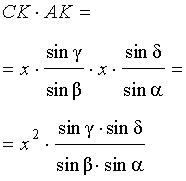
Поэтому

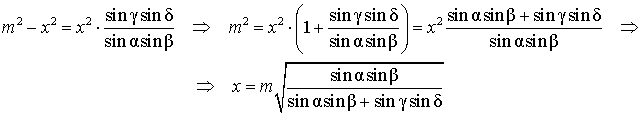
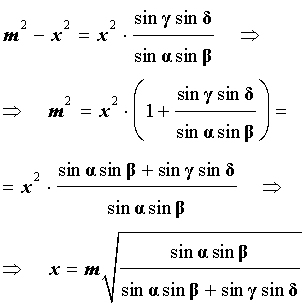
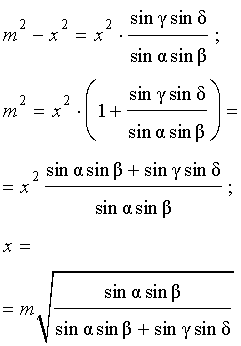
      Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL, получим равенство

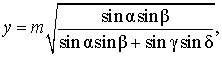
откуда вытекает равенство

x = y ,

что и завершает доказательство теоремы о бабочке.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

www.resolventa.ru

Окружность, круг, сегмент, сектор. Формулы и свойства

Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.

Определение. Единичная окружность — окружность, радиус которой равна единице.

Определение. Круг — часть плоскости, ограничена окружностью.

Определение. Радиус окружности R — расстояние от центра окружности О до любой точки окружности.

Определение. Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.

Основные свойства окружности

1. Диаметр окружности равен двум радиусам.

D = 2r

2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.

3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.

4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.

5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.

Формулы длины окружности и площади круга

Формулы длины окружности

1. Формула длины окружности через диаметр:

L = πD

2. Формула длины окружности через радиус:

L = 2πr

Формулы площади круга

1. Формула площади круга через радиус:

S = πr²

2. Формула площади круга через диаметр:

S = πD²4

Уравнение окружности

1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:

r² = x² + y²

2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

r² = (x — a)² + (y — b)²

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

{	x = a + r cos t
	y = b + r sin t

Касательная окружности и ее свойства

Определение. Касательная окружности — прямая, которая касается окружности только в одной точке.

Основные свойства касательных к окружности

1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.

2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.

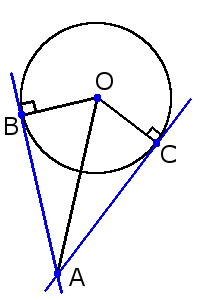3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

AB = AC

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

∠ОAС = ∠OAB

Секущая окружности и ее свойства

Определение. Секущая окружности — прямая, которая проходит через две точки окружности.

Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:

AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:

AQ ∙ BQ = CQ²

Хорда окружности ее длина и свойства

Определение. Хорда окружности — отрезок, который соединяет две точки окружности.

Длина хорды

1. Длина хорды через центральный угол и радиус:

AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:

AB = 2r sin α

Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:

если хорды AB = CD, то

дуги ◡ AB = ◡ CD

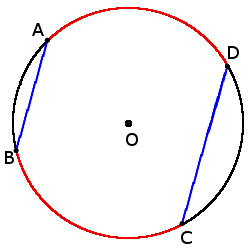2. Если хорды параллельные, то дуги между ними будут одинаковые:

если хорды AB ∣∣ CD, то

◡ AD = ◡ BC

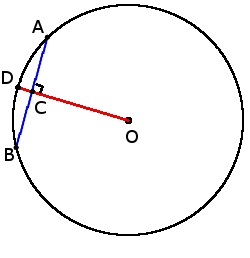3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:

если OD ┴ AB, то

AC = BC

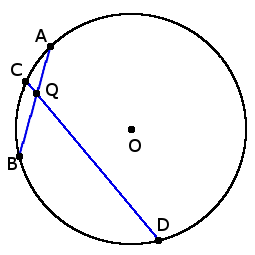4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:

AQ ∙ BQ = DQ ∙ QC

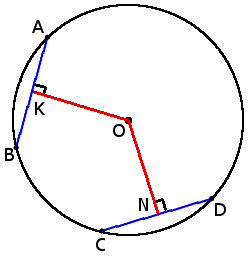5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.

если хорды AB = CD, то

ON = OK

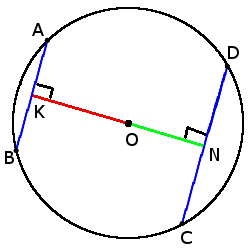6. Чем больше хорда тем ближе она к центру.

если CD > AB, то

ON < OK

Центральный угол, вписанный угол и их свойства

Определение. Центральный угол окружности — угол, вершиной которого есть центр окружности.

Определение. Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.

Основные свойства углов

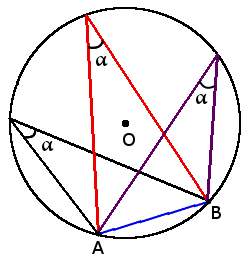1. Все вписанные углы, которые опираются на одну дугу — равны. 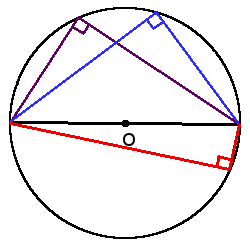2. Вписанний угол, который опирается на диаметр будет прямым (90°). 3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу

β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.

α + β = 180°

Определение. Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.

Определение. Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.

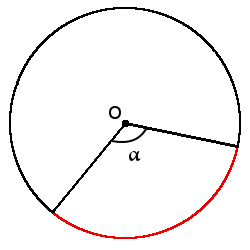Формула длины дуги через центральный угол (в градусах):

l = πr180°∙ α

Определение. Полуокружность — дуга в которой концы соединены диаметром окружности.

Определение. Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.

Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)

S = πr²360°∙ α

Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.

Определение. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.

Определение. Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.

ru.onlinemschool.com