Таблица арифметических квадратных корней – Таблица квадратных корней

Таблица квадратных корней

В таблице приведены квадратные корни натуральных чисел от 1 до 100.

√1 = 1 √4 = 2 √9 = 3 √16 = 4 √25 = 5 √36 = 6 √49 = 7 √64 = 8 √81 = 9 √100 = 10	√121 = 11 √144 = 12 √169 = 13 √196 = 14 √225 = 15 √256 = 16 √289 = 17 √324 = 18 √361 = 19 √400 = 20	√441 = 21 √484 = 22 √529 = 23 √576 = 24 √625 = 25 √676 = 26 √729 = 27 √784 = 28 √841 = 29 √900 = 30	√961 = 31 √1024 = 32 √1089 = 33 √1156 = 34 √1225 = 35 √1296 = 36 √1369 = 37 √1444 = 38 √1521 = 39 √1600 = 40	√1681 = 41 √1764 = 42 √1849 = 43 √1936 = 44 √2025 = 45 √2116 = 46 √2209 = 47 √2304 = 48 √2401 = 49 √2500 = 50
√2601 = 51 √2704 = 52 √2809 = 53 √2916 = 54 √3025 = 55 √3136 = 56 √3249 = 57 √3364 = 58 √3481 = 59 √3600 = 60	√3721 = 61 √3844 = 62 √3969 = 63 √4096 = 64 √4225 = 65 √4356 = 66 √4489 = 67 √4624 = 68 √4761 = 69 √4900 = 70	√5041 = 71 √5184 = 72 √5329 = 73 √5476 = 74 √5625 = 75 √5776 = 76 √5929 = 77 √6084 = 78 √6241 = 79 √6400 = 80	√6561 = 81 √6724 = 82 √6889 = 83 √7056 = 84 √7225 = 85 √7396 = 86 √7569 = 87 √7744 = 88 √7921 = 89 √8100 = 90	√8281 = 91 √8464 = 92 √8649 = 93 √8836 = 94 √9025 = 95 √9216 = 96 √9409 = 97 √9604 = 98 √9801 = 99 √10000 = 100

naobumium.info

Квадратный корень. Подробная теория с примерами.

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Для начала почитай комментарии внизу этой статьи, чтобы понять насколько крутой материал ты сейчас читаешь! )

А теперь давай попробуем разобраться, что это за понятие такое «квадратный корень».

К примеру, перед нами уравнение  .

Какое решение у данного уравнения? Какие числа можно возвести в квадрат и получить при этом  ?

Вспомнив таблицу умножения, ты легко дашь ответ:   и   (ведь при перемножении двух отрицательных чисел получается число положительное)!

Для упрощения математики ввели специальное понятие квадратного корня и присвоили ему специальный символ  

Давай разберемся с корнем до конца…

СОДЕРЖАНИЕ

---

 

Введение понятия арифметического квадратного корня​

Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа   называется такое неотрицательное число, квадрат которого равен  .  .

А почему же число   должно быть обязательно неотрицательным?

Например, чему равен  ?

Так-так, попробуем подобрать. Может, три? Проверим:  , а не  .

Может,  ? Опять же, проверяем:  .

Ну что же, не подбирается?

Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число!

Это надо запомнить: число или выражение под знаком корня должно быть неотрицательным!

 

Однако ты наверняка уже заметил, что в определении сказано, что «квадратным корнем из числа   называется такое неотрицательное число, квадрат которого равен

 ».

А в самом начале мы разбирали пример  , подбирали числа, которые можно возвести в квадрат и получить при этом  , ответом были   и  , а тут говорится про какое-то «неотрицательное число»!

Такое замечание вполне уместно. Здесь необходимо просто разграничить понятия квадратных уравнений и арифметического квадратного корня из числа.

К примеру,   не равносильно выражению  .

Из   следует, что

 , то есть   или  ;   (не помнишь почему так? Почитай тему «Модуль числа»!)

А из   следует, что  .

Конечно, это очень путает, но это необходимо запомнить, что знаки являются результатом решения уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.

В наше квадратное уравнение подходит как  , так и  .

Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат

.

Итак, вкратце на примере, нужно ли ставить «плюс-минус» (этот наглядный пример привёл наш читатель Игорь, спасибо ему за это):

Пусть есть две ситуации:

1)  

2)  

В первом случае у нас квадратное уравнение и его решением будет   (уже видно отличие от второго случая) и далее получаем два корня  

Во втором случае у нас НЕТ квадратного уравнения, просто х равен корню из числа и в этом случае ответ всегда «одно неотрицательное число», то есть 8.

А теперь попробуй решить такое уравнение  .

Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?

Начнем с самого начала – с нуля:   – не подходит.

Двигаемся дальше  ;   – меньше трех, тоже отметаем.

А что если  ? Проверим:   – тоже не подходит, т.к. это больше трех.

С отрицательными числами получится такая же история.

И что же теперь делать? Неужели перебор нам ничего не дал?

Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между   и  , а также между   и  .

Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.

И что дальше?

Давай построим график функции   и отметим на нем решения.

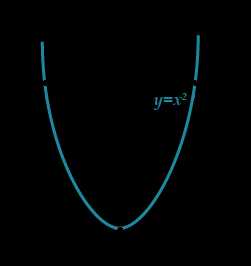
Попробуем обмануть систему и получить ответ с помощью калькулятора! Извлечем корень из  , делов-то!

Ой-ой-ой, выходит, что   Такое число никогда не кончается.

Как же такое запомнить, ведь на экзамене калькулятора не будет!?

Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение.   и   уже сами по себе ответы.

Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.

Рассмотрим еще один пример для закрепления. Разберем такую задачку: тебе необходимо пересечь по диагонали квадратное поле со стороной   км, сколько км тебе предстоит пройти?

Самое очевидное здесь рассмотреть отдельно треугольник и воспользоваться теоремой Пифагора:  .

Таким образом,  .

Так чему же здесь равно искомое расстояние?

Очевидно, что расстояние не может быть отрицательным, получаем, что  . Корень из двух приблизительно равен  , но, как мы заметили раньше,   -уже является полноценным ответом.

Извлечение корней

Чтобы решение примеров с корнями не вызывало проблем, необходимо их видеть и узнавать.

Для этого необходимо знать, по меньшей мере, квадраты чисел от   до  , а также уметь их распознавать.

То есть, тебе необходимо знать, что   в квадрате равно  , а также, наоборот, что   – это   в квадрате.

Первое время в извлечении корня тебе поможет эта таблица.

Как только ты прорешаешь достаточное количество примеров, то надобность в ней автоматически отпадет.

Попробуй самостоятельно извлечь квадратный корень в следующих выражениях:

1.  ;
2.  ;
3.  ;
4.  ;

Ответы:

 

Ну как, получилось? Теперь давай посмотрим такие примеры:

1.  ;
2.  ;
3.  .

Ответы:

 

 Свойства арифметического квадратного корня

Теперь ты знаешь, как извлекать корни и пришло время узнать о свойствах арифметического квадратного корня. Их всего 3:

• умножение;
• деление;
• возведение в степень.

Их ну просто очень легко запомнить с помощью этой таблицы и, конечно же, тренировки:

Свойство	Пример
Корень произведения равен произведению корней:
Корень из дроби — это корень из числителя и корень из знаменателя:  , если
Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение:  , при

Попробуем решить по несколько примеров на каждое свойство!

Умножение корней

Взглянул еще раз на табличку… И, поехали!

Начнем с простенького:

 

 

 

Минуууточку.   это  , а это значит, что мы можем записать вот так:

 

 

Усвоил? Вот тебе следующий:

 

 

Корни из получившихся чисел ровно не извлекаются? Не беда – вот тебе такие примеры:

 

 

 

А что, если множителей не два, а больше? То же самое! Формула умножения корней работает с любым количеством множителей:

 

 

Теперь полностью самостоятельно:

1.  
2.  
3.  

 

Ответы: Молодец! Согласись, все очень легко, главное знать таблицу умножения!

 

Деление корней

С умножением корней разобрались, теперь приступим к свойству деления.

Напомню, что формула в общем виде выглядит так:

 , если  .

А значит это, что корень из частного равен частному корней.

 

Ну что, давай разбираться на примерах:

 

 

Вот и вся наука. А вот такой пример:

 

Все не так гладко, как в первом примере, но, как видишь, ничего сложного нет.

 

А что, если попадется такое выражение:

 

Надо просто применить формулу в обратном направлении:

 

 

А вот такой примерчик:

 

 

Еще ты можешь встретить такое выражение:

 

 

Все то же самое, только здесь надо вспомнить, как переводить дроби (если не помнишь, загляни в тему дроби и возвращайся!). Вспомнил? Теперь решаем!

 

Уверена, что ты со всем, всем справился, теперь попробуем возводить корни в степени.

 

Возведение в степень

А что же будет, если квадратный корень возвести в квадрат? Все просто, вспомним смысл квадратного корня из числа   – это число, квадратный корень которого равен  .

Так вот, если мы возводим число, квадратный корень которого равен  , в квадрат, то что получаем?

Ну, конечно,  !

Рассмотрим на примерах:

 
 

 

 

Все просто, правда? А если корень будет в другой степени? Ничего страшного!

Придерживайся той же логики и помни свойства и возможные действия со степенями.

Забыл?

Почитай теорию по теме «Степень и ее свойства» и тебе все станет предельно ясно.

Вот, к примеру, такое выражение:

 

В этом примере степень четная, а если она будет нечетная? Опять же, примени свойства степени и разложи все на множители:

 

С этим вроде все ясно, а как извлечь корень из числа в степени? Вот, к примеру, такое:

 

Довольно просто, правда? А если степень больше двух? Следуем той же логике, используя свойства степеней:

 
 

Ну как, все понятно? Тогда реши самостоятельно примеры:

1.  
2.  
3.  

А вот и ответы:

 

Внесение под знак корня

Что мы только не научились делать с корнями! Осталось только потренироваться вносить число под знак корня!

Это совсем легко! 

 

 

Допустим, у нас записано число  

Что мы можем с ним сделать? Ну конечно, спрятать тройку под корнем, помня при этом, что тройка – корень квадратный из  !

 

Зачем нам это нужно? Да просто, чтобы расширить наши возможности при решении примеров:

 
Как тебе такое свойство корней? Существенно упрощает жизнь? По мне, так точно! Только надо помнить, что вносить под знак квадратного корня мы можем только положительные числа.

Реши самостоятельно вот этот пример —  
Справился? Давай смотреть, что у тебя должно получиться:

 

Молодец! У тебя получилось внести число под знак корня! Перейдем к не менее важному – рассмотрим, как сравнивать числа, содержащие квадратный корень!

 

Сравнение корней

Зачем нам учиться сравнивать числа, содержащие квадратный корень?

Очень просто. Часто, в больших и длиииинных выражениях, встречающихся на экзамене, мы получаем иррациональный ответ (помнишь, что это такое? Мы с тобой сегодня об этом уже говорили!)

Полученные ответы нам необходимо расположить на координатной прямой, например, чтобы определить, какой интервал подходит для решения уравнения. И вот здесь возникает загвоздка: калькулятора на экзамене нет, а без него как представить какое число больше, а какое меньше? То-то и оно!

Например, определи, что больше:   или  ?

Сходу и не скажешь. Ну что, воспользуемся разобранным свойством внесения числа под знак корня?

Тогда вперед:

 

 

 

Ну и, очевидно, что чем больше число под знаком корня, тем больше сам корень!

Т.е. если  , значит,  .

Отсюда твердо делаем вывод, что  . И никто не убедит нас в обратном!

 

Извлечение корней из больших чисел

До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!

 

Можно было пойти по иному пути и разложить на другие множители:

 

Что дальше? А дальше раскладываем на множители до самого конца:

 

Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.

Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:

 

Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:

А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):

 

 

Разве это конец? Не останавливаемся на полпути!

 

На простые множители разложили. Что дальше? А дальше пользуемся свойством умножение корней и записываем все под одним знаком корня:

 

Вот и все, не так все и страшно, правда?

 

Получилось  ? Молодец, все верно!

А теперь попробуй вот такой пример решить:

 

А пример-то – крепкий орешек, так сходу и не разберешься, как к нему подступиться. Но нам он, конечно, по зубам.

 

Ну что, начнем раскладывать   на множители? Сразу заметим, что можно поделить число на   (вспоминаем признаки делимости):

 

А теперь, попробуй сам (опять же, без калькулятора!):

 

Ну что, получилось  ? Молодец, все верно!

 

Подведем итоги

1. Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа   называется такое неотрицательное число, квадрат которого равен  .
    .
2. Если мы просто извлекаем квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.
3. Свойства арифметического корня:

   Свойство	Пример
   Корень произведения равен произведению корней , если
   Корень из дроби — это корень из числителя и корень из знаменателя. , если
   Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение , при

4. При сравнении квадратных корней необходимо помнить, что чем больше число под знаком корня, тем больше сам корень.

 

Как тебе квадратный корень? Все понятно?

Мы постарались объяснить тебе без воды все что нужно знать на экзамене про квадратный корень.

Теперь твоя очередь. Напиши нам сложная это для тебя тема или нет.

Узнал ты что-то новое или все было и так ясно.

Пиши в комментариях и удачи на экзаменах!

P.S. ПОСЛЕДНИЙ БЕСЦЕННЫЙ СОВЕТ 🙂

Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.

Почему?

Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!

Теперь самое главное.

Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.

Проблема в том, что этого может не хватить…

Для чего?

Для успешной сдачи ОГЭ или ЕГЭ, для перехода в 10-й класс или поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.

Я не буду тебя ни в чем убеждать, просто скажу одну вещь…

Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.

Но и это — не главное.

Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…

Но, думай сам…

Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?

НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.

На экзамене у тебя не будут спрашивать теорию.

Тебе нужно будет решать задачи на время.  

И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.

Это как в спорте — нужно много раз повторить, чтобы выиграть наверняка.  

Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!

Я рекомендую использовать для этих целей наш учебник «YouClever» (который ты сейчас читаешь, но без ограничений) и решебник и программу подготовки «100gia».

Условия их приобретения изложены здесь: кликните по этой ссылке, приобретите доступ к YouClever и 100gia и начните готовиться прямо сейчас!

 

 

И в заключение…

Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.

“Понял” и “Умею решать” — это совершенно разные навыки. Тебе нужны оба.

Найди задачи и решай!

Удачи!

youclever.org

Таблица корней

В данной статье мы с вами разберем такое понятие как квадратный корень, какие бывают виды корней, а так же рассмотрим таблицу корней и то как ей пользоваться.

Итак, что же такое квадратный корень. Для того чтобы это понять воспользуемся примерами из школьного курса и рассмотрим простое уравнение, типа: х2 = 4. Что бы его решить нужно понять какое число нужно возводить в квадрат для получения 4. Это не так уж и сложно так как таблица умножения подсказывает нам что это 2 либо -2. с целью упрощения математического решения и ввели понятие квадратного корня с присвоением ему специального символа ?.

Квадратным корнем положительного числа а, будет только положительное число квадрат от которого равняется а.

Как вы думаете почему а может быть только положительное число. Опять обратимся к примеру и найдем корень для ?(-9). И это будет 32 = 9, но не — 9, а если возьмем -3. Проверим (-3)2 = 9. Опять не получается и все это из-за того что не существует таких чисел, которые в квадрате давали бы число со знаком минус.

Можно заметить что квадратный корень в решении, может быть только положительным числом, но почему тогда в первом уравнении упоминалось как 2 так и -2? Объясняю, есть квадратные уравнения и арифметические квадратные корни от числа и это разные вещи. Например х2=4 не тоже самое что х=?4.

Да, в этом легко запутаться, но когда нужно только извлечь корень от какого либо числа, то в ответе получим исключительно положительный ответ.

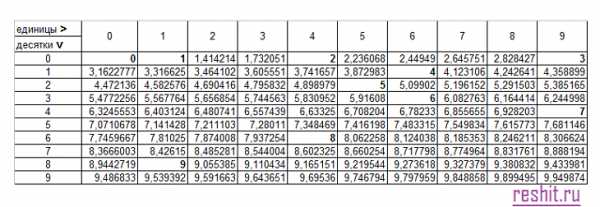
Для удобства и быстроты нахождения решений, существует таблица корней, которая содержит в себе уже готовые извлеченные корни. Пользуйтесь!
Верхняя строка содержит единицы, а левый столбец десятки. К примеру вам необходимо узнать квадратный корень числа 54. Ищем десятки с левой стороны (это будет цифра 5), а единицы с верху (это будет цифра 4). При пересечении этих значений и находится нужный нам ответ который равен 6,7082.

Таблица корней от 0 до 99

Также есть таблица квадратов, не путайте с таблицей корней. Выглядит она так:

Она удобно если вам нужно сразу получить значение двухзначного числа в квадрате. К примеру, нужно возвести 89 в квадрат. Находим 8 слева, 9 сверху, на пересечении значение квадрата — 7921.

Чем больше вы будите работать с корнями, тем реже будите пользоваться данной таблицей. Так как все значения со временем запоминаются. Это как таблица умножения, которой мы пользуемся только для изучения и запоминания.

С корнями возможно производить только три действия и это:

— умножать,
— делить,
-возводить в степень.

Свойства и Примеры объединены и показаны в таблице.

_{Когда срочно нужна курсовая работа, а времени на её написание практически нет. Стоит обратиться за помощью, которая находиться на сайте http://zakazat-kursovuyu.ru/index.php/zakaz-kursovoj. Ценой и качеством Вы будите приятно удивленны.}

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

reshit.ru

Таблица корней по алгебре

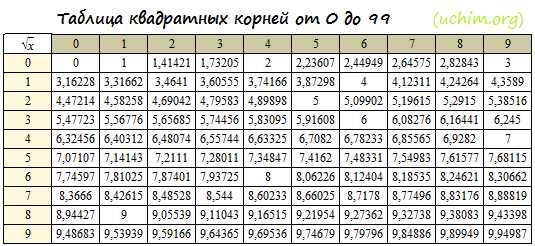
Таблица корней — это таблица, с помощью которой можно извлекать квадратные корни чисел от 0 до 99. Пользоваться таблицей очень легко. Просто выберите число десятков по вертикали и число единиц по горизонтали, результат будет на их пересечении. Например, √36=6. 3 выбирается слева, 6 — сверху. Возможно, вам также будет интересна таблица квадратов.

Извлечение корней онлайн

√

https://uchim.org/matematika/tablica-kornej — uchim.org

Таблица корней по алгебре (числа от 0 до 99, округление до пятого знака)

√x	0	1	2	3	4	5	6	7	8	9
0	0	1	1,41421	1,73205	2	2,23607	2,44949	2,64575	2,82843	3
1	3,16228	3,31662	3,4641	3,60555	3,74166	3,87298	4	4,12311	4,24264	4,3589
2	4,47214	4,58258	4,69042	4,79583	4,89898	5	5,09902	5,19615	5,2915	5,38516
3	5,47723	5,56776	5,65685	5,74456	5,83095	5,91608	6	6,08276	6,16441	6,245
4	6,32456	6,40312	6,48074	6,55744	6,63325	6,7082	6,78233	6,85565	6,9282	7
5	7,07107	7,14143	7,2111	7,28011	7,34847	7,4162	7,48331	7,54983	7,61577	7,68115
6	7,74597	7,81025	7,87401	7,93725	8	8,06226	8,12404	8,18535	8,24621	8,30662
7	8,3666	8,42615	8,48528	8,544	8,60233	8,66025	8,7178	8,77496	8,83176	8,88819
8	8,94427	9	9,05539	9,11043	9,16515	9,21954	9,27362	9,32738	9,38083	9,43398
9	9,48683	9,53939	9,59166	9,64365	9,69536	9,74679	9,79796	9,84886	9,89949	9,94987

Таблица корней в виде компактной картинки (удобно для шпаргалки, например, в 8 классе):

Всё для учебы » Математика в школе » Таблица корней по алгебре

Чтобы добавить страницу в закладки, нажмите Ctrl+D.

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:

Ссылка: https://uchim.org/matematika/tablica-kornej

Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):

uchim.org

Квадратный корень. Действия с квадратными корнями. Модуль. Сравнение квадратных корней

Факт 1.
\(\bullet\) Возьмем некоторое неотрицательное число \(a\) (то есть \(a\geqslant 0\)). Тогда (арифметическим) квадратным корнем из числа \(a\) называется такое неотрицательное число \(b\), при возведении которого в квадрат мы получим число \(a\): \[\sqrt a=b\quad \text{то же самое, что }\quad a=b^2\] Из определения следует, что \(a\geqslant 0, b\geqslant 0\). Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть \(100^2=10000\geqslant 0\) и \((-100)^2=10000\geqslant 0\).
\(\bullet\) Чему равен \(\sqrt{25}\)? Мы знаем, что \(5^2=25\) и \((-5)^2=25\). Так как по определению мы должны найти неотрицательное число, то \(-5\) не подходит, следовательно, \(\sqrt{25}=5\) (так как \(25=5^2\)).
Нахождение значения \(\sqrt a\) называется извлечением квадратного корня из числа \(a\), а число \(a\) называется подкоренным выражением.
\(\bullet\) Исходя из определения, выражения \(\sqrt{-25}\), \(\sqrt{-4}\) и т.п. не имеют смысла.  

Факт 2.
Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от \(1\) до \(20\): \[\begin{array}{|ll|} \hline 1^2=1 & \quad11^2=121 \\ 2^2=4 & \quad12^2=144\\ 3^2=9 & \quad13^2=169\\ 4^2=16 & \quad14^2=196\\ 5^2=25 & \quad15^2=225\\ 6^2=36 & \quad16^2=256\\ 7^2=49 & \quad17^2=289\\ 8^2=64 & \quad18^2=324\\ 9^2=81 & \quad19^2=361\\ 10^2=100& \quad20^2=400\\ \hline \end{array}\]

Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\] Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\), то первоначально вы должны найти значения \(\sqrt{25}\) и \(\sqrt{49}\), а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\) или \(\sqrt b\) при сложении \(\sqrt a+\sqrt b\) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt 2+ \sqrt {49}\) мы можем найти \(\sqrt{49}\) – это \(7\), а вот \(\sqrt 2\) никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt 2+7\). Дальше это выражение, к сожалению, упростить никак нельзя   \(\bullet\) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad \sqrt a:\sqrt b=\sqrt{a:b}\] (при условии, что обе части равенств имеют смысл)
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot 2}=\sqrt{64}=8\);   \(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\);   \(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}= 5\cdot 8=40\).   \(\bullet\) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\). Так как \(44100:100=441\), то \(44100=100\cdot 441\). По признаку делимости число \(441\) делится на \(9\) (так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\), то есть \(441=9\cdot 49\).
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}= \sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\] Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}= \sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{ \dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot \sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\) Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\) (сокращенная запись от выражения \(5\cdot \sqrt2\)). Так как \(5=\sqrt{25}\), то \[5\sqrt2=\sqrt{25}\cdot \sqrt2=\sqrt{25\cdot 2}=\sqrt{50}\] Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\),
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\).

 

Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число \(\sqrt2\) мы не можем. Представим, что \(\sqrt2\) – это некоторое число \(a\). Соответственно, выражение \(\sqrt2+3\sqrt2\) есть не что иное, как \(a+3a\) (одно число \(a\) плюс еще три таких же числа \(a\)). А мы знаем, что это равно четырем таким числам \(a\), то есть \(4\sqrt2\).  

Факт 4.
\(\bullet\) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака \(\sqrt {} \ \) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа \(16\) можно, потому что \(16=4^2\), поэтому \(\sqrt{16}=4\). А вот извлечь корень из числа \(3\), то есть найти \(\sqrt3\), нельзя, потому что нет такого числа, которое в квадрате даст \(3\).
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\) и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\)), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\)) и т.д.
\(\bullet\) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.  

Факт 5.
\(\bullet\) Модуль вещественного числа \(a\) – это неотрицательное число \(|a|\), равное расстоянию от точки \(a\) до \(0\) на вещественной прямой. Например, \(|3|\) и \(|-3|\) равны 3, так как расстояния от точек \(3\) и \(-3\) до \(0\) одинаковы и равны \(3\).
\(\bullet\) Если \(a\) – неотрицательное число, то \(|a|=a\).
Пример: \(|5|=5\); \(\qquad |\sqrt2|=\sqrt2\).   \(\bullet\) Если \(a\) – отрицательное число, то \(|a|=-a\).
Пример: \(|-5|=-(-5)=5\); \(\qquad |-\sqrt3|=-(-\sqrt3)=\sqrt3\).
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число \(0\), модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная \(x\) (или какая-то другая неизвестная), например, \(|x|\), про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: \(|x|\).   \(\bullet\) Имеют место следующие формулы: \[{\large{\sqrt{a^2}=|a|}}\] \[{\large{(\sqrt{a})^2=a}}, \text{ при условии } a\geqslant 0\] Очень часто допускается такая ошибка: говорят, что \(\sqrt{a^2}\) и \((\sqrt a)^2\) – одно и то же. Это верно только в том случае, когда \(a\) – полож

shkolkovo.net

Справочная таблица по теме: Арифметический квадратный корень

Арифметический квадратный корень.

Определение:

Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.

Арифметический квадратный корень из числа а обозначают .

Выражение, стоящее под знаком корня, называют подкоренным выражением.

Н,

Свойства арифметического квадратного корня:

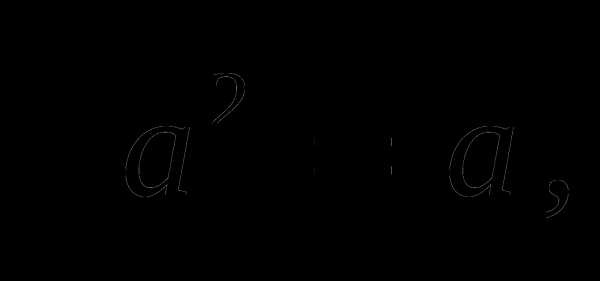где а — любое число;

где а≥0, b≥0;

где а≥0, b>0.

Н,

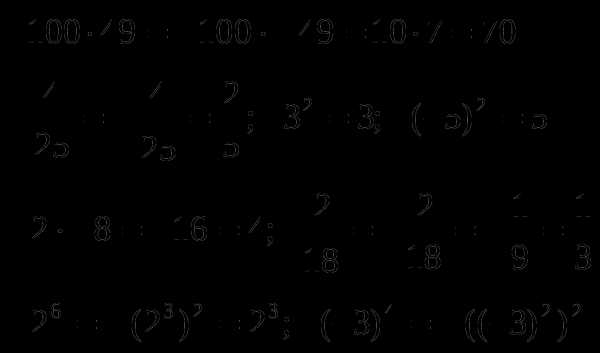
С помощью свойств корня, не применяя калькулятор и таблицы, вычислить:

Вынесение множителя из-под знака корня.

Внесение множителя под знак корня.

infourok.ru

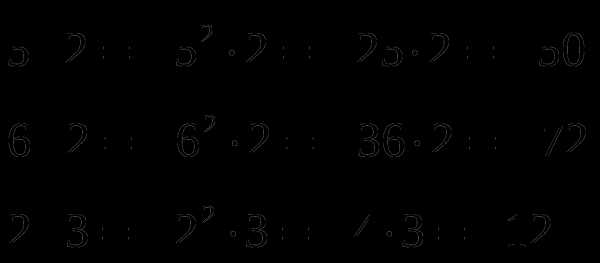
Числа / math5school.ru

2 3 5 7     11     13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103    107    109 113 127 131 137 139    149    151 157 163 167 173 179 181    191    193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277  281 283 293 307 311 313 317 331 337 347 349 353 359 367 373  379 383 389 397 401 409 419 421    431    433 439

443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811    821    823 827  829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991  997 1009 1013

1019 1021  1031  1033 1039 1049 1051  1061  1063 1069 1087 1091 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171 1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283 1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1381 1399 1409  1423 1427 1429 1433 1439 1447  1451 1453 1459 1471 1481 1483  1487  1489 1493 1499 1511 1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609 1613

1619 1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741 1747 1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861 1867 1871 1873 1877 1879 1889 1901 1907 1913 1931 1933  1949  1951 1973 1979 1987 1993 1997 1999 2003 2011 2017 2027 2029 2039 2053 2063 2069 2081 2083  2087  2089 2099 2111 2113  2129  2131 2137 2141 2143 2153 2161 2179 2203 2207 2213 2221 2237 2239 2243 2251 2267 2269 2273 2281 2287

2293 2297 2309 2311 2333 2339  2341 2347 2351 2357 2371 2377 2381 2383 2389 2393 2399 2411 2417 2423 2437 2441 2447 2459 2467 2473 2477 2503 2521 2531 2539 2543 2549 2551 2557 2579 2591 2593 2609 2617 2621 2633 2647 2657 2659 2663 2671 2677 2683 2687 2689 2693 2699 2707 2711 2713 2719 2729 2731  2741 2749 2753 2767 2777 2789 2791 2797 2801 2803 2819 2833 2837 2843 2851 2857 2861 2879 2887 2897 2903 2909 2917 2927 2939 2953

2957 2963 2969 2971  2999  3001 3011 3019 3023 3037 3041 3049 3061 3067 3079 3083 3089 3109 3119 3121 3137 3163 3167 3169 3181 3187 3191 3203 3209 3217 3221 3229 3251 3253  3257  3259 3271 3299 3301 3307 3313 3319 3323 3329 3331 3343 3347 3359 3361  3371  3373 3389 3391 3407 3413 3433 3449 3457 3461  3463  3467  3469 3491 3499 3511 3517 3527 3529 3533 3539 3541 3547 3557 3559 3571 3581 3583 3593 3607 3613 3617 3623 3631 3637 3643

3659  3671 3673 3677 3691 3697 3701 3709 3719 3727 3733 3739 3761 3767 3769 3779 3793 3797 3803 3821 3823 3833 3847 3851 3853 3863 3877 3881 3889 3907 3911 3917 3919 3923 3929 3931 3943 3947 3967 3989 4001 4003 4007 4013 4019 4021 4027 4049 4051 4057 4073 4079 4091 4093 4099 4111 4127 4129 4133  4139 4153 4157 4159 4177 4201 4211 4217 4219  4229  4231 4241 4243 4253 4259 4261  4271  4273 4283 4289 4297 4327 4337 4339 4349 4357

4363 4373 4391 4397 4409 4421  4423 4441 4447 4451 4457 4463 4481 4483 4493 4507 4513 4517 4519 4523 4547 4549 4561 4567 4583 4591 4597 4603 4621 4637 4639 4643 4649 4651 4657 4663 4673 4679 4691 4703 4721 4723 4729 4733 4751 4759 4783 4787 4789 4793 4799 4801 4813 4817 4831 4861 4871 4877 4889  4903 4909 4919 4931 4933 4937 4943 4951 4957 4967 4969 4973 4987 4993 4999 5003 5009 5011  5021  5023 5039 5051 5059 5077 5081 5087

5099 5101 5107 5113 5119 5147  5153 5167 5171 5179 5189 5197 5209 5227 5231 5233 5237 5261 5273 5279 5281 5297 5303 5309 5323 5333 5347 5351 5381 5387 5393 5399 5407 5413 5417 5419 5431 5437 5441 5443 5449 5471 5477 5479 5483 5501 5503 5507 5519 5521 5527 5531 5557 5563 5569 5573 5581 5591 5623  5639 5641 5647 5651 5653  5657  5659 5669 5683 5689 5693 5701 5711 5717 5737 5741 5743 5749 5779 5783 5791 5801 5807 5813 5821 5827

5839 5843 5849 5851 5857 5861  5867 5869  5879  5881 5897 5903 5923 5927 5939 5953 5981 5987 6007 6011 6029 6037 6043 6047 6053 6067 6073 6079 6089 6091 6101 6113 6121 6131 6133 6143 6151 6163 6173 6197 6199 6203 6211 6217 6221 6229 6247 6257 6263 6269 6271 6277 6287 6299 6301 6311 6317 6323 6329  6337 6343 6353 6359 6361 6367 6373 6379 6389 6397 6421 6427 6449 6451 6469 6473 6481 6491 6521 6529 6547 6551 6553 6563 6569 6571

6577 6581 6599 6607 6619 6637  6653 6659 6661 6673 6679 6689 6691  6701  6703 6709 6719 6733 6737 6761 6763  6779  6781 6791 6793 6803 6823 6827 6829 6833 6841 6857 6863 6869 6871 6883 6899 6907 6911 6917 6947 6949  6959  6961 6967 6971 6977 6983 6991 6997 7001 7013 7019 7027 7039 7043 7057 7069 7079  7103 7109 7121 7127 7129 7151 7159 7177 7187 7193 7207 7211 7213 7219 7229 7237 7243 7247 7253 7283 7297 7307 7309 7321 7331 7333

7349 7351 7369 7393 7411 7417  7433 7451 7457 7459 7477 7481 7487 7489 7499 7507 7517 7523 7529 7537 7541 7547 7549 7559 7561 7573 7577 7583 7589 7591 7603 7607 7621 7639 7643 7649 7669 7673 7681 7687 7691 7699 7703 7717 7723 7727 7741 7753 7757 7759 7789 7793 7817 7823 7829 7841 7853 7867 7873  7877 7879 7883 7901 7907 7919 7927 7933 7937 7949 7951 7963 7993 8009 8011 8017 8039 8053 8059 8069 8081 8087 8089 8093 8101 8111

8117 8123 8147 8161 8167 8171 8179 8191 8209 8219 8221  8231  8233 8237 8243 8263  8269 8273 8287 8291 8293 8297 8311 8317 8329 8353 8363 8369 8377 8387 8389 8419 8423 8429 8431 8443 8447 8461 8467 8501 8513 8521 8527 8537 8539 8543 8563 8573 8581 8597 8599 8609 8623 8627 8629 8641 8647 8663 8669  8677 8681 8689 8693 8699 8707 8713 8719 8731 8737 8741 8747 8753 8761 8779 8783 8803 8807 8819 8821 8831 8837 8839 8849 8861 8863

8867 8887 8893 8923 8929 8933  8941 8951 8963 8969 8971  8999  9001 9007 9011 9013 9029 9041 9043 9049 9059 9067 9091 9103 9109 9127 9133 9137 9151 9157 9161 9173 9181 9187 9199 9203 9209 9221 9227 9239 9241 9257 9277 9281 9283 9293 9311 9319 9323 9337 9341 9343 9349 9371 9377 9391 9397 9403 9413  9419 9421  9431  9433 9437 9439  9461  9463 9467 9473 9479 9491 9497 9511 9521 9533 9539 9547 9551 9587 9601 9613 9619 9623 9629 9631

9643 9649 9661 9677 9679 9689 9697 9719  9721 9733 9739 9743 9749 9767 9769 9781 9787 9791 9803 9811 9817 9829 9833 9839 9851 9857 9859  9871 9883 9887 9901 9907 9923 9929 9931 9941 9949 9967 9973

math4school.ru