Таблица корней по алгебре
Таблица корней — это таблица, с помощью которой можно извлекать квадратные корни чисел от 0 до 99. Пользоваться таблицей очень легко. Просто выберите число десятков по вертикали и число единиц по горизонтали, результат будет на их пересечении. Например, √36=6. 3 выбирается слева, 6 — сверху. Возможно, вам также будет интересна таблица квадратов.
Извлечение корней онлайн
√https://uchim.org/matematika/tablica-kornej — uchim.org
| √x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 1,41421 | 1,73205 | 2 | 2,23607 | 2,44949 | 2,64575 | 2,82843 | 3 |
| 1 | 3,16228 | 3,31662 | 3,4641 | 3,60555 | 3,74166 | 3,87298 | 4 | 4,12311 | 4,24264 | 4,3589 |
| 2 | 4,47214 | 4,58258 | 4,69042 | 4,79583 | 4,89898 | 5 | 5,09902 | 5,19615 | 5,2915 | 5,38516 |
| 3 | 5,47723 | 5,56776 | 5,65685 | 5,74456 | 5,83095 | 5,91608 | 6 | 6,08276 | 6,16441 | 6,245 |
| 4 | 6,32456 | 6,40312 | 6,48074 | 6,55744 | 6,63325 | 6,7082 | 6,78233 | 6,85565 | 6,9282 | 7 |
| 5 | 7,07107 | 7,14143 | 7,2111 | 7,28011 | 7,34847 | 7,4162 | 7,48331 | 7,54983 | 7,61577 | 7,68115 |
| 6 | 7,74597 | 7,81025 | 7,87401 | 7,93725 | 8 | 8,06226 | 8,12404 | 8,18535 | 8,24621 | 8,30662 |
| 7 | 8,3666 | 8,42615 | 8,48528 | 8,544 | 8,60233 | 8,66025 | 8,7178 | 8,77496 | 8,83176 | 8,88819 |
| 8 | 8,94427 | 9 | 9,05539 | 9,11043 | 9,16515 | 9,21954 | 9,27362 | 9,32738 | 9,38083 | 9,43398 |
| 9 | 9,48683 | 9,53939 | 9,59166 | 9,64365 | 9,69536 | 9,74679 | 9,79796 | 9,84886 | 9,89949 | 9,94987 |
Таблица корней в виде компактной картинки (удобно для шпаргалки, например, в 8 классе):
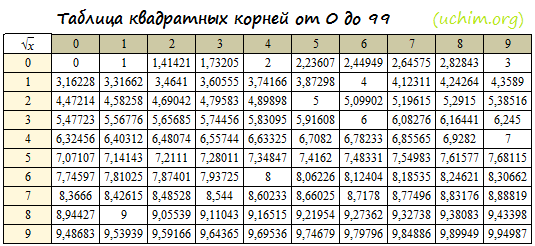
Всё для учебы » Математика в школе » Таблица корней по алгебре
Чтобы добавить страницу в закладки, нажмите Ctrl+D.
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/tablica-kornej
Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):
Таблица корней
В данной статье мы с вами разберем такое понятие как квадратный корень, какие бывают виды корней, а так же рассмотрим таблицу корней и то как ей пользоваться.
Итак, что же такое квадратный корень. Для того чтобы это понять воспользуемся примерами из школьного курса и рассмотрим простое уравнение, типа: х2 = 4. Что бы его решить нужно понять какое число нужно возводить в квадрат для получения 4. Это не так уж и сложно так как таблица умножения подсказывает нам что это 2 либо -2. с целью упрощения математического решения и ввели понятие квадратного корня с присвоением ему специального символа ?.
Квадратным корнем положительного числа а, будет только положительное число квадрат от которого равняется а.
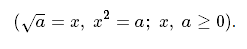
Как вы думаете почему а может быть только положительное число. Опять обратимся к примеру и найдем корень для ?(-9). И это будет 32 = 9, но не — 9, а если возьмем -3. Проверим (-3)2 = 9. Опять не получается и все это из-за того что не существует таких чисел, которые в квадрате давали бы число со знаком минус.
Можно заметить что квадратный корень в решении, может быть только положительным числом, но почему тогда в первом уравнении упоминалось как 2 так и -2? Объясняю, есть квадратные уравнения и арифметические квадратные корни от числа и это разные вещи. Например х2=4 не тоже самое что х=?4.
Да, в этом легко запутаться, но когда нужно только извлечь корень от какого либо числа, то в ответе получим исключительно положительный ответ.
Для удобства и быстроты нахождения решений, существует таблица корней, которая содержит в себе уже готовые извлеченные корни. Пользуйтесь!
Верхняя строка содержит единицы, а левый столбец десятки. К примеру вам необходимо узнать квадратный корень числа 54. Ищем десятки с левой стороны (это будет цифра 5), а единицы с верху (это будет цифра 4). При пересечении этих значений и находится нужный нам ответ который равен 6,7082.
Таблица корней от 0 до 99
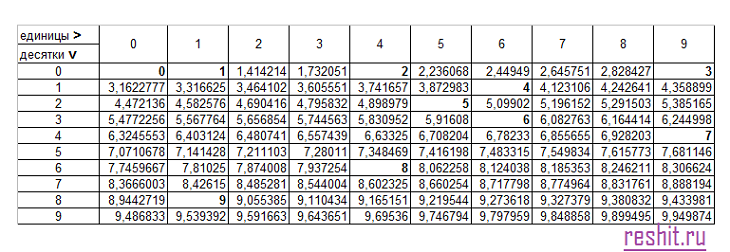
Также есть таблица квадратов, не путайте с таблицей корней. Выглядит она так:

Она удобно если вам нужно сразу получить значение двухзначного числа в квадрате. К примеру, нужно возвести 89 в квадрат. Находим 8 слева, 9 сверху, на пересечении значение квадрата — 7921.
Чем больше вы будите работать с корнями, тем реже будите пользоваться данной таблицей. Так как все значения со временем запоминаются. Это как таблица умножения, которой мы пользуемся только для изучения и запоминания.
С корнями возможно производить только три действия и это:
— умножать,
— делить,
-возводить в степень.
Свойства и Примеры объединены и показаны в таблице.

Когда срочно нужна курсовая работа, а времени на её написание практически нет. Стоит обратиться за помощью, которая находиться на сайте http://zakazat-kursovuyu.ru/index.php/zakaz-kursovoj. Ценой и качеством Вы будите приятно удивленны.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Таблица квадратных корней | Алгебра
В таблице приведены квадратные корни натуральных чисел от 1 до 100.
|
√1 = 1 √4 = 2 √9 = 3 √16 = 4 √25 = 5 √36 = 6 √49 = 7 √64 = 8 √81 = 9 √100 = 10 |
√121 = 11 √144 = 12 √169 = 13 √196 = 14 √225 = 15 √256 = 16 √289 = 17 √324 = 18 √361 = 19 √400 = 20 |
√441 = 21 √484 = 22 √529 = 23 √576 = 24 √625 = 25 √676 = 26 √729 = 27 √841 = 29 √900 = 30 |
√961 = 31 √1024 = 32 √1089 = 33 √1156 = 34 √1225 = 35 √1296 = 36 √1369 = 37 √1444 = 38 √1521 = 39 √1600 = 40 |
|
√1681 = 41 √1764 = 42 √1849 = 43 √1936 = 44 √2025 = 45 √2116 = 46 √2209 = 47 √2304 = 48 √2401 = 49 √2500 = 50 |
√2601 = 51 √2704 = 52 √2809 = 53 √2916 = 54 √3025 = 55 √3136 = 56 √3249 = 57 √3364 = 58 √3481 = 59 √3600 = 60 |
√3721 = 61 √3844 = 62 √3969 = 63 √4096 = 64 √4225 = 65 √4356 = 66 √4489 = 67 √4624 = 68 √4761 = 69 √4900 = 70 |
√5041 = 71 √5184 = 72 √5329 = 73 √5476 = 74 √5625 = 75 √5776 = 76 √5929 = 77 √6084 = 78 √6241 = 79 √6400 = 80 |
|
√6561 = 81 √6724 = 82 √6889 = 83 √7056 = 84 √7225 = 85 √7396 = 86 √7569 = 87 √7744 = 88 √7921 = 89 √8100 = 90 |
√8281 = 91 √8464 = 92 √8649 = 93 √8836 = 94 √9025 = 95 √9216 = 96 √9409 = 97 √9604 = 98 √10000 = 100 |
||
| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблицы квадратов чисел от 1. Таблица квадратов от 1 до 100. Таблица квадратных корней. Натуральных чисел от 1 до 30 и от 1 до 100. Таблица квадратов больших чисел. Квадраты чисел. Удобная расчетная таблица 1,00 — 9,99. Поделиться:
| ||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица корней с примерами
При — выражение не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу .
При решении различных математических задач часто требуются значения квадратных корней натуральных чисел. При отсутствии калькулятора посчитать их бывает затруднительно. В таблице приводятся значения корней чисел от 0 до 99 с округлением до пятого знака после запятой.
Используется таблица так: выбираем число десятков по вертикали и число единиц по горизонтали, на пересечении строчек находится результат.
Подробная таблица корней
Таблица корней может быть полезна не только при решении школьных математических задач, но при сложных вычислениях в задачах физики, механики и других прикладных задачах.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Квадратный корень. Подробная теория с примерами.
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Для начала почитай комментарии внизу этой статьи, чтобы понять насколько крутой материал ты сейчас читаешь! )
А теперь давай попробуем разобраться, что это за понятие такое «квадратный корень».
К примеру, перед нами уравнение .
Какое решение у данного уравнения? Какие числа можно возвести в квадрат и получить при этом ?
Вспомнив таблицу умножения, ты легко дашь ответ: и (ведь при перемножении двух отрицательных чисел получается число положительное)!
Для упрощения математики ввели специальное понятие квадратного корня и присвоили ему специальный символ
Давай разберемся с корнем до конца…
СОДЕРЖАНИЕ
Введение понятия арифметического квадратного корня
| Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа называется такое неотрицательное число, квадрат которого равен . . |
А почему же число должно быть обязательно неотрицательным?
Например, чему равен ?
Так-так, попробуем подобрать. Может, три? Проверим: , а не .
Может, ? Опять же, проверяем: .
Ну что же, не подбирается?
Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число!
| Это надо запомнить: число или выражение под знаком корня должно быть неотрицательным! |
Однако ты наверняка уже заметил, что в определении сказано, что «квадратным корнем из числа называется такое неотрицательное число, квадрат которого равен ».
А в самом начале мы разбирали пример , подбирали числа, которые можно возвести в квадрат и получить при этом , ответом были и , а тут говорится про какое-то «неотрицательное число»!
Такое замечание вполне уместно. Здесь необходимо просто разграничить понятия квадратных уравнений и арифметического квадратного корня из числа.
К примеру, не равносильно выражению .
Из следует, что
, то есть или ; (не помнишь почему так? Почитай тему «Модуль числа»!)
А из следует, что .
Конечно, это очень путает, но это необходимо запомнить, что знаки являются результатом решения уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.
В наше квадратное уравнение подходит как , так и .
Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.
Итак, вкратце на примере, нужно ли ставить «плюс-минус» (этот наглядный пример привёл наш читатель Игорь, спасибо ему за это):
Пусть есть две ситуации:
1)
2)
В первом случае у нас квадратное уравнение и его решением будет (уже видно отличие от второго случая) и далее получаем два корня
Во втором случае у нас НЕТ квадратного уравнения, просто х равен корню из числа и в этом случае ответ всегда «одно неотрицательное число», то есть 8.
А теперь попробуй решить такое уравнение .
Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?
Начнем с самого начала – с нуля: – не подходит.
Двигаемся дальше ; – меньше трех, тоже отметаем.
А что если ? Проверим: – тоже не подходит, т.к. это больше трех.
С отрицательными числами получится такая же история.
И что же теперь делать? Неужели перебор нам ничего не дал?
Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между и , а также между и .
Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.
И что дальше?
Давай построим график функции и отметим на нем решения.

Попробуем обмануть систему и получить ответ с помощью калькулятора! Извлечем корень из , делов-то!
Ой-ой-ой, выходит, что Такое число никогда не кончается.
Как же такое запомнить, ведь на экзамене калькулятора не будет!?
Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. и уже сами по себе ответы.
Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.
Рассмотрим еще один пример для закрепления. Разберем такую задачку: тебе необходимо пересечь по диагонали квадратное поле со стороной км, сколько км тебе предстоит пройти?

Самое очевидное здесь рассмотреть отдельно треугольник и воспользоваться теоремой Пифагора: .
Таким образом, .
Так чему же здесь равно искомое расстояние?
Очевидно, что расстояние не может быть отрицательным, получаем, что . Корень из двух приблизительно равен , но, как мы заметили раньше, -уже является полноценным ответом.
Извлечение корней
Чтобы решение примеров с корнями не вызывало проблем, необходимо их видеть и узнавать.
Для этого необходимо знать, по меньшей мере, квадраты чисел от до , а также уметь их распознавать.
То есть, тебе необходимо знать, что в квадрате равно , а также, наоборот, что – это в квадрате.
Первое время в извлечении корня тебе поможет эта таблица.

Как только ты прорешаешь достаточное количество примеров, то надобность в ней автоматически отпадет.
Попробуй самостоятельно извлечь квадратный корень в следующих выражениях:
- ;
- ;
- ;
- ;
Ответы:
Ну как, получилось? Теперь давай посмотрим такие примеры:
- ;
- ;
- .
Ответы:
- ;
- ;
- .
Свойства арифметического квадратного корня
Теперь ты знаешь, как извлекать корни и пришло время узнать о свойствах арифметического квадратного корня. Их всего 3:
- умножение;
- деление;
- возведение в степень.
Их ну просто очень легко запомнить с помощью этой таблицы и, конечно же, тренировки:
| Свойство | Пример |
|
Корень произведения равен произведению корней:
|
|
|
Корень из дроби — это корень из числителя и корень из знаменателя: , если |
|
|
Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение: , при |
Попробуем решить по несколько примеров на каждое свойство!
Умножение корней
Взглянул еще раз на табличку… И, поехали!
Начнем с простенького:
Минуууточку. это , а это значит, что мы можем записать вот так:
Усвоил? Вот тебе следующий:
Корни из получившихся чисел ровно не извлекаются? Не беда – вот тебе такие примеры:
А что, если множителей не два, а больше? То же самое! Формула умножения корней работает с любым количеством множителей:
Теперь полностью самостоятельно:
Ответы: Молодец! Согласись, все очень легко, главное знать таблицу умножения!
- ;
- ;
- .
Деление корней
С умножением корней разобрались, теперь приступим к свойству деления.
Напомню, что формула в общем виде выглядит так:
, если .
А значит это, что корень из частного равен частному корней.
Ну что, давай разбираться на примерах:
Вот и вся наука. А вот такой пример:
Все не так гладко, как в первом примере, но, как видишь, ничего сложного нет.
А что, если попадется такое выражение:
Надо просто применить формулу в обратном направлении:
А вот такой примерчик:
Еще ты можешь встретить такое выражение:
Все то же самое, только здесь надо вспомнить, как переводить дроби (если не помнишь, загляни в тему дроби и возвращайся!). Вспомнил? Теперь решаем!
Уверена, что ты со всем, всем справился, теперь попробуем возводить корни в степени.
Возведение в степень
А что же будет, если квадратный корень возвести в квадрат? Все просто, вспомним смысл квадратного корня из числа – это число, квадратный корень которого равен .
Так вот, если мы возводим число, квадратный корень которого равен , в квадрат, то что получаем?
Ну, конечно, !
Рассмотрим на примерах:
Все просто, правда? А если корень будет в другой степени? Ничего страшного!
Придерживайся той же логики и помни свойства и возможные действия со степенями.
Забыл?
Почитай теорию по теме «Степень и ее свойства» и тебе все станет предельно ясно.
Вот, к примеру, такое выражение:
В этом примере степень четная, а если она будет нечетная? Опять же, примени свойства степени и разложи все на множители:
С этим вроде все ясно, а как извлечь корень из числа в степени? Вот, к примеру, такое:
Довольно просто, правда? А если степень больше двух? Следуем той же логике, используя свойства степеней:
Ну как, все понятно? Тогда реши самостоятельно примеры:
А вот и ответы:
Внесение под знак корня
Что мы только не научились делать с корнями! Осталось только потренироваться вносить число под знак корня!
Это совсем легко!
Допустим, у нас записано число
Что мы можем с ним сделать? Ну конечно, спрятать тройку под корнем, помня при этом, что тройка – корень квадратный из !
Зачем нам это нужно? Да просто, чтобы расширить наши возможности при решении примеров:
Как тебе такое свойство корней? Существенно упрощает жизнь? По мне, так точно! Только надо помнить, что вносить под знак квадратного корня мы можем только положительные числа.
Реши самостоятельно вот этот пример —
Справился? Давай смотреть, что у тебя должно получиться:
Молодец! У тебя получилось внести число под знак корня! Перейдем к не менее важному – рассмотрим, как сравнивать числа, содержащие квадратный корень!
Сравнение корней
Зачем нам учиться сравнивать числа, содержащие квадратный корень?
Очень просто. Часто, в больших и длиииинных выражениях, встречающихся на экзамене, мы получаем иррациональный ответ (помнишь, что это такое? Мы с тобой сегодня об этом уже говорили!)
Полученные ответы нам необходимо расположить на координатной прямой, например, чтобы определить, какой интервал подходит для решения уравнения. И вот здесь возникает загвоздка: калькулятора на экзамене нет, а без него как представить какое число больше, а какое меньше? То-то и оно!
Например, определи, что больше: или ?
Сходу и не скажешь. Ну что, воспользуемся разобранным свойством внесения числа под знак корня?
Тогда вперед:
Ну и, очевидно, что чем больше число под знаком корня, тем больше сам корень!
Т.е. если , значит, .
Отсюда твердо делаем вывод, что . И никто не убедит нас в обратном!
Извлечение корней из больших чисел
До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!
Можно было пойти по иному пути и разложить на другие множители:
Что дальше? А дальше раскладываем на множители до самого конца:
Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.
Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:
Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:
А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):
Разве это конец? Не останавливаемся на полпути!
Квадратный корень. Действия с квадратными корнями. Модуль. Сравнение квадратных корней
Факт 1.
\(\bullet\) Возьмем некоторое неотрицательное число \(a\) (то есть \(a\geqslant 0\)). Тогда (арифметическим) квадратным корнем из числа \(a\) называется такое неотрицательное число \(b\), при возведении которого в квадрат мы получим число \(a\): \[\sqrt a=b\quad \text{то же самое, что }\quad a=b^2\] Из определения следует, что \(a\geqslant 0, b\geqslant 0\). Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть \(100^2=10000\geqslant 0\) и \((-100)^2=10000\geqslant 0\).
\(\bullet\) Чему равен \(\sqrt{25}\)? Мы знаем, что \(5^2=25\) и \((-5)^2=25\). Так как по определению мы должны найти неотрицательное число, то \(-5\) не подходит, следовательно, \(\sqrt{25}=5\) (так как \(25=5^2\)).
Нахождение значения \(\sqrt a\) называется извлечением квадратного корня из числа \(a\), а число \(a\) называется подкоренным выражением.
\(\bullet\) Исходя из определения, выражения \(\sqrt{-25}\), \(\sqrt{-4}\) и т.п. не имеют смысла.
Факт 2.
Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от \(1\) до \(20\): \[\begin{array}{|ll|}
\hline
1^2=1 & \quad11^2=121 \\
2^2=4 & \quad12^2=144\\
3^2=9 & \quad13^2=169\\
4^2=16 & \quad14^2=196\\
5^2=25 & \quad15^2=225\\
6^2=36 & \quad16^2=256\\
7^2=49 & \quad17^2=289\\
8^2=64 & \quad18^2=324\\
9^2=81 & \quad19^2=361\\
10^2=100& \quad20^2=400\\
\hline \end{array}\]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\] Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\), то первоначально вы должны найти значения \(\sqrt{25}\) и \(\sqrt{49}\), а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\) или \(\sqrt b\) при сложении \(\sqrt
a+\sqrt b\) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt
2+ \sqrt {49}\) мы можем найти \(\sqrt{49}\) – это \(7\), а вот \(\sqrt
2\) никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt
2+7\). Дальше это выражение, к сожалению, упростить никак нельзя
\(\bullet\) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad
\sqrt a:\sqrt b=\sqrt{a:b}\] (при условии, что обе части равенств имеют смысл)
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot
2}=\sqrt{64}=8\);
\(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\);
\(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}=
5\cdot 8=40\).
\(\bullet\) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\). Так как \(44100:100=441\), то \(44100=100\cdot 441\). По признаку делимости число \(441\) делится на \(9\) (так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\), то есть \(441=9\cdot 49\).
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}=
\sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\] Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}=
\sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{
\dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot
\sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\) Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\) (сокращенная запись от выражения \(5\cdot
\sqrt2\)). Так как \(5=\sqrt{25}\), то \[5\sqrt2=\sqrt{25}\cdot \sqrt2=\sqrt{25\cdot 2}=\sqrt{50}\] Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\),
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\).
Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число \(\sqrt2\) мы не можем. Представим, что \(\sqrt2\) – это некоторое число \(a\). Соответственно, выражение \(\sqrt2+3\sqrt2\) есть не что иное, как \(a+3a\) (одно число \(a\) плюс еще три таких же числа \(a\)). А мы знаем, что это равно четырем таким числам \(a\), то есть \(4\sqrt2\).
Факт 4.
\(\bullet\) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака \(\sqrt {} \ \) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа \(16\) можно, потому что \(16=4^2\), поэтому \(\sqrt{16}=4\). А вот извлечь корень из числа \(3\), то есть найти \(\sqrt3\), нельзя, потому что нет такого числа, которое в квадрате даст \(3\).
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\) и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\)), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\)) и т.д.
\(\bullet\) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
\(\bullet\) Модуль вещественного числа \(a\) – это неотрицательное число \(|a|\), равное расстоянию от точки \(a\) до \(0\) на вещественной прямой. Например, \(|3|\) и \(|-3|\) равны 3, так как расстояния от точек \(3\) и \(-3\) до \(0\) одинаковы и равны \(3\). 
\(\bullet\) Если \(a\) – неотрицательное число, то \(|a|=a\).
Пример: \(|5|=5\); \(\qquad |\sqrt2|=\sqrt2\).
\(\bullet\) Если \(a\) – отрицательное число, то \(|a|=-a\).
Пример: \(|-5|=-(-5)=5\); \(\qquad |-\sqrt3|=-(-\sqrt3)=\sqrt3\).
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число \(0\), модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная \(x\) (или какая-то другая неизвестная), например, \(|x|\), про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: \(|x|\).
\(\bullet\) Имеют место следующие формулы: \[{\large{\sqrt{a^2}=|a|}}\] \[{\large{(\sqrt{a})^2=a}},
\text{ при условии } a\geqslant 0\] Очень часто допускается такая ошибка: говорят, что \(\sqrt{a^2}\) и \((\sqrt a)^2\) – одно и то же. Это верно только в том случае, когда \(a\) – положительное число или ноль. А вот если \(a\) – отрицательное число, то это неверно. Достаточно рассмотреть такой пример. Возьмем вместо \(a\) число \(-1\). Тогда \(\sqrt{(-1)^2}=\sqrt{1}=1\), а вот выражение \((\sqrt {-1})^2\) вообще не существует (ведь нельзя под знак корня помещать отрицательные числа!).
Поэтому обращаем ваше внимание на то, что \(\sqrt{a^2}\) не равен \((\sqrt a)^2\)!
Пример: 1) \(\sqrt{\left(-\sqrt2\right)^2}=|-\sqrt2|=\sqrt2\), т.к. \(-\sqrt2<0\);
\(\phantom{00000}\) 2) \((\sqrt{2})^2=2\).
\(\bullet\) Так как \(\sqrt{a^2}=|a|\), то \[\sqrt{a^{2n}}=|a^n|\] (выражение \(2n\) обозначает четное число)
То есть при извлечении корня из числа, находящегося в какой-то степени, эта степень уменьшается в два раза.
Пример:
1) \(\sqrt{4^6}=|4^3|=4^3=64\)
2) \(\sqrt{(-25)^2}=|-25|=25\) (заметим, что если модуль не поставить, то получится, что корень из числа равен \(-25\); но мы помним, что по определению корня такого быть не может: у нас всегда при извлечении корня должно получаться положительное число или ноль)
3) \(\sqrt{x^{16}}=|x^8|=x^8\) (так как любое число в четной степени неотрицательно)
Факт 6.
Как сравнить два квадратных корня?
\(\bullet\) Для квадратных корней верно: если \(\sqrt a<\sqrt b\), то \(a<b\); если \(\sqrt a=\sqrt b\), то \(a=b\).
Пример:
1) сравним \(\sqrt{50}\) и \(6\sqrt2\). Для начала преобразуем второе выражение в \(\sqrt{36}\cdot \sqrt2=\sqrt{36\cdot 2}=\sqrt{72}\). Таким образом, так как \(50<72\), то и \(\sqrt{50}<\sqrt{72}\). Следовательно, \(\sqrt{50}<6\sqrt2\).
2) Между какими целыми числами находится \(\sqrt{50}\)?
Так как \(\sqrt{49}=7\), \(\sqrt{64}=8\), а \(49<50<64\), то \(7<\sqrt{50}<8\), то есть число \(\sqrt{50}\) находится между числами \(7\) и \(8\).
3) Сравним \(\sqrt 2-1\) и \(0,5\). Предположим, что \(\sqrt2-1>0,5\): \[\begin{aligned}
&\sqrt 2-1>0,5 \ \big| +1\quad \text{(прибавим единицу к обеим
частям)}\\[1ex]
&\sqrt2>0,5+1 \ \big| \ ^2 \quad\text{(возведем обе части в
квадрат)}\\[1ex]
&2>1,5^2\\
&2>2,25 \end{aligned}\] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1<0,5\).
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3<\sqrt2\) нельзя (убедитесь в этом сами)!
\(\bullet\) Следует запомнить, что \[\begin{aligned}
&\sqrt 2\approx 1,4\\[1ex]
&\sqrt 3\approx 1,7 \end{aligned}\] Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
\(\bullet\) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. Покажем, как это работает, на примере.
Возьмем \(\sqrt{28224}\). Мы знаем, что \(100^2=10\,000\), \(200^2=40\,000\) и т.д. Заметим, что \(28224\) находится между \(10\,000\) и \(40\,000\). Следовательно, \(\sqrt{28224}\) находится между \(100\) и \(200\).
Теперь определим, между какими “десятками” находится наше число (то есть, например, между \(120\) и \(130\)). Также из таблицы квадратов знаем, что \(11^2=121\), \(12^2=144\) и т.д., тогда \(110^2=12100\), \(120^2=14400\), \(130^2=16900\), \(140^2=19600\), \(150^2=22500\), \(160^2=25600\), \(170^2=28900\). Таким образом, мы видим, что \(28224\) находится между \(160^2\) и \(170^2\). Следовательно, число \(\sqrt{28224}\) находится между \(160\) и \(170\).
Попробуем определить последнюю цифру. Давайте вспомним, какие однозначные числа при возведении в квадрат дают на конце \(4\)? Это \(2^2\) и \(8^2\). Следовательно, \(\sqrt{28224}\) будет заканчиваться либо на 2, либо на 8. Проверим это. Найдем \(162^2\) и \(168^2\):
\(162^2=162\cdot 162=26224\)
\(168^2=168\cdot 168=28224\).
Следовательно, \(\sqrt{28224}=168\). Вуаля!
Таблица квадратов и квадратных корней

Используйте эту таблицу, чтобы найти квадраты и квадратные корни чисел от 1 до 100 .
Эту таблицу также можно использовать для вычисления квадратных корней из больших чисел.
- Например, если вы хотите найти квадратный корень из 2000 , посмотрите в среднем столбце , пока не найдете число, наиболее близкое к 2000. Число в среднем столбце, которое ближе всего к 2000, равно 2,025 .
- Теперь посмотрите на число слева от от 2,025 , чтобы найти его квадратный корень. Квадратный корень из 2025 равен 45 .
- Следовательно, приблизительный квадратный корень из 2000 составляет 45 .
Чтобы получить более точное число, вам понадобится калькулятор (44,721 — это более точный квадратный корень из 2000).
Готовитесь к длительной учебной сессии? Возможно, вас заинтересует наш список лучших настольных стульев 2020 года.
| НОМЕР | SQUARE | SQUARE ROOT | |||
| 1 | 1 | 1.000 | |||
| 2 | 4 | 1,414 | |||
| 3 | 9 | 1,732 | |||
| 4 | 16 | 2.000 | |||
| 5 | 25 | 2,236 | |||
| 6 | 36 | 2,449 | |||
| 7 | 49 | 2,646 | |||
| 8 | 64 | 2,828 | |||
| 9 | 81 | 3.000 | |||
| 10 | 100 | 3,162 | |||
| 11 | 121 | 3,317 | |||
| 12 | 144 | 3,464 | |||
| 13 | 169 | 3,606 | |||
| 14 | 196 | 3,742 | |||
| 15 | 225 | 3,873 | |||
| 16 | 256 | 4.000 | |||
| 17 | 289 | 4.123 | |||
| 18 | 324 | 4,243 | |||
| 19 | 361 | 4,359 | |||
| 20 | 400 | 4,472 | |||
| 21 | 441 | 4,583 | |||
| 22 | 484 | 4,690 | |||
| 23 | 529 | 4,796 | |||
| 24 | 576 | 4,899 | |||
| 25 | 625 | 5.000 | |||
| 26 | 676 | 5,099 | |||
| 27 | 729 | 5,196 | |||
| 28 | 784 | 5.292 | |||
| 29 | 841 | 5.385 | |||
| 30 | 900 | 5,477 | |||
| 31 | 961 | 5,568 | |||
| 32 | 1,024 | 5,657 | |||
| 33 | 1,089 | 5.745 | |||
| 34 | 1,156 | 5,831 | |||
| 35 | 1,225 | 5,916 | |||
| 36 | 1,296 | 6.000 | |||
| 37 | 1,369 | 6.083 | |||
| 38 | 1,444 | 6,164 | |||
| 39 | 1,521 | 6,245 | |||
| 40 | 1,600 | 6,325 | |||
| 41 | 1,681 | 6.403 | |||
| 42 | 1,764 | 6,481 | |||
| 43 | 1,849 | 6,557 | |||
| 44 | 1,936 | 6,633 | |||
| 45 46 | 2,025 | 6,708 | |||
| 2116 | 6,782 | ||||
| 47 | 2,209 | 6,856 | |||
| 48 | 2 304 | 6,928 | |||
| 49 | 2,401 | 7.000 | |||
| 50 | 2,500 | 7,071 | |||
| 51 | 2,601 | 7,141 | |||
| 52 | 2704 | 7,211 | |||
| 53 | 2,809 | 7,280 | 2,916 | 7,348 | |
| 55 | 3,025 | 7,416 | |||
| 56 | 3,136 | 7,483 | |||
| 57 | 3,249 | 7.550 | |||
| 58 | 3,364 | 7,616 | |||
| 59 | 3,481 | 7,681 | |||
| 60 | 3,600 | 7,746 | |||
| 61 | 3,721 | 7,810 | 62 | 3,844 | 7,874 |
| 63 | 3,969 | 7,937 | |||
| 64 | 4,096 | 8,000 | |||
| 65 | 4225 | 8.062 | |||
| 66 | 4,356 | 8,124 | |||
| 67 | 4,489 | 8,185 | |||
| 68 | 4,624 | 8,246 | |||
| 69 | 4,761 | 8,307 | 4,900 | 8,367 | |
| 71 | 5,041 | 8,426 | |||
| 72 | 5,184 | 8,485 | |||
| 73 | 5,329 | 8.544 | |||
| 74 | 5,476 | 8,602 | |||
| 75 | 5,625 | 8,660 | |||
| 76 | 5,776 | 8,718 | |||
| 77 | 5,929 | 8,743 | 786084 | 8,832 | |
| 79 | 6241 | 8,888 | |||
| 80 | 6,400 | 8,944 | |||
| 81 | 6,561 | 9.000 | |||
| 82 | 6,724 | 9,055 | |||
| 83 | 6,889 | 9,110 | |||
| 84 | 7,056 | 9,165 | |||
| 85 | 7,225 | 9,220 | 867,396 | 9,274 | |
| 87 | 7,569 | 9,327 | |||
| 88 | 7,744 | 9,381 | |||
| 89 | 7,921 | 9.434 | |||
| 90 | 8,100 | 9,487 | |||
| 91 | 8,281 | 9,539 | |||
| 92 | 8,464 | 9,592 | |||
| 93 | 8649 | 9,644 | 8,836 | 9,695 | |
| 95 | 9,025 | 9,747 | |||
| 96 | 9,216 | 9,798 | |||
| 97 | 9,409 | 9.849 | |||
| 98 | 9,604 | 9,899 | |||
| 99 | 9,801 | 9,950 | |||
| 100 | 10,000 | 10.000 |
ПРИМЕЧАНИЕ: Квадратные корни в этой таблице округлены до ближайшая тысячная.
Средние и медианные числа и формулы, определяющие квадратные корни.Таблица квадратного корня
Ниже представлена таблица квадратных корней, которую можно использовать в качестве быстрого справочника для проверки квадратного корня из чисел от 1 до 100. Это может быть очевидным, но посмотрите ниже, как вы можете использовать таблицу для поиска квадратного корня из числа.| N | √N | N | √N |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | 1 1.414 1,732 2 2,236 2,449 2,646 2,828 3 3,162 3,317 3,464 3,606 3,742 3,873 4 4,223 4,359 4,472 4,583 4,690 4,796 4,899 5 5,099 5,196 5,292 5,385 5.477 5,568 5,657 5,745 5,831 5,916 6 6,083 6,164 6,245 6,325 6,403 6,481 6,557 6,633 68 6,856 6,928 7 7,071 | 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 | 7.141 7,211 7,280 7,348 7,416 7,483 7,550 7,616 7,681 7,746 7,810 7,874 7,937 8 8,062 8,12485 8,062 8,12485 900 8,246 8,307 8,367 8,426 8,485 8,544 8,602 8,660 8,718 8,775 8.832 8,888 8,944 9 9,055 9,110 9,165 9,220 9,274 9,327 9,381 9,42334 9,487 9,539 9,4879,539 9,747 9,798 9,849 9,899 9,950 10 |
Как читать таблицу квадратных корней, чтобы найти квадратный корень.
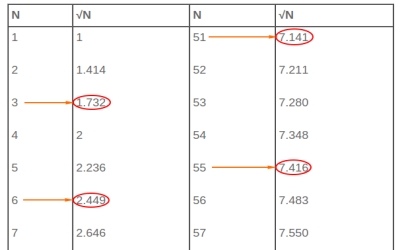
Выше мы скопировали часть таблицы квадратных корней. Из таблицы вы можете ясно видеть следующие квадратные корни.
- Квадратный корень из 3 равен 1,732
- Квадратный корень из 6 равен 2,449
- Квадратный корень из 51 равен 7,141
- Квадратный корень из 55 равен 7,416
- Квадратный корень из 7 составляет 2,646
- Квадратный корень из 53 равен 7,280
- Квадратный корень из 4 равен 2
- Квадратный корень из 78 равен 8.832
- Квадратный корень 31 равен 5,568
Краткий обзор того, что такое квадратный корень из числа.
Произведение двух одинаковых чисел — другое число. Одно из двух одинаковых чисел является квадратным корнем из другого числа.
Например, произведение 11 и 11 — это другое число или 121.
11 — квадратный корень из 121.
Новые уроки математики
Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.
.Сколько корней и корневых каналов у зубов? — таблицы / диаграммы
Количество корней и ожидаемое количество корневых каналов по типу зуба. / Таблицы и диаграммы.
Во многих видеороликах, которые мы размещаем на нашем веб-сайте, упоминается, что некоторые факторы, связанные с процессом лечения корневых каналов, зависят от того, сколько отдельных корней и корневых каналов имеет зуб.
Сюда входят: стоимость лечения, необходимое время процедуры и общая сложность случая.
Таблица: Ожидаемое количество корней и корневых каналов по типу зубов.
Если вы знаете, какой из ваших зубов будет лечиться, таблица ниже может дать вам представление о том, сколько корней и корневых каналов у него, вероятно, есть.
Фактические числа могут отличаться.
Как видно из диаграммы выше, у зубов всегда есть хотя бы один корень. И у каждого корня зуба всегда есть хотя бы один корневой канал. Но помимо этого основного формата может существовать много вариаций.
Изменчивость количества корней.
Диаграмма, показывающая количество корней для каждого типа зуба.
а) Передние (передние) зубы.
- Верхние и нижние центральные резцы, боковые резцы и клыки (клыки, глазные зубы) — у каждого всего по 1 корню.
б) Задние (задние) зубы.
- Верхние первые премоляры — 2 корня.
- Верхние 2-е премоляры — Возможны как 1, так и 2 корня.
- Нижние 1-й и 2-й премоляры (двустворчатые) — всего 1 корень.
- Верхние 1-й, 2-й и 3-й моляры — 3 корня.
- Нижние 1-й, 2-й и 3-й моляры — 2 корня.
Вариабельность количества корневых каналов.
У каждого корня зуба должен быть как минимум 1 корневой канал. Но для некоторых характерно наличие или, по крайней мере, часто больше. Вот несколько примеров распространенных вариаций, которые стоматологи должны искать.
- Нижние моляры — Ожидается, что передний (мезиальный) корень нижнего моляра (особенно 1-го моляра) будет иметь 2 канала. Нередко бывает, что задний (дистальный) корень тоже имеет 2.
- Верхние 2-е премоляры — В случае, если у этого зуба всего один корень, у него очень часто бывает 2 канала.
- Верхние моляры — Обычно передний (мезиальный) корень верхнего моляра (особенно 1-го моляра) имеет 2 канала.
- Нижние центральные и боковые резцы — Единственный корень нижнего резца иногда имеет 2 канала.
Другие варианты.
Помимо общих практических правил, приведенных выше, могут существовать и другие различия, которые даже довольно часто встречаются в реальном мире.
Стоматологические журналы забиты сообщениями о случаях, когда в зубе, подвергающемся эндодонтическому лечению, было обнаружено большее количество каналов или даже корней, чем ожидалось.
Видео, показывающие, сколько корней и корневых каналов у зубов.
Как смотреть видео. .% PDF-1.4 % ReportLab Созданный PDF-документ http://www.reportlab.com % ‘BasicFonts’: класс PDFDictionary 1 0 obj % Стандартный словарь шрифтов > endobj % ‘Annot.NUMBER1’: класс PDFDictionary 2 0 obj > / Граница [0 0 0] / Rect [219.6229 730,9469 248,7829 745.9469] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER2’: класс PDFDictionary 3 0 obj > / Граница [0 0 0] / Rect [267.4029 730,9469 290,7129 745.9469] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER3’: класс PDFDictionary 4 0 obj > / Граница [0 0 0] / Rect [293.2129 730,9469 314,8729 745.9469] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER4’: класс PDFDictionary 5 0 obj > / Граница [0 0 0] / Rect [319,8729 730,9469 343,7529 745.9469] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER5’: класс PDFDictionary 6 0 obj > / Граница [0 0 0] / Rect [367.3729 730,9469 392,9229 745.9469] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER6’: класс PDFDictionary 7 0 obj > / Граница [0 0 0] / Rect [504.4755 712,9469 530,8655 727.9469] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER7 ‘: класс PDFDictionary 8 0 объект > / Граница [0 0 0] / Rect [62.69291 697,9469 205,1629 712.9469] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘F3’: класс PDFType1Font 9 0 объект % Font Helvetica > endobj % ‘Annot.NUMBER8’: класс PDFDictionary 10 0 obj > / Граница [0 0 0] / Rect [481.2798 574 537 508,3838 586,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER9 ‘: класс PDFDictionary 11 0 объект > / Граница [0 0 0] / Rect [332.7038 544 537 350,4718 556,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER10’: класс PDFDictionary 12 0 объект > / Граница [0 0 0] / Rect [447.0638 544 537 486,1598 556,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER11’: класс PDFDictionary 13 0 объект > / Граница [0 0 0] / Rect [332.7038 526,537 358,0318 538,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER12’: класс PDFDictionary 14 0 объект > / Граница [0 0 0] / Rect [332.7038 508,537 353,5918 520,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER13’: класс PDFDictionary 15 0 объект > / Граница [0 0 0] / Rect [447.0638 508,537 472,8398 520.537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER14’: класс PDFDictionary 16 0 объект > / Граница [0 0 0] / Rect [332.7038 490,537 355,5598 502,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER15’: класс PDFDictionary 17 0 объект > / Граница [0 0 0] / Rect [447.0638 490,537 479,4958 502,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER16 ‘: класс PDFDictionary 18 0 объект > / Граница [0 0 0] / Rect [483.4958 490,537 520,8158 502,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER17’: класс PDFDictionary 19 0 объект > / Граница [0 0 0] / Rect [447.0638 478 537 475,0558 490,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER18’: класс PDFDictionary 20 0 объект > / Граница [0 0 0] / Rect [479.0558 478 537 514,5998 490,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER19’: класс PDFDictionary 21 0 объект > / Граница [0 0 0] / Rect [332.7038 460,537 346,9198 472,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER20’: класс PDFDictionary 22 0 объект > / Граница [0 0 0] / Rect [393.8878 430,537 410,5518 442.537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER21’: класс PDFDictionary 23 0 объект > / Граница [0 0 0] / Rect [447.0638 442,537 486,1598 454,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER22’: класс PDFDictionary 24 0 объект > / Граница [0 0 0] / Rect [447.0638 430,537 483.0558 442,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER23 ‘: класс PDFDictionary 25 0 объект > / Граница [0 0 0] / Rect [332.7038 412,537 342,7038 424,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER24’: класс PDFDictionary 26 0 объект > / Граница [0 0 0] / Rect [332.7038 370,537 351,3678 382,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER25’: класс PDFDictionary 27 0 объект > / Граница [0 0 0] / Rect [447.0638 370,537 471,5038 382,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER26’: класс PDFDictionary 28 0 объект > / Граница [0 0 0] / Rect [332.7038 352,537 347,8798 364,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER27’: класс PDFDictionary 29 0 объект > / Граница [0 0 0] / Rect [447.0638 352,537 483,4958 364.537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER28’: класс PDFDictionary 30 0 объект > / Граница [0 0 0] / Rect [447.0638 334 537 478,1678 346,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER29’: класс PDFDictionary 31 0 объект > / Граница [0 0 0] / Rect [482.1678 334 537 517,7118 346,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER30 ‘: класс PDFDictionary 32 0 объект > / Граница [0 0 0] / Rect [332.7038 292 537 355,0478 304,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER31’: класс PDFDictionary 33 0 объект > / Граница [0 0 0] / Rect [447.0638 292 537 479,5038 304,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER32’: класс PDFDictionary 34 0 объект > / Граница [0 0 0] / Rect [332.7038 274 537 347,3678 286,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER33’: класс PDFDictionary 35 0 объект > / Граница [0 0 0] / Rect [447.0638 274 537 481,7198 286,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER34’: класс PDFDictionary 36 0 объект > / Граница [0 0 0] / Rect [139,728 256,537 157,504 268.537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER35’: класс PDFDictionary 37 0 объект > / Граница [0 0 0] / Rect [332.7038 256,537 350,0398 268,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER36’: класс PDFDictionary 38 0 объект > / Граница [0 0 0] / Rect [447.0638 256,537 468,3918 268,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER37 ‘: класс PDFDictionary 39 0 объект > / Граница [0 0 0] / Rect [472.3918 256,537 492,3918 268,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER38’: класс PDFDictionary 40 0 объект > / Граница [0 0 0] / Rect [496.3918 256,537 523,9438 268,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER39’: класс PDFDictionary 41 0 объект > / Граница [0 0 0] / Rect [391.4478 238,537 413,8878 250,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER40’: класс PDFDictionary 42 0 объект > / Граница [0 0 0] / Rect [447.0638 238,537 472,8318 250,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER41’: класс PDFDictionary 43 0 объект > / Граница [0 0 0] / Rect [332.7038 208,537 350,7038 220.537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER42’: класс PDFDictionary 44 0 объект > / Граница [0 0 0] / Rect [447.0638 208,537 491,5038 220,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER43’: класс PDFDictionary 45 0 объект > / Граница [0 0 0] / Rect [495.5038 208,537 531.0558 220,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER44 ‘: класс PDFDictionary 46 0 объект > / Граница [0 0 0] / Rect [332.7038 190 537 355,3678 202,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER45’: класс PDFDictionary 47 0 объект > / Граница [0 0 0] / Rect [332.7038 172 537 351.0878 184,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER46’: класс PDFDictionary 48 0 объект > / Граница [0 0 0] / Rect [447.0638 172 537 480,8398 184,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER47’: класс PDFDictionary 49 0 объект > / Граница [0 0 0] / Rect [484.8398 172 537 520,8398 184,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER48’: класс PDFDictionary 50 0 объект > / Граница [0 0 0] / Rect [447.0638 160 537 488,8398 172.537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER49’: класс PDFDictionary 51 0 объект > / Граница [0 0 0] / Rect [332.7038 142,537 355,8158 154,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER50’: класс PDFDictionary 52 0 объект > / Граница [0 0 0] / Rect [447.0638 124,537 480,3918 136,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER51 ‘: класс PDFDictionary 53 0 объект > / Граница [0 0 0] / Rect [447.0638 106,537 479,5038 118,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER52’: класс PDFDictionary 54 0 объект > / Граница [0 0 0] / Rect [483.5038 106,537 521,7198 118,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER53’: класс PDFDictionary 55 0 объект > / Граница [0 0 0] / Rect [447.0638 94,53701 464,8398 106,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER54’: класс PDFDictionary 56 0 объект > / Граница [0 0 0] / Rect [468.8398 94,53701 487,9438 106,537] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER55’: класс PDFDictionary 57 0 объект > / Граница [0 0 0] / Rect [332.7038 76,53701 357.3198 88.53701] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER56’: класс PDFDictionary 58 0 объект > / Граница [0 0 0] / Rect [447.0638 76,53701 476,8318 88.53701] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER57’: класс PDFDictionary 59 0 объект > / Граница [0 0 0] / Rect [480,8318 76,53701 505,2718 88.53701] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Page1’: класс PDFPage 60 0 объект % Словарь страниц > / Повернуть 0 / Транс> / Тип / Страница >> endobj % ‘Annot.NUMBER58 ‘: класс PDFDictionary 61 0 объект > / Граница [0 0 0] / Rect [332.7038 768,7969 356,5198 780.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER59’: класс PDFDictionary 62 0 объект > / Граница [0 0 0] / Rect [447.0638 768,7969 486.6078 780.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER60’: класс PDFDictionary 63 0 объект > / Граница [0 0 0] / Rect [332.7038 750,7969 354,7038 762.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER61’: класс PDFDictionary 64 0 объект > / Граница [0 0 0] / Rect [447.0638 750,7969 468,8398 762.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER62’: класс PDFDictionary 65 0 объект > / Граница [0 0 0] / Rect [472.8398 750,7969 504.8398 762.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER63’: класс PDFDictionary 66 0 объект > / Граница [0 0 0] / Rect [332.7038 732,7969 353,8158 744.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER64’: класс PDFDictionary 67 0 объект > / Граница [0 0 0] / Rect [447.0638 732,7969 484,3838 744.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER65 ‘: класс PDFDictionary 68 0 объект > / Граница [0 0 0] / Rect [488.3838 732,7969 509,7118 744.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER66’: класс PDFDictionary 69 0 объект > / Граница [0 0 0] / Rect [447.0638 720,7969 474,6158 732.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER67’: класс PDFDictionary 70 0 объект > / Граница [0 0 0] / Rect [478.6158 720,7969 515,5118 732.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER68’: класс PDFDictionary 71 0 объект > / Граница [0 0 0] / Rect [332.7038 702,7969 346,8558 714.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER69’: класс PDFDictionary 72 0 объект > / Граница [0 0 0] / Rect [447.0638 702,7969 479.9518 714.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER70’: класс PDFDictionary 73 0 объект > / Граница [0 0 0] / Rect [483.9518 702,7969 514.1758 714.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER71’: класс PDFDictionary 74 0 объект > / Граница [0 0 0] / Rect [447.0638 690,7969 477,7278 702.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER72 ‘: класс PDFDictionary 75 0 объект > / Граница [0 0 0] / Rect [332.7038 672,7969 348,4798 684.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER73’: класс PDFDictionary 76 0 объект > / Граница [0 0 0] / Rect [447.0638 672,7969 482,6158 684.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER74’: класс PDFDictionary 77 0 объект > / Граница [0 0 0] / Rect [486.6158 672,7969 526.1678 684.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER75’: класс PDFDictionary 78 0 объект > / Граница [0 0 0] / Rect [482.1678 660,7969 518.1598 672.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER76’: класс PDFDictionary 79 0 объект > / Граница [0 0 0] / Rect [332.7038 642,7969 355.0958 654.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER77’: класс PDFDictionary 80 0 объект > / Граница [0 0 0] / Rect [447.0638 642,7969 467.0558 654.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER78’: класс PDFDictionary 81 0 объект > / Граница [0 0 0] / Rect [471.0558 642,7969 503.0558 654.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER79 ‘: класс PDFDictionary 82 0 объект > / Граница [0 0 0] / Rect [332.7038 624,7969 369,5598 636.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER80’: класс PDFDictionary 83 0 объект > / Граница [0 0 0] / Rect [447.0638 624,7969 489,7278 636.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER81’: класс PDFDictionary 84 0 объект > / Граница [0 0 0] / Rect [447.0638 612,7969 502,1678 624.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER82’: класс PDFDictionary 85 0 объект > / Граница [0 0 0] / Rect [332.7038 594,7969 348,0638 606.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER83’: класс PDFDictionary 86 0 объект > / Граница [0 0 0] / Rect [447.0638 594,7969 474.6078 606.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER84’: класс PDFDictionary 87 0 объект > / Граница [0 0 0] / Rect [478.6078 594,7969 501,2638 606.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER85’: класс PDFDictionary 88 0 объект > / Граница [0 0 0] / Rect [505.2638 594,7969 532,8158 606.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER86 ‘: класс PDFDictionary 89 0 объект > / Граница [0 0 0] / Rect [332.7038 564,7969 348,7038 576.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER87’: класс PDFDictionary 90 0 объект > / Граница [0 0 0] / Rect [488.3838 564,7969 518,5998 576.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER88’: класс PDFDictionary 91 0 объект > / Граница [0 0 0] / Rect [447.0638 552,7969 475,9438 564.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER89’: класс PDFDictionary 92 0 объект > / Граница [0 0 0] / Rect [479.9438 552,7969 502,5998 564.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER90’: класс PDFDictionary 93 0 объект > / Граница [0 0 0] / Rect [332.7038 534,7969 350.4798 546.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER91’: класс PDFDictionary 94 0 объект > / Граница [0 0 0] / Rect [447.0638 534,7969 466.6078 546.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER92’: класс PDFDictionary 95 0 объект > / Граница [0 0 0] / Rect [332.7038 516,7969 352,0318 528.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.НОМЕР93 ‘: класс PDFDictionary 96 0 объект > / Граница [0 0 0] / Rect [447.0638 516,7969 459,5038 528.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER94’: класс PDFDictionary 97 0 объект > / Граница [0 0 0] / Rect [332.7038 498,7969 351,7198 510.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER95’: класс PDFDictionary 98 0 объект > / Граница [0 0 0] / Rect [447.0638 498,7969 478.1598 510.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER96’: класс PDFDictionary 99 0 объект > / Граница [0 0 0] / Rect [482.1598 498,7969 513,2558 510.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER97’: класс PDFDictionary 100 0 объект > / Граница [0 0 0] / Rect [332.7038 468,7969 359.9998 480.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER98’: класс PDFDictionary 101 0 объект > / Граница [0 0 0] / Rect [447.0638 468,7969 488,1598 480.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER99’: класс PDFDictionary 102 0 объект > / Граница [0 0 0] / Rect [200,592 414,7969 273,936 426.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER100 ‘: класс PDFDictionary 103 0 объект > / Граница [0 0 0] / Rect [332.7038 438,7969 356,9198 450.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER101’: класс PDFDictionary 104 0 объект > / Граница [0 0 0] / Rect [447.0638 438,7969 489,4878 450.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER102’: класс PDFDictionary 105 0 объект > / Граница [0 0 0] / Rect [332.7038 396,7969 363,3678 408.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER103’: класс PDFDictionary 106 0 объект > / Граница [0 0 0] / Rect [471.0558 396,7969 503.0478 408.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER104’: класс PDFDictionary 107 0 объект > / Граница [0 0 0] / Rect [356.6478 378,7969 383.0958 390.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER105’: класс PDFDictionary 108 0 объект > / Граница [0 0 0] / Rect [447.0638 378,7969 482,1598 390.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER106’: класс PDFDictionary 109 0 объект > / Граница [0 0 0] / Rect [332.7038 360,7969 359,9278 372.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER107 ‘: класс PDFDictionary 110 0 объект > / Граница [0 0 0] / Rect [447.0638 360,7969 471,9518 372.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER108’: класс PDFDictionary 111 0 объект > / Граница [0 0 0] / Rect [475.9518 360,7969 507.0558 372.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER109’: класс PDFDictionary 112 0 объект > / Граница [0 0 0] / Rect [332.7038 342,7969 359.0878 354.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER110’: класс PDFDictionary 113 0 объект > / Граница [0 0 0] / Rect [447.0638 342,7969 471,5038 354.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER111’: класс PDFDictionary 114 0 объект > / Граница [0 0 0] / Rect [475.5038 342,7969 505.2798 354.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER112’: класс PDFDictionary 115 0 объект > / Граница [0 0 0] / Rect [447.0638 330,7969 480,8398 342.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER113’: класс PDFDictionary 116 0 объект > / Граница [0 0 0] / Rect [484.8398 330,7969 509,2798 342.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.НОМЕР114 ‘: класс PDFDictionary 117 0 объект > / Граница [0 0 0] / Rect [332.7038 312,7969 355,0638 324.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER115’: класс PDFDictionary 118 0 объект > / Граница [0 0 0] / Rect [447.0638 312,7969 468,3918 324.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER116’: класс PDFDictionary 119 0 объект > / Граница [0 0 0] / Rect [472.3918 312,7969 506.1678 324.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER117’: класс PDFDictionary 120 0 объект > / Граница [0 0 0] / Rect [332.7038 294,7969 355,5918 306.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER118’: класс PDFDictionary 121 0 объект > / Граница [0 0 0] / Rect [474.6158 294,7969 509.7278 306.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER119’: класс PDFDictionary 122 0 объект > / Граница [0 0 0] / Rect [332.7038 264,7969 354,9198 276.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER120’: класс PDFDictionary 123 0 объект > / Граница [0 0 0] / Rect [332.7038 246,7969 355,5918 258.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER121 ‘: класс PDFDictionary 124 0 объект > / Граница [0 0 0] / Rect [474.1598 246,7969 497,7038 258.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER122’: класс PDFDictionary 125 0 объект > / Граница [0 0 0] / Rect [332.7038 228,7969 351.1518 240.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER123’: класс PDFDictionary 126 0 объект > / Граница [0 0 0] / Rect [447.0638 228,7969 468,8318 240.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER124’: класс PDFDictionary 127 0 объект > / Граница [0 0 0] / Rect [332.7038 210,7969 354,4558 222.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER125’: класс PDFDictionary 128 0 объект > / Граница [0 0 0] / Rect [483.0558 210,7969 519.0558 222.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER126’: класс PDFDictionary 129 0 объект > / Граница [0 0 0] / Rect [332.7038 180,7969 345,5918 192.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER127’: класс PDFDictionary 130 0 объект > / Граница [0 0 0] / Rect [447.0638 180,7969 467.0558 192.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER128 ‘: класс PDFDictionary 131 0 объект > / Граница [0 0 0] / Rect [332.7038 162,7969 345,5918 174.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER129’: класс PDFDictionary 132 0 объект > / Граница [0 0 0] / Rect [447.0638 162,7969 488,8398 174.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER130’: класс PDFDictionary 133 0 объект > / Граница [0 0 0] / Rect [332.7038 144,7969 353,3838 156.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER131’: класс PDFDictionary 134 0 объект > / Граница [0 0 0] / Rect [447.0638 144,7969 475,0638 156.7969] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Page2’: класс PDFPage 135 0 объект % Словарь страниц > / Повернуть 0 / Транс> / Тип / Страница >> endobj % ‘Annot.NUMBER132 ‘: класс PDFDictionary 136 0 объект > / Граница [0 0 0] / Rect [417.6248 721,7102 442,9448 733.7102] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER133’: класс PDFDictionary 137 0 объект > / Граница [0 0 0] / Rect [108.6966 703,7102 130,4726 715.7102] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER134’: класс PDFDictionary 138 0 объект > / Граница [0 0 0] / Rect [134.4726 703,7102 161.1286 715.7102] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER135’: класс PDFDictionary 139 0 объект > / Граница [0 0 0] / Rect [392.2968 703,7102 424,7288 715.7102] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER136’: класс PDFDictionary 140 0 объект > / Граница [0 0 0] / Rect [428.7288 703,7102 461.1608 715.7102] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER137’: класс PDFDictionary 141 0 объект > / Граница [0 0 0] / Rect [276.047 655,7102 298 927 667.7102] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER138’: класс PDFDictionary 142 0 объект > / Граница [0 0 0] / Rect [392.2968 655,7102 420,7448 667.7102] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER139 ‘: класс PDFDictionary 143 0 объект > / Граница [0 0 0] / Rect [424.7448 655,7102 464,2888 667.7102] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER140’: класс PDFDictionary 144 0 объект > / Граница [0 0 0] / Rect [392.2968 625,7102 432,2888 637.7102] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER141’: класс PDFDictionary 145 0 объект > / Граница [0 0 0] / Rect [276.047 607,7102 297,823 619.7102] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER142’: класс PDFDictionary 146 0 объект > / Граница [0 0 0] / Rect [464.2888 607,7102 498,5048 619.7102] / Подтип / Ссылка / Тип / Аннотация >> endobj % ‘Annot.NUMBER143’: класс PDFDictionary 147 0 объект > / Borde
.
