Теорема Гюйгенса — Штейнера — Википедия
Иллюстрация теоремы для момента площадиТеоре́ма Гю́йгенса — Ште́йнера (теорема Гюйгенса, теорема Штейнера): момент инерции J{\displaystyle J} тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела JC{\displaystyle J_{C}} относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m{\displaystyle m} на квадрат расстояния d{\displaystyle d} между осями[1]:
- J=JC+md2,{\displaystyle J=J_{C}+md^{2},}
где
- J{\displaystyle J} — искомый момент инерции относительно параллельной оси,
- JC{\displaystyle J_{C}} — известный момент инерции относительно оси, проходящей через центр масс тела,
- m{\displaystyle m} — масса тела,
- d{\displaystyle d} — расстояние между указанными осями.
Теорема названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса.
Будем рассматривать абсолютно твёрдое тело, образованное совокупностью материальных точек[2].
По определению момента инерции для JC{\displaystyle J_{C}} и J{\displaystyle J} можно записать
- JC=∑i=1nmi(ri)2,{\displaystyle J_{C}=\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i})^{2},}
- J=∑i=1nmi(ri′)2,{\displaystyle J=\sum _{i=1}^{n}m_{i}(\mathbf {r} ‘_{i})^{2},}
где r{\displaystyle \mathbf {r} } — радиус-вектор точки тела в системе координат с началом, расположенным в центре масс, а r′{\displaystyle \mathbf {r} ‘} — радиус-вектор точки в новой системе координат, через начало которой проходит новая ось.
Радиус-вектор r′i{\displaystyle \mathbf {r’} _{i}} можно расписать как сумму двух векторов:
- ri′=ri+d,{\displaystyle \mathbf {r} ‘_{i}=\mathbf {r} _{i}+\mathbf {d} ,}
где d{\displaystyle \mathbf {d} } — радиус-вектор расстояния между старой (проходящей через центр масс) и новой осями вращения. Тогда выражение для момента инерции примет вид
- J=∑i=1nmi(ri)2+2∑i=1nmirid+∑i=1nmi(d)2.{\displaystyle J=\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i})^{2}+2\sum _{i=1}^{n}m_{i}\mathbf {r} _{i}\mathbf {d} +\sum _{i=1}^{n}m_{i}(\mathbf {d} )^{2}.}
Вынося d{\displaystyle \mathbf {d} } за сумму, получим
- J=∑i=1nmi(ri)2+2d∑i=1nmiri+d2∑i=1nmi.{\displaystyle J=\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i})^{2}+2\mathbf {d} \sum _{i=1}^{n}m_{i}\mathbf {r} _{i}+d^{2}\sum _{i=1}^{n}m_{i}.}
По определению центра масс, для его радиус-вектора rc{\displaystyle \mathbf {r} _{c}} выполняется
- rc=∑imiri∑imi.{\displaystyle \mathbf {r} _{c}={\frac {\sum \limits _{i}m_{i}\mathbf {r} _{i}}{\sum \limits _{i}m_{i}}}.}
Поскольку в системе координат с началом, расположенным в центре масс, радиус-вектор центра масс равен нулю, то равна нулю и сумма ∑i=1nmiri{\displaystyle \sum _{i=1}^{n}m_{i}\mathbf {r} _{i}}.
Тогда
- J=∑i=1nmi(ri)2+d2∑i=1nmi,{\displaystyle J=\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i})^{2}+d^{2}\sum _{i=1}^{n}m_{i},}
откуда и следует искомая формула:
- J=JC+md2,{\displaystyle J=J_{C}+md^{2},}
где JC{\displaystyle J_{C}} — известный момент инерции относительно оси, проходящей через центр масс тела.
Если тело состоит не из материальных точек, а образовано непрерывно распределённой массой, то во всех приведённых выше формулах суммирование заменяется интегрированием. Ход рассуждения при этом остаётся прежним.
Следствие. Из полученной формулы очевидно, что J>JC{\displaystyle J>J_{C}}. Поэтому можно утверждать: момент инерции тела относительно оси, проходящей через центр масс тела, является наименьшим среди всех моментов инерции тела относительно осей, имеющих данное направление.
Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню (назовём её осью C{\displaystyle C}) равен
- JC=mL212.{\displaystyle J_{C}={\frac {mL^{2}}{12}}.}
Тогда, согласно теореме Штейнера, его момент относительно произвольной параллельной оси будет равен
- J=JC+md2,{\displaystyle J=J_{C}+md^{2},}
где d{\displaystyle d} — расстояние между этой осью и осью C{\displaystyle C}. В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти, положив в последней формуле d=L/2{\displaystyle d=L/2}:
- J=JC+m(L2)2=mL212+mL24=mL23.{\displaystyle J=J_{C}+m\left({\frac {L}{2}}\right)^{2}={\frac {mL^{2}}{12}}+{\frac {mL^{2}}{4}}={\frac {mL^{2}}{3}}.}
Теорема Гюйгенса — Штейнера допускает обобщение на тензор момента инерции, что позволяет получать тензор J^ij{\displaystyle {\hat {J}}_{ij}} относительно произвольной точки из тензора I^ij{\displaystyle {\hat {I}}_{ij}} относительно центра масс. Пусть a{\displaystyle \mathbf {a} } — смещение от центра масс, тогда
- J^ij=I^ij+m(a2δij−aiaj),{\displaystyle {\hat {J}}_{ij}={\hat {I}}_{ij}+m(a^{2}\delta _{ij}-a_{i}a_{j}),}
где
- a=(a1,a2,a3){\displaystyle \mathbf {a} =(a_{1},a_{2},a_{3})} — вектор смещения от центра масс, а δij{\displaystyle \delta _{ij}} — символ Кронекера.
Как видно, для диагональных элементов тензора (при i=j{\displaystyle i=j}) формула имеет вид теоремы Гюйгенса — Штейнера для момента относительно новой оси.
- ↑ Тарг С. М. Краткий курс теоретической механики. — 11-е изд. — М.: «Высшая школа», 1995. — С. 268—269. — 416 с. — ISBN 5-06-003117-9.
- ↑ Абсолютно твёрдое тело, образованное совокупностью материальных точек, — это такая механическая система, у которой расстояния между составляющими её точками постоянны.
ru.wikipedia.org
Теорема Штейнера
Сначала давайте соберем в «кучку» все формулы моментов инерции для часто встречающихся тел.
Момент инерции тонкого кольца (ось вращения перпендикулярна плоскости кольца и проходит через центр)
Момент инерции полого тонкостенного цилиндра (ось вращения совпадает с осью цилиндра)
Момент инерции сплошного цилиндра (ось вращения совпадает с осью цилиндра)
Момент инерции полого толстостенного цилиндра (ось вращения совпадает с осью цилиндра)
Момент инерции диска (ось вращения совпадает с осью диска)
Момент инерции диска (ось вращения совпадает с диаметром диска)
Момент инерции шара (ось вращения совпадает с центром)
Момент инерции полой тонкостенной сферы (ось вращения совпадает с центром)
Момент инерции тонкого стержня (ось вращения совпадает с центром)
Напоминаю теорему Штейнера: момент инерции тела относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния между осями.
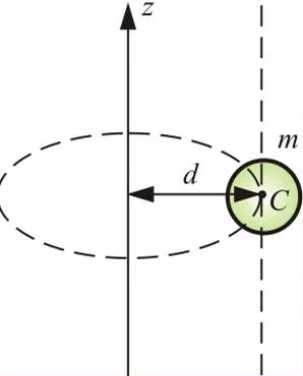
Теорема Штейнера
Теперь можно решить пару задач.
Задача 1. Найти момент инерции обруча массой и радиусом относительно оси, проходящей через его край перпендикулярно обручу.
Решение:
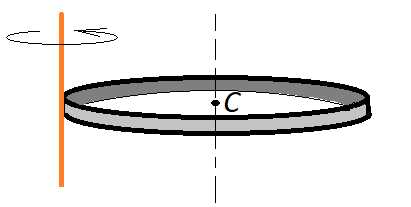
К задаче 1
По таблице определим момент инерции обруча (кольца), и прибавим произведение массы тела на квадрат расстояния между осями, а это – радиус кольца. Тогда
Ответ:
Задача 2. Найти момент инерции тонкого стержня массой и длиной относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на одну треть его длины.
Решение.
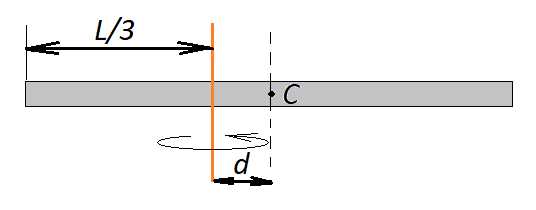
К задаче 2
Расстояние между осями
Согласно таблице момент инерции стержня равен , тогда по теореме Штейнера
Ответ:
Задача 3. Два шара радиусами см и массой г каждый скреплены тонким стержнем массой г и длиной см. Найти момент инерции системы относительно оси, перпендикулярной стержню и проходящей через центр тяжести, а также относительно оси, перпендикулярной стержню и проходящей в от его конца.
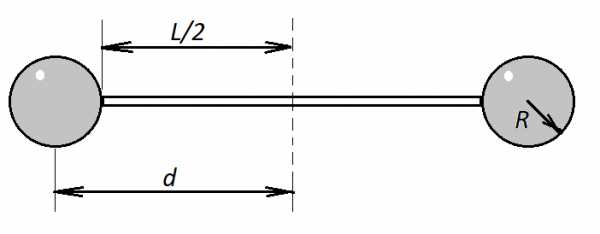
К задаче 3
Решение:
- Сначала найдем момент инерции системы относительно ее центра масс.
Здесь – момент инерции стержня, – момент инерции одного из шаров.
Момент инерции стержня определим по таблице, так как очевидно, что его центр является центром масс системы и ось вращения будет проходить через центр масс стержня.
Определим момент инерции одного из шаров по теореме Штейнера:
Тогда ответом на пункт а) будет
б) Теперь пусть ось проходит на расстоянии четверти длины стержня от его конца. Тогда момент инерции стержня будет равен по теореме Штейнера
Момент инерции шара, ближнего к оси вращения:
Момент инерции шара, дальнего от оси вращения:
Тогда ответом на пункт б) будет
Ответ: а) кг м, б) кг м.
Задача 4. Имеется диск диаметром см и массой г. В диске вырезали круглое отверстие диаметром 8 см, центр которого находится на расстоянии от центра диска. Найти момент инерции фигуры относительно оси, проходящей через центр диска и перпендикулярной его плоскости.
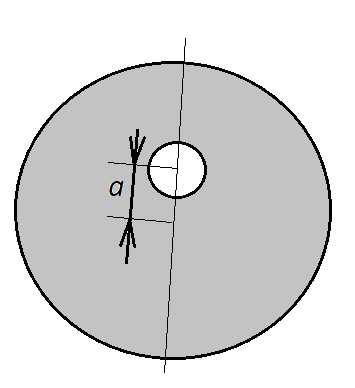
К задаче 4
Решение:
– момент инерции диска, – вырезанная часть.
– масса вырезанной части. Массу вырезанной части найдем как
, – поверхностная плотность диска.
Если – площадь диска, а – площадь вырезанной части, то
Тогда момент инерции вырезанной части
И момент инерции фигуры
Ответ: кг м.
easy-physic.ru
Теорема Штейнера.
В приведенных примерах оси проходят через центр инерции тела. Момент инерции относительно других осей вращения определяется при помощи теоремы Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции
Jc относительно параллельной оси, проходящей через центр инерции тела, и величины произведения массы тела на квадрат расстояния между ними. где m масса тела, а — расстояние от центра инерции тела до выбранной оси вращения,т.е., где m — масса тела, а — расстояние от центра
инерции тела до выбранной оси вращения.
Покажем на одном примере применение теоремы Штейнера. Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню. Прямое вычисление сводится к тому же интегралу (*),но взятому в других пределах:
Расстояние до оси, проходящей через центр масс, равно а
.
§22.Основной закон динамики вращательного движения.
Формулировка закона: Скорость изменения момента импульса относительно полюса равна главному моменту силы относительно того же полюса, т.е.
.
В
проекциях на оси координат: 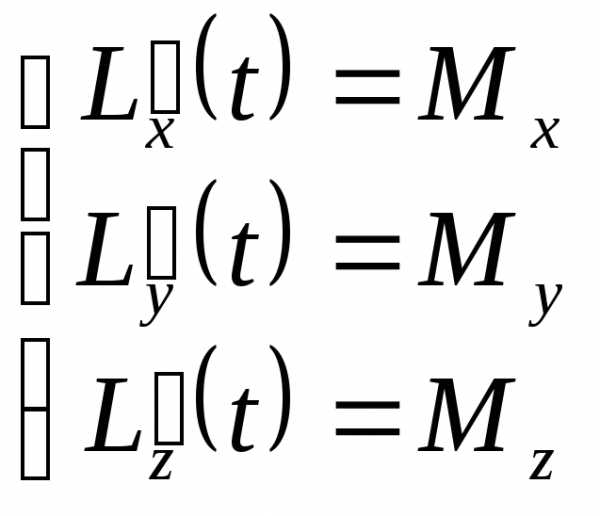 .
.
Если
вращение тела происходит относительно
неподвижной оси, то основной закон
динамики вращательного движения примет
вид:
.
В данном случае момент импульса легко
выразить через угловую скорость и момент
инерции тела относительно рассматриваемой
оси:.
Тогда основной закон динамики вращательного
движения примет вид: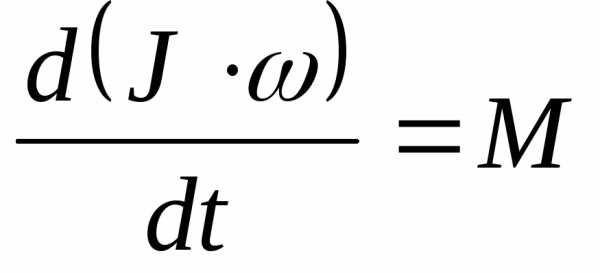 .
Если тело не рассыпается и не деформируется,
то
.
Если тело не рассыпается и не деформируется,
то
,
вследствие чего 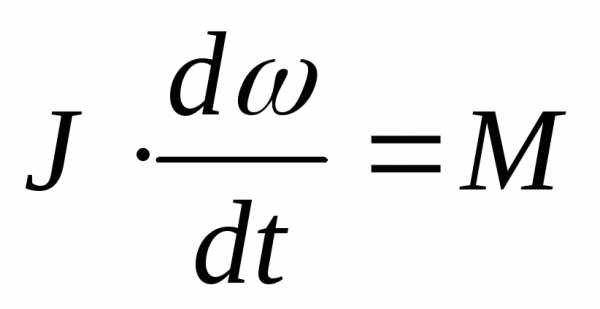 .
Если ко всему,
тои, оно равно:.
.
Если ко всему,
тои, оно равно:.
Элементарная
работа, совершаемая моментом силы, при
вращательном движении относительно
неподвижной оси вычисляется по формуле:
(*). Полная работа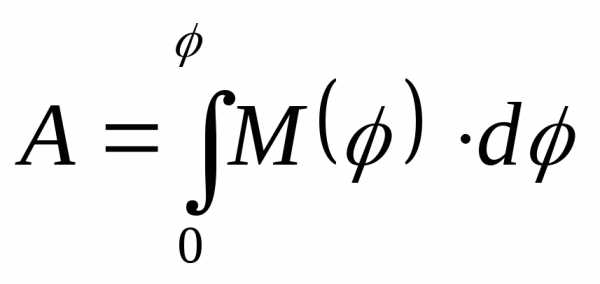 .
Если,
то.
.
Если,
то.
На
основании формулы (*), получим выражение
для кинетической энергии вращательного
движения твёрдого тела относительно
неподвижной оси. Т.к.
,
то.
После интегрирования, получим окончательный
результат для кинетической энергии
вращательного движения относительно
неподвижной оси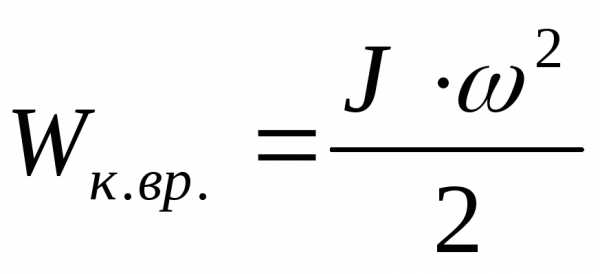 .
.
§23.Закон сохранения момента импульса.
Как уже указывалось, законы сохранения энергии и импульса связаны с однородностью времени и пространства, соответственно. Но у трехмерного пространства, в отличие от одномерного времени, имеется еще одна симметрия. Пространство само по себе изотропно,в нем нет выделенных направлений. С этой симметрией связанзакон сохранениямомента импульса.
По определению момент импульса отдельной частицы равен .
Направление вектора Lопределяется по правилу буравчика (штопора), а его величина равна L = r p sin ,где
угол между направлениями радиус-вектора частицы и ее импульса. Величина ℓ = r sinравна расстоянию от начала координатОдо прямой, вдоль которой направлен импульс частицы. Эта величина называетсяплечом импульса.ВекторLзависит от выбора начала координат, поэтому говоря о нем, обычно указывают: «момент импульса относительно точкиО«.
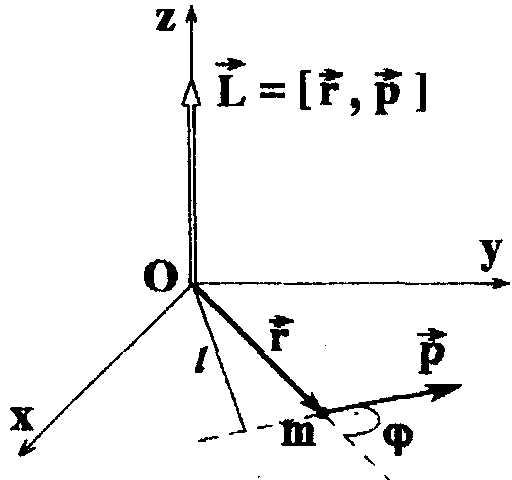
Рассмотрим производную по времени от момента импульса:
.
Первое слагаемое равно нулю, т.к. . Во втором слагаемом, согласно второму закону Ньютона, производную по импульсу можно заменить на действующую на тело силу. Векторное произведение радиус-вектора на силу называется моментом силыотносительно точкиО: .
Направление момента силы определяется тем же правилом буравчика. Его величина М = r F sin ,где
угол между радиус-вектором и силой. Аналогично тому, как это было сделано выше, определяется и плечо силы
ℓ = r sin — расстояние от точкиОдо линии действия силы. В итоге получаем уравнение движения для момента импульса частицы:.
По форме уравнение аналогично второму
закону Ньютона: вместо импульса
частицы стоит момент импульса, а вместо
силы —момент силы. Если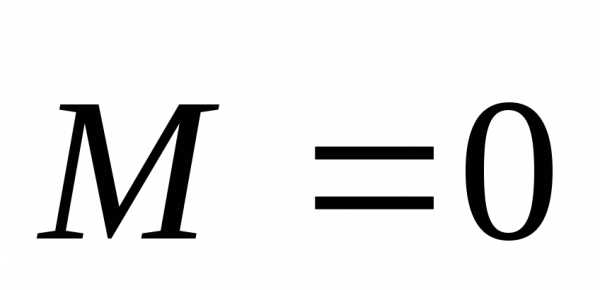 ,то
,то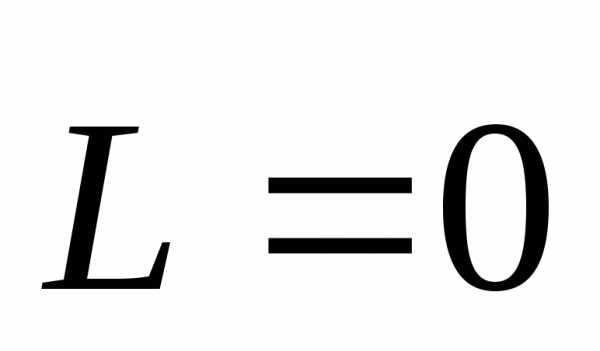
Формулировка закона: Момент импульса замкнутой системы относительно полюса не изменяется с течением времени.
В частном случае вращения относительно неподвижной оси, имеем: , где
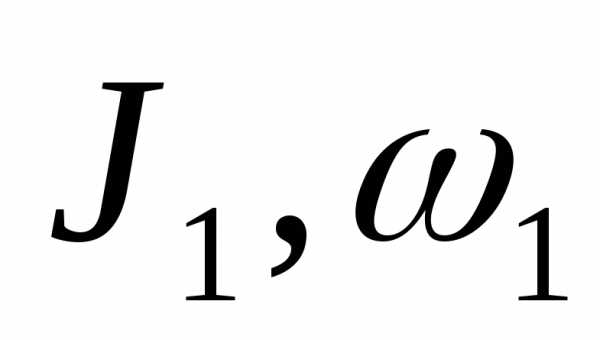 начальные
момент инерции и угловая скорость тела
относительно рассматриваемой оси, а
начальные
момент инерции и угловая скорость тела
относительно рассматриваемой оси, а
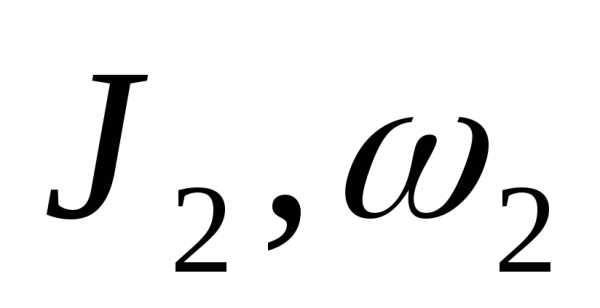 конечные
момент инерции и угловая скорость тела
относительно рассматриваемой оси.
конечные
момент инерции и угловая скорость тела
относительно рассматриваемой оси.
Закон сохранения полной механической энергии с учётом вращательного движения: полная механическая энергия консервативной системы постоянна: .
Пример: Найти скорость системы при прохождении расстояния h.
Дано: m, M, h. Найти: V — ?





studfile.net
Момент инерции — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 января 2019; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 января 2019; проверки требуют 2 правки.Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения в Международной системе единиц (СИ): кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.
Осевые моменты инерции некоторых телМоментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси[1]:
- Ja=∑i=1nmiri2,{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
- Ja=∫(m)r2dm=∫(V)ρr2dV,{\displaystyle J_{a}=\int \limits _{(m)}r^{2}dm=\int \limits _{(V)}\rho r^{2}dV,}
где:
- dm = ρ dV — масса малого элемента объёма тела dV,
- ρ — плотность,
- r — расстояние от элемента dV до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
- Ja=ρ∫(V)r2dV.{\displaystyle J_{a}=\rho \int \limits _{(V)}r^{2}dV.}
Теорема Гюйгенса — Штейнера[править | править код]
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями[1]:
- J=Jc+md2,{\displaystyle J=J_{c}+md^{2},}
где m — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
- J=Jc+md2=112ml2+m(l2)2=13ml2.{\displaystyle J=J_{c}+md^{2}={\frac {1}{12}}ml^{2}+m\left({\frac {l}{2}}\right)^{2}={\frac {1}{3}}ml^{2}.}
Осевые моменты инерции некоторых тел[править | править код]
Вывод формул[править | править код]
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
- J=∑dJi=∑Ri2dm.(1).{\displaystyle J=\sum dJ_{i}=\sum R_{i}^{2}dm.\qquad (1).}
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
- J=∑R2dm=R2∑dm=mR2.{\displaystyle J=\sum R^{2}dm=R^{2}\sum dm=mR^{2}.}
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
- J=12mR2.{\displaystyle J={\frac {1}{2}}mR^{2}.}
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен
- r=RhH,{\displaystyle r={\frac {Rh}{H}},}
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
- dm=ρdV=ρ⋅πr2dh;{\displaystyle dm=\rho dV=\rho \cdot \pi r^{2}dh;}
- dJ=12r2dm=12πρr4dh=12πρ(RhH)4dh;{\displaystyle dJ={\frac {1}{2}}r^{2}dm={\frac {1}{2}}\pi \rho r^{4}dh={\frac {1}{2}}\pi \rho \left({\frac {Rh}{H}}\right)^{4}dh;}
Интегрируя, получим
- J=∫0HdJ=12πρ(RH)4∫0Hh5dh=12πρ(RH)4h55|0H==110πρR4H=(ρ⋅13πR2H)310R2=310mR2.{\displaystyle {\begin{aligned}J=\int _{0}^{H}dJ={\frac {1}{2}}\pi \rho \left({\frac {R}{H}}\right)^{4}\int _{0}^{H}h^{4}dh={\frac {1}{2}}\pi \rho \left({\frac {R}{H}}\right)^{4}\left.{\frac {h^{5}}{5}}\right|_{0}^{H}=={\frac {1}{10}}\pi \rho R^{4}H=\left(\rho \cdot {\frac {1}{3}}\pi R^{2}H\right){\frac {3}{10}}R^{2}={\frac {3}{10}}mR^{2}.\end{aligned}}}
Сплошной однородный шар
Вывод формулы
Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
- r=R2−h3.{\displaystyle r={\sqrt {R^{2}-h^{2}}}.}
Масса и момент инерции такого диска составят
- dm=ρdV=ρ⋅πr2dh;{\displaystyle dm=\rho dV=\rho \cdot \pi r^{2}dh;}
- dJ=12r2dm=12πρr4dh=12πρ(R2−h3)2dh=12πρ(R4−2R2h3+h5)dh.{\displaystyle dJ={\frac {1}{2}}r^{2}dm={\frac {1}{2}}\pi \rho r^{4}dh={\frac {1}{2}}\pi \rho \left(R^{2}-h^{2}\right)^{2}dh={\frac {1}{2}}\pi \rho \left(R^{4}-2R^{2}h^{2}+h^{4}\right)dh.}
Момент инерции шара найдём интегрированием:
- J=∫−RRdJ=2∫0RdJ=πρ∫0R(R4−2R2h3+h5)dh==πρ(R4h−23R2h4+15h5)|0R=πρ(R5−23R5+15R5)=815πρR5==(43πR3ρ)⋅25R2=25mR2.{\displaystyle {\begin{aligned}J&=\int _{-R}^{R}dJ=2\int _{0}^{R}dJ=\pi \rho \int _{0}^{R}\left(R^{4}-2R^{2}h^{2}+h^{4}\right)dh=\\&=\pi \rho \left.\left(R^{4}h-{\frac {2}{3}}R^{2}h^{3}+{\frac {1}{5}}h^{5}\right)\right|_{0}^{R}=\pi \rho \left(R^{5}-{\frac {2}{3}}R^{5}+{\frac {1}{5}}R^{5}\right)={\frac {8}{15}}\pi \rho R^{5}=\\&=\left({\frac {4}{3}}\pi R^{3}\rho \right)\cdot {\frac {2}{5}}R^{2}={\frac {2}{5}}mR^{2}.\end{aligned}}}
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
- J0=25MR2=815πρR5.{\displaystyle J_{0}={\frac {2}{5}}MR^{2}={\frac {8}{15}}\pi \rho R^{5}.}
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
- J=dJ0dRdR=ddR(815πρR5)dR==83πρR4dR=(ρ⋅4πR2dR)23R2=23mR2.{\displaystyle {\begin{aligned}J&={\frac {dJ_{0}}{dR}}dR={\frac {d}{dR}}\left({\frac {8}{15}}\pi \rho R^{5}\right)dR=\\&={\frac {8}{3}}\pi \rho R^{4}dR=\left(\rho \cdot 4\pi R^{2}dR\right){\frac {2}{3}}R^{2}={\frac {2}{3}}mR^{2}.\end{aligned}}}
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
ru.wikipedia.org
Теорема Гюйгенса-Штейнера
Найдем связь между моментами инерции относительно двух различных параллельных осей. Она устанавливается теоремой Гюйгенса-Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно оси проходящей через центр масс, параллельно данной и произведения массы на квадрат расстояния между осями.

 .
Момент инерции тела найдем, проинтегрировав
по всем элементарным массам. Радиус-вектор
элементарной массы
.
Момент инерции тела найдем, проинтегрировав
по всем элементарным массам. Радиус-вектор
элементарной массы  относительно оси А
,
где
относительно оси А
,
где  — ее радиус-вектор относительно оси О,
— ее радиус-вектор относительно оси О,  — радиус-вектор
— радиус-вектор  ,
его модуль равен расстоянию между осями.
Таким образом
,
его модуль равен расстоянию между осями.
Таким образом. (5.11)
Умножая
обе части равенства (5.11) на  и интегрируя по всему объему, получим:
и интегрируя по всему объему, получим:
. (5.12)
Так как ось О проходит через центр масс, последний интеграл в (5.12) обращается в нуль.
 .
.
Интеграл слева дает момент инерции относительно оси А, первый интеграл справа — момент инерции относительно оси О, второй интеграл справа дает полную массу тела. Откуда
. (5.13)
Это и есть аналитическое выражение теоремы Гюйгенса-Штейнера.
Примеры вычисления моментов инерции
1. Определим момент инерции тонкого однородного стержня длиною L и массой m относительно оси, проходящей через один из его концов. (см.рис.)
Направим
ось Х вдоль стержня. Стержень будем
считать тонким. Выделим элементарную
массу  ,
имеющую длину
,
имеющую длину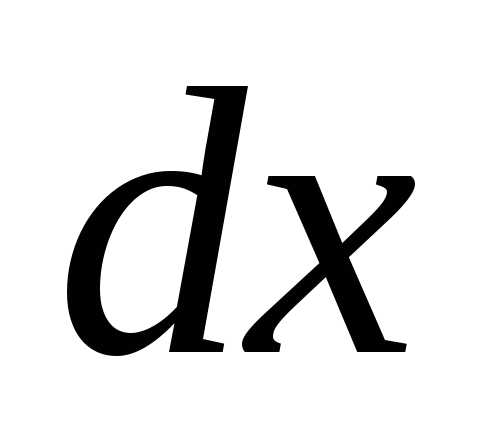 и расположенную на расстоянии Х от оси
вращения. Причем, поскольку стержень
однородный масса этого элемента
и расположенную на расстоянии Х от оси
вращения. Причем, поскольку стержень
однородный масса этого элемента
Тогда
Проинтегрировав по всей длине стержня получим:

Момент инерции этого же стержня относительно оси, проходящей через центр масс определяется как:

2. Определим момент инерции однородного диска, расположенного
перпендикулярно оси вращения, проходящей через центр масс. Радиус диска R, масса – m. Используя симметрию задачи, разобьем диск на элементарные массы в виде тонких колец радиусом r и шириной .
(см.рис.)
.
(см.рис.) Масса
этого элемента  ,
где
,
где — площадь поперечного сечения диска или
поверхностная плотность диска,- площадь кольца. Тогда
— площадь поперечного сечения диска или
поверхностная плотность диска,- площадь кольца. Тогда .
Интегрируя в пределах от 0 доR,
получим:
.
Интегрируя в пределах от 0 доR,
получим:


Выделим
элементарную массу  ,
длиной,
тогда
,
длиной,
тогда ,
здесь
,
здесь — линейная плотность массы, то есть масса
— линейная плотность массы, то есть масса
приходящаяся на единицу длины. Так как все элементарные массы расположены на одинаковом расстоянии от оси вращения (кольцо тонкое)


studfile.net
Глава 3. Динамика вращательного движения
§ 3.1 Момент силы. Момент импульса.
Пусть некоторое тело под действием силы F, приложенной в точке А, приходит во вращение вокруг оси ОО’ (рис. 1.14).
Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы. Произведение силы на плечо определяет модуль момента силы относительно точки О:
М = Fp=Frsinα.
Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы:
(3.1) Единица момента силы — ньютон-метр (Н • м).
Направление М можно найти с помощью правила правого винта.
Моментом импульса частицы называется векторное произведение радиус-вектора частицы на её импульс:
или в скалярном виде L = гPsinα
Эта величины векторная и совпадает по направлению с векторами ω.
§ 3.2 Момент инерции. Теорема Штейнера
Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, называемая моментом инерции тела относительно оси вращения.
Моментом инерции материальной точки относительно оси вращения называют произведение массы этой точки на квадрат расстояния её от оси:
Ii=miri2 (3.2)
Момент инерции тела относительно оси вращения называют сумму моментов инерции материальных точек, из которых состоит это тело:
 (3.3)
(3.3)
В общем случае, если тело сплошное и представляет собой совокупность точек с малыми массами dm, момент инерции определяется интегрированием:
 (3.4)
(3.4)
[r — расстояние от оси вращения до элемента массой dm].
Если
тело однородно и его плотность  ,
то момент инерции тела
,
то момент инерции тела
 (3.5)
(3.5)
Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.
Наиболее просто определяется момент инерции тел, имеющих правильную геометрическую форму и равномерное распределение массы по объему.
Момент инерции однородного стержня относительно оси, проходящей через центр инерции и перпендикулярной стержню
 (3.6)
(3.6)
Момент инерции однородного цилиндра относительно оси, перпендикулярной его основанию и проходящей через центр инерции,
 (3.7)
(3.7)
Момент инерции тонкостенного цилиндра или обруча относительно оси, перпендикулярной плоскости его основания и проходящей через его центр,
 (3.8)
(3.8)
 (3.9)
(3.9)
Рассмотрим пример. Определим момент инерции диска относительно оси, проходящей через центр инерции и перпендикулярной плоскости вращения. Масса диска — m, радиус — R.
Площадь кольца (рис. 3.2), заключенного между
r и r + dr, равна dS = 2πr·dr . Площадь диска S = πR2.
Следовательно,  .
Тогда
.
Тогда
 или
или 
Согласно
(3.10)
Приведенные формулы для моментов инерции тел даны при условии, что ось вращения проходит через центр инерции. Чтобы определить моменты инерции тела относительно произвольной оси, следует воспользоваться теоремой Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:
(3.11)
[m — масса тела, d — расстояние от центра масс до выбранной оси вращения (расстояние между осями)].
Единица момента инерции — килограмм-метр в квадрате (кг· м2).
Так, момент инерции однородного стержня относительно оси, проходящей через его конец, по теореме Штейнера равен
(3.12)
studfile.net
Смысл теоремы штейнера. Теорема Штейнера — формулировка
Уважаемые посетители сайта , предлагает Вашему вниманию работу по математике на тему , где представлены материалы теоретического и практического характера, рекомендации по решению задач с использованием указанной теоремы.
Теорема Штейнера , или, как именуется она в других источниках, теорема Гюйгенса-Штейнера, получила свое название в честь ее автора – Якоба Штейнера (швейцарского математика), а также благодаря дополнениям – Христиана Гюйгенса (голландского физика, астронома и математика). Рассмотрим кратко их вклад в и других наук.
Теорема Штейнера — об авторах теоремы
Якоб Штейнер
(1796—1863)
Якоб Штейнер (1796—1863) — один из , который считается основателем, как синтетической геометрии кривых линий, так и поверхностей второго и высших порядков.
Что касается Христиана Гюйгенса, то его вклад в различные науки тоже не мал. Он значительно усовершенствовал (до 92-кратного увеличения изображения), открыл кольца Сатурна и спутник его — Титан, а в 1673 году в своем довольно содержательном труде «Маятниковые часы», представил работы по кинематике ускоренного .
Теорема Штейнера — формулировка
Согласно теореме Штейнера, установлено, что момент инерции тела при расчете относительно произвольно оси соответствует сумме момента инерции тела относительно такой оси, которая проходит через центр масс и является параллельной данной оси, а также плюс произведение квадрата расстояния между осями и массы тела, по следующей формуле (1):
J= J 0 + md 2 (1)
Где в формуле принимаем соответственно величины: d – расстояние между осями ОО 1 ║О’O 1 ’;
J 0 – момент инерции тела, рассчитанный относительно оси, что проходит сквозь центр масс и будет определяться соотношением (2):
J 0 = J d = mR 2 /2 (2)
Так как d = R, тогда и момент инерции относительно оси, которая проходит через указанную на рисунке точку А будет определяется формулой (3):
J = mR 2 + mR 2 /2 = 3 / 2 mR 2 (3)
Более подробная информация о теореме представлена в реферате и презентации, которые можно скачать по ссылкам перед статьей.
Теорема Штейнера. Момент инерции – содержание работы
Введение
Часть 1. Динамика вращения твердого тела
1.1. Моменты инерции шара и диска
1.2. Теорема Гюйгенса-Штейнера
1.3. Динамика вращательного движения твердого тела — теоретические основы
Момент импульса
Момент силы
Момент инерции относительно оси вращения
Главный закон динамики вращательного движения твердого тела относительно неподвижной оси
Существует ряд геометрических задач, которые околдовывают каждого, кто по воле случая сталкивается с ними. По-видимому, это было характерно для геометрии даже в древнее время. Стоит только вспомнить три знаменитые задачи древности — удвоение куба, трисекцию угла и квадратуру круга. Попытки решить эти задачи привели к развитию новых ветвей математики. Даже сейчас существуют псевдоматематики, которые присылают в редакции «решения» этих задач и требуют публикации или доказательства ложности своих «решений».
Одна всегда возбуждавшая интерес теорема может быть сформулирована следующим образом:
Если в треугольнике две биссектрисы равны, то этот треугольник является равнобедренным.
Это с виду простое утверждение не имеет простого классического доказательства. Этот факт тем более удивителен, что заменив слово «биссектрисы» на «медианы» или «высоты», получаем утверждения, доказательства которых элементарны.
Эта теорема была послана великому шведскому геометру, члену Берлинской академии наук, Якобу Штейнеру в 1840 году Кристианом Лудольфом Лемусом, немецким математиком, профессором Берлинского университете, с просьбой дать чисто геометрическое доказательство.
Якоб Штейнер
(1796-1863 )
Штейнер дал довольно сложное доказательство, которое вдохновило многих других на поиски более простых методов. Работы по теореме Штейнера — Лемуса появлялись в различных журналах в 1842, 1844, 1848 годах и почти каждый год с 1854 года по 1864 год, а также в большом количестве и в течение следующего столетия.
Доказательство теоремы Штейнера — Лемуса
Одно из простейших доказательств опирается на следующие две леммы:
Лемма 1.
Если две хорды окружности стягивают различные острые углы с вершинами на этой окружности, то меньшему углу соответствует меньшая хорда.
Доказательство.
Две равные хорды стягивают равные углы с вершиной в центре окружности и равные углы (как их половины) с вершинами в соответствующих точках на окружности. Из двух неравных хорд более короткая, находясь дальше от центра, стягивает меньший угол с вершиной в центре и, следовательно, меньший острый угол с вершиной на окружности.
Лемма 2.
В треугольнике с двумя различными углами меньший угол обладает большей биссектрисой .
Доказательство.
Пусть ABC — треугольник, в котором угол B меньше угла C , как на рисунке выше; пусть отрезки BM и CN делят пополам углы B и C . Мы хотим доказать, что BM
∠M′CN = 1 / 2 ∠B .
Так как этот угол равен углу M′BN , то четыре точки N, B, C, М′ лежат на одной окружности. Поскольку
∠B ,
то
∠CBN
По лемме 1: CN BM′ > CN .
Вернёмся теперь непосредственно к доказательству теоремы Штейнера — Лемуса.
Часто случается, что теорема может быть выражена в форме «противоположной к обратной» — эквивалентной первоначальной. Например, вместо того, чтобы сказать: » Все люди смертны» , мы можем также сказать » Бессмертные не есть люди» . Вместо доказательства самой теоремы Штейнера — Лемуса для нас будет достаточно доказать, чтоесли в треугольнике ABC ∠B ≠ ∠C , то BM ≠ CN .
Но это есть прямое с
electric-idea.ru

