Момент инерции цилиндра, теория и примеры
Это скалярная (в общем случае тензорная) величина. Для непрерывного однородного тела, вращающегося около оси, момент инерции определяют как:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.
Для получения формулы расчета момента инерции однородного цилиндра, мы его представим как совокупность бесконечно тонких дисков, а диск, в свою очередь – совокупность бесконечно тонких колец. Поэтому мы сначала получим выражение для момента инерции кольца, затем диска и только в самом окончании цилиндра.
Момент инерции тонкого кольца
Пусть кольцо имеем радиус R. Его называют бесконечно тонким, если его ширина и толщина много меньше радиуса. Пусть кольцо вращается относительно оси Z, перпендикулярной плоскости кольца и проходит через центр кольца (рис.1).
Выделим на кольце элементарную массу (), – плотность кольца; – элементарный объем кольца.
Момент инерции бесконечно тонкого однородного диска
Пусть диск имеет радиус R. Он вращается относительно оси, которая проходит через его центр инерции, перпендикулярно его плоскости. Диск представим как систему бесконечно тонких колец, радиусы которых изменяются от нуля до R. Одно из таких колец изображено на рис.2.
Так как момент инерции тонкого кольца мы уже нашли, то его возьмем за элементарный:
где – масса выделенного кольца, равная:
Найдем момент инерции бесконечно тонкого диска, учитывая: :
массу бесконечно тонкого диска можно считать равной:
тогда момент инерции диска равен:
Момент инерции цилиндра
Для того, чтобы найти момент инерции однородного цилиндра, вращающегося относительно своей оси, представим его как совокупность дисков, толщиной .
где – высота цилиндра. Тогда момент инерции цилиндра относительно его собственной оси равен:
где масса цилиндра равна:
Примеры решения задач
Физические основы механики
Движение материальной точки характеризуется перемещением, скоростью, ускорением. Но при вращении твердого тела все его элементы имеют разные перемещения, различные скорости. Удобно найти переменные, одинаковые для всех элементов твердого тела. Мы их, собственно, уже знаем — угол поворота, угловая скорость, угловое ускорение. Соответственно, изучая динамику вращения, вместо импульса и силы мы будем оперировать их угловыми аналогами — моментом импульса и моментом силы.
Уравнение движения. В теме 4.8 было выведено уравнение движения системы материальных точек в виде
где моменты импульса и силы определялись как
Внутренние силы между телами системы, напомним, выпали из уравнений движения.
Абсолютно твердое тело можно рассматривать как систему частиц (материальных точек) с неизменными расстояниями между ними. Поэтому выписанные уравнения применимы для твердого тела, а неизменность расстояний между его точками позволяет характеризовать вращение тела вокруг неподвижной оси единственной координатой — углом поворота. Поэтому мы можем упростить приведенное выше уравнение движения. Прежде всего, нас не интересуют в данный момент напряжения, возникающие в оси. Кроме того, для описания вращения достаточно рассмотреть проекции векторов моментов импульса и силы на ось вращения.
Рис. 7.1. Момент импульса L двух шаров массы m, соединенных стержнем. Вся система вращается вокруг оси z c угловой скоростью ω
Направим ось z вдоль оси вращения и выделим в твердом теле элемент массой , положение которого характеризуется радиус-вектором (рис. 7.2).
Рис. 7.2 Вращение твердого тела вокруг неподвижной оси 0z
Момент импульса этого элемента есть
Рис.
7.3. Момент импульса системы направлен вдоль оси вращения.
Радиус-вектор можно представить как сумму его проекций на ось z и плоскость ху :
где вектор лежит в плоскости вращения и направлен от оси к выделенному элементу (см. рис. 7.1). Имеем:
Первое слагаемое — вектор, направленный противоположно Поэтому оно не дает вклада в
и
можем написать:
Суммируя по всем элементам тела, получаем
где
Величина называется моментом инерции тела.
Говоря о моменте инерции, всегда указывают, относительно какой именно оси вращения он определен (в данном случае — это ось z). Момент инерции того же тела относительно какой-то другой оси примет иное значение. Сохраняется только общее правило его вычисления: берется сумма по элементам массы, составляющим тело, умноженным на квадраты расстояний этих элементов массы до оси вращения.
В случае непрерывного распределения масс с плотностью сумма заменится на интеграл по всему объему тела:
Если тело однородно, то его плотность во всех точках постоянна и можно вынести из-под знака интеграла.
Записываем теперь уравнение движения в проекции на ось z :
Если момент инерции не зависит от времени, то дифференцировать нужно только угловую скорость, в результате получаем основное уравнение динамики вращательного движения твердого тела в виде
Производная угловой скорости по времени — это угловое ускорение
Видео 7.1. Основное уравнение динамики вращательного движения. Демонстрация, вытекающей из него связи между угловым ускорением, моментом силы и моментом инерции
Рассмотрим теперь момент внешних сил. Разложим силу на вектор в направлении оси z и вектор, ей ортогональный:
Используя снова аналогичное разложение радиус-вектора
получаем для момента внешних сил :
Первое слагаемое равно нулю.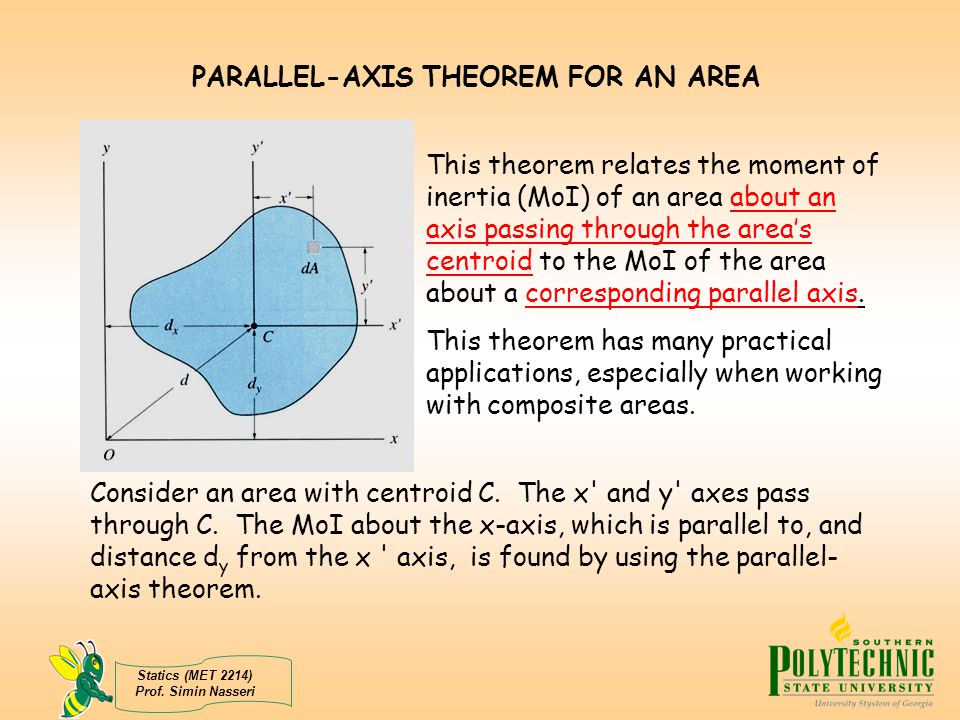
лежат в плоскости xy и, следовательно, последнее слагаемое направлено параллельно оси 0z. Если — угол между этими векторами, то
где — плечо силы (см. тему. 4.8). Силу
надо здесь понимать в алгебраическом смысле: она входит со знаком минус, если сила тормозит вращение.
Момент инерции. Найдем моменты инерции для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.
Рис. 7.4. Моменты инерции различных тел
1. Момент инерции обруча относительно оси, перпендикулярной к его плоскости и проходящей через его центр.
Обруч считается бесконечно тонким, то есть толщиной обода можно пренебречь по сравнению с радиусом . Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, можно вынести из-под знака интеграла:
где — полная масса обруча.
2. Момент инерции диска относительно оси, перпендикулярной его плоскости и проходящей через центр.
Диск считается бесконечно тонким, если его толщина много меньше радиуса . Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие обручи радиусом и шириной (рис. 7.5).
Рис. 7.5 Вычисление момента инерции диска относительно оси z, перпендикулярной его плоскости и проходящей через центр
Площадь поверхности обруча равна произведению его длины окружности на ширину: . Поскольку масса m диска распределена равномерно, масса единицы площади равна , так что масса обруча равна
Момент инерции обруча мы уже знаем:
Осталось просуммировать моменты инерции всех таких обручей:
Такой же результат получится и для момента инерции цилиндра конечной длины относительно его продольной оси.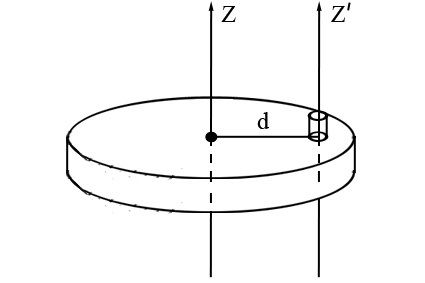
3. Момент инерции шара относительно его диаметра.
Поступим аналогичным образом: «нарежем» шар на бесконечно тонкие диски толщиной , находящиеся на расстоянии z от центра (рис. 7.6).
Рис. 7.6. Момент инерции шара относительно его диаметра
Радиус такого диска
Объем диска равен его площади, умноженной на толщину:
Массу диска находим, разделив массу шара на его объем и умножив на объем диска:
Момент инерции диска был найден выше. В применении к данному случаю он равен
Момент инерции шара находится интегрированием по всем таким дискам:
4. Момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню.
Пусть стержень имеет длину . Направим ось x вдоль стержня. Начало координат по условию находится в центре стержня (рис. 7.7).
Рис.
7.7. Момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню
Возьмем элемент стержня длиной , находящийся на расстоянии x от оси вращения. Его масса равна
а момент инерции
Отсюда находим момент инерции стержня:
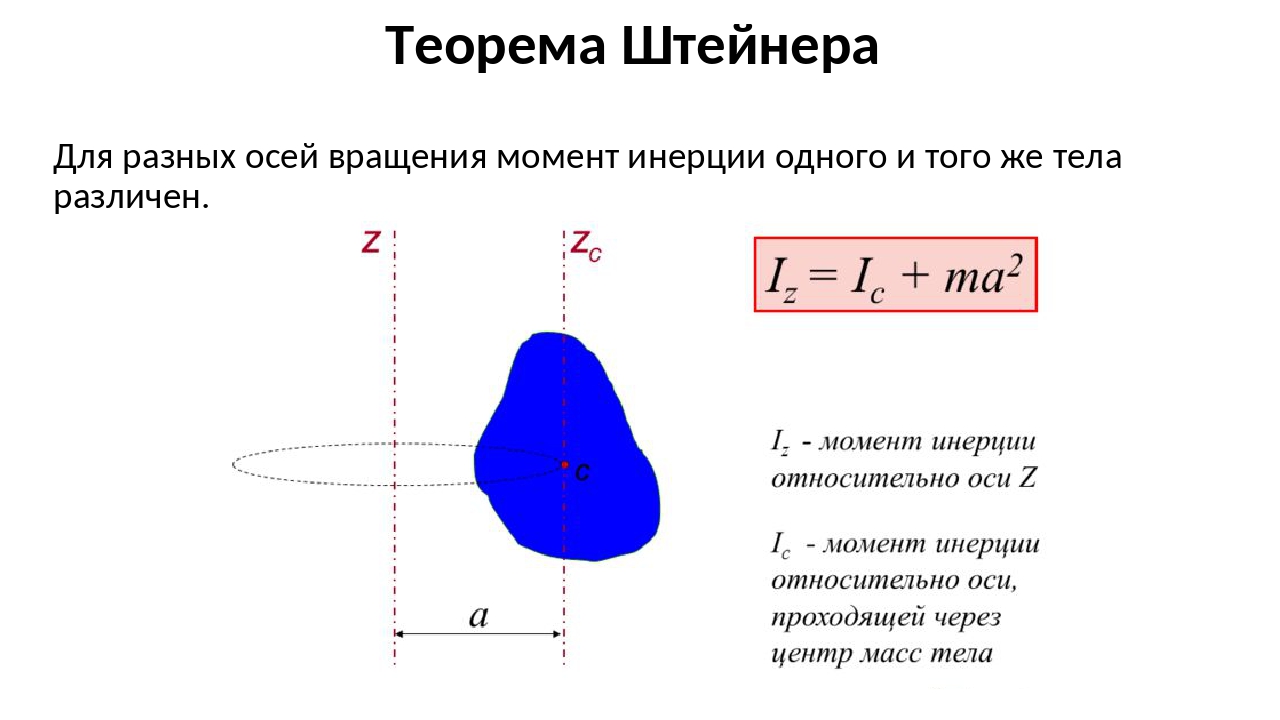
Теорема Штейнера. В приведенных примерах оси проходят через центр масс (центр инерции) тела. Момент инерции относительно других осей вращения определяется в соответствии с
Рис. 7.8. К выводу теоремы Штейнера
Момент инерции тела относительно произвольной оси равен сумме момента инерции JC относительно параллельной оси, проходящей через центр инерции тела, и величины ma2 — произведения массы тела на квадрат расстояния от центра инерции тела до выбранной оси, то есть
Продемонстрируем сначала применение теоремы Штейнера.
Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню. Прямое вычисление сводится к тому же интегралу, возникшему при вычислении момента инерции стержня относительно оси, проходящей через его середину, но взятому в других пределах:
Расстояние до оси, проходящей через центр масс, равно a = l/2. По теореме Штейнера получаем тот же результат:
Вывод теоремы Штейнера иллюстрируется рис. 7.8, 7.9
Рис. 7.9. К выводу теоремы Штейнера
Пусть одна ось проходит в направлении единичного вектора n через центр масс С твердого тела (системы тел), а другая — параллельно ей через некоторую точку 0. Из центра масс в направлении второй оси проводим ортогональный осям вектор a, который определяет положение точки 0. Радиус-векторы некоторого элемента системы массой относительно точек С и 0 обозначаем и , соответственно.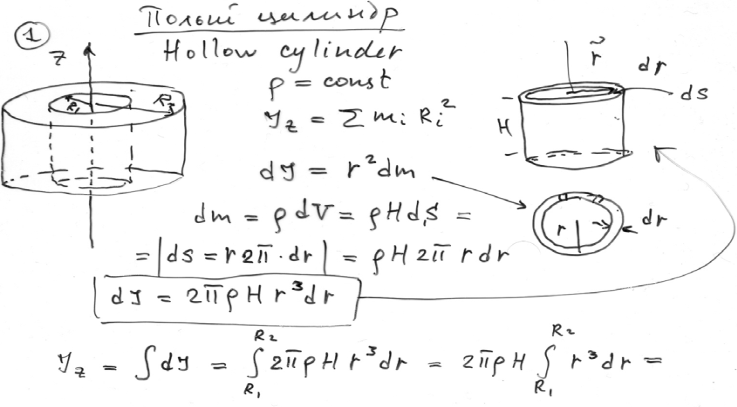
Момент инерции этого элемента относительно оси С есть
где — расстояние элемента от оси. По теореме Пифагора (см. рис. 7.9).
Катет равен проекции векторов и на ось вращения, то есть
Используя эти выражения и суммируя по всем элементам системы, находим момент инерции относительно оси, проходящей через точку С, и, аналогичным образом, момент инерции относительно параллельной оси, проходящей через точку 0 :
Здесь выражение для получено из простой заменой на .
Как видно из рис. 7.9, векторы и связаны между собой:
причем
так как векторы n и а ортогональны и их скалярное произведение
Тогда мы можем преобразовать выражение для :
Первое слагаемое в правой части — момент инерции относительно оси, проходящей через точку C. Третье слагаемое равно , где
— полная масса системы.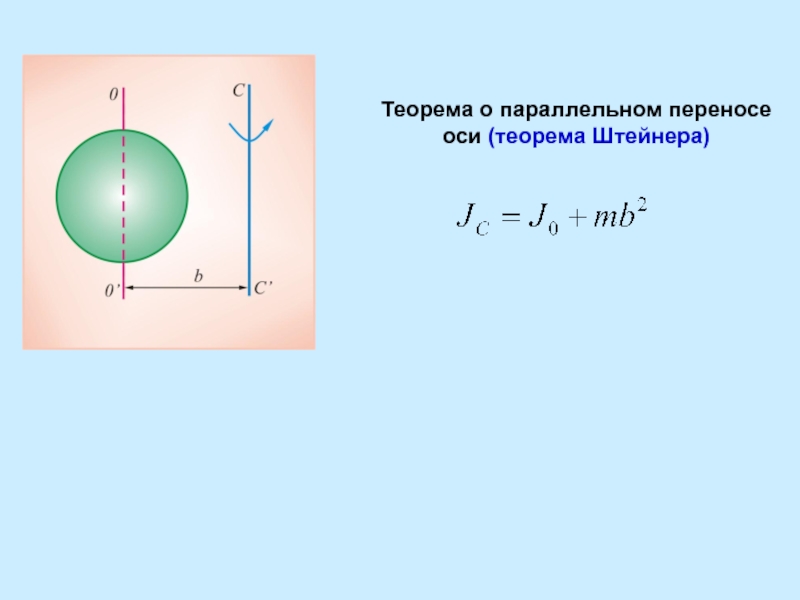
Второе слагаемое равно нулю, так как оно пропорционально радиус-вектору центра инерции относительно самого центра инерции. Окончательно:
что и требовалось доказать.
Теорема Штейнера связывает моменты инерции относительно параллельных осей. Иногда оказывается полезной другая теорема, связывающая моменты инерции относительно трех взаимно перпендикулярных осей. Однако эта теорема относится только к плоским фигурам, толщиной которых можно пренебречь по сравнению с размерами в двух других направлениях. Итак, теорема о моментах инерции плоских фигур:
Если через произвольную точку 0 плоской фигуры приведена ортогональная к фигуре ось, то момент инерции относительно этой оси равен сумме моментов инерции относительно двух взаимно перпендикулярных осей, лежащих в плоскости фигуры и проходящих через эту же точку 0.
Иными словами, берем на фигуре произвольную точку 0 и проводим координатные оси так, чтобы 0x и 0y лежали в плоскости фигуры.
Тогда, согласно теореме, момент инерции относительно оси 0z равен сумме моментов инерции относительно осей 0x и 0y:
При этом расположение осей 0x, 0y может быть произвольным; главное, чтобы они лежали в плоскости фигуры (рис. 7.10).
Рис. 7.10. Моменты инерции плоской фигуры относительно взаимно перпендикулярных осей
Из рисунка видно, что
что и требовалось доказать.
Найдем, например, момент инерции диска относительно его диаметра. Два ортогональных диаметра диска равноправны, поэтому
Согласно теореме о плоской фигуре
откуда
Теперь можно применить теорему Штейнера, чтобы найти, например, момент инерции относительно оси , параллельной диаметру и проходящей через край диска (см. рис. 7.10):
5.4. Момент инерции твердого тела
Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело
(5. 4) |
В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами , и моменты инерции тела определяется интегралом
| (5.5) |
о где — расстояние от элемента до оси вращения.
Распределение массы в пределах тела можно охарактеризовать с помощью
плотности
| (5.5) |
где m — масса однородного тела, V — его объем. Для тела с неравномерно распределенной массой это выражение даетсреднюю плотность.
Плотность в данной точке в этом случае определяется следующим образом
и тогда
| (5.6) |
Пределы интегрирования зависят от формы и размеров тела Интегрирование уравнения (5.5) наиболее просто осуществить для тех случаев, когда ось вращения проходит через центр тяжести тела.
Рассмотрим результаты интегрирования для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.
Момент инерции полого цилиндра с тонкими стенками, радиуса R.
Для полого цилиндра с тонкими стенками
Сплошной однородный диск. Ось вращения является осью диска радиуса . и массы m с плотностью Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки и массой . Для него
Весь диск можно разбить на бесконечное множество цилиндров, а затем просуммировать:
Момент инерции шара относительно оси, проходящей через центр тяжести.
Момент инерции стержня длиной L и массой m относительно оси, проходящей:
а) через центр стержня —
б) через начало стержня —
Теорема Штейнера.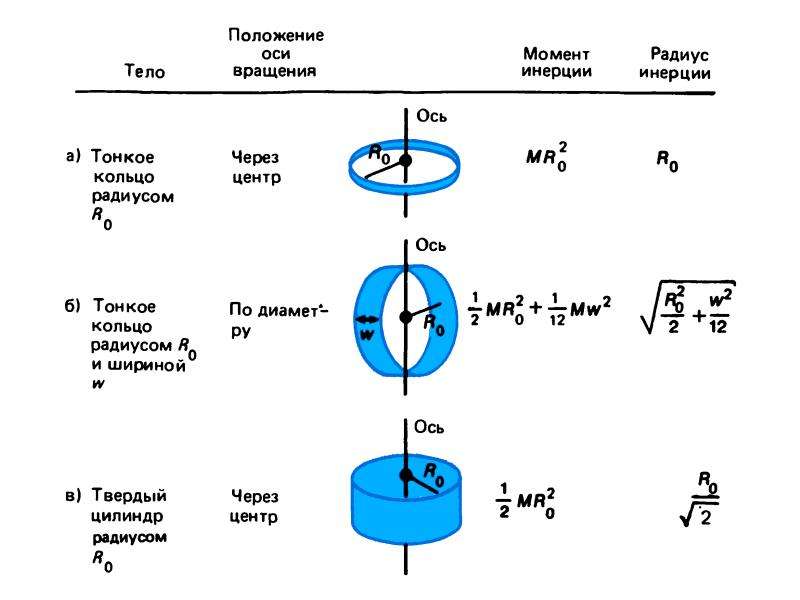
Имеем тело, момент инерции которого относительно оси, проходящей через его центр масс известен. Необходимо определить момент инерции относительно произвольно оси параллельной оси . Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями:
| (5.7) |
Механика твердого тела Момент инерции и примеры его вычисления. Теорема Штейнера.
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Лекция 5 ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Термины и понятия Метод интегрального исчисления Момент импульса Момент инерции тела Момент силы Плечо силы Реакция опоры Теорема Штейнера 5.
1. МОМЕНТ ИНЕРЦИИ ТВЕРДОГО
Динамика вращательного движения
Динамика вращательного движения План Момент импульса частицы Момент силы Уравнение моментов Собственный момент импульса Момент инерции Кинетическая энергия вращающегося тела Связь динамики поступательного
ПодробнееТема 1.4. Динамика вращательного движения
Тема 1.4. Динамика вращательного движения План 1. Момент импульса частицы. Момент силы 3. Уравнение моментов 4. Собственный момент импульса 5. Динамика твердого тела 6. Момент инерции 7. Кинетическая энергия
ПодробнееВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ (лекции 4-5)
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ (лекции 4-5) ЛЕКЦИЯ 4, (раздел 1) (лек 7 «КЛФ, ч1») Кинематика вращательного движения 1 Поступательное и вращательное движение В предыдущих лекциях мы познакомились с механикой материальной
ПодробнееДинамика вращательного движения
Восточно-Сибирский государственный университет технологий и управления Лекция 3 Динамика вращательного движения ВСГУТУ, кафедра «Физика» План Момент импульса частицы Момент силы Уравнение моментов Момент
ПодробнееЛАБОРАТОРНАЯ РАБОТА 133
ЛАБОРАТОРНАЯ РАБОТА 133 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА МАКСВЕЛЛА.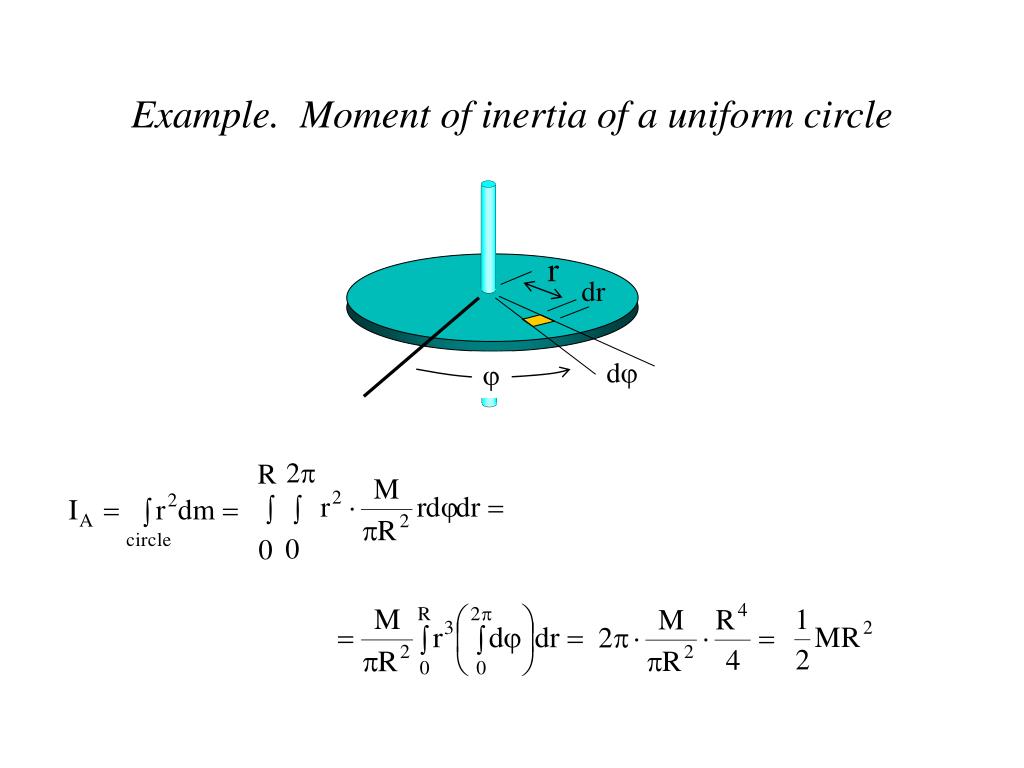
Цель работы: Целью работы является изучение основного уравнения динамики вращательного движения твердого тела и экспериментальное
Кузьмичев Сергей Дмитриевич
Кузьмичев Сергей Дмитриевич СОДЕРЖАНИЕ ЛЕКЦИИ 9 Вращение твердого тела. 1. Вращение твердого тела вокруг неподвижной оси.. Момент инерции. Теорема Гюйгенса-Штейнера. 3. Кинетическая энергия вращающегося
ПодробнееДинамика твердого тела
Динамика твердого тела Вращение вокруг неподвижной оси Момент импульса материальной точки относительно оси равен L где l — плечо импульса p — составляющая импульса перпендикулярная оси вращения При вращении
Подробнее1. Вращательные движения. Общие сведения
Цель работы. Изучить вращательное движение твердого тела с закрепленной осью вращения.
Задача. Проверить выполнимость основного закона динамики вращения для твердого тела с неподвижной осью вращения и
Генкин Б. И. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ Учебное пособие. Санкт-Петербург:, 0.. Кинетическая энергия В качестве универсальной меры различных форм движения и взаимодействия материи используют скалярную величину,
ПодробнееЗакон сохранения импульса
Закон сохранения импульса Закон сохранения импульса Замкнутая (или изолированная) система — механическая система тел, на которую не действуют внешние силы. d v ‘ ‘ d d v d… ‘ v ‘ v v ‘… ‘ v… v v
ПодробнееЧАСТЬ 2. ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ
ЧАСТЬ ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ Механика часть физики, изучающая движение и взаимодействие физических тел в пространстве и времени При этом физика имеет дело не с реальными телами: автомобилями, поездами,
ПодробнееТема: «Динамика материальной точки»
Тема: «Динамика материальной точки» 1.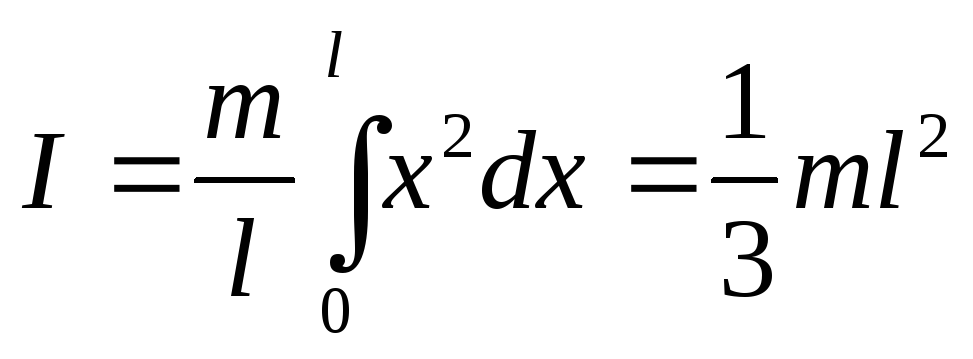
Тело можно считать материальной точкой если: а) его размерами в данной задаче можно пренебречь б) оно движется равномерно ось вращения является неподвижной угловое
ДИНАМИКА. Описание движения твердого тела
Л5 ДИНАМИКА Описание движения твердого тела 1 Прямолинейное движение Прямолинейным движением твердого тела будем называть такое движение системы материальных точек при котором скорости прямолинейного движения
ПодробнееПроверка теоремы Штейнера
Федеральное агентство по образованию РФ Ухтинский государственный технический университет 9 Проверка теоремы Штейнера Методические указания к лабораторной работе для студентов всех специальностей дневной
Подробнееε =, (6.2) I M = r, (6.3)
Методические указания к выполнению лабораторной работы 1.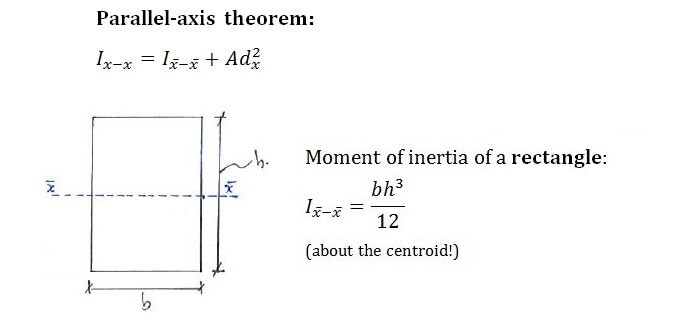
4 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА МАКСВЕЛЛА * * Аникин А.И. Механика: методические указания к выполнению лабораторных работ по физике. Архангельск:
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА.3. Динамика. Динамика это часть теоретической механики, в которой рассматривается движение материальной точки или тела под действием приложенных сил, а также устанавливается связь
ПодробнееГлава 5. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Глава 5. ДИНАМИКА ВРАЩАТЕЛЬНГ ДВИЖЕНИЯ 5.1. Момент импульса материальной точки Введем определение: моментом импульса материальной точки является векторное произведение её радиус-вектора на её импульс p.
Подробнееr 2 r. E + = 2κ a, E = 2κ a
1. Электростатика 1 1. Электростатика Урок 2 Теорема Гаусса 1.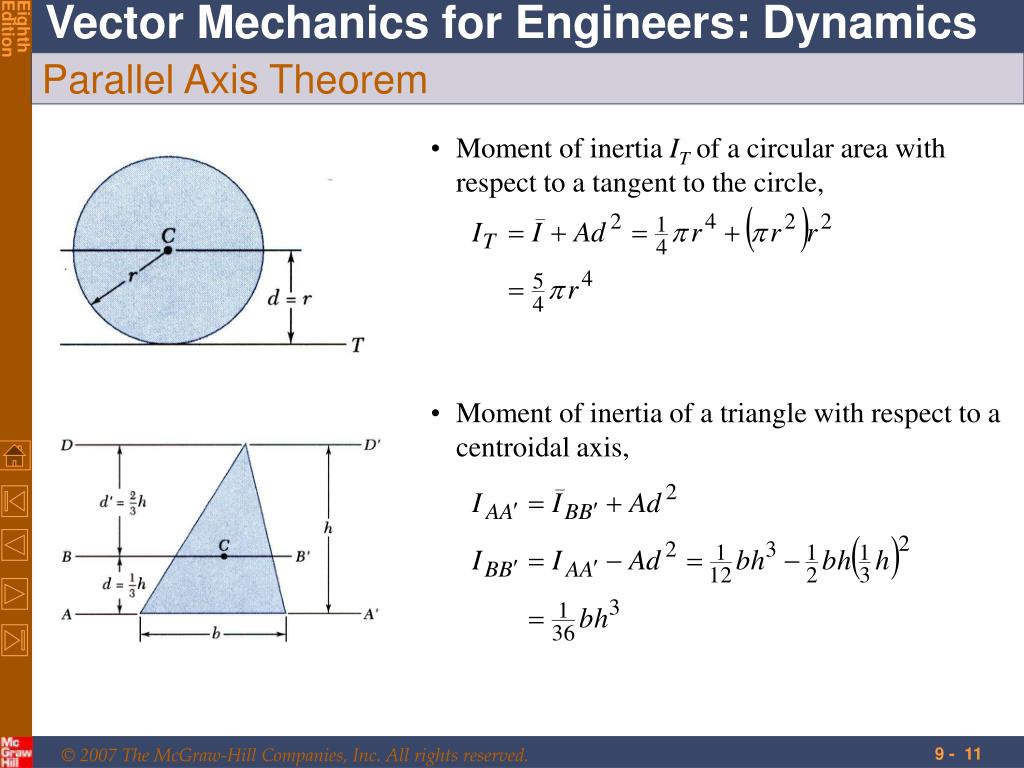
1. (1.19 из задачника) Используя теорему Гаусса, найти: а) поле плоскости, заряженной с поверхностной плотностью σ; б) поле плоского конденсатора;
КИНЕМАТИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ
КИНЕМАТИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ 2.1. Понятие механики, модели в механике 2.2. Система отсчета, тело отсчета 2.3. Кинематика материальной точки 2.3.1. Путь, перемещение 2.3.2. Скорость 2.3.3. Проекция
ПодробнееВекторный и тензорный анализ
С.Н. Зиненко Векторный и тензорный анализ Элементы дифференциальной геометрии и их приложения к механике (теория к задачам) 014 1. Естественный трехгранник кривой Теория 1 о Трехгранник кривой. На параметрическое
ПодробнееДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ Движение в инерциальной системе отсчета.
Законы динамики Ньютона. Масса скаляр, мера инерции, т.е. сопротивления внешнему воздействию. Сила вектор, мера механического действия,
Момент инерции различных тел. Теорема Штейнера
ПЕРВОЕ ВЫСШЕЕ УЧЕБНОЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ «ГОРНЫЙ»
Кафедра общей и технической физики
Лабораторная работа №5
По дисциплине Общая и техническая физика
Тема: Момент инерции различных тел. Теорема Штейнера
Автор: студент гр. ТОА-14 __________________ /Клочков Д.А./
Дата: 28.11.14
ПРОВЕРИЛ доцент_________________ /Егоров С.В./
Санкт-Петербург
2014 год
Цель работы – измерить моменты инерции различных тел. Проверить теорему Штейнера.
1. Момент инерции материальной точки массой m, находящейся на расстоянии R от оси вращения.
2. Момент инерции сплошного цилиндра.
где R, m – радиус и масса цилиндра.
3. Момент инерции полого цилиндра.
где m – масса цилиндра, – внутренний радиус,-внешний радиус.
4. Момент инерции шара массой m и радиуса R.
5. Момент инерции тонкого стержня.
6. Момент инерции вращающегося тела.
7. Теорема Штейнера.
Момент инерции относительно произвольной оси равен сумме момента инерции , относительно оси OO, параллельной данной и проходящей через центр масс тела и произведения массы тела на квадрат расстояний d между осями.
Таблицы.
Измерения для угла
F | l | M | ||
рад | H | м | Н*м | |
/2 | 0,85 | 0,05 | 0,0425 | |
1,6 | 0,05 | 0,08 | ||
3/2 | 2,1 | 0,05 | 0,105 | |
2 | 2,6 | 0,05 | 0,13 |
M (H*м)
/2 3/2 2 (рад)
Данная работа не уникальна.
Ее можно использовать, как базу для подготовки к вашему проекту.
График зависимости момента силы М от угла
0,025
Результаты измерений периода колебаний диска шара полого цилиндра, сплошного диска, стержня.
Полый цилиндр | Сплошной цилиндр | Шар | Сплошной диск | Стержень без грузов | |||
r | м | 0,05 | 0,05 | 0,07 | 0,12 | 0,3 | |
0,0025 | 0,0025 | 0,0049 | 0,0144 | 0,09 | |||
T cр | с | 1,349 | 1,030 | 1,703 | 1,766 | 2,285 | |
J | кг* | 25 * | 20* | 55,2 * | 59,3 * | 99,3 * | |
m | кг | 0,348 | 0,352 | 0,650 | 0,261 | 0,177 |
Вычисления:
1.
2
Расчёт для задания (С). Теорема Штейнера.
Ответ с учётом погрешности: J= 61* ± 7,4 * кг*м2
Вывод
Проведенный анализ гласит , что измерения момента различных тел и проверку теоремы Штейнера можно проводить методом крутильных колебаний. Данный метод дает достаточно точный результат, но здесь имеют место грубые ошибки. Результат отличается от теоретического значения, равного I= 53,1 * кг*м2
на: (I(теор) – J(эксп))/I(теор) * 100% =(37*- 33 * ) / 37* 100% = 10,8% , можно сделать вывод, что погрешность достаточно велика.
Теорема штейнера Краткая теория
При вращательном движении твердого тела вокруг неподвижной оси каждая точка тела движется в плоскости, перпендикулярной оси, по окружности, центр которой лежит на оси. Линейная скорость точки тела v связана с угловой скоростью тела.
, (1)
где r – расстояние
от точки тела до оси вращения.
Кинетическая энергия тела равна сумме кинетических энергий всех частиц тела:
, (2)
где — элементарные массы, на которые мысленно разбито тело. Подставляя скорость vi из формулы (1) в (2), получим
(3)
Величина (4)
называется моментом инерции тела. Момент инерции характеризует распределение массы в твердом теле относительно оси вращения и является мерой инертности вращающегося тела.
Выражение для кинетической энергии вращающегося тела вокруг неподвижной оси, исходя из формул (3) и (4), выглядит следующим образом:
.
Для
вычисления моментов инерции различных
тел массу
в
формуле (4) выражают
через плотность тела: = ρ ΔVi , где ΔVi –
элементарный объем тела, и переходят к
пределу ΔVi → 0.
Тогда получим
. (6)
Теорема Штейнера устанавливает связь между моментом инерции тела Iс относительно оси, проходящей через центр инерции, и моментом инерции I этого тела относительно другой оси, параллельной первой .
,
где m – масса тела, а – расстояние между осями.
Контрольные вопросы
Дайте определение динамических характеристик вращательного движения: момента силы – М, момента инерции – I, момента импульса – L.
Запишите аналитические выражения для момента инерции частицы и твердого тела. Как производится расчет момента инерции обруча, стержня, диска?
В чем состоит суть теоремы Штейнера?
Получите основное уравнение динамики вращательного движения.
Получите уравнение колебаний крутильного маятника.
Как рассчитать период колебаний крутильного маятника?
Задачи
1. Однородный диск массой m = 3 кг и радиусом R = 20 см скреплен с тонким стержнем, другой конец которого закреплен неподвижно (рис.4). Коэффициент кручения стержня (отношение приложенного вращающего момента к углу закручивания)
k = 6 Н∙м/рад. Определить частоту ω малых крутильных колебаний.
2. По данным предыдущей задачи определить амплитуду αmи начальную фазу φ колебаний, если в начальный момент
α = 0,06 рад, = 0,8 рад/с.
3. Два диска могут
вращаться без трения вокруг горизонтальной
оси. Радиус дисков R одинаков и равен 0,5 м. Массы дисков равны m1 = 0,1 кг и m2 = 3 кг.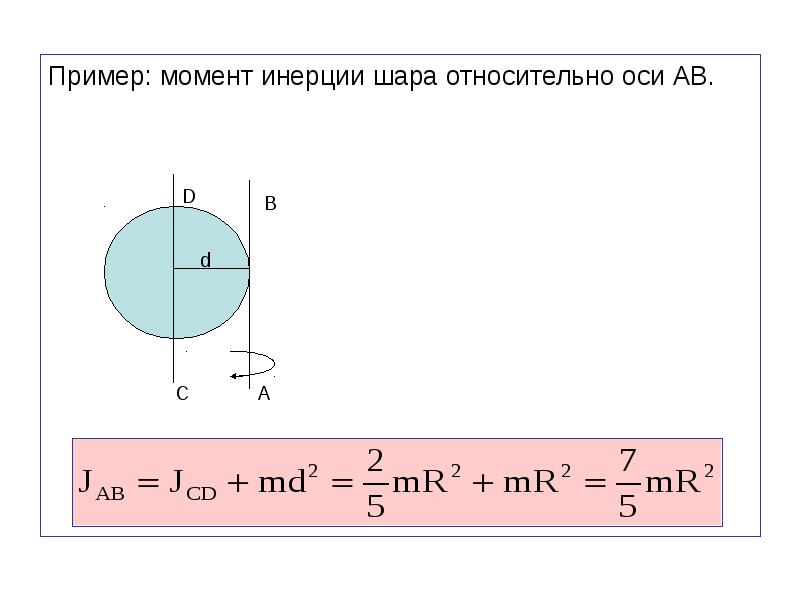
Диски соединены пружиной, у которой
коэффициент пропорциональности между
возникающим вращающим моментом и углом
закручивания равен k = 5,92 Н м /рад. Диски поворачивают в
противоположные стороны и отпускают.
Чему равен период T крутильных колебаний дисков?
4. По диаметру горизонтального диска может перемещаться, без трения по направляющему стержню небольшая муфта массой m = 0,1 кг. Муфта «привязана» к концу стержня с помощью невесомой пружины, жесткость которой k = 10 Н/м (рис. 5). Если пружина не деформирована, муфта находится в центре диска.
Найти частоту ω малых колебаний муфты в том случае, если диск вращается вокруг своей оси с угловой скоростью, равной 6 рад/с
Рис. 4 (к задаче 1) Рис. 5 (к задаче 4)
5. Сплошной однородный цилиндр массой m совершает малые колебания под действием двух пружин, суммарная жесткость которых равна k (рис. 6). Найти период этих колебаний в отсутствии скольжения.
6. Определить момент инерции системы, состоящей из четырех точечных масс m, расположенных по вершинам квадрата со стороной a, относительно оси, лежащей в плоскости квадрата и совпадающей с его диагональю.
7. По условиям предыдущей задачи определить момент инерции системы точек относительно оси, проходящей через центр квадрата перпендикулярно его плоскости.
8. Определите момент инерции медного диска радиусом
R = 5 см, в котором сделаны два выреза в виде кругов радиусами r = 2 см. Центры вырезов находятся на прямой, проходящей через центр диска на расстоянии l = 2,5 см от него (рис.7). Толщина диска h = 0,1 см. Ось вращения проходит через центр диска перпендикулярно его плоскости.
Рис. 6 (к задаче 5) Рис.7 (к задаче 8)
9. По условиям предыдущей задачи определить момент инерции диска относительно оси, проходящей через центры вырезов.
10. Плотность цилиндра длиной l – 0,1 м и радиусом
R = 0,05 м изменяется с расстоянием от оси линейно от значения
ρ1 = 500 кг/м3 до значения ρ2 = 1500 кг/м3. Найти момент инерции цилиндра относительно оси цилиндра.
7. Найти момент инерции тонкого однородного стержня относительно оси, проходящей через один из его концов с помощью теоремы Штейнера. Масса стержня m, длина l.
8. По данным предыдущей задачи найти момент инерции стержня относительно оси, проходящей на расстоянии l/4 от одного из концов.
9. Найти момент инерции диска массой m, радиусом R относительно оси, проходящей через середину радиуса перпендикулярно плоскости диска. Применить теорему Штейнера.
10. Определить момент инерции шара массой m = 2 кг радиусом R = 10 см относительно оси, проходящей через середину радиуса, используя теорему Штейнера.
11. По данным предыдущей задачи определить момент инерции шара, подвешенного на нити длиной l = 10 см относительно точки подвеса.
12. Два шара с массами m1 = 1 кги m2 = 2 кг насажены на гладкий горизонтальный стержень (рис. 8). Шары соединены между собой пружиной с жесткостью k = 24 Н/м. Левому шару сообщили начальную скорость v1 = 12 см/с. Найти частоту колебаний системы.
13. По данным предыдущей задачи найти энергию колебаний.
14. По данным предыдущей задачи найти амплитуду колебаний системы.
15. Найти циклическую частоту малых колебаний тонкого однородного стержня массой m и длиной l вокруг горизонтальной оси, проходящей через точку О (рис. 9). Жесткость пружины k. В положении равновесия стержень вертикален
Рис. 8 (к задаче 12) Рис. 9 (к задаче 15)
определение, законы, формулы для чайников
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Решение:
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Решение:
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Момент инерции, определение и примеры
Момент инерции твердого тела относительно определенной оси определяется как
(1)
(1)
где — перпендикулярное расстояние элемент массы к оси, как показано на рисунке 1. Момент инерции измеряет «сопротивление» тела изменению его состояния при вращательном движении . Момент инерции тесно связан с определением углового момента твердого тела: для твердого тела, вращающегося с угловой скоростью вокруг фиксированной оси, угловой момент равен.
Рисунок 1Определение, данное в уравнении (1), является обобщением на протяженные тела определения единственной материальной точки. Для точки массы имеем, где — масса частицы. Для набора массовых точек у нас будет конечная сумма вместо интеграла.
Принято писать для обозначения момента инерции относительно оси, проходящей через центр масс вращающегося твердого тела .
Момент инерции однородного и тонкого стержня массы и длины
Линейная плотность стержня составляет.Разница в массе равна. Следовательно, момент инерции стержня относительно оси, перпендикулярной стержню и проходящей через его центр масс , равен:
(2)
(2)
Обратите внимание, что в чтобы вычислить момент инерции , мы просто должны поместить начало системы координат точно в положение оси. Момент инерции относительно оси, перпендикулярной стержню и проходящей через конец, можно вычислить непосредственно из определения
(3)
(3)
или с помощью теоремы о параллельности оси ( Теорема Штейнера )
(4)
(4)
Какой толщины должен быть стержень?
На самом деле стержень должен быть «бесконечно тонким».Другими словами, стержень должен быть геометрической линией, действительно одномерной линией. Поэтому представленные здесь расчеты дают только приблизительное значение. Такое приближение будет хорошим, если стержень не сильно отличается от тонкой проволоки. Геометрическая форма поперечного сечения стержня не имеет значения. Таким образом, приближение справедливо и для палки, если она «достаточно тонкая».
Момент инерции однородной цилиндрической оболочки массы и радиуса
Очевидно, что все элементы массы находятся на одинаковом расстоянии от оси симметрии.Следовательно, радиус в интеграле, определяющем момент инерции , является постоянным. Результат:
(5)
(5)
Момент инерции относительно оси, лежащей на поверхности оболочки и параллельной оси симметрии, может быть вычислен с помощью теоремы Штейнера :
(6)
(6)
Оболочка должна быть тонкой, чтобы эти расчеты были хорошим приближением.Из-за симметрии высота раковины не имеет значения. Это означает, что две оболочки с одинаковой массой и радиусом, но одна из которых больше другой, будут иметь одинаковый момент инерции.
Момент инерции однородного цилиндра массы и радиуса
Предположим, что цилиндр имеет высоту. Благодаря симметрии можно рассматривать элементы массы, которые имеют форму цилиндрических оболочек радиуса для. Плотность цилиндра составляет.Таким образом, . Следовательно:
(7)
(7)
Отметим, что высота не имеет значения из-за симметрии. Момент инерции относительно оси, параллельной оси симметрии и проходящей через границу цилиндра, можно вычислить с помощью теоремы Штейнера :
(8)
/ div>
(8 )
Момент инерции: простое определение, формулы, примеры
Что такое инерция?Что такое инерция?
Инерция в физике — это способность тел сохранять состояние движения в течение определенного времени при отсутствии внешних сил.Однако понятие инерции часто используется не только в физике, но и в нашей повседневной жизни. Например, инертный человек — это человек, который вообще не проявляет никакой инициативы. Инертные люди делают только то, что им говорят другие, и делают это крайне медленно, без всякого энтузиазма. «Он движется по инерции», — говорим мы, когда хотим подчеркнуть, что что-то делается без всякого смысла, а просто из-за привычки, приобретенной с годами. Благодаря таким повседневным примерам понятие инерции становится понятным, но термин «момент инерции» требует более подробного пояснения.
Момент инерции Определение
Мы прекрасно понимаем, что масса тела является мерой его инертности. Например, если в супермаркете с силой толкают две тележки, одна из которых будет пустой, а вторая загружена разными товарами, то позже остановить тележку с товарами будет сложнее из-за ее большей массы. Другими словами, чем больше масса тела, тем больше на него действует инерция и тем больше сил требуется, чтобы изменить движение такого тяжелого тела.
В приведенном выше примере тележка движется по прямой и совершает поступательное движение. Если при поступательном движении какого-либо тела его масса является мерой его инерции, то при вращательном движении тела вокруг своей оси мерой его инерции будет величина, которая называется моментом инерции.
Момент инерции — это скалярная физическая величина, мера инерции тела, когда оно вращается вокруг оси. Обычно обозначается буквой J и измеряется в килограммах, умноженных на квадратный метр.
Формула момента инерции
Как рассчитать момент инерции? Существует общее уравнение, которое помогает физикам определять момент инерции любого тела. Если тело разделить на бесконечно малые части с массой dm, то момент инерции будет равен сумме произведения этих элементарных масс на квадрат расстояния до оси вращения. Формула будет выглядеть так:
Дж — момент инерции, r — расстояние до оси вращения.
Для материальной точки массой m, которая вращается вокруг оси на расстоянии r, эта формула будет иметь следующий вид:
Теорема Гюйгенса-Штайнера
Говоря о моменте инерции, нельзя не упомянуть теорему двух математиков Гюйгенса и Штейнера, давших формулировку определения характеристики параллельных осей.
Теорема Гюйгенса-Штейнера гласит: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси, и произведения масса тела квадратом расстояния между осями.
Если вы запишите приведенную выше математическую формулу, вы получите следующее:
Где d — расстояние между осями
Эта теорема значительно облегчает решение многих физических проблем, связанных с инерцией. Например, у вас есть объект произвольной формы, центробежная сила которого известна. Используя формулу Штейнера, мы можем вычислить момент инерции тела относительно любой оси параллельной линии, проходящей через середину фигуры.
Моменты инерции простейших объектов
Несмотря на свою простоту, вычисление моментов инерции для различных объектов требует знания интегралов, этих важных инструментов высшей математики. Для упрощения задачи создана таблица с расчетами инерции для простых геометрических фигур: круга, квадрата, цилиндра и т. Д.
Таким образом вычисляется момент инерции окружности.
Момент инерции цилиндра рассчитывается аналогично.
Предлагаем Вашему вниманию более подробные таблицы с формулами расчета момента инерции для основных геометрических фигур: диска, треугольника, сплошного цилиндра и др.
Ссылки и дополнительная литература
- Marion, JB; Торнтон, СТ (1995). Классическая динамика частиц и систем (4-е изд.). Томсон. ISBN 0-03-097302-3.
- Перейти к: a b Саймон, KR (1971). Механика (3-е изд.). Эддисон-Уэсли. ISBN 0-201-07392-7.
- Перейти к: a b Тененбаум, РА (2004).Основы прикладной динамики. Springer. ISBN 0-387-00887-X.
- Перейти к: a b c d e f g h Kane, T. R .; Левинсон, Д. А. (1985). Динамика, теория и приложения. Нью-Йорк: Макгроу-Хилл.
- Перейти к: a b Winn, Will (2010). Введение в понятную физику: Том I — Механика. АвторДом. п. 10.10. ISBN 144
30.
Момент инерции, видео
Автор: Павел Чайка, главный редактор журнала «Познавайка»
При написании этой статьи я старался сделать ее максимально интересной и полезной.Буду благодарен за любые отзывы и конструктивную критику в виде комментариев к статье. Вы также можете написать свое пожелание / вопрос / предложение на мою почту [email protected] или в Facebook.
(PDF) Оценка переменного массового момента инерции кривошипно-поршневого механизма двигателя внутреннего сгорания
Общий массовый момент инерции относительно невелик, ≈
± 1,53% от среднего значения.В случае 6-цил. рядное расположение
, периодическое изменение момента массы
инерция также имеет период 120 CA град. (Рис.), Но вариабельность
более чем в три раза больше, чем у двигателя V-6, а
достигает ± 4,65% от среднего значения.
В целом можно сделать вывод, что вариабельность момента инерции массы двигателя
зависит от расположения кривошипно-поршневого механизма двигателя
и номера цилиндра
и увеличивается с уменьшением количества цилиндров.
Учитывая, что массовый момент инерции двигателя
поршнево-кривошипно-шатунный механизм является одним из ключевых входных параметров
в динамических расчетах двигателя, использование постоянного среднего значения
этого параметра неточно.
6 ВЫВОДЫ
По результатам представленного анализа
можно сформулировать следующие выводы:
1. Расчетные характеристики и сложное движение кривошипно-поршневого механизма двигателя
дают его массовый момент
изменчивости инерции в течение одного двигателя. революция.
2. Переменный характер массового момента двигателя
инерции можно оценить, используя общее уравнение для
приведенного момента инерции массы механизма с
одной степенью свободы, которое выводится из
равенства кинетических энергия реального механизма и его приведенная модель
. В предлагаемом способе учтено реальное движение
как основных, так и вспомогательных шатунов
.Влияние неучтенных эффектов (деформация элементов
,и движение вторичных возвратно-поступательных масс)
относительно невелико. Метод может быть легко применен к
,различных механизмов поршнево-кривошипно-шатунного механизма двигателя, в
ряду и V с первичным и вторичным шатунами,
и для другого количества цилиндров.
3. Сравнение постоянного момента инерции
, рассчитанного с использованием простого метода, основанного на теореме
Гюйгенса-Штайнера, и среднего значения этого параметра
, оцененного с использованием предложенного метода, не показывает существенной разницы
.В случае V-образных двигателей
, оборудованных основными и вспомогательными шатунами
, отклонение составляет около 0,35%, а для рядного двигателя
оно несколько больше — 1,6%.
4. Изменчивость момента инерции масс
за один оборот двигателя зависит от расположения кривошипно-шатунного механизма поршня
и количества цилиндров. Это
относительно мало в случае большого количества цилиндров (≈
± 1.53% от среднего значения для двигателей V-12 и V-6), но
увеличивается с уменьшением количества цилиндров. Для одноцилиндрового двигателя
это + 18,8% и -17% от среднего значения, а для виртуальной конфигурации двигателя
V-2 + 20,65% и -21,43%.
СПИСОК ЛИТЕРАТУРЫ
[1] Гуцзоми, А. Л., Хестерман, Д. К., Стоун, Б. Дж.
Эффекты переменной инерции двигателя, включая трение поршня
и смещение кривошипа или поршневого пальца.
Proc.IMechE Vol. 222 Часть D: J. Автомобиль
Машиностроение. 2008.
[2] Раджендран1, С., Нарасимхан, М.В., Влияние инерции
Отклонение из-за возвратно-поступательных деталей и
Шатунна связанной свободной вибрации коленчатого вала
, Журнал инженерии для газа
Турбины и мощность ЯНВАРЬ 1997, Т.
119/257
[3] Fehrenbach, V.H.,. Held, W., Zuther, F.
Drehmomentbestimmung bei Verbrennungs-
motoren durch Auswertung der Kurbelwellen —
Winkelgeschwindigkeit (MTZ 1998-5).
[4] Лим, Б., Лим, И., Парк, Дж., Паэ, С., Юн, Ю. С. и
Ким, Е. С. Обнаружение пропусков зажигания в двигателе с помощью энергетической модели
(документ SAE 942059).
[5] Гуцзоми, А. Л., Хестерман, Д. К., Стоун, Б. Дж. Влияние трения поршня
на динамику блока цилиндров.
Proc.IMechE Vol. 221 Часть K: J. Multi-body
Динамика. 2007.
[6] Chen, B.C., Wu, Y.Y, Hsieh, F.C. Оценка динамики вращения двигателя
с использованием замкнутого контура оценки
с идентификацией хода для систем управления двигателем
. Proc. IMechE Vol. 219 Part
D: J. Автомобильная инженерия. 2005.
[7] Цвейри, Й. Х., Уидборн, Дж. Ф., Сеневиранте, Л. Д.,
и Алтофер, К.Сравнение динамических моделей
различной сложности для дизельных двигателей.
Том. 8, № 3, с. 273-289. Математическое и
Компьютерное моделирование динамических систем. 2002.
[8] Радонич, Д. Анализ параметров, влияющих на равномерность вращения коленчатого вала
двигателей внутреннего сгорания, используемых в транспортных средствах,
двигателей внутреннего сгорания,
транспортных средств и двигателей, YU ISSN 0350-1027,
Ноябрь 1977 г. 2 dA
, где A — площадь фигуры, а y — расстояние любой точки внутри области A от заданной оси вращения.Из определения очевидно, что момент инерции всегда должен иметь положительное значение, поскольку внутри интеграла есть только квадратный член.
Концептуально второй момент площади связан с распределением площади фигуры. В частности, более высокий момент указывает на то, что площадь формы распределена далеко от оси. Напротив, более низкий момент указывает на более компактную форму, площадь которой расположена ближе к оси. Например, на следующем рисунке обе формы имеют равные площади, тогда как правая форма имеет более высокий второй момент площади вокруг красной оси, поскольку, по сравнению с левой, ее площадь распределена значительно дальше от оси. .
Терминология
Чаще всего термин момент инерции используется для второго момента площади, особенно в инженерных дисциплинах. Однако в физике момент инерции связан с распределением массы вокруг оси и, как таковой, является свойством объемных объектов, в отличие от второго момента площади, который является свойством плоских областей. На практике для описания второго момента площади можно использовать следующие термины:
- момент инерции
- момент инерции площади
- момент инерции площади
- момент инерции поперечного сечения
- момент инерции балка
Второй момент площади (момент инерции) имеет значение только тогда, когда определена ось вращения.Тем не менее, часто можно использовать термин «момент инерции окружности», отсутствующий для обозначения оси. В таких случаях, вероятно, подразумевается ось, проходящая через центр тяжести формы.
Произведение инерции
Произведение инерции плоской замкнутой области определяется как интеграл по площади произведения расстояний от пары осей x и y:
I_ {xy} = \ iint_A xy dA
, где A — площадь формы, а x, y — расстояния любой точки внутри области A от соответствующих осей.
Если одна из двух осей также является осью симметрии, то I_ {xy} = 0.
Также обратите внимание, что в отличие от второго момента площади, произведение инерции может принимать отрицательные значения.
Дополнительная информация
Понравилась эта страница? Поделись с друзьями!
Теорема Штейнера или теорема о параллельной оси для вычисления момента инерции
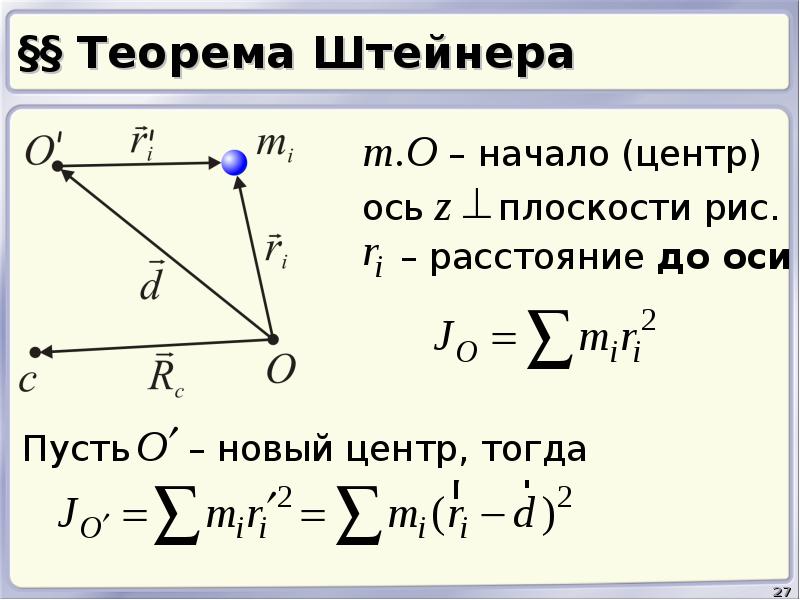
При математическом описании вращательного движения важно знать момент инерции системы относительно оси.В общем случае процедура нахождения этой величины предполагает реализацию процесса интеграции. Так называемая теорема Штейнера упрощает вычисления. Подробнее рассмотрим в статье.
Какой момент инерции?
Прежде чем сформулировать теорему Штейнера, мы должны разобраться с самой концепцией момента инерции. Предположим, есть некое тело определенной массы и произвольной формы. Это тело может быть как материальной точкой, так и любым двухмерным и трехмерным объектом (стержень, цилиндр, шар и т. Д.).). Если рассматриваемый объект совершает круговое движение вокруг определенной оси с постоянным угловым ускорением α, то мы можем записать следующее уравнение:
M = I * α
Здесь величина M представляет собой общий момент сил, который дает ускорение α всей системе. Коэффициент пропорциональности между ними — I, называется моментом инерции. Эта физическая величина рассчитывается по следующей общей формуле:
I = ∫ м (r 2 * dm)
Здесь r — расстояние между элементом с массой dm и осью вращения.Это выражение означает, что необходимо найти сумму произведений квадратов расстояний r 2 и элементарной массы dm. То есть момент инерции не является чистой характеристикой тела, что отличает его от линейной инерции. Это зависит от распределения массы по всему вращающемуся объекту, а также от расстояния до оси и от ориентации тела относительно нее. Например, стержень будет иметь другое I, если он будет вращаться вокруг центра масс и вокруг конца.
Момент инерции и теорема Штейнера
Знаменитый швейцарский математик Якоб Штайнер доказал теорему о параллельных осях и моменте инерции, которая теперь носит его фамилию. Эта теорема постулирует, что момент инерции абсолютно любого твердого тела произвольной геометрии относительно некоторой оси вращения равен сумме момента инерции относительно оси, пересекающей центр масс тела и параллельной оси вращения. во-первых, и произведение массы тела на квадрат расстояния между этими осями.Математически эта формулировка записывается следующим образом:
I Z = I O + m * l 2
I Z и I O — моменты инерции относительно оси Z и параллельно ей ось O, проходящая через центр масс тела, l — расстояние между прямыми Z и O.
Теорема позволяет, зная значение I O , вычислить любой другой момент I Z относительно оси, параллельной O.
Доказательство теоремы
Формулу теоремы Штейнера можно легко получить независимо. Для этого рассмотрим произвольное тело на плоскости xy. Пусть начало координат проходит через центр масс этого тела. Вычисляем момент инерции I O , который проходит через начало координат перпендикулярно плоскости xy. Поскольку расстояние до любой точки тела выражается формулой r = √ (x 2 + y 2 ), то получаем интеграл:
I O = ∫ м ( r 2 * dm) = ∫ m ((x 2 + y 2 ) * dm)
Теперь переместим параллельно оси x вдоль оси x на расстояние l, например, в положительном направлении, то расчет для новой оси момента инерции будет выглядеть так:
I Z = ∫ м (((x + l) 2 + y 2 ) * dm)
Раскроем полный квадрат в скобках и разделим подынтегральные выражения, получим:
I Z = ∫ m ((x 2 + l 2 + 2 * x * l + y 2 ) * dm) = ∫ m ((x 2 + y 2 ) * dm) + 2 * l * ∫ m (x * dm) + l 2 904 84 * ∫ m dm
Первый из этих членов — это I O , третий член после интегрирования дает член l 2 * m, но второй член равен нулю.Обнуление указанного интеграла связано с тем, что он берется из произведения x на элементы массы dm, что в среднем дает ноль, так как центр масс находится в начале координат. В результате получается формула теоремы Штейнера.
Рассмотренный случай на плоскости можно обобщить на трехмерное тело.
Проверка формулы Штейнера на примере стержня
Приведем простой пример, на котором продемонстрируем, как использовать рассмотренную теорему.
Известно, что для стержня длиной L и массой m момент инерции I O (ось проходит через центр масс) равен m * L 2/12, а момент I Z ( ось проходит через конец стержня) составляет м * L 2/3. Мы проверим эти данные с помощью теоремы Штейнера. Поскольку расстояние между двумя осями равно L / 2, то получаем момент I Z :
I Z = I O + m * (L / 2) 2 = m * L 2 / 12 + m * L 2/4 = 4 * m * L 2/12 = m * L 2/3
То есть мы проверили формулу Штейнера и получили такое же значение для I Z , что и в исходнике .
Аналогичные расчеты можно провести для других тел (цилиндр, шар, диск) с получением необходимых моментов инерции и без интегрирования.
Момент инерции и перпендикулярная ось
Рассматриваемая теорема касается параллельных осей. Для полноты картины полезно также привести теорему для перпендикулярных осей. Он формулируется следующим образом: для плоского объекта произвольной формы момент инерции относительно перпендикулярной к нему оси будет равен сумме двух моментов инерции относительно двух осей, взаимно перпендикулярных и лежащих в плоскости объекта, при этом все три оси должны проходить через одну точку.Математически это записывается так:
I z = I x + I y
Здесь z, x, y — три взаимно перпендикулярные оси вращения.
Существенное отличие этой теоремы от теоремы Штейнера состоит в том, что она применима только к плоским (двумерным) твердым объектам. Тем не менее на практике он широко применяется, мысленно разрезая тело на отдельные слои, а затем складывая полученные моменты инерции.2
На этой диаграмме показан объект произвольной формы с осью вращения, которая не проходит через центр масс:
Но если вы возьмете параллельную ось вращения, которая проходит через центр масс, мы можем использовать это, чтобы вычислить момент инерции, проходящий через фактическую ось вращения.
Если мы знаем или можем вычислить момент инерции через ось центра масс, Icm , измеренный в килограмм-метрах в квадрате, и мы знаем общую массу объекта, m , измеренную в килограммах. и расстояние, на котором параллельная ось находится от центра масс, r , измеряется в метрах, мы можем просто подставить эти числа и вычислить момент инерции через нашу смещенную от центра ось вращения.
Итак, теперь это, наверное, немного легче понять. Но знаете, что могло бы сделать его еще лучше? Пример.
Пример расчета
Однажды вы убираете подвал и находите действительно старую подушку для спальни. Одна из тех супер-комковатых подушек, которые следовало выбросить много лет назад. Прежде чем выбросить его, будучи физиком-любителем, вы решаете поставить над ним эксперимент. Вы бесцеремонно берете у бабушки вязальную спицу, протыкаете ее посередине и крутите подушку вокруг иглы.
Вы могли воткнуть иглу прямо посередине, но, поскольку она вся комковатая и деформированная, к сожалению, центр масс подушки уже не посередине. Центр масс подушки находится на расстоянии 0,05 метра от середины. Если бы вы воткнули вязальную спицу через центр масс, момент инерции был бы 0,00015, но вы этого не сделали. Теперь вам нужно его рассчитать. Если масса подушки составляет 0,1 килограмма, каков момент инерции подушки вокруг оси спицы?
Как решить эту проблему? Что ж, прежде всего, мы должны записать то, что мы знаем.Мы знаем, что расстояние между осью вращения и центром масс составляет 0,05 метра, это r . Мы знаем, что масса подушки 0,1 килограмма, это м . И нам сказали, что момент инерции, если бы он вращался вокруг центра масс, был бы 0,00015, это Icm , момент инерции вокруг оси центра масс.
Подставьте эти числа в теорему о параллельных осях, и вы получите:
I = 0,00015 + (0.2.
Введите это в калькулятор и решите, и вы получите 0,0004 кг м2.
Вот и все, это наш ответ.
Краткое содержание урока
Инерция вращения (также известная как момент инерции) — это число, которое представляет, сколько массы имеет вращающийся объект и как он распределяется. Объект с большей инерцией вращения сложнее ускорить. Момент инерции измеряется в кг · м2.
Теорема о параллельности осей позволяет нам вычислить момент инерции для объекта, который вращается вокруг оси, которая не проходит через центр масс.Теорема о параллельной оси утверждает, что момент инерции объекта вокруг определенной оси равен моменту инерции вокруг параллельной оси, проходящей через центр масс, плюс масса объекта, умноженная на расстояние до эта параллельная ось в квадрате.
Момент инерции вокруг центра масс — минимальное значение. Если вы переместите ось вращения в другое место, момент инерции, насколько сложно замедлить или ускорить вращение объекта, увеличивается.
Это уравнение позволяет нам вычислить это увеличенное значение, где Icm (или I-центр масс) — это момент инерции, если объект вращался вокруг параллельной оси, которая проходила через центр масс, измеренный в кг · м2, а м — масса объекта, измеренная в килограммах, а r — расстояние между параллельной осью центра масс и осью вращения, измеренное в метрах.
Результаты обучения
Каждый раздел этого урока может подготовить вас к:
- Описать инерцию вращения
- Объясните теорему о параллельности оси
- Определите форму уравнения теоремы о параллельных осях
Формула расчета момента инерции
🕑 Время чтения: 1 минута
Что такое момент инерции? Момент инерции , также называемый моментом инерции массы или угловой массой (единицы СИ кг м 2 ), является мерой сопротивления объекта изменениям скорости его вращения.Это вращательный аналог массы. То есть это инерция твердого вращающегося тела по отношению к его вращению. Момент инерции играет во вращательной динамике почти ту же роль, что и масса в базовой динамике, определяя взаимосвязь между угловым моментом и угловой скоростью, крутящим моментом и угловым ускорением, а также рядом других величин. В то время как простой скалярной обработки достаточно для многих ситуаций, более продвинутая тензорная обработка позволяет анализировать такие сложные системы, как волчки и движение гироскопа. Символ I и иногда J обычно используется для обозначения момента инерции. Момент инерции объекта относительно данной оси описывает, насколько сложно изменить его угловое движение вокруг этой оси. Например, рассмотрим два диска (A и B) одинаковой массы. Диск A имеет больший радиус, чем диск B. Предполагая, что существует однородная толщина и распределение массы, требуется больше усилий для ускорения диска A (изменения его угловой скорости), потому что его масса распределена дальше от его оси вращения: масса, которая находится дальше выходящая из этой оси при данной угловой скорости должна перемещаться быстрее, чем масса, приближающаяся к ней.В этом случае диск A имеет больший момент инерции, чем диск B. Момент инерции имеет две формы: скалярную форму I (используется, когда известна ось вращения) и более общую тензорную форму, которая не требует знания оси вращения. Скалярная форма I (часто называемая просто «моментом инерции») позволяет кратко проанализировать многие простые проблемы в динамике вращения, такие как скатывание объектов по склону и поведение шкивов. Например, в то время как блок любой формы будет скользить вниз с уменьшением трения с той же скоростью, катящиеся объекты могут спускаться с разной скоростью, в зависимости от их моментов инерции.Обруч будет опускаться медленнее, чем твердый диск той же массы и радиуса, потому что большая часть его массы расположена далеко от оси вращения, и, следовательно, ему нужно двигаться быстрее, если обруч катится с той же угловой скоростью. Однако для (более сложных) задач, в которых ось вращения может измениться, скалярная обработка неадекватна, и необходимо использовать тензорную обработку (хотя в особых случаях возможны сокращения). Примеры, требующие такой обработки, включают гироскопы, вершины и даже спутники, все объекты, выравнивание которых может изменяться.Момент инерции не следует путать с полярным моментом инерции, который является мерой способности объекта сопротивляться скручиванию (скручиванию). Формула момента инерции: Простая формула момента инерции любого объекта, будь то точечная масса или 3D-структура, задается следующим образом: где dm — масса бесконечно малой части тела и r — расстояние (перпендикулярно) от точечной массы до оси вращения. Детальный анализ (Скалярный) момент инерции точечной массы, вращающейся вокруг известной оси, определяется выражением I является аддитивным.Таким образом, для твердого тела, состоящего из N точечных масс м i с расстояниями r i до оси вращения, сумма I равна сумме моментов инерции точечной массы: Для твердого тела, описываемого непрерывной функцией плотности массы? ( r ), I относительно известной оси может быть вычислено путем интегрирования квадрата расстояния (взвешенного по плотности массы) от точки в теле до вращения. ось: где V — объем, занимаемый объектом.? — пространственная функция плотности объекта, а — координаты точки внутри тела. Диаграмма для расчета I. диска. Здесь k, — 1/2, а r — радиус, используемый для определения момента. Основываясь только на размерном анализе, I неточечного объекта должен принимать форму: где M — масса R — радиус объекта от центра масс (в некоторых случаях вместо этого используется длина объекта). k — это безразмерная константа, называемая константой инерции , которая изменяется в зависимости от рассматриваемого объекта.Инерционные константы используются для учета различий в размещении массы относительно центра вращения. Примеры включают: k = 1, тонкое кольцо или тонкостенный цилиндр вокруг его центра, k = 2/5, сплошная сфера вокруг центра k = 1/2, сплошной цилиндр или диск вокруг его центра. Теорема о параллельной оси После того, как момент инерции был вычислен для вращений вокруг центра масс твердого тела, его можно удобно пересчитать и для всех параллельных осей вращения, не прибегая к формальному определению.Если ось вращения смещена на расстояние R от оси вращения центра масс (например, вращение диска вокруг точки на его периферии, а не через его центр), смещение и центр-момент инерции связаны следующим образом: Эта теорема также известна как правило о параллельных осях и является частным случаем теоремы Штейнера о параллельных осях . Теорема о перпендикулярной оси Теорема о перпендикулярной оси для плоских объектов может быть продемонстрирована, если посмотреть на вклад в трёхосные моменты инерции от произвольного элемента массы.По моменту точечной массы вклады в каждый из осевых моментов инерции равны Композитные тела Если тело можно разложить (физически или концептуально) на несколько составных частей, то момент инерции тела относительно данной оси получается путем суммирования моментов инерции каждой составной части вокруг той же заданной оси. Моменты инерции общих форм .