Ток в замкнутой цепи – Закон Ома для полной (замкнутой) цепи

Закон Ома для полной (замкнутой) цепи

Закон Ома для полной цепи определяет значение тока в реальной цепи, который зависит не только от сопротивления нагрузки, но и от сопротивления самого источника тока. Другое название этого закона — закон Ома для замкнутой цепи. Рассмотрим смысл закона Ома для полной цепи более подробно.

Потребители электрического тока (например, электрические лампы) вместе с источником тока образуют замкнутую электрическую цепь. На рисунке 1 показана замкнутая электрическая цепь, состоящая из автомобильного аккумулятора и лампочки.

Рисунок 1. Замкнутая цепь, поясняющея закон Ома для полной цепи.

Ток, проходящий через лампочку, проходит также и через источник тока. Следовательно, проходя по цепи, ток кроме сопротивления проводника встретит еще и то сопротивление, которое ему будет оказывать сам источник тока (сопротивле­ние электролита между пластинами и сопротивление пограничных слоев электролита и пластин). Следовательно, общее сопротивление замкнутой цепи будет складываться из сопротивления лампочки и сопротивления источника тока.

Сопротивление нагрузки, присоединенной к источнику тока, принято называть внешним сопротивлением, а со­противление самого источника тока — внутренним со­противлением. Внутреннее сопротивление обозначается буквой r.

Если по цепи, изображенной на рисунке 1, протекает ток I, то для поддержания этого тока во внешней цепи согласно за­кону Ома между ее концами должна существовать раз­ность потенциалов, равная I*R. Но этот же ток I протекает и по внутренней цепи. Следовательно, для поддержания тока во внутренней цепи, также необходимо существование разности потенциалов между концами сопротивления r. Эта разность потенциалов па закону Ома должна быть равна I*r.

Поэтому для поддержания тока в цепи электродвижущая сила (ЭДС) аккумулятора должна иметь величину:

E=I*r+I*R

Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:

E=I(r+R)

или

I=E/(r+R)

Две последние формулы выражают закона Ома для полной цепи.

Закон Ома для полной замкнутой цепи формулируется так: сила тока в замкнутой цепи прямо пропорциональ­на ЭДС в цепи и обратно пропорциональ­на общему сопротивлению цепи.

Под общим со­противлением подразумевается сумма внешнего и внутреннего сопротивлений.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

www.sxemotehnika.ru

Закон Ома для замкнутой цепи

Закон Ома для замкнутой цепи показывает — значение тока в реальной цепи зависит не только от сопротивления нагрузки, но и от сопротивления источника.

Формулировка закона Ома для замкнутой цепи звучит следующим образом: величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.

Впервые зависимость тока от сопротивлений была экспериментально установлена и описана Георгом Омом в 1826 году.

Формула закона Ома для замкнутой цепи записывается в следующем виде:

где:

• I [А] – сила тока в цепи,
• ε [В] – ЭДС источника напряжения,
• R [Ом] – сопротивление всех внешних элементов цепи,
• r [Ом] – внутреннее сопротивление источника напряжения

Физический смысл закона

Потребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребитель, проходит и через источник тока, а значит, току кроме сопротивления проводника оказывается сопротивление самого источника. Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.

Физический смысл зависимости тока от ЭДС источника и сопротивления цепи заключается в том, что чем больше ЭДС, тем больше энергия носителей зарядов, а значит больше скорость их упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.

Зависимость можно показать на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения в цепи идет ток, наблюдаемый по амперметру, двигая ползунок реостата, увидим, что при изменении внешнего сопротивления ток будет меняться.

Примеры задач на применение закона Ома для замкнутой цепи

К источнику ЭДС 10 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 4 Ом. Найти силу тока в цепи и напряжение на зажимах источника.

Дано:	Решение:
ε = 10 В r = 1 Ом R = 4 Ом	Запишем закон Ома для замкнутой цепи — I=ε/(R+r) . Падение напряжения на зажимах источника найдем по формуле U=ε-Ir=εR/(R+r). Подставим заданные значения и вычислим I=(10 В)/((4+1)Ом)=2 А, U=(10 В∙4Ом)/(4+1)Ом=8 В./li> Ответ: 2 А, 8 В.

При подключении к батарее гальванических элементов резистора сопротивлением 20 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 10 Ом сила тока стала 1,5 А. Найти ЭДС и внутреннее сопротивление батареи.

Дано:

Решение:

R1 = 20 Ом R2 = 10 Ом I1 = 1 A I2 = 1.5 A

Запишем закон Ома для замкнутой цепи — I=ε/(R+r) . Отсюда для каждого сопротивления получим ε=I_1 R_1+I_1 r, ε=I_2 R_2+I_2 r. . Приравняем правые части уравнений и найдем внутреннее сопротивление r=(I_1 R_1-I_2 R_2)/(I_2-I_1 ). Подставим полученное значение в закон Ома ε=(I_1 I_2 (R_2-R_1))/(I_2-I_1 ). Произведем вычисления r=(1А∙20 Ом-1,5А∙10Ом)/(1,5-1)А=10 Ом, ε=(1А∙1,5А(20-10)Ом)/((1,5-1)А)=30 В. Ответ: 30 В, 10 Ом.

zakon-oma.ru

Закон Ома для замкнутой цепи.

Замкнутая цепь содержит: источник тока, сопротивления (потреби тока), приборы для контроля характеристик тока, провода, ключ. Приме может служить цепь, приведенная на рис.5. По отношению к источнику можно выделит внешнюю цепь, содержащую элементы, находящиеся данного источника, если проследить за током от одной его клеммы другой, и внутреннюю, к которой относят проводящую среду внутри источника обозначим сопротивление внешней цепи через

R, внутреннее сопротивление источника r. Тогда ток в цепи определяется по закону для замкнутой цепи, который гласит, что ток в замкнутой цепи прямо пропорционален величине ЭДС и обратно пропорционален сумме внутреннего и внешнего сопротивления цепи, т.е.

(8)

Из этого закона вытекают следующие частные случаи:

• Если R стремится к нулю (т.е. R << r), то ток I стремится к максимально

возможному значению I_к.з = , называемому током короткого

замыкания. Этот ток опасен для источников, поскольку вызывает перегрев источника и необратимые изменения проводящей среды внутри него.

• Если R стремится к бесконечно большой величине (т.е. при условии, что R >> r), ток I уменьшается, и падение напряжения внутри источника

Ir становится намного меньше IR, следовательно IR. Значит, величину ЭДС источника можно практически измерить с помощью вольтметра, присоединенного к клеммам источника при условии, что сопротивление вольтметра R_V >> r при разомкнутой внешней цепи.

Распределение энергии при работе источника постоянного тока

Пусть источник постоянного тока имеет ЭДС и внутреннее

сопротивление r и замкнут на сопротивление внешней нагрузки R.

Проанализируем несколько величин, характеризующих распределение энергии при работе источника постоянного тока.

а) Затраченная источником мощность Р.

Работа, совершаемая сторонними силами в замкнутой цепи по

перемещению заряда dq, равна:

dA = dq (9)

Исходя из определения, мощность, развиваемая сторонними силами в

источнике, равна:

(10)

Эта мощность расходуется источником во внешней и внутренней по отношению к источнику частях цепи. Используя закон Ома для замкнутой цепи, можно затраченную мощность представить в виде:

(11)

Если сопротивление нагрузки R уменьшается, стремясь к нулю, то Р_затP_max = Если R увеличивается, стремясь в бесконечность, то Р_зат. График зависимости затраченной сторонними силами мощности Р_зат от величины внешнего сопротивления R показан на рисунке 5.

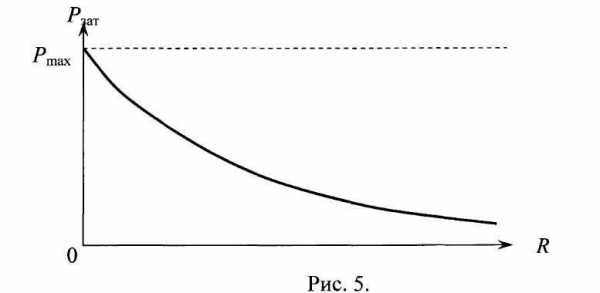
б) Полезная мощность Р_под:_

Полезной по отношению к источнику мощностью Р_под считается мощность, расходуемая источником во внешней цепи, т.е. на внешней нагрузке. Она равна:

(12)

Пользуясь законом Ома для замкнутой цепи, или заменив в последнем выражении I на /(R+r), можно представить в виде

(13)

Если числитель и знаменатель этого выражения разделить на R, то получится выражение

(13a )

наглядно демонстрирующее то, что Р_пол стремится к нулю как при уменьшении R до нуля, так и при его бесконечном увеличении, т.к. в обоих случаях знаменатель этого выражения стремится к бесконечности. Это означает, что при некотором оптимальном значении R полезная мощность достигает максимального значения

Определить оптимальное значение R, а также и значение , можно, приравняв нулю первую производную функции Р_поя

=f(R) пo R:

(14)

Как видно, полученное равенство соблюдается при условии

(15)

из чего следует, что R = r. Таким образом, при сопротивлении внешней цепи R, равном сопротивлению внутренней цепи г, полезная мощность источника тока имеет максимальное значение, которое может быть найдено по формуле:

(16)

График зависимости P_пол=f(R) показан на рисунке 6.

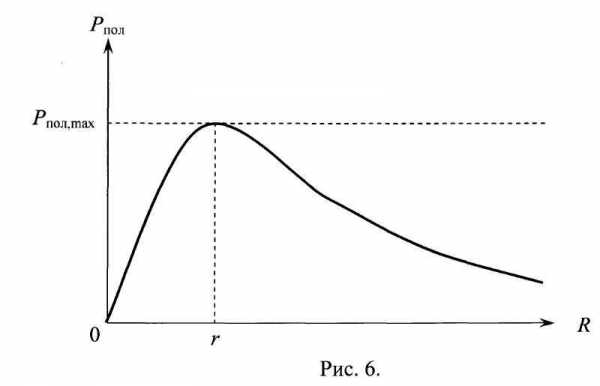
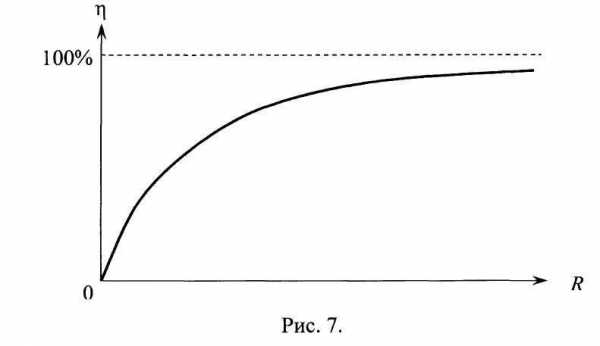
в) Коэффициент полезного действия.

Величина коэффициента полезного действия цепи г| источника тока, в соответствии с определением, составляет:

(17)

При R 0 величина 0, приR величина 100%. В последнемслучае Р

пол стремится к нулю, и такие режимы работы источника не представляют практического интереса. График зависимости КПД источника тока от величины нагрузки R показан на рисунке 7.

studfile.net

Закон Ома для замкнутой цепи

 Закон Ома для замкнутой цепи часто находит применение в работе с электричеством. Благодаря закономерности, найденной немецким физиком Георгом Омом, сегодня мы можем рассчитать величину тока, протекающего в проводе или необходимую толщину провода для подключения к сети.

История открытия

 Будущий ученый с малых лет интересовался природой электрического тока. Он провел множество испытаний, связанных с измерением напряжения и силы тока. Ввиду несовершенства измерительных приборов того времени, первые результаты исследований были ошибочны и препятствовали дальнейшему развитию вопроса. Георг опубликовал первую научную работу, в которой описывал возможную связь между напряжением и силой тока. Последующие его работы подтвердили предположения, и Ом сформулировал свой знаменитый закон. Все труды были внесены в доклад 1826 года, но научное сообщество не заметило труды молодого физика.

Через пять лет, когда известный французский учёный Пулье пришел к такому же выводу, Георга Ома наградили медалью Копли, за внесение большого вклада в развитии физика как науки.

Сегодня закон Ома используется по всему миру, признанный истинным законом природы. .

Детальное описание

  Закон Георга показывает значение электричества в определенной сети, имеющее зависимость от сопротивления к нагрузке и внутренним элементам источника питания. Рассмотрим это детально.

Условное устройство, использующее электроэнергию (например, звуковой динамик) при подключении к источнику питания образует замкнутую цепь (рисунок 1). Подсоединим динамик к аккумулятору. Следующий через динамик ток тоже следует через источник питания. Поток заряженных частиц встретит сопротивление провода и внутренней электроники устройства, а также сопротивление аккумулятора (электролит внутри банки оказывает  определенное воздействие на электрический ток). Исходя из этого, значение сопротивления закрытой сети складывается из сопротивления:

• Источника питания;
• Электрического устройства.

Подключение условного электрического прибора (динамика) к источнику питания (автомобильному аккумулятору)

Первый параметр называют внутренним, второй – внешним сопротивлением. Противодействие источника электричества маркируется символом r.

Представим, что по сети источник питания/электрическое устройство проходит определённый ток T. Для сохранения стабильного значения электричества внешней сети, в соответствии с законом, на её окончаниях должна наблюдаться потенциальная разность, которая равна R*T. Ток такой же величины проходит и внутри цепи. Вследствие этого – сохранение постоянного значения электричества внутри сети требует потенциальной разности на окончаниях сопротивления r. Она, согласно закону, должна равняться T*r. При сохранении стабильного тока в сети, значение электродвижущей силы равно:

E=T*r+T*R

 Из формулы следует, что ЭДС равна сумме падения напряжений во внутренней и внешней сети. Если вынести значение T за скобки, получим:

Е=T(r+R)

или

T=E/(r+R)

Примеры задач на применение закона для соединенной сети

1) К источнику ЭДС 15 В и сопротивлением 2 Ом подсоединен реостат с сопротивлением 5 Ом. Задача – вычислить силу тока и напряжение на зажимах.

Вычисление

• Представим закон Ома для соединенной сети: T=E/(r+R).
• Снижение напряжения вычислим по формуле: U= E-Tr=ER/(R+r).
• Подставим имеющиеся значения в формулу: T= (15 В)/((5+2) Ом) = 2.1 А, U=(15 В* 5 Ом)/(5+1) Ом = 12.5 В

Ответ: 2.1 А, 12.5 В.

  2) При подсоединении к гальваническим элементам резистора с сопротивлением 30 Ом, сила тока в сети приняла значение в 1.5 А, а при подсоединении такого же элемента с сопротивлением 15 Ом сила тока стала 2.5 А. Задача – узнать значение ЭДС и внутреннее сопротивление цепи из гальванических элементов.

Вычисление

• Запишем закон Георга Ома для соединённой сети: T=E/(r+R).
• Из него выведем формулы для внутреннего и внешнего сопротивления: E=T_1 R_1+T_1 r, E= T_2 R_2 + T 2r.
• Приравняем части формулы и вычислим внутреннее сопротивление: r=(T_1 R_1-T_2 R_2)/(T_2-T_1 ).
• Полученные значения подставим в закон: E=(T_1 T_2 (R_2-R_1))/(T_2-T_1 ).
• Проведем вычисления: r=(1.5 А∙30 Ом-2.5А∙15 Ом)/(2,5-1,5)А=7.5 Ом, E=(1.5 А∙2.5А(30-15)Ом)/((2.5-1.5)А)=56 В.

Ответ: 7.5 Ом, 56 В.

Сфера применения закона Ома для замкнутой цепи

 Закон Ома – универсальный инструмент электрика. Он позволяет правильно рассчитать силу тока и напряжение в сети. В основе принципа работы некоторых устройств лежит закон Ома. В частности, предохранителей короткого замыкания.

Короткое замыкание – случайное замыкание двух участков сети, не предусмотренное конструкцией оборудования и приводящее к неисправностям. Для предотвращения таких явлений используют специальные устройства, отключающие питание сети.

Если произойдет случайное замыкание цепи с большой перегрузкой, устройство автоматически прекратит подачу тока.

Закон Ома в данном случае находит место на участке цепи постоянного тока. В полной схеме процессов может быть гораздо больше. Многие действия при построении электрической сети или ее ремонте следует проводить с учетом закона Георга Ома.

Для полного изучения соотношения параметров тока в проводниках представлены формулы: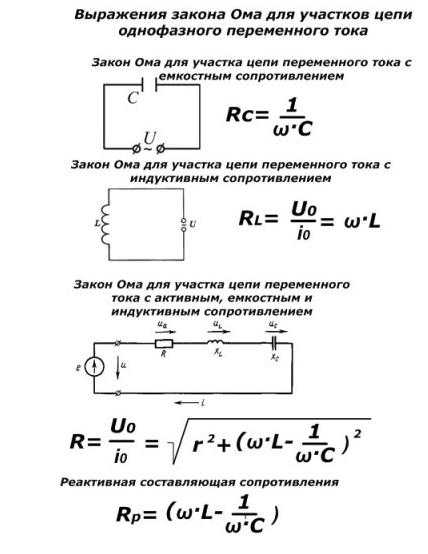

Более сложное выражение закона для практического применения: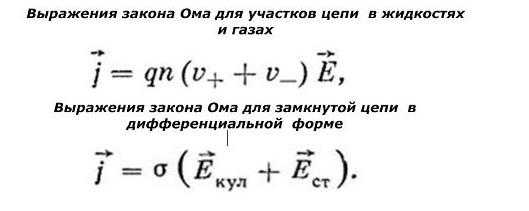

Сопротивление представлено отношением напряжения к силе тока в цепи. Если напряжение увеличить в n раз, значение тока также увеличится в n раз.

Не менее известны в электротехнике труды Густава Киргофа. Его правила находят применения в расчетах разветвленных сетей. В основе этих правил лежит закон Ома для электрической цепи.

Труды ученого нашли применение при изобретении многих повседневных вещей, таких как лампы накаливания и электрические плиты. Современные достижения в электронике многим обязаны открытиям 1825 года.

Поделиться ссылкой:

Похожее

uelektrika.ru

формула и определение, источник ЭДС

Взаимозависимость параметров системы в физике принято называть законом.

В электротехнике таковых было открыто несколько и один из главнейших — закон Ома для замкнутой цепи.

В данной статье он и все связанные с ним понятия рассматриваются подробно.

Закон Ома для замкнутой цепи

Электрическая цепь — это замкнутый контур из проводников и прочих токопроводящих элементов, по которому движутся свободные заряды, то есть протекает ток.

Какова причина их движения? Объяснить его действием электростатического поля нельзя: работа последнего при перемещении заряженной частицы по закольцованному контуру, как известно, равна нулю, а между тем в электросети в момент протекании тока явно совершается некая отличная от нуля работа — выделяется тепло, горит свет либо возникает магнитное поле.

Следовательно, должны быть какие-то иные силы, обуславливающие данное движение. Их называют сторонними (СС), а компонент электросхемы, в котором они проявляются, — источником тока (ИТ или двухполюсником). СС, преодолевая силы электростатического поля, «растаскивают» минусовые и плюсовые заряды в разные части ИТ (они называются полюсами), создавая разность потенциалов, и далее те движутся по сети под действием электростатического поля.

Аналогично подъемник «заряжает» потенциальной энергией поднимаемый груз, преодолевая силу гравитации, а циркуляционный насос — кинетической энергией частицы воды, создавая разность давлений. Электрическую сеть, включающую ИТ, называют полной или замкнутой. В противоположность ей, сеть вне двухполюсника называют внешней.

В разных ИТ сторонние силы создаются следующими способами:

1. фотонным. Разность потенциалов возникает при взаимодействии фотонов (из этих частиц состоит свет) с полупроводниковыми материалами. Действующие по такому принципу ИТ называют солнечными батареями;
2. химическим. На этом принципе основано действие гальванических элементов — батареек и аккумуляторов. К примеру, химическое разделение зарядов возникает при погружении в серную кислоту медного и цинкового электродов. Кислота изымает из каждого металла положительно заряженные ионы, но цинк отдает их легче и потому принимает относительно меди отрицательный заряд. Медный же электрод становится положительным полюсом, и если теперь соединить его с цинковым электродом проволокой, по ней потечет ток;
3. электромагнитным. СС вызываются воздействием на проводник переменного магнитного поля. Изменение его параметров, то есть его «переменность», достигается за счет движения относительно него проводника: тот совершает обороты в поле либо, наоборот, магнит вращают вокруг проводника. На этом принципе основана работа электрогенераторов (в обиходе называются динамо-машинами).

Возникновение электротока в проводнике под действием переменного электромагнитного поля, называется электромагнитной индукцией. Двигая заряды q по сети, СС совершают некую работу А. Она, очевидно, пропорциональна величине перемещаемого q, а значит, при любой величине А и Q их соотношение остается константой и может выступать характеристикой двухполюсника. Ее называют электродвижущей силой (ЭДС).

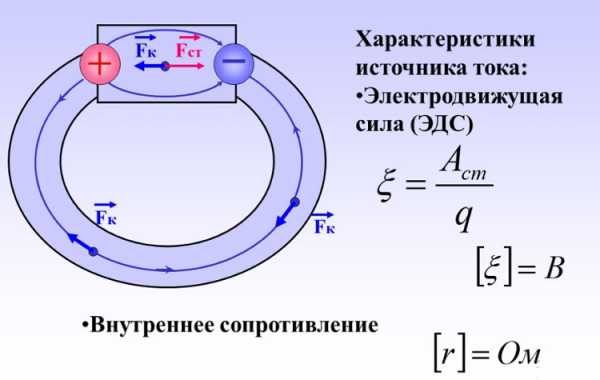
Электродвижущая сила источника тока

Математическое выражение ЭДС, обозначенной буквой Ԑ, записывается так: Ԑ = А/q. Измеряют ЭДС в тех же единицах, что и напряжение — в вольтах (В). Из последнего выражения работа СС записывается как А = Ԑ * q. С другой стороны, работа СС, согласно закону сохранения энергии, должна равняться действию электрического тока. Последняя состоит в выделении тепла (рассматривается сеть постоянного тока с активным сопротивлением).

Выделяемое тепло, в соответствии с законом Дж.-Ленца, вычисляется как произведение квадрата силы тока и электросопротивления. Последняя характеристика присуща как внешней цепи — она обозначается через R, так и ИТ (сопротивление обмоток генератора или электролита, обозначаемое через r).

Математическая запись вышесказанного:

1. теплота, выделяющаяся во внешней сети: Q1 = I² * R * t;
2. теплота, выделяющаяся в ИТ: Q2 = I² * r * t;
3. работа СС: А = Ԑ * q = I² * R * t + I² * r * t.

Силой тока I, как известно, называют количество заряда, пересекающее поперечное сечение проводника за единицу времени: I = q / t. Значит, q = I * t, соответственно, Ԑ * q = E * I * t. Тогда получим: А = Е * q = Ԑ * I * t = I² * R * t + I² * r * t. Сократив обе части равенства на I * t, получим: Ԑ = I * R + I * r. Откуда I = Ԑ / (R + r).

Последнее выражение представляет собой математическую запись закона Ома для замкнутой (полной) электросхемы. Сила тока в сети находится в прямой зависимости от ЭДС его источника и в обратной – от полного сопротивления. Как ясно из определения, сумму сопротивлений внешней цепи и ИТ (R + r) называют ее полным сопротивлением.

Таким образом, закон Ома для участка сети, выражаемый формулой I = U / R, является частным случаем закона для полной цепи, в котором двухполюсник во внимание не берут. Из него следует, что U = I * R. Возвращаясь к записи Ԑ = I *R + I * r, можно Заменить I * R на U, и тогда получится: Ԑ = U + I * r.

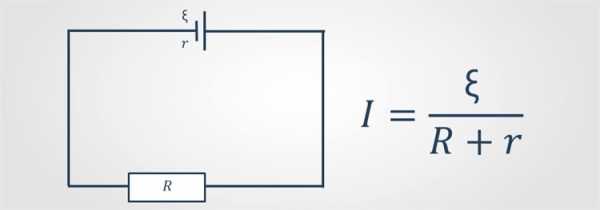
Формула закона Ома для замкнутой цепи

Поскольку через R обозначалось сопротивление всех наружных проводников, U в данном выражении определяет напряжение на ее концах, то есть на клеммах ИТ. После переноса слагаемого из одной части равенства в другую, получим: U = Ԑ – I * r.

Напряжение на клеммах двухполюсника зависит от протекающего в сети тока. Когда электросеть разомкнута и сила тока равна нулю, U = Ԑ. При коротком замыкании (КЗ), когда ток приобретает максимально возможное значение, U = 0.

Коэффициент полезного действия

Любое устройство или механизм сообщенную ему извне энергию частично расходует на всевозможные потери, а ее оставшееся количество преобразует в работу. Она именуется полезной (Апол). Отношение полезной работы к общим затратам энергии, говорит об эффективности устройства. Такую характеристику называют коэффициентом полезного действия (КПД): КПД = Апол / А.

Коэффициент полезного действия источника тока

В электротехнике «полезной» называют работу тока во внешней цепи. В самом простом случае (постоянный ток, активное сопротивление) она равна количеству тепловыделения, то есть: Апол = Qвнеш = I² * R * t. Выше было показано, что совокупная работа СС А = I² * R * t + I² * r * t, следовательно: КПД = Апол / А = I² * R * t / (I² * R * t + I² * r * t) = R / (R + r).

Приведенная формула позволяет определить КПД ИТ. В соответствии с законом сохранения энергии, он не может быть больше единицы. Принято КПД указывать в процентах. Так, при его значении, к примеру равному 0,95, говорят, что КПД составляет 95%.

Источник ЭДС

Выше было показано, что в реальном ИТ, напряжение на клеммах U зависит от силы тока в электросети. Источник ЭДС — это идеальный, теоретический ресурс напряжения (ИН) с отсутствующим внутренним сопротивлением (r = 0), то есть напряжение U на его контактах и ЭДС равны. Сила тока здесь на это равенство не влияет.

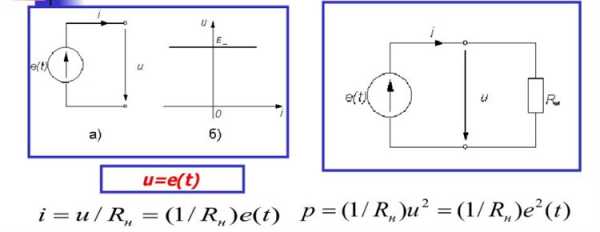
Идеальный источник напряжения

При КЗ ток становится теоретически бесконечно большим. В самом деле, если в выражении закона Ома для полной цепи: I = Ԑ / (R + r) Если полное сопротивление приравнять к нулю, сила тока I достигает бесконечности.

Поэтому источник ЭДС представляет собой теоретический бесконечный источник мощности. В реальности подобное невозможно, так как при КЗ ток в электросети ограничивается сопротивлением двухполюсника (обмоток генератора или электролита гальванического элемента).

Реальный ИН представляет собой источник конечной мощности. На схемах его обозначают как идеальный ИН с подключенным к нему последовательно элементом, соответствующим сопротивлению ИТ.

Соединение источников тока

Если одного ИТ для работы устройства недостаточно, их устанавливают несколько. Характер работы такой группы зависит от способа соединения отдельных источников.

Есть три варианта:

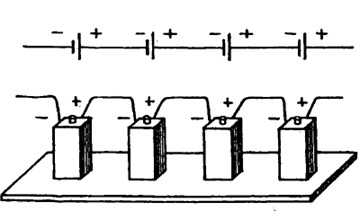
1. последовательное;
2. параллельное;
3. смешанное.

При последовательном подключении ИТ выстраивают в ряд, соединяя «плюсом» к «минусу». При этом заряды проходят по порядку через все источники, воспринимая энергию от каждого из них.

Следовательно, совокупные:

• ЭДС группы равна алгебраической сумме этих характеристик всех ИТ;
• сопротивления группы двухполюсников равно сумме соответствующих параметров каждого из них.

Если соединены n идентичных ИТ с ЭДС, равным Ԑ, и сопротивлением r, то эти параметры для группы окажутся, соответственно: Ԑ гр = n * E; Rгр = n * r. Тогда закон Ома для замкнутой цепи записывается в такой форме: I = (n * Ԑ) / (R + n * r).

Последовательное и параллельное соединение источников

Если направление от «минуса» к «плюсу» в источнике совпадает с движением часовой стрелки, то его ЭДС считается положительной. Электродвижущая сила, направленная в противоположную сторону, отрицательна.

Если внутреннее сопротивление источников в сравнении с R цепи пренебрежимо мало, а надо увеличить U на наружной сети, ИТ соединяют последовательно.

«Плюсы» ИТ, установленных параллельно, подсоединяются к одному концу системы проводников, а все «минусы» — к другому, при этом:

1. каждый заряд набирает энергию только в одном ИТ, потому ЭДС группы равна одноименному параметру одного двухполюсника: Ԑ гр = Ԑ;
2. через отдельно взятый ИТ протекает только доля потока, потому совокупное внутреннее сопротивление группы ниже внутреннего одного элемента в n раз: rгр = r / n. Здесь n — число ИТ в группе.

Здесь также рассматривается случай с одинаковыми ИТ. Закон Ома для полной цепи примет следующую форму: I = Ԑ / (R + (r / n)). Как видно, замена одного ИТ группой параллельно подключенных, приводит к увеличению I во внешней сети.

Соответственно, такой способ подключения применяют при необходимости повысить силу тока в электросети без увеличения напряжения, и сопротивление наружной сети соизмеримо с аналогичным параметром одного двухполюсника.

Видео по теме

Объяснение закона Ома для замкнутой цепи в видео:

Как видно, закон Ома для замкнутой электросхемы соотносит главные «электрические» параметры: силу тока, ЭДС источника напряжения и сопротивление. Потому его следует знать и понимать любому, кто стремится освоить электротехнику.

proprovoda.ru

Формула закона ома для замкнутой цепи

Практическое применение закона Ома.

Формула закона ома для замкнутой цепи. Германский физик Георг Ом был выдающимся ученым. Его имя связано с величайшим открытием, без него невозможно представить современную электротехнику и людей, работающих в этой сфере. В технике, безусловно, работают и многие другие физические законы, но благодаря закону Ома мы получили возможность вычислить ток, который протекает по проводнику, какую мощность он может создавать. Не этом применение его не ограничивается, используется он достаточно широко, включая нашу квартиру.

Закон Ома для замкнутой цепи определяет силу тока в сети, от которой питаются все бытовые приборы. Выглядит он таким образом: I=U/R. Физик Ом является автором и иных фундаментальных законов. Один из них – для полной цепи, где учитывается сопротивление сети и источника питания. В приведенном виде законы эти справедливы для постоянного тока, который со временем не меняет направления. Условно его характеризуют минусом и плюсом, а примером можно считать обычную батарейку.

Закон Ома для замкнутой цепи гласит, что цепь, включающая источник, содержащий внутреннее электросопротивление и нагрузку цепи, имеет силу тока, выражающуюся отношением ЭДС к сопротивлению, которое включает нагрузку и источник.

Одинаково верен этот закон и для переменного тока, но выглядит он в несколько в ином виде. В подобных сетях есть конденсаторы и индукционные катушки, которые уже рассматривались в предыдущих публикациях.

В форме закона для переменного тока присутствует полное сопротивление, включающее емкостное и индуктивное. В этом виде закон применяется для определения сопротивления ЭДС.

Как измерить силу постоянного и переменного тока мы рассматривали ранее.

Во многих случаях с ним имеют дело лишь школьники, которые после окончания школы успешно о нем не вспоминают. В подобном виде он не применяется электриком, работающим с проводкой в доме. В основном, нужен он в виде закона Ома для замкнутой цепи, который дает возможность рассчитать ЭДС по нагрузке, определить дефекты источника. ЭДС, не подходящая для низкого сопротивления, поскольку внутреннее превышает нагрузку, подходит для работы в цепи, имеющей сопротивление, превосходящее во много раз сопротивление источника.

В зависимости от мощности, которую необходимо получить при небольшом значении источника питания, получаем меньшее значение внутреннего сопротивления. По этой причине оптимальными источниками постоянного тока являются сегодня химические аккумуляторы, несмотря на то, что более выгодными могут оказаться солнечные батареи в качестве полупроводниковых источников. Наиболее благоприятной является ситуация, в которой на внутреннем сопротивлении наблюдается падение напряжения меньшее в 10 раз, чем на полезной нагрузке. Иначе говоря, учитывая мощность нагрузки, необходимо подобрать источник, импеданс которого меньший в 10 раз.

Биография ученого.

Ом родился в Германии в Эрлангене в 1789, отец его занимался воспитанием самостоятельно, поскольку мать умерла при родах. Это был очень образованный для своего времени человек и обучал сына точным наукам и философии, затем отправил его в гимназию при университете, в котором Георг продолжил изучать физику и математику. Не доучившись,

 

Ом занялся преподавательской деятельностью при монастыре. В 1809 он перебрался в Нейенбург и полностью занялся освоением математики. В 1811 вернулся к обучению в университете и благополучно завершил его, защитив дипломную работу и став доктором философии. Там же проработал на кафедре математики. Уже работая в Кельне учителем математики, он опубликовал известные труды по электричеству. Множество неприятностей не позволили ученому дальше занимать должность. Он уволен в связи с публикацией работ по физике, которые не отвечали общепринятым учениям. Ом вплотную занимается в этот период чистой наукой и делает главные свои открытия.

В 1842 Ом принят в Лондонское научное сообщество, в Мюнхене становится профессором физики. Он носил это звание до самой смерти в 1854. Ом похоронен в Мюнхене, где ему поставлен памятник. Омом теперь называют величину электрического сопротивления. Самые выдающиеся труды ученого относятся к прохождению тока по проводнику. Наиболее популярная называется законом Ома.

Открытия ученого позволили оценить количественно электрический ток, что перевернуло научный мир: все эксперименты и теоретические опыты подтвердили правоту Ома и верность его закона, который соответствует законам природы. Все последующие его труды по электричеству относились к нагреву проводов и униполярной проводимости. В 1843 в своей статье Ом изложил еще один закон, который также получил его имя. Он гласил, что ухо распознает только простые колебания, и любой тон раскладывается на составные тона, воспринимается ухом в качестве суммы тонов. Современники его не приняли, но через несколько лет после смерти ученого, была доказана справедливость закона.

ampersite.ru

Закон Ома для электрической цепи

Электрический ток, как и любое другое физическое явление подчиняется определенным законам. Так, в 1826 году, Георг Ом вывел эмпирический закон, который способен объяснить зависимость силы тока, напряжения, а также особенностей проводника в электроцепи. В дальнейшем вносились определенные изменения, сам закон Ома для электрической цепи модифицировался, и на данный момент ученые его интерпретируют в четырех вариантах, которые мы и рассмотрим.

В ходе практических исследований, на их базе, ученый смог определить зависимость силы тока и напряжения от специфики проводника, по которому протекает ток. Если быть точнее, то каждый материал имеет определенное сопротивление и на определенном участке цепи, сила тока вычисляется отношением напряжения и сопротивления.

I = U/ R,

где I – сила тока, U – напряжение, R – сопротивление проводника.

Фактически, этот закон аналогичен прохождению воды по трубам: чем больше диаметр трубы и напор, тем больше ее выльется в конечной точке.

Закон Ома для замкнутой цепи

Подобная интерпретация подразумевает наличие источника питания, а также проводника, по которому протекает ток. В этом случае, помимо сопротивления на отдельно взятом участке следует учитывать и то, которое возникает в ИП. Учитывая эти факторы, можно сказать, что сила тока будет равна отношению электродвижущей силы к сумме сопротивлений.

I = E/ Rвн+r,

где Е – ЭДС, Rвн – внешнее сопротивление, а r соответственно внутреннее.

Закон Ома для замкнутой цепи можно объяснить доступным языком. Электродвижущая сила по определению должна полноценно обеспечивать постоянную разницу потенциалов, и эта сила может иметь неприродное происхождение: химическое, если в качестве источника используется батарейка или механическая, в случае подключения к электрической цепи генератора. При подключении медной проволоки с идентичным сечением к батарейке и аккумулятору. Эффект должен быть таким, что по этому проводнику, в котором сопротивление практически отсутствует, должен пойти ток с величиной, стремящейся к бесконечности. Однако этого не происходит и разница в показателях будет существенной, а во втором случае, проволока и вовсе может перегореть. Именно поэтому в расчет берется внутреннее сопротивление источника питания, чтобы описать подобное явление.

Закон ома для неоднородного участка цепи

Перед тем, как записать формулу для подобной интерпретации закона, следует разобраться в таких понятиях, как линейные и нелинейные участки цепи.

Если сопротивление никаким образом не зависит от тока и подаваемого напряжения, то с ростом второго параметра, первый будет прямо пропорционально возрастать и наоборот, то есть зависимость можно описать прямой линией. Подобная зависимость относится к линейным участкам цепи и сопротивление имеет аналогичное название.

Однако вышеизложенный вариант считается идеальным и его можно смоделировать лишь в идеальных условиях, что фактически невозможно, ведь, как минимум, окружающая среда вносит свои коррективы. В этом случае, рост напряжения не будет прямо пропорциональным силе тока и на графике зависимость будет изображаться в виде кривой.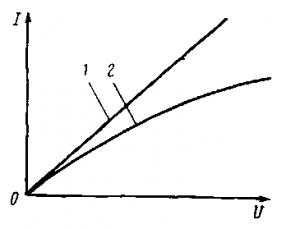

На рисунке изображено два графика, первый из которых описывает линейную зависимость, а второй нелинейную.

Чтобы отчетливо понимать разницу между этими понятиями, рассмотрим принцип работы обычной электрической лампы накаливания. При прохождении тока по нити, температура в значительной степени повышается, что приводит к заметному росту сопротивления. Соответственно, при возрастании напряжения, сила тока будет увеличиваться медленнее, то есть не линейно.

Примечание: в некоторых ситуациях, некоторыми внешними факторами пренебрегают по причине того, что они очень незначительны и в числовом эквиваленте никоим образом не могут повлиять на общую картину. Это значит, что нелинейная зависимость на графике фактически совпадает с линейной.

Учитывая вышесказанное, можно установить следующую зависимость:

I = U/ R = (f1 – f2) + E/ R,

Где f1 и f2 – потенциалы (соответственно f1 – f2 называется разницей потенциалов), E – ЭДС неоднородного участка цепи, а R – суммарное сопротивление на этом же участке.

Нужно упомянуть и о том, что электродвижущая сила не всегда в этом случае будет иметь положительное значение. Если направление тока источника будет аналогичным с направлением в электрической сети, протонов будет больше, чем электронов (положительных и отрицательных частиц), то в этом случае величина E будет иметь значение со знаком «+», в иной ситуации, этот параметр будет со знаком «-».

Закон Ома для переменного тока

Если в электроцепи имеется емкость или инертность, то этот факт следует однозначно учитывать при расчётах силы тока. Они имеют собственные показатели сопротивления, что приводит к ситуации, которая будет иметь переменный характер. В случае Закона Ома для переменного тока формула записывается следующим образом:

I = U/ Z, где

I – сила тока, U – напряжение, а Z – суммарное значение сопротивления на всех участках электрической цепи (этот параметр именуется еще, как импеданс).

Как говорилось изначально, закон Ома считается эмпирическим. Это обозначает то, что он может не всегда работать и выполнять вычисления на его основе не представляется возможным. Подобная ситуация может сложиться в нескольких случаях:

• в ситуации, когда электросеть имеет высокую частоту и электромагнитное поле может сильно изменяться за короткие промежутки времени;
• при наличии проводников, которые обладают свойствами сверхпроводимости, расположенных в условиях низких температурных показателей;
• при перегреве проводника под воздействием проходящего по нему тока, отношение напряжения и сопротивления может носить переменный, неоднородный характер;
• если проводник (диэлектрик) находится под высоким напряжением;
• светодиодных лампах;
• в полупроводниках и аналогичных устройствах.

На основе этого закона, можно произвести вывод некоторых формул математическим путем. С их помощью можно производить разнообразные расчеты.

Поделиться ссылкой:

Похожее

uelektrika.ru

No related posts.