Усилитель с общей базой – Усилительный каскад с общей базой

Усилительный каскад с общей базой

Добавлено 6 октября 2017 в 12:14

Сохранить или поделиться

Последний тип схемы усилителя на биполярном транзисторе (рисунок ниже), который мы должны изучить, это схема с общей базой. Эта конфигурация сложнее двух предыдущих и менее распространена из-за своих странных рабочих характеристик.

Усилитель с общей базой (стрелками показаны направления движения потоков электронов)

Она называется схемой с общей базой, поскольку (игнорируя источники питания постоянного напряжения) источник сигнала и нагрузка делят между собой вывод базы как общую точку (рисунок ниже).

Усилитель с общей базой: вход между эмиттером и базой, выход между коллектором и базой

Возможно, наиболее яркой характеристикой этого типа включения транзистора является то, что источник входного сигнала обеспечивать полный ток эмиттера транзистора, о чём свидетельствуют толстые стрелки на первой иллюстрации. Как известно, ток эмиттера больше, чем любой другой ток в транзисторе, так как является суммой токов базы и коллектора. В последних двух типах усилительных каскадов источник сигнала был подключен к выводу базы транзистора, таким образом, работая на минимально возможном токе.

Поскольку в этой схеме входной ток превышает все другие токи, включая выходной ток, коэффициент усиления по току на самом деле меньше 1 (обратите внимание, как R_нагр подключен к коллектору, тем самым пропуская через себя немного меньший ток, чем источник сигнала). Другими словами, эта схема ослабляет ток, а не усиливает его. В схемах с общим эмиттером и общим коллектором из всех параметров транзистора с усилением тесно был связан β. В схеме с общей базой нам нужен другой основной параметр транзистора: отношение тока коллектора к току эмиттера, который представляет собой дробное число, всегда меньше 1. Это дробное значение для любого транзистора называется коэффициентом α (альфа).

Поскольку данная схема, очевидно, не может повысить ток сигнала, было бы разумным ожидать, что она увеличит напряжение сигнала. Моделирование SPICE схемы на рисунке ниже подтвердит это предположение.

Схема с общей базой для SPICE анализа по постоянному току

common-base amplifier
vin 0 1
r1 1 2 100
q1 4 0 2 mod1
v1 3 0 dc 15
rload 3 4 5k
.model mod1 npn
.dc vin 0.6 1.2 .02
.plot dc v(3,4)
.end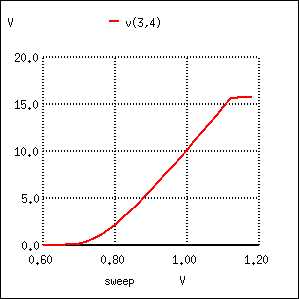

Усилитель с общей базой: график зависимости выходного напряжения от входного напряжения

Обратите внимание, что выходное напряжение изменяется практически от нуля (отсечка) до 15,75 вольт (насыщение), при этом входное напряжение меняется от 0,6 вольта до 1,2 вольта. Фактически, график выходного напряжения не показывает роста примерно до 0,7 вольта на входе и прекращает расти (выпрямляется) примерно при 1,12 вольта на входе. Это показывает довольно большой коэффициент усиления по напряжению с интервалом выходных напряжений 15,75 вольт и интервалом входных напряжений всего 0,42 вольт: коэффициент усиления составляет 37,5 раз, или 31,48 дБ. Также обратите внимание на то, как при насыщении выходное напряжение (измеренное на R

нагр) на самом деле превышает напряжение источника питания (15 вольт) из-за эффекта последовательного добавления источника входного напряжения.

Второй SPICE анализ модифицированной схемы (рисунок ниже) с источником сигнала переменного напряжения (и постоянным напряжением смещения) говорит о том же: о высоком коэффициенте усиления по напряжению.

Схема с общей базой для SPICE анализа по переменному току

common-base amplifier
vin 5 2 sin (0 0.12 2000 0 0)
vbias 0 1  dc 0.95
r1 2 1 100
q1 4 0 5 mod1
v1 3 0 dc 15
rload 3 4 5k
.model mod1 npn
.tran 0.02m 0.78m
.plot tran v(5,2) v(4)
.end

Как вы можете видеть, входной и выходной сигналы на рисунке ниже синфазны друг с другом. Это говорит о том, что усилитель с общей базой является неинвертирующим.

Усилительный каскад с общей базой: осциллограммы входного и выходного напряжений

SPICE анализ по переменному току в таблице ниже на одной частоте 2 кГц предоставляет данные о входном и выходном напряжениях для расчета коэффициента усиления.

AC анализ схемы с общей базой на частоте 2 кГц: список соединений и выходные данные

common-base amplifier
vin 5 2  ac 0.1 sin
vbias 0 1  dc 0.95
r1 2 1 100
q1 4 0 5 mod1
v1 3 0 dc 15    
rload 3 4 5k    
.model mod1 npn 
.ac dec 1 2000 2000
.print ac vm(5,2) vm(4,3) 
.end

frequency       mag(v(5,2))     mag(v(4,3))
--------------------------------------------
0.000000e+00    1.000000e-01    4.273864e+00

Значения напряжений из второго анализа (таблица выше) показывают коэффициент усиления по напряжению 42,74 (4,274 В / 0.1 В), или 32,617 дБ:

\[A_V = { V_{вых} \over V_{вх} }\]

\[A_V = { 4,274 В \over 0,10 В }\]

\[A_V = 42,74\]

\[A_{V(дБ)} = 20 \log A_{V(раз)}\]

\[A_{V(дБ)} = 20 \log 42,74\]

\[A_{V(дБ)} = 32,62 дБ\]

Вот еще один вид схемы с общей базой (рисунок ниже), на которой видны фазы и смещения по постоянному напряжению для разны сигналов в только что промоделированной схеме.

Соотношения фаз и смещений в усилителе на NPN транзисторе с общей базой

То же самое для PNP транзистора (рисунок ниже).

Соотношения фаз и смещений в усилителе на PNP транзисторе с общей базой

Для схемы усилителя с общей базой определить заранее коэффициент усиления по напряжению довольно сложно, что связано с аппроксимацией поведения транзистора, которое трудно измерить напрямую. В отличие от других типов усилительных схема, где коэффициент усиления по напряжению либо устанавливается соотношением двух резисторов (в схеме с общим эмиттером), либо фиксировался на неизменном значении (схема с общим коллектором), коэффициент усиления по напряжению в схеме с общей базой зависит во многом от величины напряжения смещения входного сигнала. Как выясняется, внутреннее сопротивление транзистора между эмиттером и базой играет важную роль в определении коэффициента усиления по напряжению, и это сопротивление изменяется в зависимости от величины тока, протекающего через эмиттер.

Хотя это явление трудно объяснить, его довольно легко продемонстрировать с помощью компьютерного моделирования. Я собираюсь запустить несколько SPICE моделирований схемы усилителя с общей базой (предыдущий рисунок), слегка изменив постоянное напряжение смещения (vbias в коде ниже), оставив теми же амплитуду входного сигнала переменного напряжения и все остальные параметры схемы. Когда в разных моделированиях коэффициент усиления по напряжению будет меняться, это будет заметно по разным амплитудам выходного напряжения.

Несмотря на то, что эти анализы будут проводиться в режиме “transfer function” (коэффициент передачи), каждый из них был сначала проверен в режиме временного анализа (построен график напряжения в зависимости от времени), чтобы гарантировать, что вся синусоида сигнала была воспроизведена точно, а не «обрезана» из-за неправильного смещения. Смотрите «*.tran 0.02m 0.78m» в коде ниже, это «закомментирование» оператора временного анализа. Вычисление коэффициента усиления не может основываться на сигналах искаженной формы. SPICE может для нас рассчитать коэффициент усиления небольшого сигнала постоянного напряжения с помощью оператора «*.tf v(4) vin«. Выходное напряжение – это v(4), а входное напряжение – это vin.

common-base amp vbias=0.85V
vin 5 2  sin (0 0.12 2000 0 0)
vbias 0 1  dc 0.85
r1 2 1 100      
q1 4 0 5 mod1   
v1 3 0 dc 15    
rload 3 4 5k    
.model mod1 npn 
*.tran 0.02m 0.78m
.tf v(4) vin
.end
 

common-base amp current gain
Iin 55 5 0A
vin 55 2  sin (0 0.12 2000 0 0)
vbias 0 1  dc 0.8753
r1 2 1 100      
q1 4 0 5 mod1   
v1 3 0 dc 15    
rload 3 4 5k    
.model mod1 npn 
*.tran 0.02m 0.78m
.tf I(v1) Iin
.end
Transfer function information:
transfer function = 9.900990e-01
iin input impedance = 9.900923e+11
v1 output impedance = 1.000000e+20

Список соединений SPICE (слева): Схема усилителя с общей базой, функция передачи (коэффициент усиления по напряжению) для различных постоянных напряжений смещения. Обратите внимание на оператор .tf v(4) vin.
Список соединений SPICE (справа): Схема усилителя с общей базой, коэффициент усиления по току; функция передачи для коэффициента усиления по постоянному току равна

I(v1)/Iin. Обратите внимание на оператор .tf I(v1) Iin

Командная строка spice -b filename.cir благодаря оператору .tf выводит следующие данные: transfer_function (коэффициент передачи), output_impedance (выходное сопротивление) и input_impedance (входное сопротивление). Сокращенный вывод команды, запущенной для напряжений смещения vbias0.85, 0.90, 0.95, 1.00 вольт, приведен ниже

Вывод SPICE: коэффициент передачи схемы с общей базой:

Circuit: common-base amp vbias=0.85V        // напряжение смещения 0,85 вольта
transfer_function = 3.756565e+01            // коэффициент передачи
output_impedance_at_v(4) = 5.000000e+03     // выходное сопротивление
vin#input_impedance = 1.317825e+02          // входное сопротивление
 
Circuit: common-base amp vbias=0.8753V Ic=1 mA  // напряжение смещения 0,8753 вольта
Transfer function information:
transfer_function = 3.942567e+01            // коэффициент передачи
output_impedance_at_v(4) = 5.000000e+03     // выходное сопротивление
vin#input_impedance = 1.255653e+02          // входное сопротивление
 
Circuit: common-base amp vbias=0.9V         // напряжение смещения 0,9 вольта
transfer_function = 4.079542e+01            // коэффициент передачи
output_impedance_at_v(4) = 5.000000e+03     // выходное сопротивление
vin#input_impedance = 1.213493e+02          // входное сопротивление
 
Circuit: common-base amp vbias=0.95V        // напряжение смещения 0,95 вольта
transfer_function = 4.273864e+01            // коэффициент передачи
output_impedance_at_v(4) = 5.000000e+03     // выходное сопротивление
vin#input_impedance = 1.158318e+02          // входное сопротивление
 
Circuit: common-base amp vbias=1.00V        // напряжение смещения 1,00 вольт
transfer_function = 4.401137e+01            // коэффициент передачи
output_impedance_at_v(4) = 5.000000e+03     // выходное сопротивление
vin#input_impedance = 1.124822e+02          // входное сопротивление
  

Тенденция в списке выше должна быть очевидна. С увеличением постоянного напряжения смещения также увеличивается и коэффициент усиления по напряжению (transfer_function). Мы видим, что коэффициент усиления по напряжению увеличивается, потому что каждео последующее моделирование (vbias = 0.85, 0.8753, 0.90, 0.95, 1.00 В) дает больший коэффициент усиления (transfer_function = 37.6, 39.4 40.8, 42.7, 44.0) соответственно. Эти изменения во многом обусловлены незначительными изменениями напряжения смещения.

Последние три строки в списке соединений выше (справа) показывают коэффициент усиления по току I(v1)/Iin = 0,99 (последние две строки выглядят неправильными). Это имеет смысл для β=100; α= β/(β+1), α=0.99=100/(100-1). Это сочетание низкого коэффициента усиления по току (всегда меньше 1) и несколько непредсказуемого коэффициента усиления по напряжению говорит не в пользу схемы с общей базой, оставляя ей лишь несколько вариантов практических применений.

Эти несколько приложений включают в себя радиочастотные усилители. База, посаженная на корпус, помогает защитить входной сигнал на эмиттере от входного сигнала на коллекторе, предотвращая нестабильность в радиочастотных усилителях. Схема с общей базой может использоваться на более высоких частотах, чем схемы с общим эмиттером и общим коллектором. Смотрите раздел «Радиочастотный усилитель мощности 750 мВт класса C с общей базой» в главе 9. Более сложную схему можно увидеть в разделе «Усилитель малых сигналов класса A с общей базой и высоким коэффициентом усиления» в главе 9.

Подведем итоги:

• Транзисторные усилители с общей базой называются так, потому что точки подачи входного напряжения и снятия выходного напряжения совместно используют вывод базы транзистора (игнорируя все источники питания).
• Коэффициент усиления по току усилителя с общей базой всегда меньше 1. Коэффициент усиления по напряжению зависит от входных и выходных сопротивлений, а также от внутреннего сопротивления перехода эмиттер-база, которое может измениться при изменении постоянного напряжения смещения. Достаточно сказать, коэффициент усиления по напряжению у усилителя с общей базой может быть очень высоким.
• Отношение тока коллектора транзистора к току эмиттера называется коэффициентом α. Значение α для любого транзистора всегда меньше единицы.

Оригинал статьи:

Сохранить или поделиться

radioprog.ru

Усилители с общей базой и общим коллектором

Усилитель с общей базой

На рис. 24.1 показан усилитель, где транзистор включен по схеме с общей базой (ОБ). Необходимое смещение создают два отдельных источника питания. Разделительный конденсатор С₁ обеспечивает передачу пере­менного входного сигнала на эмиттер транзистора (входное напряжение прикладывается между эмиттером и базой). Выходной сигнал снимается с нагрузочного резистора R₄.

На рис. 24.2 приведена практическая схема усилителя промежуточной частоты с одним источником питания. Нагрузкой усилителя являет­ся резонансный контур С₃L₁ с трансформаторной связью. С₁ – входной разделительный конденсатор, резисторы R₁ и R₂ образуют цепь смещения по постоянному току, R₃ — эмиттерный резистор. Развязывающий конденсатор С₂ обеспечивает сохранение на базе транзистора нулевого потенциала по переменному току. В данном случае развязывающий конденсатор присоединен к положительной шине источника питания, а не с шасси. Это допустимо, поскольку по переменному току (то есть для переменного сигнала) потенциал этой шины равен нулю. Потенциалы положительной шины источника питания и шасси отличаются только по постоянному току.

Усилитель с ОБ имеет низкое входное сопротивление (50-100 Ом) и низкий коэффициент усиления по сравнению с усилителем по схеме с ОЭ. Преимущество этого усилителя – хорошие частотные характеристики (широкая полоса пропускания). Поэтому усилители с ОБ используют­ся при очень высоких частотах, например в качестве усилителей РЧ в радиоприемниках и телевизорах, усилителей ПЧ в ЧМ-приемниках и т. д.

Рис. 24.1. Усилитель с ОБ. Источники питания Е₁ и Е₂ задают режим усилителя по постоянному току.

 

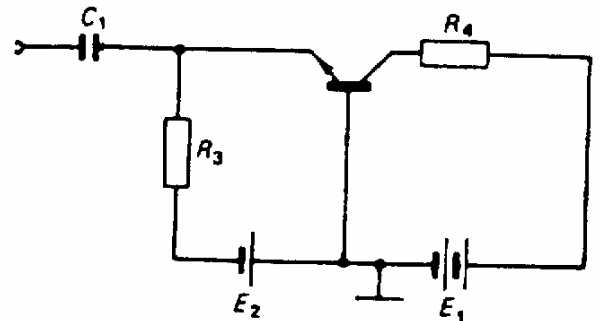
Рис. 24.2. ТипичныйУПЧ по схеме с ОБ. 

Фазовые соотношения

При уменьшении входного сигнала потенциал эмиттера уменьшается от­носительно потенциала базы, ток I_c увеличивается и увеличивает падение напряжения на коллекторном резисторе. В результате уменьшается вы­ходное напряжение. Таким образом, усилитель с ОБ не изменяет фазу входного сигнала при его усилении.

Усилитель с общим коллектором

На рис. 24.3(а) показан усилитель, где транзистор включен по схеме с об­щим коллектором. Здесь С₁ и С₂ – входной и выходной разделительные конденсаторы, резисторы R₁ и R₂ образуют цепь смещения по постоянно­му току. Коллекторный резистор отсутствует, так как выходной сигнал снимается с эмиттера. На рис. 24.3(б) представлен обычный способ изображения схемы усилителя с ОК. Выходной сигнал действует на эмиттерном резисторе R₃, и поэтому данная схема называется эмиттерным повторителем. Эмиттерный повторитель имеет высокий коэффициент усиления по току и меньший единицы коэффициент усиления по напря­жению. Такое значение коэффициента усиления по напряжению связано с действием 100 %-ной отрицательной обратной связи через резистор R₃.

Фазовые соотношения

При увеличении входного сигнала потенциал базы увеличивается отно­сительно потенциала эмиттера, т. е. увеличивается напряжение V_BE, и соответственно увеличивается падение напряжения на эмиттерном рези­сторе, являющегося выходным напряжением. Таким образом, усилитель с ОК не изменяет фазу входного сигнала при его усилении.

 

Рис. 24.3. Эмиттерный повторитель, или усилитель с ОК, (а)

и стандартное изображение его схемы (б).

Таблица 24.1. Сравнение усилителей с ОЭ, ОБ и ОК

Конфигу­рация	Входное сопротивление	Выходное сопротивление	Инвертиро­вание фазы	Преимущества
ОЭ	1-2 кОм	10-50 кОм	Да	Высокое усиление по току и мощности
ОБ	Очень низкое	Очень высокое	Нет	Хорошие частотные характеристики
ОК	Очень высокое	Очень низкое	Нет	Низкое выходное сопротивление, высокий коэффициент усиления по току

 

Добавить комментарий

radiolubitel.net

5.3. Схема с общей базой

Рис. 5.8

Схема включения транзистора с общей базой (ОБ) изображена на рис. 5.8. Входным электродом является эмиттер (входной сигнал U_вx приложен к переходу эмиттер – база, база по переменному сигналу заземлена). Выходным электродом является коллектор; с учетом того что база по переменному сигналу заземлена, можно считать, что U_выx = _к, т. е. U_выx≈ равно переменному напряжению между коллектором и базой. База является, таким образом, «общим электродом» для входного и выходного сигналов, откуда и происходит название схемы. Назначение элементов R_б1, R_б2, С_p1, С_p2 и R_к в схеме с ОБ такое же, как и в схеме с ОЭ. Дополнительным, в сравнении со схемой с ОЭ, элементом является базовая емкость (C_б), которая обеспечивает заземление базы по переменному сигналу.

Схема работает следующим образом. Когда U_вx≈ имеет положительную полярность, _Э возрастает, в результате чего U_бэ= _б– _эснижается и p–n-переход эмиттер – база частично закрывается. Ток I_э уменьшается, в результате уменьшается и ток I_к ≈ I_э, снижается падение напряжения на сопротивлении R_к, а потенциал коллектора _к= Е – I_кR_к возрастет. Так как _к≈ ≈ U_выx≈, то при увеличении мгновенного значения U_вx≈ увеличивается и мгновенное значение U_выx≈. При отрицательной полярности U_вx≈ происходят аналогичные процессы.

Входное сопротивление схемы R_вх = R_э׀׀r_бэ,где r_бэ – эквивалентное сопротивление открытого p–n-перехода эмиттер – база транзистора: оно чрезвычайно мало и обычно не превышает нескольких десятков Ом. Выходное сопротивление R_вых ненагруженной схемы определяется параллельным соединением R_к и эквивалентным сопротивлением r_кэ транзистора, включающим закрытый p–n-перехода коллектор – база, и поэтому велико. Однако если один каскад с общей базой в целях увеличения коэффициента усиления нагрузить на такой же, то выходное сопротивление резко снижается и становится меньшим, чем R_вх. Коэффициент усиления по напряжению

K_U = U_выx≈/U_вx≈ = (I_кR_к)/[I_э(R_э׀׀r_бэ)] ≈ R_к/(R_э׀׀r_бэ) = R_к/R_вх.

При каскадном соединении нескольких схем с ОБ низкоомная нагрузка шунтирует R_к и в формулу для K_U вместо этого сопротивления следует подставить значение выходного сопротивления, которое меньше R_вх: получается, что K_U < 1.

Коэффициент передачи по току К_I = I_вых/I_вх= I_к/I_э ≈ 1. Фазу сигнала схема с общей базой не меняет.

5.4. Сравнение схем включения транзисторов и их применение

Сопоставим параметры трех основных схем включения транзисторов, присваивая им соответствующие индексы:

К_UОЭ > К_{U ОБ} > К_{U ОК}, причем К_{U ОЭ}, К_{U ОБ} > 1; К_{U ОК} < 1;

К_{I ОК}> К_{I ОЭ} > К_{I ОБ}, причем К_{I ОК}, К_{I ОЭ} > 1; К_{I ОБ} < 1;

К_P у всех трех схем больше 1;

Δ_ОЭ= 180°, Δ_ОБ= 0, Δ_ОК = 0;

R_вxОК> R_вxОЭ> R_{вx ОБ}; R_выxОБ> R_выxОЭ > R_выxОК;

f_н.грОК< f_н.грОЭ< f_{н. грОБ}; f_{в.гр ОК}< f_в.грОЭ< f_{в.гр ОБ};

Δ f_ОК> Δ f_ОЭ> Δ f_ОБ (Δ f = f_в.гр– f_н.гр).

Сравнительный анализ параметров приводит к выводу о том, что схема с ОБ во многих отношениях уступает схеме с ОЭ. Этим обусловлен тот факт, что для усиления сигналов обычно применяют транзисторные схемы с общим эмиттером.

Схема с общей базой предпочтительнее лишь в случае, когда надо при небольшом усилении иметь нулевой сдвиг фаз при прохождении сигнала. Это можно обеспечить и при последовательном соединении двух схем с общим эмиттером (Δ = Δ₁ + Δ₂= 180° + 180° = 360° = 0°), но такое схемотехническое решение неэкономично.

Схема с ОК в силу своей специфики (К_U < 1) используется только как усилитель тока (при этом в эмиттерную цепь включают обмотку трансформатора, катушку электромагнита или другой «токовый» элемент, и схема отличается от изображенной на рис. 4.7). Чаще схему используют в качестве «буферного» каскада, включаемого между усилителем или генератором, с одной стороны, и низкоомной нагрузкой – с другой (например, выходной каскад измерительного прибора). При этом реализуются сразу несколько свойств схемы: сигнал при прохождении через схему с ОК мало меняется по амплитуде (К_U < 1, причем подбором величин S и R_Э удается обеспечить К_U = 0,8…0,9 и выше) и не меняется по фазе (Δ= 0), иначе говоря, выходной сигнал «повторяет» входной; высокоомное R_вxисключает шунтирование предыдущего каскада, а низкоомное R_выx позволяет подключить любую нагрузку. По этому своему основному применению схему с ОК обычно называют эмиттерным повторителем («эмиттерным» – потому что выходной сигнал снимается с эмиттера). Раньше использовался также термин «трансформатор сопротивлений», употребляемый в настоящее время очень редко.

studfiles.net

Каскад с общей базой | Основы электроакустики

 

Различают три основные схемы включения транзисто­ра в усилительных каскадах — с общей базой, общим эмиттером и общим коллектором . Общий электрод (в данном случае база) по переменному току должен быть заземлен Часть электронов теряется в базе, например, вследст­вие рекомбинации (взаимной нейтрализации противопо­ложных по знаку зарядов) электронов и дырок. Эти потери учитываются коэффициентом передачи тока эмиттера а. Так что при включении транзистора с общей базой посто­янный ток коллектора оказывается равным где 1К0 — неуправляемый ток коллектора (или обратный ток коллекторного перехода). Ток базы при этом равен 1Б = 1Э — 1к, т. е. мал, поскольку при а близком к 1 ток коллектора не намного меньше тока эмиттера.Если переменное напряжение на входе усилительного каскада на биполярном транзисторе UBX не равно нулю, то наряду с постоянной составляющей тока эмиттера появля­ется его переменная составляющая. В результате появля­ется и переменная составляющая тока коллектора. Проте­кая через резистор RK, она создает на нем переменную составляющую выходного напряжения. Если сопротивле­ние RK велико, то она может в сотни и тысячи раз превосходить UBX. Таким образом, каскад с общей базой, не усиливая ток, может усиливать напряжение и соответ­ственно и мощность.Итак, усиление по напряжению в каскаде с общей базой обусловлено тем, что переменная составляющая входного тока переносится из низкоомной цепи эмиттера в намного более высокоомную цепь коллектора. Так что коэффициент усиления оказывается близким к отноше­нию сопротивлений коллекторной и эмиттерной цепей. При этом сопротивление эмиттерной цепи (входное со­противление) очень мало, поскольку эмиттерный переход открыт. Примерно оно равно <рт/1э, где (рт — температур­ный потенциал (его значение при комнатных температу­рах порядка 25 мВ, так что при токе эмиттера 1э = 1 мА входное сопротивление будет равно всего 25 Ом). К сожалению, из-за конечного времени пролета носи­телями области базы у каскада с общим эмиттером усиле­ние на высоких частотах начинает снижаться. Оно пони­жается на 3 дБ, если частота усиливаемого сигнала достигает частоты fa (эта частота называется граничной частотой транзистора в схеме с общей базой). Многие современные транзисторы имеют fa порядка сотен МГц и выше. Емкос­ти монтажа и самого транзистора могут также ухудшить усиление на высоких частотах.

За что мы так не любим транзисторный усилитель с общей базой  Мифом № 1 является то, что довольно сложно организовать цепи питания такого каскада, вплоть до того,
что требуется дополнительный источник питания. Мало того, что такое мнение бытует среди радиолюбителей, так оно усиленно поддерживается в технической литературе. Откройте учебник с описанием работы каскада с ОБ. Первое, что вы увидите, так это горизонтальное расположение транзистора с двумя источниками питания: один в коллекторной цепи, другой в эмиттерной. После прочтения такого материала сразу пропадает какое-либо желание иметь дело с этим каскадом. Развеем этот миф. На верхнем рисунке вы видите знакомую вам схему с общим эмиттером. Легким движением мыши поворачиваем его вокруг оси и преобразуем в каскад с общей базой. По постоянному току все цепи остаются прежними. Базу по переменному току заземляем с помощью конденсатора Сф, входной сигнал подаем на эмиттер, выходной остается на прежнем месте. Каскад с общей базой готов, никаких трудностей с питанием не возникло, тем более с двумя источниками.  С включением транзистора мы разобрались, теперь приступим к изучению его работы, где мифов также достаточно.

Как же работает усилитель с общей базой?  Рассмотрим упрощенную схему включения транзистора с общей базой. Направления токов показаны условно, символизируя, что вход —  это эмиттер, выход — коллектор, часть тока ответвляется в базу.
Сразу оговорю упрощения и допущения. Обратные токи переходов, ввиду их малости, я не рассматриваю. Для понимания принципа работы и инженерных расчетов это приемлемо. Коэффициент передачи тока для каскада с общей базой меньше единицы, т.к. часть эмиттерного тока ответвляется в базу: Iэ — Iб = Iк. Соотношение токов имеет величину Iк = α * Iэ , где α< 1 -коэффициент передачи по току для ОБ.
В современных транзисторах коэффициент α близок к единице (0.98 — 0.99), поэтому в практических расчетах можно считать Iэ = Iк.  Отсутствие усиления по току совершенно не мешает получить от такого каскада усиление по напряжению, причем, немалое. Существует ещё один миф, что входное сопротивление каскада определяется резистором Rэ , который обязательно должен иметь маленький номинал.  Но это не так. Входным током каскада является ток эмиттера транзистора, поэтому входное сопротивление в основном определяется  сопротивлением эмиттерного перехода rэ = 25 /Iэ = 25Ом при токе 1мА (собственное сопротивление базы транзистора rб вносит небольшой вклад).
Ток, протекая от входной цепи к выходной, практически не изменяется, поэтому, на резисторах rэ и Rк, он создает падения напряжения пропорциональные величинам этих сопротивлений. Если Rк = 3кОм, то отношение Ku = Rк /rэ составит более 100 — это и есть коэффициент усиления по напряжению.  Таким образом, недостатками каскада являются низкое входное сопротивление и отсутствие усиления по току, но более высокая граничная частота усиления и большее выходное сопротивление. Также каскад имеет более высокую линейность по сравнению с ОЭ. Не верьте утверждениям некоторых писателей, что каскад с общей базой имеет низкое выходное сопротивление в сравнении с другими схемами.
Практические соображения по толкованию работы каскада (усилителя) с общей базой
Для работы n-p-n транзистора необходимо, чтобы потенциал базы был положительным по отношению к эмиттеру, поэтому для открытия транзистора надо эмиттер «утянуть» в минус, т.е входное напряжение должно быть отрицательным.  Проанализируем работу каскада на постоянном токе. Эмиттер транзистора с ОБ представляет собой точку с очень низким (динамическим) входным сопротивлением (около 25 Ом при токе 1мА). Поэтому можно принять, что напряжение в ней практически не меняется при изменении входного тока, (этакий виртуальный 0).
В связи с этим, предлагаю рассматривать каскад с ОБ как преобразователь ток-напряжение. Преобразование входного сигнала в выходной происходит как бы в два этапа:
— Сначала генерируем входной ток в эмиттер Iвх = (Uвх- 0.6) /Rэ,
— Затем в коллекторной нагрузке получаем падение напряжения, обусловленное этим током Uвых = Iвх * Rк (мы приняли, что Iвх = Iвых).  Не забываем, что при протекании входного тока напряжение на эмиттере будет равно прямому падению напряжения на переходе — 0.6 В. В исходном состоянии транзистор закрыт, напряжение на коллекторе равно Uпит. При подаче на вход отрицательного напряжения транзистор начинает открываться, через него протекает ток, который создает падение напряжения на коллекторном резисторе. Потенциал коллектора понижается и в пределе станет равным 0. Максимальный ток транзистора при Uк = 0 составляет: Iмакс = Uпит /Rк. Сделаем конкретный пример расчета для постоянного тока: Rэ = 1кОм (Rэ >> rэ), Rк = 10кОм, Uвх = 1В .  Входной ток равен Iвх = Iэ = (Uвх-0.6) /Rэ = 1-0.6/1 = 0.4мА. Т.к. ток коллектора равен току эмиттера, то изменение напряжения на коллекторном резисторе составит: Uк = Rк * Iк = Rк * Iэ = 10*0.4 = 4В.  Коэффициент усиления по постоянному напряжению получился равен 4. В данном случае входным сопротивлением каскада является Rэ = 1кОм. Уменьшая это сопротивление, мы увеличим входной ток, который вызывет увеличение выходного тока и выходного напряжения на нагрузке.
Этот пример демонстрирует принцип расчета и понимания работы каскада с ОБ, который оказался не так страшен, как нам его малюют.

Усилитель с общей базой для переменного сигнала Теперь нам легче понять работу усилителя на переменном сигнале. Для усиления переменного напряжения необходимо вывести транзистор на линейный участок рабочей характеристики. На рисунке 2 показаны цепи смещения транзистора, с помощью которых задается режим по постоянному току. Расчет их ничем не отличается от расчетов стандартного усилителя с ОЭ. Ток покоя Iо через транзистор устанавливается в пределах нескольких миллиампер. Переменный сигнал подается в эмиттер через конденсатор. У коллекторного тока транзистора появляется переменная составляющая, т.е. ток в некоторых пределах изменяется относительно тока покоя согласно изменениям входного напряжения. Проведем небольшие эксперименты с усилителем. Рассмотрим коэффициент передачи каскада от точки 1 до выхода с коллектора. В качестве источника сигнала возьмем генератор сигналов звуковой частоты ГНЧ с низким выходным сопротивлением, менее 100 Ом. Выходное напряжение установим 1В.  В качестве Rг поставим внешний резистор 1 кОм. В нагрузке резистор Rк = 10кОм. Для источника сигнала входным сопротивлением каскада является сумма Rг и rэ, т.к. они включены последовательно. Входной ток от источника сигнала равен Iвх = Iэ = Uг /(Rг + rэ) = . Uг /Rг, т.к.  rэ — мало. Выходное напряжение при этом составит: Uвых = Rк * Iк = Rк * α*Iэ = Rк * α* Uг /Rг.  Принимая α = 1, получим Uвых = Uг * Rк /Rг.  Коэффициент усиления равен Ku = Uвых /Uг = Rк /Rг = 10, тогда Uвых = 10 В.  Заглянем поглубже и выясним роль входного сопротивления транзистора rэ, ибо нам все уши прожужжали о низком входном сопротивлении каскада с ОБ. Посмотрим осциллографом, что происходит в точке 2. Мы обнаружим, что там присутствует весьма маленький синусоидальный сигнал, в нашем случае  25 мВ. Величина напряжения сигнала обусловлена делителем напряжения, образованным Rг и rэ: 1В * 25/1000 = 25мВ. Каким образом сигнал на выходе достигает величины в несколько вольт? Это происходит по той причине, что каскад имеет внушительный «собственный»  коэффициент усиления  по напряжению (от точки 2 до коллектора), определяемый отношением нагрузочного сопротивления и входного сопротивления транзистора:  Ku = Rк /rэ = 10000/25 = 400, тогда Uвых = Ku * Uвх = 25 * 400 = 10000 мВ или 10 В. Мы получили тот же результат, что и выше. Делаем вывод:
Результаты исследования усилителя с ОБ совпадают с результатами для каскада с ОЭ. Коэффициент усиления по переменному напряжению определяется отношением коллекторного и эмиттерного (в данном случае Rг) резисторов и не зависит от внутренних параметров транзистора при Rг > rэ.

audioakustika.ru

8 Усилительные каскады по схемам с общей базой и общим коллектором

8.1 Каскад с общей базой

С использованием эмиттерной цепи стабилизации рабочей точки построим транзисторный усилительный каскад по схеме с общей базой (рис. 8.1). Входной сигнал подается через разделительный конденсатор С1 в цепь эмиттера транзистора. База по переменной составляющей заземлена с помощью блокировочного конденсатора С_Б. Выходной сигнал снимается с коллектора. Положительное приращение входного напряжения вызывает уменьшение тока эмиттера транзистора и уменьшение падения напряжения на коллекторном сопротивлении, то есть рост напряжения на выходе. Следовательно, каскад с ОБ не инвертирует фазу сигнала при усилении.

Выбор рабочей точки и расчет резисторов можно выполнить по методике, изложенной для схемы рис. 6.1.

Приближенная эквивалентная схема для анализа каскада в области средних частот приведена на рис. 8.2 (закорачиваем все конденсаторы и источник питания Е, так как их сопротивление в рабочем диапазоне частот близко к нулю). Для физической эквивалентной схемы предполагается, что . Это допустимо при условии:

Входное сопротивление транзистора определяется соотношением

.

Входное сопротивление каскадаОно значительно меньше (десятки ом), чем в схеме с ОЭ.

Каскад не усиливает сигнал по току

Коэффициент усиления по напряжению Он такого же порядка как в схеме с ОЭ (десятки ÷ сотни).

Выходное сопротивление каскада , т.к. выходное сопротивление транзистора по схеме с ОБ равно.

Эквивалентная постоянная времени каскада в области верхних частот может быть определена по выражению Она значительно меньше, чем в схеме с ОЭ. Поэтому каскад с ОБ относится к широкополосным усилительным каскадам.

8.2 Каскад с общим коллектором

На рис. 8.3 приведен вариант построения усилителя по схеме с общим коллектором (эмиттерный повторитель). При работе в режиме малого сигнала можно выбрать в точке покоя I_Э = I₀ = =(0,5¸1) мА, U_КЭ = U₀ = E/2, ток делителя I_д = 10I_Б = и рассчитать сопротивления резисторов по формулам:

В данном каскаде сопротивления выходной цепи по постоянному и переменному току определяются соотношениями:

Коллектор транзистора по переменному току заземлен (внутреннее сопротивление источника питания Е близко к нулю). Входной сигнал через разделительный конденсатор С1 подается в цепь базы транзистора VT1, а выходной – снимается с эмиттера. В каскаде действует стопроцентная последовательная ООС по напряжению, в результате которой к участку база—эмиттер транзистора прикладывается разность входного и выходного напряжений.

Эквивалентная схема каскада для средних частот приведена на рис. 8.4. Транзистор заменен приближенной Т-образной схемой замещения. Введено обозначение

Входное сопротивление со стороны базы VT1

Входное сопротивление каскада Оно обычно значительно больше (в десятки ÷ сотни раз), чем в схеме с ОЭ.

Коэффициент усиления по напряжению

Выходное напряжение практически повторяет входное и по величине (K = 0,8 ¸0,95) и по фазе, вследствие чего каскад с ОК называют эмиттерным повторителем.

Каскад обеспечивает значительное усиление по току

Выходное сопротивление каскада мало (десятки ом):

Эквивалентная постоянная времени каскада в области верхних частот

, где .

Обычно .

Каскад с ОК не дает усиления по напряжению, усиливает сигнал по току, отличается большим входным и малым выходным сопротивлением. За счет глубокой ООС по сравнению с каскадом по схеме с ОЭ имеет более широкую полосу пропускания. Чаще всего применяется как согласующий каскад при работе с высокоомным источником сигнала или с низкоомной нагрузкой.

Для повышения входного сопротивления в схеме эмиттерного повторителя, приведенной на рис. 8.5, транзисторы VT1 и VT2 включены по схеме Дарлингтона, а также используется положительная обратная связь с помощью конденсатора C3.

Коэффициент усиления по току эквивалентного составного транзистора (составленного из транзисторов VT1 и VT2) равен произведению коэффициентов усиления тока базы каждым транзистором

h_21Э » h_21Э(1) h_21Э(2).

Емкость конденсатора выбирается достаточно большой, так что в рабочем диапазоне частот потенциал точки 3 равен потенциалу точки 2, который повторяет потенциал точки 1 (схема является повторителем напряжения). Таким образом, ток i, ответвляющийся в резистор R_б, незначителен:

где ,

Например, при К=0,9 вход будет шунтироваться сопротивлением не R_б, а 10R_б. В 10 раз уменьшится и шунтирующее влияние сопротивления коллекторного перехода транзистора VT1, включенного параллельно R_б.

Входное сопротивление каскада определяется выражением

где

и может достигать единиц мегаом.

studfiles.net

3.5. Усилительный каскад с общей базой.

Принципиальная схема каскада ОБ и его эквивалентная схема для области средних частот приведены на рис. 3.15 а и б соответственно.

Статический режим работы каскада задается источником смещения Е_см и резистором R_г, в которое также входит и внутренне сопротивление источника сигнала е_г.

Рис. 3.15

Входное сопротивление каскада. Из схемы рис. 3.15 б следует:

r_вх=U_вх/i_вх=U_эб/i_э; (3.33)

(3.34)

Тогда входное сопротивление

(3.35)

При R_к=0, r_вхr_э+r_б(1-a), так как r_к>>r_б.

При R_к>>r_к, rвх=r_э+r_б.

Практически R_к=1…5 кОм, поэтому , так какa=1. Следовательно, входное сопротивление каскада ОБ чрезвычайно мало и не превышает несколько десятков Ом, оно примерно в 1+b раз ниже входного сопротивления каскада ОЭ.

Выходное сопротивление, определенное из эквивалентной схемы рис. 3.15.б по методике для схемы каскада ОЭ:

, (3.36)

где .

Из этого выражения видно, что выходное сопротивление каскада ОБ растет с ростом R_г, стремясь к r_к. Для реальных значений R_г r_выхr_к, т.е. довольно велико.

Коэффициент усиления напряжения для средних частот усиливаемого сигнала определяется выражением

, (3.37)

так как r_к>>R_к.

Для области высоких частот

, (3.38)

где — граничная частота усиления транзистора в схеме ОБ;— постоянная времени коллекторной цепи.

Коэффициент усиления тока

. (3.39)

Таким образом, схема усилительного каскада ОБ, имея коэффициент усиления по току меньше единицы, позволяет получить значительное усиление по напряжению, а значит, и по мощности. По сравнению с другими, эта схема имеет наименьшее входное и наибольшее выходное сопротивления.

Так как емкость коллекторного перехода С_к меньше С^*_к в 1+b раз и меньшетоже в 1+b раз, то частотные свойства каскада ОБ лучше, чем каскада ОЭ тоже приблизительно в 1+b раз. В каскаде ОБ отсутствует сдвиг фазы напряжения.

3.6. Усилительный каскад с общим коллектором

Рис. 3.16

Принципиальная схема каскад ОК приведена на рис. 3.16 а, на рис. 3.16 б представлены диаграммы напряжений на входе и выходе схемы.

Коллектор транзистора в схеме рис. 3.16 а по переменной составляющей сигнала через источник питания соединен с общей шиной. Поэтому данная схема является схемой с общим коллектором.

Выходное напряжение, снимаемое с эмиттерного сопротивления R_э, совпадает по фазе со входным и отличается от него на небольшую величиную, равную напряжению на переходе база-эмиттер U_бэ открытого транзистора:

.

Следовательно, потенциал эмиттера “привязан” к потенциалу базы и повторяет его изменения. По этой причине каскад ОК получил название — эмиттерный повторитель.

Управляющим напряжением транзистора является напряжение U_бэ.

U_бэ=U_вх-U_вых. (3.40)

Поскольку , то данную схему можно рассматривать как имеющую 100%-ную последовательную отрицательную обратную связь по напряжению.

Рис. 3.17

Входное напряжение каскада может быть найдено из эквивалентной схемы рис. 3.17

; (3.41)

. (3.42)

Входное сопротивление

. (3.43)

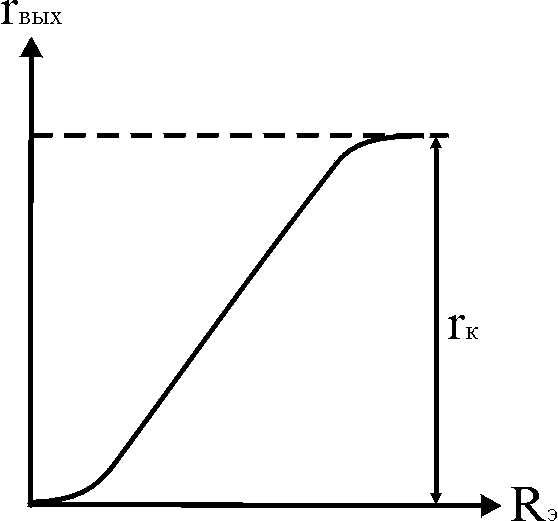
Рис. 3.18

Входное сопротивление зависит от R_э (рис. 3.18).

Если R_э=0

. (3.44)

При R_э>>r^*_к

. (3.45)

В диапазоне практических значений 100<R_э<10 кОм входное сопротивление

. (3.46)

Так как обычно R_э>>r_э, то входное сопротивление эмиттерного повторителя в нормальном рабочем режиме много больше, чем в схемах ОБ и ОЭ, но оно рпактически ограничено величиной r_к.

Выходное сопротивление определяется по той же метолике, что и для схемы ОЭ, т.е., для определения r_вых на выход схемы рис. 3.17 подаем напряжение U₂. а источник е_г закорачиваем, тогда

. (3.47)

Ток, потребляемый от источника U₂, состоит из трех составляющих:

(3.48)

Тогда выходное сопротивление

. (3.49)

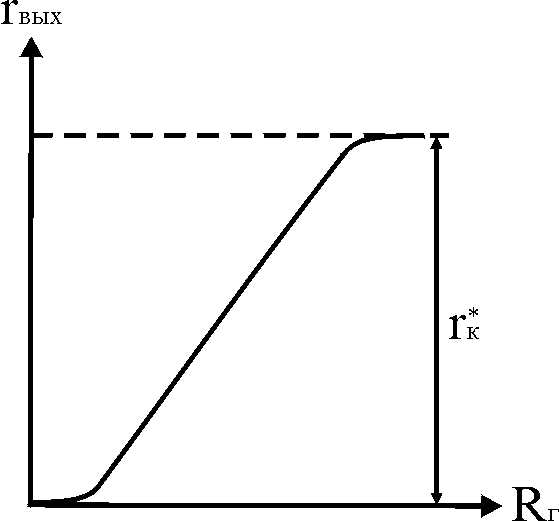
Рис. 3.19

Зависимость r_вых(R_г) представлена на рис. 3.19.

При R_г=0

(3.50)

Для R_г>>r^*_к

(3.51)

Выходное сопротивление каскада ОК в нормальном режиме много меньше выходного сопротивления каскадов ОБ иОЭ, а его изменение много больше, чем в схемах ОЭ и ОБ. Для реальных значений R_г=1…10 кОм с учетом R_э выходное сопротивление каскада

. (3.53)

Коэффициент усиления напряжения

. (3.54)

Из эквивалентной схемы каскада (рис. 3.17) найдем

. (3.55)

Входное напряжение .

Тогда (3.56)

Максимальная величина коэффициента передачи напряжения будет при выполнении условия R_э>>r^*_к>>r_э:

(3.57)

В нормальном рабочем режиме обычно выполняется условие r^*_к>>R_э>>r_э, тогда

(3.58)

Коэффициенты усиления ЭДС — К_E, тока — K_I, мощности — К_р определяются выражениями:

; (3.59)

. (3.60)

При максимальной величине K_i, которая получается при условии r^*_к>>R_э>>r_э, . Тогда

или. (3.61)

Итак, отличительными свойствами эмиттерного повторителя являются сравнительно большое входное сопротивление и малое — выходное, высокий коэффициент усиления тока и близкий к единице коэффициент передачи напряжения.

Эммитерные повторители нашли применение во входных и выходных каскадах. Их также часто используют при необходимости согласования между собой двух каскадов, например, ОБ и ОЭ и нагрузки. Следует заметить, что сопротивление внещней нагрузки оказывается включенным параллельно R_э, т.е.

(3.62)

Эммитерный повторитель на составном транзисторе

Коэффициент усиления составного транзистора СТ, выполненного из двух Т₁ и Т₂:

, (3.63)

поскольку всегда b>>1.

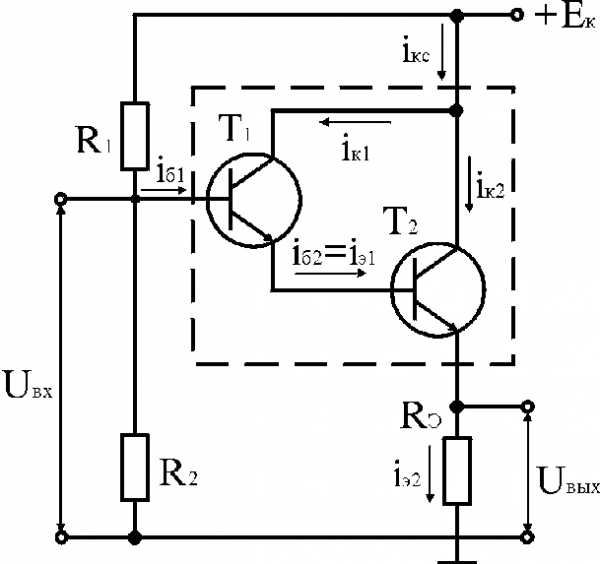
Рис. 3.20

Значение b_c может составлять несколько тысяч.

Тогда параметры повторителя на составном транзисторе могут ьыть определены по формулам (3.47)-(3.61) заменой b на b_c.Например, без учета делителя R₁—R₂ входное сопротивление схемы рис. 3.20

. (3.64)

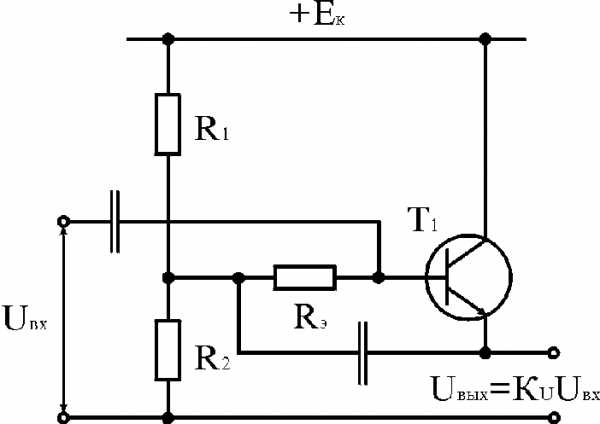
Рис. 3.21

В связи с ограмным сопротивлением таких повторителей особенно остро встает вопрос о цепи смещения базы: делать сопротивления делителя R₁—R₂ (рис. 3.20) порядка десятков Мом нельзя не только из-за температурной нестабильности, но главным образом из-за невозможности обеспечить нужный ток базы. В случае усилителей переменного тока наилучшим выходом из положения является использование отрицательной обратной связи в цепи базы (рис. 3.21). Сопротивление R₃ выбирается сравнительно низкоомным (сотни килоом), способным обеспечить необходимый ток базы, а по отношению к переменным составляющим величина Rэ повышается в 1/(1-K_U) раз за счет обратной связи с выхода повторителя. Оно может достигать десятков Мом и не будет шунтировать вход повторителя. Делитель R₁—R₂ в такой схеме может иметь любые разумные сопротивления.

studfiles.net

5.4. Резонансный усилитель с общим эмиттером

Схема резонансного усилителя показана на рис.23. Нагрузкой каскада является параллельныйLCконтур. Следует иметь в виду, что параллельно контуру включены также паразитные емкости:С_в — межвитковая емкость катушки,С_м– емкость монтажа,С_кэ– выходная емкость транзистора иС_н– паразитная емкость нагрузки. Поэтому общая емкость контура равнаС^=С_к+С_в+С_м+С_кэ+С_н. Импеданс контураZимеет максимум на резонансной частотеf₀. На рис.24 изображены резонансные кривые двух контуров, имеющих различные добротностиQ. На резонансной частоте сопротивление контура является чисто активным. Поскольку коэффициент усиления каскада пропорционален сопротивление его нагрузки, то частотная характеристика резонансного усилителя повторяет форму резонансной кривой контура (см. рис.10а).

6. Усилитель с общим коллектором

Принципиальная схема усилительного каскада с общим коллектором (ОК)  приведена на рис.25. Для упрощения рассуждений будем считать, что напряжение питанияЕ=10В. Входной сигнал подается на базу транзистора, а выходной – снимается с эмиттера. В режиме покоя постоянное напряжение на эмиттереU_э0=I_э0R_эустанавливается примерно равным половине напряжения питания Е=10В, т.е. 5В. При этом напряжение покоя набазе транзистораU_бэ=U_бU_э0.6В, для кремниевого транзистора. Таким образом, по постоянному напряжению схема охвачена стопроцентной ООС. По переменному напряжению также имеется стопроцентная ООС, и все выходное напряжение подается на вход усилителя последовательно и в противофазе с входным сигналом. Выходное напряжение немного меньше входного и схема не дает усиления по напряжениюК_U=U_вых/U_вхблизко, но немного меньше единицы.

Схема с ОК обладает существенным усилением по току К_I=I_э/I_б= (I_к+I_б)/I_б=h_21э+1. Поэтому схема усиливает мощность входного сигнала, хотя и в меньшей степени, чем схема с ОЭ.

При подаче на базу транзистора положительного напряжения базовый ток увеличивается, что приводит к увеличению эмиттерного тока и, соответствено, выходного напряжения U_вых=I_эR_э. Таким образом, выходное напряжение каскада с ОК находится в фазе с входным напряжением. Усилитель с ОК, у которого коэффициент усиления близок к единице, часто называют эмиттерным повторителем, так как напряжение на его выходе по величине и фазе повторяет напряжение на входе.

Усилитель с ОК имеет более высокое входное сопротивление и более низкое выходное сопротивление по сравнению с каскадом с ОЭ. Подробные расчеты приведены в [1] на страницах 277-280. Обычно R_вх=200300 кОм, аR_вых=100200 Ом.

Усилитель с ОК обладает более широкой полосой пропускания по сравнению с усилителем с ОЭ в области верхних частот. Как уже было сказано выше, снижение усиления на верхних частотах происходит вследствие шунтирования сопротивления нагрузки паразитными емкостями. Поскольку в усилителях с ОК и ОЭ паразитные емкости примерно одинаковы, а выходное сопротивление усилителя с ОК значительно меньше, чем усилителя с ОЭ, то и шунтирующее действие выходного сопротивления усилителя с ОК происходит на значительно больших частотах, чем для усилителя с ОЭ.

7. Усилитель с общий базой

Принципиальная схема усилительного каскада с общей базой (ОБ) показана на рис.26. Здесь входной сигнал подается на сопротивлениеR_э, включенное в цепи эмиттера, а выходной сигнал снимается с коллектора транзистора. База транзистора через конденсаторС₂подключается к общему проводу для входной и выходной цепей. Входным током является ток эмиттера I_э, а выходным – ток коллектора I_к. Из формулыI_к=I_эследует, что коэффициент усиления по токуK_I=1. При этом выходной ток изменяется в фазе с входным током, и выходное напряжение находится в фазе с входным напряжением.

Для правильной работы усилителя сопротивление R_э выбирают небольшим, порядка сотни – нескольких сотен Ом, например 200Ом, аR_квыбирают большим, порядка единиц – десятков кОм, например,R_к=10кОм. В этом случае коэффициент усиления по напряжениюK_U=U_вых/U_вх=I_кR_к/I_эR_э=I_эR_к/I_эR_эR_к/R_э=10кОм/200Ом=50, примерно такой же, как у каскада с ОЭ.

В усилителе с ОБ имеется 100% параллельная отрицательная обратная связь по току. Наличие ООС расширяет полосу пропускания в области высоких частот, поэтому схема с ОБ используется в качестве усилителя напряжения на высоких частотах. Широкое применение нашли также резонансные усилители с ОБ, обладающие высокой устойчивостью работы.

studfiles.net