Векторная диаграмма тока: Векторная диаграмма напряжений и токов онлайн

Элементы цепи синусоидального тока. Векторные диаграммы и комплексные соотношения для них. (Лекция N 4)

1. Резистор

Идеальный резистивный элемент не обладает ни индуктивностью, ни емкостью. Если к нему приложить синусоидальное напряжение (см. рис. 1), то ток i через него будет равен

(1)

Соотношение (1) показывает, что ток имеет ту же начальную фазу, что и напряжение. Таким образом, если на входе двухлучевого осциллографа подать сигналы u и i, то соответствующие им синусоиды на его экране будут проходить (см. рис. 2) через нуль одновременно, т.е. на резисторе напряжение и ток совпадают по фазе.

Из (1) вытекает:

;

Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:

;

— разделим первый из них на второй:

или

(2)

Полученный результат показывает, что отношение двух комплексов есть вещественная константа. Следовательно, соответствующие им векторы напряжения и тока (см. рис. 3) совпадают по направлению.

2. Конденсатор

Идеальный емкостный элемент не обладает ни активным сопротивлением (проводимостью), ни индуктивностью. Если к нему приложить синусоидальное напряжение (см. рис. 4), то ток i через него будет равен

(3)

Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на

/2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране будет иметь место картинка, соответствующая рис. 5.

Из (3) вытекает:

;

Введенный параметр называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление, имеет размерность Ом. Однако в отличие от R данный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при конденсатор представляет разрыв для тока, а при .

Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:

;

— разделим первый из них на второй:

или

(4)

В последнем соотношении — комплексное сопротивление конденсатора. Умножение на соответствует повороту вектора на угол по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7.

3. Катушка индуктивности

Идеальный индуктивный элемент не обладает ни активным сопротивлением, ни емкостью. Пусть протекающий через него ток (см. рис. 8) определяется выражением . Тогда для напряжения на зажимах катушки индуктивности можно записать

(5)

Полученный результат показывает, что напряжение на катушке индуктивности опережает по фазе ток на /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране (идеальный индуктивный элемент) будет иметь место картинка, соответствующая рис. 9.

Из (5) вытекает:

Введенный параметр называют реактивным индуктивным сопротивлением катушки; его размерность – Ом. Как и у емкостного элемента этот параметр является функцией частоты. Однако в данном случае эта зависимость имеет линейный характер, что иллюстрирует рис. 10. Из рис. 10 вытекает, что при катушка индуктивности не оказывает сопротивления протекающему через него току, и при

Переходя от синусоидальных функций напряжения и тока к соответствующим комплексам:

;

разделим первый из них на второй:

или

(6)

В полученном соотношении — комплексное

сопротивление катушки индуктивности. Умножение на соответствует повороту вектора на угол против часовой стрелки. Следовательно, уравнению (6) соответствует векторная диаграмма, представленная на рис. 11

4. Последовательное соединение резистивного и индуктивного элементов

Пусть в ветви на рис. 12 . Тогда

где

, причем пределы изменения

Уравнению (7) можно поставить в соответствие соотношение

которому, в свою очередь, соответствует векторная диаграмма на рис. 13. Векторы на рис. 13 образуют фигуру, называемую треугольником напряжений. Аналогично выражение

графически может быть представлено треугольником сопротивлений (см. рис. 14), который подобен треугольнику напряжений.

5. Последовательное соединение резистивного и емкостного элементов

Опуская промежуточные выкладки, с использованием соотношений (2) и (4) для ветви на рис. 15 можно записать

_.,

(8)

где

, причем пределы изменения .

На основании уравнения (7) могут быть построены треугольники напряжений (см. рис. 16) и сопротивлений (см. рис. 17), которые являются подобными.

6. Параллельное соединение резистивного и емкостного элементов

Для цепи на рис. 18 имеют место соотношения:

;

, где [См] – активная проводимость;

, где [См] – реактивная проводимость конденсатора.

Векторная диаграмма токов для данной цепи, называемая треугольником токов, приведена на рис. 19. Ей соответствует уравнение в комплексной форме

где ;

— комплексная проводимость;

Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 20.

Для комплексного сопротивления цепи на рис. 18 можно записать

Необходимо отметить, что полученный результат аналогичен известному из курса физики выражению для эквивалентного сопротивления двух параллельно соединенных резисторов.

7. Параллельное соединение резистивного и индуктивного элементов

Для цепи на рис. 21 можно записать

;

, где [См] – активная проводимость;

, где [См] – реактивная проводимость катушки индуктивности.

Векторной диаграмме токов (рис. 22) для данной цепи соответствует уравнение в комплексной форме

где ;

— комплексная проводимость;

Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 23.

Выражение комплексного сопротивления цепи на рис. 21 имеет вид:

Литература

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. В чем сущность реактивных сопротивлений?

2. Какой из элементов: резистор, катушку индуктивности или конденсатор – можно использовать в качестве шунта для наблюдения за формой тока?

3. Почему катушки индуктивности и конденсаторы не используются в цепях постоянного тока?

4. В ветви на рис. 12 . Определить комплексное сопротивление ветви, если частота тока .
Ответ: .

5. В ветви на рис. 15 . Определить комплексное сопротивление ветви, если частота тока .
Ответ: .

6. В цепи на рис. 18 . Определить комплексные проводимость и сопротивление цепи для .
Ответ: ; .

7. Протекающий через катушку индуктивности ток изменяется по закону А. Определить комплекс действующего значения напряжения на катушке.
Ответ: .

Построение векторных диаграмм

Наверняка при решении задач по электротехнике многие сталкивались с некоторыми сложностями в построении векторных диаграмм. Начнем с определения векторной диаграммы.

Векторная диаграмма — это изображение синусоидально изменяющихся величин в виде векторов на плоскости.

Векторные диаграммы применяют потому, что сложение и вычитание синусоидальных величин, неизбежные при расчете цепей переменного тока, наиболее просто выполняются в векторной форме. Кроме того векторные диаграммы отличаются простотой и наглядностью.

Построение векторной диаграммы выполняется в прямоугольной плоскости. Чтобы построить диаграмму нужно провести вектор длиною равный амплитудному значению искомой величины, под углом сдвига относительно другой величины. Возможно, вы не сразу поймете смысл сказанного, для этого нужно изучить пример.

В качестве примера рассмотрим построение векторной диаграммы для цепи, состоящей из последовательно подключенных конденсатора, резистора и катушки. Напряжение на катушке U_L=15 В, напряжение на конденсаторе U_C=20 В, напряжение на резисторе U_R=10 В, ток в цепи I=3 А. Требуется найти общее напряжение.

Катушка носит индуктивный характер, а значит, в ней напряжение опережает ток по фазе на 90°.

Конденсатор носит емкостной характер, значит, ток в нем опережает по фазе напряжение на 90°.

Резистор обладает только активным сопротивлением, и напряжение в нем совпадает по фазе с током.

Итак, для начала отложим вектор тока в масштабе. Масштаб для тока у нас будет 1 А/см.

Теперь отложим вектор напряжения на катушке, масштаб для напряжения возьмем 5 В/см, получается, что нужно отложить шесть клеток вверх, так как напряжение в катушке опережает ток. Для наглядности обозначим синим цветом.

Далее мы будем откладывать вектор активного сопротивления, так как напряжение в одной фазе с током, то мы его откладываем из конца вектора U_L параллельно вектору тока I. Обозначим его красным цветом.

Следующим шагом отложим вектор напряжения на конденсаторе, так как оно запаздывает на 90°, мы его отложим вертикально вниз, из конца вектора U_R. Обозначим желтым цветом.

И последним этапом мы отложим вектор общего напряжения, из начала координат в конец вектора U_C и обозначим его зеленым цветом.

Общее напряжение получилось равным 2,23 В, причем характер цепи емкостной, так как напряжение отстает от тока.

Аналогичным образом выполняется построение векторной диаграммы токов.

Читайте также последовательная RLС-цепь

Построение векторных диаграмм токов и напряжений — Студопедия

Порядок построения векторных диаграмм рассмотрен для случая с исправным нулевым проводом. Векторные диаграммы напряжений и токов даны на рисунках 15 и 16; на рисунке 17 дана совмещенная диаграмма токов и напряжений

1. Строятся оси комплексной плоскости: действительных величин (+1) – горизонтально, мнимых величин (j) – вертикально.

2. Исходя из значений модулей токов и напряжений и размеров полей листов, отведеных для построения диаграмм, выбираются масштабы тока mI и напряжения mU. При использовании формата А4 (размеры 210х297 мм) при наибольших модулях (см. табл. 8) тока 54 А и напряжения 433 В приняты масштабы: mI = 5 А/см, mU = 50 В/см.

3. С учетом принятых масштабов mI и mU определяется длина каждого вектора, если диаграмма строится с использованием показательной формы его записи; при использовании алгебраической формы находятся длины проекций векторов на оси действительных и мнимых величин, т.е. длины действительной и мнимой частей комплекса.

Например, для фазы А:

— длина вектора тока / 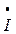ф.А / = 34,8 А/ 5 А/см = 6,96 см; длина его действительной части

I ф.А = 30 А/ 5 А/см = 6 см,

длина его мнимой части

I 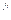ф.А = -17,8 А/5 А/см = — 3,56 см;

— длина вектора напряжения / А нагр./ = 348 В/ 50 В/см = 6,96 см; длина его действительной части

U А нагр. = 340,5 В/ 50 В/см = 6,8 см;

длина его мнимой части

U 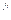Анагр. = 37,75 В/ 50 В/см = 0,76 см.

Результаты определения длин векторов, их действительных и мнимых частей отражены в таблице 9.

Таблица 9 — Длины векторов тока и напряжения, их действительных и мнимых частей для случая неповрежденного нулевого провода.

Величина	Масштаб, 1/см	Длина вектора, см	Длина действительной части, см	Длина мнимой части, см
Напряжения фаз сети	U А	50 В/см	7,6	7,6
UВ	7,6	— 3,8	— 6,56
UС	7,6	— 3,8	6,56
Напряжения фаз нагрузки	U Анагр.	50 В/см	6,96	6,8	0,76
UВ нагр.	7,4	— 4,59	— 5,8
UС нагр.	8,66	-4,59	7,32
U0	1,08	0,79	— 0,76

Продолжение таблицы 9

Токи фаз нагрузки	I ф.А	5 А/см	6,96	6.0	— 3,56
I ф.В	7,4	1,87	— 7,14
I ф.С	3,13	0,1	3,12
I 0	10,8	7,9	— 7,6

4. Построение векторной диаграммы напряжений.

4.1 На комплексной плоскости строятся векторы фазных напряжений питающей сети А, В, С; соединив их концы, получают векторы линейных напряжений АВ, ВС, СА. Затем строятся векторы фазных напряжений нагрузки А нагр., В нагр., С нагр. Для их построения можно использовать обе формы записи комплексов токов и напряжений.

Например, вектор А нагр. строится по показательной форме следующим образом: от оси +1 под углом 6 10 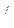, т.е. против часовой стрелки, откладывается отрезок длиной 6,96 см; по алгебраической форме его можно построить, отложив по оси +1 отрезок длиной 6,81 см, а по оси + j отрезок длиной 0,76 см, концы этих отрезков являются координатами конца вектора А нагр.

4.2 Т.к. линейные напряжения нагрузки заданы питающей сетью, для определения положения нейтрали нагрузки необходимо выполнить параллельный перенос векторов фазных напряжений нагрузки А нагр., В нагр., С нагр. так, чтобы их концы совпали с концами фазных напряжений питающей сети.

Точка 0, в которой окажутся их начала, есть нейтраль нагрузки. В этой точке находится конец вектора напряжения смещения нейтрали 0, его начало расположено в точке 0. Этот вектор можно также построить, используя данные таблицы 9.

5. Построение векторной диаграммы токов.

5.1 Построение векторов фазных токов нагрузки ф.А, ф.В, ф.С подобно построению векторов фазных напряжений.

5.2 Сложением векторов фазных токов находится вектор тока в нулевом проводе 0; его длина и длины его проекций на оси должны совпасть с указанными в таблице 8.

Векторные диаграммы токов и напряжений для случая обрыва нулевого провода строятся аналогично.

Следует выполнить анализ результатов расчета и построения векторных диаграмм и сделать выводы о влиянии несимметрии нагрузки на величину ее фазных напряжений и на напряжение нейтрали; особое внимание необходимо обратить на последствия обрыва нулевого провода сети при несимметричной нагрузке.

Примечание. Допускается совмещение диаграмм токов и напряжений при условии их выполнения разными цветами.

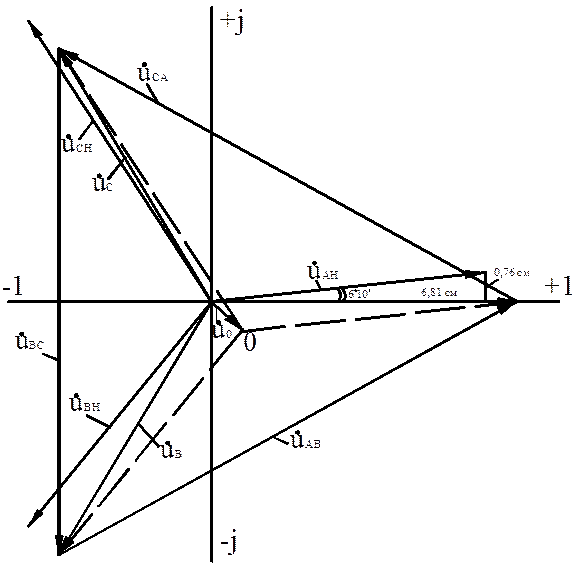
Рисунок 15. Векторная диаграмма напряжений

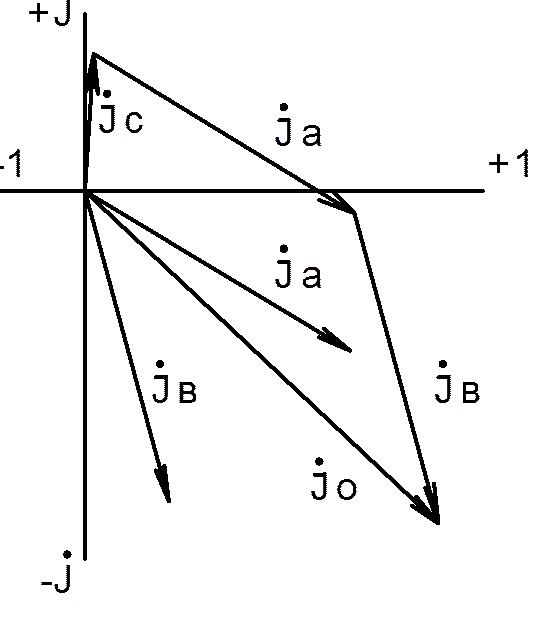
Рисунок 16. Векторная диаграмма токов.

Рисунок 17. Совмещенная векторная диаграмма напряжений и токов.

Применение векторных диаграмм для анализа несимметричных режимов (Лекция №18)

Несимметричные режимы в простейших характерных случаях (короткое замыкание и холостой ход) могут быть проанализированы на основе построения векторных диаграмм.

Рассмотрим режимы обрыва и короткого замыкания фазы при соединении в звезду для трех- и четырехпроводной систем. При этом будем проводить сопоставление с симметричным режимом работы цепи, фазные напряжения и токи в которой будут базовыми. Для этой цепи (см. рис.1,а) векторная диаграмма токов и напряжений приведена на рис. 1,б (принято, что нагрузка носит активно-индуктивный характер). Здесь

При обрыве фазы А нагрузки приходим к векторной диаграмме на рис. 2.

В этом случае

При коротком замыкании фазы А (трехпроводная система) имеет место векторная диаграмма на рис. 3. Из нее вытекает: ; ; ; ; .

При обрыве фазы А в четырехпроводной системе (нейтральный провод на рис. 1,а показан пунктиром, а вектор тока — пунктиром на рис. 1,б) ; ; .

Симметричный трехфазный приемник при соединении в треугольник и соответствующая этому случаю векторная диаграмма напряжений и токов приведены на рис. 4.

Здесь при том же способе соединения фаз генератора ; ; ; ; ; .

При обрыве провода в фазе А-В нагрузки, как это видно из схемы на рис. 5, ; , при этом сами токи и в силу автономности режима работы фаз при соединении нагрузки в треугольник такие же, как и в цепи на рис. 4,а. Таким образом,
; ; .

Цепь при обрыве линейного провода А-А’ и соответствующая этому случаю векторная диаграмма приведены на рис.6.

Здесь

; ; .

Мощность в трехфазных цепях

Мгновенная мощность трехфазного источника энергии равна сумме мгновенных мощностей его фаз:

Активная мощность генератора, определяемая как среднее за период значение мгновенной мощности, равна

Соответственно активная мощность трехфазного приемника с учетом потерь в сопротивлении нейтрального провода

реактивная

и полная

Суммарная активная мощность симметричной трехфазной системы

(1)

Учитывая, что в симметричном режиме для звезды имеют место соотношения

и для треугольника —

на основании (1) для обоих способов соединения фаз получаем

где j — угол сдвига между фазными напряжением и током.

Аналогично

Докажем теперь указанное ранее свойство уравновешенности двухфазной системы Тесла и симметричной трехфазной системы.

1. Двухфазная система Тесла

В соответствии с рис. 7

(2)

(3)

С учетом (2) и (3)

Таким образом, суммарная мгновенная мощность фаз есть величина постоянная, равная суммарной активной мощности источника.

2. Симметричная трехфазная цепь

Тогда

Отсюда

т.е. и для симметричной трехфазной цепи свойство уравновешенности доказано.

Измерение мощности в трехфазных цепях

Ниже рассмотрены практические схемы включения ваттметров для измерения мощности в трехфазных цепях.

1. Четырехпроводная система, несимметричный режим.

Представленная на рис. 8 схема называется схемой трех ваттметров.

Суммарная активная мощность цепи определяется как сумма показаний трех ваттметров

2. Четырехпроводная система, симметричный режим.

Если режим работы цепи симметричный, то для определения суммарной активной мощности достаточно ограничиться одним ваттметром (любым), включаемым по схеме на рис. 8. Тогда, например, при включении прибора в фазу А,

(4)

3. Трехпроводная система, симметричный режим.

При отсутствии доступа к нейтральной точке последняя создается искусственно с помощью включения трех дополнительных резисторов по схеме «звезда», как показано на рис. 9 – схема ваттметра с искусственной нейтральной точкой. При этом необходимо выполнение условия , где — собственное сопротивление обмотки ваттметра. Тогда суммарная активная мощность трехфазной системы определяется согласно (4).

4. Трехпроводная система, симметричный режим; измерение реактивной мощности.

С помощью одного ваттметра при симметричном режиме работы цепи можно измерить ее реактивную мощность. В этом случае схема включения ваттметра будет иметь вид по рис. 10,а. Согласно векторной диаграмме на рис. 10,б измеряемая прибором мощность

Таким образом, суммарная реактивная мощность

5. Трехпроводная система, несимметричный режим.

Представленная на рис. 11 схема называется схемой двух ваттметров. В ней сумма показаний приборов равна суммарной активной мощности цепи.

Действительно, показания приборов в данной схеме:

Тогда

В заключение отметим, что если в схеме на рис. 11 имеет место симметричный режим работы, то на основании показаний приборов можно определить суммарную реактивную мощность цепи

(5)

Литература

Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

В симметричной трехпроводной цепи произошел обрыв фазы. Что покажет вольтметр, включенный между найтральными точками источника и приемника?

Ответ: .

Во сколько раз мощность в цепи на рис. 6,а меньше мощности в цепи на рис. 4,а?

Ответ: в два раза.

В цепи на рис. 10,а симметричная нагрузка составлена из резистивных элементов. Что покажет ваттметр?

Ответ: .

В цепи на рис. 10,а симметричная нагрузка с фазным сопротивлением соединена в звезду. Линейное напряжение .

Определить показание ваттметра.

Ответ: .

В цепи на рис. 11 нагрузкой служат два одинаковых конденсатора с ХС=100 Ом, включенные между линейными проводами А и В, В и С соответственно. Линейное напряжение .

Определить показания ваттметров.

Ответ: .

На основе построения векторной диаграммы токов и напряжений для симметричного режима работы цепи на рис. 11 доказать соотношение (5).

Векторные диаграммы — Студопедия

В цепях переменного тока все токи и напряжения являются синусоидальными функциями времени. Поэтому аналитические зависимости в виде уравнений не дают представления о реальных соотношениях величин. При переходе от оригиналов функций и параметров к их изображениям в виде комплексных чисел задача анализа несущественно упрощается, т.к., в отличие от цепей постоянного тока, где все величины однозначно характеризуются одним числом, в области изображений каждая величина определяется двумя числами, каждое из которых в общем случае недостаточно для полной оценки состояния цепи. Помочь в анализе соотношений между величинами и параметрами электрический цепи может их геометрическое представление в виде векторной диаграммы.

Из курса математики известно, что любое комплексное число может быть изображено в виде точки на плоскости с ортогональной системой координат, в которой на оси абсцисс откладывается вещественная составляющая, а на оси ординат мнимая. Такое изображение соответствует алгебраической форме записи комплексного числа. Если начало координат соединить отрезком прямой с точкой изображающей комплексное число, то длина этого отрезка и его угол с вещественной осью также могут служить изображением комплексного числа. Причем, для однозначного определения угла нужно задать положительное направление отрезка, т.е. определить его как радиус-векторили просто вектор.

Векторной диаграммой называется совокупность векторов на комплексной плоскости, соответствующая комплексным величинам и/или параметрам электрической цепи и их связям.

Векторные диаграммы могут быть точными и качественными. Точные диаграммы строятся с соблюдением масштабов всех величин по результатам численного анализа. Они предназначены в основном для проверки расчетов. Качественные векторные диаграммы строятся с учетом взаимных связей между величинами и обычно предшествуют расчету или заменяют его. В качественных диаграммах масштаб изображения и конкретные значения величин несущественны, важно только, чтобы в них были правильно отражены все связи между величинами, соответствующие связям и параметрам элементов электрической цепи. Качественные диаграммы являются важнейшим инструментом анализа цепей переменного тока.

В цепях переменного тока одной из самых распространенных задач является анализ поведения цепи при изменении в широких пределах какой-либо величины или параметра.

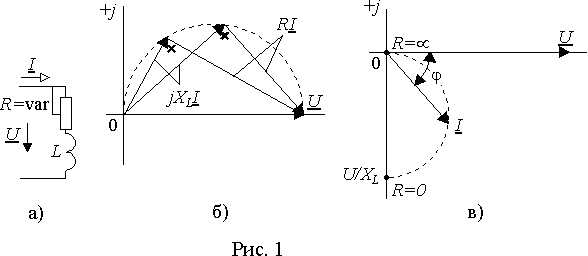
Пусть, например, требуется исследовать изменение тока в цепи, представленной на рис. 1 а), при постоянном напряжении на входе и изменении резистивного сопротивления в пределах 0 > R > µ .

Падение напряжения на входе уравновешивается суммой падений напряжения на R и L, т.е. u = u_R+u_L = Ri + Ldi/dt или для изображений

U = U_R + U_L = RI + jw LI = RI + jX_LI.

(1)

Из выражения (1) следует, что

векторы U_R и U_L всегда перпендикулярны друг другу, т.к. каждый из них представляет собой вектор тока I, умноженный на соответствующую константу (R или X_L), а в падении напряжения U_L присутствует в качестве множителя оператор поворота на 90° — j;
сумма векторов U_R и U_L постоянная и равна вектору U .

Для упрощения построений, не ограничивая в то же время общности рассуждений, совместим вектор U с вещественной осью (рис. 1 б)). Тогда в соответствии с условиями (1) при любых значениях R векторы U_R и U_L будут составлять с вектором U прямоугольные треугольники. Как известно, любой треугольник может быть вписан в окружность, причем дуги, на которые опираются углы вписанного треугольника равны двойному значению угла. Так как во всех векторных треугольниках угол между U_R и U_L равен 90° , то все они опираются на дугу в 180° , т.е. на диаметр, которым является постоянный вектор входного напряжения U. Следовательно, все треугольники векторов U_R , U_L и U вписываются в одну и ту же полуокружность, которая является геометрическим местом точек перемещения конца вектора U_R при всех изменениях значения R.

Векторная диаграмма, в которой при вариации параметров геометрическим местом точек перемещения конца какого-либо вектора является окружность или полуокружность, называется круговой диаграммой.

Так как векторы U_R и U_L связаны с вектором тока I постоянными коэффициентами, то из круговой диаграммы вектора U_R можно получить векторную диаграмму тока и она также будет круговой. Для получения вектора I, в соответствии с выражением (1), достаточно разделить все элементы треугольников U_R , U_L и U на R или jX_L. При этом мы получим подобный треугольник, одним из катетов которого будет I. Однако деление на R нецелесообразно, т.к. эта величина переменная и для сохранения масштаба треугольников следует произвести деление на jX_L. В результате диаметр полуокружности станет равным U/X_L и она вследствие деления на оператор поворота j повернется относительно начала координат на угол — 90° (рис. 1 в)). Полученная полуокружность и будет круговой диаграммой вектора входного тока I. Из нее можно заключить, что при R = 0 вектор тока отстает от напряжения на 90° и по модулю равен U/X_L. При R ® µ модуль и аргумент вектора тока стремятся к нулю.

Другой важной разновидностью векторных диаграмм являются линейные диаграммы.

Линейной диаграммой называется векторная диаграмма, в которой геометрическим местом точек конца какого-либо вектора при вариации параметра является прямая линия.

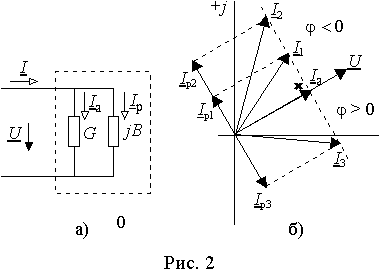Примером такой диаграммы может служить диаграмма входного тока I пассивного двухполюсника при постоянном напряжении на входе U=const и изменении его реактивной проводимости в пределах — µ > B > +µ , если активная составляющая проводимости G остается постоянной. Примером электрической цепи с такой вариацией реактивной проводимости является параллельный резонансный контур при вариации частоты 0 < w <µ .

Действительно, активная составляющая тока любого двухполюсника равна I_а=GU, а реактивная I_р=jBU, т.е. эти составляющие всегда перпендикулярны друг другу или, иначе говоря, находятся в квадратуре, т.к. являются производными от одного и того же вектора U, но I_р содержит оператор поворота на 90° — j. Входной ток представляет собой сумму активной и реактивной составляющих I = I_а+ I_р, причем, активная составляющая отличается от вектора U постоянным вещественным множителем G, поэтому всегда совпадает с ним по фазе (рис. 2 б)) и имеет постоянный модуль. Вектор реактивной составляющей имеет переменный модуль — µ < | I_р| < + µ и I_а ^ I_р , следовательно, он будет располагаться на прямой проходящей через начало координат перпендикулярно вектору U . Поэтому суммарный вектор входного тока I при изменении реактивной проводимости будет скользить своим концом по линии перпендикулярной векторам I_а и U и проходящей через конец вектора I_а.

Для качественного анализа электромагнитных процессов в электрической цепи переменного тока можно строить векторные диаграммы, пользуясь только принципиальной схемой.

Построим качественную векторную диаграмму для цепи рис. 3.

Построение всегда можно начинать с произвольно выбранной величины, но т.к. операции суммирования векторов производятся проще, чем операции разложения на составляющие, то лучше в качестве начального вектора выбирать напряжение или ток элемента цепи, расположенного как можно дальше от входа. Тогда входные величины будут получены постепенным сложением векторов.

Пусть вектор тока I₅ расположен так, как это показано на рис. 3. Ток I₅ протекает в емкости C₂, подключенной к узлам b и c цепи. Поэтому U_bc=U_C2. Но падение напряжения на емкости отстает от тока в ней на 90° , следовательно, U_bc нужно расположить на луче перпендикулярном вектору I₅ и смещенном в сторону отставания, т.е. по часовой стрелке.

Между узлами b и c помимо емкости C₂ включена ветвь, содержащая резистор r и индуктивность L. Ток в активно-резистивном двухполюснике отстает от напряжения на некоторый угол j , конкретное значение которого определяется отношением индуктивного сопротивления w L к резистивному r. Поэтому конец вектора тока I₄ в r—L ветви рис. 3 может находиться в любой точке сектора комплексной плоскости в 90° , ограниченного лучом совпадающим по направлению с U_bc и перпендикулярным ему лучом, смещенным в сторону отставания. Зададим произвольно точку конца вектора I₄ в этом секторе. Тогда падение напряжения на резисторе r должно совпадать по направлению с I₄, а падение напряжение на индуктивности L — опережать I₄ на 90°, причем в сумме U_r и U_L должны быть равны U_bc. Построение векторов U_r и U_L, удовлетворяющих этим условиям, проще всего произвести проектированием конца вектора U_bc на направление вектора I₄. Тогда вектор, совпадающий с I₄ по направлению, будет U_r, а перпендикулярный ему — U_L.

Уравнение Кирхгофа для узла b цепи можно записать в виде I₃ = I₄ + I₅, поэтому сложение векторов I₄ и I₅ по правилу параллелограмма даст нам вектор тока I₃, протекающего в резисторе R рис. 3. Падение напряжения на нем U_R = U_ab, как у любого резистора, будет совпадать по фазе с током, следовательно, его можно построить на луче совпадающем по направлению с I₃.

По второму закону Кирхгофа разность потенциалов U_ac можно представить суммой U_ac = U_ab+ U_bc = U. Соответственно, вектор входного напряжения U получается сложением по правилу параллелограмма векторов U_ab и U_bc рис. 3. Но U_ac= U_С1. Следовательно, ток в емкости C₁ должен опережать напряжение U_ac на 90° , поэтому его нужно построить на луче перпендикулярном U_ac и смещенном в сторону опережения.

Для узла a цепи справедливо I₁ = I₂ + I₃. В соответствии с этим равенством входной ток I₁ получен геометрическим суммированием векторов I₂ и I₃.

Как построить векторную диаграмму трансформатора тока

В этой статье будем строить схему замещения трансформатора тока и векторную диаграмму. Начнем со схемы замещения. Как и на векторной диаграмме, все величины мы приводим к вторичному току. Величины токов приводятся через коэффициент трансформации в первой степени, значения сопротивлений – через коэффициент трансформации в квадрате.

Первичный ток разделяется на ветвь тока намагничивания и ветвь вторичного тока.

Теперь, на основе этой схемы замещения можно построить векторную диаграмму.

Для начала строим из начала координат вектор вторичного тока I₂ и его активную составляющую I₂*R_н. Затем из конца вектора I₂*R_н откладываем на 90 градусов вектор I₂*Х_н. Сумма двух векторов будет равна U₂, т.е.:

U₂= I₂(R_н+jX_н)

Или другими словами – вторичное напряжение равно падению напряжения в сопротивлении нагрузки. Далее аналогично откладываем вектора I₂*R₂ и I₂*X₂. В итоге получим вектор ЭДС E₂

E₂=I₂(Z_н+Z₂)

Вектор между вторичным током I₂ его ЭДС E₂ обозначим «альфа». Его величина зависит от отношения активных и индуктивных сопротивлений вторичной цепи:

tg«альфа»= (R₂+ R_н)/(X₂+X_н)

Из вводной статьи про трансформаторы тока мы узнали, что первичный ток I’₁ состоит из тока намагничивания I_нам и вторичного тока I₂.

Угол между током намагничивания и ЭДС зависит от активных потерь в стали сердечника. Чем больше угол, тем меньше потери. Более подробно про углы на векторной диаграмме можно почитать в статье про погрешности в трансформаторах тока.

Угол гамма называется углом потерь и показывает отношение активной составляющей тока намагничивания к реактивной. Угол потерь определяют по экспериментальной кривой, которую снимают для конкретного трансформатора тока.

Сохраните в закладки или поделитесь с друзьями

Последние статьи

Самое популярное

Полезные сервисы

Векторная диаграмма — Знаешь как

Синусоидальные величины изображают или синусоидами, или вращающимися векторами.

Такое изображение дает возможность найти амплитуду, начальную фазу и период, т. е. все величины, определяющие синусоидальную величину.

При изображении синусоидальной величины вращающимся вектором длина вектора в определенном масштабе представляет собой амплитуду величины; угол между вектором и положительным направлением оси абсцисс в начальный момент равен начальной фазе, а угловая скорость вращения вектора равна угловой частоте. Мгновенное значение синусоидальной величины, представленной вращающимся вектором, определяется проекцией вектора на ось ординат.

Например, для изображения э. д. с. е = E_мsin (ωt + Ψ) под углом Ψ к положительному направлению оси абсцисс (рис. 5-9) проводят вектор в выбранном масштабе, выражающий амплитуду Е_м.

Рис. 5-9. Изображение синусоидальной величины вращающимся вектором.

При вращении вектора в положительном направлении (рис. 5-9) с угловой скоростью со проекции его на ось ординат (ось Y) выражают для соответствующих моментов времени мгновенные значения э. д. е., так как они в выбранном масштабе представляют величины

Е_м sin α = E_м sin (ωt + Ψ)

Ha графике (рис 5-9) для момента времени t₁ э. д. с. изображена ординатой e (t₂), равной проекции на ось Y вращающегося

вектора, расположенного в этот момент под углом α = (ωt₁ + Ψ) к оси абсцисс.

Один или несколько векторов, изображающих синусоидальные величины одной частоты, называются векторной диаграммой.

При вращении векторов, образующих векторную диаграмму, взаимное расположение их остается неизменным. Обычно интересным является сдвиг фаз между отдельными величинами. Поэтому при построении векторной диаграммы вектор, который проводится первым, направляют произвольно, а остальные векторы диаграммы располагают по отношению к нему под углами, равными углам сдвига фаз.

Рис. 5-10. Сложение двух векторов э. д. с.

Векторные диаграммы широко применяются при рассмотрении явлений в цепях переменного тока.

На рис. 5-10 показаны два вектора э. д. с. Е_м1 и Е_м₂и геометрическая сумма их — вектор суммарной э. д. с. Е_м в момент времени t = 0, Для любого момента времени

сумма проекций вращающихся векторов E_м1 и Е_м2 на ось У равна проекции на ту же ось суммарного вектора Е_мт. е. е = е₁ + е₂ так как взаимное расположение векторов при их вращении не изменяется. При сложении двух синусоидальных величин одной частоты получается синусоидальная величина той же частоты, амплитуда которой выражается длиной суммарного вектора, например:

Ē_м = Ē_м1 + Ē_м2

Черточки над буквами указывают на то, что величины являются векторами и, следовательно, сложение их производится геометрически по правилу параллелограмма (треугольника).

Вычитание двух синусоидальных величин выполняется как сложение уменьшаемой величины с обратной по знаку вычитаемой величиной, т. е.

е₁ — е₂ = е₁ + (—е₂)

Статья на тему Векторная диаграмма

векторный диаграмма PNG, бесплатно векторная диаграмма, принципиальная схема, диаграммы векторные изображения

схематическая диаграмма бизнес-информации
1200 * 2244

геометрическая векторная диаграмма
1938 * 1938

восемь диаграмм китайского языка ветер
5000 * 5000

бесплатно png векторная диаграмма деревня деревня
1200 * 1200

схема медицинского обслуживания
1200 * 1200

маленькая мышка футболка напечатанная диаграмма
500 * 500

векторная диаграмма сердца
1200 * 1200

бизнес-инфографика с желтым темно-фиолетовым красным синим кругом векторный дизайн диаграммы для презентаций и визуализации данных
5000 * 5000

вектор силуэт порта
3833 * 2427

корпус Y структурная диаграмма векторный материал
2500 * 2500

d.jpg» alt=»green leaf round frame vector diagram, Tea Pattern, Decorative Pattern, Leaf Pattern PNG and PSD»/>
зеленая круглая рамка векторной диаграммы
1200 * 1200

денежный график нисходящий медвежий тренд с символом цены доллара и золота
4250 * 4250

сердечный приступ атеросклероз хроническое заболевание медицина образование диаграмма векторная схема человеческая рука рисовать векторные иллюстрации
8333 * 8333

цветок векторная диаграмма
1200 * 1200

зигзагообразная векторная стрелка диаграмма
1200 * 1200
1200 * 1200

векторная инфографика ppt
2000 * 2000

векторная диаграмма эффекта пламени
1200 * 1200

бизнес-инфографика с желтым темно-фиолетовым красным синим квадратным векторным дизайном для презентаций и визуализации данных
5000 * 5000

e световые диаграммы
2500 * 2500

кокосовые листья
1200 * 1200

бизнес-инфографика со светло-голубым желтым индиго квадратный и круговой векторный дизайн диаграммы для презентаций и визуализации данных
5000 * 5000

90
высотное здание архитектура структура линейная диаграмма вектор
2000 * 2000

изогнутая волновая диаграмма
1200 * 1200

вектор акварель и звезды
1200 * 1200

атеросклероз хроническая болезнь медицина образование диаграмма векторная схема человеческая рука рисовать векторные иллюстрации
8333 * 8333

биткойн с графической диаграммой векторные торговые мониторы и тренд цифровые деньги концепция инвестиций криптовалюты, изолированные на белом иллюстрации
5000 * 5000

вектор фиолетовый кривая орнамент
1772 * 1772

мужчины и женщины пищеварительной системы диаграмма векторный материал
2000 * 2000

ревматоидная болезнь артрит хроническая болезнь медицина образование диаграмма векторная схема человеческая рука рисовать векторные иллюстрации
8333 * 8333

ppt шаблон векторной диаграммы
1200 * 1200

бизнес инфографики с темно-фиолетовым желтым прямоугольником и круговой диаграммой векторный дизайн для презентаций и визуализации данных
5000 * 5000
9000 векторная кривая декоративный узор
1200 * 1200

векторный колл-центр обслуживания клиентов для креативного дизайна диаграмма
850 * 1307

схематическая диаграмма бизнес-информации
1200 * 1200

ревматоид артрит хроническое заболевание ss медицина образование диаграмма векторная схема человеческая рука рисовать векторные иллюстрации
8333 * 8333

роскошный автобус векторная диаграмма
2000 * 2000

векторный диаграмма горячего кофе
1447 * 2254
.
Векторный ток | Статья о векторном токе от The Free Dictionary
На рис. 3 показаны результаты моделирования распределения электрического поля и векторной плотности тока предлагаемого поглотителя, когда E- и H-поля падают на поляризацию x и y соответственно.
Вектор плотности тока течет в направлении y, как показано на рисунке 3 (b).
Этот результат согласуется с сохранением векторного тока при слабых взаимодействиях. В среднем томе трехтомного набора учебников для серии курсов, которые заменили традиционный курс теоретической физики, Майани иллюстрирует концептуальный путь, который привел к объединение слабого и электромагнитного взаимодействий, начиная с отождествления слабого адронного тока с изотопическим спиновым током; через гипотезу консервативного векторного тока Фенмана, Гелл-Манна и других; теории Янга-Миллса и первой электрослабой теории Глэшоу.Амплитуда приложенного вектора тока статора может быть выражена током по оси d-q, а напряжение может быть выражено батареей следующим образом: Ли, первые два китайских лауреата Нобелевской премии; проведены эксперименты по бета-распаду и экспериментальное подтверждение сохранения векторного тока при бета-распаде; участвовал в Манхэттенском проекте; и была первой женщиной-президентом Американского физического общества. Как мы знаем, распределение тока на плоскости заземления обычной патч-антенны в основном концентрируется непосредственно под патчем, как показано на рисунке 3, который представляет собой векторное распределение тока резонансной частоты. 5.61 ГГц при 0 градусах. Исключением является значение кварк-конденсата, которое связано с константой распада пиона через (4). В качестве примера, давайте рассмотрим сохраняющийся векторный коррелятор тока Экспериментальные ограничения на значения [лямбда] и | [V.sub.ud] | происходят от ядерных [0.sup. +] — [0.sup. +] бета-распадов [4], унитарности CKM (предполагает сохраняющийся векторный ток, унитарность CKM и значения | [V.sub.us] | и | [V.sub.ub] | из [3]), измерения нейтронной корреляции бета-распада A [5] Не требуя поляриметрии, этот параметр распада может использоваться для измерения [лямбда] ([g.sub.a] / [g.sub.v]), тест на унитарность Кабиббо-Кобаяши-Маскава (CKM), предельные скалярные и тензорные токи и поиск нарушения заряженного векторного тока (ВАХ). Точные измерения этих параметров могут проверить унитарность матрицы Кабиббо-Кобаяши-Маскавы (CKM), обеспечивает ограничения на слабые скалярные и тензорные токи, правые токи, нарушение сохраняющегося векторного тока (CVC) и токи второго класса, а также другие возможные новые физические аспекты, выходящие за рамки Стандартной модели физика элементарных частиц. .
Соотношение фаз напряжения и тока в индуктивной цепи
Любое изменение тока в катушке (повышение или понижение) вызывает соответствующее изменение магнитного потока вокруг катушки. Поскольку ток изменяется с максимальной скоростью, когда он проходит через свое нулевое значение под углом 90 ° ( точка b на рисунке 1 ) и 270 ° (точка d), изменение магнитного потока также является наибольшим в эти моменты времени.
Следовательно, самоиндуцированная ЭДС (электромагнитное поле ) в катушке имеет максимальное (или минимальное) значение в этих точках, как показано на Рисунок 1 .
Поскольку ток не изменяется в точке, когда он проходит через свое пиковое значение при 0 ° (точка a), 180 ° (точка c) и 360 ° (точка e), изменение потока в эти моменты времени равно нулю. . Следовательно, в этих точках самоиндуцированная ЭДС в катушке находится на нулевом значении.
Рисунок 1 — Ток, самоиндуцированная ЭДС и приложенное напряжение в индуктивной цепи
В соответствии с законом Ленца , индуцированное напряжение всегда противодействует изменению тока. Ссылаясь на рисунок 1, при максимальном отрицательном значении тока ( точек на ) наведенная ЭДС имеет нулевое значение и падает.Таким образом, когда ток растет в положительном направлении (от точки a к точке c), индуцированная ЭДС имеет полярность, противоположную приложенному напряжению, и препятствует увеличению тока.
Обратите внимание, что когда ток проходит через свое нулевое значение ( точка b ), индуцированное напряжение достигает своего максимального отрицательного значения.
Теперь, когда ток имеет максимальное положительное значение (точка c), наведенная ЭДС имеет нулевое значение и растет. Поскольку ток падает до своего нулевого значения при 180 ° (от точки c к точке d), наведенная ЭДС имеет ту же полярность, что и ток, и стремится удерживать ток от падения.Когда ток достигает нулевого значения, наведенная ЭДС достигает максимального положительного значения.
Позже, когда ток увеличивается от нуля до максимального отрицательного значения на 360 ° (от точки d до точки e), индуцированное напряжение имеет полярность, противоположную полярности тока, и стремится удерживать ток от увеличения в отрицательном направлении. . Таким образом, наведенная ЭДС отстает от тока на 90 °.
Значение самоиндуцированной ЭДС изменяется как синусоида и отстает от тока на 90 °, как показано на Рисунок 1 .Приложенное напряжение должно быть всегда равным и противоположным самоиндуцированной ЭДС; следовательно, в чисто индуктивной цепи ток отстает от приложенного напряжения на 90 °.
Если приложенное напряжение (E) представлено вектором, вращающимся против часовой стрелки ( Рисунок 1b ), то ток можно выразить как вектор, который отстает от приложенного напряжения на 90 °. Диаграммы этого типа называются векторными диаграммами .
Пример
A 0.4 H Катушка с незначительным сопротивлением подключена к источнику питания 115 В, 60 Гц (см. Рисунок 2 ). Найдите индуктивное сопротивление катушки и ток в цепи. Нарисуйте векторную диаграмму, показывающую соотношение фаз между током и приложенным напряжением.
Рисунок 2 — Схема катушки и фазовая диаграмма
Решение
1. Индуктивное реактивное сопротивление катушки
X _L = 2 · π · f · L
X _L = 2 · 3.14 · 60 · 0,4
X _L = 150,7 Ом
2. Ток в цепи
I = E / X _L
I = 115 / 150,7
I = 0,76 ампер
3. Нарисуйте векторную диаграмму, показывающую соотношение фаз между током и приложенным напряжением.
Векторная диаграмма, показывающая текущее запаздывающее напряжение на 90 °, нарисована на Рис. 2b .

Сводка
Сводка по индуктивному реактивному сопротивлению
Противодействие протеканию переменного тока, вызванное индуктивностью, называется индуктивным реактивным сопротивлением (XL).
Формула для расчета XL:
.
X _L = 2 · π · f · L
.
Ток (I) отстает от приложенного напряжения (E) в чисто индуктивной цепи на фазовый угол 90 °.
.
На векторной диаграмме показан вектор приложенного напряжения (E), опережающий (вверху) вектор тока (I) на величину разности фазовых углов из-за соотношения между напряжением и током в индуктивной цепи.
ИСТОЧНИК: Справочник по электротехнике, том 3 — Загрузите его здесь [/ fancy_box]
.
Теория компенсации реактивной энергии, которую должен знать каждый инженер
Качество энергетических систем
Компенсация реактивной энергии — важный процесс повышения энергоэффективности. Это снижает энергопотребление и, следовательно, его стоимость, обеспечивает оптимальное использование установок, предотвращая их превышение размеров, и в целом улучшает качество энергосистем.
Теория компенсации реактивной энергии, которую должен знать каждый инженер (фото предоставлено VIlma Electric)
Содержание:
Введение в реактивную энергию
Чрезмерная компенсация
Параллельная RLC-схема
Диаграмма тока
Индуктивная цепь
Емкостная цепь
Группы нагрузок
Схема питания
Использование тангенса φ

1.Введение в реактивную энергию
Индуктивные нагрузки, обычно двигатели и трансформаторы, а также некоторые типы освещения с балластом, а также сварочное оборудование или индукционный нагрев, имеют особенность работы с помощью магнитного поля. Часть энергии, необходимой для создания этого магнитного поля, не преобразуется в тепло или работу.
Очень длинные линии (за счет индуктивного накопления), а также статические преобразователи (управляемые выпрямители, контроллеры мощности переменного тока и т. Д.) Также могут потреблять ненужную энергию за счет фазового сдвига тока после основного напряжения.
Энергия, соответствующая этой мощности, называется реактивной энергией . Выражается в «киловольт-ампер-реактивный час» (кварч) . Каким бы ни был источник и тип энергии: общественная распределительная система, автономный комплект, ИБП или другое, это энергия, которая потребляется без надобности.
В отличие от компенсации индуктивных цепей, компенсация преимущественно емкостных цепей требует использования индуктивностей для поглощения производимой реактивной энергии.
Эта ситуация встречается в распределительных цепях (очень длинные линии, кабельные сети), часто при низкой нагрузке на цепи.новые установки, в которых используются многочисленные электронные источники питания (центры обработки данных), также могут иметь эту особенность.
Помимо предотвращения подачи энергии обратно в систему, компенсация установки со слишком высокой емкостью необходима для ограничения переходных сверхтоков и перенапряжений , которые могут возникнуть при включении таких нагрузок, и во избежание самовосстановления. возбуждение синхронных двигателей.
Описанные ранее вредные последствия реактивной мощности на линиях электропередачи также обнаруживаются в установках:
Он увеличивает необходимый ток с риском возникновения разрушительных сверхтоков и проблемных падений напряжения, что приводит к необходимости увеличения размеров проводов.
Уменьшает доступную активную мощность, что ограничивает возможности использования источника или требует его увеличения.
Это создает дополнительные эксплуатационные расходы, связанные с ценообразованием на потребляемую реактивную энергию и измеряемую распределительной компанией.
Вернуться к содержанию ↑

1.1 Избыточная компенсация
Избыточная компенсация (Ic> Ir) увеличивает кажущийся потребляемый ток, а также увеличивает напряжение, подаваемое на оборудование.Иллюстрация векторов V2 _S (с избыточной компенсацией) и V2 (с соответствующей компенсацией) показывает это явление, которого следует избегать.
Следует проявлять осторожность при выборе компенсации энергии .
Рисунок 1 — Диаграмма чрезмерной компенсации
Вернуться к содержанию ↑

2. Параллельная цепь RLC
Промышленные системы обычно представляют собой параллельных цепей RLC . Однако каждая ветвь может сама образовывать другие сложные последовательные или последовательно / параллельные системы.Все три элемента имеют одинаковое напряжение питания.
Полный ток равен векторной сумме токов всех трех элементов: it = i _R + i _L + i _C
Рисунок 2 — Параллельная цепь RLC
Полные сопротивления индуктивная, резистивная и емкостная ветви цепи соответственно:
Z _L = Lω
Z _R = R
Z _C = –1 / Cω
Импеданс этого типа цепи равен сумма, обратная сумме обратных величин каждого импеданса:

Это уравнение показывает, что часть импеданса, обусловленная емкостью и индуктивностью, может стремиться к 0, если Lω = -1 / cω .Это явление резонанса (или, точнее, антирезонанса , поскольку U _L и U _C находятся в противофазе ), который возникает на определенных частотах, соответствующих угловой частоте:

Из-за до равенства Lω = –1 / cω , полное сопротивление цепи уменьшается на резистивной ветви R . затем ток может внезапно возрасти до опасных или даже разрушительных значений.
Это явление необходимо контролировать, в частности, при установке компенсационных конденсаторов, особенно при наличии гармоник, так как частота ω0 может быть достигнута легче, и / или при высоком импедансе L (особенно в установках малой мощности).
Мощность каждой ветви записывается следующим образом:
P _R = I _R ² × R
Q _L = I _L ² × Lω
Q _C = I _C ² × (1 / cω)
Вернуться к содержанию ↑

3. Диаграмма тока
Сдвиг фаз между токами в параллельных RLC-цепях и мощности, связанные с каждым из импедансов, составляющих эти цепи, могут быть представлены диаграммами тока Френеля и диаграммами мощности , которые демонстрируют концепции фазового сдвига (ϕ) и коэффициента мощности (PF или λ) .
Коэффициент мощности характеризует отношение активной (полезной мощности) мощности к полной мощности (сумма активной мощности и реактивной мощности).
Когда токи и напряжения полностью синусоидальны, диаграммы тока и диаграммы мощности аналогичны, а коэффициент мощности (PF или λ) идентичен косинусу ϕ угла смещения между векторами U и I .
Вернуться к содержанию ↑

3.1 Индуктивная цепь
Приведенную ниже диаграмму тока можно использовать для определения местоположения векторов, представляющих каждый из трех компонентов параллельной цепи RLC.
Рисунок 3 — Индуктивная цепь
Где:
I _R — ток в резистивной ветви
I _L — ток в индуктивной ветви
I _C — ток в емкостная ветвь
Это — полный полный ток
Напряжение u источника считается опорным. Следует отметить, что в этом примере значение I _L (реактивный ток в индуктивности) больше, чем значение I _C (реактивный ток в емкости). Угол ϕ отрицательный.
Таким образом, добавление конденсаторов позволит подавать реактивный ток, необходимый для компенсации I _L.
Вторая диаграмма является часто используемым упрощенным представлением, в котором сумма I _L и I _C записывается как Ir (для реактивного) , что не следует путать с I _R (ток резистивной ветви на левой диаграмме).
На основе этой диаграммы устанавливаются следующие соотношения:
Ia = It × cosϕ (активный ток),
Ir = It × sin ϕ (реактивный ток),
It² = Ia ² + Ir ² (полный ток).
Вернуться к содержанию ↑

3.2 Емкостная цепь
На диаграмме ниже значение I _C (реактивный ток в емкости) больше, чем значение I _L (реактивное ток в индуктивности), а угол ϕ положительный.
Для компенсации слишком высокого реактивного тока I _C необходимо использовать шунтирующие реакторы. Это не следует путать с включением индуктивностей последовательно с конденсаторами, что предназначено для ограничения риска резонанса.
Рисунок 4 — Схема емкостной цепи
Схема 2 ^nd — это часто используемое упрощенное представление, в котором сумма I _L и I _C записывается как Ir (для реактивного) .
При наличии нелинейных нагрузок вводится дополнительная мощность, называемая мощностью искажения, и равенство соотношений между мощностью и синусоидальными токами больше не проверяется.
Только измерение среднеквадратичных значений мощности даст коэффициент мощности.
Вернуться к содержанию ↑

3.3 Группы нагрузок
Аддитивные установки реактивной мощности состоят из множества групп нагрузок, соединенных параллельно (A, B, C и т. Д. В примере ниже).
Рисунок 5 — Установки, состоящие из множества групп нагрузок, соединенных параллельно (A, B, c и т. Д.)
Фазовый сдвиг тока / напряжения и общий ток, потребляемый этими группами нагрузок, являются результатом сложения текущие векторы. Это довольно сложный математический подход.
Однако реактивную мощность легко вычислить из арифметической суммы различных мощностей каждой нагрузки:
Приемник A состоит из индуктивности L ₁ и резистора R ₁,
Приемника B состоит из индуктивности L ₂ и резистора R ₂.
Рисунок 6 — Диаграмма Френеля векторов тока
Диаграмма Френеля группы приемников A и B демонстрирует взаимосвязь между векторами I _t, I ₁ и I ₂ , связанными с синусоидальными значениями i _t, i ₁ и i ₂ соответственно:
I _t × sin ϕ = I ₁ × sin ϕ ₁ + I ₂ × sin ϕ ₂
Умножение двух членов уравнения на U (общее напряжение в параллельной группе) дает:
U × I _t × sin ϕ = U × I ₁ × sin ϕ ₁ + U × I ₂ × sin ϕ ₂
Реактивная мощность группы приемников равна сумме реактивных мощностей каждого приемника, т.е.е. Q = Q1 + Q2
Это правило, которое может быть обобщено на любую группу приемников, питаемых одинаковым синусоидальным напряжением, известно как теорема Бушро (Q = ΣQn) .
Вернуться к содержанию ↑

4. Схема питания
Возможны два изображения выше, так как мощность не имеет знака. однако, по аналогии с текущей диаграммой, предпочтительнее первое представление.
Рисунок 7 — Треугольная диаграмма мощности
Где:
P = U × I × cos ϕ (активная мощность в кВт)
Q = U × I × sinϕ (реактивная мощность в квар)
S = U × I × (полная мощность в ВА)
Для линейных нагрузок:

Вернуться к содержанию ↑

5.Использование тангенса ϕ
Характеристика касательной ϕ широко используется из-за своей практичности. Чем ближе он к нулю, тем меньше потребляется реактивной энергии. Преимущество этого выражения в том, что оно характеризует баланс обмена реактивной энергией между источником питания и потребляющей установкой.
Таким образом, если компенсация мощности слишком высока, реактивная мощность Q снова становится положительной, а тангенс ϕ снова удаляется от нуля.

Допустимые значения tanϕ зависят от страны и контракта на поставку.Например, во Франции значение, при превышении которого инициируется выставление счетов (согласно тарифному периоду), составляет 0,4 (соответствует cos 0,93) со стороны измерения высокого напряжения, которая также включает реактивное потребление соединительного трансформатора.
При измерении низкого напряжения, реактивное потребление трансформатора ВН / НН добавляется на фиксированной основе , уменьшая допустимое значение tan на 0,09 . Тогда значение загара составляет 0,31 , что соответствует косинусу , равному 0.955 .
Разделение компаний, передающих и распределяющих электроэнергию, приводит к рассмотрению возможности снижения значения тангенса угла до 0,2 .
Поиск дополнительной экономии за счет снижения реактивной энергии наталкивается на техническое требование уменьшения резонансной частоты установок, вызванной слишком большим количеством конденсаторов.
Все это противоречивые элементы, которые показывают , что важно хорошо знать характеристики установки и ее приемников при реализации любого проекта компенсации .
Вернуться к содержанию ↑
Источник: Электроснабжение Legrand
.
No related posts.