Об ООО «СпецЭнергоКабель»
О НПП «Cпецкабель»
О заводе
Новости
Дайджест
Контакты

Значение косинуса – Таблица косинусов углов от 0° до 360°

Таблица косинусов (полная, градусы и значения)

В данной таблице представлены значения косинусов от 0° до 360°. Таблица косинусов нужна, чтобы узнать, чему равен косинус угла. Нужно только найти его в таблице. Для начала короткая версия таблицы.

https://uchim.org/matematika/tablica-kosinusov — uchim.org

Таблица косинусов для 0°-180°

cos(1°)0.9998
cos(2°)0.9994
cos(3°)0.9986
cos(4°)0.9976
cos(5°)0.9962
cos(6°)0.9945
cos(7°)0.9925
cos(8°)0.9903
cos(9°)0.9877
cos(10°)0.9848
cos(11°)0.9816
cos(12°)0.9781
cos(13°)0.9744
cos(14°)0.9703
cos(15°)0.9659
cos(16°)0.9613
cos(17°)0.9563
cos(18°)0.9511
cos(19°)0.9455
cos(20°)0.9397
cos(21°)0.9336
cos(22°)0.9272
cos(23°)0.9205
cos(24°)0.9135
cos(25°)0.9063
cos(26°)0.8988
cos(27°)0.891
cos(28°)0.8829
cos(29°)0.8746
cos(30°)0.866
cos(31°)0.8572
cos(32°)0.848
cos(33°)0.8387
cos(34°)0.829
cos(35°)0.8192
cos(36°)0.809
cos(37°)0.7986
cos(38°)0.788
cos(39°)0.7771
cos(40°)0.766
cos(41°)0.7547
cos(42°)0.7431
cos(43°)0.7314
cos(44°)0.7193
cos(45°)0.7071
cos(46°)0.6947
cos(47°)0.682
cos(48°)0.6691
cos(49°)0.6561
cos(50°)0.6428
cos(51°)0.6293
cos(52°)0.6157
cos(53°)0.6018
cos(54°)0.5878
cos(55°)0.5736
cos(56°)0.5592
cos(57°)0.5446
cos(58°)0.5299
cos(59°)0.515
cos(60°)0.5
cos(61°)0.4848
cos(62°)0.4695
cos(63°)0.454
cos(64°)0.4384
cos(65°)0.4226
cos(66°)0.4067
cos(67°)0.3907
cos(68°)0.3746
cos(69°)0.3584
cos(70°)0.342
cos(71°)0.3256
cos(72°)0.309
cos(73°)0.2924
cos(74°)0.2756
cos(75°)0.2588
cos(76°)0.2419
cos(77°)0.225
cos(78°)0.2079
cos(79°)0.1908
cos(80°)0.1736
cos(81°)0.1564
cos(82°)0.1392
cos(83°)0.1219
cos(84°)0.1045
cos(85°)0.0872
cos(86°)0.0698
cos(87°)0.0523
cos(88°)0.0349
cos(89°)0.0175
cos(90°)0
cos(91°)-0.0175
cos(92°)-0.0349
cos(93°)-0.0523
cos(94°)-0.0698
cos(95°)-0.0872
cos(96°)-0.1045
cos(97°)-0.1219
cos(98°)-0.1392
cos(99°)-0.1564
cos(100°)-0.1736
cos(101°)-0.1908
cos(102°)-0.2079
cos(103°)-0.225
cos(104°)-0.2419
cos(105°)-0.2588
cos(106°)-0.2756
cos(107°)-0.2924
cos(108°)-0.309
cos(109°)-0.3256
cos(110°)-0.342
cos(111°)-0.3584
cos(112°)-0.3746
cos(113°)-0.3907
cos(114°)-0.4067
cos(115°)-0.4226
cos(116°)-0.4384
cos(117°)-0.454
cos(118°)-0.4695
cos(119°)-0.4848
cos(120°)-0.5
cos(121°)-0.515
cos(122°)-0.5299
cos(123°)-0.5446
cos(124°)-0.5592
cos(125°)-0.5736
cos(126°)-0.5878
cos(127°)-0.6018
cos(128°)-0.6157
cos(129°)-0.6293
cos(130°)-0.6428
cos(131°)-0.6561
cos(132°)-0.6691
cos(133°)-0.682
cos(134°)-0.6947
cos(135°)-0.7071
cos(136°)-0.7193
cos(137°)-0.7314
cos(138°)-0.7431
cos(139°)-0.7547
cos(140°)-0.766
cos(141°)-0.7771
cos(142°)-0.788
cos(143°)-0.7986
cos(144°)-0.809
cos(145°)-0.8192
cos(146°)-0.829
cos(147°)-0.8387
cos(148°)-0.848
cos(149°)-0.8572
cos(150°)-0.866
cos(151°)-0.8746
cos(152°)-0.8829
cos(153°)-0.891
cos(154°)-0.8988
cos(155°)-0.9063
cos(156°)-0.9135
cos(157°)-0.9205
cos(158°)-0.9272
cos(159°)-0.9336
cos(160°)-0.9397
cos(161°)-0.9455
cos(162°)-0.9511
cos(163°)-0.9563
cos(164°)-0.9613
cos(165°)-0.9659
cos(166°)-0.9703
cos(167°)-0.9744
cos(168°)-0.9781
cos(169°)-0.9816
cos(170°)-0.9848
cos(171°)-0.9877
cos(172°)-0.9903
cos(173°)-0.9925
cos(174°)-0.9945
cos(175°)-0.9962
cos(176°)-0.9976
cos(177°)-0.9986
cos(178°)-0.9994
cos(179°)-0.9998
cos(180°)-1

Таблица косинусов для 181°-360°

cos(181°)-0.9998
cos(182°)-0.9994
cos(183°)-0.9986
cos(184°)-0.9976
cos(185°)-0.9962
cos(186°)-0.9945
cos(187°)-0.9925
cos(188°)-0.9903
cos(189°)-0.9877
cos(190°)-0.9848
cos(191°)-0.9816
cos(192°)-0.9781
cos(193°)-0.9744
cos(194°)-0.9703
cos(195°)-0.9659
cos(196°)-0.9613
cos(197°)-0.9563
cos(198°)-0.9511
cos(199°)-0.9455
cos(200°)-0.9397
cos(201°)-0.9336
cos(202°)-0.9272
cos(203°)-0.9205
cos(204°)-0.9135
cos(205°)-0.9063
cos(206°)-0.8988
cos(207°)-0.891
cos(208°)-0.8829
cos(209°)-0.8746
cos(210°)-0.866
cos(211°)-0.8572
cos(212°)-0.848
cos(213°)-0.8387
cos(214°)-0.829
cos(215°)-0.8192
cos(216°)-0.809
cos(217°)-0.7986
cos(218°)-0.788
cos(219°)-0.7771
cos(220°)-0.766
cos(221°)-0.7547
cos(222°)-0.7431
cos(223°)-0.7314
cos(224°)-0.7193
cos(225°)-0.7071
cos(226°)-0.6947
cos(227°)-0.682
cos(228°)-0.6691
cos(229°)-0.6561
cos(230°)-0.6428
cos(231°)-0.6293
cos(232°)-0.6157
cos(233°)-0.6018
cos(234°)-0.5878
cos(235°)-0.5736
cos(236°)-0.5592
cos(237°)-0.5446
cos(238°)-0.5299
cos(239°)-0.515
cos(240°)-0.5
cos(241°)-0.4848
cos(242°)-0.4695
cos(243°)-0.454
cos(244°)-0.4384
cos(245°)-0.4226
cos(246°)-0.4067
cos(247°)-0.3907
cos(248°)-0.3746
cos(249°)-0.3584
cos(250°)-0.342
cos(251°)-0.3256
cos(252°)-0.309
cos(253°)-0.2924
cos(254°)-0.2756
cos(255°)-0.2588
cos(256°)-0.2419
cos(257°)-0.225
cos(258°)-0.2079
cos(259°)-0.1908
cos(260°)-0.1736
cos(261°)-0.1564
cos(262°)-0.1392
cos(263°)-0.1219
cos(264°)-0.1045
cos(265°)-0.0872
cos(266°)-0.0698
cos(267°)-0.0523
cos(268°)-0.0349
cos(269°)-0.0175
cos(270°)-0
cos(271°)0.0175
cos(272°)0.0349
cos(273°)0.0523
cos(274°)0.0698
cos(275°)0.0872
cos(276°)0.1045
cos(277°)0.1219
cos(278°)0.1392
cos(279°)0.1564
cos(280°)0.1736
cos(281°)0.1908
cos(282°)0.2079
cos(283°)0.225
cos(284°)0.2419
cos(285°)0.2588
cos(286°)0.2756
cos(287°)0.2924
cos(288°)0.309
cos(289°)0.3256
cos(290°)0.342
cos(291°)0.3584
cos(292°)0.3746
cos(293°)0.3907
cos(294°)0.4067
cos(295°)0.4226
cos(296°)0.4384
cos(297°)0.454
cos(298°)0.4695
cos(299°)0.4848
cos(300°)0.5
cos(301°)0.515
cos(302°)0.5299
cos(303°)0.5446
cos(304°)0.5592
cos(305°)0.5736
cos(306°)0.5878
cos(307°)0.6018
cos(308°)0.6157
cos(309°)0.6293
cos(310°)0.6428
cos(311°)0.6561
cos(312°)0.6691
cos(313°)0.682
cos(314°)0.6947
cos(315°)0.7071
cos(316°)0.7193
cos(317°)0.7314
cos(318°)0.7431
cos(319°)0.7547
cos(320°)0.766
cos(321°)0.7771
cos(322°)0.788
cos(323°)0.7986
cos(324°)0.809
cos(325°)0.8192
cos(326°)0.829
cos(327°)0.8387
cos(328°)0.848
cos(329°)0.8572
cos(330°)0.866
cos(331°)0.8746
cos(332°)0.8829
cos(333°)0.891
cos(334°)0.8988
cos(335°)0.9063
cos(336°)0.9135
cos(337°)0.9205
cos(338°)0.9272
cos(339°)0.9336
cos(340°)0.9397
cos(341°)0.9455
cos(342°)0.9511
cos(343°)0.9563
cos(344°)0.9613
cos(345°)0.9659
cos(346°)0.9703
cos(347°)0.9744
cos(348°)0.9781
cos(349°)0.9816
cos(350°)0.9848
cos(351°)0.9877
cos(352°)0.9903
cos(353°)0.9925
cos(354°)0.9945
cos(355°)0.9962
cos(356°)0.9976
cos(357°)0.9986
cos(358°)0.9994
cos(359°)0.9998
cos(360°)1

Как легко запомнить таблицу косинусов (видео)

Существуют также следующие таблицы тригонометрических функций: таблица синусов, таблица тангенсов и таблица котангенсов.

Всё для учебы » Математика в школе » Таблица косинусов (полная, градусы и значения)

Чтобы добавить страницу в закладки, нажмите Ctrl+D.

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:


Ссылка: https://uchim.org/matematika/tablica-kosinusov

Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):

uchim.org

Таблица косинусов. Косинусы углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов углов.


Техническая информация тут
  • Перевод единиц измерения величин
  • Таблицы числовых значений
  • Алфавиты, номиналы, единицы
  • Математический справочник тут
  • Физический справочник
  • Химический справочник
  • Материалы
  • Рабочие среды
  • Оборудование
  • Инженерное ремесло
  • Инженерные системы
  • Технологии и чертежи
  • Личная жизнь инженеров
  • Калькуляторы
    • Поиск на сайте DPVAПоставщики оборудованияПолезные ссылкиО проектеОбратная связьОтветы на вопросы.Оглавление


    		Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса  / / Таблица косинусов. Косинусы углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов углов.

    Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Версия для печати.

    cos(0°)=cos(360°)=1; точная, но чуть более сложная таблица ( с точностью до 1″) здесь.

    Углы
    1° — 90°

    Углы
    91 ° — 180°

    Углы
    181° — 270°

    Углы
    271 ° — 360°

    Угол

    Cos
    1° cos= 0.9998
    2° cos= 0.9994
    3° cos= 0.9986
    4°
    cos= 0.9976
    5° cos= 0.9962
    6° cos= 0.9945
    7° cos= 0.9925
    8° cos= 0.9903
    9° cos= 0.9877
    10° cos= 0.9848
    11° cos= 0.9816
    12° cos= 0.9781
    13° cos= 0.9744
    14° cos= 0.9703
    15° cos= 0.9659
    16° cos= 0.9613
    17° cos= 0.9563
    18° cos= 0.9511
    19° cos= 0.9455
    20° cos= 0.9397
    21° cos= 0.9336
    22° cos= 0.9272
    23° cos= 0.9205
    24° cos= 0.9135
    25° cos= 0.9063
    26° cos= 0.8988
    27° cos= 0.891
    28° cos= 0.8829
    29° cos= 0.8746
    30° cos= 0.866
    31° cos= 0.8572
    32° cos= 0.848
    33° cos= 0.8387
    34° cos= 0.829
    35°    		 cos= 0.8192
    36° cos= 0.809
    37° cos= 0.7986
    38° cos= 0.788
    39° cos= 0.7771
    40° cos= 0.766
    41° cos= 0.7547
    42° cos= 0.7431
    43° cos= 0.7314
    44° cos= 0.7193
    45°    		 cos= 0.7071
    46°

    dpva.ru

    Таблица КОСИНУСОВ для углов от 0° до 360° градусов

    КОСИНУС (COS α) острого угла в прямоугольном треугольнике равен отношению прилежащего катета к его гипотенузе…

    Малая таблица значений тригонометрических функций (в радианах и градусах)
    α (радианы)0π/6π/4π/3π/2π√3π/22π
    α (градусы)0°30°45°60°90°180°270°360°
    cos α (Косинус)1√3/2√2/21/2
    0    		-101

    …

    Полная таблица косинусов для углов от 0° до  360° 
    Угол в градусах Cos (Косинус)
    0°1
    1°0.9998
    2°0.9994
    3°0.9986
    4°0.9976
    5°0.9962
    6°0.9945
    7°0.9925
    8°0.9903
    9°0.9877
    10°0.9848
    11°0.9816
    12°0.9781
    13°0.9744
    14°0.9703
    15°0.9659
    16°0.9613
    17°0.9563
    18°0.9511
    19°0.9455
    20°0.9397
    21°0.9336
    22°0.9272
    23°0.9205
    24°0.9135
    25°0.9063
    26°0.8988
    27°0.891
    28°0.8829
    29°0.8746
    30°0.866
    31°0.8572
    32°0.848
    33°0.8387
    34°0.829
    35°0.8192
    36°0.809
    37°0.7986
    38°0.788
    39°0.7771
    40°0.766
    41°0.7547
    42°0.7431
    43°0.7314
    44°0.7193
    45°0.7071
    46°0.6947
    47°0.682
    48°0.6691
    49°0.6561
    50°0.6428
    51°0.6293
    52°0.6157
    53°0.6018
    54°0.5878
    55°0.5736
    56°0.5592
    57°0.5446
    58°0.5299
    59°0.515
    60°0.5
    61°0.4848
    62°0.4695
    63°0.454
    64°0.4384
    65°0.4226
    66°0.4067
    67°0.3907
    68°0.3746
    69°0.3584
    70°0.342
    71°0.3256
    72°0.309
    73°0.2924
    74°0.2756
    75°0.2588
    76°0.2419
    77°0.225
    78°0.2079
    79°0.1908
    80°0.1736
    81°0.1564
    82°0.1392
    83°0.1219
    84°0.1045
    85°0.0872
    86°0.0698
    87°0.0523
    88°0.0349
    89°0.0175
    90°0

    …

     

    Таблица косинусов для углов от 91° до 180°
    Уголcos (Косинус)
    91°-0.0175
    92°-0.0349
    93°-0.0523
    94°-0.0698
    95°-0.0872
    96°-0.1045
    97°-0.1219
    98°-0.1392
    99°-0.1564
    100°-0.1736
    101°-0.1908
    102°-0.2079
    103°-0.225
    104°-0.2419
    105°-0.2588
    106°-0.2756
    107°-0.2924
    108°-0.309
    109°-0.3256
    110°-0.342
    111°-0.3584
    112°-0.3746
    113°-0.3907
    114°-0.4067
    115°-0.4226
    116°-0.4384
    117°-0.454
    118°-0.4695
    119°-0.4848
    120°-0.5
    121°-0.515
    122°-0.5299
    123°-0.5446
    124°-0.5592
    125°-0.5736
    126°-0.5878
    127°-0.6018
    128°-0.6157
    129°-0.6293
    130°-0.6428
    131°-0.6561
    132°-0.6691
    133°-0.682
    134°-0.6947
    135°-0.7071
    136°-0.7193
    137°-0.7314
    138°-0.7431
    139°-0.7547
    140°-0.766
    141°-0.7771
    142°-0.788
    143°-0.7986
    144°-0.809
    145°-0.8192
    146°-0.829
    147°-0.8387
    148°-0.848
    149°-0.8572
    150°-0.866
    151°-0.8746
    152°-0.8829
    153°-0.891
    154°-0.8988
    155°-0.9063
    156°-0.9135
    157°-0.9205
    158°-0.9272
    159°-0.9336
    160°-0.9397
    161°-0.9455
    162°-0.9511
    163°-0.9563
    164°-0.9613
    165°-0.9659
    166°-0.9703
    167°-0.9744
    168°-0.9781
    169°-0.9816
    170°-0.9848
    171°-0.9877
    172°-0.9903
    173°-0.9925
    174°-0.9945
    175°-0.9962
    176°-0.9976
    177°-0.9986
    178°-0.9994
    179°-0.9998
    180°-1

    …

    Таблица косинусов для углов от 180° до 270°
    Уголcos (косинус)
    181°-0.9998
    182°-0.9994
    183°-0.9986
    184°-0.9976
    185°-0.9962
    186°-0.9945
    187°-0.9925
    188°-0.9903
    189°-0.9877
    190°-0.9848
    191°-0.9816
    192°-0.9781
    193°-0.9744
    194°-0.9703
    195°-0.9659
    196°-0.9613
    197°-0.9563
    198°-0.9511
    199°-0.9455
    200°-0.9397
    201°-0.9336
    202°-0.9272
    203°-0.9205
    204°-0.9135
    205°-0.9063
    206°-0.8988
    207°-0.891
    208°-0.8829
    209°-0.8746
    210°-0.866
    211°-0.8572
    212°-0.848
    213°-0.8387
    214°-0.829
    215°-0.8192
    216°-0.809
    217°-0.7986
    218°-0.788
    219°-0.7771
    220°-0.766
    221°-0.7547
    222°-0.7431
    223°-0.7314
    224°-0.7193
    225°-0.7071
    226°-0.6947
    227°-0.682
    228°-0.6691
    229°-0.6561
    230°-0.6428
    231°-0.6293
    232°-0.6157
    233°-0.6018
    234°-0.5878
    235°-0.5736
    236°-0.5592
    237°-0.5446
    238°-0.5299
    239°-0.515
    240°-0.5
    241°-0.4848
    242°-0.4695
    243°-0.454
    244°-0.4384
    245°-0.4226
    246°-0.4067
    247°-0.3907
    248°-0.3746
    249°-0.3584
    250°-0.342
    251°-0.3256
    252°-0.309
    253°-0.2924
    254°-0.2756
    255°-0.2588
    256°-0.2419
    257°-0.225
    258°-0.2079
    259°-0.1908
    260°-0.1736
    261°-0.1564
    262°-0.1392
    263°-0.1219
    264°-0.1045
    265°-0.0872
    266°-0.0698
    267°-0.0523
    268°-0.0349
    269°-0.0175
    270°0

    …

    Таблица косинусов для углов от 270° до 360°
    УголCos (Косинус)
    271°0.0175
    272°0.0349
    273°0.0523
    274°0.0698
    275°0.0872
    276°0.1045
    277°0.1219
    278°0.1392
    279°0.1564
    280°0.1736
    281°0.1908
    282°0.2079
    283°0.225
    284°0.2419
    285°0.2588
    286°0.2756
    287°0.2924
    288°0.309
    289°0.3256
    290°0.342
    291°0.3584
    292°0.3746
    293°0.3907
    294°0.4067
    295°0.4226
    296°0.4384
    297°0.454
    298°0.4695
    299°0.4848
    300°0.5
    301°0.515
    302°0.5299
    303°0.5446
    304°0.5592
    305°0.5736
    306°0.5878
    307°0.6018
    308°0.6157
    309°0.6293
    310°0.6428
    311°0.6561
    312°0.6691
    313°0.682
    314°0.6947
    315°0.7071
    316°0.7193
    317°0.7314
    318°0.7431
    319°0.7547
    320°0.766
    321°0.7771
    322°0.788
    323°0.7986
    324°0.809
    325°0.8192
    326°0.829
    327°0.8387
    328°0.848
    329°0.8572
    330°0.866
    331°0.8746
    332°0.8829
    333°0.891
    334°0.8988
    335°0.9063
    336°0.9135
    337°0.9205
    338°0.9272
    339°0.9336
    340°0.9397
    341°0.9455
    342°0.9511
    343°0.9563
    344°0.9613
    345°0.9659
    346°0.9703
    347°0.9744
    348°0.9781
    349°0.9816
    350°0.9848
    351°0.9877
    352°0.9903
    353°0.9925
    354°0.9945
    355°0.9962
    356°0.9976
    357°0.9986
    358°0.9994
    359°0.9998
    360°1

    …

    Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите нужную часть таблицы, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».

    Пример

    Чему равен косинус 30? …

    — Ищем в таблице соответствующее значение. Правильный ответ:  0.866

    Автор: Bill4iam

    kvn201.com.ua

    Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов.

    Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°.
    cos(0°)=cos(360°)=1; точная, но чуть более сложная таблица ( с точностью до 1″) здесь.

    Углы
    1° — 90°

    Углы
    91 ° — 180°

    Углы
    181° — 270°

    Углы
    271 ° — 360°

    Угол

    Cos
    1° cos= 0.9998
    2° cos= 0.9994
    3° cos= 0.9986
    4° cos= 0.9976
    5° cos= 0.9962
    6° cos= 0.9945
    7° cos= 0.9925
    8° cos= 0.9903
    9° cos= 0.9877
    10° cos= 0.9848
    11° cos= 0.9816
    12° cos= 0.9781
    13° cos= 0.9744
    14° cos= 0.9703
    15° cos= 0.9659
    16° cos= 0.9613
    17° cos= 0.9563
    18° cos= 0.9511
    19° cos= 0.9455
    20° cos= 0.9397
    21° cos= 0.9336
    22° cos= 0.9272
    23° cos= 0.9205
    24° cos= 0.9135
    25° cos= 0.9063
    26° cos= 0.8988
    27° cos= 0.891
    28° cos= 0.8829
    29° cos= 0.8746
    30° cos= 0.866
    31° cos= 0.8572
    32° cos= 0.848
    33° cos= 0.8387
    34° cos= 0.829
    35° cos= 0.8192
    36° cos= 0.809
    37° cos= 0.7986
    38° cos= 0.788
    39° cos= 0.7771
    40° cos= 0.766
    41° cos= 0.7547
    42° cos= 0.7431
    43° cos= 0.7314
    44° cos= 0.7193
    45° cos= 0.7071
    46° cos= 0.6947
    47° cos= 0.682
    48° cos= 0.6691
    49° cos= 0.6561
    50° cos= 0.6428
    51° cos= 0.6293
    52° cos= 0.6157
    53° cos= 0.6018
    54° cos= 0.5878
    55° cos= 0.5736
    56° cos= 0.5592
    57° cos= 0.5446
    58° cos= 0.5299
    59° cos= 0.515
    60° cos= 0.5
    61° cos= 0.4848
    62° cos= 0.4695
    63° cos= 0.454
    64° cos= 0.4384
    65° cos= 0.4226
    66° cos= 0.4067
    67° cos= 0.3907
    68° cos= 0.3746
    69° cos= 0.3584
    70° cos= 0.342
    71° cos= 0.3256
    72° cos= 0.309
    73° cos= 0.2924
    74° cos= 0.2756
    75° cos= 0.2588
    76° cos= 0.2419
    77° cos= 0.225
    78° cos= 0.2079
    79° cos= 0.1908
    80° cos= 0.1736
    81° cos= 0.1564
    82° cos= 0.1392
    83° cos= 0.1219
    84° cos= 0.1045
    85° cos= 0.0872
    86° cos= 0.0698
    87° cos= 0.0523
    88° cos= 0.0349
    89° cos= 0.0175
    90° cos= 0

    Угол

    Cos
    91° cos= -0.0175
    92° cos= -0.0349
    93° cos= -0.0523
    94° cos= -0.0698
    95° cos= -0.0872
    96° cos= -0.1045
    97° cos= -0.1219
    98° cos= -0.1392
    99° cos= -0.1564
    100° cos= -0.1736
    101° cos= -0.1908
    102° cos= -0.2079
    103° cos= -0.225
    104° cos= -0.2419
    105° cos= -0.2588
    106° cos= -0.2756
    107° cos= -0.2924
    108° cos= -0.309
    109° cos= -0.3256
    110° cos= -0.342
    111° cos= -0.3584
    112° cos= -0.3746
    113° cos= -0.3907
    114° cos= -0.4067
    115° cos= -0.4226
    116° cos= -0.4384
    117° cos= -0.454
    118° cos= -0.4695
    119° cos= -0.4848
    120° cos= -0.5
    121° cos= -0.515
    122° cos= -0.5299
    123° cos= -0.5446
    124° cos= -0.5592
    125° cos= -0.5736
    126° cos= -0.5878
    127° cos= -0.6018
    128° cos= -0.6157
    129° cos= -0.6293
    130° cos= -0.6428
    131° cos= -0.6561
    132° cos= -0.6691
    133° cos= -0.682
    134° cos= -0.6947
    135° cos= -0.7071
    136° cos= -0.7193
    137° cos= -0.7314
    138° cos= -0.7431
    139° cos= -0.7547
    140° cos= -0.766
    141° cos= -0.7771
    142° cos= -0.788
    143° cos= -0.7986
    144° cos= -0.809
    145° cos= -0.8192
    146° cos= -0.829
    147° cos= -0.8387
    148° cos= -0.848
    149° cos= -0.8572
    150° cos= -0.866
    151° cos= -0.8746
    152° cos= -0.8829
    153° cos= -0.891
    154° cos= -0.8988
    155° cos= -0.9063
    156° cos= -0.9135
    157° cos= -0.9205
    158° cos= -0.9272
    159° cos= -0.9336
    160° cos= -0.9397
    161° cos= -0.9455
    162° cos= -0.9511
    163° cos= -0.9563
    164° cos= -0.9613
    165° cos= -0.9659
    166° cos= -0.9703
    167° cos= -0.9744
    168° cos= -0.9781
    169° cos= -0.9816
    170° cos= -0.9848
    171° cos= -0.9877
    172° cos= -0.9903
    173° cos= -0.9925
    174° cos= -0.9945
    175° cos= -0.9962
    176° cos= -0.9976
    177° cos= -0.9986
    178° cos= -0.9994
    179° cos= -0.9998
    180° cos= -1

    Угол

    Cos
    181° cos=-0.9998
    182° cos=-0.9994
    183° cos=-0.9986
    184° cos=-0.9976
    185° cos=-0.9962
    186° cos=-0.9945
    187° cos=-0.9925
    188° cos=-0.9903
    189° cos=-0.9877
    190° cos=-0.9848
    191° cos=-0.9816
    192° cos=-0.9781
    193° cos=-0.9744
    194° cos=-0.9703
    195° cos=-0.9659
    196° cos=-0.9613
    197° cos=-0.9563
    198° cos=-0.9511
    199° cos=-0.9455
    200° cos=-0.9397
    201° cos=-0.9336
    202° cos=-0.9272
    203° cos=-0.9205
    204° cos=-0.9135
    205° cos=-0.9063
    206° cos=-0.8988
    207° cos=-0.891
    208° cos=-0.8829
    209° cos=-0.8746
    210° cos=-0.866
    211° cos=-0.8572
    212° cos=-0.848
    213° cos=-0.8387
    214° cos=-0.829
    215° cos=-0.8192
    216° cos=-0.809
    217° cos=-0.7986
    218° cos=-0.788
    219° cos=-0.7771
    220° cos=-0.766
    221° cos=-0.7547
    222° cos=-0.7431
    223° cos=-0.7314
    224° cos=-0.7193
    225° cos=-0.7071
    226° cos=-0.6947
    227° cos=-0.682
    228° cos=-0.6691
    229° cos=-0.6561
    230° cos=-0.6428
    231° cos=-0.6293
    232° cos=-0.6157
    233° cos=-0.6018
    234° cos=-0.5878
    235° cos=-0.5736
    236° cos=-0.5592
    237° cos=-0.5446
    238° cos=-0.5299
    239° cos=-0.515
    240° cos=-0.5
    241° cos=-0.4848
    242° cos=-0.4695
    243° cos=-0.454
    244° cos=-0.4384
    245° cos=-0.4226
    246° cos=-0.4067
    247° cos=-0.3907
    248° cos=-0.3746
    249° cos=-0.3584
    250° cos=-0.342
    251° cos=-0.3256
    252° cos=-0.309
    253° cos=-0.2924
    254° cos=-0.2756
    255° cos=-0.2588
    256° cos=-0.2419
    257° cos=-0.225
    258° cos=-0.2079
    259° cos=-0.1908
    260° cos=-0.1736
    261° cos=-0.1564
    262° cos=-0.1392
    263° cos=-0.1219
    264° cos=-0.1045
    265° cos=-0.0872
    266° cos=-0.0698
    267° cos=-0.0523
    268° cos=-0.0349
    269° cos=-0.0175
    270° cos=0

    Угол

    Cos
    271° cos=0.0175
    272° cos=0.0349
    273° cos=0.0523
    274° cos=0.0698
    275° cos=0.0872
    276° cos=0.1045
    277° cos=0.1219
    278° cos=0.1392
    279° cos=0.1564
    280° cos=0.1736
    281° cos=0.1908
    282° cos=0.2079
    283° cos=0.225
    284° cos=0.2419
    285° cos=0.2588
    286° cos=0.2756
    287° cos=0.2924
    288° cos=0.309
    289° cos=0.3256
    290° cos=0.342
    291° cos=0.3584
    292° cos=0.3746
    293° cos=0.3907
    294° cos=0.4067
    295° cos=0.4226
    296° cos=0.4384
    297° cos=0.454
    298° cos=0.4695
    299° cos=0.4848
    300° cos=0.5
    301° cos=0.515
    302° cos=0.5299
    303° cos=0.5446
    304° cos=0.5592
    305° cos=0.5736
    306° cos=0.5878
    307° cos=0.6018
    308° cos=0.6157
    309° cos=0.6293
    310° cos=0.6428
    311° cos=0.6561
    312° cos=0.6691
    313° cos=0.682
    314° cos=0.6947
    315° cos=0.7071
    316° cos=0.7193
    317° cos=0.7314
    318° cos=0.7431
    319° cos=0.7547
    320° cos=0.766
    321° cos=0.7771
    322° cos=0.788
    323° cos=0.7986
    324° cos=0.809
    325° cos=0.8192
    326° cos=0.829
    327° cos=0.8387
    328° cos=0.848
    329° cos=0.8572
    330° cos=0.866
    331° cos=0.8746
    332° cos=0.8829
    333° cos=0.891
    334° cos=0.8988
    335° cos=0.9063
    336° cos=0.9135
    337° cos=0.9205
    338° cos=0.9272
    339° cos=0.9336
    340° cos=0.9397
    341° cos=0.9455
    342° cos=0.9511
    343° cos=0.9563
    344° cos=0.9613
    345° cos=0.9659
    346° cos=0.9703
    347° cos=0.9744
    348° cos=0.9781
    349° cos=0.9816
    350° cos=0.9848
    351° cos=0.9877
    352° cos=0.9903
    353° cos=0.9925
    354° cos=0.9945
    355° cos=0.9962
    356° cos=0.9976
    357° cos=0.9986
    358° cos=0.9994
    359° cos=0.9998
    360° cos=1
    таблица косинусов, косинусы углов в угловых градусах ,cos α, cosinus, сколько составляет косинус?, узнать косинус, косинус градусов

    Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций

    Доп. Инфо:

    1. Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов.
    2. Таблица синусов, она-же косинусов точная.
    3. Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов.
    4. Таблица тангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
    5. Таблица котангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg
    6. Таблица тангенсов, она же котангенсов точная.
    7. Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
    8. Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
    9. Определение и численные соотношения между единицами измерения углов в РФ. Тысячные, угловые градусы, минуты, секунды, радианы, обороты.
    10. Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.

    tehtab.ru

    определения, формулы, примеры, угол поворота

    Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии. 

    Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии. 

    Yandex.RTB R-A-339285-1

     

    Синус, косинус, тангенс и котангенс. Определения

    Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

    Определения тригонометрических функций

    Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.

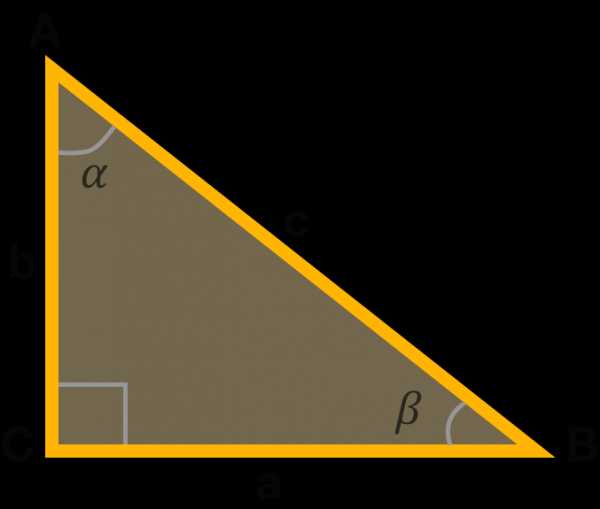
    Косинус угла (cosα) — отношение прилежащего катета к гипотенузе.

    Тангенс угла (tg α) — отношение противолежащего катета к прилежащему.

    Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.

    Данные определения даны для острого угла прямоугольного треугольника!

    Приведем иллюстрацию. 

    В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

    Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

    Важно помнить!

    Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.

    Угол поворота

    Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞. 

    В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

                                                                     

    Начальная точка A с координатами (

    zaochnik.com

    Таблица косинусов | umath.ru

    cos(271°) = 0,017452
    cos(272°) = 0,034899
    cos(273°) = 0,052336
    cos(274°) = 0,069756
    cos(275°) = 0,087156
    cos(276°) = 0,104528
    cos(277°) = 0,121869
    cos(278°) = 0,139173
    cos(279°) = 0,156434
    cos(280°) = 0,173648
    cos(281°) = 0,190809
    cos(282°) = 0,207912
    cos(283°) = 0,224951
    cos(284°) = 0,241922
    cos(285°) = 0,258819
    cos(286°) = 0,275637
    cos(287°) = 0,292372
    cos(288°) = 0,309017
    cos(289°) = 0,325568
    cos(290°) = 0,342020
    cos(291°) = 0,358368
    cos(292°) = 0,374607
    cos(293°) = 0,390731
    cos(294°) = 0,406737
    cos(295°) = 0,422618
    cos(296°) = 0,438371
    cos(297°) = 0,453990
    cos(298°) = 0,469472
    cos(299°) = 0,484810
    cos(300°) = 0,5    		cos(301°) = 0,515038
    cos(302°) = 0,529919
    cos(303°) = 0,544639
    cos(304°) = 0,559193
    cos(305°) = 0,573576
    cos(306°) = 0,587785
    cos(307°) = 0,601815
    cos(308°) = 0,615661
    cos(309°) = 0,629320
    cos(310°) = 0,642788
    cos(311°) = 0,656059
    cos(312°) = 0,669131
    cos(313°) = 0,681998
    cos(314°) = 0,694658
    cos(315°) = 0,707107
    cos(316°) = 0,719340
    cos(317°) = 0,731354
    cos(318°) = 0,743145
    cos(319°) = 0,754710
    cos(320°) = 0,766044
    cos(321°) = 0,777146
    cos(322°) = 0,788011
    cos(323°) = 0,798636
    cos(324°) = 0,809017
    cos(325°) = 0,819152
    cos(326°) = 0,829038
    cos(327°) = 0,838671
    cos(328°) = 0,848048
    cos(329°) = 0,857167
    cos(330°) = 0,866025    		cos(331°) = 0,874620
    cos(332°) = 0,882948
    cos(333°) = 0,891007
    cos(334°) = 0,898794
    cos(335°) = 0,906308
    cos(336°) = 0,913545
    cos(337°) = 0,920505
    cos(338°) = 0,927184
    cos(339°) = 0,933580
    cos(340°) = 0,939693
    cos(341°) = 0,945519
    cos(342°) = 0,951057
    cos(343°) = 0,956305
    cos(344°) = 0,961262
    cos(345°) = 0,965926
    cos(346°) = 0,970296
    cos(347°) = 0,974370
    cos(348°) = 0,978148
    cos(349°) = 0,981627
    cos(350°) = 0,984808
    cos(351°) = 0,987688
    cos(352°) = 0,990268
    cos(353°) = 0,992546
    cos(354°) = 0,994522
    cos(355°) = 0,996195
    cos(356°) = 0,997564
    cos(357°) = 0,998630
    cos(358°) = 0,999391
    cos(359°) = 0,999848
    cos(360°) = 1,0

    umath.ru

    Синус sin x косинус cos x

    Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.

    Геометрическое определение синуса и косинуса




    |BD| —  длина дуги окружности с центром в точке A.
    α — угол, выраженный в радианах.

    Определение
    Синус (sin α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.

    Косинус (cos α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.

    Принятые обозначения

    ;
    ;
    .

    ;
    ;
    .

    График функции синус, y = sin x

    График функции косинус, y = cos x

    Свойства синуса и косинуса

    Периодичность

    Функции   y = sin x   и   y = cos x   периодичны с периодом   2π.

    Четность

    Функция синус – нечетная. Функция косинус – четная.

    Область определения и значений, экстремумы, возрастание, убывание

    Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).

      y = sin x y = cos x
    Область определения и непрерывность – ∞ < x < + ∞ – ∞ < x < + ∞
    Область значений –1 ≤ y ≤ 1 –1 ≤ y ≤ 1
    Возрастание
    Убывание
    Максимумы, y = 1
    Минимумы, y = –1
    Нули, y = 0
    Точки пересечения с осью ординат, x = 0y = 0y = 1

    Основные формулы

    Сумма квадратов синуса и косинуса

    Формулы синуса и косинуса от суммы и разности

    Формулы произведения синусов и косинусов

    Формулы суммы и разности

    Выражение синуса через косинус

    Далее мы полагаем, что – целое число.

    ;
    ;
        ;
        .

    Выражение косинуса через синус

    ;
    ;
        ;
        .

    Выражение через тангенс

    ;     .

    При   , имеем:
    ;     .

    При   :
    ;     .

    Таблица синусов и косинусов, тангенсов и котангенсов

    В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.

    Выражения через комплексные переменные


    ;    

    Формула Эйлера

    Выражения через гиперболические функции

    ;    
    ;    

    Производные

    ;     .     Вывод формул > > >

    Производные n-го порядка:
    ;     .

    Интегралы

    ;    
    См. также раздел Таблица неопределенных интегралов >>>

    Разложения в ряды

        { –∞ < x < +∞ }
        { –∞ < x < +∞ }

    Секанс, косеканс

       

    Обратные функции

    Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.

    Арксинус, arcsin

       
       
       

    Арккосинус, arccos

       
       
       

    Использованная литература:
    И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

    Автор: Олег Одинцов.     Опубликовано:   Изменено:

    1cov-edu.ru

    No related posts.

    0 comments on “Значение косинуса – Таблица косинусов углов от 0° до 360°”

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    2019 © Все права защищены. Карта сайта