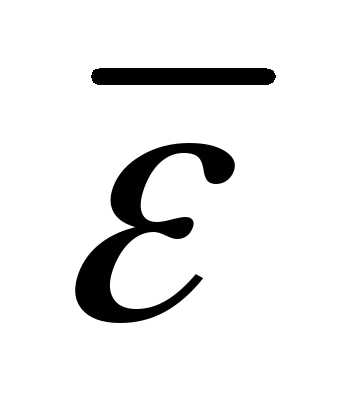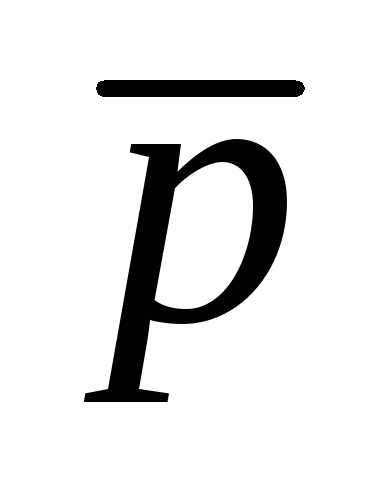Теорема штейнера для цилиндра – —

§ 4.4. Теорема Штейнера

Найдем связь между моментами инерции тела относительно двух различных параллельных осей. Предполагается, что эти оси перпендикулярны к плоскости рисунка и пересекают ее в точках О и А. Ради краткости будем называть эти самые оси также осями О и А. Разобьем мысленно тело на элементарные массы dm. Радиусы – векторы одной из них, проведенные от осей О и А параллельно плоскости рисунка, обозначим r и r , соответственно.

(На рис.4.3. изображен такой случай, когда элементарная масса dm лежит в плоскости рисунка). Тогда r

= r – a , a означает радиус-вектор .Следовательно, r ² = r² + a² – 2(ar). Учитывая, что для твердого тела момент инерции определяется через интеграл , получим

.

Интеграл слева есть момент инерции I_A тела относительно оси А, первый интеграл справа – момент инерции относительно оси О. Последний интеграл можно представить в виде , гдеR_C – радиус-вектор центра масс С тела относительно оси О (точнее, R_C есть слагающая радиуса-вектора центра масс, параллельная плоскости рисунка). Таким образом,

I_A = I_O + ma² – 2m(aR

_C). (4.12)

Допустим, что ось О проходит через центр масс С тела. Тогда R_C = 0, и предыдущая формула упрощается, принимая вид

I_A = I_C + ma². (4.13)

Это важное геометрическое соотношение называется теоремой Штейнера.

Момент инерции тела относительно какой-либо оси равен моменту инерции его относительно параллельной оси, проходящей через центр масс, сложенному с величиной ma², где а – расстояние между осями.

§ 4.5. Вычисление моментов инерции

Момент инерции тела относительно какой –либо оси можно найти вычислением. Если вещество в теле распределено непрерывно, то вычисление момента инерции его сводится к вычислению интеграла

, (4.14)

в котором r – расстояние от элемента массы dm до оси вращения.

Момент инерции тонкого однородного стержня относительно перпендикулярной оси. Пусть ось проходит через конец стержня А (рис.4.4.). Для момента инерции можно написать IA = kml2, где l – длина стержня, k – коэффициент пропорциональности. Центр стержня С является его центром масс. По теореме Штейнера IA = IC + m(l/2)2. Величину IC можно представить как сумму моментов инерции двух стержней, СА и СВ, длина каждого из которых равна l/2, масса m/2, а следовательно, момент

инерции равен 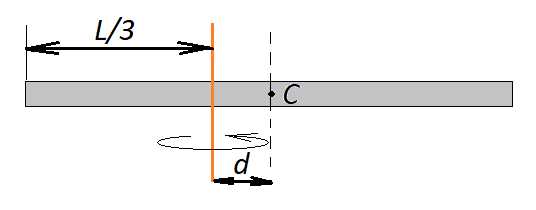. Таким образом,I_C = km(l/2)². Подставляя эти выражения в предыдущую формулу, получим

,

откуда k = 1/3. В результате находим

Момент инерции бесконечно тонкого круглого кольца (окружности). Момент инерции относительно оси Z ( рис.4.5.) равен

I_Z = mR² , (4.17)

где R – радиус кольца. Ввиду симметрии I_X = I_У .

Формула (4.17) очевидно, дает также момент инерции полого однородного цилиндра с бесконечно тонкими стенками относительно его геометрической оси.

Момент инерции бесконечно тонкого диска и сплошного цилиндра. Предполагается, что диск и цилиндр однородны, т.е. вещество распределено в них с постоянной плотностью. Пусть ось Z проходит через центр диска С перпендикулярно к его плоскости (рис.4.6.). Рассмотрим бесконечно тонкое кольцо с внутренним радиусом r и наружным радиусом r + dr. Площадь такого кольца dS = 2rdr. Его момент инерции найдется по формуле (4.17), он равен dI_z = r²dm. Момент инерции всего диска определяется интегралом 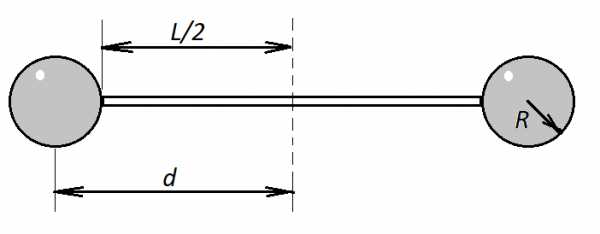Ввиду однородности диска dm =

, где S =  R ² – площадь всего диска. Вводя это выражение под знак интеграла, получим

(4.18)

Формула (4.18) дает также момент инерции однородного сплошного цилиндра относительно его продольной геометрической оси.

В

Z

m(x,y,z)

рис.4.7.

ычисление момента инерции тела относительно оси часто можно упростить, вычислив предварительномомент инерции его относительно точки. Сам по себе момент инерции тела относительно точки не играет никакой роли в динамике. Он является чисто вспомогательным понятием, служащим для упрощения вычислений. Моментом инерции тела относительно точки О называется сумма произведений масс материальных точек, из которых тело состоит, на квадраты их расстояний R до точки О:  = Σ mR

2. В случае непрерывного распределения масс эта сумма сводится к интегралу  = ∫ R²dm. Само собой понятно, что момент θ не следует смешивать с моментом инерции I относительно оси. В случае момента I массы dm умножаются на квадраты расстояний до этой оси, а в случае момента θ – до неподвижной точки.

Y X

Рассмотрим сначала одну материальную точку с массой m и с координатами x, у, z относительно прямоугольной системы координат (рис.4.7.). Квадраты расстояний ее до координатных осей Х, Y, Z равны соответственно у2 + z2, z2 + x2, x2+ у2, а моменты инерции относительно тех же осей IX = m (y2 + z2), IУ = m (z2 + x2), IZ = m (x2 + y2).

Сложим эти три равенства, получим I_X + I_У + I_Z = 2m(x² + у² + z²).

Но х² +у² + z² = R², где R – расстояние точки m от начала координат О. Поэтому

I_X

+ I_У + I_Z = 2θ. (4.19)

Это соотношение справедливо не только для одной материальной точки, но и для произвольного тела, так как тело можно рассматривать как совокупность материальных точек. Таким образом, сумма моментов инерции тела относительно трех взаимно перпендикулярных осей, пересекающихся в одной точке О, равна удвоенному моменту инерции того же тела относительно этой точки.

Момент инерции полого шара с бесконечно тонкими стенками.

Сначала найдем момент инерции θ относительно центра шара. Очевидно, он равен θ = mR². Затем применяем формулу (4.19). Полагая в ней ввиду симметрии I_X = I_У = I_Z = I. В результате находим момент инерции полого шара относительно его диаметра

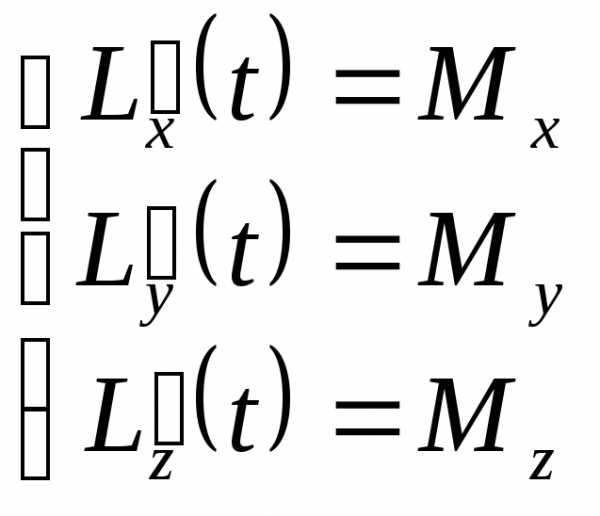. (4.20)

Момент инерции сплошного однородного шара.

Сплошной шар можно рассматривать как совокупность бесконечно тонких сферических слоев с массами dm (см. рис.4.6.). Так как шар по предположению однороден, то 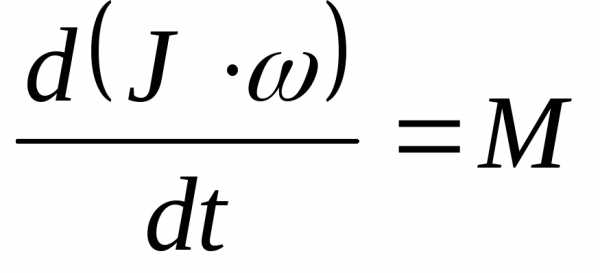, гдеdV = 4 r²dr – объем сферического слоя, а 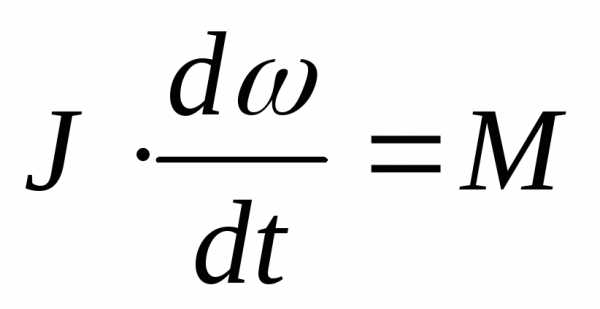– объем всего шара. По формуле (4.20) момент инерции сферического слоя относительно диаметра равен.Интегрируя, получаем момент инерции сплошного шара

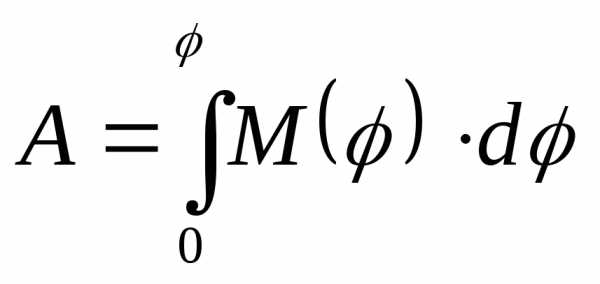. (4.21)

studfiles.net

Теорема Штейнера.

В приведенных примерах оси проходят через центр инерции тела. Мо­мент инерции относительно других осей вращения определяется при по­мощи теоремы Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции Jc относительно параллельной оси, проходящей через центр инерции тела, и величины произведения массы тела на квадрат расстояния между ними. где m масса тела, а — расстояние от центра инерции тела до выбранной оси вращения,т.е.

, где m — масса тела, а — расстояние от центра

инерции тела до выбранной оси вращения.

Покажем на одном примере применение теоремы Штейнера. Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню. Прямое вычисление сводится к тому же ин­тегралу (*),но взятому в других пределах:

Расстояние до оси, проходящей через центр масс, равно а = ℓ/2.По теореме Штейнера получаем тот же результат.

.

§22.Основной закон динамики вращательного движения.

Формулировка закона: Скорость изменения момента импульса относительно полюса равна главному моменту силы относительно того же полюса, т.е.

.

В проекциях на оси координат: .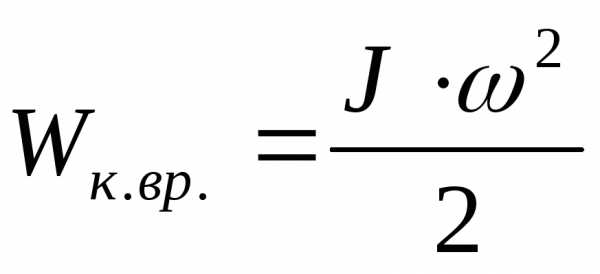

Если вращение тела происходит относительно неподвижной оси, то основной закон динамики вращательного движения примет вид: . В данном случае момент импульса легко выразить через угловую скорость и момент инерции тела относительно рассматриваемой оси:. Тогда основной закон динамики вращательного движения примет вид: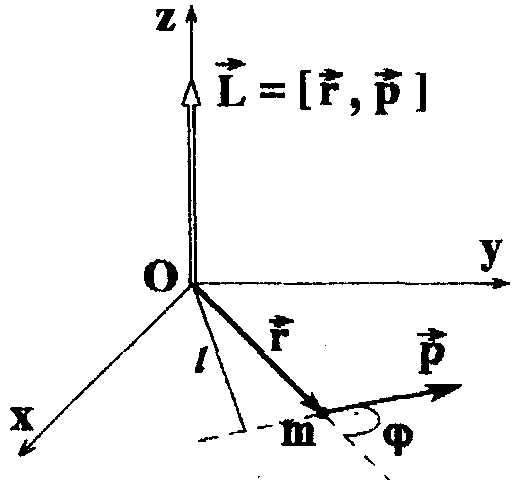. Если тело не рассыпается и не деформируется, то

, вследствие чего 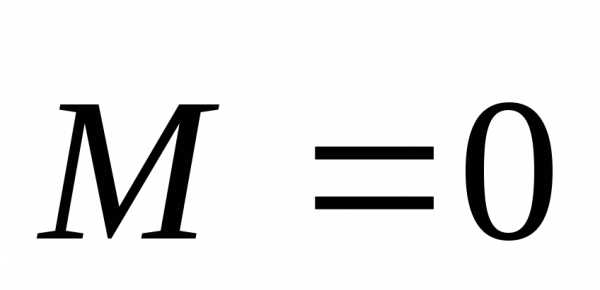. Если ко всему, тои, оно равно:.

Элементарная работа, совершаемая моментом силы, при вращательном движении относительно неподвижной оси вычисляется по формуле: (*). Полная работа. Если, то.

На основании формулы (*), получим выражение для кинетической энергии вращательного движения твёрдого тела относительно неподвижной оси. Т.к. , то. После интегрирования, получим окончательный результат для кинетической энергии вращательного движения относительно неподвижной оси.

§23.Закон сохранения момента импульса.

Как уже указывалось, законы сохранения энергии и импульса связаны с однородностью времени и пространства, соответственно. Но у трехмер­ного пространства, в отличие от одномерного времени, имеется еще одна симметрия. Пространство само по себе изотропно,в нем нет выделен­ных направлений. С этой симметрией связанзакон сохранениямомента импульса.Эта связь проявляется в том, что момент количества движе­ния, является одной из основных величин, описывающих вращательное движение.

По определению момент импульса отдельной частицы равен .

Направление вектора Lопределяется по правилу буравчика (штопора), а его величина равна L = r p sin ,где

  угол между направлениями радиус-вектора частицы и ее импульса. Величина ℓ = r sinравна рас­стоянию от начала координатОдо прямой, вдоль которой направлен импульс частицы. Эта величина называетсяплечом импульса.ВекторLзависит от выбора начала координат, поэтому говоря о нем, обычно указывают: «момент импульса относительно точкиО«.

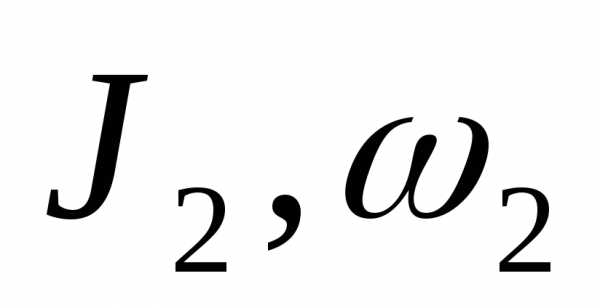
Рассмотрим производную по времени от момента импульса:

.

Первое слагаемое равно нулю, т.к. . Во втором слагаемом, согласно второму закону Ньютона, производную по импульсу можно заменить на действующую на тело силу. Векторное произведение радиус-вектора на силу называетсямоментом силыотносительно точкиО: .

Направление момента силы определяется тем же правилом буравчика. Его величина М = r F sin ,где

•  угол между радиус-вектором и силой. Аналогично тому, как это было сделано выше, определяется и плечо силы

ℓ = r sin — расстояние от точкиОдо линии действия силы. В итоге получаем уравнение движения для момента импульса частицы:.

По форме уравнение аналогично второму закону Ньютона: вместо им­пульса частицы стоит момент импульса, а вместо силы —момент силы. Если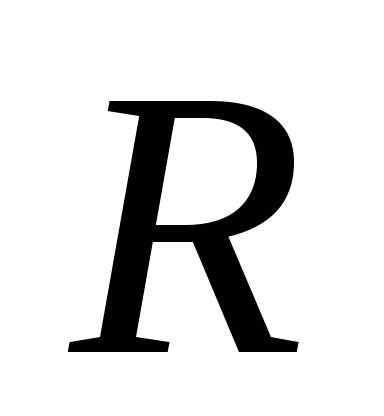,то,т.е. момент импульса постоянен в отсутствие внешних моментов сил.

Формулировка закона: Момент импульса замкнутой системы относительно полюса не изменяется с течением времени.

В частном случае вращения относительно неподвижной оси, имеем: , где

начальные момент инерции и угловая скорость тела относительно рассматриваемой оси, а

конечные момент инерции и угловая скорость тела относительно рассматриваемой оси.

Закон сохранения полной механической энергии с учётом вращательного движения: полная механическая энергия консервативной системы постоянна: .

Пример: Найти скорость системы при прохождении расстояния h.

Дано: m, M, h. Найти: V — ?

studfiles.net

Глава 3. Динамика вращательного движения

§ 3.1 Момент силы. Момент импульса.

Пусть некоторое тело под действием силы F, приложенной в точке А, приходит во вращение вокруг оси ОО’ (рис. 1.14).

Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы. Произведение силы на плечо определяет модуль мо­мента силы относительно точки О:

М = Fp=Frsinα.

Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы:

(3.1) Единица момента силы — ньютон-метр (Н • м).

Направление М можно найти с помощью правила правого винта.

Моментом импульса частицы называется векторное произведение радиус-вектора частицы на её импульс:

или в скалярном виде L = гPsinα

Эта величины векторная и совпадает по направлению с векторами ω.

§ 3.2 Момент инерции. Теорема Штейнера

Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, назы­ваемая моментом инерции тела относительно оси вращения.

Моментом инерции материальной точки относительно оси враще­ния называют произведение массы этой точки на квадрат расстояния её от оси:

I_i=m_ir_i² (3.2)

Момент инерции тела относительно оси вращения называют сумму мо­ментов инерции материальных точек, из которых состоит это тело:

(3.3)

В общем случае, если тело сплошное и представляет собой совокупность точек с малыми массами dm, момент инерции определяется интегрированием:

(3.4)

[r — расстояние от оси вращения до элемента массой dm].

Если тело однородно и его плотность , то момент инерции тела

(3.5)

Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.

Наиболее просто определяется момент инерции тел, имеющих правильную геометрическую форму и равномерное распределение массы по объему.

• Момент инерции однородного стержня относительно оси, проходящей через центр инерции и перпендикулярной стержню

(3.6)

• Момент инерции однородного цилиндра относительно оси, перпен­дикулярной его основанию и проходящей через центр инерции,

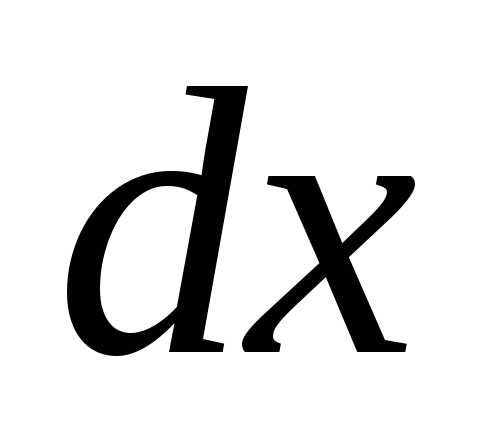(3.7)

• Момент инерции тонкостенного цилиндра или обруча относительно оси, перпендикулярной плоскости его основания и проходящей через его центр,

(3.8)

(3.9)

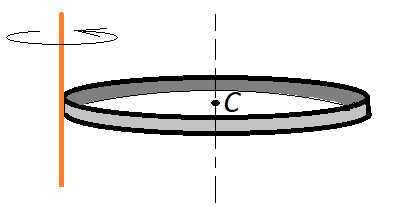
Рассмотрим пример. Определим момент инерции диска относительно оси, проходящей через центр инерции и перпендикулярной плоско­сти вращения. Масса диска — m, радиус — R.

Площадь кольца (рис. 3.2), заключенного между

r и r + dr, равна dS = 2πr·dr . Площадь диска S = πR².

Следовательно, . Тогда

или

Согласно

(3.10)

Приведенные формулы для моментов инерции тел даны при условии, что ось вращения проходит через центр инерции. Чтобы определить моменты инерции тела относительно произвольной оси, следует воспользоваться теоремой Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:

(3.11)

[m — масса тела, d — расстояние от центра масс до выбранной оси вра­щения (расстояние между осями)].

Единица момента инерции — килограмм-метр в квадрате (кг· м²).

Так, момент инерции однородного стержня относительно оси, проходящей через его конец, по теореме Штейнера равен

(3.12)

studfiles.net

Теорема Гюйгенса-Штейнера

Найдем связь между моментами инерции относительно двух различных параллельных осей. Она устанавливается теоремой Гюйгенса-Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно оси проходящей через центр масс, параллельно данной и произведения массы на квадрат расстояния между осями.

Докажем эту теорему. Пусть S сечение тела. Будем предполагать, что центр масс находится в точке О и оси, проходящие через точки О и А, перпендикулярны к рисунку. Мысленно разобьем тело на элементарные массы . Момент инерции тела найдем, проинтегрировав по всем элементарным массам. Радиус-вектор элементарной массы относительно оси А , где — ее радиус-вектор относительно оси О, — радиус-вектор , его модуль равен расстоянию между осями. Таким образом

. (5.11)

Умножая обе части равенства (5.11) на и интегрируя по всему объему, получим:

. (5.12)

Так как ось О проходит через центр масс, последний интеграл в (5.12) обращается в нуль.

.

Интеграл слева дает момент инерции относительно оси А, первый интеграл справа — момент инерции относительно оси О, второй интеграл справа дает полную массу тела. Откуда

. (5.13)

Это и есть аналитическое выражение теоремы Гюйгенса-Штейнера.

Примеры вычисления моментов инерции

1. Определим момент инерции тонкого однородного стержня длиною L и массой m относительно оси, проходящей через один из его концов. (см.рис.)

Направим ось Х вдоль стержня. Стержень будем считать тонким. Выделим элементарную массу , имеющую длинуи расположенную на расстоянии Х от оси вращения. Причем, поскольку стержень однородный масса этого элемента

Тогда

Проинтегрировав по всей длине стержня получим:

Момент инерции этого же стержня относительно оси, проходящей через центр масс определяется как:

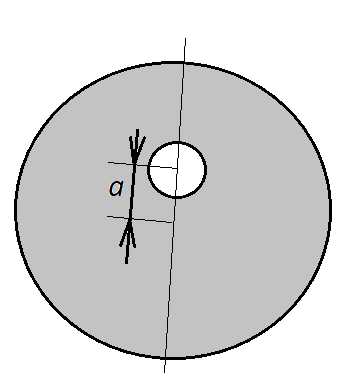
2. Определим момент инерции однородного диска, расположенного

перпендикулярно оси вращения, проходящей через центр масс. Радиус диска R, масса – m. Используя симметрию задачи, разобьем диск на элементарные массы в виде тонких колец радиусом r и шириной . (см.рис.)

Масса этого элемента , где— площадь поперечного сечения диска или поверхностная плотность диска,- площадь кольца. Тогда. Интегрируя в пределах от 0 доR, получим:

3. Тонкое однородное кольцо, расположенное перпендикулярно оси вращения, проходящей через центр масс. (см.рис.)

Выделим элементарную массу , длиной, тогда, здесь— линейная плотность массы, то есть масса

приходящаяся на единицу длины. Так как все элементарные массы расположены на одинаковом расстоянии от оси вращения (кольцо тонкое)

studfiles.net

Теорема Штейнера.

Имеется тело массой М, разбиваем его на N частей массой — каждая. Имеется 2 оси О и О^/. Вычислим момент инерции относительно оси О.

пусть ось проходит через центр масс и тогда

— теорема Штейнера

Момент инерции тела относительно производной оси О равен сумме моментов инерции этого же тела относительно оси, проходящей через центр масс и произведения массы тела на квадрат расстояния между осями.

Основное уравнение динамики вращательного движения.

Рассмотрим вращающееся вокруг оси Z твердое тело. Выделим массу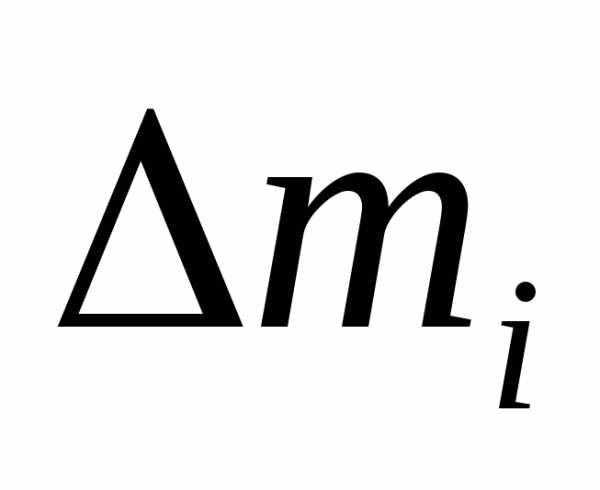;— импульс i-той части тела;— момент импульса i-той части

.

Для тела вращающегося вокруг оси симметрии

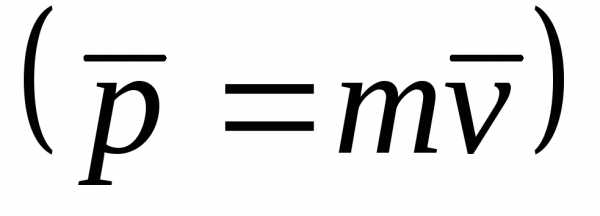
Дифференцируем левую и правую часть этого соотношения по t.

— результирующий момент сил, действующий на тело.

Данное соотношение является основным уравнением динамики вращающегося движения твердого тела и является аналогом 2-ого закона Ньютона

Поступательное движение	Вращательное движение
m	I

Кинетическая энергия вращающегося твердого тела.

Вопросы для самоконтроля

1. Что представляет момент импульса системы? Сформулируйте закон сохранения момента импульса?

2. Что называется моментом инерции тела относительно оси?

3. Что называется моментом инерции материальной точки? Моментом инерции твердого тела?

4. Сформулируйте теорему Штейнера.

5. В чем заключается основное уравнение вращательного движения твердого тела?

6. Как определяется кинетическая энергия при вращательном движении?

СПИСОК ЛИТЕРАТУРЫ

Основная

1. Детлаф, А.А. Курс физики учеб. пособие / А.А. Детлаф, Б.М. Яворский.-7-е изд. Стер.-М. : ИЦ «Академия».-2008.-720 с.

2. Савельев, И.В. Курс физики: в 3т.: Т.1: Механика .Молекулярная физика : учеб.пособие / И.В. Савельев.-4-е изд. стер. – СПб.; М. Краснодар: Лань.-2008.-352 с.

3. Трофимова, Т.И. курс физики: учеб. пособие/ Т.И. Трофимова.- 15-е изд., стер.- М.: ИЦ «Академия», 2007.-560 с.

Дополнительная

1. Фейнман, Р. Фейнмановскиелекции по физике /Р. Фейнман, Р. Лейтон, М. Сэндс. – М.: Мир.

Т.1. Современная наука о природе. Законы механики. – 1965. –232 с.

Т. 2. Пространство, время, движение. – 1965. – 168 с.

Т. 3. Излучение. Волны. Кванты. – 1965. – 240 с.

2. Берклеевский курс физики. Т.1,2,3. – М.: Наука, 1984

Т. 1. Китель, Ч. Механика / Ч. Китель, У. Найт, М. Рудерман. – 480 с.

Т. 2. Парселл, Э. Электричество и магнетизм / Э. Парселл. – 448 с.

Т. 3. Крауфорд, Ф. Волны / Ф. Крауфорд – 512 с.

3. Фриш, С.Э. Курс общей физики: в 3 т.: учеб. / С.Э. Фриш, А.В. Тиморева.- СПб.: М.; Краснодар: Лань.-2009.

Т. 1. Физические основы механики. Молекулярная физика. Колебания и волны: учебник — 480 с.

Т.2: Электрические и электромагнитные явления: учебник. – 518 с.

Т. 3. Оптика. Атомная физика : учебник– 656 с.

studfiles.net

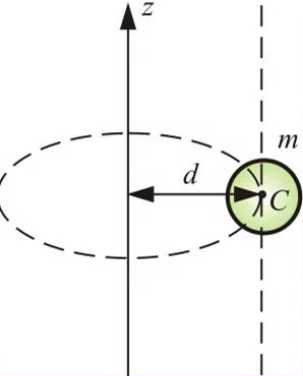
3. Теорема штейнера

Любое из тел может быть расположено на различных расстояниях от оси вращения стола (фиксация расстояний с шагом 20 мм). Для проверки теоремы Штейнера измерить моменты инерции стола с двумя цилиндрами массой m=1011г на различных расстояниях от оси вращения стола. Результаты записать в предложенную таблицу.

Таблица 6.1

Расстояние цилиндров от оси r, см	4		6		8		10
Период колебаний стола Т, мс
Момент инерции I = I0T2/T02 , г м2
Контроль: I/r2, г

; ;j = 1,2,3.

r₁ = 4 см; r₂ = 6 см; r₃ = 8 см; r₄ = 10 см.

4. Измерение момента инерции с помощью пружин известной жесткости (эксперименты на шкиве стойки стола)

Для получения колебательной системы через шкив радиуса R стойки перекидывается длинная нить, концы которой посредством двух пружин прикрепляются к зацепам на основании стойки.

k_пар = Н/м.

Момент инерции не нагруженного шкива

Период колебаний шкива Т_шк = мс при R = мм;

Момент инерции шкива I_шк = k_парR²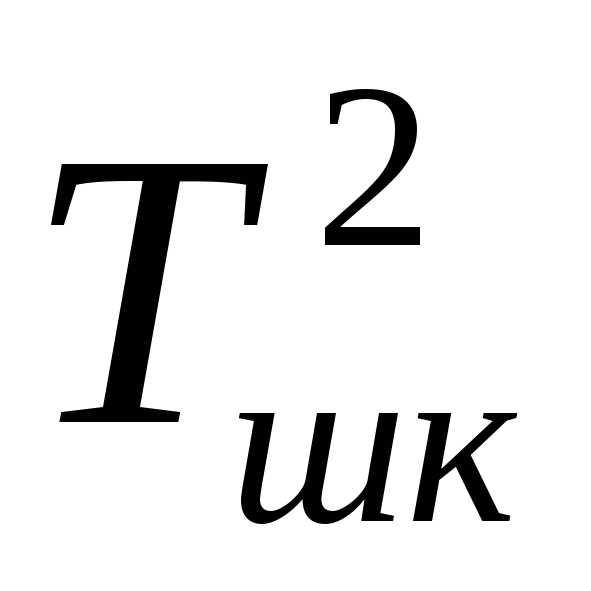/(4²) = г м².

Момент инерции стержня

L = мм, m = г

Период колебаний шкива со стержнем

Т = мс.

Момент инерции шкива со стержнем

I = k_парR²Т²/(4²) = г м².

Момент инерции стержня:

Расчётное значение:

I_ст= mL²/12 = г м².

По результатам измерений

I_cт = I – I_шк = г м².

Сделать сравнительный анализ с методом п. 2.

Лабораторная работа № 7 определение отношения Ср/Сv для воздуха по клеману-дезорму

Цель работы: познакомиться с одним из методов определения С_р/С_v.

Приборы и принадлежности: установка ЛКТ-5, шланг с грушей-помпой, переходной шланг, мембранный манометр, емкость с водой.

Краткие теоретические сведения

Состояние газа характеризуется тремя величинами – параметрами состояния: давлением Р, объемом V, и температурой Т. Уравнение связывающее эти величины, называется уравнением состояния газа. Для идеального газа уравнением состояния является уравнение Менделеева – Клапейрона:

, (7.1)

где m – масса газа,  — масса одного моля, R – универсальная газовая постоянная. Для одного моля:

. (7.2)

Теплоёмкостью тела называется количество теплоты, которое нужно сообщить телу, чтобы изменить его температуру на один градус:

(Дж/К).

Здесь dТ – изменение температуры тела при сообщении ему количества теплоты dQ.

Теплоёмкость единицы массы тела называется удельной теплоёмкостью:

(Дж/кг К).

Теплоёмкость одного моля вещества называется молярной теплоёмкостью:

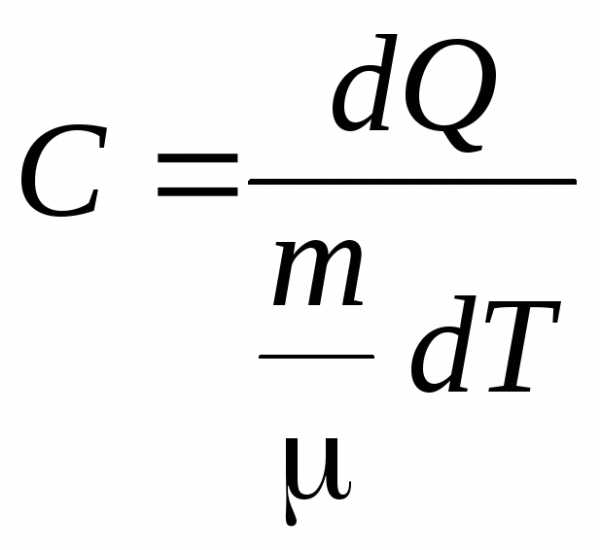(Дж/моль К). (7.3)

Величина теплоёмкости газа зависит от условий его нагревания, т.е. от того, нагревается ли газ при постоянном объёме (обозначим молярную теплоёмкость в этом случае через С_v) или процесс нагревания происходит при постоянном давлении (С_р). С_v и С_р связаны между собой. Эту связь можно получить, пользуясь уравнением состояния (7.2), написанным для одного моля газа, и первым началом термодинамики, которое можно сформулировать следующим образом: количество теплоты dQ, переданное системе, затрачивается на увеличение её внутренней энергии dU и на работу dA, совершаемую системой над внешними телами:

dQ = dU + dA. (7.4)

Элементарная работа

dA = P dV. (7.5)

Исходя из определения молярной теплоёмкости (7.3):

.

При изохорическом процессе V = const, следовательно, dV = 0 и dA = 0 (см. формулу (7.5)), и поэтому

С_v = . (7.6)

При изобарическом процессе Р = const, следовательно,

. (7.7)

Из уравнения состояния газа (7.2) получаем

Р dV + V dP = R dT.

Но dP = 0 (т.к. Р = const), а поэтому P dV = R dT.

Учитывая это равенство и заменяя dU через С_v dT, из выражения (7.7) получим

С_р = С_v + R.

Таким образом С_р > C_v: при нагревании при постоянном давлении тепло, сообщённое газу, идёт не только на изменение его внутренней энергии, но и на совершение газом работы.

Важную роль в термодинамике играет величина  = С_р/С_v , в частности,  входит в уравнение Пуассона, описывающее адиабатический процесс, т.е. процесс, протекающий без теплообмена с окружающей средой (dQ = 0). Уравнение Пуассона в переменных (Р,V) имеет вид:

РV^ = const.

Из первого начала термодинамики (7.4) для адиабатического процесса следует:

dU + dA = 0,

откуда

dA =  dU =  C_vdT,

т.е. работа в этом случае совершается за счёт изменения запаса внутренней энергии газа.

studfiles.net

3. Теорема штейнера

Любое из тел может быть расположено на различных расстояниях от оси вращения стола (фиксация расстояний с шагом 20 мм). Для проверки теоремы Штейнера измерить моменты инерции стола с двумя цилиндрами массой m=1011г на различных расстояниях от оси вращения стола. Результаты записать в предложенную таблицу.

Таблица 6.1

Расстояние цилиндров от оси r, см	4		6		8		10
Период колебаний стола Т, мс
Момент инерции I = I0T2/T02 , г м2
Контроль: I/r2, г

; ;j = 1,2,3.

r₁ = 4 см; r₂ = 6 см; r₃ = 8 см; r₄ = 10 см.

4. Измерение момента инерции с помощью пружин известной жесткости (эксперименты на шкиве стойки стола)

Для получения колебательной системы через шкив радиуса R стойки перекидывается длинная нить, концы которой посредством двух пружин прикрепляются к зацепам на основании стойки.

k_пар = Н/м.

Момент инерции не нагруженного шкива

Период колебаний шкива Т_шк = мс при R = мм;

Момент инерции шкива I_шк = k_парR²/(4²) = г м².

Момент инерции стержня

L = мм, m = г

Период колебаний шкива со стержнем

Т = мс.

Момент инерции шкива со стержнем

I = k_парR²Т²/(4²) = г м².

Момент инерции стержня:

Расчётное значение:

I_ст= mL²/12 = г м².

По результатам измерений

I_cт = I – I_шк = г м².

Сделать сравнительный анализ с методом п. 2.

Лабораторная работа № 7 определение отношения Ср/Сv для воздуха по клеману-дезорму

Цель работы: познакомиться с одним из методов определения С_р/С_v.

Приборы и принадлежности: установка ЛКТ-5, шланг с грушей-помпой, переходной шланг, мембранный манометр, емкость с водой.

Краткие теоретические сведения

Состояние газа характеризуется тремя величинами – параметрами состояния: давлением Р, объемом V, и температурой Т. Уравнение связывающее эти величины, называется уравнением состояния газа. Для идеального газа уравнением состояния является уравнение Менделеева – Клапейрона:

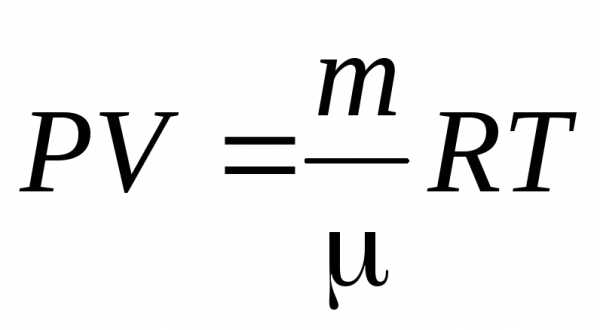, (7.1)

где m – масса газа,  — масса одного моля, R – универсальная газовая постоянная. Для одного моля:

. (7.2)

Теплоёмкостью тела называется количество теплоты, которое нужно сообщить телу, чтобы изменить его температуру на один градус:

(Дж/К).

Здесь dТ – изменение температуры тела при сообщении ему количества теплоты dQ.

Теплоёмкость единицы массы тела называется удельной теплоёмкостью:

(Дж/кг К).

Теплоёмкость одного моля вещества называется молярной теплоёмкостью:

(Дж/моль К). (7.3)

Величина теплоёмкости газа зависит от условий его нагревания, т.е. от того, нагревается ли газ при постоянном объёме (обозначим молярную теплоёмкость в этом случае через С_v) или процесс нагревания происходит при постоянном давлении (С_р). С_v и С_р связаны между собой. Эту связь можно получить, пользуясь уравнением состояния (7.2), написанным для одного моля газа, и первым началом термодинамики, которое можно сформулировать следующим образом: количество теплоты dQ, переданное системе, затрачивается на увеличение её внутренней энергии dU и на работу dA, совершаемую системой над внешними телами:

dQ = dU + dA. (7.4)

Элементарная работа

dA = P dV. (7.5)

Исходя из определения молярной теплоёмкости (7.3):

.

При изохорическом процессе V = const, следовательно, dV = 0 и dA = 0 (см. формулу (7.5)), и поэтому

С_v = . (7.6)

При изобарическом процессе Р = const, следовательно,

. (7.7)

Из уравнения состояния газа (7.2) получаем

Р dV + V dP = R dT.

Но dP = 0 (т.к. Р = const), а поэтому P dV = R dT.

Учитывая это равенство и заменяя dU через С_v dT, из выражения (7.7) получим

С_р = С_v + R.

Таким образом С_р > C_v: при нагревании при постоянном давлении тепло, сообщённое газу, идёт не только на изменение его внутренней энергии, но и на совершение газом работы.

Важную роль в термодинамике играет величина  = С_р/С_v , в частности,  входит в уравнение Пуассона, описывающее адиабатический процесс, т.е. процесс, протекающий без теплообмена с окружающей средой (dQ = 0). Уравнение Пуассона в переменных (Р,V) имеет вид:

РV^ = const.

Из первого начала термодинамики (7.4) для адиабатического процесса следует:

dU + dA = 0,

откуда

dA =  dU =  C_vdT,

т.е. работа в этом случае совершается за счёт изменения запаса внутренней энергии газа.

studfiles.net