Схемы выпрямления: разновидности, схемы, формулы и функции расчета

Что такое трехфазное выпрямление, принцип работы и схемы

В данной статье поговорим про трехфазный выпрямитель (контролируемый и неконтролируемый). Подробно опишем его принцип работы, а так же рассмотрим схемы полуволнового и полноволнового трехфазного выпрямителя.

Описание

В предыдущей статье мы видели, что процесс преобразования входного источника переменного тока в постоянный источник постоянного тока называется выпрямлением, причем наиболее популярные схемы, используемые для выполнения этого процесса выпрямления, основаны на полупроводниковых диодах. На самом деле выпрямление переменного напряжения является одним из самых популярных применений диодов, так как диоды недорогие, небольшие и надежные, что позволяет нам создавать многочисленные типы выпрямительных цепей, используя либо индивидуально подключенные диоды, либо всего один встроенный мостовой выпрямительный модуль.

Однофазные источники питания, такие как в домах и офисах, обычно имеют фазо-нейтральное напряжение 120 или 240 Врм, также называемое линией нейтрали (LN), и номиналом постоянного напряжения и частоты, которые создают переменное напряжение или ток в форму синусоидальной формы волны с сокращением «AC».

Трехфазные выпрямители, также известные как многофазные выпрямительные схемы, аналогичны предыдущим однофазным выпрямителям. Разница на этот раз в том, что мы используем три однофазных источника питания, соединенных вместе, которые были произведены одним единственным трехфазным генератором.

Преимущество здесь состоит в том, что трехфазные выпрямительные схемы могут использоваться для питания многих промышленных устройств, таких как управление двигателем или зарядка аккумулятора, которые требуют более высоких требований к мощности, чем однофазная выпрямительная схема.

Трехфазные источники питания развивают эту идею на один шаг вперед, комбинируя вместе три напряжения переменного тока одинаковой частоты и амплитуды, причем каждое напряжение переменного тока называется «фазой». Эти три фазы имеют сдвиг по фазе на 120 электрических градусов друг от друга, создавая последовательность фаз или поворот фазы на 360 ^o  ÷ 3 = 120 ^o, как показано.

Трехфазная форма волны

Преимущество здесь заключается в том, что трехфазный источник переменного тока (AC) может использоваться для подачи электроэнергии непосредственно на сбалансированные нагрузки и выпрямители. Поскольку трехфазный источник питания имеет фиксированное напряжение и частоту, он может использоваться в схеме выпрямления для получения энергии постоянного тока с постоянным напряжением, которая затем может быть отфильтрована, что приводит к выходному напряжению постоянного тока с меньшей пульсацией по сравнению с однофазной выпрямительной схемой.

Принцип работы

Видя, что 3-фазный источник питания — это просто три однофазные комбинации, мы можем использовать это многофазное свойство для создания 3-фазных цепей выпрямителя.

Как и в случае однофазного выпрямления, в трехфазном выпрямлении используются диоды, тиристоры, транзисторы или преобразователи для создания полуволновых, двухволновых, неконтролируемых и полностью управляемых выпрямительных цепей, преобразующих данный трехфазный источник питания в постоянный выходной уровень постоянного тока. В большинстве случаев трехфазный выпрямитель подается напрямую от электросети или от трехфазного трансформатора, если подключенная нагрузка требует другого уровня выхода постоянного тока.

Как и в случае предыдущего однофазного выпрямителя, наиболее простой трехфазной выпрямительной схемой является схема неуправляемого полуволнового выпрямителя, в которой используются три полупроводниковых диода, по одному диоду на фазу, как показано ниже.

Полуволновое трехфазное выпрямление

Так как же работает эта трехфазная полуволновая выпрямительная схема? Анод каждого диода подключен к одной фазе источника напряжения с катодами всех трех диодов, соединенных вместе в одну положительную точку, эффективно создавая схему диода типа «ИЛИ». Эта общая точка становится положительной (+) клеммой нагрузки, в то время как отрицательная (-) клемма нагрузки подключается к нейтрали (N) источника питания.

Предполагая, что чередование фаз красно-желто-синее (V _A  — V _B  — V _C ) и красная фаза (V _A ) начинается при 0 ^o . Первым проводящим диодом будет диод 1 ( D ₁  ), так как он будет иметь более положительное напряжение на своем аноде, чем диоды D ₂или D ₃ . Таким образом, диод D ₁ проводит для положительного полупериода V _A, в то время как D ₂ и D ₃ находятся в их обратном смещенном состоянии. Нейтральный провод обеспечивает обратный путь тока нагрузки к источнику питания.

Через 120 электрических градусов диод 2 (D ₂ ) начинает проводить для положительного полупериода V _B (желтая фаза). Теперь его анод становится более положительным, чем диоды D ₁ и D _3, которые оба «выключены», потому что они смещены в обратном направлении. Аналогичным образом , 120 ^о дальнейшем V _С(синия фаза) начинает возрастать поворачивая «ON» диод 3 (D ₃ ) в качестве анода становится более положительным, таким образом, превращая «OFF» диоды D ₁ и D ₂ .

Затем мы можем видеть, что для трехфазного выпрямления, какой бы диод не имел более положительного напряжения на своем аноде, по сравнению с двумя другими диодами, он автоматически начнет проводить, тем самым давая схему проводимости: D ₁ D ₂ D _3, как показано.

Из приведенных выше сигналов для резистивной нагрузки видно, что для полуволнового выпрямителя каждый диод пропускает ток в течение одной трети каждого цикла, а выходной сигнал в три раза больше входной частоты источника переменного тока. Следовательно, в данном цикле имеется три пика напряжения, поэтому за счет увеличения количества фаз от однофазного до трехфазного источника улучшается выпрямление источника питания, то есть выходное напряжение постоянного тока становится более плавным.

Для трехфазного полуволнового выпрямителя напряжения питания V _A V _B и V _C сбалансированы, но с разностью фаз 120 ^o, что дает:

V _A  = V _P * sin (ωt — 0 ^o )

V _B  = V _P * sin (ωt — 120 ^o )

V _C  = V _P * sin (ωt — 240 ^o )

Таким образом, среднее значение постоянного тока формы волны выходного напряжения от трехфазного полуволнового выпрямителя задается как:

Поскольку напряжение обеспечивает пиковое напряжение V _P равно V _RMS * 1,414, из этого следует, что V _P равно V _P / 1,414, что дает 0,707 * V _P , поэтому среднее выходное напряжение постоянного тока выпрямителя можно выразить через среднеквадратичное фазное напряжение, дающее:

Полноволновое трехфазное выпрямление

В двухволновой трехфазной неконтролируемой мостовой выпрямительной схеме используются шесть диодов, по два на фазу аналогично однофазному мостовому выпрямителю. Трехфазный двухполупериодный выпрямитель получается с использованием двух схем полуволнового выпрямителя. Преимущество здесь состоит в том, что схема производит более низкий пульсационный выход, чем предыдущий полуволновой 3-фазный выпрямитель, поскольку его частота в шесть раз превышает входной сигнал переменного тока.

Кроме того, двухполупериодный выпрямитель может питаться от сбалансированного 3-фазного 3-проводного треугольника, подключенного треугольником, поскольку четвертый нейтральный (N) провод не требуется. Рассмотрим ниже трехполупериодную трехфазную схему выпрямителя.

Как и раньше, при условии чередования фаз красного-желтого-синего (V _A  — V _B  — V _C) и красной фазы (V _A ) начинается при 0 ^o . Каждая фаза подключается между парой диодов, как показано на рисунке. Один диод проводящей пары питает положительную (+) сторону нагрузки, в то время как другой диод питает отрицательную (-) сторону нагрузки.

Диоды D _1, D _3, D ₂ и D ₄ образуют мостовую выпрямительную сеть между фазами A и B, аналогично диоды D ₃ D _5, D ₄ и D ₆ между фазами B и C и D _5, D _1, D ₆ и D ₂ между фазами C и А.

Таким образом, диоды D _1, D ₃ и D ₅ питают положительную шину и в зависимости от того, какая из них имеет более положительное напряжение на своем анодном выводе, проводит. Аналогично, диоды D _2, D ₄ и D ₆ питают отрицательную шину, и какой диод имеет более отрицательное напряжение на своих катодных выводах.

Тогда мы можем видеть, что для трехфазного выпрямления диоды проводят в совпадающих парах, давая схему проводимости для тока нагрузки: D _1-2 D _1-6 D _3-6 D _3-6 D _3-4 D _{5- 4} D _5-2 и D _1-2, как показано.

В трехфазных силовых выпрямителях проводимость всегда происходит в наиболее положительном диоде и соответствующем наиболее отрицательном диоде. Таким образом, когда три фазы вращаются через выводы выпрямителя, проводимость передается от диода к диоду. Затем каждый диод проводит в течение 120 ^o (одну треть) в каждом цикле питания, но так как требуется два диода для проводки в парах, каждая пара диодов будет проводить только 60 ^o (одну шестую) цикла в любой момент времени, так как показано выше.

Поэтому мы можем правильно сказать, что для трехфазного выпрямителя, питаемого от «3» вторичных обмоток трансформатора, каждая фаза будет разделена на 360 ^o / 3, таким образом, требуя 2 * 3 диода. Отметим также, что в отличие от предыдущего полуволнового выпрямителя, между входной и выходной клеммами выпрямителя нет общего соединения. Следовательно, он может питаться от звезды или от трансформатора.

Таким образом, среднее значение постоянного тока сигнала выходного напряжения от трехфазного двухполупериодного выпрямителя задается как:

Где: V _S равно (V _{L (PEAK)}  ÷ √ 3 ), а где V _{L (PEAK)} — максимальное линейное напряжение (V _L * 1,414).

Резюме трехфазного выпрямления

В этой статье мы увидели, что трехфазное выпрямление — это процесс преобразования трехфазного источника переменного тока в пульсирующее постоянное напряжение, когда выпрямление преобразует входной источник питания синусоидального напряжения и частоты в постоянное напряжение постоянного тока. Таким образом, выпрямление мощности превращает переменный источник в однонаправленный источник.

Но мы также видели, что 3-фазные неконтролируемые полуволновые выпрямители, которые используют один диод на фазу, требуют подключения в виде звезды в качестве четвертого нейтрального (N) провода для замыкания цепи от нагрузки к источнику. Трехфазный двухполупериодный мостовой выпрямитель, который использует два диода на фазу, требует только трех линий электропередачи, без нейтрали, такой как та, которая обеспечивается питанием от треугольника.

Другим преимуществом двухполупериодного мостового выпрямителя является то, что ток нагрузки хорошо сбалансирован по мосту, что повышает эффективность (отношение выходной мощности постоянного тока к подводимой входной мощности) и снижает содержание пульсаций, как по амплитуде, так и по частоте, по сравнению с полуволновой конфигурацией.

Увеличивая количество фаз и диодов в конфигурации моста, можно получить более высокое среднее выходное напряжение постоянного тока с меньшей амплитудой пульсаций, как, например, при 6-фазном выпрямлении каждый диод будет проводить только одну шестую цикла. Кроме того, многофазные выпрямители производят более высокую частоту пульсаций, что означает меньшую емкостную фильтрацию и намного более плавное выходное напряжение. Таким образом, 6, 12, 15 и даже 24-фазные неконтролируемые выпрямители могут быть разработаны для улучшения коэффициента пульсации для различных применений.

Полупроводниковые выпрямители блоков питания, схемы, онлайн расчёт

Классификация, свойства, схемы, онлайн калькулятор.
Расчёт ёмкости сглаживающего конденсатора.

«- Почему пульт не работает?
  — Я, конечно, не электрик, но, по-моему, пульт не работает, потому что телевизора нет».

— А для чего нам ещё «нахрен не упал» профессиональный электрик?
— Для чего? Да много для чего! Например, для того, чтобы быть в курсе, что без источника питания, а точнее без преобразователя сетевого переменного напряжения в постоянное, не обходится ни одно электронное устройство.
— А электрик?
— Электрик, электрик… Что электрик?… «Электрик Сидоров упал со столба и вежливо выругался…»

Итак, приступим.
Выпрямитель — это электротехническое устройство, предназначенное для преобразования переменного напряжения в постоянное.
Выпрямитель содержит трансформатор,

необходимый для преобразования напряжения сети Uc до величины U2, определяемой требованиями нагрузки;
вентильную группу (в нашем случае диодную), которая обеспечивает одностороннее протекание тока в цепи нагрузки;
фильтр, передающий на выход схемы постоянную составляющую напряжения и сглаживающий пульсации напряжения.

Расчёт трансформатора — штука громоздкая, в рамках этой статьи рассматриваться не будет, поэтому сразу перейдём к основным и наиболее распространённым схемам выпрямителей блоков питания радиоэлектронной аппаратуры.
В процессе повествования давайте сделаем допущение, что под величинами переменных напряжений и токов в цепях выпрямителей мы будем подразумевать их действующие (эффективные) значения:
U_действ = U_ампл/√2 и I_действ = I_ампл/√2.

Именно такие значения приводятся в паспортных характеристиках обмоток трансформаторов, да и большинство измерительных приборов отображают — не что иное, как аккурат эффективные значения сигналов переменного тока.

Однополупериодный выпрямитель.

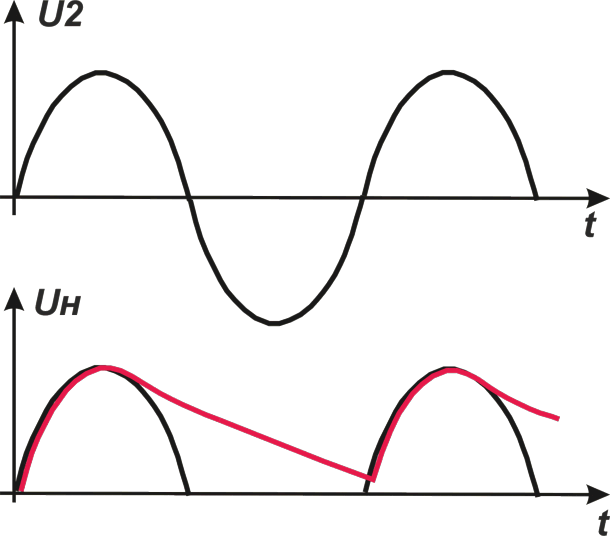
Рис.1

На Рис.1 приведена однофазная однополупериодная схема выпрямления, а также осциллограммы напряжений в различных точках (чёрным цветом — напряжение на нагрузке при отсутствии сглаживающего конденсатора С1, красным — с конденсатором).
В данном типе выпрямителя напряжение с вторичной обмотки трансформатора поступает в нагрузку через диод только в положительные полупериоды переменного напряжения. В отрицательные полупериоды полупроводник закрыт, и напряжение в нагрузку подаётся только с заряженного в предыдущий полупериод конденсатора.

Однополупериодная схема выпрямителя применяется крайне редко и только для питания цепей с низким током потребления ввиду высокого уровня пульсаций выпрямленного напряжения, низкого КПД, и неэффективного использования габаритной мощности трансформатора.

Здесь обмотка трансформатора должна обеспечивать величину тока, равную удвоенному значению максимального тока в нагрузке I_обм = 2×I_нагр  и напряжение холостого хода ~U₂ ≈ 0,75×U_н.
При выборе диода D1 для данного типа схем, следует придерживаться следующих его параметров:
U_обр > 3,14×U_н   и   I_макс > 3,14×I

н.

Едем дальше.
Двухполупериодный выпрямитель с нулевой точкой.

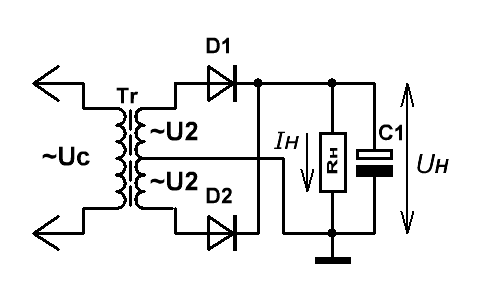
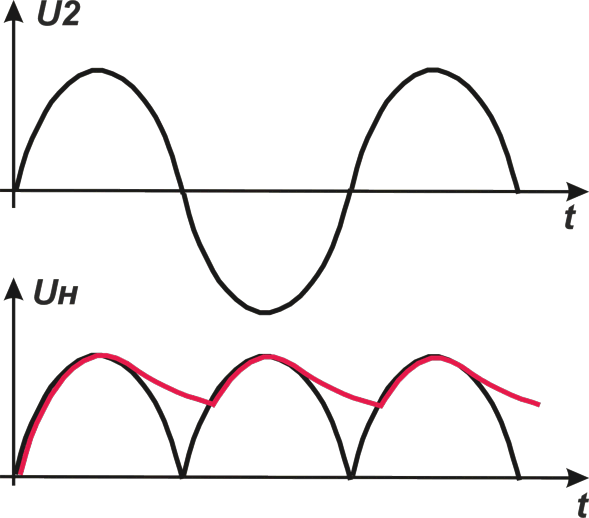
Рис.2

Схема, приведённая на Рис.2, является объединением двух противофазных однополупериодных выпрямителей, подключённых к общей нагрузке. В одном полупериоде переменного напряжения ток в нагрузку поступает с верхней половины вторичной обмотки через открытый диод D1, в другом полупериоде — с нижней, через второй открытый диод D2.
Как и любая двухполупериодная, эта схема выпрямителя имеет в 2 раза меньший уровень пульсации по сравнению с однополупериодной схемой. К недостаткам следует отнести более сложную конструкцию трансформатора и такое же, как в однополупериодной схеме — нерациональное использование трансформаторной меди и стали.

Каждая из обмоток трансформатора должна обеспечивать величину тока, равную значению максимального тока в нагрузке I_обм = I_нагр  и напряжение холостого хода ~U₂ ≈ 0,75×U_н.
Полупроводниковые диоды D1 и D2 должны обладать следующими параметрами:
U_обр > 3,14×U_н   и   I_макс > 1,57×I_н.

И наконец, классика жанра —
Мостовые схемы двухполупериодных выпрямителей.

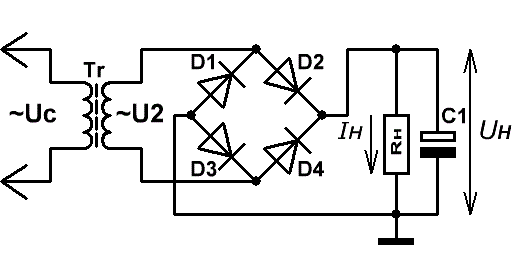
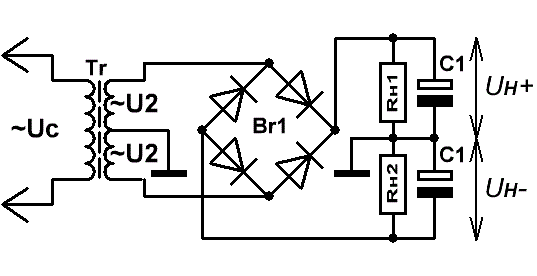
Рис.3

На Рис.3 слева изображена схема однополярного двухполупериодного мостового выпрямителя с использованием одной обмотки трансформатора. Графики напряжений на входе и выходе выпрямителя аналогичны осциллограммам, изображённым на Рис.2.
Во время положительного полупериода переменного напряжения ток протекает через цепь, образованную D2 и D3, во время отрицательного — через цепь D1 и D4. В обоих случаях направление тока, протекающего через нагрузку, одинаково.

Если сравнивать данную схему с предыдущей схемой выпрямителя с нулевой точкой, то мостовая имеет более простую конструкцию трансформатора при таком же уровне пульсаций, менее жёсткие требования к обратному напряжению диодов, а главное — более рациональное использование трансформатора и возможность уменьшения его габаритной мощности.

К недостаткам следует отнести необходимость увеличения числа диодов, что приводит к повышенным тепловым потерям за счёт большего падения напряжения в выпрямителе.

Обмотка трансформатора должна обеспечивать величину тока, равную I_обм = 1,41×I_нагр  и напряжение холостого хода ~U₂ ≈ 0,75×U_н.
Полупроводниковые диоды следует выбирать исходя из следующих соображений:
U_обр > 1,57×U_н   и   I_макс > 1,57×I_н.

При наличии у трансформатора двух одинаковых вторичных обмоток, или одной с отводом от середины выводом, однополярная схема преобразуется в схему двуполярного выпрямителя со средней точкой (Рис.3 справа).
Естественным образом, диоды в двуполярном исполнении должны выбираться исходя из двойных значений

U_обр и I_макс по отношению к однополярной схеме.

Значения U_обр и I_макс приведены исходя из величин наибольшего (амплитудного) значения обратного напряжения, приложенного к одному диоду, и наибольшего (амплитудного) значения тока через один диод при отсутствии сглаживающих фильтров на выходе.

Конденсатор С1 во всех схемах — это простейший фильтр, выделяющий постоянную составляющую напряжения и сглаживающий пульсации напряжения в нагрузке.
Для выпрямителей, не содержащих стабилизатор, его ёмкость рассчитывается по формулам:
С1 = 6400×I_н/(U_н×К_п) для однополупериодных выпрямителей и
С1 = 3200×I_н/(U_н×К_п) — для двухполупериодных,

где К_п — это коэффициент пульсаций, численно равный отношению амплитудного значения пульсирующего напряжения к его постоянной составляющей.
Для стабилизированных источников питания ёмкость С1 можно уменьшить в 5-10 раз.

«Коэффициент пульсаций выбирают самостоятельно в зависимости от предполагаемой нагрузки, допускающей питание постоянным током вполне определённой «чистоты»:
10^-3… 10^-2   (0,1-1%) — малогабаритные транзисторные радиоприёмники и магнитофоны,
10^-4… 10^-3   (0,01-0,1%) — усилители радио и промежуточной частоты,
10^-5… 10^-4   (0,001-0,01%) — предварительные каскады усилителей звуковой частоты и микрофонных усилителей.» — авторитетно учит нас печатное издание.

Ну и под занавес приведём незамысловатую онлайн таблицу.

КАЛЬКУЛЯТОР РАСЧЁТА ВЫПРЯМИТЕЛЯ ДЛЯ БЛОКА ПИТАНИЯ.

А на следующей странице рассмотрим сглаживающие фильтры силовых выпрямителей, не только ёмкостные, но и индуктивные, а также активные фильтры на биполярных транзисторах.

 

Маломощные однофазные выпрямители

Одними из самых  распространенных преобразователей тока являются выпрямители переменного тока в пульсирующий (постоянный по направлению движения носителей, но переменный по мгновенной величине) ток. Они имеют очень широкое применение. Условно их можно разделить на маломощные выпрямители (до нескольких сотен ватт  и выпрямители большой мощности (киловатты и больше)).

Содержание:

Принцип работы выпрямителя

Структурная схема выпрямителя показана ниже:

Главною его частью является выпрямляющее устройство В, образованное из диодов, объединенных особым образом. Именно здесь и происходит преобразование переменного тока в пульсирующий постоянный. Переменное напряжение подается на выпрямляющее устройство через трансформатор Тр. В некоторых случаях трансформатора может и не быть (если напряжение силовой сети отвечает той, которая необходима для работы выпрямителя). Трансформатор(если он есть) в большинстве также имеет особенности в соединении его обмоток. Пульсирующий ток , как правило не является постоянным по величине в каждое мгновение времени, и когда необходимо иметь более сглаженное его значение, чем полученный после выпрямляющего устройства, применяют фильтры Ф. В случае необходимости выпрямитель дополняют стабилизатором напряжения  или тока Ст, который поддерживает их на постоянном уровне, если параметры силовой сети изменяется по разным причинам. Структурную схему завершает нагрузка Н, которая значительно влияет на работу всего устройства и поэтому считается составляющей частью всего преобразователя.

Собственно выпрямителем является та его часть, которая обведена на рисунке выше пунктиром и состоит из трансформатора и выпрямительного устройства.

В этом подразделе рассматриваются  выпрямители малой мощности, которые необходимы для обеспечения постоянным напряжением всяких устройств в областях управления, регулирования, усилителях тока, генераторах малой мощности и так далее. Как правило, они питаются от однофазного переменного напряжения 220 или 380 В частотою 50 Гц.

Нулевая схема выпрямления

Рассмотреть принцип действия самого простого выпрямителя однофазного тока целесообразно на так называемой нулевой схеме. Хотя она сейчас встречается относительно редко (о чем речь пойдет далее), знание физических процессов, которые происходят в этой схеме, очень важны для понимания дальнейшего материала.

Нулевая схема выглядит так:

Трансформатор Тр    имеет на вторичной стороне две обмотки, соединенные последовательно таким образом, что относительно средней точки а  напряжения  на свободных концах обмоток в и с одинаковые по величине, но противоположные по фазе. Выпрямительное устройство образовано двумя диодами D1 и D2, которые соединены вместе своими катодами, тогда как каждый анод соединен с соответствующей обмоткой. Нагрузка Zн присоединена между катодами диодов и точкой трансформатора.

Рассмотрим, как возникает пульсирующее напряжение на нагрузке. Сначала будем считать нагрузку чисто активным сопротивлением, Z_н=R_н.  Когда напряжение в обмотках будет изменяться по синусоидальному закону, то в тот полупериод, когда к аноду диода приложен положительный потенциал, будет проходить прямой ток. Поскольку напряжение на диоде составляет доли вольта, пренебрежем им. Тогда вся положительная полуволна переменного напряжения будет приложена просто к нагрузке R_н.  Когда напряжение приложенное минусом к аноду, тока не будет (малым обратным током диода также пренебрежем). Таким образом, до нагрузки будем доходить лишь положительная полуволна переменного напряжения в течении половины периода. Вторая половина периода будет свободна от тока.

Вторичные обмотки соединены противофазно, нагрузка общая для обеих обмоток, таким образом, в то время, когда в одной из них (например в верхней) ток будет проходить, другая будет от него свободна и наоборот.

Поэтому в нагрузке каждый полупериод будет заполнен полуволной переменного напряжения:

И выпрямленное напряжение U_d будет иметь вид одинаковых полуволн, которые повторяются с периодом, вдвое меньшим, чем период переменного напряжения в сети питания (2π радиан). Для обобщения, что будет удобно, далее будем считать, что период изменения выпрямленного напряжения меньше 2π в m раз и равняется 2π/m (в нашем случае m-2). Если нагрузка активное сопротивление R_н, то и ток в нем i_{d ,} будет повторять кривую напряжения.

Рассмотренная схема будет иметь тот недостаток, что во вторичных обмотках по сравнению с первичной имеют место значительные пульсации тока, потому что эти обмотки работают по очереди. Поскольку они намотаны на один сердечник, магнитный поток в последнем будет переменным, поэтому и в первичной обмотке ток будет переменным, имея как положительную, так и отрицательную полуволны. Как известно из курса электротехники, действующие и средние значения тока или напряжения одинаковые только для постоянного тока. Чем больше пульсации, тем больше будет действующее значение относительно среднего. Поэтому мощности обеих сторон трансформатора не будут одинаковыми. Однако трансформатор один, и объем железа для его сердечника следует выбирать, исходя из какого-то одного значения мощности.

Поэтому условно ввели понятие типовой мощности трансформатора, которая равняется среднему мощностей обеих сторон:

Выпрямительный мост или схема Гретца

Указанный недостаток можно исправить, используя выпрямляющее устройство в виде так называемого моста (схема Гретца):

В этом случае первые полупериоды будут работать, например, диоды D2  и D4, а вторые полупериода — D1 и D3. На нагрузке каждый раз будет полная полуволна вторичного напряжения:

 Мостовая схема кроме того имеет менее сложный, более легкий и дешевый трансформатор. Как мы увидим далее, у нее есть еще несколько преимуществ.

Интересно, что эта схема появилась исторически раньше нулевой однако распространения не получила, потому что имела во-первых четыре диода вместо двух. Однако главным  было не их количество, а то что при работе каждые полупериода ток проходит через два последовательно соединенных диода, на которые падает двойное напряжение. На то время полупроводниковых диодов еще не было, а вакуумные или ртутные имели значительное падение напряжения при прохождении прямого тока, что существенно понижало коэффициент  полезного действия. Оказалось, что более сложный трансформатор нулевой схемы, но с одним диодом в кругу выпрямления тока экономично выгоднее, чем мостовая схема с удвоенным числом диодов и двойным расходом энергии на них. И только появление относительно дешевых полупроводниковых диодов с очень маленьким падением прямого напряжения позволило повернуться к мостовым схемам, которая сейчас практически вытеснила нулевую ( в этом при желании можно усмотреть проявление одного из  диалектических законов – развитие по спирали).

Основные соотношения для выпрямителя

Выведем некоторые важные формулы, которые описывают процессы, существующие в этой схеме. Будем считать, что заданными величинами являются средние значения напряжения на нагрузку U_d и среднее значение тока в нем I_d.

Среднее значение выпрямленного напряжения

Запомним это выражение на дальнейшее. В нашем случае m=2 и  . Поскольку U_d считаем заданным, то

Амплитудное значение вторичного напряжения

Из предыдущего выражения имеем:

Коэффициент трансформации трансформатора

Этот коэффициент определяет отношения питающей сети к напряжению на обмотке вторичной стороны:

Действующее значение тока вторичной обмотки

Ток вторичной обмотки в то же время есть током в нагрузке. Поскольку нагрузка чисто активная и ток в ней повторяет по форме пульсирующее напряжение, то между его средним значением и его действующим значением существует такая же зависимость, что и для напряжений, то есть

Действующее значение тока первичной обмотки

Ток в первичной обмотке повторяет с учетом n ток вторичной обмотки :

Мощность трансформатора

Мощности первичной и вторичной сторон трансформатора в этой схеме одинаковые, поэтому:

Пульсация выпрямленного напряжения

Пульсирующее напряжение состоит из среднего значения U_d   и бесконечного количества гармоничных составляющих, амплитуды которых можно определить по формулам Фурье. Если начало координат выбрать так как на рисунке, то в гармоничном составе будут присутствовать только косинусные гармоники (т.к. кривая симметрична относительна оси координат). Амплитуда k-ой гармоники определяется по формуле:

Где: l – полупериод π/m;  

Наибольшую амплитуду будет иметь первая гармоника U_(1)m, поэтому определим только ее, предположив, что k=1:

Заменив   получим:

Отношение первой гармоники к среднему значению называют коэффициентом пульсаций:

Запомним эту формулу на будущее, а сейчас отметим, что в нашем случае при m – 2, q – 2/3. Это большие пульсации – амплитуда первой гармоники составляет 67% от среднего значения выпрямленного напряжения.

 Средний ток диодов

Как мы уже видели диоды работают по очереди – каждый из них проводит в среднем половину общего тока , который есть в нагрузке. Поэтому каждый из диодов должен быть рассчитан на ток  I_в = I_d/2

Наибольшее обратное напряжение на диоде

В то время когда диод B1 проводит его можно считать замкнутым, и тогда к диоду B2 будет приложено в обратном направлении напряжение вторичной обмотки. Поэтому каждый из диодов должен быть рассчитан на ее амплитудное значение:

Однофазные схемы выпрямления — Студопедия

При небольшой мощности нагрузки (до нескольких сотен ватт) преобразование переменного тока в постоянный осуществляют с помощью однофазных выпрямителей, питающихся от одно­фазной сети переменного тока. Такие выпрямители предназначе­ны для питания постоянным током различных устройств про­мышленной электроники, обмоток возбуждения двигателей постоянного тока небольшой и средней мощности и т.д.

Однофазная однополупериодная схема выпрямления

Сущность процесса выпрямления рассмотрим на примере простейшей однофазной однополупериодной (однотактной) схемы выпрямления. В этой схеме (рисунок 76) трансформатор имеет одну вторичную обмотку, напряжение u₂которой изме­няется по синусоидальному закону. Ток в цепи нагрузки проходит только в положительные полупериоды, когда точка а вторичной обмотки, к которой присоединен анод вентиля V1, имеет положительный потенциал относительно точ­ки b, к которой через нагрузку присоединен катод.

В результа­те напряжение u₂оказывается приложенным к резистору R_d, через который начинает протекать ток нагрузки i_d.

Поскольку при активной нагрузке ток по фазе совпадает с напряжением, вентиль V1 будет пропускать ток до тех пор, пока напряжение u₂ не снизится до нуля. В отрицательные полупериоды (интервал времени t₁ – t₂ на рис. 76) к вентилю V1 прикладывается все напряжение источника U₂. Оно является для диода обрат­ным, и он будет закрыт.

Таким образом, на резисторе R_d будет пульсирующее напря­жение u_dтолько одной полярности, т.е. выпрямленное напряжение, которое будет описываться положительными полуволнами напряжения u₂ вторичной обмотки трансформато­ра Т. Ток в нагрузке i_d проходит в одном направлении, но име­ет также пульсирующий характер и представляет собой выпрямленный ток.

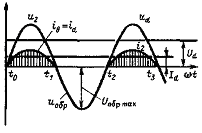
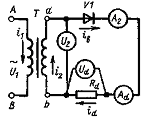
Рисунок 76 — Однофазный однополупериодный выпрямитель: схема и диаграммы напряжений и токов на элементах схемы

Выпрямленные напряжения u_dи ток i_d содержат постоянную (полезную) составляющую U_d, I_d и переменную составля­ющую (пульсации). Качественная сторона работы выпрямителя оценивается соотношениями между полезной со­ставляющей и пульсациями напряжения и тока. Коэффициент пульсаций данной схемы составляет 1,57.

Для однополупериодной схемы справедливы следующие соотношения между напряжениями, токами и мощностями в отдельных элементах вы­прямителя по отношению к соответствующим средним значениям на нагрузке.

Среднее за период значение выпрямленного напряжения при идеаль­ных вентилях и трансформаторе

U_d = 0,45 U₂

Максимальное значение обратного напряжения на вентиле

U_обр.max = √2U₂ = 3,14U_d

где U₂ — действующее значение напряжения вторичной обмотки тран­сформатора Т

Среднее значение тока, протекающего через вентиль и нагрузку

I_в.ср= I_d= I_m/π,

где I_m = U_m/R_d — амплитуда тока цепи.

Действующее значе­ние тока цепи

I₂ = I_m /2

Таким образом, в однополупериодной схеме выпрямления среднее значение выпрямленного тока в π раз меньше его амплитуды, а действу­ющее значение — в 2 раза меньше амплитуды тока.

Средняя мощность, отдаваемая в нагрузку, определяется

P_d = U_dI_d

Расчетную (типовую) мощность S_т трансформатора, определяющую его габариты, можно представить как полусумму расчетных мощностей первичной S₁ = U₁I₁ и вторичной S₂ = U₂I₂ обмоток, т.е.

S_т = (S₁ + S₂) /2 = 3,09P_d

Следовательно, расчетная мощность трансформатора, работающего на выпрямитель, больше мощности в нагрузке в 3,09 раза, так как во вто­ричной обмотке проходит несинусоидальный ток, имеющий постоянную и переменные составляющие, а в первичной обмотке кроме тока основной частоты f₁— токи высших гармоник. По отношению к сети питания эти токи являются реактивными и, не создавая полезной мощ­ности, лишь нагревают обмотки трансформатора выпрямителя. Наличие во вторичной обмотке постоянной составляющей тока I_d увеличивает степень насыщения магнитпровода трансформатора, что вызывает воз­растание тока холостого хода, и как следствие этого возникает необхо­димость в завышении расчетной мощности трансформатора.

Действующее значение тока вторичной обмотки трансформатора определяется формулой

I₂ = 1,57I_d

Действующее значение напряжения вторичной обмотки

U₂ = 2,22U_d

Действующее значение тока первичной обмотки с учетом коэффициен­та трансформации трансформатора n = U₁/U₂равно

I₁ = I₂/n

Недостатки этой схемы выпрямления следующие: плохое ис­пользование трансформатора, большое обратное напряжение на вентилях, большой коэффициент пульсации выпрямленного напряжения.

Достоинства выпрямителя: простота схемы и пи­тающего трансформатора; применяется только один вентиль или одна группа последовательно соединенных вентилей.

Двухполупериодная однофазная схема со средней точкой

Схема (рис. 77) состоит из трансформатора Т, имеющего одну первичную и две последовательно соединенные вторичные обмотки с выводом общей (нулевой) точки у этих обмоток. Коэффициент трансформации nопределяется отноше­нием U₁/U₂,где U₂ — напряжение каждой из вторичных обмо­ток (фазные напряжения), сдвинутые относительно друг друга на 180°.

Свободные концы вторичных обмоток а и Ь присоединяются к анодам вентилей V1 и V2, катоды которых соединяются вместе. Нагрузка R_dвключается между катодами вентилей, ко­торые являются положительным полюсом выпрямителя, и нуле­вым выводом 0 трансформатора, который служит отрицатель­ным полюсом.

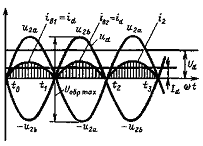
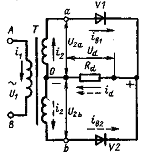
Рисунок 77 — Однофазный двухполупериодный выпрямитель со средней точкой: схема и диаграммы напряжений и токов на элементах схемы

Вентили в этой схеме, как и вторичные обмотки трансформа­тора, работают поочередно, пропуская в нагрузку ток при по­ложительных значениях анодных напряжений u_2a и u_2b.

Действительно, при изменении напряжения в точках а и b, в тот полупериод, когда напряжение в обмотке 0а положительно, ток проводит вентиль V1, анод ко­торого положителен по отношению к катоду, связанному через резистор R_dс точкой 0 вторичных обмоток. Анод вентиля V2, так же как вывод b обмотки 0b, в этот полупериод (t₀-t₁) отрицателен по отношению к нулевому выводу 0 и, следователь­но, тока не пропускает.

В следующий полупериод (интервал времени t₁-t₂ на рис. 77), когда напряжения на первичной и вторичной обмотках трансформатора изменяют свою полярность на обратную, ток бу­дет пропускать вентиль V2. Врезультате к нагрузке R_dбудет те­перь приложено напряжение u_2b, а ток i_d будет равен току i_в2 вентиля V2. Вентиль V1 выключится, так как к нему будет при­ложено обратное напряжение. Спустя полупериод, начиная с момента времени t₂, процесс повторяется: ток будет прово­дить вентиль V1, а вентиль V2 выключится и т.д.

Ток i_dв нагрузке все время течет в одном направлении — от катодов вентилей к нулевой точке 0 вторичных обмоток тран­сформатора, и на резисторе R_d появляется выпрямленное пуль­сирующее напряжение u_d содержащее постоянную и перемен­ную составляющие.

Для однофазной нулевой схемы справедливы следующие соотношения между напряжениями, токами и мощностями в отдельных элементах вы­прямителя.

Среднее значение выпрямленного напряжения

U_d = 0,9U₂,

где U₂ — действующее значение напряжения на вторичной полуобмотке,

U₂ = 1,11 U_d

Среднее значение выпрямленного тока в нагрузке

I_d = U_d/R_d

Среднее значение тока через каждый вентиль в 2 раза меньше тока I_d, проходящего через нагрузку, т.е.

I_в.ср = 0,5I_d

Действующее значение тока вентиля I_в равно действующему значению тока вторичной обмотки трансформатора I₂ и определяется формулой

I₂ = 1,57 I_в.ср

Вентиль, не работающий в отрицательную часть периода, оказывается под воздействием обратного напряжения, равного двойному фазному напряжению 2U₂. Максимальное значение обратного напряжения

U_обр.max = 2√2U₂ = 3,14U_d

Действующее значение тока первичной обмотки с учетом коэффи­циента трансформации n,выраженное через ток I_d,

I₁ = √2 I₂/n = 1.11 I_d/n

Расчетные мощности обмоток трансформатора определяют по произ­ведениям действующих значений токов и напряжений: S₁ = U₁I₁ = 1,23 P_d и S₂ = 2U₂I₂⁼ 1,74P_d, а типовую мощность — как полусум­му мощностей S₁ и S₂, т.е.

S_T = (S₁ + S₂)/2 = 1,48P_d

Оценка качества выпрямленного напряжения производится посредством коэффициента пульсации, который представляет собой отношение амплитуды первой (основной) гармонической U_d1m, как наибольшей из всех остальных к среднему значению напряжения U_dи определяется по формуле

q = U_d1m / U_d = 2/(m² -1)

где m — число фаз выпрямления, т.е. число полуволн выпрям­ленного напряжения, приходящихся на один период переменно­го тока, питающего выпрямитель.

Для рассматриваемой схемы частота первой гармоники пуль­сации f_n1 = 2f_c при частоте питающей сети f_c = 50 Гц состав­ляет 100 Гц. Подставляя в последнею формулу m = 2, определяем коэффици­ент пульсации: q = 0,67.

Однофазная мостовая схема

Состоит из трансформатора Т сдвумя обмотками и четырех диодов V1 — V4, соединенных по схеме моста (рисунок 78, а). К одной диагонали моста (точки 1,3) присоединяется вторичная обмотка, а в другую (точки 2, 4) включается нагрузка R_d. Общая точка катодов вентилей V1 и V2 является положительным полюсом выпрямителя, а отрица­тельным — точка связи анодов вентилей V3 и V4.

Вентили в этой схеме работают парами поочередно. В положи­тельный полупериод напряжения u₂ соответствующая поляр­ность которого обозначена без скобок, проводят ток вентили V1 и V3, а к вентилям V2 и V4 прикладывается обратное напряжение, и они закрыты. В отрицательный полупериод напря­жения u₂ будут проводить ток вентили V2 и V4, а вентили VI и V3 закрыты и выдерживают обратное напряжение u_обр = u₂.

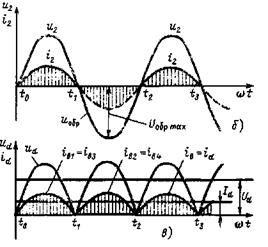
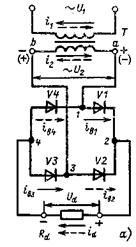
Рисунок 78 — Однофазный мостовой выпрямитель:

а — схема включения; б и в — временные диаграммы напряжений и токов на элементах схемы

Далее указанные процессы периодически повторяются. Диаг­раммы токов и напряжений на элементах схемы (рис. 78, в) будут такими же, как для однофазного двухполупериодного выпрямителя со средней точкой.

Ток i_dвнагрузке проходит все время в одном направле­нии — от соединенных катодов диодов VI и V2 к анодам дио­дов V3 и V4. Ток I₂ во вторичной обмотке трансформатора (рисунок 78, б) меняет свое направление каждые полпериода и будет синусоидальным. Постоянной составляющей тока во вторичной обмотке нет. Следовательно, не будет подмагничивания сердеч­ника трансформатора постоянным магнитным потоком. Ток i₁ в первичной обмотке трансформатора также синусоидальный.

Средние значения выпрямленного напряжения U_dи тока I_в.ср через вентиль в этой схеме получаются такими же, как и в двухполупериодной схеме с нулевой точкой.

Обратное напряжение, приложенное к закрытым вентилям, определяется напряжением U₂вторичной обмотки трансформа­тора, так как не работающие в данный полупериод вентили ока­зываются присоединенными ко вторичной обмотке трансформа­тора Т через два других работающих вентиля, падением напря­жения в которых можно пренебречь. Следовательно,

U_обр.max = √2U₂ = 1,57U_d

Токи во вторичной и первичной обмотках трансформатора определяются по формулам

I₂ = U₂/R_d I₁ = I₂/n

Типовая мощность трансформатора

S_T = 1,23P_d

На рисунке 79 также представлена однофазная мостовая схема, аналогичная рассмотренной. Чаще всего именно так изображается мостовое включение выпрямительных диодов.

 

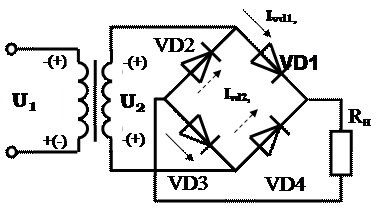Рисунок 79 – Схема однофазного мостового выпрямителя

Сравним достоинства двухполупериодных однофазных схем выпрямления.

Однофазная нулевая схема:

1) Число вентилей в 2 раза меньше, чем в однофазной мосто­вой.

2) Потери мощности в выпрямителе будут меньше, так как в нулевой схеме ток проходит через один вентиль, а в мостовой — последовательно через два.

Однофазная мостовая схема:

1) Амплитуда обратного напряжения на вентилях в 2 раза меньше, чем в нулевой схеме.

2) Вдвое меньше напряжение (число витков) вторичной обмотки трансформатора при одинаковых значениях напряжения U_d

3) Трансформатор имеет обычное исполнение, так как нет вы­вода средней точки на вторичной обмотке.

4) Расчетная мощность трансформатора на 25% меньше, чем в нулевой схеме, следовательно, меньше расходуется меди и железа, меньше будут размеры и масса.

Данная схема выпрямителя может работать и без трансфор­матора, если напряжение сети U₁ подходит по значению для по­лучения необходимого напряжения U_dи не требуется изоляции цепи выпрямленного тока от питающей сети.

Трёхфазные схемы выпрямления

Питание постоянным током потребителей средней и большой мощности производится от трехфазных выпрямителей, применение которых снижает загрузку вентилей по току, уменьшает коэффициент пульсаций и повы­шает частоту пульсации выпрямленного напряжения, что облег­чает задачу его сглаживания.

Трехфазная схема выпрямления с нулевым выводом (или трехфазная нулевая)

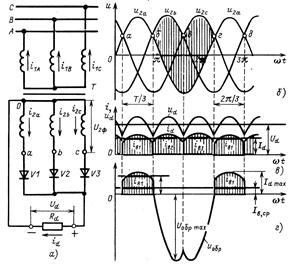
К сети трехфазного тока подключен тран­сформатор Т, три первичные обмотки которого могут быть сое­динены в звезду или треугольник, вторичные обмотки — только в звезду (рисунок 80, а). Свободные концы а, Ь, с каждой из фаз вторичной обмотки присоединяются к анодам вентилей VI, V2, V3. Катоды вентилей соединяются вместе и служат положи­тельным полюсом для цепи нагрузки R_d, а нулевая точка 0 вторичной обмотки трансформатора — отрицательным полюсом.

Рисунок 80 — Трехфазный выпрямитель с нулевой точкой:

а — схема соединения обмоток трансформатора и вентилей;

6 — г- диаграммы напряжений и токов на элементах

Из временной диаграммы на рисуноке 80 видно, что напряжения u_2a,u_2b,u_2с сдвинуты по фазе на одну треть периода (Т/3или 120°) и в течение этого интервала напряжение одной фазы выше напряжения двух других фаз относительно нулевой точки трансформатора. Ток через вентиль, связанную с ним вторич­ную обмотку и нагрузку будет протекать в течение той трети периода, когда напряжения в данной фазе больше, чем в двух других. Работающий вентиль прекращает проводить ток тогда, когда потенциал его анода становится ниже общего потенциала катодов, и к нему прикладывается обратное напряжение.

Переход тока от одного вентиля к другому (коммутация то­ка) происходит в момент пересечения кривых фазных напряже­ний (точки а, б, в и г на рис. 80, б). Выпрямленный ток i_dпроходит через нагрузку R_d непрерывно (рис. 80, в).

Напряжение u_dна выходе выпрямителя в любой момент вре­мени равно мгновенному значению напряжения той вторичной обмотки, в которой вентиль открыт, и выпрямленное напряже­ние представляет собой огибающую верхушек синусоид фазных напряжений u_2ф трансформатора Т.

Следовательно, анодный ток будет иметь форму прямо­угольника с основанием Т/3, ограниченного сверху отрезком си­нусоиды. На рисунке 80, г изображен ток фазы а, токи фаз б и с изображаются подобными кривыми, сдвинутыми на 120° от­носительно друг друга.

Для трехфазной нулевой схемы выпрямления характерны следующие соотношения между напряжениями, токами и мощностями в отдельных элементах выпрямителя.

Среднее значение выпрямленного напряжения

U_d = 1,17U_2ф,

где U_2ф — действующее значение фазного напряжения на вторичной об­мотке трансформатора.

Выпрямленное напряжение u_dсодержит постоянную составляющую U_dи наложенную на нее переменную составляющую, имеющую трехкратную частоту по отношению к частоте сети. Коэффициент пульса­ций напряжения на выходе выпрямителя

q = 2/(m² -1) = 2/(3² -1) = 0,25

Обратное напряжение U_обр приложенное к неработающему вентилю, равно междуфазному (линейному) напряжению вторичных обмоток тран­сформатора, так как анод закрытого вентиля присоединен к одной из фаз, а катод через работающий вентиль присоединен к другой фазе вто­ричной обмотки Т. На рисунок 80, г показана кривая обратного напряжения U_обр между анодом и катодом вентиля V1.

Максимальное значение U_обр равно амплитуде линейного напряжения на вторичных обмотках трансформатора, т.е.

U_обр.max = √3 √2 U_2ф = 2,09U_d

Каждый вентиль в данной схеме работает 1 раз за период в течение Т/3. Следовательно, среднее значение тока через вентиль в 3 раза меньше тока нагрузки, т.е.

I_в.ср = (1 /3)I_d

Действующее значение токов во вторичной обмотке I₂ и вентиля I_в,д определяется формулой

I₂ = I_в,д = √3I_в.ср = 0,585 I_d

Таким образом, в данной схеме токи вторичных обмоток имеют пуль­сирующий характер и содержат постоянные составляющие.

Среднее значение тока через каждый вентиль в 3 раза меньше тока I_d

I_в.ср = 0,33I_d

При одинаковом числе фаз первичной и вторичной обмоток трансфор­матора и одинаковых схемах соединения обмоток (звез­да-звезда) действующее значение первичного фазного тока I₁меньше при­веденного значения вторичного фазного тока I₂, так как в кривой тока первичной обмотки отсутствует постоянная составляющая, которая не трансформируется, т.е.

I₁ ≈ 1/n 0,47I_d

Поочередное прохождение однонаправленных токов по вторичным об­моткам трансформатора, которые не полностью компенсируются токами первичной обмотки, создает в стержнях сердечника поток Ф_о одного на­правления, значение которого составляет 20-25% основного магнитно­го потока Ф_в трансформатора и который изменяется с тройной частотой в соответствии с пульсацией анодного тока.

На­личие потока однонаправленного или вынужденного подмагничивания Ф_о в сердечнике приводит к увеличению тока холостого хода, в резуль­тате чего сердечник трансформатора насыщается, а в стальной арматуре возникают дополнительные тепловые потери. Помимо насыщения сердеч­ника трансформатора такой поток приводит к значительному возраста­нию падения напряжения в обмотках, что вызывает резкое уменьшение среднего значения выпрямленного напряжения.

Устранить эти нежелательные явления можно либо увеличением сече­ния сердечника трансформатора, а следовательно, и типовой мощности трансформатора, либо уменьшением амплитуды основного потока Ф_в. При заданной мощности трансформатора это приводит к увеличению раз­меров магнитной системы и влечет за собой повышение не только массы стали, но и массы обмоток трансформатора, поскольку с повышением пе­риметра сечения сердечника растет и средняя длина витка у обмоток.

Типовая мощность трансформатора при соединении вторичных обмо­ток в звезду

S_т = (S₁ + S₂) /2 = 1,35P_d

Трехфазная мостовая схема выпрямления

Выпрямитель в данной схеме состоит их трансформатора, первичные и вторич­ные обмотки которого соединяются в звезду или треугольник, и шести диодов, которые разделены на две группы (рис. 81, а):

1) катодную, или нечетную (диоды V1, V3 и V5), в которой электрически связаны катоды вентилей и общий вы­вод их является положительным полюсом для внешней цепи, а аноды присоединены к выводам вторичных обмоток тран­сформатора;

2) анодную, или четную (диоды V2, V4 и V6), в ко­торой электрически связаны между собой аноды вентилей, а катоды соединяются с анодами первой группы.

Общая точка связи анодов является отрицательным полюсом для внешней цепи. Нагрузка подключается между точками соединения катодов и анодов вентилей, т.е. к диагонали выпрямленного моста.

Катодная группа вентилей повторяет режим работы трехфаз­ной нулевой схемы. В этой группе вентилей в течение каждой трети периода работает вентиль с наиболее высоким потенциа­лом анода (рис. 81, 6). В анодной группе в данную часть периода работает тот вентиль, у которого катод имеет наиболее отрица­тельный потенциал по отношению к общей точке анодов.

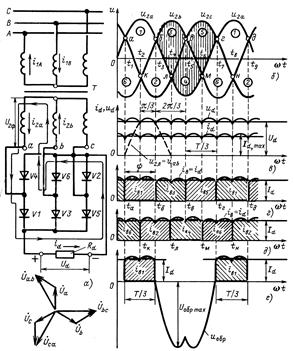
Вентили катодной группы открываются в момент пересече­ния положительных участков синусоид (точки а, 6, в и г на рис. 81, 6), а вентили анодной группы — в момент пересечения отрицательных участков синусоид (точки к, л, м и н). Каждый из вентилей работает в течение одной трети периода (Т/3, или 2π/3).

Рисунок 81 — Трехфазная мостовая схема выпрямителя:

а — схема соединения элементов; б — в-временные диаграммы на­пряжений и токов

При мгновенной коммутации тока в трехфазной мостовой схеме в любой момент времени проводят ток два вентиля — один из катодной, другой из анодной группы, при этом любой вентиль одной группы работает поочередно с двумя вентилями другой группы, соединенными с разными фазами вторичной обмотки (рис. 81, г и д). Иными словами, проводить ток будут те два накрест лежащих вентиля выпрямительного моста, между которыми действует в проводящем направлении наибольшее линейное напряжение u_2л. Например, на интервале времени t₁ – t₂ток проводят вентили V1, V6, на интервале t₂ — t₃—вен­тили V1, V2, на интервале t₃ – t₄ — вентили V3, V2 и т.д. Та­ким образом, интервал проводимости каждого вентиля состав­ляет 2π/3, или 120° (рис. 81, е), а интервал совместной ра­боты двух вентилей равен π/3, или 60°. За период напряжения питания Т = 2πпроисходит шесть переключений вентилей (шесть тактов), в связи с чем такую схему выпрямления часто называют шестипульсной.

Следует отметить, что нумерация вентилей в данной схеме не носит случайный характер, а соответствует порядку их вступле­ния в работу при условии соблюдения фазировки трансформа­тора. Через каждую фазу трансформато­ра ток i₂ будет проходить в течение 2/3 периода: 1/3 периода — положительный и 1/3 — отрицательный. Ток i_dв нагрузке все время проходит в одном направлении. Контур тока нагрузки при открытых вентилях V1 и V6 показан на схеме (рис. 81, а) тонкой черной линией.

Выпрямленное напряжение u_d в этой схеме описывается верх­ней частью кривых междуфазных (линейных) напряжений (рис. 81, е). Частота пульсаций кривой u_d равна 6f₁,коэффи­циент пульсаций напряжения на выходе выпрямителя

q = 2/(m² -1) = 2/(6² -1) = 0,25= 0,057

Обратное напряжение на закрытом вентиле определяется разностью потенциалов его катода и анода. Максимальное зна­чение обратного напряжения на вентиле в трехфазной мостовой схеме равно амплитуде линейного напряжения вторичной обмот­ки трансформатора, т.е. U_o6p.max = √2 U_2л = 1,05 U_d.При открытом состоянии двух вентилей выпрямительного моста другие четы­ре вентиля закрыты приложенным к ним обратным напряже­нием. Выпрямленный ток i_d при работе на чисто активную нагруз­ку полностью повторяет кривую напряжения u_d.

Напряжение на нагрузке по сравнению с трехфазной схемой с нулевым выводом получается вдвое большим. Это объясняется тем, что трехфазная мостовая схема выпрямителя представляет собой как бы две трехфазные схемы с нулевым выводом, выходы которых вклю­чены последовательно. Это сокращает число витков вторичных обмоток трансформатора и снижает требования к изоляции.

U₂ = π/3√6 = 0,425U_d

Среднее значение тока через каждый вентиль в 3 раза меньше тока I_d

I_в.ср = 0,33I_d

Токи во вторичной и первичной обмотках трансформатора определяются по формулам

I₂ = I_в,д = √(2/3) = 0,585I_d I₁ = I₂/n

Типовая мощность трансформатора

S_T = π/3 P_d = 1,045P_d

Диодный выпрямитель: определение, схема, прицнип работы

В статье вы узнаете что такое диодный выпрямитель, как он работает, строение данного элемента, рассмотрим как его протестировать, а так же функционал и применение выпрямителя.

Вступление

Диодный выпрямитель представляет собой полупроводниковое устройство и подпадает под действие «активных» электронных компонентов. Его основная функция — пропускать электрический токтолько в одном направлении и блокировать от другого. Это свойство также приводит к выпрямлению электрического тока при использовании источника переменного тока. Выпрямительный диод обычно распознается по его черному цвету и белому кольцу на одном из концов, что сопоставимо с цветовым кодированием резисторов, которое мы изучали в предыдущей статье. Его размер может отличаться в зависимости от мощности. У диода два конца с двумя выводами или клеммами, отсюда и название диода (в переводе с греческого означает двуногий).

Внутреннее описание

Диод, как и все полупроводники, в основном состоит из чистого кремния (более популярного в настоящее время, чем германий). По своей природе кремний является плохим проводником электричества, поэтому, смешивая в нем определенные примеси (легирование), в некоторой степени достигается проводимость. Эти примеси могут быть положительными носителями или отрицательными носителями заряда, известными как p-тип и n-тип соответственно.

В диоде кремний p-типа и кремний n- типа сплавляются вместе, образуя соединение, называемое pn-переходом. При подключении к источнику напряжения этот переход ограничит поток тока от n- типа к p-типу и позволит протекать току от p-типа к кремнию n- типа, только если напряжение превышает 0,6 вольт. Это минимальное напряжение требуется в любом кремниевом полупроводнике для инициирования проводимости электронов и известно как прямое напряжение. Вывод p-типа диода называется анодом, а вывод n- типа называется катодом и обозначается кольцом или полосой на его корпусе.

Принцип работы и функции

В электронной схеме диод действует так же, как резиновый клапан в велосипедной шине. Клапан позволяет перекачиваемому воздуху поступать с одной стороны и блокирует с другой. Аналогично, выпрямительный диод пропускает ток только в одном направлении. Таким образом, он используется в качестве защиты от полярности в электронных цепях, чтобы избежать опасности случайного изменения напряжения питания.

Другой важной функцией выпрямительного диода является выпрямление, то есть преобразование переменного тока в постоянный ток. Напряжение в переменном токе изменяется с положительного на отрицательное и наоборот количество раз в секунду. В зависимости от соединения, выпрямительный диод позволит проходить только положительному или отрицательному циклу и блокировать другой. Таким образом, результат будет либо чисто положительным, либо отрицательным. Это известно как исправление. Это свойство хорошо используется в источниках питания, адаптерах переменного / постоянного тока, зарядных устройствах и т.д. Но важно знать, что для диода потребуется минимальное входное напряжение не менее 0,7 В на нем, чтобы успешно выполнить описанную выше процедуру выпрямления или, другими словами, диоду необходимо минимум 0,7 вольт, чтобы удовлетворительно инициировать проведение электричества.

Тестирование выпрямителя

Шаги, необходимые для тестирования диодного выпрямителя, следующие:

• Возьмите качественный цифровой мультиметр;
• Установите диапазон в положение диода;
• На дисплее вы должны получить 3 или бесконечное чтение напряжения в зависимости от используемого мультиметра;
• Подключите красный зонд к катоду, а черный зонд — к аноду диода;
• Дисплей сразу покажет низкое прямое падение напряжения (выпрямительный диод) около 0,6 вольт;
• Теперь поменяйте местами соединения, дисплей вернется к своему первоначальному показанию, указывая, что диод хороший;
• Если счетчик отображает любые другие показания, диод может быть негерметичным или неисправным, а показание 0000 означает короткое замыкание.

% PDF-1.6 % 10 0 obj > endobj xref 10 103 0000000016 00000 н. 0000002727 00000 н. 0000002818 00000 н. 0000002859 00000 н. 0000003143 00000 п. 0000003756 00000 н. 0000004349 00000 п. 0000004951 00000 н. 0000004998 00000 н. 0000005047 00000 н. 0000005095 00000 н. 0000005142 00000 п. 0000005191 00000 п. 0000005239 00000 п. 0000023559 00000 п. 0000024138 00000 п. 0000043897 00000 п. 0000044273 00000 п. 0000044413 00000 п. 0000064024 00000 п. 0000082141 00000 п. 0000101582 00000 н. 0000119610 00000 н. 0000119858 00000 н. 0000119910 00000 н. 0000140915 00000 н. 0000157550 00000 н. 0000159520 00000 н. 0000159729 00000 н. 0000167883 00000 н. 0000173095 00000 н. 0000173162 00000 н. 0000173351 00000 н. 0000176509 00000 н. 0000176835 00000 н. 0000177479 00000 н. 0000179448 00000 н. 0000179671 00000 н. 0000179990 00000 н. 0000181962 00000 н. 0000182029 00000 н. 0000182218 00000 н. 0000185423 00000 н. 0000185734 00000 н. 0000186378 00000 н. 0000186591 00000 н. 0000186704 00000 н. 0000186919 00000 н. 0000187031 00000 н. 0000187626 00000 н. 0000187733 00000 н. 0000188067 00000 н. 0000188178 00000 н. 0000188722 00000 н. 0000188829 00000 н. 0000189197 00000 н. 0000189304 00000 н. 0000189648 00000 н. 0000189755 00000 н. 0000189961 00000 н. 0000190073 00000 н. 0000190610 00000 н. 0000190717 00000 н. 0000191490 00000 н. 0000191597 00000 н. 0000191974 00000 н. 0000192081 00000 н. 0000192694 00000 н. 0000192801 00000 н. 0000193102 00000 н. 0000193209 00000 н. 0000193986 00000 н. 0000194093 00000 н. 0000194383 00000 н. 0000194490 00000 н. 0000194782 00000 н. 0000194889 00000 н. 0000195283 00000 н. 0000195390 00000 н. 0000196187 00000 н. 0000196294 00000 н. 0000196872 00000 н. 0000202618 00000 н. 0000202880 00000 н. 0000205401 00000 н. 0000205733 00000 н. 0000206113 00000 н. 0000206306 00000 н. 0000208570 00000 н. 0000208870 00000 н. 0000209255 00000 н. 0000209421 00000 н. 0000212871 00000 н. 0000213269 00000 н. 0000213639 00000 н. 0000213877 00000 н. 0000214268 00000 н. 0000214501 00000 н. 0000215078 00000 н. 0000215179 00000 н. 0000215420 00000 н. 0000215614 00000 н. 0000002356 00000 н. трейлер ] >> startxref 0 %% EOF 112 0 объект > поток xb`Ha`g«_̀ X — $ @ g (5) 06030 (0 ؔ 8; 6, oHT (% @ ӋOt6`vPeke & A0c [OgkKNL ^; X44Lopbbo`QnhXR P 3͓qN Qa & L] 5D & H, oH«V`9

.

схема выпрямления — это … Что такое схема выпрямления?

Rectification Entrante — Redresseur Trois redresseurs sous forme de ponts de Graëtz Un redresseur, également appelé convertisseur alternatif непрерывный (английский выпрямитель), является un convertisseur destiné à alimenter une charge de type continuous, qu elleia en Français

Синхронное выпрямление — Синхронное выпрямление — это метод повышения эффективности преобразователей мощности в силовой электронике.Он состоит из параллельного соединения диода и транзистора (обычно силового MOSFET). Когда диод смещен в прямом направлении,…… Wikipedia

Выпрямитель — Выпрямитель — это электрическое устройство, которое преобразует переменный ток (AC) в постоянный (DC), процесс, известный как выпрямление. Выпрямители имеют множество применений, в том числе в качестве компонентов источников питания и в качестве детекторов радиосигналов. Выпрямители… Википедия

Вакуумная трубка — Эта статья про электронное устройство.Для экспериментов в откачанной трубе см свободное падение. Для транспортной системы см. Пневматическая трубка. Современные электронные лампы, в основном в миниатюрном стиле. В электронике, вакуумная лампа, электронная лампа (на Севере…… Википедия

Mesa Boogie — Логотип Mesa Boogie Mesa / Boogie (также известный как Mesa Engineering) — компания из Петалумы, Калифорния, которая производит усилители для гитар и бас-гитар. Она работает с 1969 года. Mesa была основана Рэндаллом Смитом как небольшая ремонтная мастерская…… Wikipedia

Ламповый звук — (или вентильный звук) — это характерный звук, связанный с ламповыми усилителями звука.Некоторые аудиофилы предпочитают звук, создаваемый характеристиками искажения ламповых усилителей. Звуковое значение трубки…… Википедия

Наножидкостная схема — это нанотехнология, направленная на контроль жидкостей в нанометровом масштабе. Из-за эффекта двойного электрического слоя внутри жидкостного канала, поведение наножидкости значительно отличается от его микрофлюидного…… Wikipedia

Пластинчатый детектор (радио) — Пластинчатый детектор представляет собой детекторную схему с вакуумной трубкой, используемую в A.М. радиостанции. В этой схеме используется лампа с катодом с косвенным нагревом, как правило, мю-триод среднего размера, или тетрод или пентод с резко отсеченной управляющей сеткой. Исправление R.F.…… Wikipedia

электронная трубка — электронное устройство, которое обычно состоит из герметичной стеклянной колбы, содержащей два или более электродов: используется для генерации, усиления и выпрямления электрических колебаний и переменных токов. Также называется электронной лампой. Ср. газовая трубка, вакуумная трубка… Универсал

электроника — / и лек трон икс, ее лек /, н.(используется с един. v.) наука, имеющая дело с разработкой и применением устройств и систем, использующих поток электронов в вакууме, в газовых средах и в полупроводниках. [1905 10; см. ЭЛЕКТРОННЫЙ,…… Универсальный

Умножитель напряжения — Умножитель напряжения каскада Виллара. Умножитель напряжения — это электрическая схема, которая преобразует электрическую мощность переменного тока с более низкого напряжения в более высокое постоянное напряжение, обычно посредством сети конденсаторов и диодов.Множители напряжения могут быть…… Wikipedia

.

схема выпрямления — это … Что такое схема выпрямления?

Rectification Entrante — Redresseur Trois redresseurs sous forme de ponts de Graëtz Un redresseur, également appelé convertisseur alternatif непрерывный (английский выпрямитель), является un convertisseur destiné à alimenter une charge de type continuous, qu elleia en Français

Синхронное выпрямление — Синхронное выпрямление — это метод повышения эффективности преобразователей мощности в силовой электронике.Он состоит из параллельного соединения диода и транзистора (обычно силового MOSFET). Когда диод смещен в прямом направлении,…… Wikipedia

Выпрямитель — Выпрямитель — это электрическое устройство, которое преобразует переменный ток (AC) в постоянный (DC), процесс, известный как выпрямление. Выпрямители имеют множество применений, в том числе в качестве компонентов источников питания и в качестве детекторов радиосигналов. Выпрямители… Википедия

Вакуумная трубка — Эта статья про электронное устройство.Для экспериментов в откачанной трубе см свободное падение. Для транспортной системы см. Пневматическая трубка. Современные электронные лампы, в основном в миниатюрном стиле. В электронике, вакуумная лампа, электронная лампа (на Севере…… Википедия

Mesa Boogie — Логотип Mesa Boogie Mesa / Boogie (также известный как Mesa Engineering) — компания из Петалумы, Калифорния, которая производит усилители для гитар и бас-гитар. Она работает с 1969 года. Mesa была основана Рэндаллом Смитом как небольшая ремонтная мастерская…… Wikipedia

Ламповый звук — (или вентильный звук) — это характерный звук, связанный с ламповыми усилителями звука.Некоторые аудиофилы предпочитают звук, создаваемый характеристиками искажения ламповых усилителей. Звуковое значение трубки…… Википедия

Наножидкостная схема — это нанотехнология, направленная на контроль жидкостей в нанометровом масштабе. Из-за эффекта двойного электрического слоя внутри жидкостного канала, поведение наножидкости значительно отличается от его микрофлюидного…… Wikipedia

Пластинчатый детектор (радио) — Пластинчатый детектор представляет собой детекторную схему с вакуумной трубкой, используемую в A.М. радиостанции. В этой схеме используется лампа с катодом с косвенным нагревом, как правило, мю-триод среднего размера, или тетрод или пентод с резко отсеченной управляющей сеткой. Исправление R.F.…… Wikipedia

электронная трубка — электронное устройство, которое обычно состоит из герметичной стеклянной колбы, содержащей два или более электродов: используется для генерации, усиления и выпрямления электрических колебаний и переменных токов. Также называется электронной лампой. Ср. газовая трубка, вакуумная трубка… Универсал

электроника — / и лек трон икс, ее лек /, н.(используется с един. v.) наука, имеющая дело с разработкой и применением устройств и систем, использующих поток электронов в вакууме, в газовых средах и в полупроводниках. [1905 10; см. ЭЛЕКТРОННЫЙ,…… Универсальный

Умножитель напряжения — Умножитель напряжения каскада Виллара. Умножитель напряжения — это электрическая схема, которая преобразует электрическую мощность переменного тока с более низкого напряжения в более высокое постоянное напряжение, обычно посредством сети конденсаторов и диодов.Множители напряжения могут быть…… Wikipedia

.

схема выпрямления — это … Что такое схема выпрямления?

Rectification Entrante — Redresseur Trois redresseurs sous forme de ponts de Graëtz Un redresseur, également appelé convertisseur alternatif непрерывный (английский выпрямитель), является un convertisseur destiné à alimenter une charge de type continuous, qu elleia en Français

Синхронное выпрямление — Синхронное выпрямление — это метод повышения эффективности преобразователей мощности в силовой электронике.Он состоит из параллельного соединения диода и транзистора (обычно силового MOSFET). Когда диод смещен в прямом направлении,…… Wikipedia

Выпрямитель — Выпрямитель — это электрическое устройство, которое преобразует переменный ток (AC) в постоянный (DC), процесс, известный как выпрямление. Выпрямители имеют множество применений, в том числе в качестве компонентов источников питания и в качестве детекторов радиосигналов. Выпрямители… Википедия

Вакуумная трубка — Эта статья про электронное устройство.Для экспериментов в откачанной трубе см свободное падение. Для транспортной системы см. Пневматическая трубка. Современные электронные лампы, в основном в миниатюрном стиле. В электронике, вакуумная лампа, электронная лампа (на Севере…… Википедия

Mesa Boogie — Логотип Mesa Boogie Mesa / Boogie (также известный как Mesa Engineering) — компания из Петалумы, Калифорния, которая производит усилители для гитар и бас-гитар. Она работает с 1969 года. Mesa была основана Рэндаллом Смитом как небольшая ремонтная мастерская…… Wikipedia

Ламповый звук — (или вентильный звук) — это характерный звук, связанный с ламповыми усилителями звука.Некоторые аудиофилы предпочитают звук, создаваемый характеристиками искажения ламповых усилителей. Звуковое значение трубки…… Википедия

Наножидкостная схема — это нанотехнология, направленная на контроль жидкостей в нанометровом масштабе. Из-за эффекта двойного электрического слоя внутри жидкостного канала, поведение наножидкости значительно отличается от его микрофлюидного…… Wikipedia

Пластинчатый детектор (радио) — Пластинчатый детектор представляет собой детекторную схему с вакуумной трубкой, используемую в A.М. радиостанции. В этой схеме используется лампа с катодом с косвенным нагревом, как правило, мю-триод среднего размера, или тетрод или пентод с резко отсеченной управляющей сеткой. Исправление R.F.…… Wikipedia

электронная трубка — электронное устройство, которое обычно состоит из герметичной стеклянной колбы, содержащей два или более электродов: используется для генерации, усиления и выпрямления электрических колебаний и переменных токов. Также называется электронной лампой. Ср. газовая трубка, вакуумная трубка… Универсал

электроника — / и лек трон икс, ее лек /, н.(используется с един. v.) наука, имеющая дело с разработкой и применением устройств и систем, использующих поток электронов в вакууме, в газовых средах и в полупроводниках. [1905 10; см. ЭЛЕКТРОННЫЙ,…… Универсальный

Умножитель напряжения — Умножитель напряжения каскада Виллара. Умножитель напряжения — это электрическая схема, которая преобразует электрическую мощность переменного тока с более низкого напряжения в более высокое постоянное напряжение, обычно посредством сети конденсаторов и диодов.Множители напряжения могут быть…… Wikipedia

.